Activation of electrospun carbon fibers: the effect of fiber diameter on CO₂ and steam reaction kinetics

Abstract

First, we present a fabrication process for electrospun carbon fiber mats with mean fiber diameters between 108 nm and 623 nm. The carbon fiber mats were produced by electrospinning of polyacrylonitrile (PAN) solutions and subsequent carbonization. The fiber mats feature small variations of their properties that are required for parameter studies. Second, we investigate the kinetics of steam and CO₂ activation with three different activation temperatures and times. Both activation methods result in a surface area increase depending on activation temperature and time. Detailed analysis of the macroscopic properties burn-off, surface area, and conductivity reveals insights into the microscopic activation kinetics. The different fiber diameters of the carbon fiber mats enable the distinction of surface driven and bulk processes. Our results indicate, that CO₂ activation kinetics are mass transport controlled, and that steam activation kinetics are reaction rate controlled. The turbostratic nature of PAN derived carbon and the distinct characteristics of the activation agents could explain the nonlinear behavior of the burn-off and surface area development.

Introduction

Electrospinning is a versatile tool for the production of thin fibers with diameters in the nanometer to micrometer range. Electrospinning is extensively studied in academic and industrial research due to its simplicity and the possibility for effective upscaling [1]. Electrospun materials are available for filtration, lab tissue culturing, biomedical [2] and battery applications [1]. In academic research, electrospun carbon fiber material has been used as adsorbent [3], for catalytic NO_x removal [4], for capacitive electrosorption for desalination [5], supercapacitors [6,7,8], and redox flow batteries [9]. It is also used as material for microbial fuel cells bio-electrochemical cells [10,11,12,13,14,15] due to their high porosity and large internal surface area. Electrospinning allows the processing of polymer dopes like melts, emulsions, and solutions [16]. The basic operation principle is simple: A high voltage is applied between the dope feed through a nozzle and a collector. Due to electrostatic forces on the excess charges carried by the dope, thin fibers are formed and deposited on a collector. The detailed mechanisms involved in fiber formation are discussed in detail by Reneker et al. [17]. A wide variety of electrospinning devices are available on the market. While lab-scale devices typically feature a single nozzle spinneret, production scale units boast a larger number of nozzles, i.e., NanoSpinner416 (Inovenso Ltd., Istanbul, Turkey). Sophisticated spinneret technologies such as the needleless Nanospider (Elmarco, Liberec, Czech Republic) or air stream assisted electrospinning [18] increase fiber production rates and can enhance the fiber quality by adjusting the air stream temperature [19]. The Nanospider^TM NS 8S1600U production line enables the fabrication of 1.6 m wide nanofiber mats in a continuous process. In lab-scale units, the fibers are collected on flat plates, rotating drums (this work), or conveyor belts. Drums and conveyor belts allow the fabrication of relatively large and uniform nanofiber mats using processes that may be adapted for production scale units. The collector is often wrapped with a carrier material such as aluminum foil. If the intended application requires further processing steps such as heat treatment that do not allow the use of a fiber/carrier composite, the fibers need to be separated from the carrier material. The distortion-free removal of the fiber mat can be challenging to achieve, as the electrospun nonwovens tend to stick on smooth surfaces [20]. To minimize adhesion, either rough [20], Teflon coated (4Spin Tube Collector C5, Contipro a.s., Dolní Dobrouc̆, Czech Republic) collectors or flexible non-stick carrier materials (such as acrylic gauze used in this work) can be used. The latter allows the nanofiber fabrication in a roll-to-roll process and is therefore suitable for the implementation in production scale units. The application of the electrospun fibers as electrode material requires a high electrical conductivity. Electrical conductivity of electrospun fibers can be achieved by the addition of conducting particles [21], the use of semiconducting polymers [22, 23], or the conversion of electrospun carbon precursor polymer fibers to carbon fibers. PAN, Polyvinyl alcohol (PVA) and the biopolymers lignin and cellulose were screened in pretests for their suitability for the targeted facile production of carbon fibers with tunable diameter. PVA exhibits excellent spinnability in a wide range of polymer concentrations and is soluble in water [24]. The carbon yield of PVA upon carbonization could be improved by treatment with iodine vapor [25], but a poor mechanical of the resulting carbon fibers impedes its use as precursor for this work. The fiber diameter of electropsun cellulose acetate can be tuned by the composition of the acetic acid / water solvent [26]. The deacetylated fibers (with NaOH in aqueous solution [7, 27]) were too brittle for the intended use as free standing electrode. Improving the mechanical stability by stretching during the carbonization process [28] renders impossible for randomly aligned fiber mats. The broad range of fiber diameters with Kraft-lignin/PVA/water spinning dopes reported by Ago et al. [29] could not be reproduced with the electrospinning device in the laboratory. Electrospinning and carbonization of PAN meets the requirements due to its excellent spinnability and mechanical stability of the carbon fibers. A good spinning dope can be easily prepared by dissolving the polymer in N,N-dimethylformamide (DMF), or dimethylacetamide (DMAc) [11, 30] and the resulting carbon fibers show mechanical stability after carbonization that allows further use as free-standing electrode material. The fiber diameter of PAN fibers spun from PAN/DMF dope can be tuned by the variation of polymer concentration, voltage, and needle collector distance [30] or by concentration only [11]. The carbonization of PAN is usually conducted in three steps [31,32,33]: 1) oxidative stabilization in air at temperatures ranging between 200 ^∘C and 300 ^∘C, 2) high-temperature (≤ 1600 ^∘C) pyrolysis in inert atmosphere that yields turbostratic carbon, and 3) graphitization at temperatures above 2000 ^∘C that improves the mechanical and electrical properties of fibers. The tensile strength peaks at a temperature of 1400 ^∘C, and the Young’s modulus steadily increases up to 1700 ^∘C [34] with nitrogen and hydrogen contents of the fibers dropping with increasing temperatures [35]. The according chemical reactions are summarized in Fig. S1. The chemical change is accompanied by shrinkage in length and diameter [35]. While higher pyrolysis temperatures enhance mechanical and electrical properties, the potential for activation is lowered [6]. Activation yields high specific surface area carbon materials through the introduction of pores. Hence, for applications that require high conductivity carbon and high specific surface area, i.e., electrodes for microbial fuel cells [10, 15] or supercapacitors [6, 7], a trade-off must be made. Common activation agents for physical activation are CO₂ and steam that introduce micropores in carbonaceous materials [36] and therefore increase the specific surface area. The chemical reactions for CO₂ (1) and steam (2) activation can be summarized as [37]:

$$ \mathrm{C} + \text{CO}_{2} \rightarrow 2~ \text{CO} $$

(1)

$$ \mathrm{C} + \mathrm{H}_{2}\mathrm{O} \rightarrow \text{CO}_{2} + \mathrm{H}_{2} $$

(2)

Both activation methods decrease the nitrogen content and increase the oxygen content. During CO₂ activation, hydrogen levels decrease [38], while steam activation increases the hydrogen content [39]. CO₂ and steam activation have a degrading effect on the carbon structure [39, 40]. In this work, we present a study of CO₂ and steam activation kinetics depending on the mean fiber diameter, activation temperature and time. The carbon fiber materials are characterized with respect to burn-off, electrochemically accessible surface area (ECAS), and electrical conductivity. The results enable tailoring of the material properties according to the particular requirements of the intended application. So far, literature does not provide the required level of technical detail for the fabrication of electrospun carbon fibers with small variability in their properties. However, this is a prerequisite for meaningful parameter studies [13, 14], and statistical analysis. Therefore, our study includes a comprehensive description of the fabrication of electrospun carbon fiber mats with tunable fiber diameter. The required low variability is demonstrated through process monitoring and analysis of the material properties.

Experimental

Modified electrospinning unit

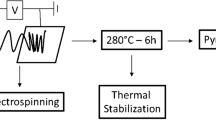
The electrospinning device used in this work is a modified Nanofiber Electrospinning Unit (KatoTech, Kyoto, Japan), as depicted in Fig. 1. The modifications pertain to the spinneret, the high voltage cable routing to the spinneret, and the purging with dry air. An air stream is heated in an electrical air heater and can be guided along the nozzle. The gas flow rate and the heating power can be adjusted. The spinneret is equipped with an electrically conducting square-shaped shield that is connected to the nozzle and the high voltage source. The shield and the routing of the high voltage cable behind the spinneret reduce distortions of the electric field. The dimensions given in the inset remain the same for all investigated polymer concentrations in the spinning dope.

Fig. 1

Schematic representation of the modified KatoTech NEU electrospinning device. The dimensions given in the inset are the same for all PAN concentrations in the dope. Δy is the range of the movement of the spinneret with 60 cm $\min \limits ^{-1}$ along the collector axis

Preparation of the electrospinning dope

Spinning dope with polymer concentrations of 6 wt%, 8 wt%, 11 wt% and 13 wt% was prepared by dissolving polyacrylonitrile (PAN, Mw 150000, Sigma-Aldrich Chemie GmbH, Munich, Germany) in dimethylacetamide (DMAc, ≥ 99%, Carl Roth GmbH + Co. KG, Karlsruhe, Germany) at 70 ^∘C using a magnetic stir bar until the solution was clear and no lumps could be observed.

Spinning parameters and fiber deposition on the collector

The fiber diameter is increasing with PAN concentration in the spinning dope [11, 41]. Therefore, 6 wt%, 8 wt%, 11 wt% and 13 wt% PAN/DMAc spinning dopes were investigated. For each of the polymer concentrations, the parameters voltage, polymer feed rate, collector drum rotation speed, airflow, and the temperature had to be individually adjusted to ensure smooth fiber mat deposition and steady fiber production and listed in Table 1. The geometrical parameters given in Fig. 1 were the same for all parameter sets. The dopes containing 6 wt% and 13 wt% polymer represent the lower and upper concentration limit with stable spinnability but already require a reduced polymer feed rate. In the case of 6 wt% dope, an increased feed rate would lead to the formation of multiple polymer jets emerging from a droplet at the nozzle tip. With the 13 wt% dope droplets of the polymer solution form at the nozzle tip. If compensated with a higher voltage, the fiber deposition extends beyond the collector drum and becomes unstable. The fibers spun from 6 wt% dope show minor beads (see Fig. 3y a) due to the low polymer concentration [42]. The 11 wt% and 13 wt% dopes require, presumably, due to their higher viscosity, hot air assisted electrospinning. The elevated temperature reduces the viscosity and enhances the drying process of the fibers [19]. The airstream along the nozzle additionally exerts a mechanical force [18] on the fibers in formation. Without hot air assistance, the fibers formed with 13 wt% dope pile up on the collector and bridge the gap between collector and nozzle. The fiber deposition on the collector was analyzed for the fabrication parameter sets given in Table 1. Figure S4 shows the polymer fiber mat area density distribution along the collector axis for each parameter set. The analysis shows that the area density deviates less than 9.4% in the 21 cm wide centerpiece on the collector used for further material processing.

Table 1 Spinning parameters for the spinning dopes with varying PAN concentration

Based on the polymer fiber deposition area density ρ_A,Polymer, the amount of polymer solution m_Dope required for carbon fiber mats with a target area density ρ_A,Carbon of 5 mg cm^− 2, was estimated. The estimated amount of polymer solution is given by

$$ m_{\text{Dope}} = \frac{\text{Shrinkage}}{\mathrm{Weight~loss}} \cdot \frac{\rho_{\mathrm{A,Carbon}}}{c_{\text{Polymer}}\cdot \rho_{\mathrm{A,Polymer}}} $$

(3)

with the polymer concentration c_Polymer, 60% weight loss, and 50% shrinkage. The total amount required for the fabrication ranged from 27.8 g for 13 wt% dope to 62.9 g for 6 wt% dope.

Fiber mat handling process

The commonly used aluminum foil as a carrier layer on the collector makes it difficult to peel off the fiber mat without distortions. Electrostatic charges, as well as the small dimensions of the fibers, further complicate the handling. Therefore, a material handling process that enables material fabrication with little variations of the material properties in one batch was developed. Figure 2 illustrates the handling steps:

• 1. The fiber mat deposited on the non-stick carrier layer (acrylic gauze fabric) wrapped around the collector drum is prepared for removal from the drum by cutting along the axis through the fiber mat and the carrier layer using a scalpel. The carrier layer and fiber mat are carefully removed from the collector and placed on a flat surface. The points of contact are limited to the cutting edges and the carrier layer. The carrier layer guarantees the dimensional stability.

• 2. A sheet of paper with markings for twelve 7×7 cm² pieces is placed on top of the fiber mat. The fiber mat is now protected from below by the carrier layer and from above by the paper sheet.

• 3. The sandwich consisting of paper, the electrospun fiber mat, and the non-stick carrier layer can now be cut easily into 7×7 cm² sized pieces that fit in the alumina sheets with a spacer of 1 mm thickness, depicted in Fig. 2 step 3, used for carbonization. As both sides of the fiber mat are now protected, the carrier layer/fiber mat/paper sandwich can be stored for later use.

• 4. Before the placement of the fiber mat pieces on the alumina sheet for carbonization, the non-stick carrier layer is removed using tweezers. The paper and the fiber mat are placed on the alumina sheets, the paper facing to the top. The paper can now be removed using tweezers. The alumina sheets are equipped on opposing sides with a rim that serves as a spacer. The stacked alumina sheets leave a 1 mm gap for the polymer fiber mat that allows shrinkage and inhibits bulging during carbonization.

Fig. 2

Illustration of the fiber mat processing handling steps that enable reproducible material fabrication. The polymer fiber mat is depicted in red. The handling steps are: 1) removal of the fiber mats from the collector 2) sandwiching of the fiber mat between carrier layer and a paper template 3) Cutting the sandwich into regular pieces as illustrated 4) Removal of the carrier layer and paper template and placement of the fiber mats between alumina sheets. The fiber mats shrink during the carbonization in size from an initial area of 7×7 cm² to the final size of $\sim$5×5 cm². The carbon fiber mat samples are cut to a size of 2×2 cm² for activation. The details are given in “Fiber mat handling process”

Carbonization

The carbonization is conducted in a two-step process using a tube furnace (SR 100-500/12, working tube dimensions: length 1.13 m, inner diameter 8.5 cm, Gero GmbH, Neuhausen, Germany): First, the PAN fibers are stabilized in air at temperatures up to 230 ^∘C [10] using a temperature ramp of 30 ^∘C h^− 1 at an airflow rate of 0.94 L $\min \limits ^{-1}$. With the slow heating ramp of 30 ^∘C h^− 1 up to 230 ^∘C during the stabilization, we aim to achieve uniform temperatures in the sample stack, sufficient gas exchange in the pores of the fiber mat. The slow heating rate also has been reported to yield more durable carbon fibers [43]. In a second step, the samples are heated to 1100 ^∘C in N₂ atmosphere at 120 ^∘C h^− 1 with a gas exchange rate of 0.94 L $\min \limits ^{-1}$. Figure S2 visualizes the carbonization process. All temperatures were measured at the sample position in the furnace.

CO₂ and steam activation

For the activation, the carbon fiber material was cut to 2×2 cm² pieces and placed on the flat alumina sheets in a furnace, as described in “Fiber mat handling process”. The furnace was heated up to the desired activation temperature under a constant nitrogen purge. Once the temperature had stabilized for one hour, the activation agent was supplied to the inside of the furnace for the desired activation time. After the activation agent supply was stopped, the furnace temperature was held at the activation temperature to allow the concentration of the activation agent to drop to 10%. The concentration of the activation agent was not directly monitored in the furnace. Instead, the extra holding time can be calculated assuming perfect mixing of the gases in the furnace using t = −τ ln(0.1) with the residence time τ. The residence time is given by $\tau = V_{\text {Furnace}}/ \dot {V}$ with the furnace volume V _Furnace and the purge gas flow rate $\dot {V}$.

Steam activation was performed in the tube furnace Gero SR 100-500/12 at a constant N₂ flow of 250 mL HCode $\min \limits ^{-1}$. Evaporating deionized water at a flow rate of 30 mL h^− 1 generated steam in the furnace. The deionized water was deaerated by stripping with N₂. CO₂ activation was conducted in a Carbolite Gero CWF 12/23 retort furnace (effective volume 16.8 L, Carbolite Gero GmbH & Co. KG, Neuhausen, Germany) at a constant N₂ flow of 250 mL HCode $\min \limits ^{-1}$. The gas supply was changed to CO₂ at a flow rate of 250 mL HCode $\min \limits ^{-1}$ once the activation temperature was reached and stable for the desired activation time. The temperatures were measured at the sample position in the furnace. As the activated carbon materials are hygroscopic, all samples were dried at 105 ^∘C in N₂ and weighed in a glovebox with a dry atmosphere.

Electrochemically accessible surface

The Electrochemically Accessible Surface Area (ECAS) method can be applied to conductive and porous materials. The method does not yield the real surface area of a sample as the measured surface area depends on the composition of the electrolyte used and the experimental conditions. ECAS is quantified by measuring the double layer capacitance [44]. The double-layer capacitance was determined by cyclic voltammetry close to the open circuit potential to minimize faradaic contributions to the current signal. The ECAS method, other than nitrogen adsorption, is a dynamic method involving transport and reorganization of ions in the electrical double-layer and the porous structure of the material investigated. Therefore, higher values with decreasing scan rates are observed, as more pores contribute to the capacitance, presumably due to slow transport between pores [45]. Low sweep rates with sufficient signal to noise ratio (10 μV s^− 1 for non-activated materials and 1 μV s^− 1 for activated materials) were chosen to evaluate the capacitance. A typical cyclic voltammogram and scan rate dependence of the derived capacitance is shown in Fig. S3. Besides the scan rate, surface chemistry affects the capacitance [46]. Hence, the double-layer capacitance and thus the ECAS is only a relative measure for the surface area, and the experimental parameters must be identical for comparability. The capacitance was related to the ECAS by comparison to a material with known specific BET surface area (C-Tex 13 [47], MAST Carbon, Basingstoke, UK) and capacitance. The resulting conversion factor is 13.15 m² F^− 1 with medium containing 187 mmol NaCl, 2.7 mmol KCl, 10 mmol Na₂HPO₄, 1.76 mmol KH₂PO₄, 9 mmol (NH₄)₂SO₄, 10 mmol MgSO₄, 1 mmol CaCl₂, and trace elements [48]. A Solartron 1470E Cell Test System (Ametek, Farnborough, UK) served as potentiostat for the capacitance measurements.

Other devices and software

Scanning electron microscopy (SEM) was conducted using a Cameca SX 100 (Cameca, Gennevilliers, France). The fiber diameter was measured manually with the software ImageJ. The area of the carbon fiber mats after carbonization was measured by counting pixels using the magic wand feature of Adobe Photoshop CS6. The statistical analysis was performed with MiniTable Sheet resistances R_S were measured in a van der Pauw configuration using a Keithley 2400 SMU (Tektronix, Beaverton, Oregon, USA) at room temperature.

Results and discussion

Shrinkage and carbon yield

The four polymer mats with different fiber diameters were subjected to the same thermal treatment for carbonization. SEM photographs of the carbon fibers and their respective PAN precursor fibers are depicted in Fig. 3. All PAN precursor fiber mats with different fiber diameters exhibit similar behavior regarding shrinkage, diameter reduction, and weight loss (Table 2). The fiber mat areas shrink in average by (49.3 ± 2.5) a% (area percent), and the quadratic shape is preserved, while the fiber diameters (see “Material properties of the non-activated fiber mats”) are reduced on average by (32.0 ± 6.6)%. This indicates that the precursor fibers shrink isotropically in length and diameter. Aligned fibers [49] or thin fiber layers fixated to alumina sheets [50] may be subjected to defined stretching during heat treatment. Sandwiching larger pieces of randomly oriented fiber mats between graphite sheets [10] or clamping in a frame during heat treatment have been shown to result in fractured carbon fiber sheets [51]. Therefore, the PAN fiber mats must be allowed to shrink freely during the carbonization process. The placement on alumina sheets together with spacers is key to the reproducible fabrication of flat and unruptured carbon fiber mats. An average weight loss of (60.1 ± 1.8) wt% is observed and is slightly higher than the value of 54.7 wt% reported for similar carbonization conditions [6]. The deviation may be explained by the higher heating rates used in this study. The weight loss translates to a carbon yield of (58.7 ± 2.6)%. The carbon yield, however, is overestimated by about 12% as fibers carbonized at 1095 ^∘C contain 2.7% nitrogen and 9.7% oxygen [6]. In one batch, shrinkage and weight loss exhibit only small variations lower than 5.0% and 1.5%, respectively. Differences between batches may be explained by variations of the carbonization conditions or the diameter of the PAN precursor fibers.

Fig. 3

Scanning electron micrograph of the electrospun PAN fibers (right) and the derived carbon fibers with mean fiber diameters from 108 nm to 623 nm (left). a to d correspond to the material fabricated using a spinning dope containing 6 wt%, 8 wt%, 11 wt% and 13 wt% PAN, respectively. Note: The surface structure of the fibers is altered by gold sputtering before imaging

Table 2 Shrinkage, diameter reduction, weight loss, and carbon yield during the carbonization

Material properties of the non-activated fiber mats

The spinning dope and electrospinning parameters are given in Table 1 result in broad but distinct PAN (carbon) fiber diameter distributions with mean fiber diameters ranging from 146 nm to 945 nm (108 nm to 623 nm) depicted in Fig. 4. Due to the asymmetrical nature of the distributions, further analysis was performed based on a log-normal distribution [52]. The resulting χ² values range between 0.0074 and 1.98 well below the critical value of 2.73 for a 95% significance level and 8 degrees of freedom. Therefore, the log-normal distribution is suitable for modeling the fiber diameter distributions. The 11 wt% and 13 wt% PAN/DMAc derived fibers exhibit a wider fiber distribution than predicted from the log-normal distribution. Branching [53] or merging of fibers during the electrospinning process might lead to multimodal fiber diameter distributions [54, 55] that are visible on the SEM photographs Fig. 3c and d causing broader distributions. The analysis yields mean fiber diameters together with an asymmetric interval given in the sub- and superscript containing 68% of the fibers (Table 3). The specific Electrochemically Accessible Surface (ECAS) of the carbon fiber materials ranges from (21.66 ± 0.60) m² g^− 1 for 108 nm fibers to (8.03 ± 0.45) m² g^− 1 for 623 nm fibers. Interestingly, the ECAS does not increase steadily with decreasing fiber diameter, as would be expected from a geometrical estimation [13]. From the geometrical estimate, one obtains the surface,

$$ A_{\mathrm{G}} = \frac{4}{\rho d}, $$

(4)

with the bulk density ρ of carbon and the fiber diameter d. With a realistic carbon density for turbostratic carbon of 1.75 g cm^− 3 [56], the estimation gives a value of 21.2 m² g^− 1 for 108 nm fibers close to the observed ECAS. The surface of the thicker fibers is underestimated by a factor between 1.6 and 3.0. The comparison of ECAS measured, and the geometrical estimation is depicted in Fig. S5. Deviations between estimation and ECAS may be explained by the non-ideal shape of the fibers that can be observed for 400 nm and 623 nm fibers (Fig. 3c and d) and variations of the surface roughness. The sheet resistance of the carbon fiber mats varies little with the fiber diameter and is about 1.6Ω. Neglecting the porous nature of the fiber mats a virtual thickness t^∗ = ρ_A ⋅ ρ^− 1 can be calculated with the area density ρ_A and the bulk carbon density ρ. With the bulk density of 1.75 g cm^− 3 [56], an electric resistivity ρ_e of about 4.7 × 10^− 5 Ω m can be calculated according to ρ_e = R_S ⋅ t^∗ from the sheet resistance. This is value more than one order of magnitude higher than the resistivity of $\sim 3 \times 10^{-6}~ {\Omega }$ m [57] reported for a PAN-based carbon film prepared under similar conditions. The fibrous morphology of the materials with a tortuosity > 1 and contact resistance between individual fibers may well explain this difference.

Table 3 Material properties of the electrospun PAN and carbon fiber mats

Fig. 4

a–d Fiber diameter distribution of the carbon fibers and their respective electrospun PAN precursor fibers produced using different polymer concentrations in the spinning dope (6 wt%, 8 wt%, 11 wt%, 13 wt%). Mean fiber diameter and the width of the distribution (see Table 3) were calculated based on log-normal distributions (n = 300), which are depicted as a continuous line. The broader distributions of 11 wt% and 13 wt% fibers may be a result of fiber branching and merging during the fiber deposition

CO₂ and steam activation

Steam activation was performed on 2×2 cm² carbon fiber mat pieces placed between alumina sheets with a spacing of 2 mm to ensure sufficient gas exchange. Activation temperatures reported in literature vary depending on the carbonization temperature and the experimental conditions between 750 ^∘C and 900 ^∘C [5, 32, 39, 58, 59]. Pretests revealed that activation temperatures above 900 ^∘C for CO₂ and 800 ^∘C for steam activation lead to non-uniform activation due to fast reaction rates and slow transport of the activation agent into the porous material. Hence, activation was performed around the temperatures that yield about 10 wt% burn-off during 4h activation time: for CO₂ (832.21 ± 0.80) ^∘C, and for steam (757 ± 0.12) ^∘C. Additionally, activation temperatures 20 ^∘C to 25 ^∘C above and below this temperature and activation times of 2 h and 8 h were studied. The four different fiber diameter materials were studied in duplicate, and error bars represent the minimum and maximum values. We report the burn-off as weigh loss during the treatment m_Start − m_Post relative to the weight of the starting material m_Start according to

$$ \mathrm{Burn\text{-off}} = (m_{\text{Start}} - m_{\text{Post}}) \cdot 100 / m_{\text{Start}} $$

in wt%.

CO₂ activation kinetics

The effect of the mean fiber diameter, CO₂ activation temperature and time on burn-off and specific ECAS are shown in Fig. 5. With respect to temperature, the burn-off during CO₂ activation increases exponentially, as shown in Fig. 5a. The corresponding apparent activation energy, according to Arrhenius, is (557 ± 11) kJ mol^− 1. The activation energies reported in the literature vary between 203 kJ mol^− 1 and 235 kJ mol^− 1 for petroleum coke [60], 185 kJ mol^− 1 to 246 kJ mol^− 1 for chars [61], and 85 kJ mol^− 1 to 368 kJ mol^− 1 for graphite [62]. Activation energies calculated neglecting mass transport tend to be overestimated as experimental conditions affect the reaction rate and mass transfer of the reactants [62, 63]. With respect to temperature, the apparent activation energy decreases with the activation temperature due to decreasing mass transfer [62]. In the investigated temperature range, the gasification reaction is controlled by the mass transfer, as shown below. Hence, the chemical reaction rate is presumably lower than the reported value. The burn-off values reported here are in a similar range, as reported previously for PAN fibers carbonized and activated under fairly comparable temperatures in a continuous constant length process [48]. With activation time, the burn-off does not steadily increase (Fig. 5b): The average burn-off after 2 h, (11.42 ± 0.92) wt%, and 4 h, (11.23 ± 0.83) wt%, do not differ significantly. After 8 h activation time, the average burn-off rises to (37.3 ± 7.0) wt%. The fact that the burn-off during 2 h and 4 h activation time does not significantly differ while the specific ECAS is steadily increasing with activation time suggests that in the early stages of the activation, the carbon pore structure changes due to molecular reorganization rather than burn-off. Carrot et al. [38] made a similar observation with a fast initial burn-off followed by slower weight losses starting at about 40 wt% burn-off. The two regimes were related to an initial removal of amorphous carbon domains that stabilize pseudo-graphitic crystallites and subsequent pore development in crystallites and their rearrangement. A slight trend to higher burn-off with decreasing fiber diameter is noticeable, consistent with the observations of Tavanai et al. [58]. CO₂ activation yields specific ECAS values up to (1254 ± 42) m² g^− 1. The specific ECAS is in good agreement with a linear increase with activation temperature and time during CO₂ activation. The activation onset temperatures determined from the x-axis intercept of the linear fits is (842.2 ± 2.3) ^∘C. Due to the relatively large variations of the specific ECAS values after CO₂ activation, a detailed statistical analysis for the correlation with the specific geometric surface A_G (4), that is inversely proportional to the fiber diameter, was conducted. For a surface driven, mass transport controlled, activation process a positive correlation is expected. The activation potential with respect to the activation temperature ζ_Temperature and time ζ_Time defined as

$$ \zeta_{\text{Temperature}} = \frac{{ECAS}_{\text{Activated}}-{ECAS}_{\mathrm{Non-activated}}}{T_{\text{Activation}}-T_{\text{Onset}}} $$

(5)

$$ \zeta_{\text{Time}} = \frac{{ECAS}_{\text{Activated}}-{ECAS}_{\mathrm{Non-activated}}}{t_{\text{Activation}}} $$

(6)

was calculated for each sample. The data points for the lowest activation temperature were excluded from the analysis due to excessive deviations. A significant positive correlation (p <.001) of both activation potentials with the specific geometric surface A_G of the fibers was found (Fig. 6).

Fig. 5

CO₂ activation: Dependence of burn-off and specific ECAS on the mean fiber diameter, activation temperature and time. The dashed lines serve as a guide for the eye

Fig. 6

Correlation analysis of the CO₂ activation potential ζ with the specific geometric surface A_G (4) for different activation temperatures in a) and activation times in b). The matchline represents the prognosis of the activation potential as function of the inverse fiber diameter. The dashed lines show the 95% prediction interval. Both linear correlations are statistically significant with 95% likelihood (p <.001). 85% of the scatter is explained by the linear regression model for activation temperature and 75% for activation time. C) shows the potentials for activation normalized to the y-axis intercept of the respective matchlines. The concurrent normalized potentials for activation indicate an equivalent correlation with the specific geometric surface

Interestingly, the normalization to the y-axis intercept of the activation potentials leads to similar slopes, indicating that the effect of activation temperature and time on the activation potential correlate equally with the geometric fiber surface. This leads to the interpretation that CO₂ activation is a surface driven process that is controlled by the diffusion of the activation agent in the porous carbon fibers. With longer activation times, the activation progresses into the bulk material, together with the pores that are introduced in the material. Further insight into the activation kinetics gives the analysis of ECAS normalized to the weight of the non-activated carbon starting material (Fig. S6 A and B), referred to as specific “ECAS^∗”, that shows a similar behavior as the specific ECAS discussed above – except the 108 nm fiber material that reaches saturation of about 700 m² g^− 1 already at a burn-off of (11.23 ± 0.97) wt%. The saturation indicates that the reaction front propagating from the fiber surface has reached the fiber core, and further gasification takes place in the activated shell. Longer activation times or higher temperatures are presumably required for full penetration of the thicker fibers.

Steam activation kinetics

Burn-off and specific ECAS of steam activated materials in dependence on the mean fiber diameter and the activation parameters temperature and time are shown in Fig. 7. Steam activation yields specific ECAS values up to (1033 ± 59) m² g^− 1, comparable to the values of CO₂ activated materials. The activation onset temperature can be determined from the x-axis intercept of linear fits to burn-off and specific ECAS. The two onset temperatures of (733.1 ± 2.8) ^∘C derived from burn-off and (731.4 ± 5.6) ^∘C derived from specific ECAS do not differ significantly. The burn-off during activation increases linearly with temperature by (0.449 ± 0.084) wt% ^∘C^− 1 and time by (3.61 ± 0.17) wt% h^− 1 (Fig. 7a and b). An exponential dependence on temperature with activation energies of 162.3 kJ mol^− 1 and 183.5 kJ mol^− 1, as reported by Park et al. [64] for pitch-based fibers with 1 μm and 10 μm diameter can not be observed. The different behavior could be explained by the broader temperature range shorter activation times compared to the present study. Surprisingly, burn-off and specific ECAS development are delayed by (1.09 ± 0.21) h and (1.863 ± 0.082) h, respectively. This apparent minimum exposure of the carbon to the heated steam required for activation may be explained by a nonlinear reaction rate dependence on the activation agent concentration that rises and drops in the furnace as determined by the residence time of the gases in the furnace. Alternatively, the delayed onset could be explained by a chemical shift due to the formation of oxygen-containing functionalities [39] in the early stages of the gasification reaction. This implies that the initial chemical shift does not promote specific ECAS development. The specific ECAS during steam activation shows an initial rapid increase, followed by an onset of saturation with respect to activation temperature and time. The saturation effect may be explained by the pore widening characteristics of steam with increasing burn-off compared to CO₂, which mainly develops microporosity [65, 66]. Figure S6c and d show the specific ECAS^* that reaches saturation of about 700 m² g^− 1 at a burn-off of (11.23 ± 0.97) wt% for all fiber diameters. The saturation indicates that the steam gasification reaction occurs throughout the whole fiber volume at activation temperatures starting from (757.08 ± 0.12) ^∘C and activation times 4 h and longer. The absence of correlation of the steam activation potential with the specific geometric surface, hence fiber diameter, suggests that the steam activation is controlled by the slow reaction rate compared to mass transport.

Fig. 7

Steam activation: dependence of burn-off a, b and specific ECAS c, d on the mean fiber diameter, activation temperature and time. The dashed lines serve as a guide for the eye

Mass transport in porous materials, however, is a complex interplay of configurational and Knudsen diffusion [66] that is sensitive to temperature and pore structure. Further clarification would require extensive material characterization and modeling efforts beyond the scope of the present study.

Electrical conductivity changes with activation

The conductivity change upon activation was analyzed by calculating the specific conductance σ = (R_S ⋅ m)^− 1 to account for weight differences between the samples. The specific conductance was then normalized to the non-activated materials to eliminate differences of the conductances between the different fiber diameter materials. Fig. 8 shows that the resulting specific conductivity changes as a function of the respective burn-off for CO₂ (a and b) and steam activation (c and d). The variations of the observed specific conductance reductions do not allow us to assess the influence of the fiber diameter. CO₂ activation temperature and time have a distinct impact on the conductivity following linear slopes of − 0.876 ± 0.033 and − 1.27 ± 0.22. The steeper slope with burn-off as a function of activation time (Fig. 8b, as compared to Fig. 8a) can be explained with the mass transport controlled activation kinetics: Longer activation times lead to deeper penetration of the activation reaction font into the carbon fiber. At longer activation times, the fraction of the activated carbon shell to non-activated core grows faster than at higher temperatures. The y-axis intercepts are close to unity (91.65 ± 0.74)% and (100.6 ± 5.1)% in both cases suggesting that the decrease of the conductivity is caused by structural changes related to the burn-off.

Fig. 8

The specific conductance change for CO₂ (steam) activation is depicted in a and b (c and d) as a function of the burn-off for all fiber diameters. The data is differentiated in activation temperature and time effects

Steam activation has a stronger impact on conductivity. Both, activation temperature and time decrease the conductivity to a similar extent with linear slopes of − 1.934 ± 0.085 and − 1.864 ± 0.029, respectively. The y-axis intercept is significantly lower than unity in both cases with (84.0 ± 1.2)% and (82.77 ± 0.47)%. A plausible explanation for the specific conductance reductions at zero burn-off are chemical or changes of the crystalline structure [67] at the early stages of the activation process. Considering the delay of burn-off and specific ECAS development discussed in Section 3, it seems more likely, that the formation of oxygen-containing functionalities is responsible for the apparent conductance changes at zero-burn-off. The different impact on the conductivity of CO₂ and steam activation becomes less relevant at higher burn-off that yields high specific ECAS values. The highest specific ECAS achieved with CO₂ activation is (1254 ± 42) m² g^− 1 with 108 nm diameter fiber material at a burn-off of (43.0 ± 1.4) wt%. This burn-off leads to a reduction of the conductivity by 54%. Thicker fibers require higher burn-off to yield high specific ECAS values. The highest specific ECAS value of steam activated materials of (1003 ± 59) m² g^− 1 is accompanied by a burn-off of (22.97 ± 0.73) wt%. Due to the lower burn-off, the conductivity is reduced by 59% only, despite the generally higher impact of steam activation on the conductivity. For applications as electrode materials, both high absolute surface area (specific ECAS^*) and high electrical conductivity are required. CO₂ activated 108 nm fiber materials, and all H₂O activated materials approach the maximum specific ECAS^∗ already at (11.23 ± 0.97) wt% and (9.9 ± 2.0) wt% burn-off respectively. The conductivity of CO₂ activated materials is reduced at this burn-off on average only by 14%, while H₂O activated materials show a higher average conductivity reduction of 36%. Hence, material fabrication with higher burn-off than about 10% appears not to be preferential for the application as electrode material.

Conclusions

First, we presented a comprehensive fabrication process for electrospun carbon fiber mats based on a modified commercial electrospinning unit. The fiber mats were spun from PAN/DMAc dopes with four different polymer concentrations between 6 wt% and 13 wt% that result in different fiber diameters. During the subsequent carbonization at 1100 ^∘C, the fiber diameter shrinks in average by (32.0 ± 7.9)%, accompanied by a shrinkage in the size of (49.3 ± 2.5)% indicating isotropic shrinkage in fiber length and diameter. The resulting carbon fibers show a log-normal fiber diameter distribution with mean fiber diameters ranging from 108 nm to 623 nm. The quantity of 12 pieces about 5x5 cm² in size produced in one batch shows only small relative variations of their properties ECAS (< 5.9%), area density (< 4.3%), and electrical sheet resistance (< 5.7%). Because of the small variations, the carbon fiber mats are suitable for parameter studies that require larger numbers of samples.

Second, we conduct a CO₂ and steam activation parameter study and analyze the activation kinetics by means of burn-off, ECAS, and electrical conductivity to elucidate implications relevant for the application as electrode material. The different fiber diameters enable to gain information on the microscopic activation kinetics. CO₂ and steam activation results in maximum ECAS values (1254 ± 42) m² g^− 1 at (43.02 ± 1.42) wt% burn-off and (1033 ± 59) m² g^− 1 at (22.97 ± 0.73) wt% burn-off respectively. The burn-off plateau at (873.21 ± 0.80) ^∘C between 2 h and 4 h activation time is attributed to an initial burn-off of the amorphous domains in the turbostratic carbon fibers. From the correlation of the specific ECAS with the specific geometric surface, we conclude that the CO₂ activation kinetics of electrospun fibers are mass transport controlled and progresses with time from the fiber surface towards the fiber core. The burn-off was found to correlate only weakly with the specific geometric surface. From the analysis of the ECAS normalized to the weight of the starting material, we deduce that the fibers, except the 108 nm fibers, are only partially activated, resulting in an activated shell enclosing a non-activated fiber core. The stronger decrease of the fiber conductivity with activation time is consistent as longer activation times lead to a thicker activated shell. Steam activation reveals no correlation of the specific ECAS and burn-off with the specific geometric surface, suggesting reaction rate controlled kinetics. The specific ECAS shows signs of saturation at higher activation temperatures and times that indicate pore widening with increasing burn-off. The specific ECAS and burn-off development show a delayed onset that presumably stems from an initial chemical shift due to oxygen uptake. This hypothesis is supported by the reduction of the conductivity at zero burn-off. Our results reveal a complex interplay between burn-off during activation, and the associated increase in ECAS as well as a loss of electrical conductivity. CO₂ activation has a lower impact on the conductivity related to burn-off as steam activation, but substantially higher burn-off is required to achieve comparably high specific ECAS values. Additionally, CO₂ activation requires a small fiber diameter starting material for high ECAS values. Therefore, we cannot deduce a preference for either CO₂ or steam activation for applications that require high specific ECAS. However, for the use of electrospun carbon materials as an electrode that requires large absolute ECAS (specific ECAS^*) a suitable trade-off with conductivity can be made: CO₂ activated 108 nm fiber material with (11.23 ± 0.97) wt% burn-off exhibits a specific ECAS^* close to the maximum, while the conductivity is reduced in average by only 14%. Last but not least, the presented fabrication process for electrospun carbon fiber mats provides a basis for the detailed CO₂ and steam activation parameter study that allows us to draw conclusions about the respective activation kinetics. The carbon materials were already used as starting material for the preparation of electrocatalysts [13, 14]. The outlined fabrication route may be used as a basis for tailoring the properties for specific applications, i.e., electrode material in bioelectrochemical systems. It may serve as a candidate for scale-up in the future.