Laws of Large Numbers for Weighted Sums of Independent Random Variables: A Game of Mass

Abstract

We consider weighted sums of independent random variables regulated by an increment sequence and provide operative conditions that ensure a strong law of large numbers for such sums in both the centred and non-centred case. The existing criteria for the strong law are either implicit or based on restrictions on the increment sequence. In our setup we allow for an arbitrary sequence of increments, possibly random, provided the random variables regulated by such increments satisfy some mild concentration conditions. In the non-centred case, convergence can be translated into the behaviour of a deterministic sequence and it becomes a game of mass when the expectation of the random variables is a function of the increment sizes. We identify various classes of increments and illustrate them with a variety of concrete examples.

1 Setup, Literature and Overview

In what follows all random variables are defined on a probability space $(\Omega , \mathcal {F}, \mathbb {P})$ and $\mathbb {E}$ denotes expectation with respect to $\mathbb {P}$. Let $\mathbb {X} {:}{=} \{\,X_k, k \in \mathbb {N}\,\}$ be a sequence of independent real valued random variables with finite mean, $\mathbb {E}[X_k] < \infty$ for all $k \in \mathbb {N}$ and let $\mathbb {A} = (a_{n,k}\in \mathbb {R}_+; n,k\in \mathbb {N})$ be a Toeplitz summation matrix, i.e., $\mathbb {A}$ satisfies

$$\begin{aligned} a_{n,k} \ge 0, \quad \forall \; n,k \in \mathbb {N}, \nonumber \\ \lim _{n} a_{n,k} = 0,\end{aligned}$$

(1.1)

$$\begin{aligned} \lim _{n} \sum _{k} a_{n,k} = 1, \end{aligned}$$

(1.2)

$$\begin{aligned} \sup _{n} \sum _{k} a_{n,k}< \infty . \end{aligned}$$

(1.3)

A simple example of Toeplitz summation matrix is $a_{n,k} = n^{-1} \mathbb {1}_{\{k \le n\}}$, more examples are given in Sect. 4. In this setup, one seeks conditions on $\mathbb {X}$ and $\mathbb {A}$ to ensure convergence in probability or almost sure convergence for the sequence $\{\,S_n,n \in \mathbb {N}\,\}$, where

$$\begin{aligned} S_n: = \sum _{k} a_{n,k} X_k. \end{aligned}$$

These questions, known as weak/strong Law of Large Numbers (LLN), have been investigated since the birth of probability theory, see [5], and have been extensively studied in the XX century, for different summation methods, such as Voronoi sums, Beurling moving averages, see [6, 7] for more summation methods. We also refer to [14] and references therein for a classical account of the subject and to [12] for a more recent account. The quest for operative conditions that apply to a wide range of $(\mathbb {X},\mathbb {A})$ and ensure weak/strong convergence of $S_n$ has been the subject of [11, 13, 15, 16].

When the elements of $\mathbb {X}$ are i.i.d. mean zero random variables, the weak LLN is equivalent to $\lim _n \max _k a_{n,k} = 0$, see [13, Theorem 1]. In [13, Theorem 2], the following sufficient conditions for the strong LLN are given:

$$\begin{aligned} \mathbb {E}\left[ \left| X_1 \right| ^{1 + \frac{1}{\gamma }}\right]<\infty \quad \text { and }\quad \limsup _{n} n^{\gamma }\max _{k} a_{n,k}< \infty , \quad \quad \text { for some } \gamma >0. \end{aligned}$$

(1.4)

For (mean-zero) independent but not identically distributed variables, similar sufficient conditions have been examined in [11, 15, 16]. In particular, in analogy with the two conditions in (1.4), these references require that the variables $X_k$’s are stochastically dominated by a random variable $X_*$ satisfying a moment condition, and that the associated coefficients $a_{n,k}$ decay sufficiently fast as a function of n.

Unlike the above references, in this paper we impose concentration conditions on $\mathbb {X}$ and obtain sufficient conditions for the weak/strong LLN when $\limsup _n \max _k a_{n,k}>0$. Here, as in [11], we consider a family of weights, referred to as masses, ${\textbf {m}}{:}{=}\left( m_k\in \mathbb {R}_+,k\in \mathbb {N} \right)$. We see ${\textbf {m}}$ as an element of $\mathbb {R}_+^{\mathbb {N}}$, i.e. we consider ${\textbf {m}}: \mathbb {N} \rightarrow \mathbb {R}_+$ to be such that ${\textbf {m}}(k) = m_k$. We assume that the mass sequence ${\textbf {m}}$ is such that

$$\begin{aligned} \sum _{k \in \mathbb {N}}m_k = \infty . \end{aligned}$$

(1.5)

Set $M_n: = \sum _{k = 1}^n m_k$ and

$$\begin{aligned} a_{n,k}: = {\left\{ \begin{array}{ll} \frac{m_k}{M_n} &{} \text {if } k \le n,\\ 0&{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(1.6)

For $\mathbb {A} = (a_{n,k}, n,k \in \mathbb {N})$, conditions (1.2) and (1.3) hold true by definition. Also, because (1.5) implies $\lim _n M_n = \infty$ it follows that (1.1) is in force and therefore $\mathbb {A}$ is a Toeplitz summation matrix. We notice in particular that if the sum in (1.5) is finite, then no LLN can be expected. Indeed, if for some k, $X_k$ is not degenerate and $m_k>0$, then the limit random variable will have finite yet strictly positive variance, what precludes convergence to a constant. To describe our results we depart from the setup of [11] and consider $X_k = X_k(m)$ to be a one parameter family of random variables.

First contribution The first goal of this paper is to provide (near to) optimal operative conditions on $\mathbb {X}$ to ensure that for any sequence of positive masses ${\textbf {m}} \in \mathbb {R}_+^{\mathbb {N}}$ that satisfies (1.5),

$$\begin{aligned} S_n = S_n ({\textbf {m}}){:}{=} \sum _{k = 1}^n \frac{m_k}{M_n} X_k(m_k) \end{aligned}$$

(1.7)

converges to zero as $n \rightarrow \infty$ both in a weak and in a strong sense. This allows us to go beyond the fast coefficient decay assumptions made in the existing literature. Due to the nature of the coefficients in (1.6) we will refer to the sum in (1.7) as incremental sum. The conditions for the weak LLN are necessary and sufficient for convergence in the centred case, see Sect. 2.3.1. This is reminiscent but not equivalent to the weak LNN for the classical average, see Theorem 1 in [9, Chap 7, p. 235] or Theorem 2.2.12 in [8].

Motivation and applications in random media Our original motivation to look at this type of incremental sums came from the analysis pursued in [1, 2, 4] of the asymptotic speed, and related large deviations, of a Random Walk (RW) in a particular class of dynamic random media, referred to as Cooling Random Environment (CRE). This model is obtained as a perturbation of another process, the well-known RWRE, by adding independence through resetting. RWCRE, denoted by $({\overline{Z}}_n)_{n\in \mathbb {N}_0}$, is a patchwork of independent RWRE displacements over different time intervals. More precisely, the classical RWRE consists of a random walk $Z_\cdot = (Z_n)_{n\in \mathbb {N}_0}$ on $\mathbb {Z}$ with random transition kernel given by a random environment sampled from some law $\mu$ at time zero. To build the dynamic transition kernel of RWCRE we fix a partition of time into disjoint intervals $\mathbb {N}_0 = \bigcup _{k\in \mathbb {N}} I_k$ then, we sample a sequence of environments from a given law $\mu$ and assign them to the time intervals $I_k$. To obtain the sum in (1.7) we let $\left| I_k \right| = m_k$ and consider $S_n = {\overline{Z}}_{M_n}/M_n$. In this case, $S_{n}$ represents the empirical speed of RWCRE at time $M_n$ and $X_k(m_k) = \frac{Z^{(k)}_{m_k}}{m_k}$, where $(Z^{(k)}_\cdot , k \in \mathbb {N})$ are independent copies of RWRE sampled from $\mu$.

This type of time-perturbation of RWRE by resetting in reality gives rise to a slightly more general sum than the incremental one in (1.7). Hence we will prove statements for the above incremental sum but also for the more general one, referred to as gradual sum, as defined in (2.2)–(2.3) below. It is worth saying that this patchwork construction can be used to perturb (in time or even in space) other models in random media, for example, to describe polymagnets [17] based on juxtaposition of independent Curie-Weiss spin-systems [10] of relative sizes $m_k$’s.

A first partial analysis of the asymptotic speed for RWCRE started in [4, Thm. 1.5] and in [1, Thm. 1.12]. The new results here offer a full characterization of when existence of the asymptotic averages in (1.7) holds.

Second contribution Our second goal is to explore, in the non-centred case, conditions on the masses ${\textbf {m}}$ that ensure convergence of the weighted sums in (1.7). In particular, we will identify different classes of masses and characterize the limit of the corresponding weighted sums. The limit in (1.7) depends on the relative weight of $m_k$ and this is what we call the game of mass. To illustrate it we construct examples for each of these classes. In Sect. 4.4 we also treat the case of random masses, a natural question when the increments sizes are regulated by a random processes, for instance, the return times to the origin of an auxiliary independent random walk.

Structure of the paper We start in the next two sections by collecting all the main new results. In Sect. 2 we state the general LLNs for centred random variables: Theorems 2.1 and 2.2, respectively, contain the weak and the strong laws for the incremental sums; Theorem 2.3 contains the strong law for the more general gradual sums. A discussion on the hypotheses in our main theorems, illustrated by counterexamples, as well as on possible extensions, is presented in Sect. 2.3.4. Section 3 is devoted to the game of mass were we explore convergence criteria for non-centred variables. The subsequent Sect. 4 illustrates in details the subtleties of the game of mass for non-centered variables by presenting a rich palette of concrete examples of various type. Section 5 contains the proofs of the main theorems organized in successive subsections, each of them starting with a brief description of the proof steps and main ideas. Finally, Appendix A covers a technical lemma adapted from [11] and used in the proof of Sect. 5.2.

2 LLNs for Mean-Zero Variables

In this section we state and discuss the general theorems in the centred case.

2.1 Incremental Sums

Let $\mathbb {X} = \{\,X_{k} (m), m \in \mathbb {R}_+, k \in \mathbb {N}\,\}$ be a family of integrable random variables that are independent in k.

Theorem 2.1

(Weak LLN) Assume that $\mathbb {X}$ satisfies the following conditions:

• (C) (Centering)

  $$\begin{aligned} \forall \,m \in \mathbb {R}_+, \, k \in \mathbb {N};\quad \mathbb {E}\left[ X_k(m) \right] = 0. \end{aligned}$$

• (W1) (Concentration)

  $$\begin{aligned} \lim _{m\rightarrow \infty } \sup _{k} \mathbb {P}\left( \left| X_k(m) \right|>\varepsilon \right) =0, \quad \forall \varepsilon >0. \end{aligned}$$

• (W2) (Uniform Integrability)

  $$\begin{aligned} \lim _{A\rightarrow \infty } \sup _{k,m} \mathbb {E} \left[ \left| X_k(m) \right| \mathbb {1}_{\left| X_k(m) \right| >A} \right] = 0. \end{aligned}$$

Let $S_n$ be as defined in (1.7). Then, for any sequence ${\textbf {m}} \in \mathbb {R}_+^\mathbb {N}$ that satisfies (1.5),

$$\begin{aligned} \lim _{n\rightarrow \infty }\mathbb {P}\left( \left| S_n \right|>\varepsilon \right) =0,\quad \forall \varepsilon >0. \end{aligned}$$

(2.1)

To obtain a strong LLN in the centred case we impose further conditions on $\mathbb {X}$. In particular the concentration condition will be strengthened by requiring a mild polynomial decay and the uniform integrability by a uniform domination.

Theorem 2.2

(Strong LLN) Assume that $\mathbb {X}$ satisfies (C) and

• (S1) (Polynomial decay) There is a $\delta >0$ such that for all $\varepsilon >0$ there is a $C = C(\varepsilon )$ for which

  $$\begin{aligned} \sup _k\mathbb {P}\left( \left| X_k(m) \right| >\varepsilon \right) <\frac{C}{m^\delta }. \end{aligned}$$

• (S2) (Uniform domination) There is a random variable $X_*$ and $\gamma >0$ such that $\mathbb {E}(\left| X_* \right| ^{2 +\gamma })<\infty$ and for all $x \in \mathbb {R}$

  $$\begin{aligned} \sup _{k,m}\mathbb {P}(X_{k}(m)>x)\le \mathbb {P}(X_*>x). \end{aligned}$$

Let $S_n$ be as defined in (1.7). Then for any sequence $\textbf{m} \in \mathbb {R}_+^\mathbb {N}$ that satisfies (1.5),

$$\begin{aligned} \mathbb {P}\left( \lim _{n\rightarrow \infty }S_n= 0 \right) = 1. \end{aligned}$$

Remarks 2.1

In general, it is not possible to remove Assumption (C) from Theorem 2.2. If $\mathbb {X}$ satisfies (S1) and (S2), the limit of $S_n$ would coincide with the limit of its mean, which may or may not exist. See Corollary (3.1) and Sect. 3 for a discussion of when this limit exists.

Random walks with independent dominated steps provide a simple class of examples for which Theorem 2.2 applies. More precisely if $X_k(m) {:}{=} m^{-1}\sum _{i = 1}^m Y_{k,i}$ with $\mathbb {E}[Y_{k,i}] = 0$, $\left| Y_{k,i} \right| \le Y_*$ a.s. for all $k,i \in \mathbb {N}$ where $Y_*$ is such that $\mathbb {E}[(Y_*)^{2 + \delta }]< \infty$. A broader class of examples for which the above applies are systems build as patchworks of finite lengths of a given converging processes, such as the above mentioned RWCRE model. In the case of RWCRE we see two applications: the limit speed and cumulant of the process can be obtained from a non-centred version of Theorem 2.2, see Theorem 1.10 and Lemma 4.2 in [1] for details.

2.2 Gradual Sums

Motivated by the random walk model in random media in [1, 4], we next focus on a more general sum by considering a time parameter t that runs on the positive real line partitioned into intervals $I_k=[M_{k-1},M_k)$ of size $m_k$: $[0,\infty )= \cup _k I_k$. As $t\rightarrow \infty$ the increments determined by the partition are gradually completed as captured in definition (2.3) below. For $\textbf{m} \in \mathbb {R}_+^{\mathbb {N}}$, let

$$\begin{aligned} \ell _t = \ell _t({{\textbf {m}}}) {:}{=} \inf \{\,\ell \in \mathbb {N}: M_\ell \ge t\,\}, \end{aligned}$$

(2.2)

and set ${\bar{t}}: = t - M_{\ell _t - 1}$. We define the gradual sum by

(2.3)

The next theorem, is an extension of Theorem 2.2 to treat the gradual sum , for which we require the following concentration condition to hold.

• (S3) (Oscillation control) For every $\varepsilon >0$ there exist $\beta >1$ and $C_\varepsilon >0$ such that for every $t,r>0$:

  $$\begin{aligned} \sup _k\mathbb {P}\left( \sup _{s \le m} \left| (r+s)X_{k}(r + s) - r X_{k}(r) \right| \ge t\varepsilon \right) \le \frac{C_\varepsilon m^\beta }{t^\beta }. \end{aligned}$$

Theorem 2.3

(Generalized strong LLN) If $\mathbb {X}$ satisfies (C), (S1), (S2), (S3) and is as defined in (2.3), then for any sequence ${\textbf {m}} \in \mathbb {R}_+^\mathbb {N}$ that satisfies (1.5)

(2.4)

Remarks 2.2

• (a) Note that the incremental sum is a subsequence of the gradual sum, as can be seen by the relation

  

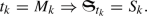
  Therefore, if $\mathbb {X}$ satisfies the conditions of Theorem 2.3 then it follows that that almost surely and in particular $S_k \rightarrow 0$ almost surely. In this sense we can see Theorem 2.3 as an extension of Theorem 2.2.

• (b) Assumption (S3) controls the oscillations between the times $M_n$’s. For example, if the sequence $sX_k(s)$ is a martingale, Doob’s $L^p$ inequality yields (S3); alternatively, if there is $f: \mathbb {R}_+ \rightarrow \mathbb {R}_+$ for which

  $$\begin{aligned} \mathbb {P}\Big (\left| (r+s)X_{k}(r + s) - r X_{k}(r) \right| \le f(s)\Big )=1 \end{aligned}$$

  (2.5)

  then one also obtains (S3). In Sect. 2.3.3 we will argue via a counter-example that an assumption like (S3) is indeed required.

• (c) Theorem 2.3 is closely related to Theorem 1.10 in [1] which deals with non-centred random variables in the case of divergent increments, i.e $m_k \rightarrow \infty$, see also Sect. 4.2. The result for gradual centred sums stated here has weaker assumptions, notably, in the context of RWRE of [1] the family $\mathbb {X}$ is satisfies (S1), (S2), and (S3) by construction. Indeed, in that framework, for any $k,m \in \mathbb {N}$, $X_k(m) = \frac{Z^{(k)}_m}{m}$, where $Z^{(k)}_m$ is the m-th step of RWRE starting from the origin. Condition (S1) is obtained from the large deviation estimates for the annealed law of RWRE under the conditions mentioned in Proposition 1.7 in [1]. The nearest neighbour property of RWRE starting from the origin implies $\mathbb {P}(\left| X_k(m) \right| \le 1) = 1$, which gives condition (S2). Finally, again the nearest neighbour property of the walk implies that (2.5) holds with $f(s) = 2\,s$, which gives condition (S3).

2.3 On the Necessity of the Hypotheses & Possible Extensions

In this section we discuss nature of the various hypotheses in the previous theorems. We start discussing the necessity of the hypotheses in Theorem 2.1. We next elaborate on the near to optimality of condition (S1) in Theorem 2.2 and the necessity of condition (S3) in Theorem 2.3, see Sects. 2.3.2 and 2.3.3 respectively. Finally possible extensions are mentioned in Sect. 2.3.4.

2.3.1 Weak LLN (Theorem 2.1): Necessity of (W1) and (W2)

Both conditions (W1) and (W2) are necessary for the weak LLN. The necessity of condition (W1) is shown in [11, Theorem 1]. We show below that condition (W2) is necessary by means of a counter-example.

Counter-example: Consider a sequence $\{\,U_k, k \in \mathbb {N}\,\}$ of i.i.d. uniform random variables on (0, 1) and $X_k(m) {:}{=} V_m(U_k)$, where

$$\begin{aligned} V_m(u) = {\left\{ \begin{array}{ll} A_m &{} \text { if } u \in [0,g(m)/2),\\ -A_m&{} \text { if } u \in (g(m)/2, g(m)],\\ 0 &{} \text{ else. } \end{array}\right. } \end{aligned}$$

with this definition, it follows that $\mathbb {P}\left( \left| X_k(m) \right| >0 \right) = g(m)$. Assume that $g:\mathbb {R}\rightarrow (0,\infty )$ is a strictly decreasing continuous function such that $\lim _{m \rightarrow \infty } g(m)=0$. Let $m_k {:}{=} \inf \{\,m: g(m)\le 1/k\,\}$. This implies that $m_k \rightarrow \infty$ as $k \rightarrow \infty$ and so (1.5) is satisfied. Furthermore by the definition of $X_k(m)$, the assumptions (C) and (W1) in Theorem 2.1 are verified. Now choose $\{\,A_{m_k}, k \in \mathbb {N}\,\}$ to be such that

$$\begin{aligned} \frac{m_n}{M_{N(n)}} A_{m_n} > 1 + \sum _{k = 1}^{n-1} A_{m_k}, \end{aligned}$$

where N(n) is such that

$$\begin{aligned} \mathbb {P}(\exists \, {n\le j \le N(n)}: X_j(m_j) \ne 0)>\frac{1}{2}. \end{aligned}$$

Such an N(n) exists and is finite. Indeed, since $\mathbb {P}(X_k(m_k) \ne 0) = g(m_k) >1/k$, we have $\sum _k g(m_k) = \infty$. Therefore, by the second Borel–Cantelli Lemma, and the continuity of probability measures:

$$\begin{aligned} 1 = \mathbb {P}(\exists \, j\ge n: X_j(m_j) \ne 0) = \lim _{N \rightarrow \infty }\mathbb {P}(\exists \,n\le j <N: X_j(m_j) \ne 0). \end{aligned}$$

With this choice of $A_{m_n}$ it follows that if there is a j, $i \le j \le N(i)$ for which $\left| X_j(m_j) \right| >0$ then $\left| S_{N(i)} \right| >1$. Therefore for any $i \in \mathbb {N}$,

$$\begin{aligned} \mathbb {P}\left( \left| S_{N(i)} \right|> 1 \right) > \frac{1}{2}. \end{aligned}$$

As $\mathbb {P}(S_{n}>0 \mid \left| S_n \right| >0) = \frac{1}{2}$, we conclude that the weak LLN does not hold.

2.3.2 Incremental SLLN (Theorem 2.2): Near Optimality of (S1)

One could try to improve the condition in (S1) by requiring a decay smaller than polynomial, that is:

$$\begin{aligned} \mathbb {P}\left( \left| X_k(m) \right| >\varepsilon \right) <\frac{C_\varepsilon }{f(m)}, \end{aligned}$$

(2.6)

for some $f: \mathbb {R}_+ \rightarrow \mathbb {R}_+$. When we look for a scale that grows slower than any polynomial, $f(m) = \log (m)$ is a natural candidate. However, as illustrated next, this already allows for counterexamples.

Counter-example: Let $\{\,U_k, k \in \mathbb {N}\,\}$ be a sequence of i.i.d. uniform random variables on (0, 1) and let $X_{k}(m) {:}{=} g_m(U_k)$ where

$$\begin{aligned} g_m(x) {:}{=} {\left\{ \begin{array}{ll} 1 &{} \text {if } x \in \left( 0,\frac{1}{2\log _2 m}\right) ,\\ -1 &{} \text {if } x \in \left[ \frac{1}{2\log _2 m}\right. , \left. \frac{1}{\log _2 m}\right) ,\\ 0 &{} \text {else}.\\ \end{array}\right. } \end{aligned}$$

Note that $\mathbb {X}$ fulfills assumptions (C), (S2), (S3), and instead of (S1) it satisfies

$$\begin{aligned} \mathbb {P}\left( X_{k}(m) = 1 \right) = \frac{1}{2\log _2m},\quad \text { and } \quad \mathbb {P}\left( X_{k}(m) = -1 \right) = \frac{1}{2\log _2m}. \end{aligned}$$

Now take $\textbf{m}$ with $m_k = 4^k$. For such an $\textbf{m}$ we see that the incremental sum $S_n$ does not satisfy the strong LLN. Indeed, as

$$\begin{aligned} \sum _{k = 1}^\infty \mathbb {P}\left( X_{k}(m_k)=1 \right) = \infty ,\quad \text { and } \quad \sum _{k = 1}^\infty \mathbb {P}\left( X_{k}(m_k) = -1 \right) = \infty \end{aligned}$$

by the second Borel–Cantelli lemma,

$$\begin{aligned} \mathbb {P}\left( X_k(m_k)=1, \text { i.o.} \right) = 1,\quad \text { and } \quad \mathbb {P}\left( X_k(m_k)=1, \text { i.o.} \right) = 1. \end{aligned}$$

Note that $M_n = (4^{n+1} - 4)/3$ and that by (1.7)

$$\begin{aligned} \left| S_n - X_{n} \right| \le 1- \frac{4^n}{M_n} + \sum _{k = 1}^{n-1}\frac{4^k}{M_n} = 2 \frac{4^n -4}{4^{n+1} - 4} \le \frac{3}{4}. \end{aligned}$$

Therefore

$$\begin{aligned} \mathbb {P}\left( \left| S_n - 1 \right|< \frac{3}{4} \text { i.o.}\right) =1,\quad \text { and } \quad \mathbb {P}\left( \left| S_n + 1 \right| < \frac{3}{4} \text { i.o.}\right) =1, \end{aligned}$$

which means that almost surely $S_n$ does not converge.

In light of the above example, we see that the condition (S1) is near to optimal. Indeed, to improve it, we would need to find f(m) in (2.6) satisfying

$$\begin{aligned} \log ^k(m)<<f(m)<< m^\delta \quad \forall \, k \in \mathbb {N}, \; \delta >0. \end{aligned}$$

2.3.3 Gradual SLLN (Theorem 2.3): Necessity of (S3)

Let $(B^{(k)}, k \in \mathbb {N})$ be independent standard Brownian motions on $\mathbb {R}$ and define

$$\begin{aligned} X_k(m): = \frac{B^{(k)}(g(k,m))}{ m\sqrt{g(k,m)}}, \end{aligned}$$

(2.7)

where $g: \mathbb {N} \times \mathbb {R}_+ \rightarrow \mathbb {R}$ is a function to be suitably chosen and which will serve to obtain $\mathbb {X}$ which satisfies (C), (S1), (S2) and for which (S3) and (2.4) fail.

Note first that (C), (S1), and (S2) hold for the variables defined in (2.7). Consider an increment sequence ${\textbf {m}} = (m_k, k \in \mathbb {N})$ with $m_k \ge 2$ for all k. We now claim that it is possible to choose g for which both (S3) and (2.4) fail. To see this, let the oscilation between points $r, t \in \mathbb {R}_+$ be defined by

Define also for any $c>0$

$$\begin{aligned} \begin{aligned} w(k,c){:}{=}\mathbb {P}\bigg (\sup _{1 \le s \le 2} |sX_k(s)|> c \bigg ). \end{aligned} \end{aligned}$$

Now note that

$$\begin{aligned} w(k,c)= & {} \mathbb {P}\bigg (\sup _{1 \le s \le 2} |sX_k(s)|> c \bigg ) \le \mathbb {P}\bigg (\sup _{1 \le s \le 2} |X_k(s)|> c/2 \bigg ) \\ {}= & {} \mathbb {P}(\omega _X(t_{k-1},t_{k-1}+2)> c/2). \end{aligned}$$

Finally, note that

$$\begin{aligned} w(k,c) = \mathbb {P}\bigg (\sup _{1 \le s \le 2} \big |sX_k(s)\big |> c \bigg ) = \mathbb {P}\bigg (\sup _{g(k,1) \le s \le g(k,2)} \bigg |\frac{B^{(k)}(g(k,s))}{ \sqrt{g(k,s)}}\bigg |> c\bigg ). \end{aligned}$$

Now, if $\lim _k g(k,2)- g(k,1) = \infty$, for example when $g(k,m) {:}{=} \exp (km)$, it follows that $\lim _k w(k,c)= 1$. Moreover, given the sequence ${\textbf {m}}$ we may choose g to be such that $w(k, M_k) \rightarrow 1$ and therefore (S3) fails. To see that (2.4) also fails, it suffices to note that if $t_k = M_k$ then by Theorem 2.2 almost surely. On the other hand

and since

$$\begin{aligned} \sum _k \mathbb {P} (\omega _X(t_{k-1},t_{k-1}+2)>1/2) \ge \sum _k w(k, M_k) = \infty , \end{aligned}$$

it follows from the second Borel–Cantelli lemma that

2.3.4 Possible Extensions

We conclude the discussion on the LLNs by commenting on possible extensions for more general weighted sums that could have been pursued.

• 1. Independence Our examples above and proofs below are based on the independence in k of $\{\,X_k(m), m \in \mathbb {R}_+, k \in \mathbb {N}\,\}$. However, for certain choices of well-behaved mass sequences $\textbf{m}$, it seems possible to adapt our arguments and still obtain a weak/strong LLN in presence of “weak enough dependence”, though the notion of “weak enough dependence” would very much depend on the weight sequence and this is why we did not pursue this line of investigation.

• 2. Relaxing condition (3.3) In the game of mass described in Sect. 3, for simplicity, we have restricted our analysis to variables with expected value independent of k, as captured in assumption (3.3). We note that this is not really needed, as we might, for example, consider $X_k(m)$’s with expected value, say, $v_m$ and $v_m'\ne v_m$ depending on the parity of k. Yet, the resulting analysis would branch into many different regimes depending on how exactly condition (3.3) is violated.

• 3. Fluctuations and large deviations It is natural to consider “higher order asymptotics”, such as large deviations or scaling limit characterizations, for the sums in (1.7) or (2.3). However, the analysis for this type of questions relies heavily on the specific distribution of the sequence of variables $\mathbb {X}$ thus preventing a general self-contained treatment. Still, it is interesting to note that these other questions can give rise to many subtleties and anomalous behaviour. This is well illustrated by the specific RWCRE model in random media introduced in [4] that motivated the present paper, we refer the interested reader to [2,3,4] for results on crossovers phenomena in related fluctuations, and to [1] for stability results of large deviations rate functions.

3 Non-centred Random Variables: The Game of Mass

If the random variables $\mathbb {X}$ are not centred, the convergence of $(S_n, n \in \mathbb {N})$ in Theorem 2.2 and the convergence of in Theorem 2.3 corresponds to the convergence of their mean. Indeed, consider $\tilde{\mathbb {X}} = \big ({\tilde{X}}_k(m), m \in \mathbb {R}_+\big )$ with ${\tilde{X}}_k(m) {:}{=} \big (X_k(m) - \mathbb {E}[X_k(m)]\big )$ and decompose the sum in (1.7) as

$$\begin{aligned} S_n =\sum _{k = 1}^n \frac{m_k}{M_n} X_k(m_k) = \sum _{k = 1}^n \frac{m_k}{M_n} {\tilde{X}}_k(m_k) + \mathbb {E}[S_n]. \end{aligned}$$

(3.1)

Similarly, decompose the sum in (2.3) as

(3.2)

Now note that $\tilde{\mathbb {X}}$ satisfies (C). If $\tilde{\mathbb {X}}$ satisfies (S1) and (S2) then, by Theorem 2.2, the random term on the right hand side of (3.1) converges to 0 almost surely. Moreover, if $\tilde{\mathbb {X}}$ also satisfies (S3), then, by Theorem 2.3 the random term on the right hand side of (3.2) converges to 0 almost surely. This gives us the following result.

Corollary 3.1

(Non-centred strong LLN) Assume that $\mathbb {X}$ satisfies (S1), (S2) and let $S_n$ be as defined in (1.7). If $\lim _n \mathbb {E}[S_n] {=}{:} v$ exists then

$$\begin{aligned} \mathbb {P}\left( \lim _{n\rightarrow \infty }S_n= v \right) = 1. \end{aligned}$$

Moreover, if $\mathbb {X}$ also satisfies (S3), is as defined in (2.3) and exists then

We remark that it is not sufficient to examine the sequence $(t_k = M_k, k \in \mathbb {N})$, as the boundary term in the gradual sum may not be negligible. For instance, if

$$\begin{aligned} \mathbb {E}[X_k(m)]= \frac{2^k - m}{\max \{2^k,m\}}, \end{aligned}$$

then for $m_k = 2^k$ we have $\mathbb {E}[X_k(m_k)] = 0$ and so for $t_k {:}{=} M_k = 2^{k+1} -2$, . However, for $t'_k {:}{=} M_{k-1} + 2^{k-1} = 2^{k} + 2^{k-1} -2$, we have $\overline{t'_k} = 2^{k-1}$, $\lim _k \mathbb {E}[ X_{\ell _{t'_k}}(\overline{t'_k})] = \frac{1}{2}$, and by equation (3.2)

Interestingly, if $\mathbb {E}[X_k(m)] = v_m$ depends only of m, one can relate the convergence of to the structure of ${\textbf {m}}$. This is what we call the game of mass and explore in the sequel.

In light of Corollary 3.1, it is natural to seek conditions on $(\mathbb {X},{\textbf {m}})$ that guarantee convergence of the full sequence . In this section, for simplicity (see Item 2. in Sect. 2.3.4), we assume that the expectation of $X_k(m)$ depends only on m and not on k, that is:

$$\begin{aligned} \mathbb {E}\left[ X_{k}(m) \right] =v_m \quad \forall \, k \in \mathbb {N}. \end{aligned}$$

(3.3)

We also assume that

$$\begin{aligned} m \mapsto v_m \quad \text {is a bounded continuous function in } \bar{\mathbb {R}}_+, \end{aligned}$$

(3.4)

where $\bar{\mathbb {R}}_+=[0,\infty ]: = \mathbb {R}_+ \cup \{\infty \}$ is the compact metric space with the metric

$$\begin{aligned} d(x,y): = \left| \arctan (x) - \arctan (y) \right| , \end{aligned}$$

(3.5)

where $\arctan (\infty ) = \pi /2$.

We first divide the mass-sequences ${\textbf {m}}$ into two classes: regular and non-regular. Roughly speaking, a sequence is regular when its empirical measure admits a weak limit. In Sect. 3.1 we give the rigorous definition of regular masses and show that, contrary to the non-regular ones, the LLN always holds true. In Sect. 3.2, we consider other notions of regularity and examine how they relate to the convergence of the empirical measures.

3.1 Regular Mass Sequences

Let $\bar{\mathcal {P}}$ be the space of probability Borel measures on $\bar{\mathbb {R}}_+$, where $\bar{\mathbb {R}}_+$ is seen as the compact metric space with metric given by (3.5). Recall (2.2) and, for a given mass sequence ${\textbf {m}} \in \mathbb {R}_+^\mathbb {N}$, let $(\mu _t(\cdot ) = \mu _{t}^{({\textbf {m}})}(\cdot ), t \ge 0 )$ be the sequence of empirical mass measures on $\bar{\mathbb {R}}_+$, where $\mu _t(\cdot )$ is given by

$$\begin{aligned} \mu _t(\cdot ): = \sum _{k = 1}^{\ell _t-1} \frac{m_k}{t} \delta _{m_k}(\cdot ) +\frac{{\bar{t}}}{t} \delta _{{\bar{t}}}(\cdot ). \end{aligned}$$

(3.6)

Given a measure $\lambda \in \bar{\mathcal {P}}$ and a measurable function $f: \bar{\mathbb {R}}_+\rightarrow \mathbb {R}$, let $\int f(m)\text {d}\lambda (m)$ represent the integral of f with respect to $\lambda$. Consider $\lambda _* \in \bar{\mathcal {P}}$, $(\lambda _t, t \ge 0)$ with $\lambda _t \in \bar{\mathcal {P}}$ for each $t \ge 0$.

Definition 3.1

(w convergence) We say that $\lambda _*$ is the w limit of $(\lambda _t, t \ge 0)$ as $t \rightarrow \infty$ and we write $\lambda _* = w \text {--}\lim \lambda _t$ or $\lambda _t \xrightarrow []{w} \lambda _*$ if for any bounded continuous function $f: \bar{\mathbb {R}}_+ \rightarrow \mathbb {R}$ we have

$$\begin{aligned} \lim _{t \rightarrow \infty } \int f(m) \text {d}\lambda _t(m) = \int f(m) \text {d}\lambda _*(m). \end{aligned}$$

Note that this definition allows for $\lambda _*(\{\infty \}) {:}{=} 1 - \lambda _*(\mathbb {R}_+)$ to be strictly positive.

Definition 3.2

(Regular mass sequence) We say that ${\textbf {m}}$ is a regular mass sequence if $(\mu _t = \mu ^{(\textbf{m})}_t, t \ge 0)$, with $\mu _t$ as in (3.6), converges weakly, i.e., if there is $\mu _* \in \bar{\mathcal {P}}$ for which

$$\begin{aligned} \mu _t\xrightarrow []{w} \mu _*. \end{aligned}$$

(3.7)

The following proposition determines the limit of for regular mass sequences.

Proposition 3.1

(Limit characterization for regular sequences) If $\mathbb {X}$ satisfies (S1)–(S3),  (3.3) and (3.4), then, for ${\textbf {m}} \in \mathbb {R}_+^{\mathbb {N}}$ and $t\ge 0$:

(3.8)

In particular, if ${\textbf {m}}$ is regular and (3.7) holds true, then

(3.9)

Proof

Note first that by (3.4) $v \in C_b(\bar{\mathbb {R}}_+)$. To prove (3.8) we note that

Now, by (3.7) we have that $\langle \mu _t, v\rangle \rightarrow \langle \mu _*, v\rangle$ and (3.9) follows from Corollary 3.1. $\square$

Remarks 3.1

When ${\textbf {m}}$ is not regular, almost sure convergence is not prevented, in fact, if $v_m = 0$ for all m, then by Theorem 2.3, converges almost surely to 0. On the other hand, Examples XI, XIII presented in Sect. 4.2 below show that almost sure convergence may not hold for irregular masses.

3.2 Regularity and Stability of Empirical Frequency

There are other possible notions of regularity rather than the one in Definition 3.2. For example, instead of the empirical measure in (3.6), we may examine the empirical mass frequency $(\textsf{F}_t = \textsf{F}_{t}^{({\textbf {m}})}, t \ge 0 )$, where $\textsf{F}_t\in \bar{\mathcal {P}}$ is given by

$$\begin{aligned} \textsf{F}_t {:}{=} \sum _{k=1}^{\ell _t-1}\frac{ \delta _{m_k}}{\ell _t} +\frac{\delta _{{\bar{t}}}}{\ell _t}. \end{aligned}$$

(3.10)

The reason we consider other notions of regularity is that it allows for a finer control of the convergence for $L^1$ bounded sequences of increments, see Example XIV below.

We note that, for any $t\ge 0$ and any arbitrary function f, the following relation between $\mu _t$ and $\textsf{F}_t$ is in force:

$$\begin{aligned} \int f(m) \, \text {d}\mu _t(m)=\frac{\ell _t}{t}\int mf(m) \, \text {d}\textsf{F}_t(m). \end{aligned}$$

(3.11)

In particular, if we take $f(m)=v_m$ and $f(m)\equiv 1$, we obtain, respectively, that

and

$$\begin{aligned} \frac{t}{\ell _t}= \int m \, \text {d}\textsf{F}_t(m). \end{aligned}$$

(3.12)

The relation in (3.11) may suggest to consider weak convergence of $\textsf{F}_t$ as an alternative notion of regularity. However, as shown in the Proposition 3.1 below, these two notions are not equivalent. We find more convenient to adopt the notion in Definition 3.2 for the following two reasons. First, there are masses for which both $(\mu _t, t \ge 0)$ and $(\textsf{F}_t, t \ge 0)$ converge weakly to some $\mu _*$ and $\textsf{F}_*$, respectively, but the limit of is determined by $\mu _*$ and not by $\textsf{F}_*$, see Examples II, IX, and VII below. Second, among the unbounded masses, those divergent in a Cesàro sense will always be regular according to Definition 3.2, while the corresponding $(\textsf{F}_t, t \ge 0)$ is not guaranteed to admit a limit, see Examples VIII and X. Yet, it is interesting to look at the LLN from the perspective of masses with “well-behaved” frequencies.

Proposition 3.2 below clarifies how the relation between $\mu _t$ and $\textsf{F}_t$ expressed in (3.11) behaves in the limit. In particular it shows how to relate the behaviour of the empirical frequencies and empirical masses under different modes of convergence, which we next define. For this proposition we introduce some definitions to deal with convergence of the integral of continuous functions which may be unbounded near 0 or $+\infty$, corresponding to Definition 3.3 and Definition 3.4 below. Consider $\lambda _* \in \bar{\mathcal {P}}$, $(\lambda _t, t \ge 0)$ with $\lambda _t \in \bar{\mathcal {P}}$ for each $t \ge 0$.

Definition 3.3

($w^{-1}$ convergence) We say that $\lambda _*$ is the $w^{-1}$ limit of $(\lambda _t, t \ge 0)$ and we write $\lambda _* = w^{-1} \text {--}\lim \lambda _t$ or $\lambda _t \xrightarrow []{w^{-1}} \lambda _*$ if $\lambda _t \xrightarrow []{w} \lambda _*$ and

$$\begin{aligned} \lim _{t \rightarrow \infty } \int m^{-1} \, \text {d}\lambda _t(m) = \int m^{-1} \, \text {d}\lambda _*(m)< \infty . \end{aligned}$$

Definition 3.4

($w^{+1}$ convergence) We say that $\lambda _*$ is the $w^{+1}$ limit of $(\lambda _t, t \ge 0)$ and we write $\lambda _* = w^{+1} \text {--}\lim \lambda _t$ or $\lambda _t \xrightarrow []{w^{+1}} \lambda _*$ if $\lambda _t \xrightarrow []{w} \lambda _*$ and

$$\begin{aligned} \lim _{t \rightarrow \infty } \int m \, \text {d}\lambda _t(m) = \int m \, \text {d}\lambda _*(m)< \infty . \end{aligned}$$

(3.13)

If a sequence ${\overline{\lambda }} = (\lambda _t, t \ge 0)$ in $\bar{\mathcal {P}}$ is such that $\lambda _t \xrightarrow []{w^{+ 1}} \lambda _*$ we say that ${\overline{\lambda }}$ is $w^{+ 1}$-stable, similarly, if $\lambda _t \xrightarrow []{w^{- 1}} \lambda _*$ we say that ${\overline{\lambda }}$ is $w^{- 1}$-stable. If the w, respectively $w^{\pm 1}$, limit does not exist for $(\lambda _t, t \ge 0)$ we write $\not \exists w$-$\lim \lambda _t$, respectively $\not \exists w^{\pm 1}$-$\lim \lambda _t$. One may note that $w^{+1}$ convergence in $\bar{\mathcal {P}}$ is the same as $L^1$ convergence of Borel real valued probability measures on $\mathbb {R}$, see [8, Thm. 4.6.3, p. 245]. The reason we use $w^{\pm 1}$ is to unify notation.

Proposition 3.2

(Regularity and stable frequencies) Assume ${\textbf {m}} \in \mathbb {R}_+^{\mathbb {N}}$ is such that for $\ell _t = \ell _t({\textbf {m}})$, the limit $A{:}{=}\lim _{t\rightarrow \infty }\frac{\ell _t}{t}\in \bar{\mathbb {R}}_+$ exists. Then:

• (a) $\textsf{F}_t \xrightarrow []{w^{+1}}\textsf{F}_* \ne \delta _0 \Rightarrow \mathsf {\mu }_t \xrightarrow []{w}\mathsf {\mu }_*$ with $\int f(m) \text {d}\mu _*(m) {:}{=} A \int m f(m)\, \text {d}\textsf{F}_*(m)$,

• (b) $\mathsf {\mu }_t \xrightarrow []{w^{-1}}\mathsf {\mu }_*\ne \delta _\infty \Rightarrow \textsf{F}_t \xrightarrow []{w}\textsf{F}_*$ with $\int f(m) \text {d}\textsf{F}_*(m) {:}{=} \frac{1}{A} \int \frac{1}{m}f(m)\, \text {d}\mu _*(m)$.

Furthermore, in both cases above $A \in (0,\infty )$.

Proof

We first prove item (a). By (3.12), (3.13) we have that

$$\begin{aligned} \frac{t}{\ell _t} = \int m \text {d}F_t(m) \rightarrow A^{-1} = \int m \text {d}F_*(m). \end{aligned}$$

(3.14)

Note that $A^{-1} \in (0,\infty )$ since by (3.13), we have that $\int m \text {d}\textsf{F}_*(m) < \infty$ and by assumption (a), we have that $\textsf{F}_* \ne \delta _0$. Finally, by (3.11) and (3.14), it follows that for any $f \in C_b(\bar{\mathbb {R}}_+)$

$$\begin{aligned} \mu _t(f) = \frac{\ell _t}{t}\int m f(m)\, \text {d}\textsf{F}_t(m) \rightarrow A \int m f(m)\, \text {d}\textsf{F}_*(m). \end{aligned}$$

We now turn to the proof of item (b). Since $\mathsf {\mu }_t \xrightarrow []{w^{-1}}\mathsf {\mu }_*$, we have the convergence of $\int f(m) \text {d}\mu _t(m)$ when $f(m)=1/m$, that is, $\int f(m) \text {d}\mu _t(m) \rightarrow \int f(m) \text {d}\mu _*(m)< \infty$. Moreover, by the assumption that $\mathsf {\mu }_*\ne \delta _\infty$ we have that $\int \frac{1}{m} \, \text {d}\mu _*(m) >0$ and thus

$$\begin{aligned} \frac{\ell _t}{t} = \int \frac{1}{m} \,\text {d}\mu _t(m) \rightarrow \int \frac{1}{m} \, \text {d}\mu _*(m) = A \in (0,\infty ). \end{aligned}$$

(3.15)

Therefore, for any $f\in C_b(\bar{\mathbb {R}}_+)$, by (3.11) and (3.15) we conclude that

$$\begin{aligned} \int f(m) \text {d}\textsf{F}_t(m) = \frac{t}{\ell _t} \int \frac{1}{m}f(m)\, \text {d}\mu _t(m) \rightarrow \frac{1}{A} \int \frac{1}{m}f(m)\, \text {d}\mu _*(m). \end{aligned}$$

$\square$

In the next section, with the help of several explicit examples, we explore more how these notions of weak and $L^1$ convergence for $(\textsf{F}_t, t \ge 0)$ relate to the regularity of $(\mu _t, t \ge 0)$, all these examples are labeled with roman numbers that can be visualized in Fig. 1.

Proposition 3.2 explains part of the different relations depicted in Fig. 1 between the dotted boxes corresponding to masses for which $(\textsf{F}_t, t \ge 0)$ convergences weakly and in $L^1$.

Fig. 1

Summary of the game of mass for $(\mathbb {X},\textbf{m})$. The above rectangle offers a visual classification of the possible different mass sequences $\textbf{m}$. The region in gray corresponds to masses for which the LLN is valid, that is, converges. The vertical line divides the masses between regular (left) and irregular (right) ones according to Definition 3.2. The horizontal line separates the mass sequences between bounded (down) and unbounded (up). Among the unbounded masses, those divergent in Cesàro sense, and in particular those divergent in a classical sense, are always regular. The dotted and dashed boxes correspond to those masses for which the related frequencies are asymptotically stable, respectively, in a weak and in a $w^{+1}$ sense, as described in the left upward corner of each box. The roman numbers in each of the different sub-classes correspond to the labels of the different illustrative examples from Sect. 4. Note that XIV is associated to two linked bullets in this diagram because it refers to random increments sampled according to a finite mean law, which may have bounded or unbounded increments. Note also that labels  IV, V, XII, XIII are associated to two linked bullets in this diagram, because convergence of irregular sequences may or may not hold true depending on the value of the speeds, for instance if the random variables have zero mean then converges, see Sect. 4 for details

4 Concrete Examples of the Game of Mass

In this section we explore the relation between these different concepts of regularity of masses and their relation to convergence of the mean. Section 4.1 is devoted to examples of bounded masses and their relation to the previously defined notions. In Sect. 4.2, we identify the regular regime of mass sequences that diverge. Finally, in Sect. 4.4 we investigate what can be said when the mass-sequence ${\textbf {m}}$ is random. The many cases of the game of mass we explore here are summarized in Fig. 1.

4.1 Bounded Masses

In the following sections, whenever the limit exists, we denote by $\mu _* = w\text {-}\lim \mu _t$, the $w\text {-}\lim$ of the empirical mass measures $(\mu _t, t \ge 0)$ as defined in (3.6) and we denote by $\textsf{F}_*= w\text {-}\lim \textsf{F}_t$, the $w\text {-}\lim$ of the empirical mass frequencies $(\textsf{F}_t, t \ge 0)$ as defined in (3.10). By Proposition 3.1 when the sequence is regular the a.s. limit of exists and is given by $v = \int v_m \, \text {d}\mu _*(m)$. The following examples show how regular masses relate with weak convergence of empirical mass frequencies.

I

(Regular + $\exists \, w$-$\lim \textsf{F}_t \ne \delta _0$) When $\sup _k m_k <\infty$, w convergence of the empirical mass frequencies plus uniform integrability implies $w^{+1}$ convergence. If $\textsf{F}_*(m) \ne \delta _0$, then the formula for the limit of can be given in terms of $\textsf{F}_*$. Indeed, by item (a) of Proposition 3.2 it follows that

II

(Regular + $\exists \,w$-$\lim \textsf{F}_t= \delta _0$) This example shows that if $\textsf{F}_* =w-\lim \textsf{F}_t= \delta _0$ then $\mu _*$ may not be given by the expression in item (a) of Proposition 3.2.

Consider the triangular array $\left( {a}_{i,j}, i,j\in \mathbb {N}, j\le i \right)$ defined by $a_{i,1} {:}{=} 1$ and for $1<j\le i$, $a_{i,j} {:}{=} 2^{-i}$, see Fig. 2.

For the sequence of increment, take $m_k$ to be the k-th term of this array, more precisely let i(k) be such that

$$\begin{aligned} \frac{(i(k)-1)i(k)}{2} \le k \le \frac{i(k) (i(k) + 1)}{2} \quad \text { and }\quad j(k) {:}{=} k - \frac{(i(k)-1)i(k)}{2}. \end{aligned}$$

(4.1)

Let

$$\begin{aligned} m_k {:}{=} a_{i(k),j(k)}. \end{aligned}$$

(4.2)

Note that

$$\begin{aligned} \sum _{k} m_k \mathbb {1}_{\{m_k<1\}} = \sum _{k} \frac{k}{2^k} < \infty . \end{aligned}$$

Therefore, in this example, $\textsf{F}_t \overset{L^1}{\rightarrow }\delta _0$ while $\mu _t \overset{w}{\rightarrow }\ \delta _1$. This shows that the $w^{+1}$ limit of $(\textsf{F}_t, t \ge 0)$ is not sufficient to describe the limit of , which is given by $v_1 = \int v_m \, \text {d}\mu _*(m)$.

Fig. 2

Triangular array representing the increment sizes of the sequence

One could think that, for bounded mass sequences, if the empirical mass measures $(\mu _t,t\ge 0)$ converge then the empirical mass frequencies $(\textsf{F}_t, t \ge 0)$ will also converge. This is not true, the following is an example of bounded regular mass sequence for which the w-$\lim$ of $(\textsf{F}_t, t \ge 0)$ does not exist.

III

(Regular + $\not \exists \,w\text {-}\lim \textsf{F}_t$) Consider the sequence ${\textbf {m}}$ defined by the algorithm below:

• (i) Set $m_1 = 1$,

• (ii) while $\textsf{F}_{M(k)}(\{1\})> 1/4$ set $m_k =a_{i(k),j(k)}$ as in (4.2). Otherwise, go to (iii),

• (iii) while $\textsf{F}_{M(k)}(\{1\})< 3/4$ set $m_k = 1$. Otherwise, go to (ii).

The difference between the mass sequence in this example and the one in Example II is that we introduced increments of size 1 in the middle of the original sequence defined in (4.2) in such a way that $3/4\ge \limsup _t \textsf{F}_t(\{1\}) \ne \liminf \textsf{F}_t(\{1\})\le 1/4$. In this case, $\mu _t \overset{w}{\rightarrow }\ \delta _1$ and $\textsf{F}_t$ does not converge.

Note that if ${\textbf {m}}$ is not regular, then depending on the function $v\in C_b(\bar{\mathbb {R}}_+)$, the sequence may not converge. If there are $K,L \in \mathbb {R}_+$ such that $v_K < v_L$, as in the example below, it is simple to construct a sequence ${\textbf {m}}$ for which does not converge.

IV

(Irregular + $\not \exists \, w$-$\lim \textsf{F}_t$) Let ${\textbf {m}}$ be the sequence composed of $A_i$ increments of size K followed by $B_i$ increments of size L where the sequences $(A_i, B_i, i \in \mathbb {N})$ will be determined later. More formally, let $(A_i, B_i, i \in \mathbb {N})$ be given, define $\tau _0 {:}{=} 0$ $\tau _n {:}{=} \tau _{n-1} + A_n + B_n$ and set

$$\begin{aligned} m_k = {\left\{ \begin{array}{ll} K &{}\text { if } \,\, k \in (\tau _n, \tau _n + A_{n+1}]\,\, \text {for some } \, n\ge 0,\\ L &{}\hbox { if}\,\, k \in (\tau _n+A_{n+1}, \tau _{n+1}]\,\, \hbox {for some}\, n \ge 0. \end{array}\right. } \end{aligned}$$

(4.3)

Choose $(A_i,B_i,i \in \mathbb {N})$ such that for all $n \in \mathbb {N}$, $A_n < A_{n+1}$, $B_n<B_{n+1}$ and

$$\begin{aligned} \frac{L(B_1 + \ldots + B_{n})}{K(A_1 + \ldots + A_{n+1})} \le \tfrac{1}{n} \quad \text { and }\quad \frac{K(A_1 + \ldots + A_{n+1})}{L(B_1 + \ldots + B_{n+1})} \le \tfrac{1}{n}. \end{aligned}$$

If $v_K < v_L$ then does not converge as

V

(Irregular + $\exists \,w^{+1}$-$\lim \textsf{F}_t$) If we combine the sequence defined in Example II with the one defined in Example IV we can construct an irregular sequence for which $F_t \overset{w}{\rightarrow }F_*$. More precisely, let $m'_{k}$ be the sequence defined in Example IV and consider a triangular array $a_{i,j}$ defined by $a_{i,1} {:}{=} m'_i$ and for $1<j\le i$, set $a_{i,j} {:}{=} 2^{-i}$. To conclude, set $m_k {:}{=} a_{i(k),j(k)}$ with i(k), j(k) as defined in (4.1). Note that this sequence is irregular even though $\textsf{F}_t\overset{L^1}{\rightarrow }\delta _0$.

By item (b) of Proposition 3.2 we see that $w^{-1}$ convergence cannot occur in any of the examples of bounded regular mass for which the empirical frequency does not converge. Indeed, all those example have a significant amount of increments of negligible mass, and as such, they modify the empirical frequency without affecting the limit of the mass sequence. We now move to the study of unbounded masses.

4.2 Unbounded Cesàro’s Divergent Masses

We say that a sequence of masses ${\textbf {m}}$ is divergent when

$$\begin{aligned} \lim _{k \rightarrow \infty } m_k = \infty , \end{aligned}$$

(4.4)

and we say that a sequence of masses ${\textbf {m}}$ is Cesàro’s divergent when

$$\begin{aligned} \lim _n \frac{m_1 + \ldots + m_n}{n} \rightarrow \infty . \end{aligned}$$

(4.5)

In either case $\mu _t \overset{w}{\rightarrow }\ \delta _\infty$. Therefore the divergent/Cesàro divergent mass sequences are always regular and by Proposition 3.1 it follows that

(4.6)

A particular case of Cesàro divergence is given by the divergent masses as captured in the next example, which is a very well-behaved class of divergent mass sequences.

VI

(Divergent mass$\Rightarrow \, w\text {-}\lim \textsf{F}_t = \delta _\infty$) Since (4.4) implies (4.5) and therefore, for any divergent mass sequence, we have that (4.6) holds true. Note also that if (4.4) holds true then $\textsf{F}_t \overset{w}{\rightarrow }\ \delta _\infty$. This is a consequence of the fact that $\lim _t \textsf{F}_t([0,A]) = 0$ for any $A>0$.

The case (4.4) is covered by Theorem 1.10 in [1] in the context of random walks in dynamic environment. Theorem 2.3 can actually be seen as a generalization of Theorem 1.10 in [1]. As mentioned in Sect. 2.3.4, the present proofs could actually cover even more general cases, if, for example, we relax the assumption in Equation (3.3). The following example shows that in the Cesàro divergent regime, the sequence $(\textsf{F}_t, t \ge 0)$ may converge, but may not be able to capture the limit of .

VII

(Cesàro divergent mass + $\exists \,w$-$\lim \textsf{F}_t$ + $\mu _* = \delta _\infty$) Consider the sequence ${\textbf {m}}$, where

$$\begin{aligned} m_k {:}{=} {\left\{ \begin{array}{ll} 1 &{}\text { if } k \text { is odd, and }\\ k &{}\text { if } k \text { is even}. \end{array}\right. } \end{aligned}$$

Informaly, half the increments are 1, and the other half diverges. More precisely,

$$\begin{aligned} \textsf{F}_t \overset{w}{\rightarrow }\frac{1}{2}\delta _1 +\frac{1}{2}\delta _\infty . \end{aligned}$$

As such, one might be tempted to say that as $t \rightarrow \infty$. This is not the case because one has to take into account the relative weights of the sequences. As it turns out, the mass of increments of size 1 for this particular sequence vanishes in the limit. Indeed, note that the sum of the first 2k increments, $M_{2k}$ is

$$\begin{aligned} M_{2k}= k(k+1) + k = k^2 + 2k. \end{aligned}$$

Now note that $\frac{k}{M_{2k}} \rightarrow 0$ and therefore

Also in this example, if $v_1\ne v_\infty$, then the weak limit of $(\textsf{F}_t, t \ge 0)$ does not determine the limit of , even if it is well defined.

As in the bounded case, see Example III, also Cesàro divergent sequences may not have well behaved empirical frequencies, as shown in the next example.

VIII

(Cesàro divergent mass + $\not \exists \, w$-$\lim \textsf{F}_t$) Take an irregular sequence ${\textbf {m}}' = (m'_k, k \in \mathbb {N})$ such as the one defined in (4.3) and intercalate it with a huge increment so that it diverges in the Cesàro sense. To be more concrete, for $k \in \mathbb {N}$ let $m_{2k -1} {:}{=} m'_k$ and $m_{2k}: =k\sum _{i = 1 }^{2k-1} m_{i}$. In this example we have that $\textsf{F}_t([A, \infty )) \rightarrow \frac{1}{2}$ for all $A>0$ but

$$\begin{aligned} \begin{aligned} \frac{1}{2}&= \limsup _t \textsf{F}_t (\{K\}) = \limsup _t \textsf{F}_t (\{L\}) \quad \text { and } \\ 0&= \liminf _t \textsf{F}_t (\{K\}) = \liminf _t \textsf{F}_t (\{L\}). \end{aligned} \end{aligned}$$

Therefore, the sequence is regular with $\mu _t\overset{w}{\rightarrow } \delta _{\infty }$, but $(\textsf{F}_t,t \ge 0)$ does not converge.

4.3 Unbounded Masses that do not Diverge in the Cesàro sense

When $\textbf{m} \in \mathbb {R}_+^{\mathbb {N}}$ is not Cesàro divergent, the sequence is not necessarily regular and more subtle scenarios may occur, as the following examples illustrate. We start with an example of a regular sequence that allows an asymptotic positive mass of increments of finite size and positive mass at infinity.

IX

(Regular $\liminf m_k<\infty$ + $\exists \, w$-$\lim \textsf{F}_t$) Let ${\textbf {m}} = (m_k, k \in \mathbb {N})$ be given by

$$\begin{aligned} m_k {:}{=} a_{i(k),j(k)} = i(k) \mathbb {1}_{\{i(k)=1\}} + \mathbb {1}_{\{j(k) \ne 1\}} \end{aligned}$$

(4.7)

where $\left( a_{i,j},i,j \in \mathbb {N}, j \le i \right)$ is represented as a triangular array in Fig. 3 with i(k), j(k) as defined in (4.1).

In this case $\textsf{F}_t \overset{w}{\rightarrow }\ \delta _1$ but $\mu _t \overset{w}{\rightarrow }\ \tfrac{1}{2} \delta _1 + \tfrac{1}{2} \delta _\infty$ and so .

The sequence above is another example of a regular sequence for which the weak limit of $\textsf{F}_t$ does not determine the limit of , even when it exists.

Fig. 3

Triangular array used to obtain the increment sizes in (4.7). The sequence interweaves terms of a divergent sequence $(m'_k = k, k \in \mathbb {N})$ with “small” terms of unit size $(m''_k = 1, k \in \mathbb {N})$, in such a way that the small terms are negligible to the empirical mass measure, while they dominate the empirical mass frequency

The next example shows a regular sequence with unbounded increments and for which the empirical frequency does not converge.

X

(Regular + $\not \exists$ w-$\lim \textsf{F}_t$) Take ${\textbf {m}}$ as in Example III but replace the k-th increment of size 1 by the k-th increment of the sequence defined in Example IX. For this example, we have that for any $\varepsilon >0$

$$\begin{aligned} \limsup _t\textsf{F}_t([0,\varepsilon ]) - \liminf _t \textsf{F}_t([0,\varepsilon ]) \ge 1/2. \end{aligned}$$

Since $\mu _t \overset{w}{\rightarrow }\ \frac{1}{2}\delta _1 +\frac{1}{2}\delta _\infty$, the mass sequence is regular but $(\textsf{F}_t, t \ge 0)$ does not converge.

XI

(Irregular + $\exists \,w$-$\lim \textsf{F}_t$) Only weak convergence of the empirical measure $(\textsf{F}_t, t \ge 0)$ does not imply convergence of . Indeed, let $(K_i,N_i, i \in \mathbb {N})$ be auxiliary sequences that we will determine later. The sequence ${\textbf {m}}$ alternates one increment of size $K_i$ with $N_i$ increments of size 1. More precisely, let $\tau (j) {:}{=} j + \sum _{i = 1}^j N_i$ and set

$$\begin{aligned} m_k {:}{=} {\left\{ \begin{array}{ll} K_j &{} \text { if } k \in \{\tau (j):j \in \mathbb {N}\}.\\ 1 &{} \text {else} \end{array}\right. } \end{aligned}$$

Now choose $(N_i,K_i, i \in \mathbb {N})$ such that

$$\begin{aligned} \frac{N_1 +\ldots +N_i}{K_i} \le \tfrac{1}{i} \text { and } \frac{K_1 + \ldots + K_i}{ N_{i+1}} \le \tfrac{1}{i}. \end{aligned}$$

Note that $\textsf{F}_t \overset{w}{\rightarrow }\ \delta _1$, but if $v_\infty < v_1$

XII

(Irregular + $\exists \,w^{+1}$-$\lim \textsf{F}_t$) In this example we construct an unbounded irregular sequence for which $(\textsf{F}_t, t \ge 0)$ converges in $w^{+1}$. In particular, from item (a) of Proposition 3.2 it follows that this limit must be $\delta _0$. Let $(A_i, i \in \mathbb {N})$ be an auxiliary sequence to be defined later. Informally, this is constructed as a combination of Example V and Example XI, where we intercalate an irregular unbounded sequence with a large number of increments of small mass. Formally, let ${\textbf {m}}'$ be the sequence defined in Example XI set $\tau (1) {:}{=} 1$ and for $j >1$ set $\tau (j) {:}{=} \tau (j-1) + A_j$. Now let

$$\begin{aligned} m_k: = {\left\{ \begin{array}{ll} m'_j &{}\text { if } j \in \{\tau (j):j \in \mathbb {N}\}.\\ 2^{-k}&{} \text {else} \end{array}\right. } \end{aligned}$$

(4.8)

Finally choose $A_i$ such that

$$\begin{aligned} \frac{1 + \sum _{k= 1}^{i+1}m'_k }{A_i} < \frac{1}{i}. \end{aligned}$$

Since $\sum _{k = 1}^\infty 2^{-k} = 1$ it follows that

$$\begin{aligned} \int m \text {d}F_t(m) \le \frac{1 + \sum _{k = 1}^{\ell _t} m'_k }{\ell _t} \rightarrow 0, \quad \text {as } t \rightarrow \infty , \end{aligned}$$

and therefore $\textsf{F}_t\overset{L^1}{\rightarrow }\delta _0$. Furthermore, the mass measure $\mu _t$ associated with the sequence $(m_k, k \in \mathbb {N})$ defined in (4.8) and the mass measure $\mu '_t$ associated with the sequence $(m'_k, k \in \mathbb {N})$ defined in Example XI satisfy for any bounded continuous function $f: \bar{\mathbb {R}}_+ \rightarrow \mathbb {R}$

$$\begin{aligned} \int f(m) \text {d}\mu _t(m) = \frac{\sigma (t)}{t}\int f(m) \text {d}\mu '_{\sigma (t)}(m) + \sum _{k = 1}^{\ell _t - 1} \mathbb {1}_{k \notin \{\tau (j) :j \in \mathbb {N}\}} f(2^{-k}) \frac{2^{-k}}{t}\nonumber \\ \end{aligned}$$

(4.9)

where $\sigma (t): = \sum _{k = 1}^{\ell _t -1} m_k \mathbb {1}_{k \in \{\tau (j):j \in \mathbb {N}\}}$ counts the mass of increments of the original sequence. Since $\sum _{k = 1}^\infty 2^{-k}$ it follows that $\left| \sigma (t) - t \right| \le 1$ and by (4.9) it follows that

$$\begin{aligned} \begin{aligned} \liminf \int v_m \text {d}\mu _t(m)&= \liminf \int v_m \text {d}\mu '_t(m)\quad \text { and }\\ \limsup \int v_m \text {d}\mu _t(m)&= \limsup \int v_m \text {d}\mu '_t(m). \end{aligned} \end{aligned}$$

As in Example XI, if $v_\infty < v_1$

For completeness, we include the following example which contains an irregular unbounded mass sequence for which the empirical measure does not converge weakly.

XIII

(Irregular + $\not \exists \,$ w-$\lim \textsf{F}_t$) To construct a sequence ${\textbf {m}}$ that is irregular and such that $\textsf{F}_t$ does not converge weakly, take the sequence defined in Example III, and replace the k-th increment of size 1 by the k-th increment of the sequence defined in XI, which itself is irregular. More precisely, let $(m'_k, k \in \mathbb {N})$ be the sequence from Example III, let $(\mu '_t, t \ge 0)$ be its empirical mass measure and let $(\textsf{F}'_t, t \ge 0)$ be its empirical mass frequency. Let the sequence $(m''_k, k \in \mathbb {N})$ be the sequence from Example XI, let $(\mu ''_t, t \ge 0)$ be its empirical mass measures and let $(\textsf{F}''_t, t \ge 0)$ be its empirical mass frequencies. We define

$$\begin{aligned} m_k ={\left\{ \begin{array}{ll} m_k' &{}\text { if } m_k' \ne 1\\ m_{N(k)}'' &{}\text { if } m_k' = 1\\ \end{array}\right. }, \end{aligned}$$

where $N(k) = \#\{j \le k :m'_k = 1\}$. Let $(\mu _t, t \ge 0)$ be the empirical mass measures and $(\textsf{F}_t, t \ge 0)$ be the empirical mass frequencies associated with $(m_k, k \in \mathbb {N})$. Recall that the sequence $(\mu ''_t, t \ge 0)$ admits different $w\text {-} \lim$ along different sub-sequences and therefore is irregular. Since $\sum _{k} m'_k \mathbb {1}_{\{m'_k \ne 1\}} < \infty$ it follows that $(\mu _t, t \ge 0)$ has the same sub-sequential w-limits as $(\mu ''_t, t \ge 0)$. This implies that ${\textbf {m}} = (m_k, k \in \mathbb {N})$ is also irregular. Finally, since $m''_k \ge 1$ it follows that

$$\begin{aligned} \begin{aligned} \limsup _t \textsf{F}'_t([0,1/2])&= \limsup _t \textsf{F}'_t([0,1/2]) \ge 3/4 \quad \text { and}\\ \liminf _t \textsf{F}'_t([0,1/2])&= \liminf _t \textsf{F}'_t([0,1/2])\le 1/4. \end{aligned} \end{aligned}$$

This allows us to conclude that ${\textbf {m}}$ is both irregular and its empirical mass frequencies do not admit a w-$\lim$.

4.4 Random Masses

In this section consider random mass sequences ${\textbf {m}}$. More specifically, we let $(m_k, k \in \mathbb {N})$ be an i.i.d. sequence of random variables, independent of $\mathbb {X}$, each distributed according to a measure $\nu$ on $\mathbb {R}_+$. There are two cases depending on weather $\nu$ has finite or infinite mean.

XIV

(Regular + (un) bounded + $\exists \,w^{+1}$-$\lim \textsf{F}_t$( Assume that $\nu (\{0\}) = 0$ and assume that $\int m\text {d}\nu (m)<\infty$. Now, let the increments $(m_k, k \in \mathbb {N})$ be i.i.d random variables with law $\nu$. By the Glivenko-Cantelli Theorem [8, Theorem 2.4.9] it follows that almost surely $(\textsf{F}_t([0,x]), t \ge 0)$ converges (uniformly in x) to $\nu ([0,x]){=}{:} F_*([0,x])$. By the classical LLN for i.i.d. random variables, almost surely, $\int m \text {d}\textsf{F}_t(m) \rightarrow \int m \text {d}\nu (m)<\infty$. Therefore the conditions of (3.13) are satisfied almost surely and so $\mathbb {P}(\textsf{F}_t \overset{w^{+1}}{\rightarrow } \textsf{F}_*) = 1$. By item (a) of Proposition 3.2 it follows that $\mathbb {P}\big (\mu _t \xrightarrow []{w} \nu \big ) = 1$. Therefore, almost surely, the sequence $\textbf{m}$ is regular and

XV

(Regular + Cesàro + $\exists \,w$-$\lim F_t$ ) Now, assume that $\int m \text {d}\nu (m) = \infty$ and again let the terms of $(m_k, k \in \mathbb {N})$ be sampled independently from $\nu$. In this case

$$\begin{aligned} \mathbb {P}\left( \frac{m_1 + \ldots + m_k }{k} \rightarrow \infty \right) =1. \end{aligned}$$

(4.10)

Then note that after k increments, the mass of increments of size smaller than $a>0$, $\mu _t([0,a])$, is bounded by $\frac{ka}{m_1 + \ldots + m_k}$ and therefore, by (4.10), for any $a>0$, almost surely $\mu _t([0,a]) \rightarrow 0.$ This implies that $\mathbb {P}(\mu _t \overset{w}{\rightarrow }\ \delta _{\infty })=1$ and therefore

5 Proofs of the Main Theorems

5.1 Weak Law of Large Numbers: Proof of Theorem 2.1

5.1.1 Proof Description

Our weak LLN is very similar to the weak LLN for sums of weighted independent random variables that can be found in [11]. The main difference in our proof is that we do not assume $m_n/M_n \rightarrow 0$. This condition is replaced by the concentration assumptions (W1) and (W2) which allows us to include the case $\limsup _n m_n/M_n >0$. We rely on this concentration assumption in the first step of the proof. Afterwards, we are following the strategy in [11] which we give here for completeness and corresponds to the second and final steps summarized below.

• First step: uniform bound on the increments We use the concentration assumptions (W1) and (W2) to restrict our analysis to the increments of bounded magnitude.

• Second step: truncation and equivalence We truncate the random variables $X_k(m_k)$ according to their relative weights at level n, i.e. we consider the truncation

  $$\begin{aligned} Y_{k,n}: = X_k(m_k) \mathbb {1}_{\big \{\left| X_k(m_k) \right| >M_n/m_k\big \}}. \end{aligned}$$

  Then we show that the weak LLN for truncated random variables is the same as the weak LLN for the original random variables.

• Final step: convergence of the mean and the variance We prove that the mean and variance of the sum of weighted truncated random variables both go to zero in the limit and conclude the proof.

Remarks 5.1

The key technical step in this proof, contained in Lemma 5.1, gives the asymptotic equivalence of the truncated random variables and the original terms in the second step. Moreover, the second part of the lemma gives control on the limit variance of the truncated terms.

5.1.2 First Step: Uniform Bound on the Increments

For each $K>0$, let $S^K_n$ represent the contribution to $S_n$ coming from the increments larger than K, i.e.

$$\begin{aligned} S^K_n {:}{=} \sum _{k = 1}^n \frac{m_k}{M_n} X_{k}(m_k) \mathbb {1}_{\{m_k>K\}}. \end{aligned}$$

Now note that due to (W1) and (W2) it follows that

$$\begin{aligned} \lim _{K \rightarrow \infty }\sup _{m>K}\sup _k\mathbb {E}\left[ \left| X_k(m) \right| \right] =0. \end{aligned}$$

(5.1)

Indeed, for any $\varepsilon >0$ and any $A>\varepsilon$

$$\begin{aligned} \begin{aligned} \mathbb {E}\left[ \left| X_k(m) \right| \right]&\le \varepsilon + A\, \mathbb {P}(\varepsilon < \left| X_k(m) \right| \le A) + \mathbb {E}\left[ \left| X_k(m) \right| \mathbb {1}_{\big \{\left| X_k(m) \right| >A\big \}} \right] . \end{aligned} \end{aligned}$$

the right hand side above can be bounded by $3 \varepsilon$ using (W1) and (W2) and since $\varepsilon >0$ is arbitrary, (5.1) follows. Now let ${\bar{S}}^K_n: = S_n - S^K_n$ be the contribution to $S_n$ coming from the increments smaller than K. By the triangle inequality and the union bound it follows that

$$\begin{aligned} \mathbb {P} \left( \left| S_n \right|> \varepsilon \right) \le \mathbb {P} \left( \left| S^K_n \right| + \left| {\bar{S}}^K_n \right|> \varepsilon \right) \le \mathbb {P} \left( \left| S^K_n \right|> \frac{\varepsilon }{2} \right) + \mathbb {P} \left( \left| {\bar{S}}^K_n \right| >\frac{ \varepsilon }{2} \right) . \end{aligned}$$

As $\sum _{k = 1}^n \frac{m_k}{M_n} \mathbb {1}_{\{m_k>K\}} \le 1$, (5.1) and Markov’s inequality imply

$$\begin{aligned} \limsup _{K \rightarrow \infty } \mathbb {P} \left( S^K_n> \varepsilon \right) =0, \end{aligned}$$

and therefore,

$$\begin{aligned} \limsup _{n \rightarrow \infty } \mathbb {P} \left( \left| S_n \right|> \varepsilon \right) \le \inf _{K}\limsup _{n\rightarrow \infty }\mathbb {P} \left( \left| {\bar{S}}^K_n \right| >\frac{ \varepsilon }{2} \right) . \end{aligned}$$

It remains to prove that the right-hand side above goes to zero for arbitrary $\varepsilon >0$.

5.1.3 Second Step: Truncation and Equivalence

We show that (2.1) is equivalent to a limit statement for truncated random variables. We consider the following truncation

$$\begin{aligned} Y_k(m_k){:}{=}X_k(m_k)\mathbb {1}_{\big \{\left| X_k(m_k) \right|< \frac{M_n}{m_k}\big \}}\mathbb {1}_{\{m_k<K\}}, \end{aligned}$$

and notice that as $M_n \rightarrow \infty$,

$$\begin{aligned} \lim _n \max _{1 \le k \le n} \frac{m_k}{M_n} \mathbb {1}_{\{m_k<K\}} = 0. \end{aligned}$$

(5.2)

Set ${\bar{s}}^K_n {:}{=}\sum _{k =1}^n \frac{m_k}{M_n}Y_n(m_k)$. We will first argue that this truncated sum ${\bar{s}}^K_n$ approximates well ${\bar{S}}^K_n$, and then show that its variance vanishes. To perform these two steps we will need the following lemma, whose proof is postponed to the end of this section and is an adaptation of the ideas in the proof Theorem 1 in [11].

Lemma 5.1

(Control over truncation) If (C), (W1), and (W2) hold true, then

$$\begin{aligned} \lim _{n \rightarrow \infty } \max _{1 \le k \le n}\frac{M_n}{m_k} \mathbb {P}\left( \left| X_k(m_k) \right| \mathbb {1}_{\{m_k<K\}}\ge \frac{M_n}{m_k} \right) =0, \end{aligned}$$

(5.3)

and

$$\begin{aligned} \lim _{n \rightarrow \infty } \max _{1 \le k \le n}\frac{m_k}{M_n}\mathbb {E}\left[ Y^2_k(m_k) \right] = 0. \end{aligned}$$

(5.4)

By the union bound, the definition of $Y_k(m_k)$, using that $\sum _{k} \frac{m_k}{M_n} \le 1$ we have that

$$\begin{aligned} \begin{aligned}&\limsup _n \mathbb {P}\left( {\bar{S}}^K_n \ne {\bar{s}}^K_n \right) \le \limsup _n \sum _{k = 1}^n \mathbb {P}\left( X_k(m_k)\mathbb {1}_{\{m_k<K\}}\ne Y_k(m_k) \right) \\&\quad = \limsup _n\sum _{k = 1}^n \mathbb {P} \left( \left| X_k(m_k) \right| \mathbb {1}_{\{m_k<K\}}\ge \frac{M_n}{m_k} \right) \\&\quad \le \limsup _n \max _{1 \le k \le n} \frac{M_n}{m_k} \mathbb {P}\left( \left| X_k(m_k) \right| \mathbb {1}_{\{m_k<K\}}\ge \frac{M_n}{m_k} \right) \sum _{k=1}^n \frac{m_k}{M_n}\\&\quad \le \limsup _n \max _{1 \le k \le n} \frac{M_n}{m_k} \mathbb {P}\left( \left| X_k(m_k) \right| \mathbb {1}_{\{m_k<K\}}\ge \frac{M_n}{m_k} \right) , \end{aligned} \end{aligned}$$

the latter can be made arbitrary small via (5.3). Hence it suffices to consider ${\bar{s}}^K_n$ instead of ${\bar{S}}^K_n$. We next control the mean and the variance of ${\bar{s}}^K_n$.

5.1.4 Final Step: Convergence to Zero of the Mean and the Variance

The mean As $(X_k(m_k), k \in \mathbb {N})$ is a uniformly integrable family of centred random variables, by (5.2) it follows that $\limsup _n \sup _{k} \mathbb {E}\left[ \left| Y_{k}(m_k) \right| \right] =0$, and so we obtain that

$$\begin{aligned} \lim _n\mathbb {E}\left( {\bar{s}}^K_n \right) = \lim _n \sum _{k = 1}^n \frac{m_k}{M_n}\mathbb {E}[Y_k(m_k)]= 0. \end{aligned}$$

The Variance By independence and (5.4) we obtain

$$\begin{aligned} \begin{aligned} \limsup _n\text {Var}\left( {\bar{s}}^K_n \right)&= \limsup _n \sum _{k=1}^n \frac{m_k^2}{M_n^2} \text {Var}(Y_k(m_k))\\&\le \limsup _n \sum _{k=1}^n \frac{m_k}{M_n} \max _{1 \le k \le n}\frac{m_k}{M_n}\text {Var}(Y_k(m_k))\\&\le \limsup _{n} \max _{1 \le k \le n}\frac{m_k}{M_n}\mathbb {E}\left[ Y^2_k(m_k) \right] = 0. \end{aligned} \end{aligned}$$

(5.5)

Finally, $\lim _n\mathbb {E}\left( {\bar{s}}^K_n \right) =0$ together with (5.5) and Chebyshev’s inequality yield

$$\begin{aligned} \limsup _{n}\mathbb {P} \left( {\bar{s}}^K_n \ge \varepsilon \right) \le \limsup _n\frac{4}{\varepsilon ^2}\text {Var}\left( {\bar{s}}^K_n \right) =0. \end{aligned}$$

$\square$

5.1.5 Proof of Lemma 5.1

Let ${\overline{T}}_n: = \inf _{1 \le k \le n} \frac{M_n}{m_k}\mathbb {1}_{\{m_k<K\}}$. Since $\lim _n {\overline{T}}_n = \infty$, equation (5.3) follows from (W2) as

$$\begin{aligned} \lim _n \frac{M_n}{m_k} P\left( \left| X_k(m_k) \right| \mathbb {1}_{\{m_k<K\}}\ge \frac{M_n}{m_k} \right) \le \lim _n \mathbb {E}\left[ \left| X_k(m_k) \right| \mathbb {1}_{\big \{\left| X_k(m_k) \right| \ge {\overline{T}}_n\big \}} \right] = 0. \end{aligned}$$

To prove (5.4), let $F_{k,m}(a): = \mathbb {P}(\left| X_k(m) \right| <a)$ and note first that integration by parts yields

$$\begin{aligned} \begin{aligned}&\int _0^T x^2 \,\text {d}F_{k,m}(x) = T^2 \mathbb {P}(\left| X_k(m) \right|<T) - 2 \int _0^T x \mathbb {P}(\left| X_k(m) \right| <x)\, \text {d}x\\&\quad = T^2 \left[ 1 - \mathbb {P}(\left| X_k(m) \right| \ge T) \right] - 2 \int _0^T x \left[ 1-\mathbb {P}(\left| X_k(m) \right| \ge x) \right] \, \text {d}x\\&\quad = -T^2 \mathbb {P}(\left| X_k(m) \right| \ge T) + 2 \int _0^T x \mathbb {P}(\left| X_k(m) \right| \ge x)\, \text {d}x. \end{aligned} \end{aligned}$$

(5.6)

Observe further that by the uniform integrability (W2)

$$\begin{aligned} \lim _{x \rightarrow \infty }\sup _{k,m} x \mathbb {P}(\left| X_k(m) \right| \ge x) = 0. \end{aligned}$$

(5.7)

Finally, since $\lim _n {\overline{T}}_n = \infty$, by (5.6), and (5.7), we have that

$$\begin{aligned} \begin{aligned}&\limsup _n \sup _{k,m}\frac{1}{{\overline{T}}_n}\int _0^T x^2 \,dF_{k,m_k}(x)\\&\quad =\limsup _n \sup _{k,m}\bigg (-{\overline{T}}_n \mathbb {P}(\left| X_k(m_k) \right| \ge {\overline{T}}_n) + 2 \int _0^{{\overline{T}}_n} \frac{x}{{\overline{T}}_n} \mathbb {P}(\left| X_k(m_k) \right| \ge x)\, \text {d}x\bigg ) = 0. \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \int _0^{\frac{M_n}{m_k}} x^2 \,dF_{k,m_k}(x) = \mathbb {E}\left[ Y^2_k(m_k) \right] , \end{aligned}$$

it follows that

$$\begin{aligned} \lim _{n \rightarrow \infty } \max _{1 \le k \le n}\frac{m_k}{M_n} \mathbb {E}\left[ Y^2_k(m_k) \right] \le \lim _{n\rightarrow \infty } \sup _{k,m} \frac{1}{{\overline{T}}_n}\int _0^{{\overline{T}}_n} x^2 \,dF_{k,m_k}(x) = 0. \end{aligned}$$

$\square$

5.2 Strong Law for the Incremental Sum: Proof of Theorem 2.2

5.2.1 Proof Description

The proof of Theorem 2.2 is a combination of the ideas in [1] with the convergence criterion in [15]. As in [1], our proof here relies on an iterative scale decomposition into “small” and “big” increments. At each scale, the small contribution is defined as the truncated sum that, thanks to the stochastic domination assumption (S2), can be dealt with the techniques of [15]. What is left, classified as “big”, is again split (in the next scale) into a “small” and a “big”. At this level, the small one is controlled in the same way as before. The iteration proceeds until we reach a scale where the condition (S1) is sufficient to ensure convergence. Here is a summary of the main steps.

• First step: recursive decomposition We first iteratively decompose the sum $S_n$ into a finite number of sums of relatively small increments and one sum of large increments.

• Second step: the large increments We show that the large increment sum converges to zero almost surely using (S1).

• Final step: the small increments Using results from [15] we prove that each of the small increments also converge to zero almost surely. For the proof one needs to consider the uniformly bounded increments and slow growing increments. The uniformly bounded increments are harder to treat because they don’t fit exactly into the hypothesis of Theorem 2 in [15]. Hence we need a subtler control as stated in Lemma A.1 whose proof is postponed to Appendix A.

Remarks 5.2

The convergence criterion of Theorem 2 in [15] is an extension of Theorem 2 in [13]. The extension fits our framework exactly as it allows one to obtain a.s. convergence of weighted sums of independent random variables that satisfy condition (S2). Importantly, the sums are weighted by coefficients $(a_{n,k}, k,n \in \mathbb {N})$ of a Toeplitz summation matrix, just as in our setup. The idea of the proof in [13] is to perform a truncation, to show equivalence of the truncated and the original sum, and finally to prove a.s. convergence for the truncated sum.

5.2.2 First Step: Recursive Decomposition

We take $\delta$ from (S1) and $\gamma$ from (S2) and fix $K = K(\delta ,\gamma ) \in \mathbb {N}$ such that

$$\begin{aligned} \delta K> 1, \quad \text { and } \quad 1 + \frac{K}{K-1}< 2 + \gamma . \end{aligned}$$

(5.8)

Now, we let ${\textbf {N}}^0 {:}{=} \mathbb {N}$, and let

$$\begin{aligned} {\textbf {N}}^{0,s}: = \left\{ j \in {\textbf {N}}^0 :m_j \le 1\right\} , \end{aligned}$$

(5.9)

and ${\textbf {N}}^1{:}{=}{} {\textbf {N}}^0 \setminus {\textbf {N}}^{0,s}$. Assume that for some $i \ge 1$ the set ${\textbf {N}}^i$ is given, if ${\textbf {N}}^i$ is finite, then we set ${\textbf {N}}^{j},{\textbf {N}}^{j,s} = \emptyset$ for all $j >i$, if ${\textbf {N}}^i$ is infinite, let $k^i:\mathbb {N} \rightarrow {\textbf {N}}^i$ be an increasing map with $k^i(\mathbb {N}) = {\textbf {N}}^i$, with the notation $k^i_j = k^i(j)$, define the (i)-st small increments by

$$\begin{aligned} {\textbf {N}}^{i,s} {:}{=} \{\,k^{i}_j \in \mathbb {N} :m_{k^{i}_j} < j^{i/K}\,\}, \end{aligned}$$

let $k^{i,s}: \mathbb {N} \rightarrow {\textbf {N}}^{i,s}$ be an increasing map with $k^{i,s}(\mathbb {N}) = {\textbf {N}}^{i,s}$ and denote $k^{i,s}_j= k^{i,s}(j)$. Now define the next level (large) increments ${\textbf {N}}^{i+1}{:}{=}{} {\textbf {N}}^i \setminus {\textbf {N}}^{i,s}$. We let the cardinality of increments in ${\textbf {N}}^i$ and ${\textbf {N}}^{i,s}$ with indices less than n be denoted by

$$\begin{aligned} J(i;n): = \#\{\,j \in {\textbf {N}}^{i}:j \le n\,\} \quad \text { and } \quad J(i,s;n): = \#\{\,j \in {\textbf {N}}^{i,s}:j \le n\,\}. \end{aligned}$$

We set $X_k {:}{=} X_{k}(m_k)$, $a^i_{n,j}: = \frac{m_{k^i_j}}{M_n}$, $a^{i,s}_{n,j} = \frac{m_{k^{i,s}_j}}{M_n}$, and $\kappa = K^2 + 1$. Since $\mathbb {N} = \bigcup _{i=0}^{\kappa - 1} {\textbf {N}}^{i,s}\cup {\textbf {N}}^{\kappa }$, we obtain

$$\begin{aligned} \begin{aligned} S_n&= \sum _{i=1}^{\kappa }\sum _{j \in {\textbf {N}}^{i,s}}\mathbb {1}_{\{j \le n\}} a_{n,j} X_{k^{i,s}_j}+ \sum _{j \in {\textbf {N}}^{\kappa }}\mathbb {1}_{\{j \le n\}} a_{n,j} X_{k^\kappa _j}\\&= \sum _{i=1}^{\kappa }\underbrace{\sum _{j=1}^{J(i,s;n)} a^{i,s}_{n,j} X_{k^{i,s}_j}} + \underbrace{\sum _{{j=1} }^{J({\kappa };n)}a^{\kappa }_{j,n} X_{k^\kappa _j}}\\&=\sum _{i=1}^{\kappa } S_n^{i,s} + S_n^{\kappa }. \end{aligned} \end{aligned}$$

(5.10)

In what follows we show that

$$\begin{aligned} \mathbb {P}\big ( \limsup _n \left| S_n^{\kappa } \right|= & {} 0\big )=1, \hspace{4cm} \end{aligned}$$

(5.11)

$$\begin{aligned} \mathbb {P}\big (\limsup _n \left| S_n^{i,s} \right|= & {} 0\big )=1, \quad \text { for } i\in \{0,1,\ldots , \kappa \}. \end{aligned}$$

(5.12)

5.2.3 Second Step: the Large Increments Sum

To prove (5.11) it is enough to show that for any $\varepsilon > 0$

$$\begin{aligned} \mathbb {P}\big (\limsup _n \left| S_n^{\kappa } \right| \le \varepsilon \big )=1 . \end{aligned}$$

(5.13)

By (S1), and the fact that $m_{k^{\kappa }_j}\ge j^K$, it follows that there is $C = C(\varepsilon )$ such that

$$\begin{aligned} \mathbb {P}\left( \left| X_{k^{\kappa }_j} \right| >\varepsilon \right) \le \frac{C}{(m_{k^{\kappa }_j})^\delta }\le \frac{C}{j^{K\delta }}. \end{aligned}$$

Since $K \delta >1$, it follows that $\sum _{j=1}^\infty \mathbb {P}(X_{k^{\kappa }_j}>\varepsilon ) <\infty$, and so, by the Borel–Cantelli Lemma,

$$\begin{aligned} \mathbb {P}\left( \limsup _j \left| X_{k^{\kappa }_j} \right| \le \varepsilon \right) =1. \end{aligned}$$

As $M_n \rightarrow \infty$ and $\sum _{j=1}^{J({\kappa },n)}m_{k^{\kappa }_j} \le M_n$, we conclude that (5.13) holds.

5.2.4 Final Step: the Small Increment Sums

The proof of (5.12) will be split in two parts, first we prove it for $i \ge 1$ and then we treat the case $i = 0$. To ease notation, for fixed $i \in \mathbb {N}$ and any $j,J \in \mathbb {N}$ set

$$\begin{aligned} {\tilde{m}}_j {:}{=}m_{k^{i,s}_j}, \quad {\tilde{M}}_J: = \sum _{j = 1}^ J {\tilde{m}}_j, \quad {\tilde{a}}_{j,J}: = \frac{{\tilde{m}}_j}{{\tilde{M}}_J}\mathbb {1}_{j\le J}, \quad \text {and let} \quad {\tilde{S}}_J = \sum _{j = 1}^ J {\tilde{a}}_{j,J} X_{k^{i,s}_j}. \end{aligned}$$

Now note that for any n

$$\begin{aligned} S^{i,s}_{n} = \frac{{\tilde{M}}_{J(i,s;n)}}{M_n}{\tilde{S}}_{J(i,s;n)}. \end{aligned}$$

As $\frac{{\tilde{M}}_{J(i,s;n)}}{M_n} \le 1$, it follows that $\limsup _n \vert {S^{i,s}_n}\vert \le \limsup _J \vert {{\tilde{S}}_J}\vert$. Therefore, it suffices to show that

$$\begin{aligned} \mathbb {P}\left( \limsup _J \left| {\tilde{S}}_J \right| = 0 \right) =1. \end{aligned}$$

(5.14)

Now note that, with the convention $k^0_j {:}{=} j$, for $i \ge 1$, we have that $k^{i,s}_j = k^{i-1}_{j'}$ with $j'\ge j$. This gives us the following upper and lower bound on $m_{k^{i,s}_j}$

$$\begin{aligned} j^{(i-1)/K} \le j'^{(i-1)/K} \le m_{k^{i-1}_{j'}}= m_{k^{i,s}_j} \le , j^{i/K}. \end{aligned}$$

(5.15)

Therefore, there are $C,c>0$ for which

$$\begin{aligned} {\tilde{M}}_{J} \ge cJ^{1 +( i-1)/K}, \qquad {\tilde{a}}_{j,J}\le \frac{C}{ J^{\frac{K-1}{K} }}. \end{aligned}$$

(5.16)

Now, as $\lim _J {\tilde{a}}_{j,J} = 0$, $\sum _{j} {\tilde{a}}_{j,J} =1$, and conditions (5.16) and (S2) hold. By the choice of K and (5.8), one can apply Theorem 2 in [15] with $\nu =\frac{K-1}{K}$ to obtain (5.14) and therefore (5.12) for $i \ge 1$. To conclude the proof of Theorem 2.2 it remains to verify that $S^{0,s}_n$ converges to 0 almost surely. This fact is given in Lemma A.1 in Appendix A and its proof is an adaptation of Theorem 4 in [11]. $\square$

5.3 Strong Law for the Gradual Sum: Proof of Theorem 2.3

5.3.1 Proof Description

As previously, we start with a summary of the main steps of the proof.

• First step: reduction to boundary terms In this step we reduce the problem o convergence of the sum from (2.3) to the study of the limit of the boundary term.

• Second step: oscillation control of small increments In this step we define a notion of “small increments” ($m_{k+1} < \alpha _k M_k$) and show (5.17) for them. The notion of “small increments” is defined in such a way that one can control the oscillations using Borel–Cantelli argument on the estimates obtained from condition (S3). The terms that do not fit into the notion of “small increments” are considered to be the “large” ones.

• Final step: oscillation control of large increments In this step we show (5.17) for the complement set, the “large increments”. The definition of small increments, given by the choice of $\alpha _k$ in the second step, ensures that the “large increments” still grow as a stretched exponential. The oscillation control condition (S3) does not give good bounds for large increments. This requires us to proceed into two stages. First, in a passage called pinning, we prove that the boundary terms converges to zero along a subsequence. For this passage, we use the polynomial decay condition (S1). Finally, in the passage called oscillations, we prove the values between the subsequence also converge to zero using condition (S3).

5.3.2 First Step: Reduction to Boundary Terms

Recall the decomposition of from (2.3). We note that is a convex combination of $S_{\ell _t}$ and the boundary term $X_{\ell _t}({\bar{t}})$ with ${\bar{t}} = t - M_{\ell _t}$. By the proof of Theorem 2.2, to prove Theorem 2.3, it remains to show that the boundary term vanishes, i.e.

$$\begin{aligned} \mathbb {P}\left( \lim _t \frac{{\bar{t}}}{t} X_{\ell _t} ({\bar{t}}) = 0 \right) =1. \end{aligned}$$

(5.17)

We divide the proof of (5.17) in two steps.

5.3.3 Second Step: The Small Increments

Let $V_n = \sup \big \{\frac{s}{(M_n + s)}\big \vert X_{n+1}(s)\big \vert :s \in [0,m_{n+1}) \big \}$ and note that

$$\begin{aligned} \limsup _t \frac{{\bar{t}}}{t}X_{\ell _t}({\bar{t}}) = \limsup _n V_n. \end{aligned}$$

(5.18)

Thanks to condition (S3), we can control the oscillations $V_n$ for small increments that satisfy a growth condition defined as follows. Fix a $\beta >1$ and for which the condition in (S3) holds, fix $a \in (\beta ^{-1},1)$, and for $j \in \mathbb {N}$, let

$$\begin{aligned} \alpha _j = \frac{1}{j^a}. \end{aligned}$$

The first small increment is defined by

$$\begin{aligned} k_1': = \inf \{k \in \mathbb {N} :M_{k+1} < (1 + \alpha _1) M_k\}, \end{aligned}$$

and define recursively the j-th small increment by

$$\begin{aligned} k'_{j+1} {:}{=} \inf \{\,k \in \mathbb {N} :k > k'_j, \quad M_{k+1} < (1 + \alpha _{j+1}) M_k \,\}. \end{aligned}$$

If for some $j, k'_{j} = \infty$ this implies there are only finitely many small increments and we do not need to worry about them in (5.18). If for all $j, k_{j}' < \infty$, we claim that almost surely

$$\begin{aligned} \limsup _j V_{k'_j} = 0. \end{aligned}$$

Indeed, as $m_{k'_j + 1}< \alpha _j M_{k'_j}$, by (S3), with $r= 0$, it follows that for any $\varepsilon >0$ there is $C_\varepsilon >0$ for which

$$\begin{aligned} \mathbb {P}(V_{k'_j}> \varepsilon ) \le \mathbb {P}\left( \sup _{s\le \alpha _j M_{k'_j}} s\vert X_{k'_j}(s)\vert >\varepsilon M_{k'_j} \right) \le C_\varepsilon \alpha _j^\beta . \end{aligned}$$

Since $\alpha _j = j^{-a}$ with $a > \beta ^{-1}$, by the Borel–Cantelli lemma we obtain

$$\begin{aligned} \quad \mathbb {P} \left( \limsup _j V_{k'_j} \le \varepsilon \right) = 1, \end{aligned}$$

(5.19)

and since $\varepsilon >0$ is arbitrary, we conclude that

$$\begin{aligned} \mathbb {P} \left( \lim _j V_{k'_j} =0 \right) = 1. \end{aligned}$$

(5.20)

$\square$

5.3.4 Final Step: The Large Increments

By (5.20) we can restrict our attention to $\{\,k^*_1,k^*_2,\ldots \,\}= \mathbb {N}{\setminus } \{\,k'_1, k'_2, \ldots \,\}$. Note that since $\alpha _j = j^{-a} \in (0, 1)$, with $a \in (0,1)$ there is some $C>0$ for which

$$\begin{aligned} (1 + \alpha _j) \ge C \exp (\alpha _j/2). \end{aligned}$$

(5.21)

Therefore, for some $c_a>0$ the following growth condition holds

$$\begin{aligned} M_{k_{i}^*}\ge \prod _{j=1}^i(1 + \alpha _j)M_1 \ge C\exp \left( \sum _{j=1}^i\frac{ \alpha _j}{2}\right) M_1 \ge \exp (c_ai^{1-a})M_1, \text { for all } i \in \mathbb {N}.\nonumber \\ \end{aligned}$$

(5.22)

The proof now proceeds in two steps, we first show that the boundary term $\frac{{\bar{t}}}{t} X_{\ell _t}({\bar{t}})$ converges to zero along a subsequence $\big \{t_{i,j}, i,j \in \mathbb {N}\cup \{0\}\big \}$, what we call pinning, and then based on this result we show that the full sequence converges to zero as we bound its oscillations on the intervals $[t_{i,j}, t_{i,j+1}]$.

Pinning We consider a subsequence that growth with rate $\big ((1 + \alpha _k), k \in \mathbb {N}\big )$. Consider the set $\{\,k^*_1,k^*_2,\ldots \,\}$, let $k^*_0 {:}{=} i(k^*_0) = 0$ and define recursively for $n\in \mathbb {N}$

$$\begin{aligned} i(k^*_{n}){:}{=} \inf \left\{ i> i(k^*_{n-1}) :\prod _{j = i(k^*_{n-1})}^i (1 + \alpha _j)M_{k^*_n} > M_{k^*_n + 1}\right\} . \end{aligned}$$

We note that (5.21) and $\sum _j \alpha _j = \infty$ imply that $i(k^*_n)< \infty$ for all n. We define the pinning sequence as follows: first let $t_{i,0}: = k^{*}_{i}$ and for $j\in \{1, \ldots , i(k^*_i) - i(k^{*}_{i-1})\}$ set

$$\begin{aligned} t_{i,j} {:}{=} {\left\{ \begin{array}{ll} (1+\alpha _{i(k^*_{i-1})+ j})t_{i,j-1} &{} \text { if } j < i(k^*_i)- i(k^{*}_{i-1}),\\ M_{k^*_i + 1} &{} \text { if } j = i(k^*_i)- i(k^{*}_{i-1}). \end{array}\right. } \end{aligned}$$

(5.23)

Now, by definition ${\bar{t}} = t - M_{\ell _t -1}$, with $\ell _t$ as in (2.2). By (5.21), it follows that for all $i,j \in \mathbb {N}$

$$\begin{aligned} {\bar{t}}_{i,j} = t_{i,j} - M_{k^*_i}= & {} M_{k^*_i}\bigg [\prod _{n =1}^{j}(1 + \alpha _{i(k^*_{i-1})+n})-1\bigg ] \nonumber \\ {}\ge & {} M_{k^*_i}\left[ C\exp \left( \sum _{n= 1}^j\alpha _{i(k^*_{i-1})+n}/2\right) -1\right] . \end{aligned}$$

(5.24)

By the polynomial decay in (S1) it follows that for any $\varepsilon >0$ there is a $C = C(\varepsilon )>0$ such that for any $i,j \in \mathbb {N}$ we have

$$\begin{aligned} \mathbb {P}\left( \left| \frac{{\bar{t}}_{i,j}}{t_{i,j}}X_{k^*_i}({\bar{t}}_{i,j}) \right| \ge \varepsilon \right) \le \mathbb {P}\left( \left| X_{k^*_i}({\bar{t}}_{i,j}) \right| \ge \varepsilon \right) \le \frac{C_\varepsilon }{\left( {\bar{t}}_{i,j} \right) ^\delta }. \end{aligned}$$

By (5.24) and (5.22), the sum over $i,j\in \mathbb {N}$ of the above probability is finite and therefore for any $\varepsilon >0$

$$\begin{aligned} \mathbb {P}\left( \frac{{\bar{t}}_{i,j}}{t_{i,j}} \left| X_{k^*_i}({\bar{t}}_{i,j}) \right| \ge \varepsilon \text { for infinitely many } (i,j) \right) = 0. \end{aligned}$$

(5.25)

Since $\varepsilon >0$ is arbitrary, it follows that

$$\begin{aligned} \mathbb {P}\left( \limsup _{i,j} \frac{{\bar{t}}_{i,j}}{t_{i,j}} \left| X_{k^*_i}({\bar{t}}_{i,j}) \right| =0 \right) = 1. \end{aligned}$$

It remains to control the oscillations of the boundary term in the intervals $[t_{i,j}, t_{i,j+1}]$.

Oscillations Now we use (S3) to compute the oscillations between the pinned values of the boundary. Fix $\varepsilon >0$ and consider the event $\Omega _{i_0}$ defined by

$$\begin{aligned} \Omega _{i_0}{:}{=} \left\{ \sup _j\left| \frac{{\bar{t}}_{i,j}}{t_{i,j}}X_{k^*_i}\left( {\bar{t}}_{k^*_i,j} \right) \right| \le \varepsilon , \quad \text { for } i >i_0 \right\} . \end{aligned}$$

Note that by (5.25) it follows that

$$\begin{aligned} \limsup _{i_0} \mathbb {P}(\Omega _{i_0}) = 1. \end{aligned}$$

(5.26)

On $\Omega _{i_0}$, for $t \in [t_{i,j}, t_{i,j+1}]$, and $j \ge 1$

$$\begin{aligned} \begin{aligned}&\left| \frac{{\bar{t}}}{t} X_{k^*_i}\left( {\bar{t}} \right) -\frac{{\bar{t}}_{i,j}}{t_{i,j}} X_{k^*_i}\left( {\bar{t}}_{i,j} \right) \right| \\&\quad = \left| \frac{1}{t}\left[ {\bar{t}} X_{k^*_i}\left( {\bar{t}} \right) - {\bar{t}}_{i,j} X_{k^*_i}\left( {\bar{t}}_{i,j} \right) \right] + \left( \frac{{t}_{i,j}}{t} - 1 \right) \frac{{\bar{t}}_{i,j}}{t_{i,j}}X_{k^*_i}\left( {\bar{t}}_{i,j} \right) \right| \\&\quad \le \frac{1}{t}\left| {{\bar{t}} X_{k^*_i}\left( {\bar{t}} \right) - {\bar{t}}_{i,j} X_{k^*_i}\left( {\bar{t}}_{i,j} \right) } \right| + \varepsilon . \end{aligned} \end{aligned}$$

(5.27)

Note that if $s: = t - t_{i,j}$ and $t\le t_{i,j+1}$, then ${\bar{t}}\le {\bar{t}}_{i,j} + s$. Note also that from (5.23) we have that $\frac{t_{i,j+1}-t_{i,j}}{t_{i,j}} \le \alpha _{i(k^*_{i-1}),j+1}$. By (5.27) and (S3), it follows that

$$\begin{aligned} \begin{aligned}&\mathbb {P} \left[ \sup _{s \le t_{i,j+1} - t_{i,j} } \left| \frac{{\bar{t}}_{i,j} + s}{t_{i,j} + s}X_{k^*_i}{({\bar{t}}_{i,j} + s)}-\frac{{\bar{t}}_{i,j}}{t_{i,j}}X_{k^*_i}{({\bar{t}}_{i,j})} \right|> 2\varepsilon , \Omega _{i_0} \right] \\&\quad \le \mathbb {P} \bigg [\sup _{s \le t_{i,j+1} - t_{i,j} } \frac{1}{t_{i,j} + s}\left| ({\bar{t}}_{i,j} + s)X_{k^*_i}({\bar{t}}_{i,j} + s)-{\bar{t}}_{i,j} X_{k^*_i}({\bar{t}}_{i,j}) \right| > \varepsilon \bigg ]\\&\quad \le \frac{C_\varepsilon (t_{i,j+1} - t_{i,j})^\beta }{t^\beta _{i,j}} \le \alpha _{i(k^*_{i-1}) +j + 1}C_\varepsilon = \frac{1}{\big (i(k^*_{i-1}) +j + 1\big )^{a \beta }}C_\varepsilon . \end{aligned} \end{aligned}$$

Since $a \in (1/\beta ,1)$, the sum of the above terms over $i\in \mathbb {N}$, $j \in \{1, \ldots , i(k^*_i) - i(k^{*}_{i-1})\}$ is finite, and therefore by (5.26)

$$\begin{aligned} \mathbb {P} \left( \limsup _k V_k \le \varepsilon \right) \ge \limsup _{i_0} \mathbb {P}\left( \limsup _k V_k \le \varepsilon ,\Omega _{i_0} \right) = \limsup _{i_0} \mathbb {P}(\Omega _{i_0})= 1.\nonumber \\ \end{aligned}$$

(5.28)

Since $\varepsilon >0$ is arbitrary, from (5.18), (5.19) and (5.28) we conclude that (5.17) holds. $\square$

A Control of Bounded Increments in Theorem 2.2

To prove the strong law for uniformly bounded increments in Theorem 2.2, we need a different approach from the one used in Sect. 5.2.4. There we obtain from (5.15) decay conditions on the coefficients in the sum of small terms, see (5.16). This allows us to use Theorem 2 in [15]. The case for uniformly bounded increments is different because we do not have a lower bound on the size of the increments and we do not obtain the decay rate in (5.16). To assess this issue we will show the following lemma.

Lemma A.1

If  $\mathbb {X}$ satisfies conditions (C), (S1), and (S2) and $S^{0,s}_n = \sum _{j=1}^n \mathbb {1}_{\{m_j \le 1\}}a_{n,j} X_j$ equivalently, with the notation of (5.9) and (5.10), $S^{0,s}_n =\sum _{j=1}^{J(0,s,n)}a^{0,s}_{n,j} X_{k_j^{0,s}}$ then

$$\begin{aligned} \mathbb {P}(\limsup _{n}\left| S_n^{0,s} \right| = 0 )=1. \end{aligned}$$

(A.1)

The proof of this lemma, given below, follows the ideas in Theorem 4 in [11] and proceeds along the following steps.

• First step: relabelling and proof reduction In this step we simplify the notation and argue that we may ignore the weight of all increments that are larger then 1. We next consider a truncation of the terms in the sum and show that the proof will require showing the equivalence of the truncated sum with the relabelled sum and prove that the truncated sum converges to zero.

• Second step: equivalence of the truncated sum Here we truncate the k-th term by the inverse of the relative weight up to k, $M_k/m_k$ and prove that the truncation is only active for finitely many terms, which implies that the limit of the original terms is the same as the limit of the truncated terms.

• Final step: convergence of the truncated sum We show that the limit of the weighted sum of truncated terms converge to zero almost surely.

1.1 A.1 First step: Relabelling and Proof Reduction

To deal with $i = 0$, the case of small increments defined in (5.9). If $\lim _{n}\sum _{i=1}^n m^{0,s}_n<\infty$ it follows that $S^{0,s}_n$ converges to 0. For this reason assume without loss of generality that

$$\begin{aligned} \lim _n \sum _{i=1}^n m^{0,0}_n \rightarrow \infty . \end{aligned}$$

For a short notation, denote $m_k = m^{0,s}_k$, let $M_n: = \sum _{k = 1}^n m^{0,s}_k$ and let $S_n = \sum a_{n,k} X_k$ where, as before, $a_{n,k} = \frac{m_k}{M_n}$. We next consider the truncated versions of $X_k$

$$\begin{aligned} Y_k: = X_k \mathbb {1}_{\big \{\vert {X_{k}\vert }\le \frac{M_k}{m_k}\big \}}. \end{aligned}$$

We next define ${\bar{S}}_n: = \sum _{k = 1}^n a_{n,k}Y_{k}$ to be the truncated sum. Finally, we reduce the proof of Lemma A.1 to the following two statements:

$$\begin{aligned} \mathbb {P} \left( Y_{k} \ne X_{k} \text { i.o.} \right) = 0, \end{aligned}$$

(A.2)

and

$$\begin{aligned} \mathbb {P} \left( \lim _n{\bar{S}}_n=0 \right) = 1. \end{aligned}$$

(A.3)

The first statement, in (A.2), implies the equivalence of the limits of the original sum and the truncated sum, i.e. it implies that

$$\begin{aligned} \mathbb {P}\left( \lim \left| S_n - {\bar{S}}_n \right| = 0\right) =1. \end{aligned}$$

The final statement, in (A.3) establishes the convergence of ${\bar{S}}_n$ and gives the desired result in (A.1).

1.2 A.2 Second Step: Equivalence of the Truncated Sum

In this Section we prove (A.2). Let $F^*(a): = \mathbb {P}(\left| X^* \right| <a)$, define

$$\begin{aligned} N(x): = \bigg \{k :\frac{M_k}{m_k} \le x \bigg \}, \end{aligned}$$

(A.4)

and note that by the domination in (S2), we have that

$$\begin{aligned} \begin{aligned} \sum _{k} \mathbb {P} \left( Y_{k} \ne X_{k} \right)&\le \sum _k \mathbb {P}\left( \left| X_{k} \right| \ge \frac{M_k}{m_k} \right) \le \sum _k \mathbb {P}\left( \left| X^* \right| \ge \frac{M_k}{m_k} \right) \\&\le \sum _k \int _{x \ge \frac{M_k}{m_k}} \,d F^*(x)= \int N(x) \,dF^*(x) = \mathbb {E}\left[ N(\left| X^* \right| ) \right] . \end{aligned} \end{aligned}$$

To obtain (A.2) it remains to prove that $\mathbb {E}\left[ N(\left| X^* \right| ) \right] <\infty$. This step follows from Lemma 2 of [11] which states that

$$\begin{aligned} \limsup \frac{N(x)}{x \log x}\le 2. \end{aligned}$$

(A.5)

By (A.5), it follows that $N(x) \le C x^{1 + \gamma }$ and by the first part of (S2), $\mathbb {E}\left[ N(\left| X^* \right| ) \right] < \infty$. $\square$

1.3 A.3 Final Step: Convergence of Truncated Sum

In this Section we prove (A.3). Since $\lim _n \mathbb {E}\left[ {\bar{S}}_n \right] = 0$, to prove (A.3) it suffices to show that

$$\begin{aligned} \sum _k \frac{m^2_k}{M^2_k} \text {Var}(Y_{k}) < \infty . \end{aligned}$$

(A.6)

As $\frac{M_k}{m_k} \rightarrow \infty$ there is $C>0$ for which $\mathbb {E}\left[ X_*^2 \right] \le C \int _{\left| x \right| \le \frac{M_k}{m_k}} x^2 \, \text {d}F^*(x)$ and so

$$\begin{aligned} \mathbb {E}\left[ Y_k^2 \right] \le \mathbb {E}\left[ X_*^2 \right] \le C \int _{\left| x \right| \le \frac{M_k}{m_k}} x^2 \, \text {d}F^*(x). \end{aligned}$$

Therefore, the sum in (A.6) can be bounded by

$$\begin{aligned} C \sum _k \frac{m^2_k}{M^2_k}\int _{\left| x \right| <\frac{M_k}{m_k}}x^2 \, \text {d}F^*(x) = C\int x^2 \sum _{k :\frac{M_k}{m_k}\ge \left| x \right| }\frac{m^2_k}{M^2_k} \text {d}F^*(x). \end{aligned}$$

To complete the proof it remains to show that the right-hand side above is finite. This follows from the following claims whose proofs are given right after:

$$\begin{aligned} \sum _{k :\frac{M_k}{m_k}\ge \left| x \right| }\frac{m^2_k}{M^2_k} \le 2 \int _{y \ge \left| x \right| }\frac{N(y)}{y^3}\, \text {d}y, \end{aligned}$$

(A.7)

and

$$\begin{aligned} \int x^2 \int _{y \ge \left| x \right| }\frac{N(y)}{y^3}\, \text {d}y\, \text {d}F^*(x)< \infty . \end{aligned}$$

(A.8)

$\square$

Proof of (A.8) By (A.5) there are $C>0$ and $\gamma \in (0,1)$ such that $N(x)\le Cx^{1 + \gamma }$. Therefore

$$\begin{aligned} \begin{aligned}&\int x^2 \int _{y \ge \left| x \right| }\frac{N(y)}{y^3}\, \text {d}y\, \text {d}F^*(x)\le \int x^2 \int _{y \ge \left| x \right| }\frac{Cy^{1 + \gamma }}{y^3}\, \text {d}y\, \text {d}F^*(x)\\&\quad = \int x^2 \int _{y \ge \left| x \right| }\frac{C}{y^{2 - \gamma }}\, \text {d}y\, \text {d}F^*(x) = \int x^{2} \frac{C}{(1 - \gamma )x^{1 - \gamma }}\, \text {d}F^*(x)\\&\quad = \frac{C}{1 - \gamma }\mathbb {E}\left[ \left| X^* \right| ^{1 + \gamma } \right] < \infty . \end{aligned} \end{aligned}$$

$\square$

Proof of (A.7) Observe that by the definition of N, see (A.4), and integration by parts

$$\begin{aligned} \begin{aligned} \sum _{k :\left| x \right|< \frac{M_k}{m_k}\le z} \frac{m^2_k}{M^2_k}&= \int _{\left| x \right|<y<z}\frac{\text {d}N(y)}{y^2}\\&= \frac{N(z)}{z^2} - \frac{N(\left| x \right| )}{x^2} + 2 \int _{\left| x \right|<y<z}\frac{N(y)}{y^3}\, \text {d}y. \end{aligned} \end{aligned}$$

Furthermore, since $N(z) \le N(y)$ for $z \le y$ and $\frac{1}{z^2} = 2\int _z^\infty \frac{1}{y^3}\, \text {d}y$ it follows from (A.8) that

$$\begin{aligned} \frac{N(z)}{z^2} \le 2\int _z^\infty \frac{N(y)}{y^3}\, \text {d}y \rightarrow 0, \quad \text {as } z \rightarrow \infty . \end{aligned}$$

Therefore

$$\begin{aligned} \begin{aligned} \sum _{k :\left| x \right|< \frac{M_k}{m_k}} \frac{m^2_k}{M^2_k}&= \lim _{z \rightarrow \infty } \sum _{k :\left| x \right|< \frac{M_k}{m_k}<z} \frac{m^2_k}{M^2_k}&\le 2 \int _{\left| x \right| <y}\frac{N(y)}{y^3}\, \text {d}y. \end{aligned} \end{aligned}$$

$\square$