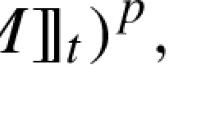1 Introduction

Throughout this article, \((f_{n})_{n\in {\mathbb {N}}}\) denotes a martingale on a filtered probability space \((\Omega ,({\mathcal {F}}_{n})_{n\in {\mathbb {N}}})\) with values in a Banach space \((X,{|}\cdot {|})\). A weight is a positive random variable on \(\Omega \). We denote martingale differences and running maxima by

$$\begin{aligned} df_{n} = f_{n}-f_{n-1}, \quad f^{*}_{n}:= \max _{n'\le n} {|}f_{n'}{|}, \quad w^{*}_{n}:= \max _{n'\le n} w_{n'}. \end{aligned}$$

We begin with the Hilbert space-valued case of our main result (Theorem 2.3).

Theorem 1.1

Let \((f_{n})_{n\in {\mathbb {N}}}\) be a martingale with values in a Hilbert space \((X=H,{|}\cdot {|})\). Let \((w_{n})_{n\in {\mathbb {N}}}\) be an adapted sequence of weights (that need not be a martingale). Then, for every \(N\in {\mathbb {N}}\), we have

$$\begin{aligned} {\mathbb {E}}\left( {|}f_{0}{|} + \frac{1}{3} \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} \right) \le {\mathbb {E}}( f^{*}_{N} ) \end{aligned}$$
(1.1)

and

$$\begin{aligned} {\mathbb {E}}\left( {|}f_{0}{|} w_{0} + \frac{1}{4} \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} w_{n} \right) \le {\mathbb {E}}( f^{*}_{N} w^{*}_{N}). \end{aligned}$$
(1.2)

A quantity similar to the left-hand side of (1.1), but with \(f^{*}_{N}\) in place of \(f^{*}_{n}\) and hence smaller, appeared in [9, §3]. Our version adds a more satisfactory equivalence to the \(L^{1}\) Burkholder–Davis–Gundy inequalities, since the n-th summand is \({\mathcal {F}}_{n}\)-measurable.

In order to relate our result to the usual martingale square function

$$\begin{aligned} Sf:= \left( \sum _{n=1}^{N} {|}df_{n}{|}^{2} \right) ^{1/2}, \end{aligned}$$

we note that, by Hölder’s inequality,

$$\begin{aligned} {\mathbb {E}}Sf \le {\mathbb {E}}\left( (f^{*}_{N})^{1/2} \left( \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} \right) ^{1/2} \right) \le \left( {\mathbb {E}}f^{*}_{N} \right) ^{1/2} \left( {\mathbb {E}}\sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} \right) ^{1/2}. \end{aligned}$$
(1.3)

By one of the Burkholder–Davis–Gundy inequalities [5], we have \({\mathbb {E}}f^{*}_{N} \le C {\mathbb {E}}Sf\) for martingales with \(f_{0}=0\) (the optimal value of C does not seem to be known; the value \(C=\sqrt{10}\) was obtained in [8, II.2.8]). Assuming that both sides are finite, this implies

$$\begin{aligned} {\mathbb {E}}Sf \le C {\mathbb {E}}\sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} \end{aligned}$$

with the same constant C.

The proof of Theorem 1.1 is based on Burkholder’s proof of the Davis inequality for the square function with the sharp constant [3] and its weighted extension by Osękowski [14]. Note, however, that the weights in the latter article are assumed to be continuous in time, so that it does not yield weighted estimates in discrete time. The estimate (1.2) is instead motivated by [13], where the Davis inequality for the martingale maximal function was proved with a similar combination of weights \((w,w^{*})\). Such weighted inequalities go back to [7], see also [11, Theorem 3.2.3] for a martingale version.

1.1 Sharpness of the Constants

Both estimates (1.1) and (1.2) are sharp, in the sense that the constants 1/3 and 1/4 cannot be replaced by any larger constants.

The sharpness of (1.1) is due to the fact that it implies the sharp version of the Davis inequality for the expectation of the martingale square function [3]. To see this, for notational simplicity, suppose \(f_{0}=0\). By (1.3) and (1.1), we have

$$\begin{aligned} {\mathbb {E}}Sf \le \sqrt{3} {\mathbb {E}}f^{*}_{N}. \end{aligned}$$

Since the constant \(\sqrt{3}\) is the smallest possible in this inequality [3, §5], also the constant in (1.1) is optimal.

The sharpness of (1.2) is proved in Sect. 4.

1.2 Consequences of the Weighted Estimate

Here, we show how Theorem 1.1 can be used to recover a number of known inequalities.

Let \(r\in [1,2]\), w be an integrable weight, \(w_{n} = {\mathbb {E}}(w|{\mathcal {F}}_{n})\), \(f^{*} = f^{*}_{\infty }\), and \(w^{*}=w^{*}_{\infty }\). For simplicity, we again assume \(f_{0}=0\). By Hölder’s inequality and (1.2), we obtain

$$\begin{aligned} \begin{aligned} {\mathbb {E}}\left( (Sf)^{r} \cdot w \right)&\le {\mathbb {E}}\left( (f^{*})^{(2-r)r/2} \left( \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} (f^{*}_{n})^{r-1} \right) ^{r/2} w \right) \\&\le \left( {\mathbb {E}}(f^{*})^{r} w \right) ^{1-r/2} \left( {\mathbb {E}}\left( \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} (f^{*}_{n})^{r-1} w \right) \right) ^{r/2} \\&= \left( {\mathbb {E}}(f^{*})^{r} w \right) ^{1-r/2} \left( {\mathbb {E}}\left( \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} (f^{*}_{n})^{r-1} w_{n} \right) \right) ^{r/2} \\&\le 2^{r} \left( {\mathbb {E}}( f^{*} )^{r} w \right) ^{1-r/2} \left( {\mathbb {E}}( f^{*} )^{r} w^{*} \right) ^{r/2}. \end{aligned} \end{aligned}$$
(1.4)

If we estimate \(w\le w^{*}\) in the first term on the right-hand side, we recover a version of the main result in [14]. Our version has a worse constant, but does not require the weights to be continuous in time. This is an important advantage, because the weights have to be chosen depending on the martingale in applications. In particular, our version is necessary in the extrapolation arguments below.

Recall that the \(A_{1}\) characteristic of a weight w is the smallest constant \([w]_{A_{1}}\) such that \(w^{*} \le [w]_{A_{1}} w\). As a direct consequence of the estimate (1.4), we obtain the estimate

$$\begin{aligned} {\mathbb {E}}\left( \left( \sum _{n=1}^{N} {|}df_{n}{|}^{2} \right) ^{1/2} w \right) \le 2 [w]_{A_{1}}^{1/2} {\mathbb {E}}( f^{*} w) \end{aligned}$$
(1.5)

for \(A_{1}\) weights w. This improves the main result of [15], where a similar estimate (with \(\sqrt{5}\) in place of 2) was proved for dyadic martingales. In view of [1, Theorem 1.3], it seems unlikely that the \(A_{1}\) characteristic in (1.5) can be replaced by a function of any \(A_{p}\) characteristic with \(p>1\), although for dyadic martingales even the \(A_{\infty }\) characteristic suffices [10, Theorem 2].

Next, we present a version of the Rubio de Francia extrapolation argument, which allows one to deduce further \(L^{p}\) weighted estimates from (1.4) (with \(r=1\)). Let \(p \in (1,\infty )\), w a weight, and \({\tilde{w}} = w^{-p'/p}\) the dual weight, where \(p'\) denotes the Hölder conjugate that is determined by \(1/p+1/p'=1\). Let also

$$\begin{aligned} Mh:= \sup _{n \in {\mathbb {N}}} {|}{\mathbb {E}}(h | {\mathcal {F}}_{n}){|} \end{aligned}$$

denote the martingale maximal operator. Then, for any function u, by (1.4) and Hölder’s inequality, we obtain

$$\begin{aligned} \begin{aligned} {\mathbb {E}}( Sf \cdot u \cdot w )&\le 2 {\mathbb {E}}( Mf \cdot M(uw) )^{1/2} \cdot {\mathbb {E}}( Mf \cdot (uw) )^{1/2}\\&\le 2 ({\mathbb {E}}(Mf)^{p} w)^{1/p} ({\mathbb {E}}(M(uw))^{p'} w^{-p'/p})^{1/(2p')} ({\mathbb {E}}u^{p'} w)^{1/(2p')}. \end{aligned} \end{aligned}$$
(1.6)

By definition of the operator norm, we have

$$\begin{aligned} ({\mathbb {E}}(M(uw))^{p'} w^{-p'/p})^{1/p'}&\le {\Vert } M {\Vert }_{L^{p'}({\tilde{w}}) \rightarrow L^{p'}({\tilde{w}})} ({\mathbb {E}}(uw)^{p'} w^{-p'/p})^{1/p'} \\&= {\Vert } M {\Vert }_{ L^{p'}({\tilde{w}}) \rightarrow L^{p'}({\tilde{w}})} ({\mathbb {E}}u^{p'} w)^{1/p'}. \end{aligned}$$

Substituting this into (1.6), we obtain

$$\begin{aligned} {\mathbb {E}}( Sf \cdot u \cdot w ) \le 2 {\Vert } M {\Vert }_{ L^{p'}({\tilde{w}}) \rightarrow L^{p'}({\tilde{w}})}^{1/2} ({\mathbb {E}}(Mf)^{p} w)^{1/p} ({\mathbb {E}}u^{p'} w)^{1/p'}. \end{aligned}$$

By duality, this implies

$$\begin{aligned} {\Vert } Sf {\Vert }_{L^{p}(w)} \le 2 {\Vert } M {\Vert }_{ L^{p'}({\tilde{w}}) \rightarrow L^{p'}({\tilde{w}})}^{1/2} {\Vert } f^{*} {\Vert }_{L^{p}(w)}. \end{aligned}$$
(1.7)

In the case \(w\equiv 1\), using Doob’s maximal inequality [11, Theorem 3.2.2], this recovers the following version of the martingale square function inequality, which matches [4, Theorem 3.2]:

$$\begin{aligned} {\Vert } Sf {\Vert }_{L^{p}} \le 2 \sqrt{p} p' {\Vert } f {\Vert }_{L^{p}}. \end{aligned}$$

More generally, an \(A_{p}\) weighted BDG inequality can be obtained from (1.7) using the \(A_{p'}\) weighted martingale maximal inequality proved in [6].

Another Rubio de Francia-type extrapolation argument, see [19, Appendix A], can be used to deduce UMD Banach space-valued estimates from either (1.2) or (1.4). This recovers one of the estimates in [18, Theorem 1.1] (the other direction similarly follows from the weighted estimate in [13]).

2 Uniformly Convex Banach Spaces

In this section, we recall a few facts about uniformly convex Banach spaces that are relevant to the Banach space-valued version of Theorem 1.1, Theorem 2.3.

Definition 2.1

Let \(q \in [2,\infty )\). A Banach space \((X,{|}\cdot {|})\) is called q-uniformly convex if there exists \(\delta >0\) such that, for every \(x,y\in X\), we have

$$\begin{aligned} \left| {\frac{x+y}{2}}\right| ^{q} + \delta \left| {\frac{x-y}{2}}\right| ^{q} \le \frac{{|}x{|}^{q} + {|}y{|}^{q}}{2}. \end{aligned}$$
(2.1)

For example, Clarkson’s inequality tells that (2.1) holds with \(\delta =1\) for \(X=L^{q}\).

We will use a different (but equivalent) characterization of uniform convexity, in terms of the convex function \(\phi : X\rightarrow {\mathbb {R}}_{\ge 0}\), \(\phi (x) = {|}x{|}^{q}\) and its directional derivative at point x in direction h, given by

$$\begin{aligned} \phi '(x)h:= \lim _{t\rightarrow 0, t>0} \frac{\phi (x+th)-\phi (x)}{t}. \end{aligned}$$
(2.2)

Convexity of \(\phi \) is equivalent to the right-hand side of (2.2) being an increasing function of t for fixed x, h. By the triangle inequality and Taylor’s formula, we have

$$\begin{aligned} {|}{|}x+h{|}^{q} - {|}x{|}^{q}{|} \le ({|}x{|}+{|}h{|})^{q} - {|}x{|}^{q} \le q{|}x{|}^{q-1}{|}h{|} + o_{{|}h{|}\rightarrow 0}({|}h{|}). \end{aligned}$$

Therefore, the quotient on the right-hand side of (2.2) is bounded from below. Hence, the limit (2.2) exists, and we have

$$\begin{aligned} {|}\phi '(x)h{|} \le q {|}x{|}^{q-1} {|}h{|}. \end{aligned}$$
(2.3)

Moreover, for every \(x\in X\), the function \(h \mapsto \phi '(x)h\) is convex, which follows directly from convexity of \(\phi \).

Lemma 2.2

A Banach space \((X,{|}\cdot {|})\) is uniformly convex if and only if, for every \(x,h\in X\), we have

$$\begin{aligned} {|}x+h{|}^{q} \ge {|}x{|}^{q} + \phi '(x) h + {\tilde{\delta }}{|}h{|}^{q}. \end{aligned}$$
(2.4)

Moreover, the largest \(\delta ,{\tilde{\delta }}\) for which (2.1) and (2.4) hold satisfy

$$\begin{aligned} \frac{\delta }{2^{q-1}-1} \le {\tilde{\delta }} \le \delta . \end{aligned}$$
(2.5)

The estimate (2.4) can only hold with \({\tilde{\delta }} \le 1\) (unless X is 0-dimensional), as can be seen by taking \(x=0\). When X is a Hilbert space, we can take \(q=2\) and \(\delta =1\) in (2.1) by the parallelogram identity and \({\tilde{\delta }}=1\) in (2.4) by (2.5).

Proof

Clearly, the sets of \(\delta \) and \({\tilde{\delta }}\) for which (2.1) and (2.4) hold are closed, so we may consider the largest such \(\delta \) and \({\tilde{\delta }}\).

To see the first inequality in (2.5), let \({\mathcal {C}}\) be the set of all constants \(c\ge 0\) such that, for every \(x,h\in X\), we have

$$\begin{aligned} \phi (x+h) \ge \phi (x) + \phi '(x) h + c \phi (h). \end{aligned}$$

By convexity of \(\phi \), we have \(0 \in {\mathcal {C}}\).

Let \(c\in {\mathcal {C}}\). For any \(x,h \in X\), using the uniform convexity assumption (2.1) with \(y=x+h\), we obtain

$$\begin{aligned} {|}x+h/2{|}^{q} + \delta {|}h/2{|}^{q} \le ({|}x{|}^{q}+{|}x+h{|}^{q})/2. \end{aligned}$$

By the definition of \(c\in {\mathcal {C}}\), it follows that

$$\begin{aligned} {|}x{|}^{q} + \phi '(x) h/2 + c {|}h/2{|}^{q} + \delta {|}h/2{|}^{q} \le ({|}x{|}^{q}+{|}x+h{|}^{q})/2. \end{aligned}$$

Rearranging this inequality, we obtain

$$\begin{aligned} {|}x{|}^{q} + \phi '(x) h + 2 c {|}h/2{|}^{q} + 2 \delta {|}h/2{|}^{q} \le {|}x+h{|}^{q}. \end{aligned}$$

Therefore, \(2^{1-q}(c+\delta ) \in {\mathcal {C}}\). Since \(c\in {\mathcal {C}}\) was arbitrary, this implies

$$\begin{aligned} \sup {\mathcal {C}}\ge \delta /(2^{q-1}-1). \end{aligned}$$

To see the second inequality in (2.5), note that convexity of \(h \mapsto \phi '(x)h\) implies \(\phi '(x)h + \phi '(x)(-h) \ge 0\). Applying (2.4) with (z, h) and (z, h), we obtain

$$\begin{aligned} {|}z+h{|}^{q} + {|}z-h{|}^{q}&\ge 2{|}z{|}^{q} + \phi '(z) h + \phi '(z)(-h) + {\tilde{\delta }}{|}h{|}^{q} + {\tilde{\delta }}{|}-h{|}^{q} \\&\ge 2{|}z{|}^{q} + 2 {\tilde{\delta }}{|}h{|}^{q}. \end{aligned}$$

With the change of variables \(x=z+h\), \(y=z-h\), we obtain (2.1) with \({\tilde{\delta }}\) in place of \(\delta \). \(\square \)

With the characterization of uniform convexity in (2.4) at hand, we can finally state our main result in full generality.

Theorem 2.3

For every \(q \in [2,\infty )\), there exists \(\gamma =\gamma (q) \in {\mathbb {R}}_{>0}\) such that the following holds.

Let \((X,{|}\cdot {|})\) be a Banach space such that (2.4) holds. Let \((f_{n})_{n\in {\mathbb {N}}}\) be a martingale with values in X, and \((w_{n})_{n\in {\mathbb {N}}}\) an adapted sequence of weights. Then,

$$\begin{aligned} {\mathbb {E}}\left( \gamma {|}f_{0}{|} w_{0} + {\tilde{\delta }} \sum _{n=1}^{\infty } \frac{{|}df_{n}{|}^{q}}{(f^{*}_{n})^{q-1}} w_{n} \right) \le \gamma {\mathbb {E}}( f^{*} w^{*}) \end{aligned}$$
(2.6)

In the case \(q=2\), we can take \(\gamma =4\). In the case \(q=2\), \({\tilde{\delta }}=1\), and \(w_{n}=1\) for all \(n\in {\mathbb {N}}\), we can take \(\gamma =3\).

In order to see that the linear dependence on \({\tilde{\delta }}\) in (2.6) is optimal, we can apply this inequality with \(w_{n} = (f^{*}_{n})^{q-1}\), followed by Doob’s maximal inequality, which gives the estimate

$$\begin{aligned} {\mathbb {E}}\left( \gamma {|}f_{0}{|}^{q} + {\tilde{\delta }} \sum _{n=1}^{\infty } {|}df_{n}{|}^{q} \right) \le \gamma {\mathbb {E}}( f^{*} )^{q} \le (q')^{q} \gamma \sup _{n\in {\mathbb {N}}} {\mathbb {E}}{|}f_{n}{|}^{q}. \end{aligned}$$

By [16, Theorem 10.6], linear dependence on \({\tilde{\delta }}\) is optimal in this inequality, and hence the same holds for (2.6).

Similarly as in Sect. 1.2, Theorem 2.3 implies several weighted extensions of the martingale cotype inequality [16, Theorem 10.59]. We omit the details.

3 The Bellman Function

The proof of Theorem 2.3 is based on the Bellman function technique; we refer to the books [12, 17] for other instances of this technique. The particular Bellman function that we use here goes back to [3]; the first weighted version of it was introduced in [14]. For \(x\in X\) and \(y,m,v \in {\mathbb {R}}_{\ge 0}\) with \({|}x{|} \le m\), we define

$$\begin{aligned} U(x,y,m,v):= {{\tilde{\delta }}} y - \frac{{|}x{|}^{q}+(\gamma -1)m^{q}}{m^{q-1}} v, \end{aligned}$$

where \(\gamma = \gamma (q)\) will be chosen later. The main feature of this function is the following concavity property.

Proposition 3.1

Suppose that \(\gamma \) is sufficiently large depending on q (see (3.8) for the precise condition). Let \((X,{|}\cdot {|})\) be a Banach space such that (2.4) holds. Then, for any \(x,h \in X\) and \(y,m,w,v \in {\mathbb {R}}_{\ge 0}\) with \({|}x{|}\le m\), we have

$$\begin{aligned} U(x\!+\!h,y+\frac{w{|}h{|}^{q}}{({|}x+h{|}\vee m)^{q-1}},{|}x+h{|}\vee m,v \vee w) \le U(x,y,m,v) - \frac{v \phi '(x) h}{m^{q-1}}.\nonumber \\ \end{aligned}$$
(3.1)

Proof of Theorem 2.3 assuming Proposition 3.1

Using (3.1) with

$$\begin{aligned} x= & {} f_{n}, \quad y = {\tilde{S}}_{n}:= \gamma {|}f_{0}{|} w_{0} + {\tilde{\delta }} \sum _{j=1}^{n} \frac{{|}df_{j}{|}^{q}}{(f^{*}_{j})^{q-1}} w_{j}, \quad m = f^{*}_{n},\\ w= & {} w_{n}, \quad v=w^{*}_{n}, \quad h = df_{n+1}, \end{aligned}$$

we obtain

$$\begin{aligned} U(f_{n+1},{\tilde{S}}_{n+1},f^{*}_{n+1},w^{*}_{n+1}) \le U(f_{n},{\tilde{S}}_{n},f^{*}_{n},w^{*}_{n}) - \frac{\phi '(f_{n}) df_{n+1}}{(f^{*}_{n})^{q-1}} w_{n}^{*}. \end{aligned}$$
(3.2)

By convexity of \(h \mapsto \phi '(x)h\), we have

$$\begin{aligned} {\mathbb {E}}\left( \frac{\phi '(f_{n}) df_{n+1}}{(f^{*}_{n})^{q-1}} w_{n}^{*} | {\mathcal {F}}_{n} \right) = \frac{w_{n}^{*}}{(f^{*}_{n})^{q-1}} {\mathbb {E}}( \phi '(f_{n}) df_{n+1} | {\mathcal {F}}_{n} ) \ge 0. \end{aligned}$$

Taking expectations, we obtain

$$\begin{aligned} {\mathbb {E}}U(f_{n+1},{\tilde{S}}_{n+1},f^{*}_{n+1},w^{*}_{n+1}) \le {\mathbb {E}}U(f_{n},{\tilde{S}}_{n},f^{*}_{n},w^{*}_{n}). \end{aligned}$$

Iterating this inequality, we obtain

$$\begin{aligned}{} & {} {\mathbb {E}}\left( \gamma {|}f_{0}{|} w_{0} + {\tilde{\delta }} \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{q}}{(f^{*}_{n})^{q-1}} w_{n} - \gamma f^{*}_{N} w^{*}_{N} \right) \\{} & {} \quad \le {\mathbb {E}}U(f_{N},{\tilde{S}}_{N},f^{*}_{N},w^{*}_{N}) \le {\mathbb {E}}U(f_{0},{\tilde{S}}_{0},f^{*}_{0},w^{*}_{0}) = 0. \end{aligned}$$

\(\square \)

Remark 3.2

The above proof in fact shows the pathwise inequality

$$\begin{aligned} \gamma {|}f_{0}{|} w_{0} + {\tilde{\delta }} \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{q}}{(f^{*}_{n})^{q-1}} w_{n} \le \gamma f^{*}_{N} w^{*}_{N} - \sum _{n=1}^{N} \frac{\phi '(f_{n}) df_{n+1}}{(f^{*}_{n})^{q-1}} w_{n}^{*}. \end{aligned}$$

This can be used to improve the first part of [2, Theorem 1.1]. For simplicity, consider the scalar case \(X={\mathbb {C}}\) (so that \(q=2\) and \({\tilde{\delta }}=1\)) with \(f_{0}=0\) and \(w_{n}=1\). The above inequality then simplifies to

$$\begin{aligned} \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{q}}{f^{*}_{n}} \le 3 f^{*}_{N} - \sum _{n=1}^{N} \frac{2 f_{n} df_{n+1}}{f^{*}_{n}}. \end{aligned}$$

Using (1.3), the above inequality, and concavity of the function \(x\mapsto x^{1/2}\), we obtain

$$\begin{aligned} S_{N}f&\le (f^{*}_{N})^{1/2} \left( \sum _{n=1}^{N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} \right) ^{1/2}\\&\le (f^{*}_{N})^{1/2} \left( 3 f^{*}_{N} - \sum _{n=1}^{N} \frac{2 f_{n} df_{n+1}}{f^{*}_{n}} \right) ^{1/2} \\&\le (f^{*}_{N})^{1/2} \left( (3 f^{*}_{N})^{1/2} - \frac{1}{2}(3 f^{*}_{N})^{-1/2} \sum _{n=1}^{N} \frac{2 f_{n} df_{n+1}}{f^{*}_{n}} \right) \\&= \sqrt{3} f^{*}_{N} - \sum _{n=1}^{N} \frac{f_{n} df_{n+1}}{\sqrt{3} f^{*}_{n}}. \end{aligned}$$

Proof of Proposition 3.1

If \({|}x+h{|}\le m\), then

$$\begin{aligned}&U(x+h,y+\frac{w{|}h{|}^{q}}{({|}x+h{|}\vee m)^{q-1}},{|}x+h{|}\vee m,v \vee w) \\&\quad = {\tilde{\delta }}\left( y+\frac{w{|}h{|}^{q}}{m^{q-1}}\right) -\frac{{|}x+h{|}^{q}+(\gamma -1)m^{q}}{m^{q-1}} (v\vee w) \\&\quad \le {\tilde{\delta }}\left( y+\frac{w{|}h{|}^{q}}{m^{q-1}}\right) - \frac{{|}x{|}^{q} + \phi '(x) h + {\tilde{\delta }}{|}h{|}^{q}+(\gamma -1)m^{q}}{m^{q-1}} (v\vee w)\\&\quad \le {\tilde{\delta }} y - \frac{{|}x{|}^{q} + \phi '(x) h +(\gamma -1)m^{q}}{m^{q-1}} (v\vee w)\\&\quad \le {\tilde{\delta }} y - \frac{{|}x{|}^{q} + \phi '(x) h + (\gamma -1)m^{q}}{m^{q-1}} v \\&\quad = U(x,y,m,w,v) - \frac{\phi '(x) h}{m^{q-1}} v. \end{aligned}$$

In the last inequality, we used

$$\begin{aligned}{} & {} {|}\phi '(x)h{|} \le q {|}x{|}^{q-1} {|}h{|}\nonumber \\{} & {} \quad \le q {|}x{|}^{q-1} ({|}x{|} + m) \le {|}x{|}^{q} + (2q-1) m^{q} \le {|}x{|}^{q} + (\gamma -1) m^{q}, \end{aligned}$$
(3.3)

which holds provided that \(\gamma \ge 2q\).

If \({|}x+h{|}>m\), then we need to show

$$\begin{aligned}{} & {} {\tilde{\delta }}\left( y+\frac{w{|}h{|}^{q}}{{|}x+h{|}^{q-1}}\right) - \frac{{|}x+h{|}^{q} + (\gamma -1) {|}x+h{|}^{q}}{{|}x+h{|}^{q-1}} (v\vee w) \\{} & {} \quad \le {\tilde{\delta }}y - \frac{{|}x{|}^{q} + (\gamma -1)m^{q}}{m^{q-1}} v - \frac{\phi '(x) h}{m^{q-1}} v. \end{aligned}$$

This is equivalent to

$$\begin{aligned} \frac{{\tilde{\delta }}{|}h{|}^{q}w - \gamma {|}x+h{|}^{q} (v\vee w)}{{|}x+h{|}^{q-1}} \le \frac{-{|}x{|}^{q} v-(\gamma -1)m^{q}v}{m^{q-1}} - \frac{\phi '(x) h}{m^{q-1}} v. \end{aligned}$$
(3.4)

Assuming that \(\gamma \ge 2^{q}{\tilde{\delta }}\), we have

$$\begin{aligned} {\tilde{\delta }} {|}h{|}^{q} \le {\tilde{\delta }} ({|}x+h{|} + {|}x{|})^{q} \le {\tilde{\delta }} (2 {|}x+h{|})^{q} \le \gamma {|}x+h{|}^{q}, \end{aligned}$$
(3.5)

and it follows that the left-hand side of (3.4) is

$$\begin{aligned} \le (v\vee w) \frac{{\tilde{\delta }}{|}h{|}^{q}-\gamma {|}x+h{|}^{q}}{{|}x+h{|}^{q-1}} \le v \frac{{\tilde{\delta }}{|}h{|}^{q}-\gamma {|}x+h{|}^{q}}{{|}x+h{|}^{q-1}}. \end{aligned}$$

Hence, it suffices to show

$$\begin{aligned} \frac{{\tilde{\delta }}{|}h{|}^{q}-\gamma {|}x+h{|}^{q}}{{|}x+h{|}^{q-1}} \le \frac{-{|}x{|}^{q}-(\gamma -1)m^{q}}{m^{q-1}} - \frac{\phi '(x) h}{m^{q-1}}. \end{aligned}$$
(3.6)

Let \(t:= {|}x+h{|}/m > 1\) and \({\tilde{t}}:= {|}h{|}/m\). Note that \({|}t-{\tilde{t}}{|} = {|}{|}x+h{|}-{|}h{|}{|}/m \le {|}x{|}/m \le 1\). We will show (3.6) in two different ways, depending on the values of \(t,{\tilde{t}}\).

Estimate 1. By (2.4), the inequality (3.6) will follow from

$$\begin{aligned} \frac{{\tilde{\delta }}{|}h{|}^{q}-\gamma {|}x+h{|}^{q}}{{|}x+h{|}^{q-1}} \le \frac{-{|}x+h{|}^{q}+{\tilde{\delta }}{|}h{|}^{q}-(\gamma -1)m^{q}}{m^{q-1}}. \end{aligned}$$

This is equivalent to

$$\begin{aligned} {\tilde{\delta }}{\tilde{t}}^{q}/t^{q-1}-\gamma t \le -t^{q}+{\tilde{\delta }}{\tilde{t}}^{q}-(\gamma -1), \end{aligned}$$

or

$$\begin{aligned} \gamma \ge \frac{1}{t-1} \left( t^{q}-1 - {\tilde{\delta }} {\tilde{t}}^{q}(1-1/t^{q-1}) \right) . \end{aligned}$$

Estimate 2. The inequality (3.6) is implied by

$$\begin{aligned} \frac{{\tilde{\delta }}{|}h{|}^{q}}{{|}x+h{|}^{q-1}} + \frac{{|}x{|}^{q}+(\gamma -1)m^{q}}{m^{q-1}} + \frac{{|}\phi '(x) h{|}}{m^{q-1}} \le \gamma {|}x+h{|}. \end{aligned}$$

This is equivalent to

$$\begin{aligned} \frac{{\tilde{\delta }}{\tilde{t}}^{q}}{t^{q-1}} + \frac{{|}x{|}^{q}}{m^{q}} + (\gamma -1) + \frac{{|}\phi '(x) h{|}}{m^{q}} \le \gamma t. \end{aligned}$$

Using (2.3), we see that the left-hand side is bounded by

$$\begin{aligned} \frac{{\tilde{\delta }} {\tilde{t}}^{q}}{t^{q-1}} + 1 + (\gamma -1) + \frac{q {|}x{|}^{q-1} \cdot {|}h{|}}{m^{q}} \le \frac{{\tilde{\delta }} {\tilde{t}}^{q}}{t^{q-1}} + \gamma + q {\tilde{t}}. \end{aligned}$$

Hence, it suffices to assume

$$\begin{aligned} \frac{{\tilde{\delta }} {\tilde{t}}^{q}}{t^{q-1}} + \gamma + q (t+1) \le \gamma t, \end{aligned}$$

or, in other words,

$$\begin{aligned} \gamma \ge \frac{1}{t-1} \left( \frac{{\tilde{\delta }} {\tilde{t}}^{q}}{t^{q-1}} + q {\tilde{t}} \right) . \end{aligned}$$

Combining the two estimates, we see that (3.6) holds provided that

$$\begin{aligned} \gamma \ge \sup _{t>1, {|}t-{\tilde{t}}{|} \le 1} \frac{1}{t-1} \min \left( t^{q}-1 - {\tilde{\delta }} {\tilde{t}}^{q}(1-1/t^{q-1}), \frac{{\tilde{\delta }} {\tilde{t}}^{q}}{t^{q-1}} + q {\tilde{t}} \right) . \end{aligned}$$
(3.7)

In order to obtain a more easily computable bound, we estimate

$$\begin{aligned} \textrm{RHS}(3.7) \le \sup _{t\ge 1} \sup _{K\ge 0} \frac{1}{t-1} \min \left( t^{q}-1 - K(1-1/t^{q-1}), K/t^{q-1} + q (t+1) \right) . \end{aligned}$$

Since we are taking the minimum of an increasing and a decreasing function in K, the supremum over K is achieved for the value of K for which these functions take equal values, or for \(K=0\) if the latter value is negative. Hence, substituting \(K=\max (t^{q}-1-q(t+1),0)\), we obtain

$$\begin{aligned} \textrm{RHS}(3.7) \le \sup _{t\ge 1} \frac{1}{t-1} \left( t^{q}-1 - \max (t^{q}-1-q(t+1),0)(1-1/t^{q-1}) \right) , \end{aligned}$$

The function \(t \mapsto t^{q}-1-q(t+1)\) is strictly monotonically increasing, so there is a unique solution \(t_{0}\) to \(t_{0}^{q}-1-q(t_{0}+1) = 0\). The supremum is then assumed for \(t=t_{0}\), since

$$\begin{aligned} \frac{\mathop {}\!\textrm{d}}{\mathop {}\!\textrm{d}t} \frac{t^{q}-1}{t-1} = \frac{(q-1)t^{q}+1-qt^{q-1}}{(t-1)^{2}} \ge 0 \end{aligned}$$

by the AMGM inequality, and

$$\begin{aligned} \frac{\mathop {}\!\textrm{d}}{\mathop {}\!\textrm{d}t} \frac{1}{t-1} \left( q(t+1) + \frac{t^{q}-1}{t^{q-1}} \right) = - \frac{2q}{(t-1)^{2}} - \frac{t^{q-2}}{(t^{q}-t^{q-1})^{2}} (t^{q}-qt+(q+1)) \le 0. \end{aligned}$$

Hence,

$$\begin{aligned} \textrm{RHS}(3.7) \le \frac{q(t_{0}+1)}{t_{0}-1}. \end{aligned}$$

Collecting the conditions on \(\gamma \) in the proof, we see that it suffices to assume

$$\begin{aligned} \gamma \ge \max ( \frac{q(t_{0}+1)}{t_{0}-1}, 2q, 2^{q}). \end{aligned}$$
(3.8)

For \(q=2\), we have \(t_{0}=3\), so we can take \(\gamma = 4\).

In the case \(v=w=1\), we do not use (3.3) and (3.5), so the only condition on \(\gamma \) is given by (3.7). If we additionally assume \(q=2\) and \({\tilde{\delta }} = 1\), that condition can be further simplified in the same way as in [14]. Namely, it suffices to ensure

$$\begin{aligned} \gamma \ge \sup _{t>1, {|}t-{\tilde{t}}{|} \le 1} \frac{1}{t-1} \left( t^{2}-1 - {\tilde{t}}^{2}(1-1/t) \right) . \end{aligned}$$

The supremum in \({\tilde{t}}\) is assumed for \({\tilde{t}} = (t-1)\), so this condition becomes

$$\begin{aligned}{} & {} \gamma \ge \sup _{t>1} \frac{1}{t-1} \left( t^{2}-1 - (t-1)^{2}(1-1/t) \right) \\{} & {} \quad = \sup _{t>1} t+1 - (t-1)^{2}/t = \sup _{t>1} 3 - 1/t = 3. \end{aligned}$$

This is the bound used in (1.1). \(\square \)

4 Optimality

In this section, we show that the inequality (1.2) fails if 1/4 is replaced by any larger number, already if the weights constitute a (positive) martingale.

Let \(\Omega = {\mathbb {N}}_{\ge 1}\) with the filtration \({\mathcal {F}}_{n}\) such that the n-th \(\sigma \)-algebra \({\mathcal {F}}_{n}\) is generated by the atoms \(\{1\},\dotsc ,\{n\}\). Let \(k\in {\mathbb {R}}_{>0}\) be arbitrary. The measure on \((\Omega ,{\mathcal {F}}=\vee _{n\in {\mathbb {N}}} {\mathcal {F}}_{n})\) is given by \(\mu (\{\omega \}) = k(k+1)^{-\omega }\). The martingale and the weights are given by

$$\begin{aligned} f_{n}(\omega ) = {\left\{ \begin{array}{ll} (-1)^{\omega +1} \frac{k+2}{k}, &{} \omega \le n,\\ (-1)^{n}, &{} \omega>n, \end{array}\right. } \quad w_{n}(\omega ) = {\left\{ \begin{array}{ll} 0, &{} \omega \le n,\\ (k+1)^{n}, &{} \omega > n. \end{array}\right. } \end{aligned}$$

Note that both these processes are indeed martingales. Their running maxima are given by

$$\begin{aligned} f^{*}_{n}(\omega ) = {\left\{ \begin{array}{ll} \frac{k+2}{k}, &{} \omega \le n,\\ 1, &{} \omega>n, \end{array}\right. } \quad w^{*}_{n}(\omega ) = {\left\{ \begin{array}{ll} (k+1)^{\omega -1} &{} \omega \le n,\\ (k+1)^{n}, &{} \omega > n. \end{array}\right. } \end{aligned}$$

Now, we compute both sides of (1.2):

$$\begin{aligned} {\mathbb {E}}\sum _{n \le N} \frac{{|}df_{n}{|}^{2}}{f^{*}_{n}} w_{n} = \sum _{n \le N} \mu ({\mathbb {N}}_{>n}) \frac{2^{2}}{1} (k+1)^{n} = \sum _{n \le N} (k+1)^{-n} \frac{2^{2}}{1} (k+1)^{n} = 4N, \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}(f^{*}_{N} w^{*}_{N})&= \sum _{\omega \le N} \mu (\{\omega \}) \frac{k+2}{k} (k+1)^{\omega -1} + \mu ({\mathbb {N}}_{>N}) \cdot 1 \cdot (k+1)^{N}\\&= \sum _{\omega \le N} k(k+1)^{-\omega } \frac{k+2}{k} (k+1)^{\omega -1} + (k+1)^{-N} \cdot 1 \cdot (k+1)^{N} \\&= N \frac{k+2}{k+1} + 1. \end{aligned}$$

Since k and N can be arbitrarily large, we see that the constant in (1.2) is optimal.