Backward Euler–Maruyama Method for the Random Periodic Solution of a Stochastic Differential Equation with a Monotone Drift

Abstract

In this paper, we study the existence and uniqueness of the random periodic solution for a stochastic differential equation with a one-sided Lipschitz condition (also known as monotonicity condition) and the convergence of its numerical approximation via the backward Euler–Maruyama method. The existence of the random periodic solution is shown as the limit of the pull-back flows of the SDE and the discretized SDE, respectively. We establish a convergence rate of the strong error for the backward Euler–Maruyama method with order of convergence 1/2.

1 Introduction

Periodicity is widely exhibited in a large number of natural phenomena like oscillations, waves, or even lying behind many complicated ensembles such as biological and economic systems. However, periodic behaviors are often found to be subject to random perturbation or under the influence of noise. Physicists have attempted to study random perturbations to periodic solutions for some time by considering a first linear approximation or asymptotic expansions in small noise regime, but this approach restricted its applicability to the small fluctuation (c.f. Van Kampen [13], Weiss and Knoblock [16]). It was only until recently that the random periodic solution was endowed with a proper definition (c.f. Zhao and Zheng [19], Feng, Zhao and Zhou [8]), which is compatible with definitions of both the stationary solution (also termed as random fixed points) and the deterministic periodic solution. It gives a rigorous and clearer understanding to physically interesting problems of certain random phenomena with a periodic nature and also represents a long time limit of the underlying random dynamical system.

Let us recall the definition of the random periodic solution for stochastic semi-flows given in [8]. Let H be a separable Banach space. Denote by $(\Omega ,\mathcal{F},{\mathbb {P}},(\theta _s)_{s\in {\mathbb {R}}})$ a metric dynamical system and $\theta _s:\Omega \rightarrow \Omega$ is assumed to be measurably invertible for all $s\in {\mathbb {R}}$. Denote $\Delta :=\{(t,s)\in {\mathbb {R}}^2, s\le t\}$. Consider a stochastic semi-flow $u: \Delta \times \Omega \times H\rightarrow H$, which satisfies the following standard condition

$$\begin{aligned} u(t,r,\omega )=u(t,s,\omega )\circ u(s,r,\omega ), \end{aligned}$$

(1)

for all $r\le s\le t$, $r, s,t\in {\mathbb {R}}$, for a.e. $\omega \in \Omega$. We do not assume the map $u(t,s,\omega ): H\rightarrow H$ to be invertible for $(t,s)\in \Delta ,\ \omega \in \Omega$.

Definition 1

A random periodic path of period $\tau$ of the semi-flow $u: \Delta \times \Omega \times H\rightarrow H$ is an $\mathcal{F}$-measurable map $y:{\mathbb {R}}\times \Omega \rightarrow H$ such that

$$\begin{aligned} \Big \{\begin{array}{l}u(t,s, y(s,\omega ), \omega )=y(t,\omega ),\ \ \forall t\ge s\\ y(s+\tau ,\omega )=y(s, \theta _\tau \omega ),\ \ \forall s\in {\mathbb {R}} \end{array} \end{aligned}$$

(2)

for any $\omega \in \Omega$.

Building on this new concept, there have been more recent progresses toward understanding the random periodicity of various stochastic systems. The existence of random periodic solutions to stochastic differential equations (SDEs) and stochastic partial differential equations (SPDEs) are initially studied in [8] and [4], with additive noise. Instead of following the traditional geometric method of establishing the Poincaré mapping, a new analytical method for coupled infinite horizon forward-backward integral equations is introduced. It was then followed by the study on the anticipating random periodic solutions (c.f. Feng, Wu and Zhao: [6] and [7]). Regarding applications, Chekroun, Simonnet and Ghil [3] employed random periodic results to climate dynamics, and Wang [14] observed random periodicity behavior in the study of bifurcations of stochastic reaction diffusion equations.

In general, random periodic solutions cannot be solved explicitly. One may treat the numerical approximation that stay sufficient close to the true solution as a good substitute to study stochastic dynamics. It is worth mentioning here that this is a numerical approximation of an infinite time horizon problem. The classical numerical approaches including the Euler–Marymaya method and a modified Milstein method to simulate random period solutions of a dissipative system with global Lipschitz condition have been investigated in [5], which is the first paper that numerical schemes were used to approximate the random period trajectory.

In this paper, we study the random periodic solutions of stochastic differential equations with weakened conditions on the drift term compared to [5] and simulate them via the backward Euler–Maruyama method. Let $W :{\mathbb {R}} \times \Omega \rightarrow {\mathbb {R}}^d$ be a standard two-sided Wiener process on the probability space $(\Omega , {\mathcal {F}}, {\mathbb {P}})$, with the filtration defined by ${\mathcal {F}}_s^{t}:=\sigma \{W_u-W_v:s<v\le u<t\}$ and ${\mathcal {F}}^{t}={\mathcal {F}}^{t}_\infty =\vee _{s\le t}{\mathcal {F}}^{t}_s$. Throughout this paper, we shall use $\vert \cdot \vert$ for the Euclidean norm, $\Vert u\Vert :=\sqrt{{\mathbb {E}}[\vert u\vert ^2]}$ and $\Vert u\Vert _p:=\root p \of {{\mathbb {E}}[\vert u\vert ^p]}$. We are interested in the ${\mathbb {R}}^d$-valued random periodic solution to a SDE of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathrm {d}{X^{t_0}_t} = \big [-A X^{t_0}_t + f(t,X^{t_0}_t) \big ] \mathrm {d}{t}+g(t)\mathrm {d}{W_t},&{} \quad \text {for } t \in (t_0,T],\\ X^{t_0}_{t_0} = \xi ,&{} \end{array}\right. } \end{aligned}$$

(3)

where $\xi$ is a ${\mathcal {F}}^{t_0}$-measurable random initial condition. In addition, A, f, and g, and $\xi$ satisfy the following assumptions:

Assumption 1

The linear operator $A :{\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$ is self-adjoint and positive definite.

Assumption 1 implies the existence of a positive, increasing sequence $(\lambda _i)_{i\in [d]} \subset {\mathbb {R}}$ such that $0<\lambda _1 \le \lambda _2 \le \cdots \lambda _d$, and of an orthonormal basis $(e_i)_{i\in [d]}$ of ${\mathbb {R}}^d$ such that $A e_i = \lambda _i e_i$ for every $i \in [d]$, where $[d]:=\{1,\ldots ,d\}$.

Assumption 2

The mapping $f :{\mathbb {R}} \times {\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$ is continuous and periodic in time with period $\tau$. Moreover, there exists a $C_f \in (0,\infty )$ such that

$$\begin{aligned}&\langle u_1-u_2, f(t,u_1) - f(t,u_2) \rangle \le C_f \vert u_1 - u_2\vert ^2\\&\langle u, f(t,u) \rangle \le C_f (1+\vert u\vert ^2) \end{aligned}$$

for all $u,u_1, u_2 \in {\mathbb {R}}^d$ and $t \in [0,\tau )$.

Assumption 3

The diffusion coefficient functions $g :{\mathbb {R}} \rightarrow {\mathbb {R}}$ is continuous and periodic in time with period $\tau$. Moreover, we assume there exists a constant $\sigma >0$ such that $\sup _{s\in [0,\tau )}\vert g(s)\vert <\sigma$ and $\vert g(t_1)-g(t_2)\vert \le \sigma \vert t_2-t_1\vert$ for all $t_1,t_2 \in [0,\tau )$.

It is well known that under these assumptions the solution $X_{\cdot }^{t_0} :[t_0,T] \times \Omega \rightarrow {\mathbb {R}}^d$ to (3) is uniquely determined by the variation-of-constants formula

$$\begin{aligned} X^{t_0}_t(\xi ) = e^{-A(t-t_0)} \xi + \int _{t_0}^t e^{-A(t-s)} f(s,X^{t_0}_s) \mathrm {d}{s} + \int _{t_0}^t e^{-A(t-s)}g(s) \mathrm {d}{W_s}. \end{aligned}$$

(4)

1.1 The Pull-Back

We know there exists a standard ${\mathbb {P}}$-preserving ergodic Wiener shift $\theta$ such that $\theta _t (\omega )(s)=W_{t+s}-W_{t}$ for $s,t\in {\mathbb {R}}$. We will show that when $k\rightarrow \infty$, the pull-back $X^{-k\tau }_t(\xi )$ has a limit $X^* _t$ in $L^2(\Omega )$ and $X^* _t$ is the random periodic solution of SDE (3), satisfying

$$\begin{aligned} X^*_t = \int _{-\infty }^t e^{-A(t - s)} f(s,X^{*}_s) \mathrm {d}{s} + \int _{-\infty }^t e^{-A(t - s)} g(s) \mathrm {d}{W_s}. \end{aligned}$$

(5)

To achieve it, we need additional assumptions on $\xi$ and f.

Assumption 4

$C_f<\lambda _1$.

Assumption 5

There exists a constant $C_\xi$ such that $\Vert \xi \Vert <C_\xi$.

Assumption 6

There exists a constant ${\hat{C}}_f$ such that $\Big \vert f(t,u)-\frac{\langle f(t,u),u\rangle }{\vert u\vert ^2}u\Big \vert \le {\hat{C}}_f(1+\vert u\vert )$ for $u\in {\mathbb {R}}^d, t\in [0,\tau )$.

Assumption 6 together with Assumptions 1 to 3 ensures the existence of a global semiflow generated from SDE (3) with additive noise [11]. Section 3 is devoted to the first main result, which claims the existence and uniqueness of random periodic solutions to the SDE (3) under the one-sided Lipschitz condition on the drift.

Theorem 7

Under Assumptions 1 to 6, there exists a unique random periodic solution $X^{*}_t(\cdot )\in L^2(\Omega )$ such that the solution of (3) satisfies

$$\begin{aligned} \lim _{k\rightarrow \infty }\Vert X^{-k\tau }_t(\xi )-X^*_t\Vert =0. \end{aligned}$$

(6)

In Sect. 4, we derive additional properties of the solution such as the uniform boundedness for a higher moment of $X^{-k\tau }_t$ and solution regularity under an additional Assumption 13, which imposes superlinearity of f and assumes a larger lowerbound for $\lambda _1$ compared to Assumption 4. Those properties will play an important role in proving the order of convergence of the backward Euler–Maruyama in Theorem 19.

1.2 The Backward Euler–Maruyama

For stiff ordinary differential equations, the implicit method is preferred due to its good performance even on a time grid with a large step size [15]. For its stochastic counterpart such as (3), we shall approximate the solution using the backward Euler–Maruyama method, the simplest version of implicit methods for SDEs.

Let us fix an equidistant partition ${\mathcal {T}}^h:=\{jh,\ j\in {\mathbb {Z}} \}$ with stepsize $h\in (0,1)$. Note that ${\mathcal {T}}^h$ stretches along the real line because eventually we are dealing with an infinite time horizon problem in the form of (5). Then to simulate the solution to (3) starting at $-k\tau$, the backward Euler–Maruyama method on ${\mathcal {T}}^h$ is given by the recursion

$$\begin{aligned} \begin{aligned} {\hat{X}}_{-k\tau +(j+1)h}^{-k\tau } =&{\hat{X}}_{-k\tau +jh}^{-k\tau } - Ah{\hat{X}}_{-k\tau +(j+1)h}^{-k\tau }+h f\big ((j+1)h, {\hat{X}}_{-k\tau +(j+1)h}^{-k\tau } \big )\\&+ g(jh)\Delta W_{-k\tau +jh} \end{aligned} \end{aligned}$$

(7)

for all $j \in {\mathbb {N}}$, where the initial value ${\hat{X}}_{-k\tau }^{-k\tau } = \xi$, and $\Delta W_{-k\tau +jh}:=W_{-k\tau +(j+1)h}-W_{-k\tau +jh}$. Note that due to the periodicity of f (c.f. Assumption 2), we write $f(-k\tau +jh, {\hat{X}}_{-k\tau +jh}^{-k\tau } )$ as $f(jh, {\hat{X}}_{-k\tau +jh}^{-k\tau })$, and similar arguments for the g term.

The implementation of (7) requires solving a nonlinear equation at each iteration. Theorem 16 ensures the well-posedness of difference equation (7) under Assumptions 1 to 4. We explore the random periodicity of its solution in Sect. 5 and prove the second main result in our paper:

Theorem 8

Under Assumptions 1 to rm 5, for any $h\in (0,1)$ with $\tau =nh$, $n\in {\mathbb {N}}$, the backward Euler–Maruyama method (7) admits a random period solution on ${\mathcal {T}}^h$.

We also determine a strong order 1/2 for the backward Euler–Maruyama method in Theorem 19 and Corollary 20. Compared to Theorem 3.4 and Theorem 4.2 in [5] which imposed condition on the size of h (to be sufficient small) because of the implementation of explicit numerical methods, we benefit a flexible choice of stepsize h from using the backward Euler–Maruyama method even in the infinite horizon case.

Finally we assess the performance of the backward Euler–Maruyama method via a numerical experiment and compare it with the one of the classical Euler–Maruyama method under various steps. The result shows that the backward Euler–Maruyama method is able to converge to the random periodic solution when the stepsize is fairly large while Euler–Maruyama method diverges.

2 Preliminaries

In this section, we present a few useful mathematical tools for later use.

Lemma 9

(The Grönwall inequality: a continuous version [1]) Let I denote a time interval in form of $[I_-,I^+]$. Let a, b and u be real-valued functions defined on I. Assume that a and b are continuous and that the negative part of a is integrable on every closed and bounded subinterval of I. Then if b is nonnegative and if u satisfy the following inequality

$$\begin{aligned} u(t)\le a(t)+\int _{I_-}^{t}b(s)u(s)\mathrm {d}s, \end{aligned}$$

(8)

then

$$\begin{aligned} u(t)\le a(t)+\int _{I_-}^t a(s)b(s)\exp {\Big (\int _s^t b(r)\mathrm {d}r\Big )}\mathrm {d}s. \end{aligned}$$

(9)

If in addition, the function a is non-decreasing, then

$$\begin{aligned} u(t)\le a(t)\exp {\Big (\int _{I_-}^t b(r)\mathrm {d}r\Big )}. \end{aligned}$$

(10)

Lemma 10

(The Grönwall inequality: a discrete version [17, 18]) Consider two nonnegative sequences $(u_n)_{n\in {\mathbb {N}}}, (a_n)_{n\in {\mathbb {N}}} \subset {\mathbb {R}}$ which for some given $w \in [0,\infty )$ satisfy

$$\begin{aligned} u_n \le a_n + w\sum _{j=1}^{n-1} u_j,\quad \text { for all } n \in {\mathbb {N}}. \end{aligned}$$

Then, for all $n \in {\mathbb {N}}$, it also holds true that

$$\begin{aligned} u_n \le a +\frac{w}{c_{n-1}}\big (u_0+\sum _{j=1}^{n-1} a_jc_j \big ), \end{aligned}$$

where $c_j:=\frac{1}{(1+w)^j}$ for $j\in {\mathbb {N}}$.

Also the crucial but simple equality for the analysis of the backward Euler–Maruyama is

$$\begin{aligned} \vert b\vert ^2-\vert a\vert ^2+\vert b-a\vert ^2=2\langle b-a, b\rangle . \end{aligned}$$

(11)

3 Existence and Uniqueness of the Random Periodic Solution

In this section, we focus on the existence and uniqueness of the random periodic solution to SDE (3). To achieve it, we first show there is a uniform bound for the second moment of its solution under necessary assumptions.

Lemma 11

For SDE (3) with given initial condition $\xi$ and satisfying Assumptions 1 to 5, we have

$$\begin{aligned} \sup _{k\in {\mathbb {N}}}\sup _{t>-k\tau }{\mathbb {E}}[\vert X_{t}^{-k\tau }(\xi )\vert ^2]\le C_{\xi }^2+\frac{2K_2\lambda _1}{2(\lambda _1-C_f)}, \end{aligned}$$

(12)

where $K_2:=\frac{\sigma ^2+2C_f}{2\lambda _1}$.

Proof of Lemma 11

Applying Itô formula to $e^{2\lambda _1 t}\Vert X_{t}^{-k\tau }(\xi )\Vert ^2$ and taking the expectation yield

$$\begin{aligned} \begin{aligned} e^{2\lambda _1 t}{\mathbb {E}}[\vert X_{t}^{-k\tau }(\xi )\vert ^2]=&e^{-2\lambda _1 k\tau }{\mathbb {E}}[\vert \xi \vert ^2]+2\lambda _1 \int _{-k\tau }^t e^{2\lambda _1 s}{\mathbb {E}}[\vert X_{s}^{-k\tau }\vert ^2]\mathrm {d}s\\&-2\int _{-k\tau }^te^{2\lambda _1 s}{\mathbb {E}}\langle X_{s}^{-k\tau }, AX_{s}^{-k\tau }\rangle \mathrm {d}s\\ {}&+2\int _{-k\tau }^te^{2\lambda _1 s}{\mathbb {E}}\langle X_{s}^{-k\tau }, f(s,X_{s}^{-k\tau })\rangle \mathrm {d}s\\&+\int _{-k\tau }^t e^{2\lambda _1 s}\vert g(s)\vert ^2\mathrm {d}s. \end{aligned} \end{aligned}$$

(13)

Note that $2(\lambda _1I-A)$ is non-positive definite. Then making use of Assumptions 2 and 3 gives

$$\begin{aligned} e^{2\lambda _1 t}\Vert X_{t}^{-k\tau }(\xi )\Vert ^2&\le e^{-2\lambda _1 k\tau }\Vert \xi \Vert ^2+2C_f\int _{-k\tau }^te^{2\lambda _1 s}\Vert X_{s}^{-k\tau }\Vert ^2\mathrm {d}s\\&\quad \quad +(\sigma ^2+2C_f)\int _{-k\tau }^t e^{2\lambda _1 s}\mathrm {d}s\\&\le e^{-2\lambda _1 k\tau }\Vert \xi \Vert ^2+\frac{(\sigma ^2+2C_f)}{2\lambda _1}(e^{2\lambda _1 t}-e^{-2\lambda _1 k\tau })\\&\quad \quad +2C_f\int _{-k\tau }^te^{2\lambda _1 s}\Vert X_{s}^{-k\tau }\Vert ^2\mathrm {d}s. \end{aligned}$$

Denote $K_1:= e^{-2\lambda _1 k\tau }\big (\Vert \xi \Vert ^2-\frac{\sigma ^2+2C_f}{2\lambda _1}\big )$, $K_2:=\frac{\sigma ^2+2C_f}{2\lambda _1}$ and $K_3:=2C_f$. Note that $K_3\le 2\lambda _1$ because of Assumption 4. By the Grönwall inequality, we have that

$$\begin{aligned} e^{2\lambda _1 t}\Vert X_{t}^{-k\tau }(\xi )\Vert ^2&\le K_1+K_2 e^{2\lambda _1 t}+\int _{-k\tau }^t( K_1+K_2 e^{2\lambda _1 s})K_3e^{K_3(t-s)}\mathrm {d}s\\&\le K_1e^{K_3(k\tau +t)}+K_2 e^{2\lambda _1 t}+\frac{K_2K_3}{2\lambda _1-K_3}(e^{2\lambda _1 t}-e^{-2\lambda _1 k\tau })\\&\le (K_1e^{2\lambda _1k\tau }+K_2) e^{2\lambda _1 t}+\frac{K_2K_3}{2\lambda _1-K_3}e^{2\lambda _1 t}. \end{aligned}$$

Note that $K_1e^{2\lambda _1 k\tau }+K_2=\Vert \xi \Vert ^2$. By Assumption 5, it leads to

$$\begin{aligned} \Vert X_{t}^{-k\tau }(\xi )\Vert ^2\le \Vert \xi \Vert ^2+\frac{K_2K_3}{2\lambda _1-K_3}\le C_{\xi }^2+\frac{2K_2\lambda _1}{2\lambda _1-K_3}. \end{aligned}$$

$\square$

Then we explore the solution dependence on initial conditions.

Lemma 12

Let Assumptions 1 to 3 hold. Denote by $X_t^{-k\tau }$ and $Y_t^{-k\tau }$ two solutions of SDE (3) with different initial values $\xi$ and $\eta$. Then

$$\begin{aligned} \Vert X_t^{-k\tau }-Y_t^{-k\tau }\Vert ^2\le e^{(C_f-\lambda _1)(t+k\tau )}\Vert \xi -\eta \Vert ^2. \end{aligned}$$

In addition, if Assumption 4 holds, then for every $\epsilon >0$, there exists a $t\ge -k\tau$ such that it holds

$$\begin{aligned} \Vert X_{{\tilde{t}}}^{-k\tau }-Y_{{\tilde{t}}}^{-k\tau }\Vert ^2<\epsilon \end{aligned}$$

(14)

whenever ${\tilde{t}}\ge t$.

Proof of Lemma 12

Define $E_t^{-k\tau }:=X_t^{-k\tau }-Y_t^{-k\tau }$. From (4), we have that

$$\begin{aligned} \begin{aligned}&E_t^{-k\tau } = (\xi -\eta )+\int _{-k\tau }^{t} e^{-A(t - s)} \big (f(s,X^{-k\tau }_s)- f(s,Y^{-k\tau }_s) \big )\mathrm {d}{s}. \end{aligned} \end{aligned}$$

(15)

Similar as the proof of Lemma 11, we apply Itô formula to $e^{2\lambda _1 t}\vert E_t^{-k\tau }\vert ^2$, take the expectation, make use of Assumption 2 and get

$$\begin{aligned} \begin{aligned} e^{2\lambda _1 t}\Vert E_t^{{-}k\tau }\Vert ^2&\le e^{{-}2\lambda _1 k\tau }\Vert \xi {-}\eta \Vert ^2+2\int _{{-}k\tau }^te^{2\lambda _1 s}{\mathbb {E}}\Big \langle E_s^{{-}k\tau }, f(s,X_{s}^{{-}k\tau })-f(s,Y_{s}^{{-}k\tau })\Big \rangle \mathrm {d}s\\&\le e^{-2\lambda _1 k\tau }\Vert \xi -\eta \Vert ^2{+}2C_f\int _{-k\tau }^te^{2\lambda _1 s}\Vert E_{s}^{-k\tau }\Vert ^2\mathrm {d}s. \end{aligned} \end{aligned}$$

(16)

Applying Eqn. (10) gives the desired inequality. The claim in (14) follows if Assumption 4 holds. $\square$

With Lemmas 11, 12 and Assumption 6, the main result Theorem 7 can be shown by following the same argument in the proof of Theorem 2.4 in [5].

4 More Results on the Solution

In this section, we explore some properties of the solution to 3 for analysis later.

Assumption 13

There exists a constant $q\in (1,\infty )$ and a positive L such that

$$\begin{aligned} \vert f (t_1,u_1)-f (t_2,u_2)\vert \le L(1+\vert u_1 \vert ^{q-1}+\vert u_2 \vert ^{q-1})\vert u_1-u_2\vert , \end{aligned}$$

for $t_1,t_2\in [0,\tau )$ and $u_1,u_2\in {\mathbb {R}}^d$. In addition, there exists a positive number $p\in [4q-2,\infty )$ such that

$$\begin{aligned} \gamma _p:=\big (C_f+\frac{(p-1)\sigma ^2}{2}\Big )(2+p+2^{p+1})<p\lambda _1. \end{aligned}$$

The first property we will show is the uniform boundedness for the p-th moment of the SDE solution.

Proposition 14

Under Assumptions 1 to 5 and 13, the solution to (3) satisfies

$$\begin{aligned} \sup _{k\in {\mathbb {N}}}\sup _{t>-k\tau }{\mathbb {E}}[\vert X_{t}^{-k\tau }(\xi )\vert ^p_p]<\infty . \end{aligned}$$

(17)

Proof of Proposition 14

From the proof of Lemma 11, we know that

$$\begin{aligned} \mathrm {d}e^{2\lambda _1 t}\vert X_{t}^{-k\tau }\vert ^2=&2\lambda _1 e^{2\lambda _1 t}\vert X_{t}^{-k\tau }\vert ^2\mathrm {d}t-2e^{2\lambda _1 t}\langle X_{t}^{-k\tau }, AX_{t}^{-k\tau }\rangle \mathrm {d}t\\&+2e^{2\lambda _1 t}\langle X_{t}^{-k\tau }, f(t,X_{t}^{-k\tau })\rangle \mathrm {d}t+2e^{2\lambda _1 t}\vert g(t)\vert ^2\mathrm {d}t\\&+2e^{2\lambda _1 t}\langle X_{t}^{-k\tau }, g(t)\rangle \mathrm {d}W_t. \end{aligned}$$

Then applying Itô formula to $e^{p\lambda _1 t}\vert X_{t}^{-k\tau }\vert ^p=\big (e^{2\lambda _1 t}\vert X_{t}^{-k\tau }\vert ^2\big )^{p/2}$ and taking into consideration $2(\lambda _1I-A)$ being non-positive definite give

$$\begin{aligned} {\mathbb {E}}[e^{p\lambda _1 t}\vert X_{t}^{-k\tau }\vert ^p]\le&e^{-p\lambda _1k\tau }\Vert \xi \Vert ^p_p\\&+p \int _{-k\tau }^{t}{\mathbb {E}}\Big [e^{(p-2)\lambda _1 s}\vert X_{s}^{-k\tau }\vert ^{p-2}e^{2\lambda _1 s}\langle X_{s}^{-k\tau }, f(t,X_{s}^{-k\tau })\rangle \Big ]\mathrm {d}s\\&+\frac{p(p-1)}{2} \int _{-k\tau }^{t}{\mathbb {E}}\Big [e^{(p-2)\lambda _1 s}\vert X_{s}^{-k\tau }\vert ^{p-2}e^{2\lambda _1 s}\Big ]g(s)^2\mathrm {d}s. \end{aligned}$$

Now by the Young inequality

$$\begin{aligned} a^{p-2}b\le \frac{p-2}{p}a^p+\frac{2}{p}b^{p/2}, \forall a,b\ge 0, \end{aligned}$$

and the inequality from fundamental calculus,

$$\begin{aligned} \big (a^2+b^2\big )^{\frac{p}{2}}\le 2^p(a^p+b^p), \forall a,b\ge 0, \end{aligned}$$

we have that

$$\begin{aligned} {\mathbb {E}}[e^{p\lambda _1 t}\vert X_{t}^{-k\tau }\vert ^p]&\le e^{-p\lambda _1k\tau }\Vert \xi \Vert ^p_p\\&\quad +p\Big (C_f{+}\frac{(p{-}1)\sigma ^2}{2}\Big ) \int _{-k\tau }^{t}e^{p\lambda _1 s}{\mathbb {E}}\Big [\vert X_{s}^{-k\tau }\vert ^{p-2}\big (1{+}\vert X_{s}^{-k\tau }\vert ^{2}\big )\Big ]\mathrm {d}s\\&\le e^{-p\lambda _1k\tau }\Vert \xi \Vert ^p_p+\gamma _p \int _{-k\tau }^{t}e^{p\lambda _1 s}\big (1+\Vert X_{s}^{-k\tau }\Vert ^{p}_p\big )\mathrm {d}s\\&\le {\hat{K}}_1+\gamma _p e^{p\lambda t}+\gamma _p \int _{-k\tau }^{t}{\mathbb {E}}[e^{p\lambda _1 s}\vert X_{s}^{-k\tau }\vert ^{p}]\mathrm {d}s, \end{aligned}$$

where ${\hat{K}}_1:= e^{-p\lambda _1 k\tau }\big (\Vert \xi \Vert ^p_p-\gamma _p\big )$. Because of Assumption 13, the rest simply follows the same way as the end of the proof for Lemma 11. $\square$

Following a similar argument as in Proposition 5.4 and 5.5 [2], we can easily get the following bounds for analysis later.

Proposition 15

Let Assumptions 1 to 5 and 13 hold. Then there exists a positive constant $C_{q,A,f}$ which depends on q, d, A,$C_f$ only, such that

$$\begin{aligned} \Vert X_{t_1}^{-k\tau }-X_{t_2}^{-k\tau }\Vert \le C_{q,A,f}\big (1+\sup _{k\in {\mathbb {N}}}\sup _{t\ge -k\tau }\Vert X_{t}^{-k\tau }\Vert ^q_{2q}\big )\vert t_2-t_1\vert ^{\frac{1}{2}}, \end{aligned}$$

(18)

for all $t_1,t_2\ge -k\tau$. Moreover,

$$\begin{aligned} \begin{aligned}&\int _{t_1}^{t_2}\big \Vert A\big (X_{s}^{-k\tau }-X_{t_4}^{-k\tau }\big )+f\big (s,X_{s}^{-k\tau }\big )-f\big (t_3,X_{t_4}^{-k\tau }\big )\big )\big \Vert \mathrm {d}s\\&\le C_{q,A,f}\big (1+\sup _{k\in {\mathbb {N}}}\sup _{t\ge -k\tau }\Vert X_{t}^{-k\tau }\Vert ^{2q-1}_{4q-2}\big )\vert t_2-t_1\vert ^{\frac{3}{2}}, \end{aligned} \end{aligned}$$

(19)

for all $t_3,t_4\in [t_1,t_2]$.

5 The Random Periodic Solution of the Backward Euler–Maruyama Scheme

In this section, we will prove that the backward Euler–Maruyama method (7) admits a unique discretized random period solution. To achieve this, let us first show the existence and uniqueness of solution to the targeted scheme.

Theorem 16

(Well-posedness) Let Assumptions 1 to 4 be satisfied. Then for any $h\in (0,1)$, there exists a unique ${\mathbb {R}}^d$-valued sequence $({\hat{X}}^{-k\tau }_{jh})_{h\in {\mathbb {N}}}$ satisfying the difference equation (7) on the associated time grid ${\mathcal {T}}^h$.

Proof of Theorem 16

Let $h \in (0,1)$ and define $G :{\mathbb {R}}^d \rightarrow {\mathbb {R}}^d$ by $G_(\zeta ) = \zeta +Ah\zeta - h f(t, \zeta )$ for all $\zeta \in {\mathbb {R}}^d$ and $t\in [0,\tau )$. Then it holds

$$\begin{aligned} \langle G_t(\varsigma ) - G_t(\zeta ), \varsigma - \zeta \rangle&= (I+Ah)\vert \varsigma - \zeta \vert ^2 - h \langle f(t,\varsigma ) - f(t,\zeta ), \varsigma - \zeta \rangle \\&\ge (1 +\lambda _1h- C_f h) \vert \varsigma - \zeta \vert ^2. \end{aligned}$$

Because of Assumption 4, we have $L_{G_t} :=1 +\lambda _1h- C_f h>1$. Hence, the uniform monotonicity theorem¹ (c.f. Proposition 3.5 in [10]) is applicable. In particular, the sequence $({\hat{X}}^{-k\tau }_{jh})_{h\in {\mathbb {N}}}$ defined by

$$\begin{aligned} {\hat{X}}^{-k\tau }_{(j+1)h} := G_{(j+1)h}^{-1}\big ({\hat{X}}^{-k\tau }_{jh} + g(jh)\Delta W_{-k\tau +jh}) \end{aligned}$$

for every $j \in {\mathbb {N}}$ satisfies (7). $\square$

The next Lemma claims there is a uniform bound for the second moment of the numerical solution under necessary assumptions.

Lemma 17

Under Assumptions 1 to 5, for any $h\in (0,1)$, it holds for the backward Euler–Maruyama method (7) on ${\mathcal {T}}^h$ that

$$\begin{aligned} \sup _{k,N\in {\mathbb {N}}}{\mathbb {E}}[\vert {\hat{X}}_{-k\tau +Nh}^{-k\tau } (\xi )\vert ^2]< \infty . \end{aligned}$$

(20)

Proof of Lemma 17

First note that from (11), we have that for any $N\in {\mathbb {N}}$

$$\begin{aligned} \begin{aligned}&\vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }\vert ^2-\vert {\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\vert ^2+\vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\vert ^2\\&\quad =2\langle {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau },{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle . \end{aligned} \end{aligned}$$

(21)

From (7), we have that

$$\begin{aligned} \begin{aligned}&2\langle {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau },{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle \\&\quad =-2h\langle A{\hat{X}}_{-k\tau +Nh}^{-k\tau },{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle +2h\langle f\big (Nh,{\hat{X}}_{-k\tau +Nh}^{-k\tau }\big ),{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle \\&\quad \ +2\langle g\big ((N-1)h\big )\Delta W_{-k\tau +(N-1)h},{\hat{X}}_{-k\tau +Nh}^{-k\tau }\rangle . \end{aligned} \end{aligned}$$

(22)

Note that ${\mathbb {E}}\langle g\big ((N-1)h\big )\Delta W_{-k\tau +(N-1)h},{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\rangle =0$. Taking the expectation of both sides of (22) and making use of Assumption 2 give

$$\begin{aligned}&\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }\Vert ^2-\Vert {\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\Vert ^2+\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\Vert ^2\\&\quad =2{\mathbb {E}}\langle {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau },{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle \\&\quad \le -2h{\mathbb {E}} \langle (A-C_fI){\hat{X}}_{-k\tau +Nh}^{-k\tau },{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle +h(2C_f+\sigma ^2)\\&\quad \quad +\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\Vert ^2. \end{aligned}$$

Then cancelling the same term on both side gives

$$\begin{aligned}&\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }\Vert ^2-\Vert {\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\Vert ^2\\&\quad \le -2h{\mathbb {E}} \langle (A-C_fI){\hat{X}}_{-k\tau +Nh}^{-k\tau },{\hat{X}}_{-k\tau +Nh}^{-k\tau } \rangle +h(2C_f+\sigma ^2)\\&\quad \le -2h (\lambda _1-C_f)\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }\Vert ^2+h(2C_f+\sigma ^2). \end{aligned}$$

Let $\alpha :=\frac{2C_f+\sigma ^2}{2(\lambda _1-C_f)}$. Rearranging the terms above gives

$$\begin{aligned} \big (1+2h(\lambda _1-C_f)\big )\big (\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }\Vert ^2-\alpha \big )\le \Vert {\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }\Vert ^2-\alpha . \end{aligned}$$

(23)

By iteration, this leads to

$$\begin{aligned} \Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }\Vert ^2\le \frac{1}{\big (1+2h(\lambda _1-C_f)\big )^N}\big (\Vert \xi \Vert ^2-\alpha \big )+\alpha . \end{aligned}$$

(24)

Because of Assumptions 4 and 5, the term on the right-hand side above can be bounded by $\Vert \xi \Vert ^2+\alpha$, which is independent of k, N and h. $\square$

The next result shows two numerical solutions starting from different initial conditions can be arbitrarily close after sufficiently many iterations.

Lemma 18

Under Assumptions 1 to 5, define ${\hat{X}}_{-k\tau +Nh}^{-k\tau }$ and ${\hat{Y}}_{-k\tau +Nh}^{-k\tau }$ solutions of the backward Euler–Maruyama scheme on ${\mathcal {T}}^h$. Then there exists an $N^*$ such that for any $N\ge N^*$, $\Vert {\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{Y}}_{-k\tau +Nh}^{-k\tau }\Vert <\epsilon$.

Proof of Lemma 18

Define $D_N:={\hat{X}}_{-k\tau +Nh}^{-k\tau }-{\hat{Y}}_{-k\tau +Nh}^{-k\tau }$. Let us use (11) again, which allows us to examine the following term:

$$\begin{aligned} 2{\mathbb {E}} \langle D_N-D_{N-1} ,D_N\rangle&=-2h{\mathbb {E}}\langle AD_N,D_N\rangle \\&\quad +2h{\mathbb {E}}\langle f\big (Nh,{\hat{X}}_{-k\tau +Nh}^{-k\tau }\big )-f\big (Nh,{\hat{Y}}_{-k\tau +Nh}^{-k\tau }\big ),D_N \rangle \\&\quad \le 2h{\mathbb {E}}\langle (-A+C_fI)D_N,D_N\rangle . \end{aligned}$$

Following a similar argument as in the proof of Lemma 17, this leads to

$$\begin{aligned} (1+2h(\lambda _1-C_f))\Vert D_N\Vert ^2\le \Vert D_{N-1}\Vert ^{2}. \end{aligned}$$

By iteration, we have

$$\begin{aligned} \Vert D_N\Vert ^{2}\le \frac{1}{(1+2h(\lambda _1-C_f))^N}\Vert D_{0}\Vert ^{2}=\frac{1}{(1+2h(\lambda _1-C_f))^N}\Vert \xi -\eta \Vert ^{2}. \end{aligned}$$

Because of $\lambda _1>C_f$, the assertion follows. $\square$

Proof of Theorem 8

First we shall show that there exists a limit of ${\hat{X}}_{t}^{-k\tau }$ in $L^2(\Omega )$. Note from Lemma 17, it holds ${\hat{X}}_{-k\tau +Nh}^{-k\tau }\in L^2(\Omega )$ for $N\in {\mathbb {N}}$. For $t=-k\tau +Nh$, by using the semi-flow property we have for $m\in {\mathbb {N}}$

$$\begin{aligned} {\hat{X}}^{-k\tau -m\tau }_t={\hat{X}}^{-k\tau }_t\circ {\hat{X}}^{-k\tau -m\tau }_{-k\tau }. \end{aligned}$$

Both sides are the same process and ${\hat{X}}^{-k\tau }_t$ on the RHS has a different initial condition. Denote $M:=nk$, then by Lemma 18 we have for $\epsilon >0$ there exists a $M^*$ such that for $M\ge M^*$

$$\begin{aligned} \big \Vert {\hat{X}}^{-k\tau -m\tau }_t-{\hat{X}}^{-k\tau }_t\big \Vert =\big \Vert {\hat{X}}^{-(M+nm)h}_t-{\hat{X}}^{-Mh}_t\big \Vert <\epsilon . \end{aligned}$$

Then we construct the Cauchy sequence $({\hat{X}}^{-k\tau }_t)_{k\in {\mathbb {N}}}$ converging to some limit ${\hat{X}}^*_t$ in $L^2(\Omega )$. Also it is not hard to show that the convergence is independent of the initial point. For $k\rightarrow \infty$, we have from Lemma 18

$$\begin{aligned} \big \Vert {\hat{X}}^*-{\hat{X}}^{-k\tau }_t(\eta )\big \Vert \le \big \Vert {\hat{X}}^*-{\hat{X}}^{-k\tau }_t(\xi )\big \Vert + \big \Vert {\hat{X}}^{-k\tau }_t(\xi )-{\hat{X}}^{-k\tau }_t(\eta )\big \Vert \rightarrow 0. \end{aligned}$$

Now let us verify the random periodicity of the backward Euler–Maruyama scheme by induction. Let us examine two terms ${\hat{X}}_{-k\tau +Nh}^{-k\tau }(\theta _\tau \omega )$ and ${\hat{X}}_{-(k-1)\tau +Nh}^{-(k-1)\tau }(\omega )$, where $t=-k\tau +Nh$. For ${\hat{X}}_{-k\tau +Nh}^{-k\tau }(\theta _\tau \omega )$, we have the expression

$$\begin{aligned} {\hat{X}}_{-k\tau +Nh}^{-k\tau }(\theta _\tau \omega )&= {\hat{X}}_{-k\tau +(N-1)h}^{-k\tau }(\theta _\tau \omega )-Ah{\hat{X}}_{-k\tau +Nh}^{-k\tau }(\theta _\tau \omega ) \\&\quad +h f\big (Nh, {\bar{X}}_{-k\tau +Nh}^{-k\tau }(\theta _\tau \omega ) \big )+ g({(N-1)h})\Delta W_{-k\tau +(N-1)h}(\theta _\tau \omega ), \end{aligned}$$

where

$$\begin{aligned} \Delta W_{-k\tau +(N-1)h}(\theta _\tau \omega )=W_{-(k-1)\tau +Nh}-W_{-(k-1)\tau +(N-1)h}=\Delta W_{-(k-1)\tau +(N-1)h}(\omega ). \end{aligned}$$

For ${\hat{X}}_{-(k-1)\tau +Nh}^{-(k-1)\tau }(\omega )$, we have its expression given by

$$\begin{aligned} {\hat{X}}_{-(k-1)\tau +Nh}^{-(k-1)\tau }(\omega ) =&{\hat{X}}_{-(k-1)\tau +(N-1)h}^{-(k-1)\tau }(\omega )-Ah{\hat{X}}_{-(k-1)\tau +Nh}^{-(k-1)\tau }(\omega )\\&f( Nh, {\bar{X}}_{-(k-1)\tau +Nh}^{-(k-1)\tau } ( \omega )\big ){+} g({(N-1)h})\Delta W_{-(k-1)\tau +(N-1)h}(\omega ). \end{aligned}$$

By induction and by the pathwise uniqueness of the solution of the backward Euler–Maruyama scheme (Theorem 16), we have that

$$\begin{aligned} {\hat{X}}_{-k\tau +Nh}^{-k\tau }\big (\theta _\tau \omega ,\xi (\theta _\tau \omega )\big ) =\theta _\tau {\hat{X}}_{-k\tau +Nh}^{-k\tau }\big (\omega ,\xi (\omega )\big ) = {\hat{X}}_{-(k-1)\tau +Nh}^{-(k-1)\tau }\big ( \omega ,\xi (\omega )\big ). \end{aligned}$$

Finally from (5) and the fact $t=-k\tau +Nh$, we have

$$\begin{aligned}&\big \Vert {\hat{X}}_{t}^*(\theta _\tau \omega )-{\hat{X}}_{t+\tau }^{*}( \omega )\big \Vert \\&\quad \le \big \Vert X_{t}^{-k\tau }\big (\theta _\tau \omega ,\xi (\theta _\tau \omega )\big )-{\hat{X}}_{t}^*(\theta _\tau \omega )\big \Vert {+}\big \Vert {\hat{X}}_{t+\tau }^{-(k-1)\tau }\big ( \omega ,\xi (\omega )\big ){-}{\hat{X}}_{t+\tau }^{*}( \omega )\big \Vert \overset{k\rightarrow \infty }{\longrightarrow }0. \end{aligned}$$

Therefore, ${\hat{X}}_{t}^*(\theta _\tau \omega )={\hat{X}}_{t+\tau }^{*}( \omega )$ ${\mathbb {P}}$-a.s. $\square$

6 Error Analysis

Theorem 19

Under Assumptions 1 to 5 and 13, for any $h\in (0,1)$ with $\tau =nh$, $n\in {\mathbb {N}}$, there exists a constant C that depends on q, A, f, g and d such that the backward Euler–Maruyama method (7) approximates the true solution of (3) on ${\mathcal {T}}^h$ with

$$\begin{aligned} \sup _{k,N}\big \Vert X^{-k\tau }_{-k\tau +Nh}-{\hat{X}}^{-k\tau }_{-k\tau +Nh}\big \Vert \le C h^{1/2}. \end{aligned}$$

(25)

Proof of Theorem 19

First note that

$$\begin{aligned} \begin{aligned}&X^{-k\tau }_{-k\tau +Nh}=X^{-k\tau }_{-k\tau +(N-1)h}-\int _{-k\tau +(N-1)h}^{-k\tau +Nh}AX^{-k\tau }_{s}\mathrm {d}s\\&\quad +\int _{-k\tau +(N-1)h}^{-k\tau +Nh}f\big (s,X^{-k\tau }_{s}\big )\mathrm {d}s+\int _{-k\tau +(N-1)h}^{-k\tau +Nh}g(s)\mathrm {d}W_s\\&=X^{-k\tau }_{-k\tau +(N-1)h}-\int _{-k\tau +(N-1)h}^{-k\tau +Nh}A\big (X^{-k\tau }_{s}-X^{-k\tau }_{-k\tau +Nh}\big )\mathrm {d}s-hAX^{-k\tau }_{-k\tau +Nh}\\&\quad +\int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (f\big (s,X^{-k\tau }_{s}\big )-f\big (s,X^{-k\tau }_{-k\tau +Nh}\big )\Big )\mathrm {d}s+hf\big (s,X^{-k\tau }_{-k\tau +Nh}\big )\\&\quad +\int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (g(s)-g\big ((N-1)h\big )\Big )\mathrm {d}W_s+g\big ((N-1)h\big )\Delta W_{-k\tau +(N-1)h}. \end{aligned} \end{aligned}$$

(26)

Define $e_N:=X^{-k\tau }_{-k\tau +Nh}-{\hat{X}}^{-k\tau }_{-k\tau +Nh}$. Then

$$\begin{aligned}&2{\mathbb {E}} \langle e_N-e_{N-1} ,e_N\rangle \\&\quad =-2h{\mathbb {E}}\langle Ae_N,e_N\rangle +2h{\mathbb {E}}\langle f\big ({Nh},X_{-k\tau +Nh}^{-k\tau }\big )-f\big ({Nh},{\hat{X}}_{-k\tau +Nh}^{-k\tau }\big ),e_N \rangle \\&\qquad +2{\mathbb {E}}\Big \langle -\int _{-k\tau +(N-1)h}^{-k\tau +Nh}A\big (X^{-k\tau }_{s}-X^{-k\tau }_{-k\tau +Nh}\big )\mathrm {d}s ,e_N\Big \rangle \\&\qquad +2{\mathbb {E}}\Big \langle \int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (f\big (s,X^{-k\tau }_{s}\big )-f\big (s,X^{-k\tau }_{-k\tau +Nh}\big )\Big )\mathrm {d}s ,e_N\Big \rangle \\&\qquad +2{\mathbb {E}}\Big \langle \int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (g(s)-g\big ((N-1)h\big )\Big )\mathrm {d}W_s ,e_N\Big \rangle . \end{aligned}$$

By the Young’s inequality

$$\begin{aligned}2ab\le \epsilon ^2a^2+\frac{b^2}{\epsilon ^2}, \forall a,b>0,\end{aligned}$$

and Assumption 2, we are able to choose $\epsilon _0^2:=h(\lambda _1-C_f){/3}$ such that

$$\begin{aligned}&2{\mathbb {E}} \langle e_N-e_{N-1} ,e_N\rangle \\&\quad \le 2h{\mathbb {E}}\langle (-A+C_fI)e_N,e_N\rangle +3\epsilon _0^2 \Vert e_N\Vert ^2\\&\qquad +\frac{1}{\epsilon ^2_0}\Big \Vert -\int _{-k\tau +(N-1)h}^{-k\tau +Nh}A\big (X^{-k\tau }_{s}-X^{-k\tau }_{-k\tau +Nh}\big )\mathrm {d}s\Big \Vert ^2\\&\qquad +\frac{1}{\epsilon ^2_0}\Big \Vert \int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (f\big (s,X^{-k\tau }_{s}\big )-f\big (s,X^{-k\tau }_{-k\tau +Nh}\big )\Big )\mathrm {d}s\Big \Vert ^2\\&\qquad +\frac{1}{\epsilon ^2_0}\Big \Vert \int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (g(s)-g\big ((N-1)h\big )\Big )\mathrm {d}W_s\Big \Vert ^2. \end{aligned}$$

By Proposition 15, we know there exists a constant C depending on q, A, f and g such that

$$\begin{aligned}&\Big \Vert -\int _{-k\tau +(N-1)h}^{-k\tau +Nh}A\big (X^{-k\tau }_{s}-X^{-k\tau }_{-k\tau +Nh}\big )\mathrm {d}s\Big \Vert ^2\\&\quad +\Big \Vert \int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (f\big (s,X^{-k\tau }_{s}\big )-f\big (s,X^{-k\tau }_{-k\tau +Nh}\big )\Big )\mathrm {d}s\Big \Vert ^2\\&\quad +\Big \Vert \int _{-k\tau +(N-1)h}^{-k\tau +Nh}\Big (g(s)-g\big ((N-1)h\big )\Big )\mathrm {d}W_s\Big \Vert ^2\\&\quad \le Ch^3\Big (1+\sup _{k,N} \Vert X^{-k\tau }_{-k\tau +Nh}\Vert _{4q-2}^{2q-1}\Big ):=\beta h^3. \end{aligned}$$

Note that $\beta$ is bounded because of Proposition 15. Then from (11) and the estimate above, we have that

$$\begin{aligned} \Vert e_N\Vert ^2-\Vert e_{N-1}\Vert ^2&\le 2{\mathbb {E}} \langle e_N-e_{N-1} ,e_N\rangle \\&\le 2h{\mathbb {E}}\langle (-A+C_fI)e_N,e_N\rangle +3\epsilon _0^2 \Vert e_N\Vert ^2+\frac{\beta h^3}{\epsilon ^2_0}. \end{aligned}$$

Define ${\hat{\alpha }}:=\frac{\beta h}{(\lambda _1-C_f)^2}$. The inequality above can be rearranged to

$$\begin{aligned} \Big (1+h(\lambda _1-C_f)\Big )\big (\Vert e_N\Vert ^2-{\hat{\alpha }}\big ) \le \Vert e_{N-1}\Vert ^2-{\hat{\alpha }}. \end{aligned}$$

By iteration and assuming ${\hat{X}}^{-k\tau }_{-k\tau }=X^{-k\tau }_{-k\tau }=\xi$, we have

$$\begin{aligned} \Vert e_N\Vert ^2\le \Big (1-\frac{1}{1+h(\lambda _1-C_f)^N}\Big )\frac{\beta h}{(\lambda _1-C_f)^2} \end{aligned}$$

Finally due to Assumption 4 (alternatively, Assumption 13), we have $\Vert e_N\Vert ^2\le \frac{\beta h}{(\lambda _1-C_f)^2}.$ Then the assertion follows. $\square$

Corollary 20

Under Assumptions 1 to 6 and 13, for any $h\in (0,1)$ with $\tau =nh$, $n\in {\mathbb {N}}$, there exists a constant C that depends on q, A, f, g and d such that the exact and numerical random periodic solutions of (7) given in Theorems 7 and 8 satisfy

$$\begin{aligned} \sup _{t\in {\mathcal {T}}^h} \big \Vert X^*_t-{\hat{X}}^*_t\big \Vert \le C h^{\frac{1}{2}}. \end{aligned}$$

(27)

Proof of Corollary 20

The result simply follows from

$$\begin{aligned} \big \Vert X^*_t-{\hat{X}}^*_t\big \Vert \le \limsup _{k}\Big [\big \Vert X^*_t-{\hat{X}}^{-k\tau }_t\big \Vert +\big \Vert X^{-k\tau }_t-{\hat{X}}^{-k\tau }_t\big \Vert +\big \Vert {\hat{X}}^{-k\tau }_t-{\hat{X}}^*_t\big \Vert \Big ]. \end{aligned}$$

$\square$

7 Numerical Analysis

In this section, we consider the following one-dimensional SDE example

$$\begin{aligned} \mathrm {d}X_t^{t_0}=-10\pi X_t^{t_0}\mathrm {d}t+\sin {(2\pi t)}\mathrm {d}t+0.05\mathrm {d}W_t. \end{aligned}$$

(28)

It is easily verified that the associated period is 1 and Assumptions 1 to 6 and 13 are fulfilled with $\lambda _1=10$, $C_f=2$ and $\sigma =0.05$. Thus, (28) has a random periodic solution according to Theorem 7 and its backward Euler–Maruyama simulation also admits a random periodic path. First, let us show, the scheme converges to its random periodic path regardless its initial condition. To achieve this, we choose the time grid between $t_0=-10$ and $T=0$ with stepsize 0.05, generate a Brownian realization on the time grid, and set two initial conditions to be 0.2 and $-0.3$. Two simulated paths can then be obtained in Fig. 1 by applying the backward Euler–Maruyama method in (7) iteratively on the time grid, with given initial condition and shared Brownian realization. As shown in Fig. 1, two paths coincide shortly after the start. Note in theory ${\hat{X}}_{t}^{*}={\hat{X}}_{t}^{-\infty }$, but we take pull-back time $-10$ as this is already enough to generate a good convergence to the random periodic paths for $t\ge -9$.

Fig. 1

Two paths generated by backward Euler–Maruyama method from differential initial conditions

As discussed in [5], there are two ways to demonstrate the periodicity. The easier approach is to simulate the processes ${\hat{X}}_{t}^{*}(\omega )=X^{-30}_t(\omega ,0.2)$for $t\in [-4,-1]$ and ${\hat{X}}_{t}^{*}(\theta _{-1}\omega )=X^{-30}_t(\theta _{-1}\omega ,0.2)$ for $t\in [-3,0]$. We can observe that the two segmented processes are identical in Fig. 2 due to ${\hat{X}}_{t-1}^{*}(\omega )={\hat{X}}_{t}^{*}(\theta _{-1}\omega )$.

Fig. 2

Two paths with generated by backward Euler–Maruyama method on different realizations

Fig. 3

The pull-back path ${\hat{X}}^{-30}(t,\theta _{-t}\omega )$ generated by backward Euler–Maruyama method

The other way to check random periodicity of path X with period $\tau$ is to verify whether or not ${\hat{X}}^{*}(t,\theta _{-t}\omega )$ is periodic with period $\tau$. To test it, we need to consider $X_t^{t_0}(\theta _{-t}\omega )$. Note that for any fixed $r\in {\mathbb {R}}$ we have that

$$\begin{aligned} \begin{aligned} \mathrm {d}X_t^{t_0}(\theta _{-r}\omega )&=-10\pi X_t^{t_0}(\theta _{-r}\omega )\mathrm {d}t+\sin {(2\pi t)}\mathrm {d}t+0.05\mathrm {d}W_{t}(\theta _{-r}\omega )\\&=-10\pi X_t^{t_0}(\theta _{-r}\omega )\mathrm {d}t+\sin {(2\pi t)}\mathrm {d}t+0.05\mathrm {d}W_{t-r}. \end{aligned} \end{aligned}$$

(29)

Now set $t_0=0$, and $X_{0}^{0}(\theta _{-r}\omega )=x_0$. For each fixed r, we simulate the path of Eqn. (29) through the backward Euler–Maruyama method up to $t=r$. Then we obtain the evaluation of ${\hat{X}}^{0}(r,\theta _{-r}\omega )$. To allow convergence, we look at the path pattern from $t=2$ to $t=5$ in Fig. 3. Apparently we have obtained a periodic pull-back path as expected, which in turn shows the random periodicity of the original path.

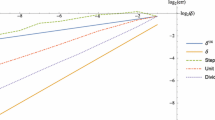
Finally, we test the order of convergence of the backward Euler–Maruyama method and compare the performance with (forward) Euler–Maruyama method. For its approximation, we first generated a reference solution with a small step size of $h_{\text {ref}}=2^{-15}$. This reference solution was then compared to numerical solutions with larger step sizes $h\in \{2^{-i}: i=4,5,6,7,8\}$. The error plot is shown in Fig. 4. We plot the Monte Carlo estimates of the root-mean-squared errors versus the underlying temporal step size, i.e., the number i on the x-axis indicates the corresponding simulation is based on the temporal step size $h = 2^{-i}$. Both methods give the order of convergence above 1, which is beyond the theoretical order of convergence. When the stepsize is large, say, $h=2^{-4}$, the Euler–Maruyama method has the error 0.048 which is almost five times of the error 0.011 from the backward Euler–Maruyama method. Indeed if we relax the stepsize to $h=2^{-3}$, the Euler–Maruyama diverges while the backward Euler–Maruyama method still converges as expected. This further supports Theorem 8 and the advantage of backward Euler–Maruyama method: the backward Euler–Maruyama method converges regardless the size of stepsize ($h<1$).

Fig. 4

Numerical experiment for simulating the random periodic solution of SDE (28): Step sizes versus $L^2$ error