Skip to main content
SpringerLink
Log in

TWO-WEIGHTED COMPOSITION OPERATORS ON SOBOLEV SPACES AND QUASICONFORMAL ANALYSIS

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

Abstract

We establish some equivalent conditions for a homeomorphism \(\varphi : D\rightarrow D'\) of Euclidean domains in \(\mathbb R^n\), \(n\ge 2\), to induce a bounded composition operator \(\varphi ^*: {L}^1_p(D';\omega ) \cap \text {Lip}_l(D')\rightarrow L^1_q(D;\theta )\), where \(1< q \le p<\infty\), by the composition rule: \(\varphi ^*(f)=f\circ \varphi\). Here \(\omega :D'\rightarrow (0,\infty )\) is an arbitrary weight function on the domain \(D'\), and \(\theta :D\rightarrow (0,\infty )\) is some weight function in Muckenhoupt’s \(A_{q}\)-class on the domain D. Moreover, we prove that the class of homeomorphisms under consideration is completely determined by the controlled variation of the weighted capacity of cubical condensers whose shells are concentric cubes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The definition of generalized derivatives assumes that \(\frac{\partial u}{dy_j}\in L_{1,\text {loc}}(D')\).

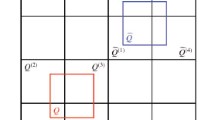
  2. For our description of a cubical condenser, see Definition 3.

  3. Recall that the norm \(|x|_p\) of a vector \(x=(x_1,x_2,\dots ,x_n)\in \mathbb R^n\) is defined as \(|x|_p=\bigl (\sum \nolimits _{k=1}^n|x_k|^p\bigr )^\frac{1}{p}\) for \(p\in [1,\infty )\) and \(|x|_\infty =\max \nolimits _{k=1,\dots ,n}|x_k|\). Each ball of the norm \(|x|_2\) or \(|x|_\infty\) is an Euclidean ball B or cube Q respectively.

  4. Instead of cubes, we can use balls as elementary sets.

  5. We understand (9) in the sense that any function \(u\in {L}^1_p(W;\omega ) \cap \overset{\circ }{\text {Lip}}_l(W)\) extended by zero beyond W belongs to \({L}^1_p(D';\omega ) \cap \text {Lip}_l(D')\).

  6. Henceforth, \(B_\delta\) is an arbitrary ball \(B(z,\delta )\subset D'\) containing y.

  7. It is not required that \(u_i\in \mathcal R(U_i)\) and \(v_i=\varphi ^*u_i\).

References

  1. Vodopyanov S. K. Basics of the quasiconformal analysis of a two-index scale of spatial mappings. Dokl. Akad. Nauk 2019;484(2):142–146.

  2. Vodopyanov S. K. Basics of the Quasiconformal Analysis of a two-index Scale of Space Mappings. Sib. Math. J. 2018;59(5):805–834.

  3. Vodopyanov S. K. Differentiability of mappings of the Sobolev space Wn-11with conditions on the distortion function. Sib. Math. J. 2018;59(6):983–1005.

  4. Vodopyanov S. K. Composition operators in weighted Sobolev spaces and the theory of Qp-homeomorphisms. Dokl. Akad. Nauk, 2020, vol. 494(5), p. 21–25. https://doi.org/10.31857/S268695432005046X

  5. Vodopyanov S. K. On analytical and geometrical properties of mappings in the theory of Qq,p-homeomorphisms. Mat. Zametki, 2020, vol. 108(6), p. 924–928.

  6. Vodopyanov S. K. The regularity of inverses to Sobolev mappings and the theory of Qq,p-homeomorphisms. Sib. Math. J. 2020, vol. 61(6), p. 1257–1299. https://doi.org/10.1134/S0037446620060051

  7. Vodopyanov S. K. and Tomilov A. O. Functional and analytical properties of a class of mappings of the quasiconformal analysis Izv. Ross. Akad. Nauk Ser. Mat., 2021, vol. 85(5), 883–931. https://doi.org/10.1070/IM9082

  8. Vodopyanov S. K. The Taylor Formula and Function Spaces. Novosibirsk: Novosibirsk Univ., 1988.

  9. Vodopyanov S. K. Mappings of homogeneous groups and imbeddings of functional spaces. Sib. Math. J., 1989, vol. 30(5), p. 685–698.

  10. Vodopyanov S. K. Weighted Sobolev spaces and mapping theory. Abstracts: All-Russia Mathematical School “Potential Theory” (Katsiveli, 26 June–3 July 1991). Kiev: Inst. Mat. Akad. Nauk USSR, Kiev. 1991. p. 7.

  11. Vodopyanov S. K. Geometric Aspects of Spaces of General Differentiable Functions. Extended Abstract of Doct. Sci. Dissertation. Novosibirsk: Sobolev Institute of Mathematics. 1992.

  12. Ukhlov A. D. On mappings generating the embeddings of Sobolev spaces. Sib. Math. J., 1993, vol. 34(1), p. 165–171.

  13. Vodopyanov S. K. and Ukhlov A. D. Sobolev spaces and (P-Q)-quasiconformal mappings of Carnot groups. Sib. Math. J., 1998, vol. 39(4), p. 665–682.

  14. Vodopyanov S. K. and Ukhlov A. D. Superposition operators in Sobolev spaces. Russian Math. (Iz. VUZ), 2002, vol. 46(10), p. 9–31.

  15. Vodopyanov S. K. Regularity of mappings inverse to Sobolev mappings. Sb. Math., 2012, vol. 203(10), p. 1383–1410.

  16. Sobolev S. L. On some transformation groups of an n-dimensional space. Dokl. Akad. Nauk SSSR, 1941, vol. 32(6), p. 380–382.

  17. Mazya V. G. Classes of Sets and Embedding Theorems of Function Classes. Some Problems of the Theory of Elliptic Operators. Extended Abstract of Cand. Sci. Dissertation. Leningrad: Leningrad Univ., 1961.

  18. Mazya V. G. Sobolev Spaces. Springer: Berlin, 2011.

  19. Reshetnyak Yu. G. Space Mappings with Bounded Distortion. Amer. Math. Soc., Providence. 1989.

  20. Mostow G. D. Quasi-conformal mappings in n-space and the rigidity of hyperbolic space forms. Inst. Hautes Études Sci. Publ. Math., 1968, vol. 34(1), p. 53–104.

  21. Reiman M.Über harmonishe Kapazität und quasikonforme Abbildungen in Raum. Comm. Math. Helv., 1969, vol. 44, p. 284–307.

  22. Väisälä J. Lectures on n-Dimensional Quasiconformal Mappings. Lecture Notes in Math.; V. 229. Springer: Berlin, 1971.

  23. Gehring F. W. Lipschitz mappings and the p-capacity of rings in n-space. Advances in the Theory of Riemann Surfaces. Princeton: Princeton Univ., 1971. P. 175–193

  24. Lelong-Ferrand J. Etude d’une classe d’applications liées à des homomorphismes d’algèbres de fonctions et généralisant les quasi-conformes. Duke Math., 1973, vol. 40, p. 163–186.

  25. Vodopyanov S. K. and Goldshtein V. M. Lattice isomorphisms of the spaces Wn1and quasiconformal mappings. Sib. Math. J., 1975, vol. 16(2), p. 174–189.

  26. Vodopyanov S. K. and Goldshtein V. M. Functional characteristics of quasi-isometric mappings. Sib. Math. J., 1976, vol. 17(4), p. 580–584.

  27. Romanov A. S. A change of variable in the Bessel and Riesz potential spaces. Functional Analysis and Mathematical Physics. Novosibirsk: Inst. Mat. 1985. P. 117–133.

  28. Vodopyanov S. K. Lp-Potential theory and quasiconformal mappings on homogeneous groups. Modern Problems of Geometry and Analysis. Novosibirsk: Nauka. 1989. P. 45–89.

  29. Vodopyanov S. K. Composition operators on Sobolev spaces. Complex Analysis and Dynamical Systems. II: A Conf. in Honor of Professor Lawrence Zalcman’s Sixtieth Birthday, June 9–12, 2003, Nahariya, Israel. Eds.: M. Agranovsky, L. Karp, D. Shoikhet. Amer. Math. Soc., 2005. P. 327–342.

  30. Vodopyanov S. K. and Evseev N. A. Isomorphisms of Sobolev spaces on Carnot groups and quasi-isometric mappings. Sib. Math. J., 2014, vol. 55(5), p. 817–848.

  31. Vodopyanov S. K. and Evseev N. A. Isomorphisms of Sobolev spaces on Carnot groups and metric mapping properties. Dokl. Math., 2015, vol. 82(2), p. 232–236.

  32. Vodopyanov S. K. and Evseev N. A. Isomorphisms of Sobolev spaces on Carnot groups and quasiconformal mappings. Sib. Math. J., 2015, vol. 56(5), p. 789–821.

  33. Vodopyanov S. K.On admissible changes of variables for Sobolev functions on (sub)Riemannian manifolds. Dokl. Math., 2016, vol. 93(3), p. 318–321.

  34. Vodopyanov S. K. Admissible changes of variables for Sobolev functions on (sub-)Riemannian manifolds. Sb. Math., 2019, vol. 210(1), p. 59–104.

  35. Vodopyanov S. K. Isomorphisms of Sobolev spaces on Riemannian manifolds and quasiconformal mappings. Sib. Math. J., 2019, vol. 60(5), p. 774–804.

  36. Molchanova A. and Vodopyanov S. Injectivity almost everywhere and mappings with finite distortion in nonlinear elasticity. Calculus of Variations and PDE, 2020, vol. 59(17), p. 774–804. https://doi.org/10.1007/s0052601916714

  37. Ball J. M. Global invertibility of Sobolev functions and the interpenetration of matter. Proc. Roy. Soc. Edinburgh Sect. A, 1981, vol. 88(3–4), p. 315–328.

  38. Ambrosio L. and Tilli P. Topics on Analysis in Metric Spaces. Oxford University, New York. 2004.

  39. Baykin A. N. and Vodopyanov S. K. Capacity estimates, Liouville’s Theorem, and singularity removal for mappings with bounded (p-q)-distortion. Sib. Math. J., 2015, vol. 56(2), p. 237–261.

  40. Ukhlov A. D. and Vodopyanov S. K. Mappings associated with weighted Sobolev spaces. Complex Analysis and Dynamical Systems. III. AMS Contemp. Math.; V. 455.. Amer. Math. Soc., 2008, p. 369–382.

  41. Kilpeläinen T. Weighted Sobolev spaces and capacity. Annales Academiæ Scientiarum Fennicæ Series A. I. Mathematica, 1994, vol. 19, p. 95–113.

  42. J. Heinonen, T. Kilpeläinen, O. Martio. Nonliner potential theory of degenerate elliptic equations. Oxford: Clarendon Press. 1993.

  43. Vodopyanov S. K. and Ukhlov A. D. Sobolev spaces and (P-Q)-quasiconformal mappings of Carnot groups. Sib. Math. J., 1998, vol. 39(4), 665–682.

  44. Rado I. and Reichelderfer P. V. Continuous Transformations in Analysis with an Introduction to Algebraic Topology. Springer: Berlin, 1955.

  45. Vodopyanov S. K. and Ukhlov A. D. Superposition operators in the Lebesgue spaces and differentiability of quasiadditive set functions. Vladikavkaz. Mat. Zh., 2002, vol. 4(1), p. 11–33.

  46. Vodop’yanov S. K. and Ukhlov A. D. Set functions and their applications in the theory of Lebesgue and Sobolev spaces. I. Siberian Adv. Math., 2004, vol. 14(4), p. 78–125.

  47. Rickman S. Quasiregular Mappings. Springer, 1993.

  48. Federer H. Geometric Measure Theory. Springer: New York, 1960.

  49. Evans L. C. and Gariepy R. F. Measure Theory and Fine Properties of Functions. CRC: Boca Raton. 1992.

  50. Vodopyanov S. K. Moduli inequalities for Wn-1,loc1-mappings with weighted bounded (q,p)-distortion. Complex Variables and Elliptic Equations, 2020, vol. 66(6–7), p. 1037–1072. https://doi.org/10.1080/17476933.2020.1825396

  51. Hajł asz P. Change of variables formula under minimal assumptions. Colloq. Math., 1993, vol. LXIV(1), p. 93–101.

  52. Reshetnyak Yu. G. Some geometrical properties of functions and mappings with generalized derivatives. Sib. Math. J., 1966, vol. 7(4), p. 704–732.

  53. Martio O. and Malý J. Lusin’s condition (N) and mappings of the class W1,n. J. Reine Angew. Math., 1995, vol. 48(5), p. 19–36.

  54. Vodopyanov S. K. Differentiability of maps of Carnot groups of Sobolev classes. Sb. Math., 2003, vol. 194(6), p. 857–877.

  55. Martio O., Ryazanov V., Srebro U., and Yakubov E. Moduli in Modern Mapping Theory. Springer: New York. 2008.

  56. Folland G. B., Stein E. M. Hardy spaces on homogeneous group. Princeton: Princeton University Press, 1982.

  57. Brudnyi Yu. A., Kotlyar B. D. A certain problem of combinatorial geometry. Siberian Math. J., 1970, vol. 11(5), p. 870–871.

  58. Shvartsman P. A. A Continuation Theorem for Function Spaces Defined by Local approximation. Extended Abstract of Cand. Sci. Dissertation. Yaroslavl: Yaroslavsk. Univ., 1983.

  59. Koskela P., Panka P., and Zhang Yi Ru-Ya. Ahlfors reflection theorem for p-morphisms. arXiv preprint arXiv: 1912.09200.

Download references

Author information

Authors and Affiliations

  1. Sobolev Institute of Mathematics, Acad. Koptyug av.4, 630090, Novosibirsk, Russia

    S. K. Vodopyanov

Authors
  1. S. K. Vodopyanov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. K. Vodopyanov.

Additional information

The paper is dedicated to the anniversary of Professor S. Samko.

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The study was carried out within the framework of the State contract of the Sobolev Institute of Mathematics, project No. FWNF-2022-0006.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vodopyanov, S.K. TWO-WEIGHTED COMPOSITION OPERATORS ON SOBOLEV SPACES AND QUASICONFORMAL ANALYSIS. J Math Sci 266, 491–509 (2022). https://doi.org/10.1007/s10958-022-05903-y

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-022-05903-y

Keywords

MSC2010

Search

Navigation