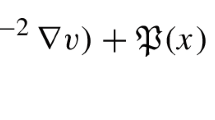Skip to main content
SpringerLink
Log in

Asymptotics of Eigenvalues in Spectral Gaps of Periodic Waveguides with Small Singular Perturbations

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

The asymptotics of eigenvalues appearing near the lower edge of a spectral gap of the Dirichlet problem is studied for the Laplace operator in a d-dimensional periodic waveguide with a singular perturbation of the boundary by creating a hole with a small diameter ε. Several versions of the structure of the gap edge are considered. As usual, the asymptotic formulas are different in the cases d ≥ 3 and d = 2, where the eigenvalues occur at distances O(ε2(d−2)) or O(ε2d) and O(|ln ε|−2) or O(ε4), respectively, from the gap edge. Other types of singular perturbation of the waveguide surface and other types of boundary conditions are discussed, which provide the appearance of eigenvalues near both edges of one or several gaps.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. O. A. Ladyzhenskaya , Boundary Value Problems of Mathematical Physics, Springer-Verlag, New York etc. (1985).

    Book  Google Scholar 

  2. M. Sh. Birman and M. Z. Solomyak, Spectral Theory of Selfadjoint Operators in Hilbert Space [in Russian], Leningrad Univ., Leningrad (1980).

    Google Scholar 

  3. A. V. Sobolev and J. Walthoe, “Absolute continuity in periodic waveguides,” Proc. London Math. Soc., 85, No. 1, 717–741 (2002).

    Article  MathSciNet  Google Scholar 

  4. T. A. Suslina and R. G. Shterenberg, “Absolute continuity of the spectrum of the magnetic Schrödinger operator with a metric in a two-dimensional periodic waveguide,” Algebra Analiz, 14:2, 159–206 (2002).

    MATH  Google Scholar 

  5. I. Kachkovskii and N. Filonov, “Absolute continuity of the spectrum of a periodic Schrödinger operator in a multidimensional cylinder,” Algebra Analiz, 21:1, 133–152 (2009).

    MATH  Google Scholar 

  6. I. M. Gel’fand, “Expansion in eigenfunctions of an equation with periodic coefficients,” Dokl. Akad. Nauk SSSR, 73, 1117–1120 (1950).

    Google Scholar 

  7. S. A. Nazarov, “Elliptic boundary value problems with periodic coefficients in a cylinder,” Izv. Akad. Nauk SSSR, Ser. Mat., 45:1, 101–112 (1981).

    MathSciNet  MATH  Google Scholar 

  8. S. A. Nazarov and B. A. Plamenevskii, Elliptic Problems in Domains With Piecewise Smooth Boundaries [in Russian], Nauka, Moscow (1991).

    Google Scholar 

  9. T. Kato, Perturbation Theory for Linear Operators, Grundlehren Math. Wiss., 132, Springer-Verlag, New York (1966).

  10. M. M. Skriganov, “Geometric and arithmetic methods in the spectral theory of multidimensional periodic operators,” Trudy Mat. Inst. Steklov., 171, 3–122 (1985).

    MathSciNet  Google Scholar 

  11. P. Kuchment, Floquet Theory for Partial Differential Equations, Birchäuser, Basel (1993).

    Book  Google Scholar 

  12. P. A. Kuchment, “Floquet theory for partial differential equations,” Uspekhi Mat. Nauk, 37:4 (226), 3–52 (1982).

    MathSciNet  MATH  Google Scholar 

  13. P. Kuchment, “The mathematics of photonic crystals,” Chap. 7 in Mathematical Modeling in Optical Science, in: Frontiers in Applied Mathematics, SIAM, 22 (2001), pp. 207–272.

  14. S. A. Nazarov, “Properties of spectra of boundary value problems in cylindrical and quasicylindrical domain Sobolev Spaces in Mathematics,” Vol. II (Maz’ya V., Ed.) Intern. Math. Series, 9, 261–309 (2008).

  15. W. Bulla, F. Gesztesy, W. Renger, and B. Simon, “Weakly coupled bound states in quantum waveguides,” Proc. Amer. Math. Soc., 125, No. 8, 1487–1495 (1997).

    Article  MathSciNet  Google Scholar 

  16. V. V. Grushin, “On the eigenvalues of finitely perturbed Laplace operators in infinite cylindrical domains,” Mat. Zamet., 75:3, 360–371 (2004).

    Article  MathSciNet  Google Scholar 

  17. R. R. Gadyl’shin, “Local perturbations of quantum waveguides,” Teoret. Mat. Fiz., 145:3, 358–371 (2005).

    Article  MathSciNet  Google Scholar 

  18. D. I. Borisov, “The discrete spectrum of a pair of nonsymmetric waveguides connected by a window,” Mat. Sborn., 197, No. 4, 3–32 (2006).

    Article  Google Scholar 

  19. S. A. Nazarov, “Variational and asymptotic methods for finding eigenvalues below the continuous spectrum threshold,” Sibirsk. Mat. Zh., 51, No. 5, 1086–1101 (2010).

    MathSciNet  Google Scholar 

  20. M. Sh. Birman and M. Z. Solomyak, “Discrete negative spectrum under nonregular perturbations (polyharmonic operators, Schr¨odinger operators, with a magnetic fields, periodic operators),” in: Rigorous Results in Quantum Dynamics (Liblice, 1990), World Sci. Publishing, River Edge, NJ (1991), pp. 25–36.

  21. M. Sh. Birman, ”The discrete spectrum of the periodic Schrödinger operator perturbed by a decreasing potential,” Algebra Analiz, 8, No. 1, 3–20 (1996).

  22. M. Sh. Birman, “The discrete spectrum in gaps of the perturbed periodic Schrödinger operator. I. Regular perturbations,” in: Boundary Value Problems, Schrödinger Operators, Deformation Quantization. Math. Top., Akademie Verlag, Berlin, 8 (1995), pp. 334–352.

  23. M. Sh. Birman, “The discrete spectrum in gaps of the perturbed periodic Schrödinger operator. II. Nonregular perturbations,” Algebra Analiz, 9, No. 6, 62–89 (1997).

    MATH  Google Scholar 

  24. A. Figotin and A. Klein, “Midgap defect modes in dielectric and acoustic media,” SIAM J. Appl. Math., 58, No. 6, 1748–1773 (1998).

    Article  MathSciNet  Google Scholar 

  25. H. Ammari and F. Santosa, “Guided waves in a photonic bandgap structure with a line defect,” SIAM J. Appl. Math., 64, No. 6, 2018–2033 (2004).

    Article  MathSciNet  Google Scholar 

  26. D. Miao and F. Ma, “On guided waves created by line defects,” J. Stat. Phys., 130, 1197–1215 (2008).

    Article  MathSciNet  Google Scholar 

  27. S. A. Nazarov, “Gaps and eigenfrequencies in the spectrum of a periodic acoustic waveguide,” Akustik Zh., 59, No. 3, 312–321 (2013).

    Google Scholar 

  28. B. M. Brown, V. Hoang, M. Plum, and I. Wood, “Spectrum created by line defects in periodic structures,” Math. Nachr., 287, 1972–1985 (2014).

    Article  MathSciNet  Google Scholar 

  29. S. A. Nazarov, “Bounded solutions in a T-shaped waveguide and the spectral properties of the Dirichlet ladder,” Zh. Vychisl. Mat. Mat. Fiz., 54, No. 8, 1299–1318 (2014).

    MathSciNet  MATH  Google Scholar 

  30. B. Delourme, S. Fliss, P. Joly, and E. Vasilevskaya, “Trapped modes in thin and infinite ladder like domains. Part 1: Existence results,” Asymptotic Analysis, 103, No. 3, 103–134 (2017).

    Article  MathSciNet  Google Scholar 

  31. S. A. Nazarov, “Asymptotics of eigenvalues in spectral gaps under regular perturbations of walls of a periodic waveguide,” Probl. Mat. Analiz., Novosibirsk, Vol. 89, 63–98 (2017).

  32. S. A. Nazarov, “Almost standing waves in a periodic waveguide with resonator, and nearthreshold eigenvalues,” Algebra Analiz, 28, No. 3, 111–160 (2016).

    Google Scholar 

  33. D. V. Evans, M. Levitin, and D. Vasil’ev, “Existence theorems for trapped modes,” J. Fluid Mech., 261, 21–31 (1994).

    Article  MathSciNet  Google Scholar 

  34. S. A. Nazarov, “Asymptotic expansions of eigenvalues in the continuous spectrum of a regularly perturbed quantum waveguide,” Theoret. Mat. Fiz., 167, No. 2, 239–262 (2011).

    Article  MathSciNet  Google Scholar 

  35. S. A. Nazarov, “Enforced stability of a simple eigenvalue in the continuous spectrum,” Funkt. Anal. Prilozhen., 47, No. 3, 37–53 (2013).

    Article  Google Scholar 

  36. I. C. Gokhberg and M. G. Kreyn, Introduction to the Theory of Linear not Self-Adjoint operators, Nauka, Moscow (1965).

    Google Scholar 

  37. M. M. Vainberg and V. A. Trenogin, Theory of Branching of Solutions of Non-Linear Equations [in Russian], Nauka, Moscow (1969).

    MATH  Google Scholar 

  38. W. G. Mazja, S. A. Nazarov, and B. A. Plamenewski, Asymptotische Theorie Elliptischer Randwertaufgaben in Singulär Gestörten Gebieten, Vol. 1, Akademie-Verlag, Berlin (1991).

  39. M. Van Dyke, Perturbation Methods in Fluid Mechanics [Russian translation], Mir, Moscow (1967).

    MATH  Google Scholar 

  40. A. M. Il’in, Matching of Asymptotic Expansions of Solutions of Boundary-Value Problems [in Russian], Nauka, Moscow (1989).

    Google Scholar 

  41. S. A. Nazarov, “Opening a gap in the continuous spectrum of a periodically perturbed waveguide,” Mat. Zamet., 87, No. 5, 764–786 (2010).

    Article  MathSciNet  Google Scholar 

  42. F. L. Bakharev, S. A. Nazarov, and K. M. Ruotsalainen, “A gap in the spectrum of the Neumann–Laplacian on a periodic waveguide,” Appl. Analys., 88, 1–17 (2012).

    MATH  Google Scholar 

  43. D. Borisov and K. Pankrashkin, “Quantum waveguides with small periodic perturbations: gaps and edges of Brillouin zones,” J. Physics A: Math. Theor., 46, No. 23, 203–235 (2013).

    Article  MathSciNet  Google Scholar 

  44. S. A. Nazarov, “Asymptotic behavior of spectral gaps in a regularly perturbed periodic waveguide,” Vestn. St.-Petersb. Univ., Ser. 1,2, No. 7, 54–63 (2013).

  45. V. G. Maz’ya, S. A. Nazarov, and B. A. Plamenevskii, “Asymptotic expansions of eigenvalues of boundary value problems for the Laplace operator in domains with small holes,” Izv. Akad. Nauk SSSR, Ser. Mat., 48, No. 2, 347–371 (1984).

    Article  Google Scholar 

  46. G. Polya and G. Szegö, Isoperimetric Inequalities in Mathematical Physics [Russian translation], Fizmatgiz, Moscow (1962).

    MATH  Google Scholar 

  47. N. S. Landkof, Foundations of Modern Potential Theory [in Russian], Nauka, Moscow (1966).

    Google Scholar 

  48. V. A. Kondrat’ev, “Boundary-value problems for elliptic equations in domains with conical or corner points,” Trudy Moskov. Mat. Obshch., 16, 209–292 (1967).

    Google Scholar 

  49. S. A. Nazarov, “On the constants in the asymptotic expansion of solutions of elliptic boundary value problems with periodic coefficients in a cylinder,” Vestn. Leningr. Univ., Ser. 1,3, No. 15, 16–22 (1985).

  50. S. A. Nazarov, “The asymptotics of frequencies of elastic waves trapped by a small crack in an anisotropic waveguide,” Mekh. tverd. tela, No. 6, 112–122 (2010).

  51. S. A. Nazarov, M. Specovius-Neugebauer, and J. Sokolowski, “Polarization matrices in anisotropic heterogeneous elasticity,” Asymp. Analys., 68, No. 4, 189–249 (2010).

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. St. Petersburg State University, St. Petersburg, Russia

    S. A. Nazarov

Authors
  1. S. A. Nazarov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. A. Nazarov.

Additional information

Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 471, 2018, pp. 168–210.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nazarov, S.A. Asymptotics of Eigenvalues in Spectral Gaps of Periodic Waveguides with Small Singular Perturbations. J Math Sci 243, 746–773 (2019). https://doi.org/10.1007/s10958-019-04576-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-019-04576-4

Search

Navigation