Skip to main content
SpringerLink
Log in

Optimal Synthesis in the Control Problem of an n-Link Inverted Pendulum with a Moving Base

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

Abstract

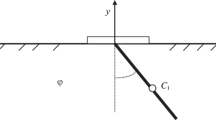
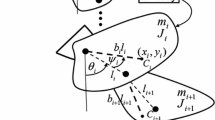
In this paper, we consider the problem of stabilization of an n-link inverted pendulum on a movable base (cart). A cart is allowed to move along the horizontal axis. A force applied to the cart is considered as a control. The problem is to minimize the mean square deviation of the pendulum from the vertical line. For the linearized model, we show that, for small deviations from the upper unstable equilibrium position, the optimal regime contains trajectories with more and more frequent switchings. Namely, the optimal trajectories with infinite number of switchings are shown to attain, in finite time, the singular surface and then continue these motion with singular control over the singular surface, approaching the origin in an infinite time. It is shown that the costructed solutions are globally optimal.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Awrejcewicz, G. Wasilewski, G. Kudra, and S. A. Reshmin, “An experiment with swinging up a double pendulum using feedback control,” J. Comput. Syst. Sci. Int., 51, No. 2, 176–182 (2012).

    Article  MATH  Google Scholar 

  2. V. G. Boltyanskii, Mathematical Methods of Optimal Control, Holt, Reinhart and Winston (1971).

    Google Scholar 

  3. V. Borisov, M. Zelikin, and L. Manita, “Optimal synthesis in an infinite-dimensional space,” Tr. Mat. Inst. Steklova, 271, 34–52 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  4. M. Z. Borshchevskii and I. V. Ioslovich, “The problem of the optimum rapid braking of an axisymmetric solid rotating around its center of mass,” J. Appl. Math. Mech., 49, No. 1, 24–30 (1985).

    Article  MATH  Google Scholar 

  5. O. Yu. Cherkasov and A. G. Yakushev, “Singular arcs in the optimal evasion against a proportional navigation vehicle,” J. Optim. Theory Appl., 113, No. 2 (2002).

  6. A. M. Formal’skii, On stabilization of an inverted double pendulum with one control torque,” J. Comput. Syst. Sci. Int., 45, No. 3, 337–344 (2006).

    Article  MATH  Google Scholar 

  7. A. M. Formal’skii, “Global stabilization of a double inverted pendulum with control at the hinge between the links,” Mech. Solids, 43, No. 5, 687–697 (2008).

    Article  Google Scholar 

  8. I. M. Gelfand, Lectures on Linear Algebra, Dover, New York (1989).

    Google Scholar 

  9. V. A. Ilyin and E. G. Poznyak, Linear Algebra, Mir, Moscow (1990).

  10. P. L. Kapitsa, “Pendulum with a vibrating suspension,” Usp. Fiz. Nauk, 44, No. 7, 7–20 (1951).

    Article  Google Scholar 

  11. H. J. Kelley, R. E. Kopp, and H. G. Moyer, “Singular extremals,” in: Topics in Optimization (G. Leitmann, ed.), Academic Press, New York (1967), pp.63–103.

  12. L. V. Lokutsievskiy, “The Hamiltonian property of the flow of singular trajectories,” Mat. Sb., 205, No. 3, 432 (2014).

  13. L. A. Manita, “Optimal singular and chattering modes in the problem of controlling the vibrations of a string with clamped ends,” J. Appl. Math. Mech., 74, 661–616 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  14. Yu. G. Martynenko and A. M. Formal’skii,” “Cotrolled pendulum on a movable base,” Mech. Solids, 43, No. 5, 687–697 (2008).

  15. S. N. Osipov and A. M. Formal’skii, “The problem of the time-optimal turning of a manipulator,” J. Appl. Math. Mech., 52, No. 6, 725–731 (1988).

    Article  MATH  Google Scholar 

  16. S. A. Reshmin and F. L. Chernous’ko, “Time-optimal control of an inverted pendulum in the feedback form,” J. Comput. Syst. Sci. Int., 45, No. 3, 383–394 (2006).

    Article  MATH  Google Scholar 

  17. M. I. Zelikin and V. F. Borisov, “Regimes with increasingly more frequent switchings in optimal problems,” Tr. Mat. Inst. Steklova, 1. 95–186 (1993).

  18. M. I. Zelikin and V. F. Borisov, Theory of Chattering Control with Applications to Astronautics, Robotics, Economics, and Engineering, Birkhäuser, Boston-Basel-Berlin (1994).

  19. M. I. Zelikin and V. F. Borisov, “Singular optimal regimes in problems of mathematical economics,” J. Math. Sci., 130, No. 1 (2005).

Download references

Author information

Authors and Affiliations

  1. National Research University Higher School of Economics, Moscow, Russia

    L. A. Manita

  2. Moscow Institute of Electronics and Mathematics, Moscow, Russia

    L. A. Manita

  3. M. V. Lomonosov Moscow State University, Moscow, Russia

    M. I. Ronzhina

Authors
  1. L. A. Manita
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. I. Ronzhina
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. A. Manita.

Additional information

Translated from Sovremennaya Matematika. Fundamental’nye Napravleniya (Contemporary Mathematics. Fundamental Directions), Vol. 56, Dynamical Systems and Optimal Control, 2015.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Manita, L.A., Ronzhina, M.I. Optimal Synthesis in the Control Problem of an n-Link Inverted Pendulum with a Moving Base. J Math Sci 221, 137–153 (2017). https://doi.org/10.1007/s10958-017-3222-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-017-3222-x

Search

Navigation