Skip to main content
SpringerLink
Log in

Asymptotics of the frequency of a surface wave trapped by a slightly inclined barrier in a liquid layer

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

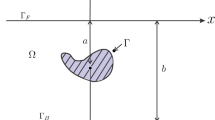
A two-dimensional statement of the scattering problem for an oblique incident surface wave by an obstacle in the form of a submerged barrier is considered. If the barrier is vertical, the discrete spectrum of the problem is shown to be empty, but for an inclined barrier an eigenvalue appears below the threshold of the continuous spectrum and the corresponding trapped made decays exponentially in the direction perpendicular to the obstacle. The behavior of the eigenvalue is analyzed for small values of the angle of inclination from the vertical. Bibliography: 48 titles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. N. Kuznetsov, V. Maz’ya, and B. Vainberg, Linear Water Waves, Cambridge Univ. Press, Cambridge (2002).

    Book  MATH  Google Scholar 

  2. O. A. Ladyzhenskaya, Boundary Value Problems in Mathematical Physics [in Russian], Nauka, Moscow (1973).

    Google Scholar 

  3. T. H. Havelock, “Forced surface waves on water,” Phil. Mag., 8, 569-576 (1929).

    MATH  Google Scholar 

  4. S. A. Nazarov, “A simple way of finding trapped modes in problems of the linear theory of surface waves,” Dokl. RAN, 429, No. 6, 746-749 (2009).

    Google Scholar 

  5. S. A. Nazarov, “Sufficient conditions of appearance of trapped modes in problems of the linear theory of surface waves,” Zap. Nauchn. Semin. POMI, 369, 202-223 (2009).

    Google Scholar 

  6. M. Sh. Birman and M. Z. Solomyak, Spectral Theory of Self-Adjoint Operators in Hilbert Space [in Russian], Izd. Leningrad. Univ., Leningrad (1980).

    Google Scholar 

  7. F. Ursell, “Trapping modes in the theory of surface waves,” Proc. Camb. Phil. Soc., 47, 347-358 (1951).

    Article  MathSciNet  MATH  Google Scholar 

  8. F. Ursell, “Mathematical aspects of trapping modes in the theory of surface waves,” J. Fluid Mech., 183, 421-437 (1987).

    Article  MathSciNet  MATH  Google Scholar 

  9. R. M. Garipov, “On the linear theory of gravity waves: the theorem of existence and uniqueness,” Arch. Rat. Mech. Anal., 24, 352-362 (1967).

    Article  MathSciNet  MATH  Google Scholar 

  10. S. A. Nazarov, “Concentration of trapped modes in problems of the linear theory of waves on the surface of a liquid,” Mat. Sb., 199, No. 12, 53-78 (2008).

    Article  Google Scholar 

  11. F. Ursell, “The effect of a fixed vertical barrier on surface waves in deep water,” Proc. Camb. Phil. Soc., 43, 374-382 (1947).

    Article  MathSciNet  MATH  Google Scholar 

  12. F. John, “Waves in the presence of an inclined barrier,” Comm. Pure Appl. Math., 1, 149-200 (1948).

    Article  MATH  Google Scholar 

  13. D. V. Evans, “Diffraction of water-waves by a submerged vertical plate,” J. Fluid Mech., 40, 433-451 (1970).

    Article  MATH  Google Scholar 

  14. P. McIver, “Scattering of water waves by two surface-piercing vertical barriers,” IMA J. Appl. Math., 35, 339-355 (1985).

    Article  MathSciNet  MATH  Google Scholar 

  15. D. C. Shaw, “Perturbational results for diffraction of water-waves by nearly-vertical barriers,” IMA J. Appl. Math., 34, 99-117 (1985).

    Article  MathSciNet  MATH  Google Scholar 

  16. X. Yu and A. T. Chwang, “Analysis of wave scattering by submerged circular disk.” J. Eng. Mech., 119, 1804-1817 (1993).

    Article  Google Scholar 

  17. N. F. Parsons and P. A. Martin, “Scattering of water waves by submerged curved plates and by surface-piercing flat plates,” Appl. Ocean Res., 16, 129-139 (1994).

    Article  Google Scholar 

  18. L. Farina and P. A. Martin, “Scattering of water waves by a submerged disc using a hypersingular integral equation,” Appl. Ocean Res., 20, 121-134 (1998).

    Article  Google Scholar 

  19. M. D. Groves, “On the existence of trapped modes in channels of arbitrary cross-sections,” Math. Meth. Appl. Sci., 20, 521-545 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  20. P. A. Martin, N. F. Parsons, and L. Farina, “Interaction of water waves with thin plates,” in: Mathematical Techniques for Water Waves (B. N. Mandal ed.), Computational Mechanics Publications (1997), pp. 197-229.

  21. C. M. Linton and D. V. Evans, “Trapped modes above a submerged horizontal plate,” Q. J. Mech. Appl. Math., 44, 487-506 (1991).

    Article  MathSciNet  MATH  Google Scholar 

  22. N. F. Parsons and P. A. Martin, “Trapping of water waves by submerged plates using hyper-singular integral equations,” J. Fluid Mech., 284, 359-375 (1995).

    Article  MathSciNet  MATH  Google Scholar 

  23. C. M. Linton and N. G. Kuznetsov, “Nonuniqueness in two-dimensional water wave problems: numerical evidence and geometrical restrictions,” Proc. R. Soc. Lond. A., 453, 2437-2460 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  24. N. Kuznetsov, P. McIver, and C. M. Linton, “On uniqueness and trapped modes in the water-wave problem for vertical barriers,” Wave Motion., 33, 283-307 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  25. I. V. Kamotski and S. A. Nazarov, “Exponentially damped solutions of the problem of diffraction on a hard periodic grid,” Mat. Zam., 73, No. 1, 138-140 (2003).

    Article  Google Scholar 

  26. S. A. Nazarov, “Variational and asymptotic methods of searching eigenvalues below the threshold of the continuous spectrum,” Sib. Mat. Zh., 51, No. 5, 1086-1101 (2010).

    Article  Google Scholar 

  27. S. A. Nazarov and J. H. Videman, “Existence of edge waves along three-dimensional periodic structures,” J. Fluid Mech., 659, 225-246 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  28. T. Kato, Perturbation Theory of Linear Operators [Russian translation], Mir, Moscow (1972).

    Google Scholar 

  29. J. Sanchez-Hubert and E. Sanchez-Palencia, Vibration and Coupling of Continuous Systems. Asymptotic Methods, Springer-Verlag, Heidelberg (1989).

    Book  MATH  Google Scholar 

  30. W. G. Mazja, S. A. Nasarow, and B. A. Plamenewski, Asymptotische Theorie elliptischer Randwertaufgaben in singulär gestörten Gebieten. 1, Akademie-Verlag, Berlin (1991).

    Google Scholar 

  31. W. Bulla, F. Gesetesy, W. Renrer, and B. Simon, “Weakly coupled bound states in quantum waveguides,” Proc. Amer. Math. Soc., 125, No. 8, 1487-1495 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  32. P. Exner and S. A. Vugalter, “Bound-states in a locally deformed waveguide: the critical case,” Lett. Math. Phys., 39, No. 1, 59-68 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  33. D. Borisov, P. Exner, R. Gadyl’shin, and D. Krejčiřik, “Bound states in weakly deformed strips and layers,” Ann. H. Poincaré, 2, 553-571 (2001).

    Article  MATH  Google Scholar 

  34. W. P. Maslov, “Asymptotics of eigenfunctions of the equation ∆u + k 2 u = 0 with boundary conditions on equidistant curves and scattering of electromagnetic waves in a waveguide,” Dokl. Akad. Nauk SSSR, 123, No. 4. 631-633 (1958).

    Google Scholar 

  35. P. Duclos and P. Exner, “Curvature-induced bound states in quantum waveguides in two and three dimensions,” Rev. Math. Phys., 7, No. 1, 73-102 (1995).

    Article  MathSciNet  MATH  Google Scholar 

  36. Y. Avishai, D. Bessis, B. G. Giraud, and G. Mantica, “Quantum bound states in open geometries,” Phys. Rev. B, 44, No. 15, 8028-8034 (1991).

    Article  Google Scholar 

  37. V. V. Grushin, “On eigenvalues of the finitely perturbed Laplace operator in infinite cylindrical domains,” Mat. Zam., 75, No. 3, 360-371 (2004).

    Article  MathSciNet  Google Scholar 

  38. R. R. Gadyl’shin, “On local perturbations of quantum waveguides,” Teor. Mat. Fiz., 145, No. 3, 358-371 (2005).

    Article  MathSciNet  Google Scholar 

  39. A. M. Il’in, Agreement of Asymptotic Expansions of Solutions of Boundary Value Problems [in Russian], Nauka, Moscow (1989).

    Google Scholar 

  40. V. A. Kondratiev, “Boundary value problems for elliptic equations in domains with conic and corner points,” Trudy Mosk. Mat. Obshch., 16, 219-292 (1963).

    Google Scholar 

  41. V. G. Maz’ya and B. A. Plamenevskii, “On coefficients in the asymptotics of solutions of elliptic boundary value problems in a domain with conic points,” Math. Nachr., 76, 29-60 (1977).

    Article  MathSciNet  MATH  Google Scholar 

  42. V. G. Maz’ya and B. A. Plamenevskii, “Estimates in L p and in the Hölder classes and the Miranda-Agmon maximum principle for solutions of elliptic boundary-value problems in domains with singular points on the boundary,” Math. Nachr., 77, 25-83 (1979).

    Google Scholar 

  43. S. A. Nazarov, “Polynomial property of self-adjoint elliptic boundary value problems and algebraic description of their attributes,” Usp. Mat. Nauk, 54, No. 5, 77-142 (1999).

    Google Scholar 

  44. S. A. Nazarov and B. A. Plamenevskii, Elliptic Problems in Domains with Piecewise Smooth Boundaries, Walter de Gruyter, Berlin, New York (1994).

    Book  MATH  Google Scholar 

  45. S. A. Nazarov, “Properties of spectra of boundary value problems in cylindrical and quasicylindrical domains,” in: Sobolev Spaces in Mathematics, Vol. II, Maz’ya V. (Ed.), International Mathematical Series, Vol. 9 (2008), pp. 261-309.

  46. M. Van Dyke, Perturbation Methods in Fluid Mechanics [Russian translation], Mir, Moscow (1967).

    Google Scholar 

  47. J. Hadamard, “Mémoire sur le problème d’ana1yse relatif à l’éuilibre des plaques élastiques encastréecs,” (Euvres, 2, 515-631 (1968).

    Google Scholar 

  48. S. A. Nazarov, “Scenarios of a quasistatic grow of cracks under weak bends and breaks,” Prikl. Mat. Mekh., 72, No. 3, 507-525 (2008).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. CEMAT/Departamento de Matematica, Instituto Superior Tercnico, Lisboa, Portugal

    J. H. Videman

  2. Institute of Problems in Mechanical Engineering, St. Petersburg, Russia

    S. A. Nazarov

  3. Politenico of Torino, Torino, Italy

    V. Chiado Piat

Authors
  1. J. H. Videman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. A. Nazarov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. Chiado Piat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to J. H. Videman, S. A. Nazarov or V. Chiado Piat.

Additional information

Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 393, 2011, pp. 46-79.

Translated by V. Chiado Piat, J. Videman, and S. A. Nazarov.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Videman, J.H., Nazarov, S.A. & Piat, V.C. Asymptotics of the frequency of a surface wave trapped by a slightly inclined barrier in a liquid layer. J Math Sci 185, 536–553 (2012). https://doi.org/10.1007/s10958-012-0937-6

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-012-0937-6

Keywords

Search

Navigation