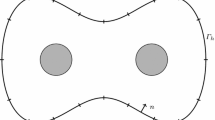
Abstract
Considering the example of a mixed boundary value problem for the Helmholtz operator we discuss two methods for finding eigenvalues below the continuous spectrum threshold: one variational and the other—asymptotic. We construct asymptotics for the eigenvalue arising near the threshold as a small obstacle appears in the cylindrical waveguide. The resulting asymptotic formula, its derivation and justification differ substantially from the case of a bounded domain.
Similar content being viewed by others
References
Ladyzhenskaya O. A., Boundary Value Problems of Mathematical Physics, Springer-Verlag, New York etc. (1985).
Birman M. Sh. and Solomyak M. Z., Spectral Theory of Selfadjoint Operators in Hilbert Space, D. Reidel Publ. Co., Dordrecht (1987).
Alonso A. and Simon B., “The Birman-Krein-Vishik theory of selfadjoint extensions of semibounded operators,” J. Operator Theory, 4, No. 2, 251–270 (1980).
Nazarov S. A., “Selfadjoint extensions of the Dirichlet problem operator in weighted function spaces,” Math. USSR-Sb., 65, No. 1, 229–247 (1990).
Nazarov S. A., “Selfadjoint extensions of the operator of the Dirichlet problem in a 3-dimensional region with an edge,” J. Appl. Industr. Math., 3, No. 3, 377–390 (2009).
Kamotskiĭ I. V. and Nazarov S. A., “Elastic waves localized near periodic families of defects,” Dokl. Phys., 44, No. 10, 715–717 (1999).
Kamotskiĭ I. V. and Nazarov S. A., “Exponentially decreasing solutions of diffraction problems on a rigid periodic boundary,” Math. Notes, 73, No. 1, 129–131 (2003).
Mazja W. G., Nasarow S. A., and Plamenewski B. A., Asymptotische Theorie elliptischer Randwertaufgaben in singulär gestörten Gebieten. 2, Akademie-Verlag, Berlin (1991).
Il’in A. M., Matching Asymptotic Expansions for Solutions of Boundary Value Problems [in Russian], Nauka, Moscow (1989).
Jones D. S., “The eigenvalues of ▽ 2u + λu = 0 when the boundary conditions are given on semi-infinite domains,” Proc. Cambridge Philos. Soc., 49, 668–684 (1953).
Bonnet-Bendhia A.-S. and Starling F., “Guided waves by electromagnetic gratings and non-uniqueness examples for the diffraction problem,” Math. Methods Appl. Sci., 77, 305–338 (1994).
Evans D. V., Levitin M., and Vassiliev D., “Existence theorems for trapped modes,” J. Fluid Mech., 261, No. 1, 21–31 (1994).
Sukhinin S. V., “Waveguide, anomalous, and whispering properties of a periodic chain of obstacles,” Sibirsk. Zh. Industr. Mat., 1, No. 2, 175–198 (1998).
Kamotskiĭ I. V. and Nazarov S. A., “The augmented scattering matrix and exponentially decaying solutions of an elliptic problem in a cylindrical domain,” J. Math. Sci. (New York), 111, No. 4, 3657–3666 (2002).
Nazarov S. A., “A criterion for the existence of decaying solutions in the problem on a resonator with a cylindrical waveguide,” Funct. Anal. Appl., 40, No. 2, 97–107 (2006).
Linton C. M. and McIver P., “Embedded trapped modes in water waves and acoustics,” Wave Motion, 45, 16–29 (2007).
Nazarov S. A., “Properties of spectra of boundary value problems in cylindrical and quasicylindrical domains,” Sobolev Spaces in Mathematics. II (Maz’ya V., Ed.), 2008, pp. 261–309 (Intern. Math. Ser.; V. 9).
Gindikin S. G., Tales of Mathematicians and Physicists, Springer-Verlag, Berlin (2007).
Linton C. M. and McIver P., “The existence of Rayleigh-Bloch surface waves,” J. Fluid Mech., 470, 85–90 (2002).
Maz’ya V. G., Nazarov S. A., and Plamenevskiĭ B. A., “Asymptotic expansions of the eigenvalues of boundary value problems for the Laplace operator in domains with small holes,” Math. USSR-Izv., 24, No. 2, 321–345 (1985).
Polya G. and Szegö G., Isoperimetric Inequalities in Mathematical Physics [Russian translation], Fizmatgiz, Moscow (1962).
Kondrat’ev V. A., “Boundary value problems for elliptic equations in domains with conical or angular points,” Trudy Moskov. Mat. Obshch., 16, 209–292 (1967).
Nazarov S. A. and Plamenevsky B. A., Elliptic Problems in Domains with Piecewise Smooth Boundaries, Walter de Gruyter, Berlin and New York (1994).
Maz’ya V. G. and Plamenevskiĭ B. A., “On coefficients in asymptotic expansions of solutions to elliptic boundary value problems in domains with conical points,” Math. Nachr., Bd 76, 29–60 (1977).
Maz’ya V. G. and Nazarov S. A., “Paradoxes of limit passage in solutions of boundary value problems involving the approximation of smooth domains by polygonal domains,” Math. USSR-Izv., 29, No. 3, 511–533 (1987).
Vishik M. I. and Lyusternik L. A., “Regular degeneration and a boundary layer for linear differential equations with a small parameter,” Uspekhi Mat. Nauk, 12, No. 5, 3–122 (1957).
Nazarov S. A. and Sokolowski J., “Spectral problems in shape optimization. Singular boundary perturbations,” Asymptotic Anal., 56, No. 3-4, 159–196 (2008).
Kamotskiĭ I. V. and Nazarov S. A., “Spectral problems in singularly perturbed domains and self-adjoint extensions of differential operators,” Trans. Amer. Math. Soc. Ser. 2, 199, 127–181 (2000).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text Copyright © 2010 Nazarov S. A.
Translated from Sibirskiĭ Matematicheskiĭ Zhurnal, Vol. 51, No. 5, pp. 1086-1101, September-October, 2010
Rights and permissions
About this article
Cite this article
Nazarov, S.A. Variational and Asymptotic Methods for Finding Eigenvalues below the Continuous Spectrum Threshold. Sib Math J 51, 866–878 (2010). https://doi.org/10.1007/s11202-010-0087-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11202-010-0087-3