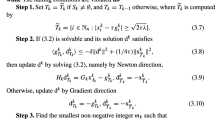1 Introduction

In this paper, we consider smooth continuous optimization problems with sparsity constraints, i.e., problems where the number of nonzero components of solutions are upper-bounded by a certain threshold. This class of problems has a wide range of applications, from subset selection in regression [28] and the compressed sensing technique used in signal processing [15] to portfolio optimization [10, 29]. Such a problem can be reformulated into equivalent different mixed-integer problems and is known to be \(\mathcal{N}\mathcal{P}\)-hard [10, 30, 31].

For the cases where the objective function is convex, exact methods (see, e.g., [9, 10, 31, 32]), typically based on branch-and-bound or branch-and-cut strategies, have been proposed in the literature to solve these problems up to certified global optimality. In recent works [7, 8], numerical strategies have been devised that make methods of this kind computationally sustainable even at a quite large scale.

On the other hand, the approaches proposed in the literature for the solution of this problem in the general case include: methods that handle suitable reformulations of the problem based on orthogonality constraints (see, e.g., [12,13,14, 16]); penalty decomposition methods, where penalty subproblems are solved by a block coordinate descent method [23, 26]; methods that identify points satisfying tailored optimality conditions related to the problem [3, 4]; heuristics like evolutionary algorithms [1], particle swarm methods [11, 18], genetic algorithms, tabu search and simulated annealing [17], and also neural networks [21].

We observe sparsity-constrained problems are generally hard to solve because both the objective function and the feasible set (due to the combinatorial nature of the sparsity constraint) are nonconvex. The inherently combinatorial flavor of the given problem makes the definition of proper optimality conditions and, consequently, the development of algorithms that generate points satisfying those conditions a challenging task. A number of ways to address these issues are proposed in the literature (see, e.g., [3, 4, 14, 23, 26]). However, some of the optimality conditions proposed do not fully take into account the combinatorial nature of the problem, whereas some of the corresponding algorithms [3, 26] require to exactly solve a sequence of nonconvex subproblems and this may be practically prohibitive. Moreover, due to the theoretical tools involved in the analysis, it is anyway not easy to relate the different approaches with each other.

In this paper, we hence give a unifying view on this matter. More specifically, we consider the mixed-integer reformulation of the problem proposed in [14] and use it to define a suitable optimality condition. This condition is then embedded into an algorithmic framework aimed at finding points satisfying the resulting optimality criterion. The algorithm combines inexact minimizations with a strategy that explores tailored neighborhoods of a given feasible point. Those features make it easy to handle the nonconvexity in both the objective function and the feasible set also from a practical point of view. We prove the convergence of the algorithmic scheme, establishing that its limit points satisfy the specific optimality condition. We then show that different conditions proposed in the literature (see, e.g., [3, 14, 26]) can be easily derived from ours. We finally perform some numerical tests on sparse logistic regression in order to show that the devised method is also computationally viable.

The paper is organized as follows: in Sect. 2, we provide basic definitions and preliminary results related to optimality conditions of problem (1). In Sect. 3, we describe our proposed algorithmic framework and show (Sect. 3.1) the convergence analysis without constraint qualifications. In Sect. 4, we analyze the asymptotic convergence properties of the algorithm when constraint qualifications hold. Finally, we report numerical experiments in Sect. 5 and give some concluding remarks in Sect. 6. We also provide in Sect. 1 some insights on the relationship between classical stationarity conditions for convex problems with and without constraints qualifications.

2 Basic Definitions and Preliminary Results

We consider the following sparsity-constrained problem:

$$\begin{aligned} \min _x f(x)\quad \text {s.t.} \quad \Vert x \Vert _0 \le s,\quad x \in X, \end{aligned}$$
(1)

where \(f:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is a continuously differentiable function, \(\Vert x\Vert _0\) denotes the cardinality of the vector x, \(X \subseteq {\mathbb {R}}^n\) is a closed and convex set, and \(s<n\) is a properly chosen integer value. We further use \(\mathcal {X}\) to indicate the overall feasible set \(X\cap \{x\in {\mathbb {R}}^n\mid \Vert x\Vert _0\le s\}\).

Even though problem (1) is a continuous optimization problem, it has an intrinsic combinatorial nature and in applications the interest often lies in finding a good, possibly globally optimal configuration of active variables. Being 1 a continuous problem, \(x^*\in \mathcal {X}\) is a local minimizer if there exists an open ball \(\mathcal {B}(x^*,\epsilon )\) such that \(f(x^*)=\min \{f(x)\mid x\in \mathcal {X}\cap \mathcal {B}(x^*,\epsilon )\}\). In some works from the literature (e.g., [14, 26]) necessary conditions of local optimality have been proposed. However, for this particular problem every local minimizer for a fixed active set of s variables is a local minimizer of the given problem. Hence the number of local minimizers grows as fast as \(\left( {\begin{array}{c}n\\ s\end{array}}\right) \) and is thus of low practical usefulness.

In [3, 4], the authors propose necessary conditions for global optimality that go beyond the concept of local minimum described above, thus allowing to consider possible changes to the structure of the support set, and reducing the pool of optimal candidates. However, these conditions are either tailored to the “unconstrained case”, or limited to moderate changes in the support, or involve hard operations, such as exact minimizations or projections onto nonconvex sets.

In order to introduce a general and affordable necessary optimality condition that also takes into account the combinatorial nature of the problem, we consider in our analysis the equivalent reformulation of problem (1) described in [14]:

$$\begin{aligned} \begin{aligned} \min _{x,y}\;&f(x)\\ \text {s.t. }&e^\top y \ge n - s, \quad x_i y_i = 0 \; \; \forall \, i=1,\ldots ,n,\\&x \in X,\quad y \in \{ 0, 1 \}^n. \end{aligned} \end{aligned}$$
(2)

From here onwards, we will use the following notation:

$$\begin{aligned} \mathcal {Y}= \left\{ y \mid y \in \{0,1\}^n, e^\top y \ge n - s\right\} ,\qquad \mathcal {X}(y) = \{ x \in X \mid x_i y_i = 0 \ \forall \, i=1,\ldots ,n \}. \end{aligned}$$

We further define the support set of a vector z and its complement by

$$\begin{aligned} I_1(z) = \{ i \mid z_i \ne 0 \},\qquad I_0(z) = \{ i \mid z_i = 0 \}. \end{aligned}$$

Moreover, we recall the concept of super support set [4].

Definition 2.1

Let \(z\in \mathcal {X}\) be a feasible solution of problem (1). A set \(J\subseteq \{1,\ldots ,n\}\) is referred to as a super support set for z if it is such that \(I_1(z)\subseteq J\) and \(|J|=s\). We denote the set of all super support sets at z by \(\mathcal {J}(z)\).

A super support set substantially identifies a subset of components of z that could be moved jointly without breaking the cardinality constraint. Clearly, if z has full support, then the only super support set for z is \(I_1(z)\) itself.

We denote by \(z_I\) the subvector of z identified by the components contained in an index set I. We also denote by \(\Pi _C\) the orthogonal projection operator over the closed convex set C. We notice that given a feasible point (x, y) of problem (2), the components \(I_0(y)\) give an active subspace for x, i.e., those components identify the subspace where the nonzero components of x lay. We thus have that \(I_1(x)\subseteq I_0(y)\). In order to suitably manage the mixed-integer structure of problem (2), inspired by [24, 27], we need to introduce the notion of discrete neighborhood mapping, which is a point-to-set mapping defined as follows.

Definition 2.2

Let \(\mathcal {N}:\mathcal {X}(y)\times \mathcal {Y}\rightarrow 2^ {\mathcal {X}(y)\times \mathcal {Y}}\) be a point-to-set mapping. We say that \(\mathcal {N}\) is a discrete neighborhood mapping if for any \(({\bar{x}},{\bar{y}})\in \mathcal {X}({\bar{y}})\times \mathcal {Y}\) we have:

  • \(({\bar{x}},{\bar{y}})\in \mathcal {N}({\bar{x}},{\bar{y}})\);

  • \(|\mathcal {N}({\bar{x}},{\bar{y}})|<\infty \).

Basically, given a feasible point \(({{\bar{x}}}, {{\bar{y}}})\), a discrete neighborhood mapping \(\mathcal {N}\) defines a discrete neighborhood \(\mathcal {N} ({{\bar{x}}},{{\bar{y}}})\), which is a finite set of feasible points that contains \(({{\bar{x}}},{{\bar{y}}})\) itself. Of course, in order for the concept of neighborhood to be practically meaningful, the points in it should be close, to some extent, to the point \(({{\bar{x}}}, {{\bar{y}}})\); however, the formalization of this feature will be deferred to the definition of each specific discrete neighborhood mapping.

Note that the discrete neighborhood mapping is the rule for generating the discrete neighborhood of any feasible point.

Now, a notion of local optimality for problem (2), depending on the considered discrete neighborhood, can be introduced.

Definition 2.3

A point \((x^\star ,y^\star )\in \mathcal {X}(y^\star )\times \mathcal {Y}\) is a local minimizer of problem2 with respect to the discrete neighborhood \(\mathcal {N}(x^\star ,y^\star )\) if there exists an \(\epsilon > 0\) such that for all \(({\hat{x}},{\hat{y}})\in \mathcal {N}(x^\star ,y^\star )\) it holds \(f(x^\star )\le f(x)\;\; \forall \, x \in \mathcal {B}({\hat{x}},\epsilon )\cap \mathcal {X}({\hat{y}}).\)

Note that in the above definition the continuous nature of the problem, expressed by the variables x, is taken into account by means of the standard ball \(\mathcal {B} ({\hat{x}}, \epsilon )\). The given definition clearly depends on the choice of the discrete neighborhood. A larger neighborhood \(\mathcal {N}(x^*, y^*)\) should give a better local minimizer, but the computational effort needed to locate the solution may increase.

Inspired by the definition of local optimality for problem (2), we introduce a necessary optimality condition for problem that depends on a given discrete neighborhood mapping \({\mathcal {N}}\), and allows to take into account possible, beneficial changes of the support, thus properly capturing, from an applied point of view, the essence of the problem. Such a condition relies on the use of stationary points related to continuous problems obtained by fixing the binary variables in problem (2), i.e., for a fixed \({{\bar{y}}} \in \mathcal {Y}\),

$$\begin{aligned} \min _x \; f(x)\quad \text {s.t. } x \in \mathcal {X}({{\bar{y}}}). \end{aligned}$$
(3)

Definition 2.4

(\(\mathcal {N}\)-stationarity) A point \((x^\star , y^\star )\in \mathcal {X}(y^\star )\times \mathcal {Y}\) is a stationary point with respect to the discrete neighborhood \(\mathcal {N}(x^\star , y^\star )\) if

  1. (i)

    the point \(x^\star \) is a stationary point of the continuous problem

    $$\begin{aligned} \min _x \; f(x) \quad \text {s.t. } \quad x \in \mathcal {X}(y^\star ); \end{aligned}$$
  2. (ii)

    every \(({\hat{x}}, {\hat{y}}) \in \mathcal {N}(x^\star , y^\star )\) satisfies \(f({\hat{x}}) \ge f(x^\star )\) and if \(f({\hat{x}}) = f(x^\star )\), the point \({\hat{x}}\) is a stationary point of the continuous problem

    $$\begin{aligned} \min _x \; f(x) \quad \text {s.t. } \quad x \in \mathcal {X}({\hat{y}}). \end{aligned}$$

It is easy to see that the following result holds.

Theorem 2.1

Let \(x^\star \) be a minimum point of problem (1). Then there exists a point \(y^\star \in {\mathcal {Y}}\) such that \((x^\star , y^\star )\in \mathcal {X}(y^\star )\times \mathcal {Y}\) and is a stationary point with respect to a discrete neighborhood \(\mathcal {N}(x^\star , y^\star )\).

We will show later in this work that the definition of \(\mathcal {N}\)-stationarity allows to retrieve in a unified view most of the known optimality conditions, if a suitable neighborhood \(\mathcal {N}\) is employed. In Definition 2.4 we generically refer to stationary points of problem (3), namely, to points satisfying suitable optimality conditions. Then, concerning the assumptions on the feasible set \(\mathcal {X}({{\bar{y}}})\), we distinguish the two cases: (i) no constraint qualifications holds; (ii) constraint qualifications are satisfied and the usual KKT theory can be applied.

In case (i), we will refer to the following definition (cfr. [6]) of stationary point of problem (3).

Definition 2.5

Given \({{\bar{y}}} \in \mathcal {Y}\) and \({{\bar{x}}}\in \mathcal {X}({{\bar{y}}})\), we say that \({{\bar{x}}}\) is a stationary point of problem (3) if and only if

$$\begin{aligned} {{\bar{x}}}=\Pi _{\mathcal {X}({{\bar{y}}})}\left[ {{\bar{x}}}-\nabla f(\bar{x})\right] . \end{aligned}$$

We notice that \(\mathcal {X}({{{\bar{y}}}})\) is a convex set when X is convex, then the condition given above is a classic stationarity condition for the problem (3). Case (ii) will be considered later.

As we have seen, the definition of discrete neighborhood for problem (2) is general. Now, we introduce a specific discrete neighborhood mapping that can be implemented at a reasonable computational cost, and will also help us to relate our analysis to the other theoretical tools available in the literature. In order to better motivate the introduction of the general definition of discrete neighborhood, we will present another example of point-to-set mapping in Sect. 3.

Consider a set \(I\subseteq \{1,\ldots ,n\}\) and a function \({H}_{I}: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) defined as

$$\begin{aligned} ({H}_{I}(x))_h = \left\{ \begin{array}{ll} 0, &{} \text {if }h\in I\\ x_h &{} \text {otherwise.} \end{array}\right. \end{aligned}$$

This function basically sets to zero all the components with indices in I of a given vector x. As said before, we introduce an example of discrete neighborhood mapping for problem (2) and based on the above function.

Definition 2.6

Let \(d_H:\{0,1\}^n\times \{0,1\}^n\rightarrow \mathbb {N}\) denote the Hamming distance. Moreover, let \(\Delta (y,{\hat{y}})=\{i\mid y_i\ne {\hat{y}}_i\}\). Then, given \(\rho \in \mathbb {N}\), the discrete neighborhood mapping \(\mathcal {N}_\rho \) is defined as

$$\begin{aligned} \mathcal {N}_\rho (x,y)=\left\{ ({\hat{x}},{\hat{y}})\mid {\hat{y}}\in \mathcal {Y},\mathcal {X}({\hat{y}})\ne \emptyset ,\;\;d_H({\hat{y}},y)\le \rho ,\; {\hat{x}}=\Pi _{\mathcal {X}({\hat{y}})}(H_{\Delta (y,{\hat{y}})}(x))\right\} . \end{aligned}$$
(4)

Basically, the discrete neighborhood mapping \(\mathcal {N}_\rho \) is such that the discrete neighborhood \(\mathcal {N}_\rho (x,y)\) contains points \(({\hat{x}},{\hat{y}})\) with at most \(\rho \) components of \({\hat{y}}\) differing from y; \({\hat{x}}\) is obtained by zeroing components of x as needed to maintain feasibility w.r.t. the complementarity constraints and then by projecting the result onto the (convex) active feasible set \(X({\hat{y}})\). In other words, this particular definition of discrete neighborhood allows to take into account the potential “change of status” of up to \(\rho \) variables in the vector \({{\hat{y}}}\) defining an active subspace.

Example 2.1

Consider the problem (2) with \(X={\mathbb {R}}^3\), \(n=3\) and \(s=2\) and let \(\rho = 2\). Let (x, y) be a feasible point defined as follows

$$\begin{aligned} (x,y)= \left( \begin{array}{l} 1\\ 2\\ 0 \end{array} \right) \left( \begin{array}{l} 0\\ 0\\ 1 \end{array} \right) . \end{aligned}$$

The neighborhood \({{\mathcal {N}}}_\rho (x,y)\) is given by

$$\begin{aligned} {{\mathcal {N}}}_2(x,y)=\left\{ \left( \begin{array}{l} 1\\ 2\\ 0 \end{array}\right) \left( \begin{array}{l} 0\\ 0\\ 1 \end{array}\right) , \; \left( \begin{array}{l} 1\\ 0\\ 0 \end{array}\right) \left( \begin{array}{l} 0\\ 1\\ 0 \end{array}\right) , \; \left( \begin{array}{l} 0\\ 2\\ 0 \end{array}\right) \left( \begin{array}{l} 1\\ 0\\ 0 \end{array}\right) , \; \left( \begin{array}{l} 1\\ 0\\ 0 \end{array}\right) \left( \begin{array}{l} 0\\ 1\\ 1 \end{array}\right) , \; \left( \begin{array}{l} 0\\ 2\\ 0 \end{array}\right) \left( \begin{array}{l} 1\\ 0\\ 1 \end{array}\right) , \; \left( \begin{array}{l} 0\\ 0\\ 0 \end{array}\right) \left( \begin{array}{l} 1\\ 1\\ 1 \end{array}\right) \right\} . \end{aligned}$$

3 Algorithmic Framework

Here, we discuss an algorithmic framework for the solution of problem (1) that exploits the reformulation given in problem (2). The proposed approach is somehow related to classic methods for mixed variable programming proposed in the literature (see, e.g., [24, 27]).

The approach aims at finding points satisfying the newly defined \(\mathcal {N}\)-stationarity condition. The algorithm combines inexact minimizations with a strategy that explores discrete neighborhoods of a given feasible point. Those features make it easy to handle the nonconvexity in both the objective function and the feasible set also from a practical point of view.

Roughly speaking, the approach, at each iteration k, computes a discrete neighborhood \(\mathcal {N}\left( x^k, y^k\right) \) of the current point \(\left( x^k,y^k\right) \), and performs local exploratory moves around the points of the neighborhood with respect to the continuous variables.

Specifically, the continuous exploration move consists of a local search performed by an Armijo-type line search along the projected gradient direction, where the feasible set \(\mathcal {X}(y)\) for the continuous variables is induced by the binary variables y that implicitly define an active set. The procedure is formalized in Algorithm 1.

figure a

The proposed framework, which we refer to as Sparse Neighborhood Search (SNS), is formally defined in Algorithm 2, where it is assumed that a discrete neighborhood mapping \(\mathcal {N}\) is employed. In brief, the instructions of our algorithmic framework are carried out as follows:

  1. (i)

    starting from the current iterate \(\left( x^k,y^k\right) \), the PGLS is performed to obtain the point \({\tilde{x}}^k\) (see step 3);

  2. (ii)

    any point \(\left( {\hat{x}}^k, {\hat{y}}^k\right) \in \mathcal {N}\left( {\tilde{x}}^k, y^k\right) \) that is not significantly worse (in terms of objective function value) than the current candidate, is considered in the neighborhood exploration, i.e., a local continuous search around \({\hat{x}}^k\) is performed (see step 4 and while cycle - steps 6–18);

  3. (iii)

    the local search is given by multiple steps of PGLS and is stopped when the point is approximately stationary (steps 6–18);

  4. (iv)

    we skip to the next iteration as soon as a point providing a sufficient decrease of the objective value is found (successful iteration, see steps 11– 15) or when there is no point left to analyze in the neighborhood;

  5. (v)

    in the latter case, the success of the iteration will be established by the decrease in the objective value attained by \({\tilde{x}}^k\) (see steps 19– 25).

Remark 3.1

The value of parameter \(\mu _k\) controls the approximation degree of stationarity considered to stop, at step 16, local optimizations in the exploration phase. In the definition of Algorithm 2, the value of \(\mu _k\) decreases at each iteration, asymptotically going to zero, so that the accuracy of the exploration phase gradually increases. However, the value of \(\mu _k\) does not have an impact in the convergence analysis, as long as it remains strictly positive; convergence can indeed be established thanks to the properties of the PGLS. The analysis in Sect. 3.1 for example is not impacted if the value \(\mu \) is kept fixed, as we did in our numerical experiments.

figure b

3.1 Convergence Analysis

In this section, we prove a set of results concerning the properties of the sequences produced by Algorithm 2. Note that in this section we employ the concept of stationarity (24). First, we state some suitable assumptions.

Assumption 3.1

The gradient \(\nabla f(x)\) is Lipschitz-continuous, i.e., there exists a constant \(L > 0\) such that \(\left\| \nabla f(x) - \nabla f({\bar{x}}) \right\| \le L \left\| x - {\bar{x}} \right\| \) for all \(x, {\bar{x}} \in {\mathbb {R}}^n\).

Assumption 3.2

Given \(y^0 \in \mathcal {Y}\), \(x^0 \in \mathcal {X}\left( y^0\right) \) and a scalar \(\xi > 0\), the level set \( \mathcal {L}\left( x^0, y^0\right) = \left\{ (x,y) \in \mathcal {X}(y) \times \mathcal {Y}\mid f(x) \le f\left( x^0\right) + \xi \right\} \) is compact.

First, note that when we deal with both continuous and integer variables, the usual notion of convergence to a point needs to be tweaked. In particular, we have the following definition.

Definition 3.1

A sequence \(\{ \left( x^k, y^k\right) \}\) converges to a point \(({\bar{x}}, {\bar{y}})\) if for any \(\epsilon > 0\) there exists an index \(k_\epsilon \) such that for all \(k \ge k_\epsilon \) we have that \(y^k = {\bar{y}}\) and \(\Vert x^k - {\bar{x}} \Vert < \epsilon \).

To ensure convergence to meaningful points, we need a “continuity” assumption on the discrete neighborhood mapping \(\mathcal {N}\) we exploit.

Assumption 3.3

Let \(\left\{ \left( x^k, y^k\right) \right\} \) be a sequence converging to \(({\bar{x}}, {\bar{y}})\). Then, for any \(({\hat{x}}, {\hat{y}}) \in \mathcal {N}({\bar{x}}, {\bar{y}})\), there exists a sequence \(\{ \left( {\hat{x}}^k, {\hat{y}}^k\right) \}\) converging to \(({\hat{x}}, {\hat{y}})\) such that \(\left( {\hat{x}}^k, {\hat{y}}^k\right) \in \mathcal {N}\left( x^k, y^k\right) \).

The assumption above requires the lower semicontinuity of the point-to-set mapping \(\mathcal {N}\) (see, e.g., [5]). Note that this assumption is necessary to ensure property (ii) of \(\mathcal {N}\)-stationarity given in Definition 2.4.

First we show that the neighborhood \(\mathcal {N}_\rho \) considered in Definition 2.6 satisfies Assumption 3.3. To this aim we separately analyze the cases \(X={\mathbb {R}}^n\) and \(X\subset {\mathbb {R}}^n\). Then we will present another example of neighborhood satisfying Assumption 3.3.

Proposition 3.1

The point-to-set map \(\mathcal {N}_\rho \) given in Definition 2.6 satisfies Assumption 3.3 when \(X={\mathbb {R}}^n\).

Proof

Let \(\left\{ x^k,y^k\right\} \) be a sequence convergent to \(\{{\bar{x}},{\bar{y}}\}\). Then, for any \(\epsilon >0\), there exists \(k_\epsilon \) such that \(y^k={\bar{y}}\) and \(\Vert x^k-{\bar{x}}\Vert \le \epsilon \) for all \(k>k_\epsilon \). Let \(({\hat{x}},{\hat{y}})\in \mathcal {N}_\rho ({\bar{x}},{\bar{y}})\). For k sufficiently large, since \(y^k={\bar{y}}\), we have \(\{y\mid y\in \mathcal {Y},\; d_H\left( y,y^k\right) \le \rho \}=\{y\mid y\in \mathcal {Y},\; d_H(y,{\bar{y}})\le \rho \}\), hence \({\hat{y}}\in \{y\mid d_H(y,y^k)\le \rho \}\) for all k. Let us then consider the sequence \(\{{\hat{x}}^k,{\hat{y}}^k\}\) where \({\hat{y}}^k={\hat{y}}\) and \({\hat{x}}^k=H_{\Delta (y^k,{\hat{y}})}(x^k)\). We can observe that \(({\hat{x}}^k,{\hat{y}}^k)\in \mathcal {N}_\rho (x^k,y^k)\). Now, let \(j\in \{1,\ldots ,n\}\). The set \(\Delta (y^k,{\hat{y}}^k)=\Delta ({\bar{y}},{\hat{y}})=\Delta \) is constant for k sufficiently large. Noting that, being \(X={\mathbb {R}}^n\), \(\Pi _{\mathcal {X}({\hat{y}})}(H_\Delta (x)) = H_{\Delta }(x)\), we have for \(j\notin \Delta \)

$$\begin{aligned} \lim _{k\rightarrow \infty }{\hat{x}}^k_j = \lim _{k\rightarrow \infty }x^k_j={\bar{x}}_j = {\hat{x}}_j. \end{aligned}$$

On the other hand, if \(j\in \Delta \), \({\hat{x}}^k_j=0\) and \({\hat{x}}_j=0\). Hence \(\lim _{k\rightarrow \infty }{\hat{x}}^k={\hat{x}}\) and we thus get the thesis. \(\square \)

The result still holds in the case \(X\subset {\mathbb {R}}^n\).

Proposition 3.2

Let \(\{(x^k, y^k)\}\) be a sequence converging to \(({\bar{x}}, {\bar{y}})\). Then, the point-to-set map \(\mathcal {N}_\rho (x,y)\) defined in Definition 2.6 satisfies Assumption 3.3.

Proof

The proof follows exactly as in Proposition 3.1, recalling the continuity of the projection operator \(\Pi _{\mathcal {X}({\hat{y}})}\). \(\square \)

Before presenting another example of discrete neighborhood mapping and turning to the convergence analysis of the algorithm, we prove a further useful preliminary result concerning the discrete neighborhood mapping \(\mathcal {N}_\rho \).

Lemma 3.1

Let \(y\in \mathcal {Y}\) and \(x\in \mathcal {X}(y)\) with \(\delta =\Vert x\Vert _0\). Let us consider the set

$$\begin{aligned} \bar{\mathcal {N}}(x)=\{({\hat{x}},{\hat{y}})\mid {\hat{y}}\in \{0,1\}^n,\; {\hat{x}} = x,\;e^\top {\hat{y}}=n-s,\; I_0({\hat{y}})\supseteq I_1(x)\; \}. \end{aligned}$$

We have that \(\bar{ \mathcal {N}}(x)\subseteq \mathcal {N}_\rho (x,y),\) when \(\rho \ge 2(s-\delta )\).

Proof

Let \(({\hat{x}}, {\hat{y}})\) be any point in \(\bar{\mathcal {N}}(x)\). From the feasibility of (x, y) we have

$$\begin{aligned} \delta \le |I_0(y)|\le s\qquad n-s\le |I_1(y)|\le n-\delta . \end{aligned}$$
(5)

Moreover, from the definition of \(\bar{\mathcal {N}}(x)\), we have \(|I_0({\hat{y}})|=s\) and \(|I_1({\hat{y}})| = n-s.\) Now, it is easy to see that

$$\begin{aligned} d_H(y,{\hat{y}}) = n - |I_0(y) \cap I_0({\hat{y}})| - |I_1(y)\cap I_1({\hat{y}})|. \end{aligned}$$
(6)

We can note that, since \(I_0(y)\supseteq I_1(x)\) and \(I_0({\hat{y}})\supseteq I_1(x)\), it has to be \(I_0(y)\cap I_0({\hat{y}}) \supseteq I_1(x)\). Therefore

$$\begin{aligned} |I_0(y) \cap I_0({\hat{y}})| \ge |I_1(x)| = \delta . \end{aligned}$$
(7)

We can now turn to \(I_1(y)\cap I_1({\hat{y}})\). Since the latter set can be equivalently written, by De Morgan’s law, as \(\{1,\ldots ,n\}\setminus (I_0(y)\cup I_0({\hat{y}}))\), we can obtain

$$\begin{aligned} \begin{aligned} |I_1(y)\cap I_1({\hat{y}})|&= |\{1,\ldots ,n\}\setminus (I_0(y)\cup I_0({\hat{y}}))|\\ {}&= n - |I_0(y)\cup I_0({\hat{y}})|\\ {}&=n - (|I_0(y)| + |I_0({\hat{y}})| - |I_0(y)\cap I_0({\hat{y}})|)\\ {}&= n - |I_0(y)| - s + |I_0(y)\cap I_0({\hat{y}})|\\&\ge n - s - s + \delta \\ {}&= n -2s + \delta , \end{aligned} \end{aligned}$$

where the second last inequality comes from (5) and (7). Putting everything together back in (6), we get \(d_H(y,{\hat{y}}) \le n - \delta - n+2\,s - \delta = 2(s-\delta ).\) Taking into account that \(\rho \ge 2(s-\delta )\) in the definition of \(\mathcal {N}_\rho (x,y)\), we obtain \(({\hat{x}}, {\hat{y}})\in \mathcal {N}_\rho (x,y),\) thus getting the desired result. \(\square \)

Another example of discrete neighborhood mapping satisfying Assumption 3.3 is reported below and is inspired by the coordinate descent type algorithms proposed in [3, 4]. The basic idea of these coordinate methods is that of updating the support at each iteration by one or two variables. In particular, the methods perform in some cases the swap between pairs of variables.

Example 3.1

An \(n\times n\) permutation matrix \(\Sigma \) is a square matrix obtained from the \(n\times n\) identity matrix by a permutation of rows. Let us assume that we are dealing with a convex set X that is type-1 symmetric according to [4], i.e., any permutation of variables preserves feasibility. Formally, for any point \(x\in X\) and any permutation matrix \(\Sigma \), we have \(\Sigma x\in X\). Feasible sets of this kind include very relevant cases, such as the entire Euclidean space, the unit simplex, p-balls and boxes.

Now, let us denote by H a permutation matrix obtained by interchanging only two rows of the identity, say i and j. The point \( {{\hat{x}}}=Hx \) is such that

$$\begin{aligned} {{\hat{x}}}_i=x_j, \quad {{\hat{x}}}_j=x_i,\quad {{\hat{x}}}_h=x_h \text { for } h\ne i,j, \end{aligned}$$

so that \(\Vert {{\hat{x}}}\Vert _0=\Vert x\Vert _0\). With symmetric sets, not only swap operations are guaranteed to maintain feasibility, but also have a semantic meaning as variables are on equal scales. We are thus motivated to define a set \(\Gamma =\{H_1,H_2,\ldots ,H_p\}\) of permutation matrices obtained by interchanging two rows. Note that the maximum cardinality p of \(\Gamma \) is \({{n(n-1)}\over {2}}\). We can finally define the discrete neighborhood \(\mathcal {N}_\Gamma (x, y)\) as follows:

$$\begin{aligned} \mathcal {N}_\Gamma (x,y)=\left\{ \left( {{\hat{x}}}^l,{{\hat{y}}}^l\right) \mid \ {{\hat{x}}}^l=H_lx, \;{{\hat{y}}}^l=H_ly, \ l=1,\ldots ,p\}\cup \{(x,y)\right\} , \end{aligned}$$

i.e., \(\mathcal {N}_\Gamma (x,y)\) is obtained by swapping pairs of variables (both continuous and binary). Since all points in \(\mathcal {N}_\Gamma (x,y)\) are feasible and \((x,y)\in \mathcal {N}_\Gamma (x,y)\), this mapping indeed satisfies all the properties required by Definition 2.2.

Proposition 3.3

The point-to-set map \(\mathcal {N}_\Gamma (x,y)\) defined in Example 3.1 satisfies Assumption 3.3.

Proof

If \(\{(x^k, y^k)\}\) converges to \(({\bar{x}}, {\bar{y}})\), then for any \(\epsilon > 0\) there exists an index \(k_\epsilon \) such that for all \(k \ge k_\epsilon \) we have that \(y^k = {\bar{y}}\) and \(\Vert x^k - {\bar{x}} \Vert < \epsilon \). Let \(({\hat{x}}, {\hat{y}}) \in \mathcal {N}_\Gamma ({\bar{x}}, {\bar{y}})\), i.e., for some \(l\in \{1,\ldots ,p\}\) we have \( {\hat{x}}=H_l {{\bar{x}}}\) and \( {\hat{y}}=H_l{{\bar{y}}}. \) Let \(\{({\hat{x}}^k, {\hat{y}}^k)\}\) be the sequence such that \(({\hat{x}}^k, {\hat{y}}^k) = (H_lx^k, H_ly^k)\) for all k. Note that \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}_\Gamma (x^k, y^k)\) for all k since \(H_l\in \Gamma \).

For k sufficiently large we have \(y^k = {\bar{y}}\). This implies that \({\hat{y}}^k = H_ly^k=H_l{{\bar{y}}}={\hat{y}}\). Moreover we can write

$$\begin{aligned} \lim _{k\rightarrow \infty }{{\hat{x}}}^k= \lim _{k\rightarrow \infty } H_lx^k=H_l{{\bar{x}}}={{\hat{x}}}, \end{aligned}$$

and hence we may conclude that \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}_\Gamma (x^k, y^k)\) and \(\{ ({\hat{x}}^k, {\hat{y}}^k)\}\) converges to \(({\hat{x}}, {\hat{y}})\). \(\square \)

We can now focus on the algorithms. First, we give a definition that is useful for the analysis.

Definition 3.2

A function \(\sigma : {\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) is a forcing function if, for any sequence \(\{t_k\}\), \(t_k\in [0,+\infty )\), we have that \(\lim \limits _{k\rightarrow \infty } \sigma (t_k) = 0 \) implies \( \lim \limits _{k\rightarrow \infty }t_k=0.\)

Then, we prove a property of Algorithm 1 that will play an important role in the convergence analysis of Algorithm 2.

Proposition 3.4

Given a feasible point \((x, y)\in \mathcal {X}(y)\times \mathcal {Y}\), Algorithm 1 produces a feasible point \(({\tilde{x}}, y)\) such that \( f({\tilde{x}}) \le f(x) - \sigma \left( \left\| x - \Pi _{\mathcal {X}(y)} \left[ x - \nabla f(x)\right] \right\| \right) . \)

Proof

By definition, \(d = {\hat{x}} - x\), where \({\hat{x}} = \Pi _{\mathcal {X}(y)} \left[ x - \nabla f(x)\right] \). By the properties of the projection operator, we can write \((x - \nabla f(x) - {\hat{x}})^\top (x - {\hat{x}}) \le 0,\) which, with simple manipulations, implies that

$$\begin{aligned} \nabla f(x)^\top d \le - \left\| d \right\| ^2 = - \left\| x - \Pi _{\mathcal {X}(y)}\left[ x - \nabla f(x)\right] \right\| ^2. \end{aligned}$$
(8)

By the instructions of the algorithm, either \(\alpha =1\) or \(\alpha < 1\).

If \(\alpha = 1\), then \({\tilde{x}} = x + d\) satisfies

$$\begin{aligned} f({\tilde{x}}) \le f(x) + \gamma \nabla f(x)^\top d \le f(x) - \gamma \left\| x - \Pi _{\mathcal {X}(y)} \left[ x - \nabla f(x)\right] \right\| ^2. \end{aligned}$$
(9)

If \(\alpha < 1\), we must have that

$$\begin{aligned} f(x + \alpha d) \le f(x) + \gamma \alpha \nabla f(x)^\top d, \end{aligned}$$
(10)
$$\begin{aligned} f\left( x + \frac{\alpha }{\delta } d\right) > f(x) + \gamma \frac{\alpha }{\delta } \nabla f(x)^\top d. \end{aligned}$$
(11)

Applying the mean value theorem to equation (11), we get

$$\begin{aligned} \nabla f\left( x + \theta \frac{\alpha }{\delta } d\right) ^\top d > \gamma \nabla f(x)^\top d, \end{aligned}$$

where \(\theta \in (0,1)\). Adding and subtracting \(\nabla f(x)^\top d\), and rearranging, we get

$$\begin{aligned} (1 - \gamma ) \nabla f(x)^\top d > \left[ \nabla f(x) - \nabla f\left( x + \theta \frac{\alpha }{\delta } d\right) \right] ^\top d. \end{aligned}$$

By the Lipschitz-continuity of \(\nabla f(x)\), we can write

$$\begin{aligned} \left[ \nabla f(x) - \nabla f\left( x + \theta \frac{\alpha }{\delta } d\right) \right] ^\top d \ge -L \frac{\alpha }{\delta } \left\| d \right\| ^2, \end{aligned}$$

which means that

$$\begin{aligned} (1 - \gamma ) \nabla f(x)^\top d > -L \frac{\alpha }{\delta } \left\| d \right\| ^2. \end{aligned}$$

Rearranging, we get

$$\begin{aligned} \frac{\delta }{L}(1 - \gamma ) \nabla f(x)^\top d > -\alpha \left\| d \right\| ^2. \end{aligned}$$

This last inequality, together with (8), yields

$$\begin{aligned} \frac{\delta }{L}(1 - \gamma ) \nabla f(x)^\top d > \alpha \nabla f(x)^\top d, \end{aligned}$$

and substituting in equation (10) we finally get

$$\begin{aligned}{} & {} f({\tilde{x}}) < f(x) + \gamma \frac{\delta }{L}(1 - \gamma ) \nabla f(x)^\top d \\ {}{} & {} \quad \le f(x) - \gamma \frac{\delta }{L}(1 - \gamma ) \left\| x - \Pi _{\mathcal {X}(y)} \left[ x - \nabla f(x)\right] \right\| ^2. \end{aligned}$$

This last inequality, together with (9), implies that

$$\begin{aligned} f({\tilde{x}}) \le f(x) - \sigma \left( \left\| x - \Pi _{\mathcal {X}(y)} \left[ x - \nabla f(x)\right] \right\| \right) \end{aligned}$$

where

$$\begin{aligned} \sigma \left( t \right) = \gamma \min \left\{ 1,\frac{\delta }{L}(1-\gamma ) \right\} t^2. \end{aligned}$$

\(\square \)

We can now state a couple of preliminary theoretical results. We first show that Algorithm 2 is well-posed.

Proposition 3.5

For each iteration k, the loop between steps 9 and 18 of Algorithm 2 terminates in a finite number of steps.

Proof

Suppose by contradiction that Steps 9-18 generate an infinite loop, so that an infinite sequence of points \(\{z^j\}\) is produced for which

$$\begin{aligned} \left\| z^j - \Pi _{\mathcal {X}(y^\prime )} \left[ z^j - \nabla f(z^j)\right] \right\|> \mu _k > 0 \quad \forall j. \end{aligned}$$
(12)

By Proposition 3.4, for each j we have that

$$\begin{aligned} f(z^{j+1}) - f(z^j) \le -\sigma \left( \left\| z^j - \Pi _{\mathcal {X}(y^\prime )} \left[ z^j - \nabla f(x^j)\right] \right\| \right) , \end{aligned}$$
(13)

where \(\sigma \left( \cdot \right) \ge 0\). The sequence \(\{ f(z^j) \}\) is therefore nonincreasing. Moreover, equation (13) implies that

$$\begin{aligned} \left| f(z^{j+1}) - f(z^j)\right| \ge \sigma \left( \left\| z^j - \Pi _{\mathcal {X}(y^\prime )} \left[ z^j - \nabla f(z^j)\right] \right\| \right) . \end{aligned}$$
(14)

By Assumption 3.2, \(\{ f(x^j) \}\) is lower bounded. Therefore, recalling that \(\{ f(z^j) \}\) is nonincreasing, we get that \(\{ f(z^j) \}\) converges, which implies that

$$\begin{aligned} \left| f(z^{j+1}) - f(z^j)\right| \rightarrow 0. \end{aligned}$$

By (14), we get that \({\sigma \left( \left\| z^j - \Pi _{\mathcal {X}(y^\prime )} \left[ z^j - \nabla f(z^j)\right] \right\| \right) \rightarrow 0}\), and, by the properties of \(\sigma \left( \cdot \right) \), we finally get that \(\left\| z^j - \Pi _{\mathcal {X}(y^\prime )} \left[ z^j - \nabla f(z^j)\right] \right\| \rightarrow 0\), and this contradicts (12). \(\square \)

We now define a set of indices that will be useful in the convergence analysis:

$$\begin{aligned} K_u = \{k \mid \eta _k < \eta _{k-1} \}, \end{aligned}$$
(15)

that is the set of indices related to the points generated at unsuccessful iterations (see Steps 19– 25 of Algorithm 2). The next proposition shows some properties of the sequences generated by the algorithm, which will play an important role in the subsequent analysis.

Proposition 3.6

Let \(\{ (x^k, y^k) \}\), \(\{\mu _k\}\) and \(\{ \eta _k\}\) be the sequences produced by Algorithm 2. Then:

  1. (i)

    the sequence \(\{ f\left( x^k\right) \}\) is nonincreasing and convergent;

  2. (ii)

    the sequence \(\{ \left( x^k, y^k\right) \}\) is bounded;

  3. (iii)

    the set \(K_u\) defined in (15) is infinite;

  4. (iv)

    \(\lim _{k \rightarrow \infty } \mu _k = 0\);

  5. (v)

    \(\lim _{k \rightarrow \infty } \eta _k = 0\);

  6. (vi)

    \(\lim _{k \rightarrow \infty } \left\| x^k - \Pi _{\mathcal {X}(y^k)} \left[ x^k - \nabla f(x^k)\right] \right\| = 0\).

Proof

  1. (i)

    The instructions of the algorithm and Proposition 3.4 imply that \(\{ f\left( x^k\right) \}\) is nonincreasing, and Assumption 3.2 implies that \(\{ f\left( x^k\right) \}\) is lower bounded. Hence, \(\{ f\left( x^k\right) \}\) converges.

  2. (ii)

    The instructions of the algorithm imply that each point \(\left( x^k, y^k\right) \) belongs to the level set \(\mathcal {L}\left( x^0, y^0\right) \), which is compact by Assumption 3.2. Therefore, \(\{ \left( x^k, y^k\right) \}\) is bounded.

  3. (iii)

    Suppose that \(K_u\) is finite. Then there exists \({\bar{k}} > 0\) such that all iterates satisfying \(k > {\bar{k}}\) are successful, i.e., \( f(x^k) \le f(x^{k-1}) - \eta _{k-1},\) and \(\eta _k = \eta _{k-1} = \eta > 0\) for all \(k \ge {\bar{k}}\). Since \(\eta > 0\), this implies that \(\{f(x^k)\}\) diverges to \(-\infty \), in contradiction with (i).

  4. (iv)

    Since, for all k, \(\mu _{k+1} = \delta \mu _k\), where \(\delta \in (0, 1)\), the claim holds.

  5. (v)

    If \(k \in K_u\), then \(\eta _{k} = \theta \eta _{k-1}\), where \(\theta \in (0,1)\). Since \(K_u\) is infinite and \(\eta _{k}=\eta _{k-1}\) if \(k\notin K_u\), the claim holds.

  6. (vi)

    By Proposition 3.4, we have that

    $$\begin{aligned} f({\tilde{x}}^k) - f(x^k) \le -\sigma \left( \left\| x^k - \Pi _{\mathcal {X}(y^k)} \left[ x^k - \nabla f(x^k)\right] \right\| \right) . \end{aligned}$$

    By the instructions of the algorithm, \(f(x^{k+1}) \le f({\tilde{x}}^k)\), and so we can write

    $$\begin{aligned} f(x^{k+1}) - f(x^k) \le -\sigma \left( \left\| x^k - \Pi _{\mathcal {X}(y^k)} \left[ x^k - \nabla f(x^k)\right] \right\| \right) , \end{aligned}$$

    i.e.,

    $$\begin{aligned} \left| f(x^{k+1}) - f(x^k) \right| \ge \sigma \left( \left\| x^k - \Pi _{\mathcal {X}(y^k)} \left[ x^k - \nabla f(x^k)\right] \right\| \right) . \end{aligned}$$

    Since \(\{ f(x^k) \}\) converges, we get that \({\sigma \left( \left\| x^k - \Pi _{\mathcal {X}(y^k)} \left[ x^k - \nabla f(x^k)\right] \right\| \right) \rightarrow 0}\). By the properties of \(\sigma \left( \cdot \right) \), we get that \(\left\| x^k - \Pi _{\mathcal {X}(y^k)} \left[ x^k - \nabla f(x^k)\right] \right\| \rightarrow 0\).

\(\square \)

Before stating the main theorem of this section, it is useful to summarize some theoretical properties of the subsequence \(\{(x^k, y^k)\}_{K_u}\). As the proof shows, the next proposition follows easily from the theoretical results we have shown above.

Proposition 3.7

Let \(\{(x^k, y^k)\}\) be the sequence of iterates generated by Algorithm 2, and let \(K_u\) be defined as in (15). Then:

  1. (i)

    \(\{(x^k, y^k)\}_{K_u}\) admits accumulation points;

  2. (ii)

    for any accumulation point \((x^*, y^*)\) of the sequence \(\{(x^k, y^k)\}_{K_u}\), every point \({({\hat{x}}, {\hat{y}})\in \mathcal {N}(x^*, y^*)}\) is an accumulation point of a sequence \(\{({\hat{x}}^k, {\hat{y}}^k)\}_{K_u}\) where \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}(x^k, y^k)\).

Proof

  1. (i)

    By Proposition 3.6, (ii), \(\{(x^k, y^k)\}\) is bounded. Therefore, \(\{(x^k, y^k)\}_{K_u}\) is also bounded, and so it admits accumulation points.

  2. (ii)

    Assumption 3.3 implies that every \(({\hat{x}}, {\hat{y}}) \in \mathcal {N}(x^*, y^*)\) is an accumulation point of a sequence \(\{({\hat{x}}^k, {\hat{y}}^k)\}_{K_u}\), where \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}(x^k, y^k)\).

\(\square \)

We can now prove the main theoretical result of this section.

Theorem 3.1

Let \(\{(x^k, y^k)\}\) be the sequence generated by Algorithm 2. Every accumulation point \((x^*,y^*)\) of \(\{(x^k, y^k)\}_{K_u}\) is a stationary point w.r.t \(\mathcal {N}(x^*,y^*)\) of problem (2).

Proof

Let \((x^*, y^*)\) be an accumulation point of \(\{(x^k, y^k)\}_{K_u}\). We must show that conditions (i)-(iii) of Definition 2.4 are satisfied.

  1. (i)

    From the instructions of Algorithm 2 the iterates \((x^k,y^k)\) belong to the set \({\mathcal {L}}(x^0,y^0)\), which is closed from Assumption 3.2. Any limit point \((x^*,y^*)\) belongs to \(\mathcal {L}(x^0,y^0)\) and is thus feasible for problem (2).

  2. (ii)

    The result follows from Proposition 3.6, (iv).

  3. (iii)

    Considering the way the set \(K_u\) is defined in (15), we can observe that for all \(k\in K_u\) we have \(x^k={\tilde{x}}^{k-1},\quad y^k=y^{k-1}.\) We can thus denote

    $$\begin{aligned} \mathcal {N}^k=\mathcal {N}(x^k,y^k)=\mathcal {N}({\tilde{x}}^{k-1},y^{k-1}). \end{aligned}$$

    Since \(k\in K_u\), for all \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}^k\) either the test at step 11 failed or the point was not included in \(W_{k-1}\) and hence \(f({\hat{x}}^k) > f({\tilde{x}}^{k-1}) - \eta _{k-1} = f({x}^{k}) - \eta _{k-1}.\) Since the sequence \(\{f(x^k)\}\) is nonincreasing (Proposition 3.6, (i)), we can write \(f(x^*) \le f(x^k) < f({\hat{x}}^k) + \eta _{k-1}.\) for all \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}^k\). Taking limits, we get from Proposition 3.6, (iii), Assumption 3.3, and by the continuity of f that \(f(x^*)\le f({\hat{x}})\) for all \(({\hat{x}}, {\hat{y}}) \in \mathcal {N}(x^*, y^*)\). Now, note that (i) of Proposition 3.6 ensures the existence of \(f^* \in {\mathbb {R}}\) satisfying

    $$\begin{aligned} \lim \limits _{k \rightarrow \infty } f(x^k) = f(x^*) = f^*. \end{aligned}$$
    (16)

    Consider any \(({\hat{x}}, {\hat{y}}) \in \mathcal {N}(x^*, y^*)\) such that

    $$\begin{aligned} f({\hat{x}}) = f^*. \end{aligned}$$
    (17)

    Proposition 3.7 implies that the point \(({\hat{x}}, {\hat{y}})\) is an accumulation point of a sequence \(\{({\hat{x}}^k, {\hat{y}}^k)\}_{K_u}\), where \(({\hat{x}}^k, {\hat{y}}^k) \in \mathcal {N}^k\). Therefore, by (16) and (17) we get, for k sufficiently large, \(f({\hat{x}}^k) < f(x^k) + \xi =f({\tilde{x}}^{k-1})+\xi .\) Thus, for such values of k, we have

    $$\begin{aligned} ({\hat{x}}^k, {\hat{y}}^k) \in W_{k-1}=\{(x,y)\in \mathcal {N}^k\mid f(x)\le f({\tilde{x}}^{k-1})+\xi \}. \end{aligned}$$

    Steps 9-18 produce the points \(z_{k-1}^2,\ldots ,z_{k-1}^{j_{k-1}^*}\) (where \(j_{k-1}^*\) is the finite number of iterations of steps 9-18 until the test at step 16 is passed), which, by the instructions at Step 10 and by Proposition 3.4, satisfy

    $$\begin{aligned} f({\hat{x}}^k) \ge f(z_{k-1}^2) \ge \ldots \ge f(z_{k-1}^{j_{k-1}^*}). \end{aligned}$$
    (18)

    Again, since \(k \in K_u\), the test at step 11 is not passed at iteration \(k-1\), and we can write

    $$\begin{aligned} f(z_{k-1}^{j_{k-1}^*}) > f({\tilde{x}}^{k-1}) - \eta _{k-1} = f(x^k) - \eta _{k-1}. \end{aligned}$$
    (19)

    Moreover, as the sequence \(\{({\hat{x}}^k, {\hat{y}}^k)\}_{K_u}\) converges to the point \(({\hat{x}}, {\hat{y}})\), by (16), (17), (18), (19), and by (iii) of Proposition 3.6, we obtain

    $$\begin{aligned} f^* = \lim \limits _{k \rightarrow \infty , k \in K_u} f({\hat{x}}^k) = \lim \limits _{k \rightarrow \infty , k \in K_u} f(z^2_{k-1}) = \lim \limits _{k \rightarrow \infty , k \in K_u} f(x^k) = f^*. \end{aligned}$$

    By Proposition 3.4, we have that

    $$\begin{aligned} f(z_{k-1}^2) \le f({\hat{x}}^k) - \sigma \left( \left\| {\hat{x}}^k - \Pi _{\mathcal {X}({\hat{y}}^k)} \left[ {\hat{x}}^k - \nabla f({\hat{x}}^k)\right] \right\| \right) , \end{aligned}$$

    which can be rewritten as

    $$\begin{aligned} \left| f(z_{k-1}^2) - f({\hat{x}}^k) \right| \ge \sigma \left( \left\| {\hat{x}}^k - \Pi _{\mathcal {X}({\hat{y}}^k)} \left[ {\hat{x}}^k - \nabla f({\hat{x}}^k)\right] \right\| \right) . \end{aligned}$$

    Taking limits for \(k \rightarrow \infty , k \in K_u\), we get \(\left\| {\hat{x}} - \Pi _{\mathcal {X}({\hat{y}})} \left[ {\hat{x}} - \nabla f({\hat{x}})\right] \right\| = 0,\) and the claim finally holds.

\(\square \)

The above theorem states that, if any discrete neighborhood mapping \(\mathcal {N}\) satisfying the continuity Assumption 3.3 is employed, then all limit points of the sequence \(K_u\) produced by the SNS algorithm are \(\mathcal {N}\)-stationary. Now, we show that a suitable choice of the neighborhood to be used within Algorithm 2 allows to obtain convergence toward points satisfying relevant optimality conditions from the literature. In [4], the concept of basic feasibility (BF) introduced in [3] is extended to problem (1):

Definition 3.3

A feasible point \(x^*\) of problem (1) is referred to as basic feasible if, for every super support set \(J\in \mathcal {J}(x^*)\), letting \(y_J\in \{0,1\}^n\) such that \(y_i=0\) if \(i\in J\) and \(y_i=1\) otherwise, there exists \(L>0\) such that:

$$\begin{aligned} x^* = \Pi _{\mathcal {X}(y_J)}(x^*+d),\qquad d_i={\left\{ \begin{array}{ll} -\frac{1}{L}\nabla _if(x^*)&{} \text {if } i\in J\\ 0&{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

Note that BF stationarity requires that, for any \(y_J\) defining a super support set, \(x^*=\Pi _{\mathcal {X}(y_J)}[x^*+d]\), where \(d_J=-\frac{1}{L}\nabla _J f(x^*)\) and \(d_{{\bar{J}}}=0,\) whereas the condition in Definition 2.5 requires \(x^*=\Pi _{\mathcal {X}(y_J)}[x^*-\nabla f(x^*)]\). In fact, in the case of our problem the two conditions are equivalent, as we show below.

Lemma 3.2

Let \(y\in \mathcal {Y}\) and \(x^*\in \mathcal {X}(y)\). Then \(x^*\) satisfies

$$\begin{aligned} x^*=\Pi _{\mathcal {X}(y)}(x^*+d), \end{aligned}$$

where \(d_{I_0(y)}=-\frac{1}{L}\nabla _{I_0(y)} f(x^*)\) and \(d_{I_1(y)}=0,\) if and only if it satisfies

$$\begin{aligned} x^*=\Pi _{\mathcal {X}(y)}(x^*-\nabla f(x^*)). \end{aligned}$$

Proof

By the definition of projection, we have for all \(z\in {\mathbb {R}}^n\) that

$$\begin{aligned} \Pi _{\mathcal {X}(y)}(z)&= \mathop {\mathrm {\arg \min }}\limits _{\begin{array}{c} (x_{I_0(y)},x_{I_1(y)})\in X\\ x_{I_1(y)}=0 \end{array}}\left\| \begin{array}{c} x_{I_0(y)}-z_{I_0(y)}\\ x_{I_1(y)}-z_{I_1(y)} \end{array}\right\| ^2\\ {}&= \left[ \begin{array}{c} \mathop {\mathrm {\arg \min }}\limits \limits _{x_{I_0(y)}:(x_{I_0(y)},0)\in X}\Vert x_{I_0(y)}-z_{I_0(y)}\Vert ^2\\ 0 \end{array}\right] . \end{aligned}$$

Hence, we have

$$\begin{aligned} \Pi _{\mathcal {X}(y)}(x^*-\nabla f(x^*)) = \left[ \begin{array}{c} \mathop {\mathrm {\arg \min }}\limits \limits _{x_{I_0(y)}:(x_{I_0(y)},0)\in X}\Vert x_{I_0(y)}-(x^*_{I_0(y)}-\nabla _{I_0(y)} f(x^*))\Vert ^2\\ 0 \end{array}\right] \end{aligned}$$

and

$$\begin{aligned} \Pi _{\mathcal {X}(y)}(x^*+d) = \left[ \begin{array}{c} \mathop {\mathrm {\arg \min }}\limits \limits _{x_{I_0(y)}:(x_{I_0(y)},0)\in X}\Vert x_{I_0(y)}-(x^*_{I_0(y)}-\frac{1}{L}\nabla _{I_0(y)} f(x^*))\Vert ^2\\ 0 \end{array}\right] . \end{aligned}$$

To prove the statement, it is sufficient to show that if

$$\begin{aligned} x^*_{I_0(y)} = \mathop {\mathrm {\arg \min }}\limits \limits _{x_{I_0(y)}:(x_{I_0(y)},0)\in X}\left\| x_{I_0(y)}-(x^*_{I_0(y)}-\frac{1}{L}\nabla _{I_0(y)} f(x^*))\right\| ^2 \end{aligned}$$

for some \(L>0\), then

$$\begin{aligned} x^*_{I_0(y)} = \mathop {\mathrm {\arg \min }}\limits \limits _{x_{I_0(y)}:(x_{I_0(y)},0)\in X} \left\| x_{I_0(y)}-(x^*_{I_0(y)}-\frac{1}{L_2}\nabla _{I_0(y)} f(x^*))\right\| ^2 \end{aligned}$$

for all \(L_2>0\). Thus, let us assume by contradiction that there exists \(L_2>0\), \(L_2\ne L\), such that

$$\begin{aligned} {\hat{x}}_{I_0(y)} = \mathop {\mathrm {\arg \min }}\limits \limits _{x_{I_0(y)}:(x_{I_0(y)},0)\in X}\left\| x_{I_0(y)}-(x^*_{I_0(y)}-\frac{1}{L_2}\nabla _{I_0(y)} f(x^*))\right\| ^2, \end{aligned}$$

with \({\hat{x}}_{I_0(y)}\ne x^*_{I_0(y)}.\) By the properties of the projection operator over a convex set, we get:

$$\begin{aligned}&\left( x^*_{I_0(y)}-\left( x^*_{I_0(y)}-\frac{1}{L}\nabla _{I_0(y)} f(x^*)\right) \right) ^\top \\ {}&\quad (x_{I_0(y)}^*-x_{I_0(y)})\le 0\quad \forall \,x_{I_0(y)}:(x_{I_0(y)},0)\in X \end{aligned}$$

and

$$\begin{aligned}&\left( {\hat{x}}_{I_0(y)}-\left( x^*_{I_0(y)}-\frac{1}{L_2}\nabla _{I_0(y) f(x^*)}\right) \right) ^\top \\ {}&\quad ({\hat{x}}_{I_0(y)}-x_{I_0(y)})\le 0\quad \forall \,x_{I_0(y)}:(x_{I_0(y)},0)\in X. \end{aligned}$$

From the first of the above equations we then obtain

$$\begin{aligned} \nabla _{I_0(y)} f(x^*)^\top (x_{I_0(y)}^*-{\hat{x}}_{I_0(y)})\le 0, \end{aligned}$$

whereas from the second we can write

$$\begin{aligned} \left( {\hat{x}}_{I_0(y)}-\left( x^*_{I_0(y)}-\frac{1}{L_2}\nabla _{I_0(y) f(x^*)}\right) \right) ^\top ({\hat{x}}_{I_0(y)}-x^*_{I_0(y)})\le 0, \end{aligned}$$

and then

$$\begin{aligned} \Vert {\hat{x}}_{I_0(y)}-x^*_{I_0(y)}\Vert ^2\le \frac{1}{L_2}\nabla _{I_0(y)} f(x^*)^\top (x_{I_0(y)}^*-{\hat{x}}_{I_0(y)})\le 0, \end{aligned}$$

which is absurd. \(\square \)

We can show that, by using the discrete neighborhood mapping \(\mathcal {N}_\rho \), with a sufficiently large value of \(\rho \), the SNS procedure described in Algorithm 2 converges to basic feasible solutions.

Theorem 3.2

Let \(\{(x^k, y^k)\}\) be the sequence of iterates generated by Algorithm 2 equipped with \(\mathcal {N}_\rho \) as discrete neighborhood mapping and \(\mathcal {A}^*\) the set of the accumulation points of the sequence \(\{(x^k, y^k)\}_{K_u}\). If \(\rho \ge 2(s-\delta ^*)\), in the definition of \({\mathcal {N}}_\rho \), and \(\delta ^*=\min \{\Vert x^*\Vert _0\ |\ (x^*,y^*)\in {\mathcal {A}^*}\}\), then given a point \((x^*,y^*)\in {\mathcal {A}}^*\), \(x^*\) is basic feasible for problem (1).

Proof

Let \(J\in \mathcal {J}(x^*)\) and consider the vector \({\hat{y}}\) such that \( {\hat{y}}_j=1\; \forall j\notin J \) and zero otherwise. As \(|J|=s\), we have \(e^\top {\hat{y}}=n-s\). Moreover, \(I_1(x^*)\subseteq I_0({\hat{y}})\), thus, using Lemma 3.1, we have \((x^*,{\hat{y}}) \in \bar{ \mathcal {N}}(x^*)\subseteq \mathcal {N}_\rho (x^*, y^*)\). By taking into account Theorem 3.1, we finally get that \((x^*,y^*)\) is an \(\mathcal {N}_\rho \)-stationary point of problem (2) and that \(x^*\) is also a stationary point of

$$\begin{aligned} \min \; f(x)\quad \text {s.t. } \quad x \in \mathcal {X}({\hat{y}}), \end{aligned}$$

that is, \(x^*=\Pi _{\mathcal {X}({\hat{y}})}(x^*-\nabla f(x^*)).\) Then, by Lemma 3.2, recalling that \({\hat{y}}_i=0\) if and only if \(i\in J\), we obtain that \(x^*\) is basic feasible. \(\square \)

Remark 3.2

Due to the non-availability of the \(\delta ^*\) value, Theorem 3.2 may at a first glance appear as an ex post result. However, by taking into account that \(\delta ^*\ge 0\), we know a priori that the BF property will hold at limit points if we set \(\rho = 2s\). We shall also note that in most cases \(\delta ^*\) will be not so far from s, hence small values of \(\rho \) should typically be enough to enforce the basic feasibility of solutions.

4 Convergence Results under Constraint Qualifications

Continuing with the discussion started at the end of the previous section, we show that, under constraint qualifications and by choosing suitable neighborhoods, it is possible to state convergence results similar to those considered in important works of the related literature [14, 26]. Here, we assume that \(X = \{x\in {\mathbb {R}}^n\mid g(x)\le 0, \;h(x) = 0\}\), where \(h_i\), \(i=1,\ldots ,p\) are affine functions and \(g_i\), \(i=1,\ldots ,m\), are convex functions. First we state the following assumption which implicitly involves constraint qualifications.

Assumption 4.1

Given \({\bar{y}} \in \mathcal {Y}\) and \({\bar{x}}\in \mathcal {X}({\bar{y}})\), we have that \({\bar{x}}\) is a stationary point of problem (3) if and only if there exist multipliers \(\lambda \in {\mathbb {R}}^m\), \(\mu \in {\mathbb {R}}^p\) and \(\gamma \in {\mathbb {R}}^n\) such that

$$\begin{aligned} \begin{array}{r} \displaystyle \nabla f({\bar{x}}) + \sum _{i=1}^m \lambda _i \nabla g_i({\bar{x}}) + \sum _{i=1}^p \mu _i \nabla h_i({\bar{x}}) + \sum _{i=1}^n \gamma _i e_i = 0,\\ \lambda _i \ge 0, \ \lambda _i g_i({\bar{x}}) = 0, \ \forall i = 1, \ldots , m,\\ \gamma _i = 0, \ \forall \; i \text { such that } {\bar{y}}_i=0. \end{array} \end{aligned}$$

The above assumption states that \({{\bar{x}}}\) is a stationary point of problem (3) if and only if it is a KKT point of the following problem

$$\begin{aligned} \begin{aligned} \min _{x}\;&f(x) \\ \text {s.t. }&h_i(x) = 0, \quad \forall i=1,\ldots ,p,\\&g_i(x) \le 0, \quad \forall i=1,\ldots ,m,\\&x_i {\bar{y}}_i= 0, \quad \; \forall i=1,\ldots ,n, \\ \end{aligned} \end{aligned}$$

which can be equivalently rewritten as follows

$$\begin{aligned} \begin{aligned} \min _{x}\;&f(x) \\ \text {s.t. }&h_i(x) = 0, \quad \forall i=1,\ldots ,p,\\&g_i(x) \le 0, \quad \forall i=1,\ldots ,m,\\&x_i = 0, \qquad \; \forall i\in I_1({\bar{y}}). \end{aligned} \end{aligned}$$

Remark 4.1

As shown in Appendix A, Assumption 4.1 holds when, e.g., the functions \(g_i\) are strongly convex with constant \(\mu _i>0\), for \(i=1,\ldots ,m\), the functions \(h_j\), for \(j=1,\ldots ,p\) are affine, and some Cardinality Constraint-Constraint Qualification (CC-CQ) is satisfied. For instance, a standard CC-CQ is the Cardinality Constraint-Linear Independence Constraint Qualification (CC-LICQ), requiring the linear independence of gradients

$$\begin{aligned} \nabla g_i({\bar{x}})\qquad&\text { for all } i: g_i({\bar{x}}) = 0,\\ \nabla h_i({\bar{x}})\qquad&\text { for all } i=1,\ldots ,p,\\ e_i\qquad&\text { for all } i\in I_1({\bar{y}}). \end{aligned}$$

From Theorem 3.1 and Assumption 4.1 we get the following result.

Theorem 4.1

Let \(\{(x^k, y^k)\}\) be the sequence generated by Algorithm 2. Every accumulation point \((x^*,y^*)\) of the sequence of unsuccessful iterates \(\{(x^k, y^k)\}_{K_u}\) is such that there exist multipliers \(\lambda \in {\mathbb {R}}^m\), \(\mu \in {\mathbb {R}}^p\) and \(\gamma \in {\mathbb {R}}^n\) satisfying the following equation:

$$\begin{aligned} \begin{array}{r} \displaystyle \nabla f(x^*) + \sum _{i=1}^m \lambda _i \nabla g_i(x^*) + \sum _{i=1}^p \mu _i \nabla h_i(x^*) + \sum _{i=1}^n \gamma _i e_i = 0,\\ \lambda _i \ge 0, \ \lambda _i g_i(x^*) = 0, \ \forall i = 1, \ldots , m,\\ \gamma _i = 0, \ \forall \; i\in I_0(y^*). \end{array} \end{aligned}$$
(20)

Remark 4.2

Condition (20) is the S-stationarity concept introduced in [14]. Basically, the limit points of the sequence \(\{(x^k,y^k)\}_{K_u}\) produced by Algorithm 2 are always guaranteed to be S-stationary. This implies, by the results in [14], that \(x^*\) is also Mordukhovich-stationary for problem (1). In fact, under Assumption 4.1, it is easy to see that \(\mathcal {N}\)-stationarity is a stronger condition than M-stationarity, from points (i)-(ii) of Definition 2.4.

In order to state stronger convergence results, we can to use the discrete neighborhood mapping \(\mathcal {N}_\rho \) with a sufficiently large value of \(\rho \) in the algorithm.

Theorem 4.2

Let \(\{(x^k, y^k)\}\) be the sequence generated by Algorithm 2 equipped with the discrete neighborhood mapping \(\mathcal {N}_\rho \) and \(\mathcal {A}^\star \) the set of the accumulation points of the sequence \(\{(x^k, y^k)\}_{K_u}\) of unsuccessful iterates. If \(\rho \ge 2(s-\delta ^\star )\), in the definition of \(\mathcal {N}_\rho \), and \(\delta ^\star =\min \{\Vert x^\star \Vert _0\ |\ (x^\star ,y^\star )\in {\mathcal {A}^\star }\}\), then given a point \((x^\star ,y^\star )\in {\mathcal {A}}^\star \) and for every super support set \(J\in \mathcal {J}(x^\star )\), we have that there exist multipliers \(\lambda \in {\mathbb {R}}^m\), \(\mu \in {\mathbb {R}}^p\) and \(\gamma \in {\mathbb {R}}^n\) such that

$$\begin{aligned} \begin{array}{r} \displaystyle \nabla f(x^\star ) + \sum _{i=1}^m \lambda _i \nabla g_i(x^\star ) + \sum _{i=1}^p \mu _i \nabla h_i(x^\star ) + \sum _{i=1}^n \gamma _i e_i = 0,\\ \lambda _i \ge 0, \ \lambda _i g_i(x^\star ) = 0, \ \forall i = 1, \ldots , m,\\ \gamma _i = 0, \ \forall \; i \in J, \end{array} \end{aligned}$$
(21)

i.e., \(x^\star \) satisfies strong Lu-Zhang conditions for problem (1).

Proof

Let \(J\in \mathcal {J}(x^\star )\) and consider the vector \({{\hat{y}}}\) such that \( {{\hat{y}}}_j=1\; \forall j\notin J \) and zero otherwise. We have \(I_1(x^\star )\subseteq I_0({{\hat{y}}})\) and, as \(|J|=s\), \(e^\top {{\hat{y}}}=n-s\). Hence, \((x^\star ,{{\hat{y}}}) \in \bar{\mathcal {N}}(x^\star )\subseteq \mathcal {N}_\rho (x^\star , y^\star )\), where we used Lemma 3.1. By taking into account Theorem 3.1, we finally get that \((x^\star ,y^\star )\) is an \(\mathcal {N}_\rho \)-stationary point of problem (2) and that \(x^*\) is also a stationary point of

$$\begin{aligned} \min \; f(x) \quad \text {s.t. } \quad x \in \mathcal {X}({{\hat{y}}}). \end{aligned}$$

Then, by Assumption 4.1, recalling that \({{\hat{y}}}_i=0\) if and only if \(i\in J\), we obtain that (21) holds. \(\square \)

Remark 4.3

Condition (21) is the necessary optimality condition first defined in [26]. It is actually interesting to note that the PD algorithm proposed in the referenced work is not guaranteed to converge to a point satisfying such a condition for every super support set (this only happens when the limit point has full support). In the general case, the PD method indeed generates points satisfying (21) for at least one super support set. Our SNS algorithm would have the same exact convergence results if we used the neighborhood

$$\begin{aligned} \mathcal {N}(x^k,y^k)=\{(x,y)\mid x=x^k,\;e^{\top }y=n-s,\;y_ix_i^k=0\,\forall \,i\}. \end{aligned}$$

The above neighborhood basically checks all the super support sets at the current iterate \(x^k\), but it does not satisfy the continuity Assumption 3.3, hence failing to guarantee that condition (21) is satisfied by all super support sets at the limit point.

5 Numerical Experiments

From a computational point of view, we are particularly interested in studying two relevant aspects. Specifically, here we want to:

  • analyze the benefits and the costs of increasing the size of the neighborhood;

  • assess the performance of the proposed approach, compared to the Greedy Sparse-Simplex (GSS) method proposed in [3] and the Penalty Decomposition (PD) approach [26].

To these aims, we considered the problem of sparse logistic regression, where the objective function is continuously differentiable and convex, but the solution of the problem for a fixed support set requires the adoption of an iterative method. Note that we preferred to consider a problem without other constraints in addition to the sparsity one, in order to simplify the analysis of the behavior of the proposed algorithm.

The problem of sparse logistic regression [22] has important applications, for instance, in machine learning [2, 33]. Given a dataset having N samples \(\{z^1,\ldots ,z^N\}\), with n features and N corresponding labels \(\{t_1,\ldots , t_N\}\) belonging to \(\{-1,1\}\), the problem of sparse maximum likelihood estimation of a logistic regression model can be formulated as follows

$$\begin{aligned} \min _w\;L(w) =\sum _{i=1}^{N} \log \left( 1+\exp \left( -t_i(w^{\top }z^i)\right) \right) \quad \text { s.t. }\quad \Vert w\Vert _0\le s. \end{aligned}$$
(22)

The benchmark for this experiment is made up of problems of the form (22), obtained as described hereafter. We employed 6 binary classification datasets, listed in Table 1. All the datasets are from the UCI Machine Learning Repository [20]. For each dataset, we removed data points with missing variables; moreover, we one-hot encoded the categorical variables and standardized the other ones to zero mean and unit standard deviation. For every dataset, we chose different values of s, as specified later in this section.

Table 1 List of datasets used for experiments on sparse logistic regression
Full size table

Algorithms SNS, PD and GSS have been implemented in Python 3.7, mainly exploiting libraries numpy and scipy. The convex subproblems of both PD and GSS have been solved up to global optimality by using the L-BFGS algorithm (in the implementation from [25], provided by scipy). We also employed L-BFGS for the local optimization steps in SNS. All algorithms start from the feasible initial point \(x^0=0\in {\mathbb {R}}^n\). For the PD algorithm, we set the starting penalty parameter to 1 and its growth rate to 1.05. The algorithm stops when \(\Vert x^k-y^k\Vert <0.0001\), as suggested in [26]. AS for the GSS, we stop the algorithm as soon as \(\Vert x^{k+1}-x^k\Vert \le 0.0001\).

Concerning our proposed Algorithm 2, the parameters have been set as follows:

$$\begin{aligned} \xi = 10^{3},\qquad \theta = 0.5,\qquad \eta _0 = 10^{-5}. \end{aligned}$$

For what concerns \(\mu _0\) and \(\delta \), we actually keep the value of \(\mu \) fixed to \(10^{-6}\). We again employ the stopping criterion \(\Vert x^{k+1}-x^k\Vert \le 0.0001\).

For all the algorithms, we have also set a time limit of \(10^4\) seconds. All the experiments have been carried out on an Intel(R) Xeon E5-2430 v2 @2.50GHz CPU machine with 6 physical cores (12 threads) and 16 GB RAM.

As benchmark for our experiments, we considered 18 problems, obtained from the 6 datasets in Table 1 and setting s to 3, 5 and 8 in (22). For SNS and GSS we consider the computational time employed to find the best solution. We take into account four versions of Algorithm 2, with neighborhood radius \(\rho \in \{1,2,3,4\}\).

In Fig. 1 the performance profiles [19] w.r.t. the objective function values and the runtimes (intended as the time to find the best solution) attained by the different algorithms are shown. We do not report the runtime profile of SNS(1) since it is much faster than all the other methods and thus would dominate the plot, making it poorly informative. We can however note that unfortunately its speed is outweighed by the very poor quality of the solutions.

Fig. 1
figure 1

Performance profiles for the considered algorithms on 18 sparse logistic regression problems

Full size image

We can observe that increasing the size of the neighborhood consistently leads to higher quality solutions, even though the computational cost grows. We can see that SNS (with a sufficiently large neighborhood) has better performances than the other algorithms known from the literature; in particular, while the neighborhood radius \(\rho =1\) only allows to perform forward selection, with poor outcomes, \(\rho \ge 2\) makes swap operations possible, with a significant impact on the exploration capabilities. The GSS has worse quality performance than SNS(2), which is reasonable, since its move set is actually smaller and optimization is always carried out w.r.t. a single variable and not the entire active set. However, it also proved to be slower than the SNS, mostly because of two reasons: it always tries all feasible moves, not necessarily accepting the first one that provides an objective decrease, and it requires many more iterations to converge, since it considers one variable at a time. Finally, the PD method appears not to be competitive from both points of view: it is slow at converging to a feasible point and it has substantially no global optimization features that could guide to globally good solutions.

It is interesting to remark how considering larger neighborhoods appears to be particularly useful in problems where the sparsity constraint is less strict and thus combinatorially more challenging. As an example, we show the runtime-objective tradeoff for the breast, spam and a2a problems for \(s=3\) and \(s=8\) in Fig. 2. We can observe that for \(s=3\), SNS finds good, similar solutions for either \(\rho =2,3\) or 4, with a similar computational cost. On the other hand, as s grows to 8, using \(\rho =4\) allows to significantly improve the quality of the solution without a significant increase in terms of runtime.

Fig. 2
figure 2

Quality/cost trade-off for the algorithms on sparse logistic regression problems from datasets breast, spam and a2a

Full size image

6 Conclusions

In this paper we have analyzed sparsity-constrained optimization problems. For this class of problems, we have defined a necessary optimality condition, namely, \(\mathcal {N}\)-stationarity, exploiting the concept of discrete neighborhood associated with a well-known mixed integer equivalent reformulation, that allows to take into account potentially advantageous changes on the set of active variables.

We have afterwards proposed an algorithmic framework to tackle the family of problems under analysis. Our SNS method alternates continuous local search steps and neighborhood exploration steps; the algorithm is then proved to produce a sequence of iterates whose cluster points are \(\mathcal {N}\)-stationary. Moreover, we proved that, by suitably employing a tailored neighborhood, the limit points also satisfy other optimality conditions from the literature, based on both gradient projection and Lagrange multipliers, thus providing stronger optimality guarantees than other state-of-the-art approaches.

Finally, we studied the features and the benefits of our proposed procedure from a computational perspective. Specifically, we compared the performance of the SNS as the size of the neighborhood increases, observing that using wider neighborhoods consistently provides higher quality solutions with a reasonable increase of the computational cost, especially when the required cardinality is not that small. Moreover, when comparing SNS with the Penalty Decomposition method and the Greedy Sparse-Simplex method, we observed that our approach has higher exploration capability, thus getting a nice match between theory and practice, and it is affordable in terms of computational cost, being even faster than the other considered methods.