1 Introduction

We consider optimal piecewise linear (pwl.) interpolations of the bilinear nonconvex function \( F:\mathbb {R}^2 \rightarrow \mathbb {R}, F(x, y) = xy \) over the rectangular domain \( D = [\underline{x}, {\bar{x}}] \times [\underline{y}, {\bar{y}}] \). A pwl.interpolation \( f :D \rightarrow \mathbb {R}\) of F is uniquely defined by its underlying triangulation \( {\mathcal {T}}\mathrel {{\mathop :}{=}}\{T_1, \ldots ,T_k\} \subseteq \mathbb {R}^2 \), \( k \in \mathbb {N}\) of the domain D, where f is linear over each simplex \( T_i \). The approximation error between F and f is defined as the maximum pointwise deviation over D. For any prescribed approximation accuracy \( \varepsilon > 0 \), we are interested in triangulations that lead to pwl.interpolations with an approximation error less than \( \varepsilon \) and that are minimal with respect to the number of simplices they contain. To the best of our knowledge, finding triangulations which are optimal in this sense is still an open problem. Furthermore, there have been no attempts so far to prove approximation guarantees for existing triangulation schemes in the literature either.

Contribution. In this paper, we make several important steps toward efficient triangulation schemes for the pwl.interpolation of bilinear functions. At first, we construct triangulations that provably minimize the approximation error with up to five simplices. We show that these triangulations are in turn optimal for approximation accuracies up to over the unit box. Using these basic triangulations as building blocks, we derive an approximation algorithm for the optimal triangulation problem which we call crossing swords, based on its underlying geometric idea. We prove that this scheme can be used to create triangulations consisting of at most -times the number of simplices in an optimal triangulation. To be more precise, the crossing swords algorithm is an - approximation algorithm for all with \( i \in \mathbb {N}\). For any intermediate value, the approximation guarantee is . In this sense, the crossing swords scheme is an asymptotic -approximation algorithm for small prescribed accuracies. Furthermore, we prove that crossing swords produces optimal triangulations for all with \( i \in \mathbb {N}\) if we require each simplex to have one axis-parallel edge. We will show that crossing swords triangulations are superior to the most-widely used triangulation schemes in the literature, i.e., K1, J1 [21], longest-edge bisection [10, 14], maximum error bisection [13, 20] and red refinement [4, 8]. Although we show that longest-edge bisection is also a - approximation algorithm, it produces more simplices than crossing swords expect for certain specific values of \( \varepsilon \), where the two are equivalent. Furthermore, we introduce a generalized version of the K1-triangulation scheme and show that it is a \(\sqrt{5}\)-approximation algorithm. This also applies to the red refinement scheme. Since the approximation accuracies in crossing swords triangulations can be adjusted more finely, our scheme is by a factor of two better than previous methods in many cases. The overall dominance of the crossing swords scheme is underlined by numerical results for an indicative example.

Literature Review. Pwl.interpolations of bilinear functions are studied in the literature in various contexts. On the one hand, such approximations are important in many applications. For example, in computer visualization, nonlinear surfaces are usually represented by pwl.functions based on triangulations. This also applies to nonlinear shapes in architectural design, which in some cases can be realized in practice only via pwl.approximations, cf.[19]. On the other hand, several very efficient algorithmic frameworks for solving quadratic optimization problems rely on pwl.approximations [1, 6, 8, 13, 14]. However, finding optimal pwl.interpolations of xy over rectangular domains is still an unsolved problem. The only attempt to find provably minimal triangulations is represented by [15]. Here, the author develops a mixed-integer quadratic program which models the optimal triangulation problem. However, due to its size and inherent complexity, the presented model cannot even be solved for trivial instances by state-of-the-art solvers. Besides that, there exist several heuristic triangulation approaches in the literature. In [23], the author uses regular uniform triangulations, namely J1- and K1-triangulations, which were first presented in [21]. In [11] and [20], the authors go a step further and develop triangulations which are specifically designed for the approximation of xy over rectangular domains. In [9, 13, 14], triangulations are constructed adaptively, using red, maximum error or longest-edge refinements. For all mentioned triangulation schemes, we derive relations between the approximation accuracy and the resulting number of simplices. Most importantly, we introduce a new, more efficient triangulation scheme for which we can prove that it dominates the previously known methods.

On a more general basis, the authors of [19] are interested in optimal triangulations of xy over the whole plane \( \mathbb {R}^2 \). They show how to construct so-called optimal simplices, i.e., triangles which fulfill a prescribed approximation accuracy while maximizing their area. They prove that \( \mathbb {R}^2 \) can be tiled with optimal simplices only and thus obtain an optimal triangulation. A natural idea would be to use optimal simplices to triangulate rectangular domains as well. However, due to their geometry, it is not possible to use solely optimal simplices to triangulate rectangular regions. Instead, we will use this idea to derive a lower bound on minimal triangulations over any given compact domain. This bound is essential in proving the above-mentioned approximation guarantees for the different triangulations schemes.

Structure. Our work is structured as follows. In Sect. 2, we introduce the general notation and concepts that are used throughout the article. After that, in Sect. 3 we focus on optimal triangulations for the pwl.interpolation of xy over rectangular domains. We show that the problem can be reduced from general rectangular domains to the unit box. In Sect. 3.1, we construct optimal triangulations consisting of up to five simplices. We use them as building blocks to develop our - approximation algorithm called crossing swords in Sect. 3.2. It even yields optimal triangulations if we require that each simplex has one axis-parallel edge. In addition, we also prove approximation guarantees for a generalized version of K1-triangulations, the red refinement and the longest-edge bisection scheme. In Sect. 3.4, we prove the dominance of the crossing swords triangulation compared to the known triangulations from the literature and provide numerical results on an exemplary instance that underline the theoretical results. Finally, we conclude in Sect. 4.

2 Piecewise Linear Functions and Approximations

We start by introducing the basic concepts of triangulations and piecewise linear functions and discuss their use in approximating nonlinear functions. For the sake of simplicity, we restrict ourselves to continuous functions over polytopal domains.

A function is called piecewise linear (pwl.) if it is linear over each element of a given domain partition. To partition a domain, it is possible to use any family of polytopes. However, in practice most often triangulations are used, see, e.g., [22]. This is without loss of generality, since a pwl.function defined with respect to a partition by polytopes can always be represented by a pwl.function over a triangulation, namely by triangulating each polytope. Therefore, we define pwl.functions over triangulations. In the following, we formally introduce the relevant definitions in this context. Throughout this work, we use the notation V(P) for the vertex set and A(P) for the area of a polytope \( P \subset \mathbb {R}^d \). The following definitions are formulated in a general way for pwl.function in \(\mathbb {R}^d\). In Sect. 3, we only consider the special case \(d=2\) and therein triangulations formed by full-dimensional simplices, i.e., the special case \(d=k=2\).

Definition 1.1

A k-simplex T is the convex hull of \( k + 1 \) affinely independent points in \( \mathbb {R}^d \). We call T a full-dimensional simplex if \( k = d \) holds.

A triangulation is a partition consisting of full-dimensional simplices.

Definition 1.2

A finite set of full-dimensional simplices \( {\mathcal {T}}\mathrel {{\mathop :}{=}}\{T_1, \ldots ,T_k\} \subseteq \mathbb {R}^d \), \( k \in \mathbb {N}\), is called a triangulation of a polytope \( P \subseteq \mathbb {R}^d \) if \( P = \cup _{i = 1}^k T_i \) and the intersection \( T_i \cap T_j \) of any two simplices \( T_i, T_j \in {\mathcal {T}}\) is a proper face of \(T_i\) and \(T_j\). Further, we denote the nodes \( N({\mathcal {T}}) \) of the triangulation \( {\mathcal {T}}\) as \( N({\mathcal {T}}) \mathrel {{\mathop :}{=}}\cup _{i = 1}^k V(T_i) \).

We use the concept of triangulations to define pwl.functions.

Definition 1.3

Let \( P \subset \mathbb {R}^d \) be a polytope. A continuous function \( g:P \rightarrow \mathbb {R}\) is called piecewise linear if there exist vectors \( m_i \in \mathbb {R}^d \) and constants \( c_i \in \mathbb {R}\) for \( i = 1, \ldots , k \) and a triangulation \( {\mathcal {T}}\mathrel {{\mathop :}{=}}\{T_1, \ldots , T_k\} \), \( k \in \mathbb {N}\), of P such that

$$\begin{aligned} g (x) = m_i^\top x + c_i \quad \text {if } x \in T_i. \end{aligned}$$

Pwl.functions can be used to approximate nonlinear functions. We consider the case where the pwl.approximation coincides with the nonlinear function at the nodes of the triangulations. In this way, we can ensure continuity of the approximation if the nonlinear function is continuous.

Definition 1.4

Let \( P \subset \mathbb {R}^d \) be a polytope, and let \( {\mathcal {T}}\mathrel {{\mathop :}{=}}\{T_1, \ldots , T_k\} \), \( k \in \mathbb {N}\), be a triangulation of P. We call a pwl.function \( g:P \rightarrow \mathbb {R}\) a pwl.interpolation of a continuous function \( G:P \rightarrow \mathbb {R}\) if \( g(x) = G(x) \) holds for all \( x \in N({\mathcal {T}}) \).

Usually, the error of a pwl.approximation is measured by the maximum absolute pointwise deviation between the pwl.approximation itself and the nonlinear function to be approximated; see, e.g., [11, 13, 18, 23]. In the following, we also use this definition of the approximation error.

Definition 1.5

Consider a triangulation \( {\mathcal {T}}\) of a polytope \( P \subset \mathbb {R}^d \) and let \( g :P \rightarrow \mathbb {R}\) be a pwl.interpolation of a function \( G:P \rightarrow \mathbb {R}\) w.r.t.to \( {\mathcal {T}}\). We call

$$\begin{aligned} E_{g, G}:P \rightarrow \mathbb {R}, \quad E_{g, G}(x) \mathrel {{\mathop :}{=}}g(x) - G(x) \end{aligned}$$

the error function w.r.t.g and G and

$$\begin{aligned} \varepsilon _{g, G}(T) \mathrel {{\mathop :}{=}}\max _{x \in T} |E_{g, G}(x)| \end{aligned}$$

the approximation error on a simplex \( T \in {\mathcal {T}}\). Consequently, we define the approximation error of g (or, equivalently, of \( {\mathcal {T}}\)) w.r.t.G over the domain P as

$$\begin{aligned} \varepsilon _{g, G}({\mathcal {T}}) \mathrel {{\mathop :}{=}}\max _{T \in {\mathcal {T}}} \varepsilon _{g, G}(T). \end{aligned}$$

Given some \( \varepsilon > 0 \), we call g an \( \varepsilon \)-interpolation and \( {\mathcal {T}}\) an \( \varepsilon \)-triangulation if the approximation error is smaller than or equal to \( \varepsilon \).

Finally, we formulate the concept of optimal triangulations for pwl.interpolations of nonlinear functions; see also [15].

Definition 1.6

Let \(P \subseteq \mathbb {R}^d\) be a polytope and \(g :P \rightarrow \mathbb {R}\) a pwl.\(\varepsilon \)-interpolation of \(G :P \rightarrow \mathbb {R}\) with respect to the triangulation \({\mathcal {T}}\). We call \({\mathcal {T}}\) \(\varepsilon \)-optimal if \(|{\mathcal {T}}|\) is minimal among all \(\varepsilon \)-triangulations.

It is not obvious how to determine \(\varepsilon \)-optimal triangulations in general. We tackle this problem for bilinear functions in the following.

3 Triangulations for the Interpolation of xy Over Box Domains

In this section, we focus on finding optimal triangulations for pwl.interpolations of the bilinear function

$$\begin{aligned} F:\mathbb {R}^2 \rightarrow \mathbb {R}, F(x, y) = xy \end{aligned}$$

over the rectangular domain \( D = [\underline{x}, {\bar{x}}] \times [\underline{y}, {\bar{y}}] \), i.e., we treat the following problem:

Problem 1

Given some \(\varepsilon >0\), find an \( \varepsilon \)-optimal triangulation of D w.r.t.F.

Our main contribution will be the derivation of a novel approximation algorithm for Problem 1. We begin by stating a known result from the literature for the approximation of F over a single simplex.

Lemma 1.7

(Approximation error) [19] Given a pwl.interpolation \( f:D \rightarrow \mathbb {R}\) of F defined by a triangulation \( {\mathcal {T}}\) of D, the approximation error \( \varepsilon _{f,F}(T) \) over a simplex \( T \in {\mathcal {T}}\) is attained at the center of one of its facets. Further, if \( (x_0, y_0) \) and \( (x_1, y_1) \) are the endpoints of a facet, we have

$$\begin{aligned} \varepsilon _{f,F}(T) = \left|E_{f,F} \left( \tfrac{x_1 - x_0}{2}, \tfrac{y_1 - y_0}{2}\right) \right|= \tfrac{1}{4}|(x_1 - x_0) (y_1 - y_0)|. \end{aligned}$$
(1)

Since the error on each simplex is attained on one of its facets, we know the following for the approximation error over D.

Lemma 1.8

Let \( f:D \rightarrow \mathbb {R}\) be a pwl.interpolation of F defined by a triangulation \( {\mathcal {T}}\) of D. Then, the approximation error \( \varepsilon _{f,F}({\mathcal {T}}) \) is attained on a facet of some simplex T of \( {\mathcal {T}}\) that is not on the boundary of D.

Proof

The proof follows directly from Lemma 3.1 and the fact that all boundary facets are axis-parallel. This implies that the approximation error is zero there as either \( x_1 = x_0 \) or \( y_1 = y_0 \) holds in Eq. (1). \(\square \)

A geometric view on Lemma 3.1 is sketched in Fig. 1. Here, the maximum approximation error on the facet \(e_{v_1,v_2}\) is illustrated. The yellow rectangle is the facet enclosing axis-parallel rectangle, and the area of the red rectangle equals the maximum approximation error on \(e_{v_1,v_2}\). It is one quarter of the area of the yellow rectangle.

Fig. 1
figure 1

Geometrical visualization of the approximation error on an edge of a simplex

Full size image

We use Lemma 3.1 to show that we can reduce the triangulation problem over D to the unit box \( U \mathrel {{\mathop :}{=}}[0, 1] \times [0, 1] \) by scaling the prescribed accuracy with the area of the box. In particular, we show how to transform any \( \varepsilon \)-triangulation \( {\mathcal {T}}_U \) of U into an \( \nu \varepsilon \)-triangulation \( {\mathcal {T}}_D \) of D such that \( |{\mathcal {T}}_U| = |{\mathcal {T}}_D| \) holds, with \( \nu {:}{=}({\bar{x}} - \underline{x})({\bar{y}} - \underline{y}) \) being the area of D. The triangulation \( {\mathcal {T}}_D \) is obtained by a linear mapping of the nodes \( N({\mathcal {T}}_U) \).

Lemma 1.9

(Invariance of triangulations under scaling and shifting) Let \( f_U :U \rightarrow \mathbb {R}\) be a pwl.\( \varepsilon \)-interpolation of F defined by a triangulation \( {\mathcal {T}}_U \) of the unit box U. Further, let \( L :\mathbb {R}^2 \rightarrow \mathbb {R}^2, L(x, y) = \left( \underline{x} + x({\bar{x}} - \underline{x}), \underline{y} + y({\bar{y}} - \underline{y})\right) \). Let \( {\mathcal {T}}_D \) be the triangulation of the box D such that each simplex \( T_D \in {\mathcal {T}}_D \) corresponds to a simplex \( T_U \in {\mathcal {T}}_U \) via the mapping L on the respective vertex sets, i.e., \( V(T_D) = \{L(P) \mid P \in V(T_U)\} \). Further, let \( \nu {:}{=}({\bar{x}} - \underline{x})({\bar{y}} - \underline{y}) \) be the area of D. Then, \( {\mathcal {T}}_D \) is a \( \nu \varepsilon \)-triangulation of D and \( |{\mathcal {T}}_D| = |{\mathcal {T}}_U| \). Additionally, if \({\mathcal {T}}_U\) is an \(\varepsilon \)-optimal triangulation of U, then \({\mathcal {T}}_D\) is an \(\nu \varepsilon \)-optimal triangulation of D.

Proof

By construction, it is clear that \( |{\mathcal {T}}_D| = |{\mathcal {T}}_U| \) holds. We have to show that \( {\mathcal {T}}_D \) is a \( \nu \varepsilon \)-triangulation of D. Let \( e_D \) be a facet of an arbitrary simplex \( T_D \in {\mathcal {T}}_D \) with endpoints \( (x_0^D, y_0^D) \) and \( (x_1^D, y_1^D) \). The endpoints of \( e_D \) are nodes of \( {\mathcal {T}}_D \) and therefore the result of a linear mapping of two vertices \( (x_0^U, y_0^U) \) and \( (x_1^U, y_1^U) \) that are the endpoints of some face \( e_U \) in \( {\mathcal {T}}_U \):

$$\begin{aligned} (x_0^D, y_0^D)&= L((x_0^U, y_0^U)) = (\underline{x} + x_0^U({\bar{x}} - \underline{x}), \underline{y} + y_0^U({\bar{y}} - \underline{y})),\\ (x_1^D, y_1^D)&= L((x_1^U, y_1^U)) = (\underline{x} + x_1^U({\bar{x}} - \underline{x}), \underline{y} + y_1^U({\bar{y}} - \underline{y})). \end{aligned}$$

Further, let \( \varepsilon _e \in [0, \varepsilon ] \) be the approximation error over \( e_U \). The approximation error over \( e_D \), attained at its center \( (x^*,y^*) \), is calculated as follows:

$$\begin{aligned} E_{f_D,G}((x^*, y^*))&= \tfrac{1}{4} (x_1^D - x_0^D)(y_1^D - y_0^D)\\&= \tfrac{1}{4} (\underline{x} + x_1^U({\bar{x}} - \underline{x}) - \underline{x} - x_0^U({\bar{x}} - \underline{x}))\\&\hspace{1.5cm} (\underline{y} + y_1^U({\bar{y}} - \underline{y}) - \underline{y} - y_0^U({\bar{y}} - \underline{y}))\\&= \underbrace{\tfrac{1}{4} (x_1^U - x_0^U)(y_1^U - y_0^U)} _{\varepsilon _e} \underbrace{({\bar{x}} - \underline{x})({\bar{y}} - \underline{y})}_{\nu } = \varepsilon _e \nu . \end{aligned}$$

Thus, the approximation error on each facet of \( {\mathcal {T}}_D \) is \( \nu \) times the error on the corresponding facet in \( {\mathcal {T}}_U \). Since we assumed that \( {\mathcal {T}}_U \) is an \( \varepsilon \)-interpolation, \( \varepsilon _e \nu \le \varepsilon \nu \) holds for each facet e of \( {\mathcal {T}}_D \). This means \( {\mathcal {T}}_D \) is an \( \nu \varepsilon \)-triangulation.

Next, we prove that if \({\mathcal {T}}_U\) is \(\varepsilon \)-optimal, then \( {\mathcal {T}}_D \) is \( \nu \varepsilon \)-optimal. Assume \({\mathcal {T}}_U\) is \(\varepsilon \)-optimal and there exists a \( \nu \varepsilon \)-triangulation \({\mathcal {S}}_D\) of D such that \(|{\mathcal {S}}_D|<|{\mathcal {T}}_D|\). If we apply the inverse of L to the node set of \({\mathcal {S}}_D\), we obtain a triangulation \({\mathcal {S}}_U\) of U, i.e., for every simplex \(S_D\in {\mathcal {S}}_D\) we get a simplex \(S_U\in {\mathcal {S}}_U\) with \( V(S_U) = \{L^{-1}(P) \mid P \in V(S_D)\} \). Let \( e_U \) be a facet of an arbitrary simplex \( S_U \in {\mathcal {S}}_U \) with endpoints \( (x_0^U, y_0^U) \) and \( (x_1^U, y_1^U) \). The endpoints of \( e_U \) are nodes of \( {\mathcal {S}}_U \) and therefore the result of a linear mapping of two vertices \( (x_0^D, y_0^D) \) and \( (x_1^D, y_1^D) \) that are the endpoints of some face \( e_D \) in \( {\mathcal {S}}_D \):

$$\begin{aligned} (x_0^U, y_0^U)&= L^{-1}((x_0^D, y_0^D)) = (\tfrac{x_0^D-\underline{x}}{{\bar{x}} - \underline{x}}, \tfrac{y_0^D-\underline{y}}{{\bar{y}} - \underline{y}}),\\ (x_1^U, y_1^U)&= L^{-1}((x_1^D, y_1^D)) = (\tfrac{x_1^D-\underline{x}}{{\bar{x}} - \underline{x}}, \tfrac{y_1^D-\underline{y}}{{\bar{y}} - \underline{y}}). \end{aligned}$$

Further, let \( \nu \varepsilon _e\) with \(\varepsilon _e \in [0, \nu \varepsilon ] \) be the approximation error over \( e_D \). The approximation error over \( e_U \), attained at its center \( (x^*,y^*)\), is calculated as follows:

$$\begin{aligned} E_{f_D,G}((x^*, y^*))&= \tfrac{1}{4} (x_1^U - x_0^U)(y_1^U - y_0^U)\\&= \tfrac{1}{4} (\tfrac{x_1^D-\underline{x}}{{\bar{x}} - \underline{x}}-\tfrac{x_0^D-\underline{x}}{{\bar{x}} - \underline{x}}) (\tfrac{y_1^D-\underline{y}}{{\bar{y}} - \underline{y}}-\tfrac{y_0^D-\underline{y}}{{\bar{y}} - \underline{y}})\\&= \underbrace{\tfrac{1}{4} (x_1^U - x_0^U)(y_1^U - y_0^U)}_{\nu \varepsilon _e} \underbrace{\tfrac{1}{({\bar{x}} - \underline{x})({\bar{y}} - \underline{y})}}_{\nu ^{-1}} = \varepsilon _e. \end{aligned}$$

Thus, the approximation error on each facet of \( {\mathcal {S}}_U \) is less than or equal to \(\varepsilon \). This means that \({\mathcal {S}}_U\) is an \(\varepsilon \)-triangulation of U with \(|{\mathcal {S}}_U|<|\mathcal {{\mathcal {T}}}_U|\), which contradicts the assumption that \({\mathcal {T}}_U\) is \(\varepsilon \)-optimal. It follows that under the assumption that \({\mathcal {T}}_U\) is an \(\varepsilon \)-optimal triangulation, there is no \(\nu \varepsilon \)-triangulation of D with fewer simplices than \({\mathcal {T}}_D\), proving that \({\mathcal {T}}_D\) is \(\nu \varepsilon \)-optimal.

\(\square \)

Note that in Lemma 3.3 the bound \(\nu \varepsilon \) is tight if \(\varepsilon \) is a tight bound for the approximation over U, i.e., if the approximation error \(\varepsilon \) is attained at some point \((x,y)\in U\), then an approximation error of \(\nu \varepsilon \) is attained at \(L(x,y)\in D\). As a result of Lemma 3.3, we can consider the approximation of F over U w.l.o.g. in the following:

Problem 2

Given some \( \varepsilon > 0 \), find an \( \varepsilon \)-optimal triangulation of U w.r.t.F.

3.1 Solving the Optimal Triangulation Problem for up to Five Simplices and a General Lower Bound

In the following, we solve Problem 2 for a fixed number of simplices up to five and give a general lower bound with respect to the approximation quality \(\varepsilon >0\). Finding a general scheme that solves Problem 2 for arbitrary values of \( \varepsilon \) is an open problem. However, in [15] it is shown that Problem 2 can be formulated as a mixed-integer quadratically constrained program (MIQCP). The author takes advantage of the fact that the approximation error is attained on one of the facets of the simplices and can therefore exploit the representability of a triangulation by a fully connected planar graph. This representation allows for the modeling of Problem 2 by an MIQCP with a finite number of constraints and variables. To the best of our knowledge, this is the only work trying to determine provably \( \varepsilon \)-optimal triangulations over box domains. Unfortunately, due to the size of the resulting MIQCP, this approach is computationally intractable even for trivial instances. Nevertheless, we will later use its underlying idea of representing a triangulation as a planar graph to prove the optimality of triangulations consisting of up to five simplices.

A lower bound for \(\varepsilon \)-optimal triangulations. We begin our examination of Problem 2 in deriving a general lower bound for \( \varepsilon \)-optimal triangulations. This lower bound enables us later to determine approximation guarantees for specific triangulation schemes. The idea of the presented lower bound goes back to the work of Pottmann et al. [19], who studied optimal triangulations of the plane \( \mathbb {R}^2 \). The authors showed that an \( \varepsilon \)-optimal triangulation of \(\mathbb {R}^2\), in the sense that the individual simplices have maximal area, is obtained by using so-called \( \varepsilon \)-optimal simplices. An \( \varepsilon \)-optimal simplex satisfies a prescribed accuracy \( \varepsilon \) while maximizing its area. The area of an \( \varepsilon \)-optimal simplex is \( 2\sqrt{5}\varepsilon \). As it is possible to tile the \( \mathbb {R}^2 \) with \( \varepsilon \)-optimal simplices only, such triangulations are optimal. In Fig. 2, we illustrate two different 0.25-optimal simplices. For more information on \( \varepsilon \)-optimal simplices, we refer the reader to [19] and [2]. We use the following lemma from [5], to give a general lower bound for the triangulation of polytopal domains.

Lemma 1.10

(Lower bound) [5] Let \( P \subset \mathbb {R}^2 \) be a polytopal domain with an area of A(P) . Then, any \( \varepsilon \)- triangulation \( {\mathcal {T}}_P \) of P w.r.t.F contains at least simplices.

Fig. 2
figure 2

Optimal simplices with an approximation error of 0.25

Full size image

The proof is straightforward. If we assume that we can triangulate P solely by \(\varepsilon \)-optimal simplices, which have an area of \(2\sqrt{5}\varepsilon \), we obtain the indicated lower bound immediately. For the approximation of F over U, Lemma 3.4 thus sets the following lower bound:

Corollary 1.11

An \( \varepsilon \)-optimal triangulation \( {\mathcal {T}}\) of U w.r.t.F requires at least simplices.

However, it is unclear whether or how to use \( \varepsilon \)-optimal simplices to triangulate U. Furthermore, the lower bound from Lemma 3.4 is not always tight. In [17], the author proves that one cannot triangulate a rectangle with an odd number of simplices such that all simplices have the same area. This means for those prescribed approximation accuracies \( \varepsilon > 0 \) for which the lower bound is an odd number, we need at least one additional simplex. We now show that this lower bound can even be improved if we require that each simplex has at least one axis-parallel edge. This lemma has also been presented in the dissertation of the fourth author [15].

Lemma 1.12

Let \(\varepsilon >0\) be a prescribed approximation accuracy for the interpolation of F over a simplex T. If T has at least one axis-parallel edge, then the maximum area of T is \(4\varepsilon \).

Proof

Let T be a simplex with vertices \(v_1=(x_1,y_1)\), \(v_2=(x_2,y_2)\) and \(v_3=(x_3,y_3)\). W.l.o.g., we assume \(e_{v_1,v_2}\) is parallel to the x-axis. The area of T can then be calculated using the areas of the axis-parallel edge-enclosing rectangles of \(e_{v_1,v_3}\) and \(e_{v_2,v_3}\):

$$\begin{aligned} A(T)=\tfrac{1}{2}\left| (x_3-x_1)(y_3-y_1)\right| + \tfrac{1}{2}\left| (x_3-x_2)(y_3-y_2)\right| . \end{aligned}$$

Further, for the edges \(e_{v_1,v_3}\) and \(e_{v_2,v_3}\), the approximation error has to be less than or equal to \(\varepsilon \), i.e.,

$$\begin{aligned} \left| \tfrac{(x_3-x_1)(y_3-y_1)}{4}\right| \le \varepsilon \quad \wedge \quad \left| \tfrac{(x_3-x_2)(y_3-y_2)}{4}\right| \le \varepsilon . \end{aligned}$$

Now, obviously A(T) attains its maximum possible value of \(4\varepsilon \) if

$$\begin{aligned} (x_3-x_1)(y_3-y_1) = 4\varepsilon \quad \wedge \quad (x_3-x_2)(y_3-y_2) = -4\varepsilon \end{aligned}$$

holds. Since we assumed \(e_{v_1,v_2}\) to be parallel to the x-axis, \(y_1=y_2\) holds and we get a simplex of maximum area \(4\varepsilon \) if the vertices have the following positions:

$$\begin{aligned} v_1=(x_1,y_1),\,v_2=(x_2,y_1),\,v_3=\left( \tfrac{x_1+x_2}{2}, \tfrac{8\varepsilon }{x_2-x_1}+y_1\right) . \end{aligned}$$

\(\square \)

Corollary 1.13

An \( \varepsilon \)-optimal triangulation \( {\mathcal {T}}\) of U w.r.t.F where each simplex has at least one axis-parallel edge requires simplices.

Euler relations for triangulations. The following optimality proofs exploit the representation of a triangulation by a fully connected planar graph. In this sense, the vertices and facets of the simplices become the nodes and edges of a graph. This allows us to translate the well-known Euler relations for planar graphs to triangulations, see also [3].

Let \( {\mathcal {T}}\) be a triangulation of some polytope \( P \subset \mathbb {R}^2 \), then it holds that

$$\begin{aligned} K = 2 |N({\mathcal {T}})| - |{\mathcal {T}}| - 2 \end{aligned}$$
(2)

and

$$\begin{aligned} E = 3 |N({\mathcal {T}})| - K - 3, \end{aligned}$$
(3)

where K is the number of vertices that lie on the boundary of P and E is the number of edges of \( {\mathcal {T}}\). For K, we further know that

$$\begin{aligned} K \le |N({\mathcal {T}})|, \end{aligned}$$
(4)

which together with (2) gives

$$\begin{aligned} |N({\mathcal {T}})| \le |{\mathcal {T}}| +2. \end{aligned}$$
(5)

If P is a rectangle, then it obviously also holds that

$$\begin{aligned} K \ge 4. \end{aligned}$$
(6)

Optimal triangulations with up to five simplices. We use the Euler relations to derive optimal triangulations of U for the interpolation of F under the restriction that the number of simplices is fixed a priori. These triangulations in turn yield \( \varepsilon \)-optimal triangulations in the sense of Problem 2 for specific value ranges of \( \varepsilon \). Let \( {\mathcal {T}}_n^* \) be a triangulation with a minimal approximation error among all triangulations of U consisting of n simplices, and let \( \varepsilon _n^* \) be the corresponding minimal approximation error. This means that \( {\mathcal {T}}_n^* \) is an \( \varepsilon \)-optimal triangulation for all \( \varepsilon \in (\varepsilon _{n + 1}^*, \varepsilon _n^*] \).

Fig. 3
figure 3

Triangulations with \(|{\mathcal {T}}|\le 5\); (*) a, b, c and i are optimal triangulations with respect to the number of simplices used

Full size image

In the following, we determine optimal triangulations \({\mathcal {T}}\) of U for \(|{\mathcal {T}}|=2,3,4,5\).

We start with \( \mathbf {|{\mathcal {T}}| = 2} \): Relations (2)–(6) reduce the set of possible triangulations to those where \( |N({\mathcal {T}})| = 4 \), \( K = 4 \) and \( E = 5 \). Therefore, only two triangulations of U are possible, namely the ones using one of the diagonals to triangulate U. Either diagonal leads to an optimal triangulation as they produce the same approximation error of , attained at their center. We refer to these equivalent triangulations by \( {\mathcal {T}}_2^* \), and one example is shown in Fig. 3a.

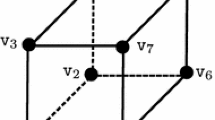
Next we consider \( \mathbf {|{\mathcal {T}}| = 3} \): Relations (2)–(6) only allow for triangulations with \( |N({\mathcal {T}})| \in \{4, 5\} \). Assuming \( |N({\mathcal {T}})| = 4 \), we obtain \( K = 3 \), which is a contradiction to Eq. (4). Assuming \( |N({\mathcal {T}})| = 5 \) instead, we obtain \( K = 5 \). The latter implies that all nodes have to be on the boundary of U. Due to symmetry, it does not matter if the additional node is on a facet which is either parallel to the x-axis or the y-axis. In both cases, the following linear program defines the optimal position of the fifth node:

$$\begin{aligned} \begin{aligned} \varepsilon _3^* \mathrel {{\mathop :}{=}}\min _x \tfrac{1}{4}\; x_1 \\ \mathrm {s.t.}\quad \quad - x_1 + x_2&\le 0\\ \,-x_1 - x_2 + 1&\le 0\\ x \in [0, 1]^2&. \end{aligned} \end{aligned}$$
(7)

In Problem 7 and the following optimization problems, we do not give specific names to variables. Instead, we use the variable notation \(x_i\) as it is conform to the standard definition of quadratic programs, which we use in Lemma 3.8. Nevertheless, in Problem 7 and in the subsequent optimization problems, \( \tfrac{1}{4}x_1 \) always models the bound on the approximation error that is minimized, see Lemma 3.1 for the calculation of the approximation error. All further variables \(x_i\) model the axis-lengths of the inner edges which can be chosen freely in the respective configuration. Each constraint models the approximation error on an inner edge of the considered triangulation. The approximation error on an outer edge is always zero. Figures 3(a)–3(i) illustrate which constraint models which edge. In Fig. 3b, we have two inner edges that both have a y-axis length of 1 and an x-axis length of \(x_2\) and \(1-x_2\), resulting in maximum approximation errors on these edges of \(\tfrac{1}{4}x_2\) and \(\tfrac{1}{4}(1-x_2)\). Since both errors must be less than or equal to the bound \(\tfrac{1}{4}x_1\), the constraints in Problem 7 are obtained after transformation:

$$\begin{aligned} \quad \tfrac{1}{4}x_2\, \le \,\tfrac{1}{4}x_1 \Rightarrow -x_1 +x_2 \le 0,\\ \,\tfrac{1}{4}(1-x_2)\, \le \,\tfrac{1}{4}x_1 \Rightarrow -x_1 - x_2 +1 \le 0. \end{aligned}$$

The optimal solution to Problem 7 is \( x^* = \left( \tfrac{1}{2}, \tfrac{1}{2}\right) \) with a corresponding approximation error of \( \varepsilon _3^* = \tfrac{1}{8} \). We refer to these equivalent triangulation by \( {\mathcal {T}}_3^* \), and an example is shown in Fig. 3b.

We continue with \( \mathbf {|{\mathcal {T}}| = 4} \): Again, from relations (2)–(6) we know that \( |N({\mathcal {T}})| \in \{4, 5, 6\} \). If \( |N({\mathcal {T}})| = 4 \), we obtain \( K = 2 \), which is a contradiction to (6). If \( |N({\mathcal {T}})| = 5 \), we obtain \( K = 4 \) and \( E = 8 \). Triangulations that fulfill this property have one inner vertex that is connected to all four corners of U. We can find the optimal position of the inner vertex by solving this quadratic program:

$$\begin{aligned} \begin{aligned} \varepsilon _4^* \mathrel {{\mathop :}{=}}\min _x \tfrac{1}{4}\; x_1\\ \mathrm {s.t.}-x_1 + x_2x_3&\le 0\\ -x_1 + x_3 - x_2x_3&\le 0\\ -x_1 -x_2 - x_3 + x_2x_3 + 1&\le 0\\ x \in [0, 1]^3. \end{aligned} \end{aligned}$$
(8)

In Fig. 3c, we have four inner edges with maximum approximation errors of \(\tfrac{1}{4}x_2x_3\), \(\tfrac{1}{4}(1-x_2)x_3\), \(\tfrac{1}{4}x_2(1-x_3)\), and \(\tfrac{1}{4}(1-x_2)(1-x_3)\). All errors have to be less than or equal to \(\tfrac{1}{4}x_1\), which after transformation leads to the constraints in Problem 8. The optimal solution to Problem 8 is \( x^* = \left( \tfrac{1}{4}, \tfrac{1}{2}, \tfrac{1}{2}\right) \), with an approximation error of \( \varepsilon _4^* = \frac{1}{16} \). We refer to the corresponding optimal triangulation by \({\mathcal {T}}_4^*\), see Fig. 3c. Finally, if \( |N({\mathcal {T}})| = 6 \), we obtain \( K = 6 \), which means that all nodes have to be on the boundary of U. Due to symmetry, the remaining two free nodes can either be positioned on adjacent, opposite or both on the same boundary facet. If both nodes are placed on the same boundary facet of U, we have a similar case to \(|{\mathcal {T}}|=3\) and the minimal possible approximation error is \(\tfrac{1}{8}\). An example of this triangulation is shown in Fig. 3d. If the two nodes are placed on adjacent boundary facets, we can minimize the approximation error by solving the following quadratic program:

$$\begin{aligned} \begin{aligned} \min _x \tfrac{1}{4}\; x_1\\ \mathrm {s.t.}-x_1 +x_2x_3&\le 0\\ -x_1 + x_3 -x_2x_3&\le 0\\ -x_1 - x_3 + 1&\le 0\\ x \in [0, 1]^3.&\end{aligned} \end{aligned}$$
(9)

In Fig. 3d, we have three inner edges with maximum approximation errors of \(\tfrac{1}{4}x_2x_3\), \(\tfrac{1}{4}(1-x_2)\), \(\tfrac{1}{4}x_2(1-x_3)\), and \(\tfrac{1}{4}(1-x_3)\). All errors have to be less than or equal to \(\tfrac{1}{4}x_1\), which after transformation leads to the constraints in Problem 9. The optimal value of Problem 9 is . Thus, this configuration can also not be optimal, see Fig. 3e, for example. If the two additional nodes are placed on opposite boundary facets, we can minimize the approximation error by solving the following linear program:

$$\begin{aligned} \begin{aligned} \min _x \tfrac{1}{4}\; x_1\\ \mathrm {s.t.}-x_1 - x_2&\le 0\\ -x_1 - x_3 +1&\le 0\\ -x_1 + x_3 - x_2&\le 0\\ x \in [0, 1]^3. \end{aligned} \end{aligned}$$
(10)

In Fig. 3e, we have three inner edges with maximum approximation errors of \(\tfrac{1}{4}x_2\), \(\tfrac{1}{4}(1-x_3)\), \(\tfrac{1}{4}(x_2-x_3)\), and \(\tfrac{1}{4}(1-x_3)\). All errors have to be less than or equal to \(\tfrac{1}{4}x_1\), which after transformation leads to the constraints in Problem 9. The optimal solution to Problem 10 is \( x = (\tfrac{1}{3}, \tfrac{1}{3}, \tfrac{2}{3}) \), with an approximation error of \( \tfrac{1}{12} \). Thus, this configuration can also not yield an optimal triangulation, see Fig. 3f for an example. Consequently, we know that holds and that \( {\mathcal {T}}_4^* \) is optimal.

Finally, we consider the case \( \mathbf {|{\mathcal {T}}| = 5} \): From relations (2)–(6), it follows that \( |N({\mathcal {T}})| \in \{6, 7\} \). If \( |N({\mathcal {T}})| = 6 \), we obtain \( K = 5 \). This means we have one free node on the boundary of U and one free inner node. In this case, there are three different ways to connect the nodes such that we have a triangulation with exactly five simplices. It is obvious that two of them are not optimal, see Fig. 3g and h. The approximation error of the third configuration is minimized by the following nonconvex quadratically constrained quadratic program (QCQP), visualized in Fig. 3i:

$$\begin{aligned} \begin{aligned} \varepsilon _5^*\mathrel {{\mathop :}{=}}\min _x \tfrac{1}{4}\; x_1\\ \mathrm {s.t.}-x_1 - x_2 + 1&\le 0\\ -x_3x_4 + x_2x_3 -x_1&\le 0\\ x_3x_4 - x_1&\le 0\\ -x_3x_4 + x_4 - x_1&\le 0\\ x_3x_4 - x_3 - x_4 - x_1 + 1&\le 0\\ x \in [0, 1]^4. \end{aligned} \end{aligned}$$
(11)

In Fig. 3i, we have five inner edges with maximum approximation errors of \(\tfrac{1}{4}(1-x_2)\), \(\tfrac{1}{4}x_3(x_2-x_4)\), \(\tfrac{1}{4}x_3x_4\), \(\tfrac{1}{4}(1-x_3)x_4\) and \(\tfrac{1}{4}(1- x_3)(1-x_4)\). All errors have to be less than or equal to \(\tfrac{1}{4}x_1\), which after transformation leads to the constraints in Problem 11. By geometric reasoning, we guess

$$\begin{aligned} x^* =\left( \sqrt{5} - 2, 3 - \sqrt{5}, \tfrac{(\sqrt{5} - 1)}{2}, \tfrac{(3 - \sqrt{5})}{2}\right) ^T \end{aligned}$$

as a candidate for an optimal solution, which entails an approximation error of \( \varepsilon _5^* = \tfrac{(\sqrt{5} - 2)}{4} \). In the following, we prove the optimality of \(x^*\). In general, we can prove that a vector is globally optimal for a nonconvex QCQP by checking two conditions which together are sufficient.

Lemma 1.14

(Global optimality in nonconvex QCQPs) [16] Consider a quadratic program of the form

$$\begin{aligned} \min x^T Q_0 x + c_0^T x\\ \mathrm {s.t.}\, x^T Q_i x +c_i^T x - b_i&\le 0 \quad \forall i = 1, \ldots , m, \end{aligned}$$

where all \( Q_i \) are \( n \times n \) real symmetric matrices and \( c_i \in \mathbb {R}^n \). A vector \( x^* \in \mathbb {R}^n \) is globally optimal for this problem if there exists a vector \( \lambda ^* \in \mathbb {R}^m \) such that

$$\begin{aligned} \begin{aligned} \left( \sum _{i = 0}^m Q_i\right) x^* + c_0 + \sum _{i = 0}^m \lambda ^*_i c_i&= 0\\ x^{*T} Q_i x^* + c_i^T x^* - b_i&\le 0&\forall i = 1, \ldots , m\\ \lambda _i^*&\ge 0&\forall i = 1, \ldots , m\\ \lambda ^*_i \left( x^{*T} Q_i x^* + c^T x^* - b_i\right)&= 0&\forall i = 1, \ldots , m&. \end{aligned} \end{aligned}$$
(12)

and

$$\begin{aligned} Q_0+\sum _{i = 1}^m \lambda _i^* Q_i \succcurlyeq 0 \end{aligned}$$
(13)

hold.

We use Lemma 3.8 to prove that \( x^* \) is optimal for Problem 11.

Proposition 1.15

The vector \( x^* = (\sqrt{5} - 2, 3 - \sqrt{5}, \tfrac{(\sqrt{5} - 1)}{2}, \tfrac{(3 - \sqrt{5})}{2})^T \) is globally optimal for the nonconvex quadratic program (11).

Proof

First, we show that \( x^* \) is a locally optimal solution, applying the KKT conditions from (12). This means we have to find a vector \( \lambda \in \mathbb {R}^5 \) that solves the following system:

$$\begin{aligned} \begin{aligned} \lambda _1 + \lambda _2 + \lambda _3 + \lambda _4 + \lambda _5&= 1\\ (\sqrt{5} - 1) - 2\lambda _1&= 0\\ -\lambda _5&= 0\\ \lambda _4 - \lambda _5&= 0\\ \lambda _4&=0\\ \lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5&\ge 0. \end{aligned} \end{aligned}$$
(14)

Note that we can neglect the dual variables for the constraints \(x \in [0, 1]^4\), since they must all be zero for \(x^*\) anyway due to \(0<x^*_i < 1\). We can easily check that \( \lambda ^* = (\tfrac{(\sqrt{5} - 1)}{2}, \tfrac{(1 + \sqrt{5})}{2}, 0, 0, 0)^T \) is feasible for (14), and therefore, \( (x^*,\lambda ^*) \) is feasible for (12). According to Lemma 3.8, \( (x^*,\lambda ^*) \) is globally optimal for Problem (11) if \( Q_0 + \sum _{i = 1}^5 {\lambda _i^*}^T Q_i \succeq 0 \) holds. As the matrix

$$\begin{aligned} Q^* \mathrel {{\mathop :}{=}}Q_0 + \sum _{i = 1}^5 {\lambda _i^*}^T Q_i = \left( \begin{matrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \lambda _2^* &{} 0\\ 0 &{} 0 &{} 0 &{} - \lambda _2^*\\ 0 &{} 0 &{} 0 &{} 0 \end{matrix}\right) \end{aligned}$$

is strictly upper triangular, its only eigenvalue is 0. It is therefore a positive semidefinite matrix, and consequently, \( x^* \) is a globally optimal solution to Problem 11. \(\square \)

As a result of Proposition 3.9, the minimal approximation error of the configuration modeled in Problem 11 is \( \varepsilon _5^* = \tfrac{\sqrt{5} - 2}{4} \). This means that the corresponding triangulation \( {\mathcal {T}}_5^* \) is optimal for the case of five simplices.

3.2 Crossing Swords: A \(\sqrt{5}/2\)-Approximation Algorithm for Optimal Triangulations

We use the optimal triangulations consisting of up to five simplices from Sect. 3.1 to derive our novel triangulation scheme crossing swords stated in Algorithm 1. The algorithm takes as input an integer N and returns a triangulation of U with N simplices that has an approximation error of less than \( \tfrac{1}{4(N - 1)} \). We will use this approximation accuracy depending on the number of simplices to prove that the crossing swords scheme is a -approximation algorithm for Problem 2.

The general idea of crossing swords triangulations is to use the optimal triangulations consisting of up to five simplices as partial triangulations to construct arbitrarily fine triangulations of U. The algorithm takes as input a number of simplices N and starts with a partition of U into n smaller rectangles, where n depends on the modulus of N by 4. The first \(n-1\) rectangles must have the same area, and they are triangulated with four simplices in fashion of \({\mathcal {T}}^*_4\). The n-th rectangle can have a different area, and its subtriangulation is either \( {\mathcal {T}}_2^* \), \( {\mathcal {T}}_3^* \), \( {\mathcal {T}}_4^* \) or \( {\mathcal {T}}_5^* \), also depending on the modulus of the input N by 4. The areas of the rectangles in Algorithm 1 are chosen such that the approximation error on all simplices is equal, which we use as a heuristic rule to minimize the (overall) approximation error. The repeated use of the \( {\mathcal {T}}_4^* \) triangulation motivates the name crossing swords.

Algorithm 1
figure a

Crossing Sword Triangulation Scheme (for the unit box U)

Full size image
Fig. 4
figure 4

Visualization of skinny vs. quadratic crossing swords triangulations with the same approximation error

Full size image

Lemma 1.16

(Crossing Sword Triangulations) Algorithm 1 is correct, i.e., for any input N it returns a triangulation of U with an approximation error according to Eq. (15).

Proof

In the following, we prove the correctness of the approximation error stated in Eq. (15) with respect to the modulus of N by 4. For the sake of simplicity, we speak of \( {\mathcal {T}}_i^*\) -triangles ( ) whenever a rectangle is triangulated in fashion of  \( {\mathcal {T}}_i^* \) with \( i \in \{2, 3, 4, 5\} \). Via the scaling formulas established in Lemma 3.3, the approximation error of these subtriangulations on arbitrary rectangles D with an area of A(D) is given as follows (cf.Fig. 3):

We now distinguish the four cases of Eq. (15), and examples of these with \(N=6,7,8,9\) are shown in Fig. 5. To this end, we check that the areas of the rectangles sum up to one and that the approximation error postulated in Eq. (15) is fulfilled by the returned triangulation \( {\mathcal {T}}_{\text {cs}}^N\) of Algorithm 1.

Case \( \mathbf {N \equiv 0 \mathop {\textbf{mod}} 4}\): Each \( U_i \) has an area of \( A(U_i) = \tfrac{4}{N} \), and therefore,

$$\begin{aligned} \sum _{i = 1}^n A(U_i) = \tfrac{N}{4} \cdot \tfrac{4}{N} = 1 \end{aligned}$$

holds. The approximation error on each \( {\mathcal {T}}_4^* \)-triangle, and thus also the one arising from \( {\mathcal {T}}_{\text {cs}}^N\), is given as

Case \( \mathbf {N \equiv 1 \mathop {\textbf{mod}} 4}\): The rectangles \( U_1, \ldots , U_{n - 1} \) have an area of

$$\begin{aligned} A(U_i) = \tfrac{4(\sqrt{5} - 2)}{(\sqrt{5} - 2)(N - 5) + 1}, \end{aligned}$$

and \( U_n \) has an area of \( A(U_n) = \tfrac{1}{(\sqrt{5} - 2)(N - 5) + 1} \). This means

$$\begin{aligned} \sum _{i = 1}^n A(U_i) = \tfrac{N - 5}{4} \cdot \tfrac{4(\sqrt{5} - 2)}{(\sqrt{5} - 2)(N - 5) + 1} + \tfrac{1}{(\sqrt{5} - 2)(N - 5) + 1} = 1. \end{aligned}$$

The corresponding approximation errors are given as

Case \( \mathbf {N \equiv 2 \mathop {\textbf{mod}} 4} \): The rectangles \( U_1, \ldots , U_{n - 1} \) have an area of \( A(U_i) = \tfrac{4}{N - 1} \), and \( U_n \) has an area of \( A(U_n) = \tfrac{1}{N - 1} \). Therefore, we have

$$\begin{aligned} \sum _{i = 1}^n A(U_i) = \tfrac{N - 2}{4} \cdot \tfrac{4}{N - 1} + \tfrac{1}{N - 1} = 1. \end{aligned}$$

The corresponding approximation errors are given as

Case \( \mathbf {N \equiv 3 \mathop {\textbf{mod}} 4} \): The rectangles \( U_1, \ldots , U_{n - 1} \) have an area of \( A(U_i) = \tfrac{4}{N - 1} \), and \( U_n \) has an area of \( A(U_n) = \tfrac{2}{N - 1} \). This leads to

$$\begin{aligned} \sum _{i = 1}^n A(U_i) = \tfrac{N - 3}{4} \cdot \tfrac{4}{N - 1} + \tfrac{2}{N - 1} = 1. \end{aligned}$$

The corresponding approximation errors are given as

\(\square \)

Fig. 5
figure 5

Congruence classes of crossing sword triangulations

Full size image

As a direct result of Lemma 3.10, for any approximation accuracy \( \varepsilon > 0 \) there exists an \( \varepsilon \)-triangulation consisting of at most simplices.

Proposition 1.17

(Upper bound on \( \varepsilon \)-optimal triangulations) For any approximation accuracy \( \varepsilon > 0 \), there exists an input to Algorithm 1 such that the returned triangulation \( {\mathcal {T}}_{cs }^{N_{\varepsilon }}\) is an \( \varepsilon \)-triangulation.

Proof

The proof results directly from calling Algorithm 1 with . \(\square \)

We use Proposition 3.11 to prove that Algorithm 1 is an approximation algorithm for Problem 2.

Theorem 1.18

Given an approximation accuracy \( \varepsilon > 0 \), calling Algorithm 1 with input is a \( (\tfrac{\sqrt{5}}{2} + 4\sqrt{5}\varepsilon ) \)- approximation algorithm for Problem 2.

Proof

From Proposition 3.11, we know that \( {\mathcal {T}}_{\text {cs}}^{N_{\varepsilon }}\) is an \( \varepsilon \)-triangulation with . Using the lower bound for the number of simplices in an \( \varepsilon \)-optimal triangulation from Proposition 3.5, we can prove the proclaimed approximation guarantee of crossing swords triangulations:

\(\square \)

This upper estimate of the approximation guarantee of crossing swords triangulations can be strengthened when only considering certain discrete values of approximation accuracies.

Theorem 1.19

Let \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{16i} \) for some \( i \in \mathbb {N}\). Then, calling Algorithm 1 with input \( N_{\varepsilon }\mathrel {{\mathop :}{=}}\tfrac{1}{4\varepsilon } \) is a \( \tfrac{\sqrt{5}}{2} \)-approximation algorithm for Problem 2.

Proof

By the choice of \( \varepsilon \), we have \( N_{\varepsilon }\in \mathbb {N}\). Further, we know from Eq. (15) that \( N_{\varepsilon }\equiv 0 \mod 4 \) holds and that Algorithm 1 called with \( N_{\varepsilon }\) returns an \( \varepsilon \)-triangulation \( {\mathcal {T}}_{\text {cs}}^{N_{\varepsilon }}\). Again, by using the lower bound from Proposition 3.5, we can prove the proclaimed approximation quality of crossing swords triangulations:

\(\square \)

Next, we show that crossing swords produces optimal triangulations for \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{16 i} \) with \( i \in \mathbb {N}\) if we additionally require that each simplex has at least one axis-parallel edge.

Theorem 1.20

Let \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{16i} \) for some \( i \in \mathbb {N}\). Then, calling Algorithm 1 with input \( N_{\varepsilon }\mathrel {{\mathop :}{=}}\tfrac{1}{4\varepsilon } \) yields an \(\varepsilon \)-optimal triangulation for Problem 2 if we require that each simplex has at least one axis-parallel edge.

Proof

In Corollary 3.7, we showed that under the condition that each simplex has an axis-parallel edge, the lower bound for the number of simplices in an \(\varepsilon \)-optimal triangulation is \(\lceil \tfrac{1}{4\varepsilon }\rceil \). Further, we know from Eq. (15) that \( N_{\varepsilon }\equiv 0 \mod 4 \) holds and that Algorithm 1 called with \( N_{\varepsilon }\) returns an \( \varepsilon \)-triangulation \( {\mathcal {T}}_{\text {cs}}^{N_{\varepsilon }}\), where \(|{\mathcal {T}}_{\text {cs}}^{N_{\varepsilon }}|= \tfrac{1}{4\varepsilon }\).

\(\square \)

Note that in Algorithm 1, we do not explicitly state how to construct the rectangular partition of the domain. In fact, a partition with given areas of the rectangles always exists as we explain now. One way to create such a partition is to line up rectangles along the x-axis that have a full height of one. In this arrangement, it is easy to choose the area of these rectangles as required based on their width, whereas it is not obvious how to do this for other arrangements. A corresponding version of Algorithm 1 is stated in the appendix as Algorithm 2. However, this arrangement inherently leads to very skinny simplices for large values of N, see Fig. 4 for an example with \(N=16\). Skinny simplices in turn can lead to numerical difficulties in evaluating the function values of the pwl.interpolation. Although irrelevant from a theoretical point of view, it would be desirable in practice to partition U into rectangles that are “as square as possible” to avoid skinny simplices. In [7], two problems are studied that address this very question of partitioning “as square as possible”. One is called PERI-SUM, which aims at minimizing the sum of all perimeters for a given set of rectangular areas. The second one is PERI-MAX, which has the goal to minimize the largest perimeter over all rectangles for a given set of rectangular areas. Both problems are NP-complete. For certain inputs, namely \( N = 4^i \) with \( i \in \mathbb {N}\), all rectangles have the same area and a partition into squares is possible. The longest-edge bisection scheme described in Sect. 3.3 yields exactly such crossing swords triangulations with square partition elements for \( N = 4^i \). For general areas as inputs to PERI-SUM, [12] gives a modeling as an MIQCP. In order to find high-quality solutions fast, the authors also present a polynomial time \( \tfrac{3}{\sqrt{2}} \)- approximation algorithm.

Finally, we make the conjecture that Algorithm 1 indeed yields optimal triangulations for a special sequence of errors converging to zero which we previously used in Theorem 3.14. The following conjecture is equivalent to Theorem 3.14 without the requirement of axis-parallel edges and yields triangulations with \(N_{\varepsilon }\equiv 0 \mod 4\) many triangles.

Conjecture 1.21

Let \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{16i} \) for some \( i \in \mathbb {N}\). Then, calling Algorithm 1 with input \( N_{\varepsilon }\mathrel {{\mathop :}{=}}\tfrac{1}{4\varepsilon } \) yields an \(\varepsilon \)-optimal triangulation for Problem 2.

Remark 3.16

According to Lemma 3.3, we can apply Algorithm 1 and the lower bound from Lemma 3.4 to general box domains \( D = [\underline{x}, {\bar{x}}] \times [\underline{y}, {\bar{y}}] \). Therefore, the approximation guarantees from Theorems 3.12 and 3.13 are also valid for arbitrary box domains.

3.3 Approximation Qualities of Widely Used Triangulation Schemes

In this section, we prove approximation guarantees for several popular triangulation schemes from the literature. For this purpose, we proceed analogously to Theorem 3.13 and consider only discrete values of approximation accuracies converging to zero.

Generalized K1-triangulations We start by analyzing the uniform triangulation schemes J1 and K1. Furthermore, we develop a generalized version of the K1, for which we prove an approximation guarantee of \( \sqrt{5} \). In Fig. 6a and b, we show a K1- and a J1-triangulation consisting of 32 simplices each. Both triangulation schemes are defined over a grid that partitions the domain into axis-parallel squares. Each square is triangulated in fashion of \( {\mathcal {T}}_2^* \). Note that J1 and K1 only differ in the orientation of the diagonals. However, the orientation of the diagonals does not matter for the resulting approximation error. Therefore, both triangulation schemes are equally efficient in terms of the number of simplices.

Proposition 1.23

For any given uniform rectangular grid, K1- and J1-triangulations have the same approximation error.

Fig. 6
figure 6

Uniform triangulations J1 and K1

Full size image

In the way, K1- and J1-triangulations have been used in the literature so far; they require the same uniform partitioning along both axes. Therefore, they offer only limited flexibility to generate good triangulations for most prescribed approximation accuracies. To add somewhat more flexibility, we generalize the K1-triangulation scheme by allowing subdivisions of different granularities for each axis—see also Fig. 6c, where we show a generalized K1-triangulation over a \( 4 \times 2 \)-grid. The approximation error of the generalized K1-triangulation scheme is uniquely determined by the underlying grid.

Proposition 1.24

Let L be a uniform grid over U with i intervals on the x-axis and j intervals on the y-axis. Further, let \({\mathcal {T}}_{\text {K}1}^{ij}\) be a generalized K1-triangulation of U with respect to L. Then,

$$\begin{aligned} |{\mathcal {T}}_{\text {K}1}^{ij}| = 2ij \end{aligned}$$

and

$$\begin{aligned} \varepsilon ({\mathcal {T}}_{\text {K}1}^{ij}) = \tfrac{1}{4ij} = \tfrac{1}{2|{\mathcal {T}}_{\text {K}1}^{ij}|} \end{aligned}$$

hold.

Proof

Each rectangle of the underlying grid has an area of \( \tfrac{1}{ij} \). From Lemma 3.3, we know that the approximation error of a \( {\mathcal {T}}_2^* \) triangulations is \( \tfrac{1}{4} \) times the area of the triangulated rectangle, which finishes the proof. \(\square \)

We can use the lower bound from Lemma 3.4 to prove an approximation guarantee for generalized K1-triangulations.

Theorem 1.25

Let \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{4ij} \) for some \( i, j \in \mathbb {N}\). Then, the generalized K1-triangulation scheme is an \(\sqrt{5}\)-approximation algorithm for Problem 2.

Proof

Let L be a uniform grid over U with i intervals in x-direction and j intervals in y-direction, and let \({\mathcal {T}}_{\text {K}1}^{ij}\) be the corresponding K1-triangulation. From Proposition 3.18, it follows that \( \varepsilon ({\mathcal {T}}_{\text {K}1}^{ij}) = \tfrac{1}{4ij} = \varepsilon \) and \( |{\mathcal {T}}_{\text {K}1}^{ij}| = 2ij \). As a result, we can prove the proclaimed approximation quality by using the lower bound from Proposition 3.5:

\(\square \)

Together with Theorem 3.13, this means that generalized K1-triangulations need twice the number of simplices than crossing swords triangulations to fulfill the same approximation accuracy. This observation is visualized in Fig. 6d, where we show how to convert a J1-triangulation with 32 simplices into a crossing swords triangulation of 16 simplices that has the same approximation accuracy by removing certain edges.

3.3.1 Approximation Quality of Iterative Refinement Schemes Starting with \({\mathcal {T}}_2^*\).

In the following, we show approximation qualities for triangulations generated by refinement schemes. A refinement scheme specifies how the simplices of a given triangulation are subdivided into smaller simplices. In the context of pwl.approximations, a refinement is performed to reduce the approximation error. In the following, we always assume that the initial triangulation of U is \( {\mathcal {T}}_2^* \). Subsequently, we perform iterative refinements on all simplices where the approximation error is greater than an a prescribed accuracy \( \varepsilon > 0 \) and repeat the refinements until we end up with an \( \varepsilon \)-triangulation.

Longest-edge bisection. The longest-edge bisection subdivides a simplex by adding a new vertex at the center of its longest edge and connects it with the opposite vertex, see Fig. 7. Algorithm 3 in the appendix gives a detailed version of this procedure. We define \( {\mathcal {T}}_{\text {L}}^{i}\) as the triangulation resulting from the i-th longest-edge refinement of \( {\mathcal {T}}_{\text {L}}^0 \mathrel {{\mathop :}{=}}{\mathcal {T}}_2^* \). This strategy also results in a \( \tfrac{\sqrt{5}}{2} \)- approximation algorithm for specific values of \( \varepsilon \).

Theorem 1.26

Let \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{2^{i + 3}} \) for some odd \( i \in \mathbb {N}\). Taking the triangulation \( {\mathcal {T}}_{\text {L}}^{i}\) resulting from the i-th refinement of \( {\mathcal {T}}_{\text {L}}^0 \) by a longest-edge bisection yields a \( \tfrac{\sqrt{5}}{2} \)-approximation algorithm for Problem 2.

Proof

The error on an edge e with endpoints \( (x_0, y_0) \) and \( (x_1, y_1) \) is always attained at its midpoint and has a value of \( \tfrac{1}{4} |(x_1 - x_0) (y_1 - y_0)| \). If e is now bisected, the approximation error on the resulting edges reduces by a factor of \( \tfrac{1}{4} \). As we start with \( {\mathcal {T}}_{\text {L}}^0 = {\mathcal {T}}_2^* \), the approximation error in both initial simplices is attained at the midpoint of the diagonal edge and is \( \tfrac{1}{4} \). The longest-edge bisection is now performed on both simplices at the midpoint of the diagonal, see Fig. 7b. The resulting four simplices each have one of the outer edges of U as their longest edge, with a constant approximation error of 0 along that edge. However, the maximum approximation error on each simplex is on one of the new diagonal edges and has a value of \( \tfrac{1}{16} \). If we now perform a longest-edge bisection again, we bisect exclusively on axis-parallel edges. This is because adding a new node on an axis-parallel edge, along which the pwl.interpolation corresponds to F anyway, leaves the pwl.interpolation unchanged. The resulting eight simplices shown in Fig. 7c therefore have the same approximation error as the four from the previous iteration. In this way, we continue the refinement and obtain an increase in the number of simplices by a factor of two in each refinement iteration, while the approximation error is reduced by a factor of \( \tfrac{1}{4} \) in the odd refinement iterations only. This leads to the fact that the triangulation \( {\mathcal {T}}_{\text {L}}^{i}\) from the i-th longest-edge refinement consists of \( 2^{i + 1} \) simplices and has an approximation error of \( \tfrac{1}{2^{i + 3}} \). Therefore, we obtain the proclaimed approximation guarantee of \( \sqrt{5}/2 \) only for the resulting triangulation after odd iterations of the longest-edge refinement strategy:

\(\square \)

Fig. 7
figure 7

Longest-edge bisection

Full size image

Red refinement The red refinement procedure subdivides a simplex into four smaller simplices by adding a new vertex at the center of each edge and new edges that connect these new vertices, see Fig. 8. Algorithm 4 in the appendix gives a detailed version of this procedure. We define \( {\mathcal {T}}_{\text {R}}^{i}\) as the triangulation resulting from the i-th red refinement of \( {\mathcal {T}}_{\text {R}}^0 \mathrel {{\mathop :}{=}}{\mathcal {T}}_2^* \). This strategy results in a \( \sqrt{5} \)-approximation algorithm for specific values of \( \varepsilon \).

Theorem 1.27

Let \( \varepsilon \mathrel {{\mathop :}{=}}\tfrac{1}{2^{2i}} \) for some \( i \in \mathbb {N}_0 \). Taking the triangulation \( {\mathcal {T}}_{\text {R}}^{i}\) resulting from the i-th red refinement of \( {\mathcal {T}}_{\text {R}}^0 \mathrel {{\mathop :}{=}}{\mathcal {T}}_2^* \) yields an \(\sqrt{5}\)-approximation algorithm for Problem 2.

Proof

According to Lemma 3.1, the error on an edge e with endpoints \( (x_0, y_0) \) and \( (x_1, y_1) \) is attained at its midpoint and has a value of \( \tfrac{1}{4}|(x_1 - x_0)(y_1 - y_0)| \). The red refinement strategy refines a simplex into four simplices by bisecting all edges of the initial simplex. Therefore, the approximation error reduces by a factor of \( \tfrac{1}{4} \). As we start with \( {\mathcal {T}}_{\text {R}}^0 = {\mathcal {T}}_2^* \), the approximation error in both initial simplices is attained at the midpoint of the diagonal edge and is \( \tfrac{1}{4} \). The red refinement is then performed on both simplices at the midpoints of the respective edges. The resulting eight simplices each have an approximation error of \( \tfrac{1}{16} \), and the triangulation can be viewed as a union of four identical \( {\mathcal {T}}_2^* \)-triangulations. In this pattern, we increase the number of simplices by a factor of four, while the approximation error is reduced by a factor of \( \tfrac{1}{4} \) in each iteration. Consequently, the triangulation \( {\mathcal {T}}_{\text {R}}^{i}\) from the i-th red refinement consists of \( 4^{i + \tfrac{1}{2}} \) simplices and has an approximation error of \( \tfrac{1}{2^{2i}} \). Therefore, we obtain the proclaimed approximation guarantee of \( \sqrt{5} \) for the red refinement scheme:

\(\square \)

Fig. 8
figure 8

Red refinement

Full size image

3.4 Comparison of the Different Triangulation Schemes

We close this section with a comparative discussion of the presented triangulation schemes and provide exemplary numerical results on the number of simplices for several indicative approximation accuracies.

The following corollaries show that for arbitrary approximation accuracies \( \varepsilon >0 \) crossing swords triangulations always use at most as many simplices as the known methods from the literature. However, in most cases, they outperform them clearly. In Fig. 9, these results are graphically represented as well. We see that crossing swords stays very close to the lower bound and due to its fine adjustability dominates the other triangulations most of the time.

Fig. 9
figure 9

Comparison of triangulation scheme in terms of the number of simplices for prescribed approximation accuracies

Full size image

Corollary 1.28

(Crossing swords dominates K1-triangulations) For any \( \varepsilon > 0 \), the crossing swords triangulation scheme produces triangulations that have at most the number of simplices than a generalized K1-triangulation. For \( \varepsilon < \tfrac{1}{4} \), the number is strictly lower.

Proof

By Proposition 3.18, the discrete approximation errors attained exactly by the generalized K1-triangulations are all \( \varepsilon _{ij} \mathrel {{\mathop :}{=}}\tfrac{1}{4ij} \) with \( i, j \in \mathbb {N}\). For these approximation errors, we know that generalized K1 is an \( \sqrt{5} \)-approximation algorithm and that crossing swords is an \( \sqrt{5}(\tfrac{1}{2} + 4\varepsilon _{ij}) \)- approximation algorithm. For \( i, j = 1 \), i.e., \( \varepsilon _{1, 1} = \tfrac{1}{4} \), both schemes produce equivalent triangulations consisting of two simplices. For \( i = 1 \) and \( j = 2 \) or \( i = 2 \) and \( j = 1 \), i.e., \( \varepsilon _{1, 2} = \varepsilon _{2, 1} = \tfrac{1}{8} \), the generalized K1-triangulation produces four simplices, while crossing swords returns only three simplices. For all other values of i and j, \( \varepsilon _{i, j} < \tfrac{1}{8} \) holds, and therefore, crossing swords has a guaranteed approximation quality of less than \( \sqrt{5} \). \(\square \)

Corollary 1.29

(Crossing swords dominates longest-edge bisection) For any \( \varepsilon > 0 \), the crossing swords triangulation scheme produces triangulations that have at most the number of simplices as a triangulation constructed by longest-edge bisection.

Proof

By Theorem 3.20, longest-edge bisection has an approximation quality of \( \tfrac{\sqrt{5}}{2} \) for all \( \varepsilon _i \mathrel {{\mathop :}{=}}\tfrac{1}{2^{i + 3}} \) with \( i \in \mathbb {N}\). These values are a subset of the approximation errors \( \varepsilon _j \mathrel {{\mathop :}{=}}\tfrac{1}{16j} \), for which the crossing swords triangulation also has an approximation quality of \( \tfrac{\sqrt{5}}{2} \). Further, for all \( \varepsilon \) with \( \tfrac{1}{16\cdot 2^i - 1}< \varepsilon < \tfrac{1}{16 \cdot 2^{i - 1}} \) and \( i \in \mathbb {N}\) crossing swords produces strictly less simplices. \(\square \)

With a similar proof as for Corollary 3.22, we also obtain that crossing swords outperforms red-refinement.

Corollary 1.30

(Crossing swords dominates red-refinement) For any \( \varepsilon > 0 \), the crossing swords triangulation scheme produces triangulations that have at most the number of simplices as a triangulation constructed by longest-edge bisection. For \( \varepsilon < \tfrac{1}{4} \), the number is strictly lower.

Table 1 Efficiencies of triangulations for \( D = [0, 6] \times [0, 2] \). (*) General pwl.approximations (not an interpolation)
Full size table
Fig. 10
figure 10

Triangulations for a prescribed accuracy of \( \varepsilon = 0.5 \)

Full size image

In addition to these theoretical proofs, we also give a numerical example that underlines the presented properties. We consider the domain \( D = [0, 2] \times [2, 6] \) and approximation accuracies of \( \{1, 0.5, 0.25, 0.1, 0.05\} \). The results are summarized in Table 1. Here, we list the prescribed approximation accuracy \(\varepsilon \), the number of simplices and the exact approximation error of the respective triangulation. The stated results underline the efficiency and adaptability of the crossing swords triangulation scheme. For the finest approximation accuracy \( \varepsilon = 0.05 \), the crossing swords scheme produces a triangulation with only 60 simplices, while the other schemes need a factor of at least 1.5 times more simplices. The next best triangulation scheme is that by [20], which is based on a maximum error bisection refinement strategy. However, they consider general pwl.approximations instead of interpolations. Thus, since they solve a generalization of Problem 2, the results are not directly comparable. Nevertheless, the crossing swords scheme seems to provide more efficient triangulations even for this generalized problem. Crossing swords as well as generalized K1 is the only schemes which are able to fulfill the given accuracies exactly. However, the number of simplices in generalized K1-triangulations growths much faster than in crossing swords triangulations with increasing accuracy. For \( \varepsilon = 0.05 \), K1 requires even factor twice as many simplices as crossing swords. The poor adaptability to the prescribed approximation error exhibited by the refinement methods, i.e., red-refinement, longest-edge bisection and max-error refinement, can be seen from the fact that in order to satisfy an accuracy of \( \varepsilon = 0.5 \), they produce triangulations that have actual approximation errors of 0.1875 and 0.2344, respectively. To visualize the observed results, the triangulations of the considered triangulation schemes for an accuracy of \( \varepsilon = 0.5 \) are shown in Fig. 10a. Besides the mere number of simplices, it is especially noticeable that the maximum error scheme produces relatively skinny simplices, which can lead to numerical problems in the evaluation of the approximation for small errors.

4 Conclusion

In this work, we have introduced a novel triangulation scheme called crossing swords to interpolate bivariate products xy over rectangular domains. We showed that a crossing swords triangulation requires at most \( \sqrt{5} / 2 \) times as many simplices as an \( \varepsilon \)-optimal triangulation for any approximation accuracy \( \varepsilon > 0 \). Crossing swords thus outperforms all previously known triangulation schemes in the literature, which we have proved theoretically and also underlined by exemplary numerical results. We have also proved that crossing swords triangulations are \(\varepsilon _i\)-optimal under the condition that each simplex has one axis-parallel edge and with \(i\in \mathbb {N}\) holds. Supported by computational tests, we conjecture that this also holds if the simplices are not required to be axis-parallel. Future research could address the extension of interpolations to general approximations. In [2], it was shown that optimal triangulations of \(\mathbb {R}^2\) consist of slightly fewer triangles if, instead of interpolations, approximations with a deviation by a constant factor are considered. A similar result is presumably achievable for box domains. In addition, triangulations for polytopes other than the rectangular box domains are canonical candidates for further investigations.