Continuous-Time Markowitz’s Mean-Variance Model Under Different Borrowing and Saving Rates

Abstract

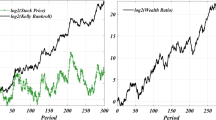
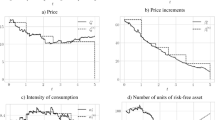
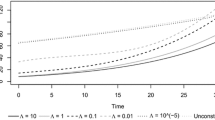
We study Markowitz’s mean-variance portfolio selection problem in a continuous-time Black–Scholes market with different borrowing and saving rates. The associated Hamilton–Jacobi–Bellman equation is fully nonlinear. Using a delicate partial differential equation and verification argument, the value function is proven to be $C^{3,2}$ smooth. It is also shown that there are a borrowing boundary and a saving boundary which divide the entire trading area into a borrowing-money region, an all-in-stock region, and a saving-money region in ascending order. The optimal trading strategy turns out to be a mixture of continuous-time strategy (as suggested by most continuous-time models) and discontinuous-time strategy (as suggested by models with transaction costs): one should put all the wealth in the stock in the middle all-in-stock region and continuously trade it in the other two regions in a feedback form of wealth and time. It is never optimal to short sale the stock. Numerical examples are also presented to verify the theoretical results and to give more financial insights beyond them.

Appendix: Proof of Theorem 5.1

In this section, we prove Theorem 5.1 by approximation method.

Firstly, for each fixed $0<\varepsilon <1$, define a continuous function

$$\begin{aligned} \Gamma _\varepsilon (\xi ,\eta ):=A\Big (\frac{\xi }{\eta +\varepsilon }\Big ),\quad (\xi ,\eta )\in (-\infty ,+\infty )\times [0,+\infty ). \end{aligned}$$

Note that

$$\begin{aligned} {\partial }_\xi \Gamma _\varepsilon (\xi ,\eta )=A^{\prime }\Big (\frac{\xi }{\eta +\varepsilon }\Big ) \frac{1}{\eta +\varepsilon }= \left\{ \begin{array}{ll} -\frac{1}{\eta +\varepsilon }\in [-\frac{1}{\varepsilon },0),&{}\quad \text{ if }\;a_2<-\frac{\xi }{\eta +\varepsilon }<a_1,\\ 0,&{}\quad \text{ if }\;-\frac{\xi }{\eta +\varepsilon }>a_1 \;\hbox {or}\; -\frac{\xi }{\eta +\varepsilon }<a_2, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} {\partial }_\eta \Gamma _\varepsilon (\xi ,\eta )= & {} A^{\prime }\Big (\frac{\xi }{\eta +\varepsilon }\Big ) \frac{-\xi }{(\eta +\varepsilon )^2}\\ {}= & {} \left\{ \begin{array}{ll} \frac{\xi }{\eta +\varepsilon }\frac{1}{\eta +\varepsilon }\in [-\frac{a_1}{\varepsilon },0),&{}\quad \text{ if }\; a_2<-\frac{\xi }{\eta +\varepsilon }<a_1,\\ 0,&{}\quad \text{ if }\; -\frac{\xi }{\eta +\varepsilon }>a_1\;\hbox {or}\;-\frac{\xi }{\eta +\varepsilon }<a_2, \end{array} \right. \end{aligned}$$

so the function $\Gamma _\varepsilon (\cdot ,\cdot )$ is Lipschitz continuous in $(-\infty ,+\infty )\times [0,+\infty )$. Moreover, for each fixed $c>0$, ${\partial }_\xi \Gamma _\varepsilon (\xi ,\eta )$ and ${\partial }_\eta \Gamma _\varepsilon (\xi ,\eta )$ are uniformly bounded for all $(\xi ,\eta , \varepsilon )\in (-\infty ,+\infty )\times [c,+\infty )\times [0,1]$.

Now, consider an approximation equation in a bounded domain $Q_T^N:=(-N,N)\times [0,T]$,

$$\begin{aligned} \begin{array}{ll} &{}w^{\varepsilon ,N}_s-\frac{1}{2}\sigma ^2A^2\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )w^{\varepsilon ,N}_{zz} +\Big (\mu -\frac{1}{2}\sigma ^2A^2\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) -\sigma ^2A\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )\Big )w^{\varepsilon ,N}_z\\ &{}+\Big (\mu -\sigma ^2A\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )\Big )w^{\varepsilon ,N}=0 \quad \hbox {in} \quad Q_T^N,\\ &{}(w^{\varepsilon ,N}-w^{\varepsilon ,N}_z)(-N,s)=-e^{-r_2 s }d,\quad w^{\varepsilon ,N}_z(N,s)=\frac{1}{2} e^{\theta _1 s } e^N,\quad s\in [0,T],\\ &{}w^{\varepsilon ,N}(z,0)=\frac{1}{2}e^z-d,\quad -N<z<N, \end{array} \end{aligned}$$

(54)

The Leray-Schauder fixed point theorem (see [14] Theorem 4, p.541) and embedding theorem (see [29] Theorem 6.8) imply the existence of $C^{1+\alpha ,\frac{1+\alpha }{2}}\big (\overline{Q_T^N}\big )$ (for some $\alpha \in (0,1)$) solution to the problem (54). Moreover, the Schauder estimation (see [29] Theorem 4.23) implies

$$\begin{aligned} w^{\varepsilon ,N}\in C^{2+\alpha ,1+\frac{\alpha }{2}}\big (\overline{Q_T^N}\big ). \end{aligned}$$

In the proceeding proof, we will frequently use the following fact without claim:

$$\begin{aligned} 0<a_2\le A(\xi )\le a_1,\quad |A'(\xi )| \le 1,\quad a_2\le |A'(\xi )\xi | \le a_1,\quad a_2^2\le |A'(\xi )\xi ^2| \le a_1^2. \end{aligned}$$

We first establish the estimates

$$\begin{aligned} \frac{1}{2} e^{\theta _2 s } e^z-e^{-r_1 s } d\le w^{\varepsilon ,N} \le \frac{1}{2} e^{\theta _1 s } e^z-e^{-r_2 s }d. \end{aligned}$$

(55)

Denote

$$\begin{aligned} \psi (z,s)=\frac{1}{2} e^{\theta _2 s } e^z-e^{-r_1 s } d,\quad A(\cdot \cdot )=A\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ). \end{aligned}$$

Using the definitions of $\theta _2$, $a_1$ and $a_2$ as well as the bounds on A and $A'$, we get

$$\begin{aligned}{} & {} \!\!\!\psi _s-\frac{1}{2}\sigma ^2A^2(\cdot \cdot )\psi _{zz}+\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot ) -\sigma ^2A(\cdot \cdot )\Big )\psi _z+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )\psi \\= & {} \frac{1}{2}e^{\theta _2 s } e^z\Big (\theta _2-\frac{1}{2}\sigma ^2A^2(\cdot \cdot ) +\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )\Big )+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )\Big )\\{} & {} +e^{-r_1 s } d\Big (r_1-(\mu -\sigma ^2A(\cdot \cdot ))\Big )\\\le & {} \frac{1}{2}e^{\theta _2 s } e^z\Big (\theta _2-\sigma ^2a_2^2-2\sigma ^2a_2+2\mu \Big ) +e^{-r_1 s } d\Big (r_1-(\mu -\sigma ^2a_1)\Big )\\= & {} 0. \end{aligned}$$

Notice $\theta _1>\theta _2$, so

$$\begin{aligned}&\psi (z,0)=\frac{1}{2}e^z-d=w^{\varepsilon ,N}(z,0), -N<z<N, \nonumber \\&(\psi -\psi _z)(-N,s)=-e^{-r_1 s } d\le -e^{-r_2 s }d=(w^{\varepsilon ,N}-w^{\varepsilon ,N}_z)(-N,s), s\in [0,T], \nonumber \\&\psi _z(N,s)=\frac{1}{2} e^{\theta _2 s } e^N\le \frac{1}{2} e^{\theta _1 s } e^N=w^{\varepsilon ,N}_z(N,s), s\in [0,T]. \end{aligned}$$

Applying the comparison principle for linear equations, the first inequality in (55) is established.

Similarly, let

$$\begin{aligned} \Psi (z,s)=\frac{1}{2}e^{\theta _1 s }e^{z}-e^{-r_2 s }d. \end{aligned}$$

Then by the definitions of $\theta _1$, $a_1$ and $a_2$,

$$\begin{aligned}{} & {} \Psi _s-\frac{1}{2}\sigma ^2A^2(\cdot \cdot )\Psi _{zz}+\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot ) -\sigma ^2A(\cdot \cdot )\Big )\Psi _z+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )\Psi \\= & {} \frac{1}{2}e^{\theta _1 s }e^{z}\Big (\theta _1-\frac{1}{2}\sigma ^2A^2(\cdot \cdot ) +\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )\Big )+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )\Big )\\{} & {} +e^{-r_2 s }d\Big (r_2-(\mu -\sigma ^2A(\cdot \cdot ))\Big )\\\ge & {} \frac{1}{2}e^{\theta _1 s }e^{z}\Big (\theta _1-\sigma ^2a_1^2-2\sigma ^2a_1+2\mu \Big ) +e^{-r_2 s }d\Big (r_2-(\mu -\sigma ^2a_2)\Big )\\= & {} 0. \end{aligned}$$

Moreover,

$$\begin{aligned}&\Psi (z,0)=\frac{1}{2}e^{z}-d=w^{\varepsilon ,N}(z,0), -N<z<N, \nonumber \\&(\Psi -\Psi _z)(-N,s)=-e^{-r_2 s }d=(w^{\varepsilon ,N}-w^{\varepsilon ,N}_z)(-N,s), s\in [0,T], \nonumber \\&\Psi _z(N,s)=\frac{1}{2} e^{\theta _1 s } e^N=w^{\varepsilon ,N}_z(N,s), s\in [0,T], \end{aligned}$$

by the comparison principle, the second inequality in (55) is established.

Due to the setting of boundary conditions, we cannot establish $w^{\varepsilon ,N}_z\ge \frac{1}{2}e^{-\kappa s} e^z$. Instead, we first prove

$$\begin{aligned} w^{\varepsilon ,N}_z\ge -e^{-\theta _3 s} d, \end{aligned}$$

(56)

where

$$\begin{aligned} \theta _3=\min \{\mu -\sigma ^2 a_1(a_1+3),r_1\}. \end{aligned}$$

Differentiating the equation in (54) w.r.t. z we have

$$\begin{aligned}&{\partial }_s w^{\varepsilon ,N}_z-\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdot \cdot ){\partial }_zw^{\varepsilon ,N}_z\Big ) +\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )\Big ){\partial }_zw^{\varepsilon ,N}_z\\&\quad +\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )w^{\varepsilon ,N}_z\\&\quad -\sigma ^2A'(\cdot \cdot )\Big (\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon } -\frac{w^{\varepsilon ,N}}{(|w^{\varepsilon ,N}_z|+\varepsilon )^2}\textrm{sgn}(w^{\varepsilon ,N}_z)w^{\varepsilon ,N}_{zz}\Big ) \Big (A(\cdot \cdot )+1\Big )w^{\varepsilon ,N}_z\\&\quad -\sigma ^2A'(\cdot \cdot )\Big (\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon } -\frac{w^{\varepsilon ,N}}{(|w^{\varepsilon ,N}_z|+\varepsilon )^2}\textrm{sgn}(w^{\varepsilon ,N}_z)w^{\varepsilon ,N}_{zz}\Big ) w^{\varepsilon ,N}=0. \end{aligned}$$

After reorganizing, we get an equation for $w^{\varepsilon ,N}_z$ in the divergence form:

$$\begin{aligned}&{\partial }_s w^{\varepsilon ,N}_z-\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdot \cdot ){\partial }_zw^{\varepsilon ,N}_z\Big ) +\Big (-\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )+\mu \Big ){\partial }_zw^{\varepsilon ,N}_z \nonumber \\&+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )w^{\varepsilon ,N}_z-\sigma ^2A'(\cdot \cdot )\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon } \Big (A(\cdot \cdot )+1\Big )w^{\varepsilon ,N}_z \nonumber \\&+\sigma ^2A'(\cdot \cdot )\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) \Big (\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) \Big (A(\cdot \cdot )+1\Big )\textrm{sgn}(w^{\varepsilon ,N}_z){\partial }_zw^{\varepsilon ,N}_z \nonumber \\&+\sigma ^2A'(\cdot \cdot ) \Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )^2 \textrm{sgn}(w^{\varepsilon ,N}_z){\partial }_zw^{\varepsilon ,N}_z-\sigma ^2A'(\cdot \cdot ) \frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } w^{\varepsilon ,N}_z =0. \end{aligned}$$

(57)

It is not hard to check that all the coefficients in (57) are bounded. Denote $\psi (z,s)=-e^{-\theta _3 s} d$, then

$$\begin{aligned}&{\partial }_s \psi -\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdot \cdot ){\partial }_z \psi \Big ) +\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )\Big ){\partial }_z \psi \\&+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )\psi -\sigma ^2A'(\cdot \cdot )\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon } \Big (A(\cdot \cdot )+1\Big )\psi \\&+\sigma ^2A'(\cdot \cdot )\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) \Big (\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) \Big (A(\cdot \cdot )+1\Big )\textrm{sgn}(w^{\varepsilon ,N}_z){\partial }_z \psi \\&+\sigma ^2A'(\cdot \cdot ) \Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )^2 \textrm{sgn}(w^{\varepsilon ,N}_z){\partial }_z \psi -\sigma ^2A'(\cdot \cdot ) \frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } \psi \\&=e^{-\theta _3 s}d\Big (\theta _3-\mu +\sigma ^2A(\cdot \cdot ) +\sigma ^2A'(\cdot \cdot )\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon } \Big (A(\cdot \cdot )+1\Big )\\ {}&\quad +\sigma ^2A'(\cdot \cdot ) \frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } \Big )\\&\le e^{-\theta _3 s}d (\theta _3-\mu +\sigma ^2 a_1+\sigma ^2 a_1(a_1+1)+\sigma ^2 a_1 )\le 0, \end{aligned}$$

thanks to the definition of $\theta _3$. Moreover,

$$\begin{aligned}&w^{\varepsilon ,N}_z(z,0)=\frac{1}{2}e^{z}\ge 0\ge \psi (z,0), \nonumber \\&w^{\varepsilon ,N}_z(-N,s)=w^{\varepsilon ,N}(-N,s)+e^{-r_2 s }d>-e^{-r_1 s} d\ge \psi (-N,s), \quad {(\mathrm by \;(55))}\nonumber \\&w^{\varepsilon ,N}_z(N,s)=\frac{1}{2} e^{\theta _1 s } e^N\ge 0\ge \psi (N,s). \end{aligned}$$

Using the comparison principle for divergence forms (see [29] Corollary 6.16), we obtain $w^{\varepsilon ,N}_z\ge \psi$, giving (56).

We next to prove

$$\begin{aligned} w^{\varepsilon ,N}_z\le \frac{1}{2}e^{k s}e^z. \end{aligned}$$

(58)

Denote $g^{\varepsilon ,N}(z,s)=e^{-z}w^{\varepsilon ,N}_z(z,s)$. According to (57), we have

$$\begin{aligned}&{\partial }_s g^{\varepsilon ,N}-\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdot \cdot )g^{\varepsilon ,N}_z\Big ) -\sigma ^2A^2(\cdot \cdot )g^{\varepsilon ,N}_z -\frac{\sigma ^2}{2}A^2(\cdot \cdot )g^{\varepsilon ,N} \nonumber \\&-\sigma ^2A(\cdot \cdot )A'(\cdot \cdot ) \Big (\frac{w^{\varepsilon ,N}_z}{w^{\varepsilon ,N}_z+\varepsilon }g-\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) {\Big (\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )\textrm{sgn}(w^{\varepsilon ,N}_z)}\big (g^{\varepsilon ,N}_z+g^{\varepsilon ,N} \big )\Big ) \nonumber \\&+\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )\Big )\big (g^{\varepsilon ,N}_z+g^{\varepsilon ,N} \big ) \nonumber \\&+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )g^{\varepsilon ,N} -\sigma ^2A'(\cdot \cdot ) \Big (A(\cdot \cdot )+1\Big )g^{\varepsilon ,N} \nonumber \\&+\sigma ^2A'(\cdot \cdot )\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } \Big (A(\cdot \cdot )+1\Big )\textrm{sgn}(w^{\varepsilon ,N}_z)\big (g^{\varepsilon ,N}_z+g^{\varepsilon ,N} \big ) \nonumber \\&+\sigma ^2A'(\cdot \cdot ) \Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )^2\textrm{sgn}(w^{\varepsilon ,N}_z)\big (g^{\varepsilon ,N}_z+g^{\varepsilon ,N} \big )-\sigma ^2A'(\cdot \cdot ) \frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } g^{\varepsilon ,N} =0. \end{aligned}$$

(59)

On the other hand, denote $\Psi (z,s)=\frac{1}{2}e^{k s}$, then

$$\begin{aligned}&{\partial }_s \Psi -\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdot \cdot )\Psi _z\Big ) -\sigma ^2A^2(\cdot \cdot )\Psi _z-\frac{\sigma ^2}{2}A^2(\cdot \cdot )\Psi \\&-\sigma ^2A(\cdot \cdot )A'(\cdot \cdot ) \Big (\frac{w^{\varepsilon ,N}_z}{w^{\varepsilon ,N}_z+\varepsilon }\Psi -\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big ) {\Big (\frac{w^{\varepsilon ,N}_z}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )\textrm{sgn}(w^{\varepsilon ,N}_z)}\big (\Psi _z+\Psi \big )\Big )\\&+\Big (-\frac{1}{2}\sigma ^2A^2(\cdot \cdot )-\sigma ^2A(\cdot \cdot )+\mu \Big )\big (\Psi _z+\Psi \big )\\&+\Big (\mu -\sigma ^2A(\cdot \cdot )\Big )\Psi -\sigma ^2A'(\cdot \cdot ) \Big (A(\cdot \cdot )+1\Big )\Psi \\&+\sigma ^2A'(\cdot \cdot )\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } \Big (A(\cdot \cdot )+1\Big )\textrm{sgn}(w^{\varepsilon ,N}_z)\big (\Psi _z+\Psi \big )\\&+\sigma ^2A'(\cdot \cdot ) \Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )^2\textrm{sgn}(w^{\varepsilon ,N}_z) \big (\Psi _z+\Psi \big )-\sigma ^2A'(\cdot \cdot ) \frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon } \Psi \\&\ge \frac{1}{2}e^{ks}{\Big (k-\frac{1}{2}\sigma ^2 a_1^2-\sigma ^2 a_1^2-\frac{1}{2}\sigma ^2 a_1^2-\sigma ^2 a_1(a_1+1)-\sigma ^2 a_1^2-\sigma ^2 a_1\Big )} \ge 0, \end{aligned}$$

thanks to the definition of k. Notice $k\ge \theta _1$, so

$$\begin{aligned}&g^{\varepsilon ,N} (z,0)=\frac{1}{2}=\Psi (z,0),\nonumber \\&g^{\varepsilon ,N} (-N,s)=e^{N}(w^{\varepsilon ,N}+e^{-r_2 s}d)(-N,s)\le \frac{1}{2} e^{\theta _1 s} \le \frac{1}{2} e^{k s}=\Psi (-N,s),\quad {(\mathrm by \;(55))}\nonumber \\&g^{\varepsilon ,N} (N,s)=\frac{1}{2} e^{\theta _1 s } \le \frac{1}{2} e^{k s}=\Psi (N,s). \end{aligned}$$

Using the comparison principle for divergence forms, we obtain $g^{\varepsilon ,N}\le \Psi$, proving (58).

Thanks to (55), (56) and (58), for each $a<b$, when $N>\max \{|a|,|b|\}$, taking the $C^{\alpha ,\frac{\alpha }{2}}$ interior estimate (see [29] Theorem 6.33) to the equations in (54) and (57) respectively, we obtain

$$\begin{aligned} \Big |w^{\varepsilon ,N}\Big |_{C^{\alpha ,\frac{\alpha }{2}}([a,b]\times [0,T])}, \quad \Big |w^{\varepsilon ,N}_z\Big |_{C^{\alpha ,\frac{\alpha }{2}}([a,b]\times [0,T])}\;\le C.\end{aligned}$$

where C is independent of $\varepsilon$ and N. Since $\Gamma _\varepsilon (\cdot ,\cdot )$ is Lipschitz continuous in $(-\infty ,+\infty )\times [0,+\infty )$, we have

$$\begin{aligned} \;\bigg |\;A\Big (\frac{w^{\varepsilon ,N}}{|w^{\varepsilon ,N}_z|+\varepsilon }\Big )\; \bigg |\;_{C^{\alpha ,\frac{\alpha }{2}}([a,b]\times [0,T])}\le C_\varepsilon \end{aligned}$$

(60)

i.e. the coefficients in the equation of (54) belong to $C^{\alpha ,\frac{\alpha }{2}}([a,b]\times [0,T])$, so we can take the Schauder interior estimate to the equation in (54) to get

$$\begin{aligned} \Big |w^{\varepsilon ,N}\Big |_{C^{2+\alpha ,1+\frac{\alpha }{2}}([a,b]\times [0,T])}\;\le C_\varepsilon . \end{aligned}$$

(61)

where the above two $C_\varepsilon$s are independent of N. Therefore, there exists $w^\varepsilon \in C^{2+\alpha ,1+\frac{\alpha }{2}}\big (\overline{Q_T}\big )$ such that, for any region $Q=(a,b)\times (0,T]\subset Q_T$, there exists a subsequence of $w^{\varepsilon ,N}$, which we still denote by $w^{\varepsilon ,N}$, such that $w^{\varepsilon ,N}\rightarrow w^\varepsilon$ in $C^{2,1}(\overline{Q})$ when $N\rightarrow \infty$. So $w^\varepsilon$ satisfies the initial problem

$$\begin{aligned} \begin{array}{ll} &{}w^\varepsilon _s-\frac{1}{2}\sigma ^2A^2\big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\big )w^\varepsilon _{zz} +\Big (\mu -\frac{1}{2}\sigma ^2A^2\big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\big )-\sigma ^2A\big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\big )\Big )w^\varepsilon _z\\ &{}+\Big (\mu -\sigma ^2A\big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\big )\Big )w^\varepsilon =0 \quad \hbox {in} \quad Q_T,\\ &{}w^\varepsilon (z,0)=\frac{1}{2}e^z-d. \end{array} \end{aligned}$$

(62)

The exponential growth conditions on $w^\varepsilon$ and $w^\varepsilon _z$ come from the estimates (55), (56) and (58).

We now prove

$$\begin{aligned} w^\varepsilon _z\ge \frac{1}{2}e^{-\kappa s}e^{z}. \end{aligned}$$

(63)

Denote

$$\begin{aligned} g^\varepsilon (z,s)=e^{-z}w^\varepsilon _z(z,s),\quad A(\cdots )=A\big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\big ). \end{aligned}$$

Letting $N\rightarrow \infty$ in (59), we obtain

$$\begin{aligned}&{\partial }_s g^\varepsilon -\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdots ) g^\varepsilon _z\Big ) -\sigma ^2A^2(\cdots ) g^\varepsilon _z -\frac{\sigma ^2}{2}A^2(\cdots ) g^\varepsilon \\&-\sigma ^2A(\cdots )A'(\cdots ) \Big ({\frac{w^\varepsilon _z}{|w^\varepsilon _z|+\varepsilon } g^\varepsilon -\Big (\frac{w^{\varepsilon }}{|w^{\varepsilon }_z|+\varepsilon }\Big )\Big (\frac{w^\varepsilon _z}{|w^\varepsilon _z|+\varepsilon }\Big )\textrm{sgn}(w^\varepsilon _z)}\big ( g^\varepsilon _z+g^\varepsilon \big )\Big )\\&+\Big (\mu -\frac{1}{2}\sigma ^2A^2(\cdots )-\sigma ^2A(\cdots )\Big )\big ( g^\varepsilon _z+g^\varepsilon \big )\\&+\Big (\mu -\sigma ^2A(\cdots )\Big ) g^\varepsilon -\sigma ^2A'(\cdots ) \Big (A(\cdots )+1\Big ) g^\varepsilon \\&+\sigma ^2A'(\cdots )\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon } \Big (A(\cdots )+1\Big )\textrm{sgn}(w^\varepsilon _z)\big ( g^\varepsilon _z+g^\varepsilon \big )\\&+\sigma ^2A'(\cdots ) \Big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\Big )^2\textrm{sgn}(w^\varepsilon _z)\big ( g^\varepsilon _z+g^\varepsilon \big )-\sigma ^2A'(\cdots ) \frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon } g^\varepsilon =0. \end{aligned}$$

On the other hand, denote $\Psi (z,s)=\frac{1}{2}e^{-\kappa s}$, we have

$$\begin{aligned}&{\partial }_s \Psi -\frac{\sigma ^2}{2}{\partial }_z\Big (A^2(\cdots )\Psi _z\Big ) -\sigma ^2A^2(\cdots )\Psi _z -\frac{\sigma ^2}{2}A^2(\cdots )\Psi \\&-\sigma ^2A(\cdots )A'(\cdots ) \Big ({\frac{w^\varepsilon _z}{|w^\varepsilon _z|+\varepsilon } \Psi -\Big (\frac{w^{\varepsilon }}{|w^{\varepsilon }_z|+\varepsilon }\Big )\Big (\frac{w^\varepsilon _z}{|w^\varepsilon _z|+\varepsilon }\Big )\textrm{sgn}(w^\varepsilon _z)}\big (\Psi _z+\Psi \big )\Big )\\&+\Big (-\frac{1}{2}\sigma ^2A^2(\cdots )-\sigma ^2A(\cdots )+\mu \Big )\big (\Psi _z+\Psi \big )\\&+\Big (\mu -\sigma ^2A(\cdots )\Big )\Psi -\sigma ^2A'(\cdots ) \Big (A(\cdots )+1\Big )\Psi \\&+\sigma ^2A'(\cdots )\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon } \Big (A(\cdots )+1\Big )\textrm{sgn}(w^\varepsilon _z)\big (\Psi _z+\Psi \big )\\&+\sigma ^2A'(\cdots ) \Big (\frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon }\Big )^2\textrm{sgn}(w^\varepsilon _z)\big (\Psi _z+\Psi \big )-\sigma ^2A'(\cdots ) \frac{w^\varepsilon }{|w^\varepsilon _z|+\varepsilon } \Psi \\&\le \frac{1}{2}e^{-\kappa s}{\Big (-\kappa +\sigma ^2 a_1(1+a_1)+\mu +\mu +\sigma ^2(a_1+1)+\sigma ^2a_1(a_1+1)+\sigma ^2a_1^2+\sigma ^2a_1\Big )}=0, \end{aligned}$$

thanks to the definition of $\kappa$. Moreover, $g(z,0)=\frac{1}{2}=\Psi (z,0)$. By the comparison principle, we have $g\ge \Psi$; hence, (63) is proved.

Thanks to (58) and (63), $w^\varepsilon _z$ has positive lower and upper bounds which are independent of $\varepsilon$ in any bounded region, noting that the bounds of $|{\partial }_\eta \Gamma _\varepsilon (\xi ,\eta )|$ and $|{\partial }_\eta \Gamma _\varepsilon (\xi ,\eta )|$ are independent of $\varepsilon$ when $\eta$ has a positive lower bound, so the constants $C_\varepsilon$s in the estimates (60) and (61) are independent of $\varepsilon$. Let $\varepsilon \rightarrow 0$ in (62), we obtain a limit w that satisfies (17). Moreover, (18) and (19) are the direct consequences of (55), (58), (63).