Gaining or Losing Perspective for Piecewise-Linear Under-Estimators of Convex Univariate Functions

Abstract

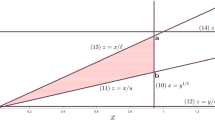
We study mixed-integer nonlinear optimization (MINLO) formulations of the disjunction $x\in \{0\}\cup [\ell ,u]$, where z is a binary indicator for $x\in [\ell ,u]$ ($0 \le \ell <u$), and y “captures” f(x), which is assumed to be convex and positive on its domain $[\ell ,u]$, but otherwise $y=0$ when $x=0$. This model is very useful in nonlinear combinatorial optimization, where there is a fixed cost c for operating an activity at level x in the operating range $[\ell ,u]$, and then, there is a further (convex) variable cost f(x). So the overall cost is $cz+f(x)$. In applied situations, there can be N 4-tuples $(f,\ell ,u,c)$, and associated (x, y, z), and so, the combinatorial nature of the problem is that for any of the $2^N$ choices of the binary z-variables, the non-convexity associated with each of the $(f,\ell ,u)$ goes away. We study relaxations related to the perspective transformation of a natural piecewise-linear under-estimator of f, obtained by choosing linearization points for f. Using 3-d volume (in (x, y, z)) as a measure of the tightness of a convex relaxation, we investigate relaxation quality as a function of f, $\ell$, u, and the linearization points chosen. We make a detailed investigation for convex power functions $f(x):=x^p$, $p>1$.

Appendix

Lemma A.1

For $x\in (0,1)\cup (1,\infty )$, $p>1$,

$$\begin{aligned} x^p + (p-1) - px>0, \quad (p-1)x^p + 1 - px^{p-1}>0. \end{aligned}$$

Proof

$x^p + (p-1) - px = x^p - 1 - p(x-1)>0$ because of the strict convexity of $x^p$ on $(0,\infty )$ for $p>1$. $(p-1)x^p + 1 - px^{p-1} = 1 - x^p - px^{p-1}(1-x)>0$ because of the strict convexity of $x^p$ on $(0,\infty )$ for $p>1$. $\square$

Lemma A.2

Letting $h(x):=(p-2)(x^p-1) - p(x^{p-1}-x)$, we have

• (i) if $1<p<2$, then $h(x)>0$ for $x\in (0,1)$;

• (ii) if $p>2$, then $h(x)<0$ for $x\in (0,1)$.

Proof

We have

$$\begin{aligned} h'(x)&= (p-2)px^{p-1} - p(p-1)x^{p-2} + p\\ h''(x)&= (p-2)(p-1)px^{p-3}(x-1) \end{aligned}$$

(i) If $1<p<2$, then $h''(x)>0$ on (0, 1), which implies that $h'(x)$ is increasing. Thus, $h'(x)<h'(1)=0$, which implies that h(x) is decreasing. Therefore, $h(x)>h(1)=0$. (ii) Similarly, we could prove that h(x) is increasing and $h(x)<0$ on (0, 1). $\square$

Remark A.1

Notice that $h(x) = -x^p h(1/x)$, we have $h(x)<0$ on $(1,\infty )$ when $1<p<2$, and $h(x)>0$ on $(1,\infty )$ when $p>2$.

Lemma A.3

Letting $\delta (x) := (x^{p-1}-1)^2 - (p-1)^2 x^{p-2}(x-1)^2$, we have

• (i) if $1<p<2$, then $\delta (x)<0$ on $(0,1)\cup (1,\infty )$;

• (ii) if $p>2$, then $\delta (x)> 0$ on $(0,1)\cup (1,\infty )$.

Proof

Notice that $\delta (x) = x^{2p-2}\delta (1/x)$, we only need to show the results on (0, 1). Letting

$$\begin{aligned} \varphi (x):= 1-x^{p-1} - (p-1)x^{\frac{p-2}{2}}(1-x), \end{aligned}$$

we have

$$\begin{aligned} \varphi '(x) = -(p-1)x^{\frac{p-4}{2}}\left( x^{\frac{p}{2}}-1 -\frac{p}{2}(x-1)\right) . \end{aligned}$$

(i) $\varphi '(x)> 0$ because of the strict concavity of $x^{p/2}$ when $1<p<2$. Along with $\varphi (1)=0$, we obtain that $\varphi (x)<0$ on (0, 1). (ii) Similarly, because of the strict convexity of $x^{p/2}$ when $p>2$, we obtain that $\varphi (x)>0$ on (0, 1). $\square$

Lemma A.4

For $x\in (0,1)\cup (1,\infty )$,

$$\begin{aligned} \phi (x):= p(p-1)(1-x)x^{p-1}\log x + (x^{p-1}-1)(x^p-1)>0. \end{aligned}$$

Proof

We have

$$\begin{aligned} \phi '(x)&= p(p-1)((p-1)x^{p-2}-px^{p-1})\log x +p(p-1)(1-x)x^{p-2} \\&\quad + (p-1)x^{p-2}(x^p-1)+px^{p-1}(x^{p-1}-1).\\ \frac{\phi '(x)}{x^{p-2}}&=((p-1)-px)p(p-1)\log x +p(p-1)(1-x) \\&\quad + (p-1)(x^p-1) +p(x^p-x).\\ \frac{d}{dx}\left( \frac{\phi '(x)}{x^{p-2}}\right)&=-p^2(p-1)\log x +\frac{p(p-1)^2}{x} - p^3 +p(2p-1)x^{p-1}\\&=p^2(x^{p-1}-1-\log x^{p-1}) +p(p-1)\left( \frac{p-1+x^p-px}{x}\right) . \end{aligned}$$

By Lemma A.1 and the inequality $t-1\ge \log t$, we have $\frac{d}{dx}\left( \frac{\phi '(x)}{x^{p-2}}\right) >0$. Because $\phi '(1)=0$, we have $\phi '(x)<0$ for $x\in (0,1)$ and $\phi '(x)>0$ for $x\in (1,\infty )$. Combined with $\phi (1)=0$, we obtain $\phi (x)>0$ for $x\in (0,1)\cup (1,\infty )$, which proves the lemma. $\square$

Lemma A.5

For $1<p<2$, $x\in (0,1)$,

$$\begin{aligned} \frac{x^p+(p-1)-px}{1+(p-1)x^p-p x^{p-1}} > x^{\frac{2-p}{3}}. \end{aligned}$$

Proof

Let $K(x):=x^{\frac{2-p}{3}}(1+(p-1)x^p-p x^{p-1})-x^p-(p-1)+px$.

$$\begin{aligned} K'(x)&= \frac{2-p}{3}x^{-\frac{p+1}{3}} + (p-1)\frac{2(p+1)}{3}x^{\frac{2p-1}{3}} -p\frac{2p-1}{3}x^{\frac{2p-4}{3}} -px^{p-1} +p\\&=x^{-\frac{p+1}{3}}\left( \frac{2-p}{3}+\frac{2(p-1)(p+1)}{3}x^{p} - \frac{p(2p-1)}{3}x^{p-1} - px^{\frac{4p-2}{3}}+ px^{\frac{p+1}{3}}\right) \\&=:x^{-\frac{p+1}{3}} K_1(x).\\ K_1'(x)&=\frac{d }{dx}\left( x^{\frac{p+1}{3}}K'(x)\right) \\&=\frac{2p(p^2-1)}{3}x^{p-1} - \frac{p(p-1)(2p-1)}{3}x^{p-2} - \frac{p(4p-2)}{3}x^{\frac{4p-5}{3}}+ \frac{p(p+1)}{3}x^{\frac{p-2}{3}}\\&= \frac{p}{3}x^{\frac{p-2}{3}}\left( 2(p^2-1)x^{\frac{2p-1}{3}} - (2p-1)(p-1)x^{\frac{2p-4}{3}} - 2(2p-1)x^{p-1}+ (p+1)\right) \\&=:\frac{p}{3}x^{\frac{p-2}{3}}K_2(x).\\ K_2'(x)&=\frac{d}{dx}\left( \frac{3}{p}x^{\frac{2-p}{3}}\frac{d }{dx}\left( x^{\frac{p+1}{3}}K'(x)\right) \right) \\&= 2(2p-1)(p-1)x^{\frac{2p-7}{3}}\left( \frac{p+1}{3}x - \frac{p-2}{3} - x^{\frac{p+1}{3}}\right) \\&= -2(2p-1)(p-1)x^{\frac{2p-7}{3}}\left( (x^{\frac{p+1}{3}}-1)- \frac{p+1}{3}(x-1)\right) > 0. \end{aligned}$$

The last inequality follows from the strict concavity of function $x^{\frac{p+1}{3}}$ when $1<p<2$. Because $K_2(1)=0$, we have $K_2(x)< 0$ on (0, 1), which implies $K_1(x)$ is decreasing on (0, 1). Along with $K_1(1)=0$, which implies $K_1(x)> 0$ on (0, 1). Therefore, K(x) is increasing on (0, 1), and $K(x)< K(1)=0$, which proves the lemma. $\square$

Proof of Theorem 3.13

For $p>2$, we know that for $k\ge 0$,

$$\begin{aligned} F(x^{k+1}) \le F(x^k) + F'(x^k) (x^{k+1} -x^k) =0, \end{aligned}$$

because of the concavity of $F_i(x)$ from Lemma 3.8 (ii). Along with $F(x^0)\le 0$ (Proposition 3.12) and $[F'(x^k)]^{-1}\ge 0$ from Lemma 3.7 (ii), we know that $x^{k+1}\ge x^k$ for $k\ge 0$. Also by concavity, we have

$$\begin{aligned} 0\le F(u{\mathbf {1}}) - F(x^k) \le F'(x^k)(u{\mathbf {1}}-x^k), \end{aligned}$$

which implies $x^k\le u{\mathbf {1}}$ because $[F'(x^k)]^{-1}$ is nonnegative. Therefore, the increasing bounded sequence $\{x^k\}$ has a limit $x^*=\lim _{k\rightarrow \infty } x^k$ and $F(x^*) = 0$.

For $1<p<2$, similarly, we know that for $k\ge 0$,

$$\begin{aligned} F(x^{k+1}) \ge F(x^k) + F'(x^k) (x^{k+1} -x^k) =0, \end{aligned}$$

because of the convexity of $F_i(x)$ from Lemma 3.8 (i). Along with $F(x^0)\ge 0$ (Proposition 3.12), we know that $[F'(x^k)]^{-1}\ge 0$ from Lemma 3.7 (i). we know that $x^{k+1}\le x^k$ for $k\ge 0$. Also by convexity, we have

$$\begin{aligned} 0\ge F(\ell {\mathbf {1}}) - F(x^k) \ge F'(x^k)(\ell {\mathbf {1}}-x^k), \end{aligned}$$

which implies $x^k\ge \ell {\mathbf {1}}$ because $[F'(x^k)]^{-1}$ is nonnegative. Therefore, the decreasing bounded sequence $\{x^k\}$ has a limit $x^*=\lim _{k\rightarrow \infty } x^k$ and $F(x^*) = 0$. $\square$

Proof of Claim in Theorem 3.19 (i)

Letting

$$\begin{aligned} \varTheta (t)&:=2t[(1-t^{p-1})^2-(p-1)^2t^{p-2}(1-t)^2] \\&\quad -(p-1)(1-t)[(p-2)(1-t^p)-p(t-t^{p-1})], \end{aligned}$$

the claim is for $1<p<2$, $0<t<1$, $\varTheta (t)>0$. We have

$$\begin{aligned} \varTheta '(t)&= 2(2p-1)t^{2p-2} -(p^2-1)(3p-4)t^p+2p(3(p-1)^2-2)t^{p-1}\\&\quad -(p-1)^2(3p-2)t^{p-2}-2p(p-1)t+(2p^2-4p+4).\\ \varTheta ''(t)&= (p-1)[4(2p-1)t^{2p-3}-p(p+1)(3p-4)t^{p-1}\\&\quad +2p(3(p-1)^2-2)t^{p-2} -(p-1)(3p-2)(p-2)t^{p-3}-2p].\\ \varTheta '''(t)&= (p-1)t^{p-4}[4(2p-1)(2p-3)t^p-p(p+1)(3p-4)(p-1)t^2\\&\quad +2p(3(p-1)^2-2)(p-2)t-(p-1)(3p-2)(p-2)(p-3)]\\&=(p-1)t^{p-4}\Big [2(p-1)^2[6t^p-p(p+1)t^2+2p(p-2)t-(p-2)(p-3)]\\&\quad +p(p-2)[4t^p-(p^2-1)t^2+2(p^2-2p-1)t-(p-3)(p-1)]\Big ]. \end{aligned}$$

Let $\varTheta _1(t):=6t^p-p(p+1)t^2+2p(p-2)t-(p-2)(p-3)$, $\varTheta _2(t):=4t^p-(p^2-1)t^2+2(p^2-2p-1)t-(p-3)(p-1)$. We first show that $t^p-1-p(t-1)\le (p-1)(1-t)^2$. This follows from the fact that

$$\begin{aligned} \frac{d}{dt}\left( \frac{t^p-1-p(t-1)}{(1-t)^2}\right) = \frac{(p-2)(1-t^p)-p(t-t^{p-1})}{(1-t)^3}<0 \quad \text {(Lemma A.2(i))}. \end{aligned}$$

Then we have

$$\begin{aligned} \varTheta _1(t)&=6(t^p-1-p(t-1))-p(p+1)(1-t)^2\\&\le 6(p-1)(1-t)^2-p(p+1)(1-t)^2\\&= -(p-2)(p-3)(1-t)^2<0.\\ \varTheta _2'(t)&= 4pt^{p-1} -2(p^2-1)t + 2(p^2-2p-1).\\ \varTheta _2''(t)&= 2(p-1)t^{p-2}(2p - (p+1)t^{2-p})>0. \end{aligned}$$

Thus, $\varTheta _2'(t)<\varTheta _2'(1) = 0$, which implies $\varTheta _2(t)$ is decreasing and $\varTheta _2(t)>\varTheta _2(1)=0$. Because $\varTheta _1(t)<0$ and $\varTheta _2(t)>0$, we have that $\varTheta '''(t)<0$. Therefore, $\varTheta ''(t)>\varTheta ''(1)=0$, which implies that $\varTheta '(t)$ is increasing. Thus, $\varTheta '(t)<\varTheta '(1)=0$, which implies $\varTheta (t)$ is decreasing, i.e., $\varTheta (t)>\varTheta (1)=0$. Then the claim follows directly. $\square$

Proof of Claim in Theorem 3.19 (ii)

Letting

$$\begin{aligned} \varPhi (t)&:=pt[(1-t^{p-1})^2-(p-1)^2t^{p-2}(1-t)^2] \\&\quad - (p-1)(1-t^p)[(p-2)(1-t^p)-p(t-t^{p-1})], \end{aligned}$$

the claim is for $p>2$, $0<t<1$, $\varPhi (t)<0$. We have

$$\begin{aligned} \varPhi '(t)&= p[-2(p-1)(p-2)t^{2p-1} + p(2p-1)t^{2p-2}-p(p^2-1)t^p \\&\quad + 2(p-2)(p^2+p-1)t^{p-1} -p(p-1)^2t^{p-2}+p].\\ \varPhi ''(t)&= p(p-1)t^{p-3}[-2(p-2)(2p-1)t^{p+1} +2p(2p-1)t^p -p^2(p+1)t^2\\&\quad +2(p-2)(p^2+p-1)t - p(p-1)(p-2)]. \end{aligned}$$

Let $\varPhi _1(t):=\frac{\varPhi ''(t)}{p(p-1)t^{p-3}} = -2(p-2)(2p-1)t^{p+1} +2p(2p-1)t^p -p^2(p+1)t^2 +2(p-2)(p^2+p-1)t - p(p-1)(p-2)$. Then

$$\begin{aligned} \varPhi _1'(t)&= -2(p-2)(2p-1)(p+1)t^p + 2p^2(2p-1)t^{p-1} \\&\quad -2p^2(p+1)t +2(p-2)(p^2+p-1);\\ \varPhi _1''(t)&= -2(p-2)(2p-1)(p+1)p t^{p-1} +2p^2(2p-1)(p-1)t^{p-2} \\&\quad -2p^2(p+1);\\ \varPhi _1'''(t)&= -2p(p-2)(2p-1)(p-1)t^{p-3}[(p+1)t - p]. \end{aligned}$$

Therefore, we have that $\varPhi _1''(t)$ is increasing on $(0,\frac{p}{p+1})$ and decreasing on $(\frac{p}{p+1},1)$. We have $\varPhi _1''(t)\le \varPhi _1''(\frac{p}{p+1})=2p^2(2p-1)\left( \frac{p}{p+1}\right) ^{p-2}-2p^2(p+1)$. Letting $\varPhi _2(p):=(p-2)\log \left( \frac{p}{p+1}\right) -\log \left( \frac{p+1}{2p-1}\right)$, we have

$$\begin{aligned} \varPhi _2'(p)&=\frac{p-2}{p} +\log (p) -\frac{p-1}{p+1} -\log (p+1) +\frac{2}{2p-1};\\ \varPhi _2''(p)&=\frac{(p-2)(8p^2+p-1)}{p^2(p+1)^2(2p-1)^2}>0. \end{aligned}$$

Therefore, $\varPhi _2'(p)$ is increasing on $(2,\infty )$. Along with $\lim _{p\rightarrow \infty }\varPhi _2'(p)=0$, we have that $\varPhi _2'(p)<0$ on $(2,\infty )$, which implies that $\varPhi _2(p)<\varPhi _2(2)=0$. Thus, $\varPhi _1''(t)<0$. Then we have that $\varPhi _1'(t)$ is decreasing on (0, 1), which implies that $\varPhi _1'(t)>\varPhi _1'(1) =0$. Therefore, we have $\varPhi _1(t)<\varPhi _1(1)=0$, i.e., $\varPhi ''(t)<0$. Then we conclude that $\varPhi '(t)$ is decreasing on (0, 1), which implies that $\varPhi '(t)>\varPhi (1)=0$. Therefore, $\varPhi (t)$ is increasing on (0, 1) and $\varPhi (t)<\varPhi (1)=0$, which proves the claim. $\square$