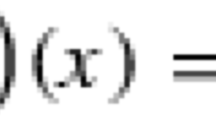1 Introduction

In this paper, we consider finite dimensional parametric optimization problems. We are interested in approximating the solution as a function of the parameters. The properties of parametric optimization problems are discussed in detail in [1]. For a theoretical treatment of parametric programming, or perturbation analysis, we refer to [2, 8, 15].

There are two classical approaches to tackle this problem. The first one starts with a complementarity function to reformulate the first-order necessary optimality conditions as a nonlinear parameterized equation system. An analysis of the resulting system can be found for example in [14, 17]. Then, one solves this equation system for a single given parameter, for example with a Newton method. An implicit function theorem guarantees the existence of a sufficiently smooth solution path in the neighborhood under some nonsingularity assumption. This solution path is followed in order to obtain the solution for a different parameter close to the first one. The path-following algorithm is often a predictor corrector method, where the prediction is based on data evaluated at the current point of the solution path, and the corrector step is some kind of (semismooth) Newton method to project the predicted point back on the solution path, and hence get an approximate solution for a new parameter. Details for such approaches can be found for example in [11, 12, 18]. Following the solution path, one can compute an approximation of the solution function on a given parameter set. Whilst this works very well for a one-dimensional parameter set, it is much more involved for higher dimensions. But there are also algorithms available, see for example [22]. A related approach is based on the parametric sensitivity analysis in [8, 9] and the concept of solution differentiability, which is exploited in [4] to obtain approximations to perturbed solutions in real-time using a Taylor expansion of the solution mapping in some nominal parameter. This approach requires second-order sufficient conditions, linear independence constraint qualification, and strict complementarity to hold at the nominal parameter. Under these conditions local differentiability of the solution mapping is guaranteed, but only in some (in general) unknown neighborhood of the nominal parameter. For large deviations to the nominal parameter, smoothness of the solution map in general is not given and Taylor expansion is not justified anymore. An attempt to overcome this difficulty can be found in [23], where the neighborhoods are estimated and databases of solutions and sensitivities are used to obtain a real-time capable approximation method.

The second and obvious approach is to compute for several parameter values the solution function and then use an interpolation technique for the scattered data to get an approximate solution for the function on the entire parameter set. If the scatter has some structure one can use finite elements method, multi-linear or spline interpolation. For non-structured data one requires a meshless interpolation method. Here, the use of radial basis functions, first introduced in a cartography application in [13], is a successful technique. The approach in [23] follows this spirit, too, but uses sensitivity updates instead of interpolation.

In this paper we suggest a new approach that directly computes an interpolation function without first solving several instances of our optimization problem for different parameters. Instead, we use the nonlinear equation reformulation of the first-order necessary optimality conditions and replace the primal and dual solutions with a linear combination of approximating functions. Defining a residual function and summing over some test parameters, we obtain a single nonlinear least-squares optimization problem in the basis function coefficients as variables. The resulting approximation is well suited for real-time optimization tasks as it is able to cover large parameter regions while the cost for evaluating the approximate function is very cheap. It is important to stress that the approach does not require to solve instances of the parametric optimization problem. Our standing assumption throughout is that it is too expensive to solve the parametric optimization problems explicitly, e.g., within a real-time application.

The detailed problem setting will be given in Sect. 2. Through the number of basis functions we can adapt the dimension of the least-squares problem. We show in Section 3, that by solving this nonlinear least-squares problem we obtain directly an interpolation function for the desired solution function. Further, we show that stationary points are global minima of the least-squares problem under mild assumptions, which allows to solve the problem globally. In Section 4, we present criteria to estimate the error of the obtained approximate solution at a new parameter, which is only based on a cheap function evaluation. Some preliminary numerical results are given in Sect. 5, before we conclude our paper in Sect. 6.

2 Problem Setting

Consider the parametric nonlinear optimization problem:

$$\begin{aligned} \min \, f(x,p) \qquad \text {s.t.}\quad h(x,p) = 0, \quad g(x,p) \le 0. \end{aligned}$$
(1)

Herein, \(x\in {\mathbb R}^{n_x}\), \(p\in {\mathbb R}^{n_p}\), \(f:{\mathbb R}^{n_x}\times {\mathbb R}^{n_p} \rightarrow {\mathbb R}\), \(g:{\mathbb R}^{n_x}\times {\mathbb R}^{n_p} \rightarrow {\mathbb R}^{n_g}\), \(h:{\mathbb R}^{n_x}\times {\mathbb R}^{n_p} \rightarrow {\mathbb R}^{n_h}\). For abbreviation define

$$\begin{aligned} m :=n_x+n_g+n_h. \end{aligned}$$

For a given parameter p let x(p) denote the optimal solution of (1). We are interested in the mapping \(x : P \rightarrow {\mathbb R}^{n_x}\), \(p \mapsto x(p)\), for a set of parameters \(P\subset {\mathbb R}^{n_p}\).

In the following we will use the notation \(J_x h(x,p) \in {\mathbb R}^{n_h \times n_x}\) for the Jacobian of h with respect to x and \(\nabla _x h(x,p)=(J_x h(x,p))^\top \in {\mathbb R}^{n_x \times n_h}\) for the transposed matrix. The notation will be used analogous for the other appearing functions.

Let us consider the necessary KKT conditions, which read as follows:

$$\begin{aligned} 0&= \nabla _x f(x(p),p) + \nabla _x g(x(p),p) \lambda (p) + \nabla _x h(x(p),p) \mu (p) ,\\ 0&= h(x(p),p), \\ 0&\le \lambda (p), \quad \lambda (p)^\top g(x(p),p) = 0,\quad g(x(p),p) \le 0. \end{aligned}$$

Let \(z(p) :=(x(p)^\top ,\lambda (p)^\top ,\mu (p)^\top )^\top \) denote a KKT point for a given parameter \(p \in P\) and define the Lagrange function where

$$\begin{aligned} L(z,p) :=f(x,p) + \lambda ^\top g(x,p) + \mu ^\top h(x,p). \end{aligned}$$

Using a suitable NCP-function, e.g., the Fischer–Burmeister function

$$\begin{aligned} \varphi : {\mathbb R}\times {\mathbb R}\rightarrow {\mathbb R}, \quad \varphi (a,b) = \sqrt{a^2 + b^2}-a-b \end{aligned}$$
(2)

and the function

$$\begin{aligned} \Phi : {\mathbb R}^{n_g} \times {\mathbb R}^{n_g} \rightarrow {\mathbb R}^{n_g}, \quad \Phi _i(a,b)= \varphi (a_i,b_i) \quad i=1,\dots ,n_g, \end{aligned}$$

the KKT conditions can be reformulated as a nonlinear system of equations

$$\begin{aligned} 0 = F(z(p),p) :=\begin{pmatrix} \nabla _x L(z(p),p) \\ h(x(p),p) \\ \Phi (-g(x(p),p),\lambda (p)) \end{pmatrix}. \end{aligned}$$
(3)

The function \(F:{\mathbb R}^{m} \times {\mathbb R}^{n_p} \rightarrow {\mathbb R}^m\) is not differentiable everywhere, since the Fischer–Burmeister function is not. However, using the implicit function theorem for Lipschitz functions from [5, Section 7.1], we get under a full rank assumption on the generalized Jacobian of F with respect to z, that the solution function \(z(\cdot )\) is Lipschitz in a neighborhood of the considered nominal parameter. But, there is no information on the size of such a neighborhood. Another way to argue for smoothness of the solution in the neighborhood of a nominal parameter is given in [21]. Therein, it is shown that, under smoothness conditions on f, g, h, the Mangasarian–Fromovitz constraint qualification (MFCQ), a second-order condition on the Lagrangian function and a constant rank condition on the set of equality and active inequality constraints in a neighborhood of the nominal parameter, the solution \(x(\cdot )\) is at least locally Lipschitz, but the multipliers need not be continuous.

In our approach we will not exploit an implicit function theorem. Our idea is to approximate z(p) by a linear combination of some basis functions. Let

$$\begin{aligned} \Psi :{\mathbb R}^{n_p} \times {\mathbb R}^{n_p} \rightarrow {\mathbb R}, \quad \Psi (p,q):=\psi (\Vert p-q\Vert ) \end{aligned}$$

be any radial basis function, for example a Gaussian one

$$\begin{aligned} \psi (p,q) = \exp (-c^2 \Vert p-q\Vert ^2) \qquad \text {with a constant } c\ne 0. \end{aligned}$$
(4)

For textbooks on the theory of radial basis functions, we refer to [3, 24]. Let us mention that the use of basis functions is independent of the dimension of the parameter space. It is viable for any dimension \(n_p \in {\mathbb N}\).

For our approach we define for a set of \(K \in {\mathbb N}\) basis parameters \(\hat{p}_k,\) and weight vectors \(\alpha ^k \in {\mathbb R}^{n_x}, \beta ^k \in {\mathbb R}^{n_g}, \gamma ^k \in {\mathbb R}^{n_h}\) for \(k=1,\dots ,K,\) the approximation

$$\begin{aligned} \tilde{x}(p)&:=\sum _{k=1}^K \alpha ^k \, \Psi (p,\hat{p}_k) ,&\tilde{\lambda }(p)&:=\sum _{k=1}^K \beta ^k \, \Psi (p,\hat{p}_k),\\ \tilde{\mu }(p)&:=\sum _{k=1}^K \gamma ^k \, \Psi (p,\hat{p}_k) ,&\tilde{z}(p)&:=\begin{pmatrix} \tilde{x}(p)\\ \tilde{\lambda }(p)\\ \tilde{\mu }(p) \end{pmatrix} \in {\mathbb R}^{n_x+n_g+n_h} . \end{aligned}$$

We consider the ordering of the weights by the components, i.e., we define

$$\begin{aligned} \alpha&:=(\alpha ^1_1,\dots ,\alpha ^K_1,\dots ,\alpha ^1_{n_x},\dots ,\alpha ^K_{n_x}),\\ \beta&:=(\beta ^1_1,\dots ,\beta ^K_1,\dots ,\beta ^1_{n_g},\dots ,\beta ^K_{n_g}),\\ \gamma&:=(\gamma ^1_1,\dots ,\gamma ^K_1,\dots ,\gamma ^1_{n_h},\dots ,\gamma ^K_{n_h}). \end{aligned}$$

In order to determine good weights for the approximate functions, we choose a number of N test parameters \(p_i,i=1,\dots ,N\), and solve the following nonlinear least-squares problem:

$$\begin{aligned} \min _{\alpha ,\beta ,\gamma } \quad \frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2. \end{aligned}$$
(5)

The advantage of this approach is, that instead of solving (1) for every parameter \(p \in P\) we now solve a single nonlinear least-squares problem in \(K \cdot m\) variables in order to get an approximation for the KKT points of (1) for \(p \in P\).

We like to emphasize that our approach aims at approximating KKT points. We cannot guarantee to obtain minimizers. For instance it is possible to obtain non-optimal critical points as defined in [16].

3 Global Minima

In this section we will show that under suitable assumptions stationary points of (5) are global minima and hence we obtain exact solutions at the test points. To do so, we have to compute the gradient of the function

$$\begin{aligned} R(\alpha ,\beta ,\gamma ) :=\frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2. \end{aligned}$$

Note, that through the square in the definition of this function it is continuously differentiable although the function \(F(\tilde{z}(p),p)\) is only semismooth but not differentiable due to the Fischer–Burmeister function.

Let us first introduce some notation. By \(\partial _{\tilde{z}} F(\tilde{z}(p),p)\) we will denote the generalized Jacobian (in the sense of Clarke) of \(F(\tilde{z}(p),p)\) with respect to \(\tilde{z}(p)\). Further, we define the vector

$$\begin{aligned} \overline{\Psi }(p):=\left( \Psi (p,\hat{p}_1), \dots , \Psi (p,\hat{p}_K) \right) \in {\mathbb R}^K, \end{aligned}$$

and the block diagonal matrix

$$\begin{aligned} \widehat{\Psi }_{m}(p) :={{\,\textrm{blockdiag}\,}}\left( \overline{\Psi }(p),\dots ,\overline{\Psi }(p) \right) \in {\mathbb R}^{m\times mK}. \end{aligned}$$

In the following we will require that the chosen radial basis functions and parameters \(p_i\) lead to nonsingularity of a certain matrix. Hence we make the following assumption.

Assumption 1

Let the radial basis function \(\Psi \), the basis and test parameters \(\hat{p}_k\), \(k=1,\dots ,K\), and \(p_i, i=1,\dots ,N\), respectively, be chosen such that the matrix

$$\begin{aligned} \begin{pmatrix} \overline{\Psi }(p_1)^\top&\dots&\overline{\Psi }(p_N)^\top \end{pmatrix} \in {\mathbb R}^{K \times N} \end{aligned}$$

has full column rank.

This assumption in particular requires that \(N \le K\), meaning that we do not consider more test parameters than basis parameters. It is satisfied if we use the Gaussian radial basis functions from (4). Now, we develop the gradient formula. By chain rule we have

$$\begin{aligned} \nabla _{(\alpha ,\beta ,\gamma )} \left( \frac{1}{2}\Vert F(\tilde{z}(p),p) \Vert ^2 \right) = J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p)^\top \, \partial _{\tilde{z}} F(\tilde{z}(p),p)^\top \, F(\tilde{z}(p),p). \end{aligned}$$

The Jacobian \(J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p)\) of \(\tilde{z}(p)\) with respect to \((\alpha ,\beta ,\gamma )\) is given by

$$\begin{aligned} J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p)&:=\begin{pmatrix} J_{\alpha } \tilde{x} (p) &{} J_{\beta } \tilde{x}(p)&{} J_{\gamma } \tilde{x}(p)\\ J_{\alpha } \tilde{\lambda }(p) &{} J_{\beta } \tilde{\lambda }(p)&{} J_{\gamma } \tilde{\lambda }(p)\\ J_{\alpha } \tilde{\mu }(p) &{} J_{\beta } \tilde{\mu }(p)&{} J_{\gamma } \tilde{\mu }(p)\end{pmatrix}\\&= \begin{pmatrix} J_{\alpha } \tilde{x} (p) &{} 0&{} 0\\ 0 &{} J_{\beta } \tilde{\lambda }(p)&{} 0\\ 0 &{} 0&{} J_{\gamma } \tilde{\mu }(p)\end{pmatrix} = \widehat{\Psi }_{m}(p). \end{aligned}$$

The generalized Jacobian \(\partial _{\tilde{z}} F(\tilde{z}(p),p)\) of \(F(\tilde{z}(p),p)\) with respect to \(\tilde{z}(p)\) is given by

$$\begin{aligned}&\partial _{\tilde{z}} F(\tilde{z}(p),p)\\&\quad =\begin{pmatrix} \nabla _{xx}^2 L(\tilde{z}(p),p) &{} \nabla _x g(\tilde{x}(p),p) &{} \nabla _x h(\tilde{x}(p),p) \\ J_x h(\tilde{x}(p),p) &{} 0 &{} 0\\ - D_g(-g(\tilde{x}(p),p),\tilde{\lambda }(p)) J_x g(\tilde{x}(p),p) &{} D_\lambda (-g(\tilde{x}(p),p),\tilde{\lambda }(p)) &{} 0 \end{pmatrix}, \end{aligned}$$

with diagonal matrices \(D_g(-g(\tilde{x}(p),p),\tilde{\lambda }(p)), D_\lambda (-g(\tilde{x}(p),p),\tilde{\lambda }(p)) \in {\mathbb R}^{n_g \times n_g}\) whose entries are given by

$$\begin{aligned}&\left( (D_g(-g(\tilde{x}(p),p),\tilde{\lambda }(p)))_{jj}, (D_\lambda (-g(\tilde{x}(p),p),\tilde{\lambda }(p)))_{jj} \right) \\&\qquad {\left\{ \begin{array}{ll} = \frac{(- g_i(\tilde{x}(p),p),\tilde{\lambda }_i(p) )}{\sqrt{(\tilde{\lambda }_i(p))^2 + g_i (\tilde{x}(p),p)^2}} - (1,1) , &{}\text {if}~(\tilde{\lambda }_i(p) , - g_i (\tilde{x}(p),p)) \ne ( 0, 0), \\ \in \mathbb {B}_1(0,0) - (1,1) , &{} \text {if}~(\tilde{\lambda }_i(p), - g_i (\tilde{x}(p),p)) = ( 0, 0 ), \end{array}\right. } \end{aligned}$$

for all \(j=1,\dots ,n_g\), where \(\mathbb {B}_1(0,0)\) denotes the closed unit ball centered at (0, 0) with radius 1. With the explicit gradient formula, we can now state our stationarity result.

Theorem 3.1

Let Assumption 1 hold and assume that for all \(i=1,\dots ,N\)

  • \(\nabla _{xx}^2 L(\tilde{z}(p_i),p_i)\) is positive semi-definite and

    $$\begin{aligned} d^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i) d > 0 \end{aligned}$$

    holds for every

    $$\begin{aligned} d \in \{d \in {\mathbb R}^{n_x}\setminus \{0\} \mid J_x h(\tilde{x}(p_i),p_i) d = 0, J_x g(\tilde{x}(p_i),p_i) d = 0\}. \end{aligned}$$

  • \(\nabla _x h(\tilde{x}(p_i),p_i)\) has full column rank \(n_h\), i.e., the gradients of the equations are linearly independent.

Then, every weight vector \((\alpha ,\beta ,\gamma )\) that is a stationary point of

$$\begin{aligned} \frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2 \end{aligned}$$

with respect to \((\alpha ,\beta ,\gamma )\) defines a mapping \(\tilde{z}(p)\) that satisfies \(F(\tilde{z}(p_i),p_i)=0\) for all \(i=1,\dots ,N,\) and thus, \(\tilde{z}(p_i)\) is a KKT point of (1) for every test parameter \(p_i,\) \( i=1,\dots ,N\).

Proof

Let an arbitrary stationary point be given. Then, we must have

$$\begin{aligned} 0 =&\nabla _{(\alpha ,\beta ,\gamma )} \left( \frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2 \right) \\ =&\sum _{i=1}^N J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p_i)^\top \, \partial _{\tilde{z}} F(\tilde{z}(p_i),p_i)^\top \, F(\tilde{z}(p_i),p_i)\\ =&\begin{pmatrix}J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p_1)^\top \cdots J_{(\alpha ,\beta ,\gamma )}\tilde{z}(p_N)^\top \end{pmatrix} \cdot \\&\begin{pmatrix} \partial _{\tilde{z}} F(\tilde{z}(p_1),p_1)^\top &{} &{} \\ &{} \ddots &{} \\ &{} &{} \partial _{\tilde{z}} F(\tilde{z}(p_N),p_N)^\top \end{pmatrix} \begin{pmatrix} F(\tilde{z}(p_1),p_1) \\ \vdots \\ F(\tilde{z}(p_N),p_N) \end{pmatrix} . \end{aligned}$$

Now, for the first matrix we have

$$\begin{aligned}&\begin{pmatrix}J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p_1)^\top \cdots J_{(\alpha ,\beta ,\gamma )}\tilde{z}(p_N)^\top \end{pmatrix}\\&\quad = \begin{pmatrix}\widehat{\Psi }_{m}(p_1)^\top \cdots \widehat{\Psi }_{m}(p_N)^\top \end{pmatrix}\\&\quad = \begin{pmatrix} \overline{\Psi }(p_1)^\top &{} &{} &{} &{} \overline{\Psi }(p_N)^\top &{} &{} \\ &{} \ddots &{} &{}\ddots &{} &{} \ddots &{} \\ &{} &{} \overline{\Psi }(p_1)^\top &{} &{} &{} &{} \overline{\Psi }(p_N)^\top \end{pmatrix}. \end{aligned}$$

After some row permutations , we see that this is a block-diagonal matrix with the matrix \(\begin{pmatrix} \overline{\Psi }(p_1)^\top&\cdots&\overline{\Psi }(p_N)^\top \end{pmatrix}\) from Assumption 1 on the diagonal. Thus, the entire matrix has full column rank by Assumption 1. This implies

$$\begin{aligned} 0&= \begin{pmatrix} \partial _{\tilde{z}} F(\tilde{z}(p_1),p_1)^\top &{} &{} \\ &{} \ddots &{} \\ &{}&{} \partial _{\tilde{z}} F(\tilde{z}(p_N),p_N)^\top \end{pmatrix} \begin{pmatrix} F(\tilde{z}(p_1),p_1) \\ \vdots \\ F(\tilde{z}(p_N),p_N) \end{pmatrix}. \end{aligned}$$

Hence, for all \(i \in \{1, \dots ,N\}\) we have

$$\begin{aligned} 0=\partial _{\tilde{z}} F(\tilde{z}(p_i),p_i)^\top F(\tilde{z}(p_i),p_i). \end{aligned}$$
(6)

Consider an arbitrary \(i \in \{1, \dots ,N\}\). For better readability we use the abbreviations

$$\begin{aligned} D_g[i]:=&D_g(-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)),\\ D_\lambda [i]:=&D_\lambda (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)). \end{aligned}$$

Then, from (6) we have

$$\begin{aligned} 0=&\partial _{\tilde{z}} F(\tilde{z}(p_i),p_i)^\top F(\tilde{z}(p_i),p_i) \nonumber \\ =&\begin{pmatrix} \nabla _{xx}^2 L(\tilde{z}(p_i),p_i)^\top &{} \nabla _x h(\tilde{x}(p_i),p_i) &{} - \nabla _x g(\tilde{x}(p_i),p_i) D_g[i]\\ J_x g(\tilde{x}(p_i),p_i) &{} 0 &{} D_\lambda [i]\\ J_x h(\tilde{x}(p_i),p_i) &{} 0 &{} 0 \end{pmatrix} \cdot \nonumber \\&\begin{pmatrix} \nabla _x L(\tilde{z}(p_i),p_i) \\ h(\tilde{x}(p_i),p_i) \\ \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)) \end{pmatrix}. \end{aligned}$$
(7)

From the third block we obtain

$$\begin{aligned} J_x h(\tilde{x}(p_i),p_i) \nabla _x L(\tilde{z}(p_i),p_i) =0, \end{aligned}$$

and from the second block

$$\begin{aligned} -J_x g(\tilde{x}(p_i),p_i) \nabla _x L(\tilde{z}(p_i),p_i) = D_\lambda [i] \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)). \end{aligned}$$

Multiplying the first block with \(\nabla _x L(\tilde{z}(p_i),p_i)^\top \) from the left side and using the last two equations we get

$$\begin{aligned} 0 =&\nabla _x L(\tilde{z}(p_i),p_i)^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i)^\top \nabla _x L(\tilde{z}(p_i),p_i)\\&+ \underbrace{\nabla _x L(\tilde{z}(p_i),p_i)^\top \nabla _x h(\tilde{x}(p_i),p_i)}_{=0} h(\tilde{x}(p_i),p_i)\\&\underbrace{- \nabla _x L(\tilde{z}(p_i),p_i)^\top \nabla _x g(\tilde{x}(p_i),p_i)}_{= \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))^\top D_\lambda [i]} D_g[i]\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))\\ =&\nabla _x L(\tilde{z}(p_i),p_i)^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i)^\top \nabla _x L(\tilde{z}(p_i),p_i)\\&+ \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))^\top D_\lambda [i] D_g[i]\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)) . \end{aligned}$$

Since \(\nabla _{xx}^2 L(\tilde{z}(p_i),p_i)\) is positive semi-definite, the first term is non-negative. The product matrix \(D_\lambda [i] D_g[i]\) is positive semidefinite, because by definition all entries of both diagonal matrices are non-positive. Hence, also the second term is non-negative. This implies that both terms must be zero, i.e.,

$$\begin{aligned} 0=&\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))^\top D_\lambda [i] D_g[i]\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)), \end{aligned}$$
(8)
$$\begin{aligned} 0=&\nabla _x L(\tilde{z}(p_i),p_i)^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i)^\top \nabla _x L(\tilde{z}(p_i),p_i). \end{aligned}$$
(9)

If \((D_g(-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))_{jj}=0\) or \((D_\lambda (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))_{jj} =0\) we also must have \(\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))_j=0,\) which can be seen from the definition. Thus, we can deduce from (8) that

$$\begin{aligned} \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))=0. \end{aligned}$$

Using this in (7), we get in the second and third block

$$\begin{aligned} \begin{pmatrix} J_x g(\tilde{x}(p_i),p_i) \\ J_x h(\tilde{x}(p_i),p_i)\end{pmatrix} \nabla _x L(\tilde{z}(p_i),p_i)=0. \end{aligned}$$

Then, with \(d = \nabla _x L(\tilde{z}(p_i),p_i)\) we know from the positive definiteness assumption and from (9) that

$$\begin{aligned} \nabla _x L(\tilde{z}(p_i),p_i)=0. \end{aligned}$$

Finally, the full column rank assumption on \(\nabla _x h(\tilde{x}(p_i),p_i) \) and equation (7) yield

$$\begin{aligned} h(\tilde{x}(p_i),p_i)=0. \end{aligned}$$

Since \(i \in \{1, \dots ,N\}\) was arbitrarily chosen, we have shown that

$$\begin{aligned} F(\tilde{z}(p_i),p_i)=0 \end{aligned}$$

must hold for all \(i=1,\dots ,N\). Since every \(\tilde{z}(p)\) with \(F(\tilde{z}(p_i),p_i)=0\) is a KKT point, the proof is complete. \(\square \)

This theorem justifies that the obtained weights determined by any optimization algorithm finding stationary points, are suitable to define an approximation function \(\tilde{z}(p)\) of the true function z(p) through the linear combination of basis functions. The theorem guarantees that \(\tilde{z}(p)\) interpolates the function z(p) for all test parameters \(p_i\), \(i=1,\dots ,N\), if a stationary point exists. Furthermore, if no stationary point exists, then for at least one of the parameters \(p_i\), \(i=1,\dots ,N\), we do not have any KKT point.

Note that including test parameters for which no KKT point exists leads to difficulties in the optimization, since we no longer have a stationary point. Even if the used solver stops at an approximate stationary point, the computed solution may contain some very large weights and we may be far from the exact solution at all test parameters, even those that have a KKT point.

Furthermore, besides the non-existence of a KKT point, non uniqueness of KKT points can lead to problems as well. In order to illustrate this issue, we look at the following example.

Example 3.1

Consider the parametric optimization problem

$$\begin{aligned} \min _x \quad&-\frac{1}{4} x^4+\frac{1}{3}px^3+\frac{1}{2}x^2-px \\ \text {s.t.}\quad&-\frac{1}{2}(p^2+1) \le x \le \frac{1}{2}(p^2+1) \end{aligned}$$

for \(p \in [-1,1]\). The corresponding KKT points \((x(p),\lambda _1(p),\lambda _2(p))\) can be easily computed and are given by:

$$\begin{aligned} p \in \{-1,1\} \quad \Rightarrow{} & {} {}&x(p)\in \{-1,1\},\quad{} & {} \lambda _1(p) = \lambda _2(p) = 0. \\ p \in (-1,1) \quad \Rightarrow{} & {} {}&x(p)=p,\quad{} & {} \lambda _1(p) = \lambda _2(p) = 0. \end{aligned}$$

We observe that for \(p \in \{-1,1\}\) the problem admits two KKT points.

Fig. 1
figure 1

Results for Example 3.1: feasible set (gray area), contour lines of the objective function, KKT points (black), possible approximation (dashed red).

Full size image

In Figure 1 the feasible set is superimposed to the objective function visualized using contour lines and to the set of KKT points. In case that we would use the parameters \(p=-1,0,1\) for the training of our approximation function, a valid linear interpolated approximation of the KKT points is depicted as a red dashed line. This clearly differs significantly from the actual solution of the parametric optimization problem and also from the actual KKT points. \(\diamond \)

Clearly, strong convexity of the functions \(f(\cdot ,p)\) for fixed parameters p together with only affine linear constraints are sufficient for the positive definiteness assumption on \(\nabla ^2_{xx}L(\tilde{z}(p_i),p_i)\) in Theorem 3.1. Further, if we have \(n_x\) linear independent gradients of g and h the set

$$\begin{aligned} \{d \in {\mathbb R}^{n_x}\setminus \{0\} \mid J_x h(\tilde{x}(p_i),p_i) d = 0, J_x g(\tilde{x}(p_i),p_i) d = 0\} \end{aligned}$$

is empty, and we only assume positive semi-definiteness of \(\nabla ^2_{xx}L(\tilde{z}(p_i),p_i)\). As we can see in the proof, the assumptions, except Assumption 1, guarantee nonsingularity of the generalized Jacobian of F(z(p), p) with respect to z. Thus, they also allow to use an implicit function theorem [5, Section 7.1], to get the existence of the solution functions in a neighborhood.

Let us present a similar result, which does not require the positive semidefiniteness of \(\nabla _{xx}^2 L(\tilde{z}(p_i),p_i)\) on the entire space, but sharpens the positive definiteness assumption. To do so, we partition the inequality constraints by the sign of the corresponding component of \(\Phi (-g(\tilde{x}(p),p),\tilde{\lambda }(p))\), and use the abbreviations

$$\begin{aligned} g_{(\Phi >0)}(\tilde{x}(p),p) ,\quad g_{(\Phi =0)}(\tilde{x}(p),p) ,\quad \text { and } \quad g_{(\Phi <0)}(\tilde{x}(p),p) , \end{aligned}$$

to distinguish the components of g with positive, zero and negative values of \(\Phi (-g(\tilde{x}(p),p),\tilde{\lambda }(p))\), respectively.

Theorem 3.2

Let Assumption 1 hold and assume that for all \(i=1,\dots ,N\)

  • \(d^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i) d > 0\) for all \(d \in K(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i) \setminus \{0\}\) with

    $$\begin{aligned} K(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i):=\{d \in {\mathbb R}^{n_x} \mid&J_x h(\tilde{x}(p_i),p_i) d = 0,\\&J_x g_{(\Phi>0)}(\tilde{x}(p_i),p_i) d > 0, \\&J_x g_{(\Phi =0)}(\tilde{x}(p_i),p_i) d = 0,\\&J_x g_{(\Phi<0)}(\tilde{x}(p_i),p_i) d < 0\}. \end{aligned}$$

  • \(\nabla _x h(\tilde{x}(p_i),p_i)\) has full column rank \(n_h\), i.e., the gradients of the equations are linearly independent.

Then, every weight vector \((\alpha ,\beta ,\gamma )\) that is a stationary point of

$$\begin{aligned} \frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2 \end{aligned}$$

with respect to \((\alpha ,\beta ,\gamma )\) defines a mapping \(\tilde{z}(p)\) that satisfies \(F(\tilde{z}(p_i),p_i)=0\) for all \(i=1,\dots ,N,\) and thus, \(\tilde{z}(p_i)\) is a KKT point of (1) for every test parameter \(p_i\), \(i=1,\dots ,N\).

Proof

Let an arbitrary stationary point be given. We follow the proof of Theorem 3.1 until (7). From the second block of (7) we get

$$\begin{aligned} J_x g(\tilde{x}(p_i),p_i) \nabla _x L(\tilde{z}(p_i),p_i) = - D_\lambda [i] \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)). \end{aligned}$$

By definition of \(\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))\) and \(D_\lambda [i]\) we have

$$\begin{aligned} \left( -D_\lambda [i] \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)) \right) _j \left\{ \begin{array}{ll}>0, &{}\text {if } \varphi (-g_j(\tilde{x}(p_i),p_i),\tilde{\lambda }_j(p_i)) > 0 ,\\ =0, &{}\text {if } \varphi (-g_j(\tilde{x}(p_i),p_i),\tilde{\lambda }_j(p_i)) = 0, \\<0, &{}\text {if } \varphi (-g_j(\tilde{x}(p_i),p_i),\tilde{\lambda }_j(p_i)) < 0. \end{array} \right. \end{aligned}$$

This, together with \(J_x h(\tilde{x}(p_i),p_i) \nabla _x L(\tilde{z}(p_i),p_i) = 0\) from the third block of (7), yields

$$\begin{aligned} \nabla _x L(\tilde{z}(p_i),p_i) \in K(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i). \end{aligned}$$

As in the proof of Theorem 3.1, we have

$$\begin{aligned} 0 =&\nabla _x L(\tilde{z}(p_i),p_i)^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i)^\top \nabla _x L(\tilde{z}(p_i),p_i)\\&+ \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))^\top D_\lambda [i] D_g[i]\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)) \end{aligned}$$

with a non-negative second summand. Then, the first summand cannot be positive. Since \(\nabla _x L(\tilde{z}(p_i),p_i) \in K(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i)\) this is by our positive definiteness assumption of \(\nabla _{xx}^2 L(\tilde{z}(p_i),p_i)\) on \(K(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i) \setminus \{0\}\) only possible if

$$\begin{aligned} \nabla _x L(\tilde{z}(p_i),p_i) = 0. \end{aligned}$$

This in turn means

$$\begin{aligned} 0 = \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))^\top D_\lambda [i] D_g[i]\Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)). \end{aligned}$$
(10)

The rest of the proof is analogous to that of Theorem 3.1. \(\square \)

Remark 3.1

Let the Strong Second-Order Sufficient Condition (SSOSC) hold for all \(i=1,\dots ,N,\) at all points \((\tilde{x}(p_i),\tilde{\lambda }(p_i))\), i.e., assume

$$\begin{aligned} d^\top \nabla _{xx}^2 L(\tilde{z}(p_i),p_i) d > 0 \text { for all } d \in K_1(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i) \setminus \{0\} \end{aligned}$$

with

$$\begin{aligned} K_1(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i):=\{d \in {\mathbb R}^{n_x} \mid J_x h(\tilde{x}(p_i),p_i) d = 0, J_x g_{J_+}(\tilde{x}(p_i),p_i) d = 0\}, \end{aligned}$$

where \(J_+ :=\{j \in \{1,\ldots ,n_g\} \mid g_j(\tilde{x}(p_i),p_i)=0,\tilde{\lambda }_j(p_i)>0 \}\). Then, since \(j \in J_+\) implies \(\varphi (-g_j(\tilde{x}(p_i),p_i),\tilde{\lambda }_j(p_i))=0\), we have

$$\begin{aligned} K(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i) \subseteq K_1(\tilde{x}(p_i),\tilde{\lambda }(p_i),p_i), \end{aligned}$$

and hence, SSOSC implies the definiteness assumption in Theorem 3.2.

In general, stationary points with negative multipliers \(\tilde{\lambda }(p_i)\) may exist as soon as we have at least one nonlinear inequality constraint, since the positive (semi-)definiteness of \(\nabla ^2_{xx}L(\tilde{z}(p_i),p_i)\) may be destroyed even for convex optimization problems. Let us give an explicit example having non-optimal stationary points:

Example 3.2

Consider the parametric convex optimization problem

$$\begin{aligned} \min \, 2 x_1^2 +3 x_2^2 +\frac{28}{5} x_1-p x_2 \qquad \text {s.t.}\quad x_1^2+x_2^2 \le 8 \end{aligned}$$

for \(p \in {\mathbb R}\). Now we choose the point \(\tilde{x}(p)=(2,0)^\top \) and \(\tilde{\lambda }(p)=-3\). Then, we get for any \(p \in {\mathbb R}\)

$$\begin{aligned}&\partial _{\tilde{z}} F(\tilde{z}(p),p)^\top F(\tilde{z}(p),p)\\&\quad =\begin{pmatrix} \nabla _{xx}^2 L(\tilde{z}(p),p)^\top &{} - \nabla _x g(\tilde{x}(p),p) D_g(-g(\tilde{x}(p),p),\tilde{\lambda }(p))\\ J_x g(\tilde{x}(p),p) &{} D_\lambda (-g(\tilde{x}(p),p),\tilde{\lambda }(p)) \end{pmatrix} \begin{pmatrix} \nabla _x L(\tilde{z}(p),p) \\ \Phi (-g(\tilde{x}(p),p),\tilde{\lambda }(p)) \end{pmatrix} \\&\quad =\begin{pmatrix} 4+2\tilde{\lambda }(p) &{} 0 &{} -2 \tilde{x}_1(p) D_g(4,-3)\\ 0 &{} 6+2\tilde{\lambda }(p) &{} -2 \tilde{x}_2(p) D_g(4,-3) \\ 2 \tilde{x}_1(p) &{} 2 \tilde{x}_2(p) &{} D_\lambda (4,-3) \end{pmatrix} \begin{pmatrix} 4 \tilde{x}_1(p) + \frac{28}{5} + 2 \tilde{x}_1(p) \tilde{\lambda }(p)\\ 6 \tilde{x}_2(p)-p + 2 \tilde{x}_2(p) \tilde{\lambda }(p)\\ \phi (4,-3) \end{pmatrix}\\&\quad =\begin{pmatrix} -2 &{} 0 &{} \frac{4}{5}\\ 0 &{} 0 &{} 0 \\ 4 &{} 0 &{} -\frac{8}{5} \end{pmatrix} \begin{pmatrix} \frac{8}{5} \\ -p \\ 4 \end{pmatrix} =0. \end{aligned}$$

Since this holds for every \(p \in {\mathbb R},\) we obtain

$$\begin{aligned}&\nabla _{(\alpha ,\beta ,\gamma )} \left( \frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2 \right) \\&\quad = \sum _{i=1}^N J_{(\alpha ,\beta ,\gamma )} \tilde{z}(p_i)^\top \, \partial _{\tilde{z}} F(\tilde{z}(p_i),p_i)^\top \, F(\tilde{z}(p_i),p_i) = 0 \end{aligned}$$

for any test parameter set \(p_i\), \(i=1,\dots ,N\). Hence, we have a stationary point which obviously does not satisfy \(F(\tilde{z}(p_i),p_i) = 0\) for any \(i=1,\dots ,N,\) and hence the conclusion of Theorem 3.1 or Theorem 3.2 does not hold. \(\diamond \)

It follows from the example above that, if nonlinear constraints are present, we cannot avoid the positive (semi-)definiteness assumptions in the Theorems. Let us stress that solving an instance of the parameterized problem for a fixed parameter p via minimization of the merit function \(\Vert F(\cdot ,\cdot ,p) \Vert ^2\) might result in obtaining non-optimal stationary points, and this is not a consequence of our approach with basis functions.

From a numerical point of view, the approximated multipliers can also become negative, because of approximation errors. Nevertheless, we can distinguish these stationary points from those with actual negative multipliers by checking if the merit function \(\Vert F(x,\lambda ,p) \Vert ^2\) for this corresponding point is close to zero. The merit function vanishes only if the multiplier is greater than or equal to zero, because of the Fisher-Burmeister function. If the approximation error is not acceptable, then a re-training could be used to improve the approximation by adding the respective parameter to the training set. The re-training process uses the pre-trained approximation as an initial guess and it can be expected that it requires only a few iterations. This would even permit to perform the re-training online. We will investigate this aspect and its potential in a future research.

Next, we consider the special case of a parameterized linear problem, where the functions \(f(\cdot ,p)\), \(g(\cdot ,p)\), and \(h(\cdot ,p)\) are affine linear for every fixed parameter p. Then, we can show the following version.

Theorem 3.3

Consider a parameterized linear problem. Let Assumption 1 hold and assume that for all \(i=1,\dots ,N\)

  • \(\nabla _x h(\tilde{x}(p_i),p_i)\) has full column rank \(n_h\), i.e., the gradients of the equations are linear independent.

  • The matrix \(\begin{pmatrix} Jh(x) \\ Jg(x) \end{pmatrix}\) has full column rank \(n_x\).

Then, every weight vector \((\alpha ,\beta ,\gamma )\) that is a stationary point of

$$\begin{aligned} \frac{1}{2} \sum _{i=1}^N \Vert F(\tilde{z}(p_i),p_i) \Vert ^2 \end{aligned}$$

with respect to \((\alpha ,\beta ,\gamma )\) defines a mapping \(\tilde{z}(p)\) that satisfies \(F(\tilde{z}(p_i),p_i)=0\) for all \(i=1,\dots ,N,\) and thus \(\tilde{z}(p_i)\) is a KKT point for every \(i=1,\dots ,N\).

Proof

We follow the proof of Theorem 3.1. Considering an arbitrary index \(i \in \{1, \dots ,N\}\) and replacing \(\nabla _{xx}^2 L(\tilde{z}(p_i),p_i)=0\), we also obtain (8) and

$$\begin{aligned} \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))=0. \end{aligned}$$

Using this in (6), we get

$$\begin{aligned} 0&= \partial _{\tilde{z}} F(\tilde{z}(p_i),p_i)^\top F(\tilde{z}(p_i),p_i)\\ \nonumber&= \begin{pmatrix} 0 &{} \nabla _x h(\tilde{x}(p_i),p_i) &{} - \nabla _x g(\tilde{x}(p_i),p_i) D_g(-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))\\ J_x g(\tilde{x}(p_i),p_i) &{} 0 &{} D_\lambda (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i))\\ J_x h(\tilde{x}(p_i),p_i) &{} 0 &{} 0 \end{pmatrix} \cdot \\&\qquad \begin{pmatrix} \nabla _x L(\tilde{z}(p_i),p_i) \\ h(\tilde{x}(p_i),p_i) \\ \Phi (-g(\tilde{x}(p_i),p_i),\tilde{\lambda }(p_i)) \end{pmatrix}\\&= \begin{pmatrix} \nabla _x h(\tilde{x}(p_i),p_i) \cdot h(\tilde{x}(p_i),p_i) \\ \begin{pmatrix}J_x g(\tilde{x}(p_i),p_i) \\ J_x h(\tilde{x}(p_i),p_i) \end{pmatrix} \cdot \nabla _x L(\tilde{z}(p_i),p_i) \end{pmatrix}. \end{aligned}$$

Now, the full rank assumptions imply that

$$\begin{aligned} h(\tilde{x}(p_i),p_i)=0 \qquad \text {and} \qquad \nabla _x L(\tilde{z}(p_i),p_i)=0 \end{aligned}$$

for all \(i=1,\dots ,N\). Finally, the assertion of the theorem follows as in the proof of Theorem 3.1. \(\square \)

4 Error Estimate

In this section we will provide an error bound result showing that also for parameters \(p \in P \setminus \{p_1,\dots ,p_N\}\) we have a good approximation of the function z(p) through \(\tilde{z}(p)\).

Defining for \( y \in {\mathbb R}^n\) the component wise maximum function

$$\begin{aligned} (y)^+ :=\max \{ 0,y \}, \end{aligned}$$

and using [19, Theorem 5.1] we get the following Hölderian error bound.

Lemma 4.1

Let \(p \in P\) be fixed. Let f, g, h be analytic functions and the set of KKT points

$$\begin{aligned} S_p:=\{z =(x,\lambda ,\mu )\in {\mathbb R}^{n_x+n_g+n_h} \mid F(z,p)=0\} \end{aligned}$$

be nonempty. Then, for any compact set \(C \subset {\mathbb R}^{n_x} \times {\mathbb R}^{n_g}\times {\mathbb R}^{n_h}\) we have constants \(\tau _p >0\) and \(\delta _p >0\) such that

$$\begin{aligned} {{\,\textrm{dist}\,}}(z, S_p) \le \tau _p \, r(z,p)^{\delta _p} \qquad \forall z \in C, \end{aligned}$$

where

$$\begin{aligned} r(z,p):=\Vert \nabla _x L(z,p)\Vert + \Vert h(x,p)\Vert + \Vert (-\lambda )^+\Vert + \Vert (g(x,p))^+\Vert + |\lambda ^\top g(x,p) |. \end{aligned}$$

Assuming that the parameter set P is compact, no sequence of constants \(\{\tau _p\}\) or \(\{\delta _p\}\) for \(p \in P\) can be unbounded, since it must have an accumulation point. Hence, we can define on a compact set P constants independent of the parameter

$$\begin{aligned} \tau :=\max _{p \in P} \tau _p \qquad \text {and} \qquad \delta :=\max _{p \in P} \delta _p. \end{aligned}$$

Now slightly adapting [7, Lemma 3 and Lemma 4] for the Fischer–Burmeister function instead of the penalized Fischer–Burmeister function, we obtain

$$\begin{aligned} r(z,p) \le \Vert F(z,p)\Vert . \end{aligned}$$

Together, we now have the following error bound.

Lemma 4.2

Let P be compact, let f, g, h be analytic functions and the set of KKT points

$$\begin{aligned} S_p :=\{ z =(x,\lambda ,\mu )\in {\mathbb R}^{n_x+n_g+n_h} \mid F(z,p)=0 \} \end{aligned}$$

be nonempty. Then for any compact set \(C \subset {\mathbb R}^{n_x} \times {\mathbb R}^{n_g}\times {\mathbb R}^{n_h}\) we have constants \(\tau >0\) and \(\delta >0\) such that

$$\begin{aligned} {{\,\textrm{dist}\,}}(z, S_p) \le \tau \Vert F(z,p)\Vert ^{\delta } \qquad \forall z \in C. \end{aligned}$$

Applying this lemma yields that for any \(p \in P\) there is one KKT point z(p) such that

$$\begin{aligned} \Vert \tilde{z}(p) - z(p)\Vert = {{\,\textrm{dist}\,}}((\tilde{x}(p),\tilde{\lambda }(p),\tilde{\mu }(p)), S_p) \le \tau \Vert F(\tilde{z}(p),p)\Vert ^{\delta }. \end{aligned}$$

Hence, by reducing the value of \(\Vert F(\tilde{z}(p),p)\Vert \) we improve the approximation property of the function \(\tilde{z}(p)\). Thus, we have a cheap criterion (function evaluation of F) to check the approximation property and we do not need to solve the optimization problem (1) to do so. Then, if the error at a chosen new parameter is above a certain tolerance, we can include the parameter in the parameter test set and find a better approximation by computing a new interpolating function.

5 Numerical Results

In this Section, we test our approach numerically, considering examples drawn from parametric linear programming, multi-objective optimization, and optimal control. We will use the Fischer–Burmeister NCP-function and Gaussian radial basis functions, as defined in (2) and (4), respectively. Therein, we choose the constant

$$\begin{aligned} c = \frac{\sqrt{\ln (2)}}{\Delta p} > 0 , \end{aligned}$$

where \(\Delta p > 0\) is related to the distance between basis parameters. Selecting a uniform lattice for the basis parameters, this means that direct neighbors have an influence of 0.5 on each other. This heuristic value seems to yield good results in practice. Note, that the optimization problem is highly sensitive to the choice of this scaling parameter c. We solve the nonlinear least-squares problem (5) by invoking the MATLAB routine lsqnonlin, without providing the Jacobian of F.

Example 5.1

(LP) For the parametric linear program

$$\begin{aligned} \min _x \quad&(-100,-250) x&\text {s.t.}\quad&\begin{pmatrix} 1 &{} 1\\ 40&{}120 \\ 6 &{} 12 \\ -1 &{} 0\\ 0 &{} -1 \end{pmatrix} x \le \begin{pmatrix} 40 \\ 2400+p \\ 312 \\ 0 \\ 0 \end{pmatrix} , \end{aligned}$$

the solution is given by

$$\begin{aligned} x(p) = {\left\{ \begin{array}{ll} \begin{pmatrix} 0 \\ 26 \end{pmatrix} ,&{} \text {if}~720 \le p, \\ \begin{pmatrix} 36 - p/20 \\ 8 + p/40 \end{pmatrix} ,&{} \text {if}~160 \le p< 720, \\ \begin{pmatrix} 30 - p/80 \\ 10 + p/80 \end{pmatrix} ,&{} \text {if}~-800 \le p< 160, \\ \begin{pmatrix} 60 + p/40 \\ 0 \end{pmatrix} ,&{} \text {if}~-2400 \le p< -800, \\ \text {no solution} ,&{} \text {if}~p < -2400. \end{array}\right. } \end{aligned}$$

We consider parameters p in the interval \(P = [-2400, 2400]\), where the problem admits a solution. Further, we take the same \(K = N = 16\) test and basis parameters, equidistant distributed on P, and set \(\Delta p = 4800/(K-1) = 320\).

The optimization problem was successfully solved with high accuracy to the global minimum: the sum of squares reaches the value \(5.6 \cdot 10^{-17}\) after 23 iterations, taking approximately 0.7 seconds. Both the solutions x(p) and the multipliers \(\lambda (p)\) are well approximated, as one can see in Figure 2.

Let us stress again, that we solve only a single nonlinear least-squares problem with \(K (n_x + n_g)\) variables to obtain this solution; for the results depicted in Figure 2 this amounts to 112 variables. At the marked test parameters, the approximating function fits the exact solution. Although with some spurious oscillations, also the multipliers \(\lambda (p)\) are well approximated, despite their discontinuities. \(\diamond \)

Fig. 2
figure 2

Results for Example 5.1: exact solution (blue line), approximation (red line), basis and test points (red circles). The multiplier \(\lambda _5\) (omitted) is analogous to \(\lambda _4\).

Full size image

Example 5.2

(Pareto) Consider the nonlinear optimization problem:

$$\begin{aligned} \min _x \quad&p_1 \left( x_1^2 - x_1 x_2 - x_1 \right) + (1 - p_1) \left( x_2^2 - x_1 x_2/2 - 2 x_2 \right) \\ \text {s.t.}\quad&x_1 \ge 0 ,\quad x_2 \ge 0 ,\quad x_1 + x_2 \le p_2 . \end{aligned}$$

Here, parameters \(p_1\) and \(p_2\) affect the cost function and the constraints, respectively. We used a scalarization approach to reformulate a multi-objective optimization problem as a parameterized problem. For \(p_1 \in [0,1]\) we obtain all Pareto optimal points of the corresponding multi-objective optimization problem. Parameter \(p_2\) is an upper bound on the common constraint. The feasible set is nonempty whenever \(p_2 \ge 0\).

We consider parameters \(p_1 \in [0,1]\) and \(p_2 \in [0,5]\), where the problem always admits a solution. We take the same \(K = N = 12\) test and basis parameters from a uniform lattice, selecting 3 equidistant values for \(p_1\) and 4 for \(p_2\). Finally, we set \(\Delta p = 1\).

The optimization problem was successfully solved with high accuracy to the global minimum: the sum of squares reaches the value \(1.8 \cdot 10^{-16}\) after 20 iterations, taking approximately 0.3 seconds. The corresponding solutions x(p) are sampled on a grid in the parameter space and depicted in Figure 3 against the exact solution, obtained analytically. We can observe some deviations but the overall approximation is fairly satisfactory. \(\diamond \)

Fig. 3
figure 3

Results for Example 5.2: exact solution (surface) and approximation at sample parameters (red circles).

Full size image

Example 5.3

(Hanging chain) Consider the problem of finding the chain suspended between two points with minimal potential energy. The chain is inextensible and uniformly dense. We need to determine a function \(x_1 : [0,1] \rightarrow {\mathbb R}\) describing the chain profile. Various formulations of this problem are possible. We use the optimal control formulation from [6, §4], in terms of the horizontal coordinate s, the vertical coordinate \(x_1\), the control u, the partial potential energy \(x_2\) and the partial length \(x_3\):

$$\begin{aligned} \min _{x,u}\quad&x_2(1) \\ \text {s.t.}\quad&x_1^\prime (s) = u(s){} & {} s \in [0,1] \\&x_2^\prime (s) = x_1(s) \sqrt{1 + u^2(s)}{} & {} s \in [0,1] \\&x_3^\prime (s) = \sqrt{1 + u^2(s)}{} & {} s \in [0,1] \\&x_1(0) = x_2(0) = x_3(0) = 0 \\&x_1(1) = 1 + p_1 ,\quad x_3(1) = 2 + p_2 . \end{aligned}$$

Here, parameters \(p_1\) and \(p_2\) affect the end-point height and the chain length, respectively. The problem admits a solution if \(p_2 \ge \sqrt{p_1^2 + 2 p_1 + 2} - 2\).

A direct approach for optimal control problems consists in solving numerically the nonlinear program resulting from their full discretization. We consider \(\nu \in {\mathbb N}\) intervals of uniform size \(\Delta s = 1/\nu \), piecewise constant control approximation and adopt the trapezoidal rule for integration of the dynamics. Let \(f_k\) denote the finite difference approximation of function f(s) evaluated at \(s_k = k \Delta s\), \(k=0,\dots ,\nu \). Then, direct discretization yields the following nonlinear program:

$$\begin{aligned} \min _{x,u}\quad&x_{2,\nu } \\ \text {s.t.}\quad&x_{1,k+1} = x_{1,k} + \Delta s \; u_{k+\nicefrac {1}{2}}{} & {} k=0,\dots ,\nu -1 \\&x_{2,k+1} = x_{2,k} + \Delta s \; f_{2,k+\nicefrac {1}{2}}{} & {} k=0,\dots ,\nu -1 \\&x_{3,k+1} = x_{3,k} + \Delta s \sqrt{1 + u_{k+\nicefrac {1}{2}}^2}{} & {} k=0,\dots ,\nu -1 \\&x_{1,0} = x_{2,0} = x_{3,0} = 0 \\&x_{1,\nu } = 1 + p_1 ,\quad x_{3,\nu } = 2 + p_2 \end{aligned}$$

where

$$\begin{aligned} f_{2,k+\nicefrac {1}{2}}&:=\frac{x_{1,k} + x_{1,k+1}}{2} \sqrt{1 + u_{k+\nicefrac {1}{2}}^2}{} & {} k=0,\dots ,\nu -1 . \end{aligned}$$

This nonlinear program has the form of (1) with \(n_x = 4 \nu - 6\) decision variables, \(n_g = 0\) inequality and \(n_h = 3 \nu \) equality constraints. We consider \(\nu = 10\) discretization intervals and parameters \(p_1 \in [-0.25, 0.25]\) and \(p_2 \in [0, 1]\). We take the same \(K = N = 5\) test and basis parameters, drawn from a uniform random distribution over the parameter space, and set \(\Delta p = 5\).

The optimization problem was successfully solved with high accuracy to the global minimum: the sum of squares reaches the value \(8.6 \cdot 10^{-18}\) after 31 iterations, taking approximately 3.6 seconds. The corresponding solutions x(p) are visualized in Figure 4 and seem to yield a valid approximation. In particular, we notice the end-point constraints are satisfied in all cases. \(\diamond \)

Fig. 4
figure 4

Results for Example 5.3: approximate solutions \(x_1(p)\) and \(x_3(p)\), for 8 equidistant values of \(p_1\) and \(p_2 = 0\) (left) and for 8 equidistant values of \(p_2\) and \(p_1 = 0\) (right).

Full size image

6 Conclusion and Outlook

In this paper, we introduced a new approach for approximating parameter-dependent solutions of parametric optimization problems. The approximation is performed by a linear combination of basis functions, whose corresponding weights in the solution approximation can be found by minimizing a nonlinear least squares problem. It was shown that, under mild assumptions, a stationary point of this minimization problem fulfills the optimality conditions of the initial problem. In addition, we introduced an error estimate for a given parameter set. This estimate strongly depends on the corresponding residual, which allows us to monitor the approximation error for each parameter set. Therefore, a reduction of the approximation error can be obtained by including parameters with a high approximation error to the least squares problem during the optimization. We justified our theoretical results by some numerical examples, where we successfully found parameter-dependent solutions of a linear program, a nonlinear optimization problem and a discretized optimal control problem.

As mentioned in Section 3, non-existent or multiple KKT points can lead to problems in the training. Investigating these problems and finding avoidance strategies could become part of future works. An option could be to use online or offline re-training strategies whenever an inaccurate approximation is detected. Another possible extension of the underlying work could include numerical study of more involved optimization problems as well as different approximation strategies. A straightforward idea is to use artificial neural networks as a solution approximation, in particular one can exploit the idea of physics-informed neural networks [20], since it is based on a residual minimization and thus, fits into the approach presented in this paper. Moreover, possessing the result from Sect. 4, one could investigate an adaptive solution strategy, especially in case of high dimensional problems, in order to maintain the computational time close to real-time applications. One of such applications could be, e.g., the intersection management problem formulated in [10].