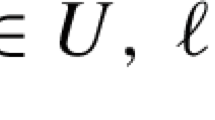1 Introduction

In recent years, tremendous progress has been made in developing algorithms for mixed-integer nonlinear optimization problems (MINLP). Nevertheless, they remain one of the most challenging optimization problems studied to date, and in particular, the global solution of even reasonably-sized instances can be out of reach. In addition, optimization problems are typically prone to uncertainties in the input data due to measurement errors, fluctuations or insufficient knowledge of the underlying applications’ characteristics. Ignoring these uncertainties might lead to decisions that are not only suboptimal but even infeasible.

In robust optimization, we typically first define uncertainty sets containing the realizations we wish to protect against. Decisions that are feasible for all realizations within the uncertainty sets are termed robust feasible and from these, the ones with the best objective value are called robust optimal. This results in an optimization problem of the form

$$\begin{aligned} \begin{aligned} \min _{x, y} \quad&C(x,y) \\ {{\,\mathrm{s.t.}\,}}\quad&V_{i}(x,y, u) \le 0 \quad \forall u\in \mathcal {U}, i\in \{1,\ldots ,n\}\\&x \in X , y \in Y \cap \mathbb {Z}^{n_y}, \end{aligned} \end{aligned}$$
(1)

with decision variables x, y and an uncertain parameter u. The task to determine the worst-case realization of the uncertainty for a candidate solution is called adversarial problem. For (1), this reads \(\max _{ u \in \mathcal {U}, i\in [n]}V_{i}(x,y, u)\). Although robust optimization problems are not tractable in general, practically efficient solution approaches have been developed for broad classes of problems, for example for robust combinatorial and for mixed-integer linear optimization. However, robust mixed-integer nonlinear problems are still very challenging both in theory and in practice, where the development of general approaches is still in its infancy. For a recent review of the current state-of-the-art, we refer to [26].

Reformulations of the robust counterparts to an algorithmically tractable problem rely on strong assumptions on the problem structure. In particular, it is usually necessary for such exact reformulation approaches to assume that the problem is convex in the decisions (x, y in (1)) and fulfills properties such as (hidden) concavity in the uncertainty (u in (1)) [6]. In the non-convex case, one may use a reformulation of a robust MINLP as polynomial optimization problem, which works if the contributing functions are polynomials and the uncertain parameters are contained in a semialgebraic set (see, e.g., [24, 25]). In this paper, we pursue a different direction. Rather than an exact reformulation approach or constraining functions to be polynomials, we choose a direct outer approximation approach. For this, we consider problems that are of convex type with respect to the decision variables (see Assumption 3.1). On the other hand, we allow for nonsmoothness, a general non-concave dependence on uncertainties and inexact worst case evaluations. Moreover, our only assumption for the uncertainty set is compactness.

Our approach then yields solutions that are robust feasible up to a tolerance and we consider both discrete and continuous decisions to be taken in the robust problem. The considered class of problems for example occurs in robust gas transport problems with discrete-continuous control decisions, nonlinear physical constraints and uncertainties in physics and demand.

In order to develop the algorithm, robust MINLPs are rewritten as nonsmooth MINLPs using an optimal value function of the adversarial problem. For an overview of state-of-the-art methods for nonsmooth MINLPs we refer to [13], where, among others, outer approximation approaches, extended level bundle methods and extended cutting plane methods are discussed. Our approach relies on the outer approximation concept to treat the nonsmooth MINLP. Outer approximation (OA) is an algorithm that is used for solving MINLPs in wide contexts. For an introduction and references, we refer to [17]. In the algorithm, a mixed-integer and typically linear master problem is solved to global optimality, as originally proposed in [10] and [14]. Iteratively, for fixed integral decisions, continuous subproblems are solved. Outer approximation for nonsmooth MINLP was first discussed in [12, 34, 35]. For the practical application of such a method, a concept for the solution of the arising nonsmooth subproblems is required. [9] suggests to use a proximal bundle method for the latter and demonstrates how appropriate cutting planes can be extracted at a solution.

Our Contribution Our approach follows the same lines, but we face an additional challenge: for a general non-convex adversarial problem, the determination of the worst case, which is required for the evaluation of the optimal value function, is itself not tractable in general. Thus, to achieve algorithmic tractability, we allow for inexact worst-case evaluations. In order to cope with this inexactness on the level of the subproblems, we modify an adaptive bundle method from [23], which was recently developed for the solution of nonlinear robust optimization problems with continuous variables. Due to the inexactness, in contrast to [9], we only have access to an outer approximation of the exact subdifferential. Nevertheless, we are able to show that cutting planes for the outer approximation can be extracted, which are valid up to a quantifiable error. With this, we are able to prove correctness and finite convergence of the OA method in the presence of inexactness. In detail, we are able to guarantee that the approximate solution determined by our OA algorithm is optimal up to a given tolerance. Moreover, the robust constraints are satisfied up to a tolerance, which is determined by the inexactness in the worst-case evaluation. The OA algorithm with the adaptive bundle method is outlined as a general algorithm independent from algorithmic details on the approximate solution of the adversarial problem. Here, we use piecewise linear relaxations of non-convexities and solve them via a mixed-integer linear optimizer. However, we point out that our approach can also be used with alternative methods that find an approximate worst case. To evaluate the performance of the novel algorithm, we specify it for the robust gas transport problem with discrete-continuous decisions. We demonstrate its efficiency by showing that our approach efficiently solves large realistic instances that could not be solved before.

We note that another avenue to treat inexactness in MINLP problems is described in [1], where an inexact version of a Benders’ decomposition is used. The combinatorial setting considered there allows for binary decisions and continuous subproblems are allowed to be solved inexactly by an oracle. In contrast to our method, finite convergence is ensured via no-good cuts. The oracle’s response then only has to result in valid inequalities that do not necessarily cut off the current iterate. Also for smooth MINLPs, alternative concepts exist, which can handle inexactness. Among them is the one in [27], where approximately fulfilled optimality conditions for the subproblems are required.

Structure This work is structured as follows. Although the presented algorithm is fully general, we prefer to start with an example application that falls into the considered class of problems in order to ease understanding of the subsequently introduced technical considerations. Thus, in Sect. 2, we briefly introduce the robust gas transport problem. In Sect. 3, we then derive the general setting of a nonsmooth MINLP that models a robust MINLP and present the framework of an OA method for this. The adaptive bundle method for continuous subproblems and resulting optimality conditions are presented in Sect. 4. In Sect. 5, we derive an OA algorithm that can deal with inexactness in function values, subgradients, and hence cutting planes obtained from subproblem solutions. The type of inexactness thereby matches our results for the bundle method’s output. We also prove convergence of the OA algorithm. Finally, we present and discuss computational results for the gas transport problem in Sect. 6.

2 An Example Application for the Class of Problems Studied Here

We consider the stationary discrete-continuous gas transport problem, see [21], under uncertainties. A decomposition approach for the continuous robust two-stage gas transport problem is presented in [3] and a set containment approach for deciding robust feasibility of this problem is proposed in [4].

In this problem, we aim to find a control of active elements, such as compressors, valves or control valves, that minimizes the costs while ensuring that all demands are satisfied and that no technical or physical constraints are violated. Feasibility needs to be maintained even under uncertainties in demand and pressure loss coefficients.

A gas network is modeled by a directed graph \(\mathcal {G}= (\mathcal {V}, {\mathcal {A}})\) with \(\vert \mathcal {V}\vert = n\), \(\vert {\mathcal {A}}\vert = m\) and an incidence matrix \({A}\in \{-1,0,1\}^{n\times m}\). The arcs model pipes, compressors and valves. A state variable \(q\in \mathbb {R}^m\) denotes the gas flow, \(d\in \mathbb {R}^n\) denotes the given balanced demand and flow conservation must hold: \(A q = d\). Squared pressure values at the nodes are denoted by \(\pi \in \mathbb {R}^n\) and must fulfill bounds. For one root node \(r\in \mathcal {V}\), the pressure value is assumed to be fixed. The pressure change at compressors is associated with a convex and differentiable cost function \(w(\cdot )\), which is to be minimized.

The pressure loss on an arc \(a\in {\mathcal {A}}\), i.e., the difference between squared pressures at connected nodes depends on the type of arc and we distinguish between pipes and compressors. The pressure losses on pipes depend on the flow values and directions as well as on pressure loss coefficients \(\lambda _a>0\). In detail, we have for every pipe \(a=(u, v)\) the non-convex behavior [21]

$$\begin{aligned} \pi _v - \pi _u = - \lambda _a q_a \vert q_a \vert . \end{aligned}$$
(2)

For compressors, we use a linear compressor model where a pressure loss is assigned to every compressor \(a\in {\mathcal {A}}\) and depends on continuous and binary decision variables, x and y, respectively. The binary variables y determine if a compressor is active and the continuous variables x determine the pressure increase at active compressors. The pressure loss at every active compressor \(a=(u, v)\) is then evaluated as

$$\begin{aligned} \pi _v - \pi _u = x\cdot y, \end{aligned}$$
(3)

which leads to a non-convex cost function \(w(x\cdot y)\). Compressors in bypass mode and open valves both behave like pipes with no pressure loss. We have further binary decisions y on the opening of valves.

We robustly protect against uncertainties in demand and pressure loss coefficients that are contained in a compact uncertainty set, i.e., \((d, \lambda )\in \mathcal {U}\). After uncertain parameters d and \(\lambda \) are realized, the second-stage state variables q and \(\pi \) uniquely adjust themselves by fulfilling flow conservation and the pressure loss constraints (2)–(3). We require that the pressure values are bounded both from above and from below by \(\pi \in [{\underline{\pi }}, {\overline{\pi }}]\). Further, we can write the pressure values, due to their uniqueness, as a function of the decision variables (x, y) and the uncertain parameters \((d,\lambda )\). This results in the following discrete-continuous robust gas transport problem.

figure a

The function \(\pi _v(\cdot )\) can be evaluated by solving a system of nonlinear and non-convex equations that involve, e.g., (2). This formulation relies on reformulation results in [3, 16]. Now, with

$$\begin{aligned} V_v\big (x,y, (d,\lambda )\big ):=\max \Big \{ {\underline{\pi }}_v - \pi _v( x,y; d, \lambda ), \pi _v( x,y; d, \lambda ) - {\overline{\pi }}_v\Big \}, \end{aligned}$$
(4)

we can rewrite the robust constraints via one constraint by

$$\begin{aligned} \begin{aligned} G(x,y) =&\max _{(d, \lambda ) \in \mathcal {U}} \sum _{v\in \mathcal {V}} V_v^+\big (x,y, (d,\lambda )\big ) \le 0, \end{aligned} \end{aligned}$$
(5)

where the superscript ‘\(+\)’ denotes the positive part. With this, we write the discrete-continuous robust gas transport problem in (\(P_{gas}\)) as

figure b

For the case that no compressor is part of a cycle, it turns out that the constraint function G is convex with respect to the continuous variable x. We refer to [2] for a discussion of the appropriateness of this assumption.

Lemma 2.1

Under the assumption that no compressor is part of a cycle, the function G(x, y) is convex in x.

This lemma follows from the analysis in [3] and we omit the proof here.

We have outlined this example application already here in order to ease understanding of the subsequent sections where the general class of discrete-continuous robust nonlinear problems is defined and where we present the novel OA algorithm that is able to solve them.

3 Outer Approximation for Mixed-Integer Nonlinear Robust Optimization

We write a robust optimization problem with a compact uncertainty set \(\mathcal {U}\subseteq {\mathbb {R}}^{n_u}\) as

$$\begin{aligned} \begin{aligned} \min _{x, y} \quad&C(x,y) \\ {{\,\mathrm{s.t.}\,}}\quad&V_{i}(x,y, u) \le 0 \quad \forall u\in \mathcal {U}, i\in \{1,\ldots ,n\}\\&x \in X , y \in Y \cap \mathbb {Z}^{n_y}. \end{aligned} \end{aligned}$$
(6)

The variables have dimensions \(n_x\) and \(n_y\), respectively. We have that X is a full-dimensional box of form \(X = [{\underline{x}}, {\overline{x}}]\subseteq \mathbb {R}^{n_x}\) and that Y is compact. Moreover, the objective function \(C:{\mathbb {R}}^{n_x+ n_y}\rightarrow {\mathbb {R}}\) and the constraint functions \(V_i:{\mathbb {R}}^{n_x+ n_y + n_u}\rightarrow {\mathbb {R}}\) are locally Lipschitz continuous and satisfy the following convexity-type assumption.

Assumption 3.1

The functions \(C(\cdot , \cdot )\) and \(V_{i}(\cdot , \cdot , u)\), for every \(u\in \mathcal {U}\), \(i\in [n]\), fulfill the following generalized convexity assumption when denoted by f. The function \(f: X \times Y \cap \mathbb {Z}^{n_y} \rightarrow {\mathbb {R}}\) is convex with respect to x and it is true that for any pair \(({x}, {y}) \in X \times Y \cap \mathbb {Z}^{n_y}\), there exists a joint subgradient \((s^{x}, s^{y})\) such that the following subgradient inequality is satisfied:

$$\begin{aligned} f(x, y) + \begin{pmatrix} s^{x}\\ s^{y} \end{pmatrix}^T \begin{pmatrix} {\bar{x}} - x\\ {\bar{y}} - y \end{pmatrix} \le f({\bar{x}}, {\bar{y}}) \quad \forall ({\bar{x}}, {\bar{y}}) \in X \times Y \cap \mathbb {Z}^{n_y}. \end{aligned}$$
(7)

A sufficient condition for this assumption is joint convexity of the function f on \(X \times Y\). The other way round, our assumption only implies convexity in the continuous variable x. It is worth mentioning that, when we rely on Assumption 3.1, we have to make sure that all subgradients we use indeed satisfy inequality (7), while this is automatically true if convexity is assumed. More generally, it also suffices to specify how to derive subgradients that fulfill (7). This covers the setting of the gas transport, in which the functions are convex in the continuous decisions (see Lemma 2.1) and, despite a lack of convexity (see (3)), one can derive subgradients with respect to the binary decisions that fulfill (7). Further, here, we do not require convexity or concavity in the uncertain parameter u. This hence covers the gas transport setting with the non-convex dependence of pressure values on the uncertain parameters. Now, we reformulate the robust optimization problem (6) as a nonsmooth MINLP with finitely many constraints using the nonsmooth function

$$\begin{aligned} G(x,y):=\max _{u\in \mathcal {U}} V(x,y,u) :=\max _{u\in \mathcal {U}} \sum _{i=1}^n V_i^+(x,y,u) \end{aligned}$$

as a constraint function. We obtain

figure c

We note that the assumed generalized convexity of the functions \(V_i(x, y, u)\) directly carries over to \(G\). To evaluate \(G\), it is necessary to solve an adversarial problem that determines a worst-case parameter maximizing the constraint violation. To make this concept clear, we mention that in the robust gas transport problem, the adversarial problem, i.e., to evaluate the function \(G\) in (4)–(5), is to find for fixed control decisions a realization of demand and physical parameters that maximizes the violation of pressure bounds.

The goal is to solve the MINLP (P) via an outer approximation approach. We sketch the general framework of an OA method for (P) here by closely following [14, 35]. In an OA method, a master problem and a subproblem are solved in every iteration. The master problem is a mixed-integer linear problem (MIP) that is a relaxation of the original problem (P). Solving an MIP is in general NP-hard. However, many algorithmic enhancements were developed so that MIPs can typically be solved to global optimality by modern available solvers, even for large instances (see, e.g., [7]). The linear relaxation of the original problem (P) in iteration \(K\) is the master problem:

figure d

where \(\Theta ^K\in {\mathbb {R}}\) denotes the objective value of the current best known solution and \(\epsilon _{oa}>0\) is a previously fixed optimality tolerance as typically used in an OA method (e.g., by [14]). We detail below the linearized constraints, which are generated via function values and subgradients. After termination, one has detected infeasibility or has found a feasible \(\epsilon _{oa}\)-optimal solution. By \(\epsilon _{oa}\)-optimality, we mean that the objective value deviates from the optimal objective value by at most \(\epsilon _{oa}\).

Every OA iteration involves the solution of a subproblem where all integer variables are fixed and one determines best values only for the continuous variables. However, the subproblems are nonlinear. The solution of a subproblem, i.e., the resulting mixed-integer candidate solution, is then used to generate linearized constraints that are valid for all feasible solutions of the original problem (P) that still need to be considered. These constraints act as cutting planes that are added to the master problem (\(MP^{K}\)) and strengthen the relaxation of (P). Further, they are chosen such that every feasible integer assignment is visited only once, so that the OA method converges finitely with a global \(\epsilon _{oa}\)-optimal solution to the original MINLP.

In each iteration, one candidate integer solution from the feasible set Y is fixed. For this fixed integer assignment, we solve a subproblem. This is either a continuous subproblem of (P) or, in the case of its infeasibility, a so-called feasibility problem that minimizes the violation of constraints. For a fixed integer assignment \({y_{K}}\), the continuous subproblem is

figure e

If the continuous subproblem is infeasible, we solve the feasibility problem, which minimizes the violation of the constraint \(G(x,y) \le 0\) and is written as

figure f

Next, we detail the linearized constraints, i.e., the cutting planes in the master problem (\(MP^{K}\)). We first split the set of integer points in Y into two sets, depending on whether the corresponding continuous subproblem is feasible or not:

$$\begin{aligned}&T = \{y\in Y\cap \mathbb {Z}^{n_y}\mid (NLP(y_{K}))\text { is feasible}\}, \\&S = \{y\in Y\cap \mathbb {Z}^{n_y}\mid (NLP(y_{K}))\text { is infeasible}\}. \end{aligned}$$

In the course of an OA algorithm, we collect the investigated integer points in subsets \(T^K\subseteq T\), \(S^K\subseteq S\). For fixed \({y_{K}}\), we denote by \({x_{K}}\) a continuous solution to (\(NLP(y_{K})\)) or (\(F(y_{K})\)). To strengthen the relaxation of the master problem, we collect linearizations at the mixed-integer candidate solutions \(({x_{K}}, {y_{K}})\). In detail, we approximate the functions C and G (or only G in the case of infeasibility) by linearizations generated by function values and subgradients, \((\alpha _K, \beta _K)\), \((\xi _K, \eta _K)\), evaluated at \(({x_{K}}, {y_{K}})\). In an iteration \(K\), the linearized constraints (i.e., the constraints in (\(MP^{K}\))) are of the form

$$\begin{aligned} \begin{aligned}&C(x_J, y_J) + (\alpha _J^T, \beta _J^T) \begin{pmatrix} x - x_J\\ y - y_J\end{pmatrix} \le \theta \qquad \qquad \! \forall y_J\in T^{K}\\&G(x_J, y_J) + (\xi _J^T, \eta _J^T) \begin{pmatrix} x - x_J\\ y - y_J\end{pmatrix} \le 0 \qquad \qquad \forall y_J\in T^{K}\\&G(x_L, y_L) + (\xi _L^T, \eta _L^T) \begin{pmatrix} x - x_L\\ y - y_L\end{pmatrix} \le 0 \qquad \qquad \forall y_L\in S^{K}. \end{aligned} \end{aligned}$$
(8)

These cutting planes are then added to the master problem. To avoid cutting off an optimal solution to the original problem (P), the cutting planes must be valid in the following sense: they cut off a point only if it is infeasible or does not improve the current best objective value by more than \(\epsilon _{oa}\). Further, to ensure finite convergence of the algorithm, the cutting planes must cut off the current assignment of integer variables. To ensure this and hence correctness of an OA method, one usually requires in a nonsmooth setting that the function values and subgradients fulfill KKT conditions of the subproblem and therefore assumes that Slater’s condition holds (see, e.g., [9, 35]). We proceed similarly and also assume that Slater’s condition holds in the following form.

Assumption 3.2

If (\(NLP(y_{K})\)) is feasible, then there is an \(x\in int(X)\) with \(V_i(x,y_K,u) <0~ \forall u\in \mathcal {U}, i\in [n]\).

To illustrate this assumption, we briefly concretize it for the gas transport problem from the preceding section: there, we require that for every possible realization of the uncertain parameters, i.e., demand and pressure loss coefficients, there exists a control of the active elements such that all pressure bounds are strictly fulfilled, i.e., \(\pi \in ({\underline{\pi }}, {\overline{\pi }})\).

In the presented setting, the solution of the subproblems (\(NLP(y_{K})\)) and (\(F(y_{K})\)) is a challenging task that is not accessible by standard methods. In particular, we face non-concavities in the uncertain parameters so that the constraint function G, i.e., the adversarial problem \(G(x,y)=\max _{u \in \mathcal {U}} V(x, y, u)\) for given x, y, may be only approximately evaluable. In the next section, we investigate which properties can be ensured for solutions to the subproblems in the presence of such inexact worst-case evaluations.

4 An Adaptive Bundle Method for the Continuous Subproblems

To solve continuous nonsmooth optimization problems, bundle methods are a practically efficient approach. As the latter are usually applied in an unconstrained setting, we write the subproblems as unconstrained problems and penalize constraint violation in the objective. Instead of (\(NLP(y_{K})\)), we aim to solve the following unconstrained problem with an \(l_1\)-penalty term \(P_X(x) = \sum _{i=1}^{n_x} \max \{0,x_i - {\overline{x}}, {\underline{x}} - x_i\}\) and sufficiently large penalty parameters \(\psi , \psi _X>0\):

figure g

The existence of finite penalty parameters is ensured by Assumption 3.2. In particular, it ensures the existence of finite penalty parameters such that a point \({x_{K}}\) solves (\(NLP_{\psi }({y_{K}})\)) if and only if it solves (\(NLP(y_{K})\)). This can be seen by using, e.g., [33, Theorem 7.21] and we omit the details here. To treat (\(F(y_{K})\)), we also use a penalty formulation with a sufficiently large penalty parameter \(\psi _X\):

figure h

In practice, we simply choose certain penalty parameters \(\psi , \psi _X\) at the beginning, which are then increased if required (see end of this section). We present in this section an algorithm for the approximate solution of the penalized subproblems. We first write the objective functions in the abstract form

$$\begin{aligned} \min _{x \in \mathbb {R}^{n_x}} f(x) = \min _{x \in \mathbb {R}^{n_x}} \max _{ u \in \mathcal {U}} v(x,u), \end{aligned}$$
(9)

where

$$\begin{aligned} f(x){} & {} = C(x, {y_{K}}) + \psi G(x, {y_{K}}) + \psi _{X} P_X(x), \\ v(x, u){} & {} = C(x, {y_{K}}) + \psi V(x, {y_{K}}, u) + \psi _{X} P_X(x). \end{aligned}$$

For the feasibility problem (\(F_{\psi }({y_{K}})\)), we set \(C\equiv 0\) and \(\psi =1\), so that no separate discussion is required. We further note that the integer variable \({y_{K}}\) is fixed during the solution of a subproblem, so that we largely omit it in the remainder of this section.

Due to the unconstrained and nonsmooth character of (9), in principal a proximal bundle type method can be applied for its solution. However, as (9) is solved in the context of an outer approximation scheme, not only an (approximate) solution \(x_K\) of (9) is required, but also cutting planes in the sense of (8) have to be extracted. While in a continuously differentiable setting, appropriate cutting planes can be determined a posteriori by computing the gradients of the objective and constraints at the solution \(x_K\), in a nonsmooth setting, the situation is more involved. Roughly speaking, the reason is that the subgradients at the solution \(x_K\) are not unique and one has to choose them such that they fulfill first-order optimality conditions. To overcome this, suitable sequences of subgradients have to be constructed while the bundle algorithm is carried out. This is demonstrated in [9] using an exact penalization proximal bundle algorithm. While in principle the same idea can be applied to our setting, we are facing the additional difficulty that every evaluation of the function f requires the solution of the adversarial problem

$$\begin{aligned} \max _{ u \in \mathcal {U}} V(x,y,u). \end{aligned}$$
(10)

This is in general a hard problem if the constraint functions \(V_i\) are non-concave in the uncertain parameter u as in the robust gas transport problem from Sect. 2. Thus, we follow [23] and use in the following the relaxed assumption that problem (10) can only be solved with a prescribed finite precision \(\epsilon _f > 0\). This means that there is an oracle, which provides for every given x and \(\epsilon _f\) an approximate worst case

$$\begin{aligned} {u_{x}}\in \{ {u_{x}}\in \mathcal {U}\mid v(x,{u_{x}})\ge \max _{u\in \mathcal {U}} v(x,u) -\epsilon _f \}, \end{aligned}$$
(11)

so that \({v}(x,{u_{x}})\ge f(x)-\epsilon _f\). Using this, we can define an overestimator for f as

$$\begin{aligned} f_a(x):={v}(x,{u_{x}})+\epsilon _f. \end{aligned}$$
(12)

Furthermore, as a consequence of the inexactness, instead of an element from the exact Clarke subdifferential of f at x, the best we can hope for is the following approximate subgradient of f (see [23]).

$$\begin{aligned} g_{x}\in \partial _x v(x, u_x). \end{aligned}$$

This is an element of the Clarke subdifferential of \(v(\cdot , {u_{x}})\) with \({u_{x}}\) defined by the choice in (11). This approximate subgradient lies in the following set, which is the convex hull that contains \(\partial _x v(x, u_x)\) and the subdifferentials for all uncertain parameters that better approximate the worst case.

$$\begin{aligned} \tilde{\partial }_{a}{f}({x}):=\text {conv}\{g\mid g\in \partial _x v(x,u), u\in \mathcal {U}, \, v(x,u)\ge v(x,{u_{x}})\}. \end{aligned}$$
(13)

This set can be interpreted as an outer approximation of the exact Clarke subdifferential at x. In [23], an adaptive proximal bundle method is suggested for this setting. This algorithm—as most bundle methods—generates a sequence of serious and trial iterates. The serious iterates form a sequence, which approach an approximate solution of (9). For each serious iterate, one generates a sequence of trial iterates that improve the local approximation of f around the serious iterate by information about function values and subgradients. The algorithm is able to work with elements from the approximate subdifferential (13) if the error in (12) is chosen as follows: given a current trial iterate \(x^k\) (with inner loop counter k) and current serious iterate x, the error bound \(\epsilon _f^k\) for \(f_a(x^k)\) is set to

$$\begin{aligned} {\epsilon _f^{k}} =\epsilon '' \Vert x-x^k\Vert ^2. \end{aligned}$$
(14)

Here, \(\epsilon ''\) is a previously chosen algorithmic parameter. For this, the following convergence result is derived in [23].

Corollary 4.1

[23, Corollaries 2, 3, 4] Let \(x_1\) be such that \(\Omega :=\{x\in \mathbb {R}^{n_x}{:} f(x)\le f_a(x_1)\}\) is bounded and let f be lower \(C^1\). Let us use [23, Algorithm 1] with a stopping tolerance \(\tilde{\epsilon }=0\) in line 3 there. Then two different situations can occur:

  1. (1)

    The algorithm stops with a serious iterate \(x_j\) after finitely many iterations. Then we set \({\bar{x}}:=x_j\).

  2. (2)

    All inner loops terminate finitely, but the outer loop does not terminate finitely. In this case, the sequence of serious iterates \(x_j\) has at least one accumulation point; we denote this by \({\bar{x}}\).

In either of the cases, it holds that \( 0\in \tilde{\partial }_{a}{f}({{\bar{x}}}). \)

Now, applying the adaptive bundle method to problem (9) for an approximate solution \(x_K\), we obtain \(0\in \tilde{\partial }_{a}{f}({x_K})\) or—exploiting the structure of f—\(0\in \tilde{\partial }_{a}{(C+ \psi G + \psi _{X} P_X)}({x_K}).\) Given that \(C\) and \(P_X\) do not depend on u and by exploiting the convexity of \(C, G\) and \(P_X\) with respect to x, this can be rewritten as

$$\begin{aligned} 0\in \partial C(x_K) + \psi \tilde{\partial }_{a}{G}({x_K}) + \psi _{X} \partial {P_X}({x_K}). \end{aligned}$$
(15)

The challenge for the remainder of this section is now to construct elements \({\alpha } \in \partial C({x_{K}})\), \(\tilde{\xi } \in \tilde{\partial }_{a}{G}({{x_{K}}})\) and \(\zeta \in \partial P_X({x_{K}})\), such that

$$\begin{aligned} {\alpha } + \psi \tilde{\xi } + \psi _{X} \zeta = 0, \end{aligned}$$
(16)

i.e., to construct suitable (approximate) subgradients of \( C\), \(G\) and \(P_X\) that realize the optimality condition (15). It will turn out later that \(\alpha \) and \(\tilde{\xi }\) can then be used to construct cutting planes in the sense of (8). As already outlined above, such realizations cannot be computed solely on the basis of the knowledge of \(x_K\). Rather than this, a deeper insight into the algorithm from [23] and a couple of modifications, which we outline in the sequel, are required. The full modified algorithm is detailed in Algorithm 2 in Appendix A. We first require that whenever in Algorithm 2 an approximate subgradient of f at a point x is evaluated, it is computed as

$$\begin{aligned} g_x = s_{C}^{x} + \psi s_{G}^{x} + \psi _X s_X^{x}, \end{aligned}$$
(17)

where \(s_{C}^{x} \in \partial C(x), s_{G}^{x} \in \partial _x V(x, u_x), s_X^{x} \in \partial P_X(x)\), and \(u_x\) is an approximate worst case in the sense of (11). This is realized in lines 20-21 of Algorithm 2.

Next, we make use of the so-called aggregate subgradient, which—together with (17)—will be the key for deriving \(\alpha \) and \(\tilde{\xi }\) in (16) and played already a crucial role in the convergence proof in [23]. To introduce this, we repeat the definition of the convex working model used in [23]. This is, at a serious iterate x, the piecewise linear function

$$\begin{aligned} \phi _{k}(\cdot , x):=\max \{m_l(\cdot , x)\mid 0\le l \le k-1\}. \end{aligned}$$

Here, \(m_l(\cdot , x)\) are cutting planes that are generated using approximate function values and subgradients. More precisely,

$$\begin{aligned} m_0(\cdot , x):=f_a(x)+{g_{x}}^T (\cdot -x), \end{aligned}$$

with \({g_{x}}\in \partial _x v(x,u_x)\), is a so-called exactness plane at the serious iterate x, and

$$\begin{aligned} m_l(\cdot , x):=t_l(\cdot ) -{r_{l}}, \ l=1,\ldots ,k-1 \end{aligned}$$

are cutting planes at trial iterates \(x^l\), where \(t_l(\cdot )\) is the tangent plane at \(x^l\) and \({r_{l}}\) a downshift with respect to the serious iterate x. Then, in every iteration the following convex problem is solved in order to generate a new trial iterate \(x^k\).

$$\begin{aligned} \min _{z\in \mathbb {R}^{n_x}} \phi _k(z,x) + (z-x)^\top Q_x (z-x)+ \frac{\tau _k}{2}\Vert z-x\Vert ^2. \end{aligned}$$
(18)

Here, \(\tau _k > 0\) is a proximity control parameter and \(Q_x\) a symmetric matrix, which can be used to model second-order information. Now the aggregate subgradient \({g^*_{k}}\) is defined as

$$\begin{aligned} {g^*_{k}} = (Q_x + \tau _k\mathcal {I})(x-x^k). \end{aligned}$$

As \(x^k\) is the unique minimizer of (18), \({g^*_{k}}\) is a subgradient of the current working model, i.e., \({g^*_{k}} \in \partial \phi _k(x^k, x)\).

Now, we carry out the following three steps: First, we see that \({g^*_{k}}\) tends to 0 along a suitable subsequence. The claim is detailed in Lemma 4.1. We omit its proof as the latter is a straight-forward combination of arguments from the convergence analysis in [23]. Based on this, we introduce a stopping criterion for the bundle method. Second, we show that every \({g^*_{k}}\) can be split according to the partition in (17) and construct the output of the bundle method. Third, we prove in Theorem 4.1 that the limits of the individual parts of \({g^*_{k}}\) satisfy the optimality condition (16). This implies that the modified bundle method, with the proposed stopping criterion and output, generates subgradients that fulfill the optimality condition (16).

Lemma 4.1

[23, proofs of Lemma 6, Theorem 1, Corollaries 3, 4]; [28, proofs of Lemma 4, 7] We use the same assumptions as in Corollary 4.1 and use [23, Algorithm 1] without any stopping criterion. Then one of the following situations occur:

  1. (1)

    The inner loop at a serious iterate x does not terminate finitely. Then \(x^k\rightarrow x\), and there is a subsequence of the inner loop indices k such that \(\phi _k(x^k, x)\rightarrow f_a(x)\), and \({g^*_{k}}\rightarrow 0 \in \tilde{\partial }_{a}{f}({{x}})\).

  2. (2)

    All inner loops terminate finitely, but the outer loop does not terminate finitely. The sequence of all trial and serious iterates is bounded and there is a choice of pairs of outer and inner loop indices (j, k(j)) and a subsequence of the outer loop indices j such that \(x_j\rightarrow {\bar{x}}\), \(x^{k(j)}\rightarrow {\bar{x}}\), \(\phi _{k(j)}(x^{k(j)}, x_j) \rightarrow f_a({\bar{x}})\) and \({g^*_{k(j)}}\rightarrow 0\in \tilde{\partial }_{a}{f}({{\bar{x}}})\).

Now, in order to make sure that we stop the proximal bundle algorithm at a point, where the aggregate subgradient is small, we apply the following modification: rather than using the abstract convergence criterion \(0\in \tilde{\partial }_{a}{f}({x})\), we apply the criterion \(\Vert {g^*_{k}} \Vert \le \epsilon ^*\) with a tolerance \(\epsilon ^*= 0\) (see Algorithm 2, line 8). Hence, in the cases in which the bundle algorithm does not terminate finitely, we have a sequence of aggregate subgradients that converges to \(g^*=0 \in \tilde{\partial }_{a}{f}({{\bar{x}}})\). In the case of finite termination, we find \({g^*_{k}}=0\) for a finite k.

Next we derive a partition of an aggregate subgradient \({g^*_{k}}\), which is analogous to the partition by which subgradients were derived in (17). In order to do so, we first denote the subgradients at former trial iterates \(x^l\) by \(g_l\), so that \(g_l \in \tilde{\partial }_{a}{f}({x^l})\), and elements of the exactness plane via the index \(l=0\). As \(\phi _k(\cdot , x)\) is convex and piecewise affine linear with slopes \(g_l\), the aggregate subgradient \({g^*_{k}} \in \partial \phi _k(x^k, x)\) is a convex combination of subgradients \(g_l\) with \(l<k\):

$$\begin{aligned} {g^*_{k}} = \sum _{l=0}^{k-1} \lambda ^k_l g_l, \quad \sum _{l=0}^{k-1} \lambda _l^k = 1. \end{aligned}$$
(19)

Further, \(\lambda _l^k >0\) for an \(l \in \{0,\ldots ,k-1\}\) only if \(m_l(x^k, x) = \phi _k(x^k, x)\). As in the course of the former bundle iterations, \(g_l \in \tilde{\partial }_{a}{f}({x_l})\) with \(l<k\) has been computed via (17), we have the following partitions.

$$\begin{aligned} g_l = s_{C}^{l} + \psi s_{G}^l + \psi _X s_X^{l},\quad s_{C}^{l} \in \partial _{x} C(x^l), s_{G}^l \in \tilde{\partial }_{a}{G}({x^l}), s_X^{l} \in \partial P_X(x^l). \end{aligned}$$
(20)

Accordingly, we define, denoting by j the outer loop counter of the current serious iterate x,

$$\begin{aligned} \begin{aligned}&\alpha _j^k = \sum _{l=0}^{k-1} \lambda _l^{k} s_{C}^{l},\qquad \tilde{\xi }_j^k = \sum _{l=0}^{k-1} \lambda _l^{k} s_{G}^l, \qquad {\zeta }_j^k= \sum _{l=0}^{k-1} \lambda _l^{k} s_{G}^l. \end{aligned} \end{aligned}$$
(21)

We note that the weights \(\lambda _l^k , l \in \{0,\ldots ,k-1\}\) can be computed by solving a linear system of equations in line 11 of Algorithm 2.

In practice, we choose a \(\epsilon ^*>0\) and stop the bundle method as soon as \(\Vert {g^*_{k}}\Vert \) is sufficiently small at an iteration k with a solution \({x_{K}}= x^{k}\). As subgradients for the current iteration \(K\) of the outer approximation algorithm, we then choose

$$\begin{aligned} \begin{aligned}&\alpha _{{K}} = \alpha _j^k,\quad \tilde{\xi }_{{K}} = \tilde{\xi }_j^k. \end{aligned} \end{aligned}$$
(22)

In Theorem 4.1, we finally formalize and justify this choice from a theoretical perspective, i.e., for \(\epsilon ^*=0\). In detail, we show that the choice (22) is correct in the sense of the optimality condition (16) if we have \(\Vert {g^*_{k}}\Vert = 0\) for a finite k. Moreover, we prove that in all cases where the algorithm does not finitely converge, we can define a suitable limit of (22) instead. We distinguish the following three cases of output of the bundle method.

(1) In the case that the algorithm converges finitely within an inner loop at a serious iterate \(x_j\) with \(\Vert {g^*_{k}}\Vert = 0\), we choose

$$\begin{aligned} x_K{} & {} = x_j, \; \epsilon _G^{K} = {\epsilon _f^{x_j}}, \; \tilde{G}(x_K, y_K)= V(x_j, y_K, u_{x_j}), \nonumber \\ \alpha _K{} & {} = \alpha _j^k, \; \tilde{\xi }_K= \tilde{\xi }_j^k, \; \zeta _K= \zeta _j^k. \end{aligned}$$
(23)

(2) In the case that the algorithm converges with infinitely many iterations in an inner loop at a serious iterate \(x_j\), we choose a subsequence of iterates k as in Lemma 4.1, (1), and set

$$\begin{aligned} \begin{aligned}&x_K= x_j, \quad \epsilon _G^{K} = {\epsilon _f^{x_j}}, \quad \tilde{G}(x_K, y_K)= V(x_j, y_K, u_{x_j}),\\&\alpha _K= \lim _{k\rightarrow \infty } \alpha _j^k, \quad \tilde{\xi }_K= \lim _{k\rightarrow \infty } \tilde{\xi }_j^k, \quad \zeta _K= \lim _{k\rightarrow \infty } \zeta _j^k. \end{aligned} \end{aligned}$$
(24)

(3) In the case that the algorithm does not converge in an inner loop, we choose a cluster point of the serious iterates as a solution. We choose a cluster point \({\bar{x}}\) and a sequence of indices k(j) as in Lemma 4.1, (2):

$$\begin{aligned} \begin{aligned}&x_K= {\bar{x}}, \quad \epsilon _G^{K} = 0, \quad \tilde{G}(x_K, y_K)= \lim _{j\rightarrow \infty }V(x_j, y_K, u_{x_j}),\\&\alpha _K= \lim _{j\rightarrow \infty } \alpha _j^{k(j)}, \quad \tilde{\xi }_K= \lim _{j\rightarrow \infty } \tilde{\xi }_j^{k(j)}, \quad \zeta _K= \lim _{j\rightarrow \infty } \zeta _j^{k(j)}. \end{aligned} \end{aligned}$$
(25)

It is noted that in (1) and (2) above, \( {\epsilon _f^{x_j}}\) denotes the error, which was required to compute the serious iterate \(x_j\) (see (14)). The choices in (23), (24) and (25) are justified by the following result.

Theorem 4.1

The adaptive bundle method with subgradient generation in Algorithm 2 with \(\epsilon ^*=0\), with (23), (24) and (25) as output, and under the assumptions as in Corollary 4.1, generates subgradients \({\alpha }_K \in \partial C(x_K)\), \(\tilde{\xi }_K \in \tilde{\partial }_{a}{G}({x_K})\) and \(\zeta _K \in \partial P_X(x_K)\) with \({\alpha }_K + \psi \tilde{\xi }_K + \psi _{X} \zeta _K = 0\).

One of the key tools for the proof of this theorem is a suitable choice of a convex overestimator of the working model \(\phi _k(\cdot , x)\) at a serious iterate x. In detail, we use as an overestimator the point-wise supremum of all cutting planes that could be generated at potential trial iterates z. These take the form \( m_{z}(\cdot , x) = f_a(z) + {g_{z}}^T(\cdot - z) - {r_{z}}, \) where \(f_a(z)\) and \(g_z\in \partial _x v(z, {u_{z}})\) are approximate function values and approximate subgradients at z, and \({r_{z}}\) a downshift with respect to x. With these, the overestimator is defined as

$$\begin{aligned} \phi (\cdot ,x):=\sup \Big \{{} & {} \big \{m_{z}(\cdot ,x)\vert {u_{z}}\in \mathcal {U}, v(z,{u_{z}}) \ge f(z) - \epsilon ''\Vert x-z\Vert ^2, z\in B(0,M)\setminus \{x\}\big \}\nonumber \\{} & {} \cup \big \{m_{0}(\cdot ,x)\vert {u_{x}}'\in \mathcal {U}, v(x,{u_{x}}') = v(x,{u_{x}}) \big \}\Big \}, \end{aligned}$$
(26)

where M is chosen such that x and all possible trial iterates lie in B(0, M) (see [23]). In an analogous way, we define an overestimator for \(G\) only:

$$\begin{aligned} \phi ^G(\cdot ,x):=\sup \Big \{{} & {} \big \{m_{z}^G(\cdot ,x)\vert {u_{z}}\in \mathcal {U}, v(z,{u_{z}}) \ge f(z) - \epsilon ''\Vert x-z\Vert ^2, z\in B(0,M)\setminus \{x\}\big \} \nonumber \\{} & {} \cup \big \{m_{0}^G(\cdot ,x)\vert {u_{x}}'\in \mathcal {U}, v(x,{u_{x}}') = v(x,{u_{x}}) \big \}\Big \}, \end{aligned}$$
(27)

with cutting planes \( m_{z}^G(\cdot , x) = G_a(z) + {s_{G}^{z}}^T(\cdot - z) - {r_{z}} \) at z with approximate function value \(G_a(z)\) and approximate subgradient \(s_{G}^{z}\in \partial _x \big (\sum _{i=1}^n V(z, {u_{z}})\big )\). Before we move on to the proof of Theorem 4.1, we import an auxiliary result from [23].

Lemma 4.2

[23, Lemma 3] For the first-order model \(\phi (\cdot ,x)\), as defined in (26), the following properties hold:

  1. (1)

    \(\phi (x,x)=f_a(x)\),

  2. (2)

    \(\partial \phi (x,x)\subseteq \tilde{\partial }_{a}{f}({x})\),

  3. (3)

    \(\phi _k(\cdot , x)\le \phi (\cdot , x)\) for the working model \(\phi _k(\cdot , x)\).

The same holds if we replace \(\phi \) by the first-order model \(\phi ^G\) defined in (27) and f by G.

Proof of Theorem 4.1

We divide the proof into two claims concerning convergence in the inner or the outer loop, respectively.

Claim 4.1

If the inner loop at a serious iterate \(x = x_j\) does not terminate finitely, then there is a subsequence of the indices k such that the limits of subsequences \(\alpha :=\lim _{k\rightarrow \infty }\alpha _j^k\), \(\tilde{\xi }:=\lim _{k\rightarrow \infty } \tilde{\xi }_j^k\) and \(\zeta :=\lim _{k\rightarrow \infty } \zeta _j^k\) exist and fulfill

$$\begin{aligned} {\alpha } \in \partial C(x), ~\tilde{\xi } \in \tilde{\partial }_{a}{G}({x}), ~\zeta \in \partial P_X(x), ~ 0 = {\alpha } + \psi \tilde{\xi } + \psi _{X} \zeta . \end{aligned}$$
(28)

Proof

We recall that the aggregate subgradients at the trial iterates \(x^k\) are given by (19)-(20). From Lemma 4.1, (1), we have \(x^k\rightarrow x\), so that, with local boundedness of the Clarke subdifferential [8] and compactness of \(\mathcal {U}\), we obtain boundedness of the sequences \((s_{C}^{k})_k,(s_{G}^{k})_k,(s_X^{k})_k\). The sequences \((\alpha ^k_j)_k\), \((\tilde{\xi }_j^k)_k\), \((\zeta ^k_j)_k\) as their respective convex combinations thus are bounded as well. For the aggregate subgradient \({g^*_{k}}\), it holds that

$$\begin{aligned} {g^*_{k}} = \alpha ^k_j+ {\psi _{}}\tilde{\xi }_j^k +{\psi _{X}}\zeta ^k_j. \end{aligned}$$
(29)

By Lemma 4.1, (1), \({g^*_{k}}\) converges, passing to a subsequence, to 0. We pass to a suitable subsequence of this such that the limits \(\alpha \), \(\tilde{\xi }\) and \(\zeta \) are well-defined. Further, it follows from (29) that \(0 = {\alpha } + \psi \tilde{\xi } + \psi _{X} \zeta \).

It remains to prove the first part of (28). We use the definition of the first-order models in (26) and (27). As the functions \(C\) and the \(l_1\)-penalty function \(P_X\) are convex and not affected by inexactness, we have

$$\begin{aligned} \phi (\cdot , x) = C(\cdot ) + {\psi _{}}\phi ^G(\cdot , x) + {\psi _{X}} P_X(\cdot ). \end{aligned}$$
(30)

This first-order model \(\phi \) is approximated by the working model \(\phi _{k}(\cdot , x)\), which is refined in every iteration. At the iterate \(x^k\), we have \(\phi _k(x^k, x) = m_{l}(x^k, x)\) for l with \(\lambda _k^l >0\), so that the working model’s value can be written as \(\phi _k(x^k, x) = \sum _{l=0}^{k-1} \lambda ^k_l m_{l}(x^k, x)\). We now partition the cutting planes \(m_{l}(\cdot , x)\) analogously to (17). First, we recall that every cutting plane is generated by a tangent plane and a downshift term: \( m_{l}(\cdot , x)= t_l(\cdot ) -{r_{l}}\). The slope of the tangent plane \(t_l(\cdot )\) is \(g_l\), derived via \(g_l = s_{C}^l + \psi s_{G}^l + \psi _X s_X^l\). As we have this partition at hand, we can partition the cutting plane \( m_{l}(\cdot , x)\) into

$$\begin{aligned} m_{l}(\cdot , x) = m_{l}^C(\cdot , x)+ {\psi _{}} m^{G}_{l}(\cdot , x)+ {\psi _{X}} m^{X}_{l}(\cdot , x), \end{aligned}$$

with \(m_{l}^C(\cdot , x)= t^{C}_l(\cdot )\), \(m^{G}_{l}(\cdot , x)= t^{G}_l(\cdot )-{r_{l}}\) and \(m^{X}_{l}(\cdot , x)= t^{X}_l(\cdot )\). The slopes of these cutting planes are \(s_{C}^{l}, s_{G}^{l}\) and \(s_X^{l}\), respectively. Further, they underestimate \(C(\cdot )\), \(\phi ^G(\cdot ,x)\) and \(P_X(\cdot )\), respectively, so that the following subgradient inequalities hold for every \(l<k\) and any z:

$$\begin{aligned}&m_{l}^C(x^k, x)+s_{C}^{l}(z-x^k)\le C(z), \end{aligned}$$
(31a)
$$\begin{aligned}&m^{G}_{l}(x^k, x)+s_{G}^{l}(z-x^k)\le \phi ^G(z, x), \end{aligned}$$
(31b)
$$\begin{aligned}&m^{X}_{l}(x^k, x)+s_X^{l}(z-x^k)\le P_X(z). \end{aligned}$$
(31c)

From this, we derive subgradient inequalities for the functions \(C(\cdot )\), \(\phi ^G(\cdot ,x)\) and \(P_X(\cdot )\) as follows: We multiply the inequalities by the corresponding factors \(\lambda _l^k\), sum over \(l<k\) and add a zero-term to the left-hand side. It follows for any z that

$$\begin{aligned}&C(x^k) - C(x^k) + \sum _{l=0}^{k-1} \lambda ^k_l m_{l}^C(x^k, x)+\sum _{l=0}^{k-1} \lambda ^k_ls_{C}^{l}(z-x^k)\le C(z), \end{aligned}$$
(32a)
$$\begin{aligned}&\phi ^G(x^k, x)-\phi ^G(x^k, x)+\sum _{l=0}^{k-1} \lambda ^k_l m^{G}_{l}(x^k, x)+\sum _{l=0}^{k-1} \lambda ^k_ls_{G}^{l}(z-x^k)\le \phi ^G(z, x), \end{aligned}$$
(32b)
$$\begin{aligned}&P_X(x^k) - P_X(x^k) +\sum _{l=0}^{k-1} \lambda ^k_l m^{X}_{l}(x^k, x)+\sum _{l=0}^{k-1} \lambda ^k_l s_X^{l}(z-x^k)\le P_X(z). \end{aligned}$$
(32c)

Using the convex \(\epsilon \)-subdifferential (see, e.g., [5]) and (21), we have

$$\begin{aligned} \alpha ^k_j&\in \partial ^{[\epsilon _{C}^k]}{C}({x^k}), \quad \epsilon _{C}^k = C(x^k) - \sum _{l=0}^{k-1} \lambda _l^k m^{C}_{l}(x^k, x), \end{aligned}$$
(33a)
$$\begin{aligned} \tilde{\xi }_j^k&\in \partial ^{[\epsilon _{G}^k]}{\phi ^{G}}({x^k, x}), \quad \epsilon _{G}^k = \phi ^G(x^k, x) - \sum _{l=0}^{k-1} \lambda _l^k m^{G}_{l}(x^k, x), \end{aligned}$$
(33b)
$$\begin{aligned} \zeta _j^k&\in \partial ^{[\epsilon _{X}^k]}{{P_X}}({x^k}), \quad \epsilon _{X}^k = {P_X}(x^k) - \sum _{l=0}^{k-1} \lambda _l^k m^{X}_{l}(x^k, x). \end{aligned}$$
(33c)

Further, we have for every \(l<k\) with \(\lambda ^k_l>0\) that \(\phi _k(x^k, x) = m^{C}_{l}(x^k) + {\psi _{}} m^{G}_{l}(x^k) + {\psi _{X}} m^{X}_{l}(x^k)\).

By (30), it thus holds that

$$\begin{aligned} \begin{aligned} \phi (x^k, x) - \phi _k(x^k, x)&= \epsilon _{C}^k + {\psi _{}}\epsilon _{G}^k + {\psi _{X}}\epsilon _{X}^k. \end{aligned} \end{aligned}$$
(34)

From Lemma 4.1, (1), we have that \(x^k\rightarrow x\). Further, from Lemma 4.1, (1), and Lemma 4.2, (1), it follows that \(\phi _k(x^k, x)\rightarrow f_a(x) = \phi (x,x)\). Thus, \(\phi (x^k, x) - \phi _k(x^k, x)\rightarrow 0\). As the summands on the right side of (34) are non-negative, they also converge to 0.

We thus have convergence of \(\epsilon _C^k, \epsilon _G^k\) and \(\epsilon _{X}^k\) to 0, convergence of \(x^k\rightarrow x\), and convergence of \(\alpha _j^k\), \(\tilde{\xi }_j^k\) and \(\zeta _j^k\) to \(\alpha , \tilde{\xi }\) and \(\zeta \), respectively. With (33), it thus follows that \(\alpha \in \partial C(x), \tilde{\xi } \in \partial \phi ^G(x,x)\) and \(\zeta \in \partial P_X(x)\) (see, e.g., [20, Proposition 4.1.1]). The claim \(\tilde{\xi } \in \tilde{\partial }_{a}{G}({x})\) follows by the result \(\phi (x,x)\subseteq \tilde{\partial }_{a}{f}({x})\) from Lemma 4.2, (2), which holds analogously for \(\phi ^G\). \(\square \)

We note that the proof for the case of finite termination (i.e., (23)) follows as a special case of the proof of Claim 4.1. From the definition of the aggregate subgradient \({g^*_{k}}\), we see that \({g^*_{k}}=0\) implies that the trial iterate \(x^k\) and the serious iterate x coincide. With this, we can follow the proof of Claim 4.1 until we arrive at formula (33). Now, using \(x^k=x\), it is straight-forward to show that \(\epsilon _{C}^k = \epsilon _{G}^k = \epsilon _{X}^k = 0\) without passing to the limit.

Claim 4.2

If the outer loop does not terminate finitely with serious iterates \(x_j\) and a cluster point \({\bar{x}}\), then there is a choice of a subsequence of inner loop indices k(j) such that the limits of subsequences \(\alpha :=\lim _{j\rightarrow \infty } \alpha _j^{k(j)}\), \(\tilde{\xi }:=\lim _{j\rightarrow \infty } \tilde{\xi }_j^{k(j)}\) and \(\zeta :=\lim _{j\rightarrow \infty } \zeta _j^{k(j)}\) exist and fulfill

$$\begin{aligned} {\alpha } \in \partial C({\bar{x}}), ~\tilde{\xi } \in \tilde{\partial }_{a}{G}({{\bar{x}}}), ~\zeta \in \partial P_X({\bar{x}}), ~ 0 = {\alpha } + \psi \tilde{\xi } + \psi _{X} \zeta . \end{aligned}$$

Proof

The proof can be conducted by following the proof of Claim 4.1. Minor changes have to be made as follows: We do not consider a fixed serious iterate but rather a sequence \((x_j)\) of serious iterates with a cluster point \({\bar{x}}\). As a sequence of trial iterates, we consider a sequence \((x^{k(j)})_j\) that has the properties as ensured by Lemma 4.1, (2). This sequence has \({\bar{x}}\) as a cluster point and it holds by Lemma 4.1, (2), and Lemma 4.2, (1), that \(\phi _{k(j)}(x^{k(j)}, x_j) \rightarrow f_a({\bar{x}}) = \phi ({\bar{x}}, {\bar{x}})\). Finally, the claim follows analogously to the proof of Claim 4.1\(\square \)

With this, we have handled all cases in Theorem 4.1. \(\square \)

Remark 4.1

From convexity of C and \(V_i\) (\(i\in [n]\)) in x, we infer that the approximate subdifferential \(\tilde{\partial }_{a}{f}({\cdot })\) is contained in a convex \(\epsilon \)-subdifferential (see, e.g., [29]): with \({g_{x}}\in \partial _x v(x, u_x)\) and denoting the error in the evaluation of G(x) by \(\epsilon _G^p = f(x) - v(x, u_x)\), we have

$$\begin{aligned} \begin{aligned}&~v(x, u_x) + g_x^T(z-x) \le v(z, u_x) ~\forall z\in {\mathbb {R}}^{n_x} \Rightarrow ~ v(x, u_x) + g_x^T(z-x) \le f(z) ~\forall z\in {\mathbb {R}}^{n_x}\\&\Rightarrow ~ f(x) + g_x^T(z-x) \le f(z) + \epsilon _G^{p} ~\forall z\in {\mathbb {R}}^{n_x} \Rightarrow ~ g_x \in \partial ^{[\epsilon _G^{p}]}{f}({x}). \end{aligned} \end{aligned}$$

This shows \(\tilde{\partial }_{a}{f}({x}) \subset \partial ^{[\epsilon _G^{p}]}{f}({x})\). Thus, the approximate optimality condition \(0\in \tilde{\partial }_{a}{f}({x})\) already implies \(f(x) \le \min _{x} f(x) + \epsilon _G^{p}\), i.e., that the point x is \(\epsilon _G^{p}\)-optimal.

We further note that in practice, we may not have access to \(\epsilon _G^p\), but we have the required precision of the corresponding function evaluation \(\epsilon _G^{K}\), determined by (14) and specified in (23)-(25) for the three different termination scenarios, which is an upper bound for the exact error \(\epsilon _G^p\).

Subgradients w.r.t. Integer Variables We now provide formulas for subgradients with respect to integer variables. Having generated \(\tilde{\xi }_{K}\) via the adaptive bundle method as described above, we have \( \tilde{\xi }_{K} = \sum _{l=0}^{k-1} \lambda ^{k} s_G^l \) with k the bundle iteration index at which we stopped and \(s_{G}^l \in \partial _xV(x^l, y_K, u_{x^l})\). Now, we compute in every bundle iteration a subgradient \(s_{G, y}^l\) such that \((s_{G}^l, s_{G, y}^l)\) fulfills the subgradient inequality (7) for \(V(\cdot , \cdot , u_{x^l})\) at \((x^l, {y_{K}})\) and choose

$$\begin{aligned} \tilde{\eta }_{K} = \sum _{l=0}^{k-1} \lambda _l^{k} s_{G, y}^l, \end{aligned}$$

with weights \( \lambda _l^{k}\) from (19) as an integer subgradient. Analogously, we compute

$$\begin{aligned} \beta _{K} = \sum _{l=0}^{k-1} \lambda _l^{k} s_{C, y}^l. \end{aligned}$$

These subgradients, \(\beta _{K}\) and \(\tilde{\eta }_{K}\), fulfill the subgradient inequality (7) for \(C(\cdot , \cdot )\) at \(({x_{K}}, {y_{K}})\) and for \(G(\cdot , \cdot )\) at \(({x_{K}}, {y_{K}})\) up to the error \(\epsilon _G^p\) in \(\tilde{G}({x_{K}}, {y_{K}})\). For a theoretical justification, the proof of Theorem 4.1 can be extended in a straight-forward way. In particular, the required subgradient inequalities can be derived from an appropriate extension of (31) and (32).

Inexactness in Solution Output We finally comment on the inexactness in the solution output (23)-(25) and possibilities to enhance its quality. In particular, it is in an OA approach of interest to decide on the feasibility of the continuous subproblem (\(NLP(y_{K})\)).

If we approximately solve the feasibility problem (\(F(y_{K})\)) with the adaptive bundle method and obtain an output \(\tilde{G}({x_{K}}, {y_{K}})>0\), then we know that (\(NLP(y_{K})\)) is indeed infeasible. Otherwise, if we solve (\(F(y_{K})\)) with output \(\tilde{G}({x_{K}}, {y_{K}})=0\), or (\(NLP(y_{K})\)) with any value for \(\tilde{G}({x_{K}}, {y_{K}})\), we do not know if (\(NLP(y_{K})\)) is feasible or not. For the latter case, we have the following three options. As preferred option, we can always simply increase \(\epsilon _G^{K}\) by \(\tilde{G}({x_{K}}, {y_{K}})\), then set, in (23)-(25), \(\tilde{G}({x_{K}}, {y_{K}})\) to 0 and correctly label the problem as feasible with tolerance \(\epsilon _G^{K}\). If this leads to a larger feasibility error \(\epsilon _G^{K}\) than desired, we can re-run the bundle method with increased penalty parameter and we can use a refinement strategy in the bundle method that has been proposed in [23, Corollary 5]. This strategy involves re-evaluations of function values at serious iterates and leads to an exact convergence result, i.e., to \(0\in \partial f({\bar{x}})\) in Corollary 4.1. This option can however be rather expensive. We note that Assumption 3.2 ensures that, if (\(NLP(y_{K})\)) is feasible, then this strategy of exactly solving the penalized problem (\(NLP_{\psi }({y_{K}})\))) leads to a feasible and optimal solution to (\(NLP(y_{K})\)).

In contrast to inexactness in the feasibility with respect to \(G({x_{K}}, {y_{K}})\), we require exact feasibility with respect to the constraint \(x\in X\). To achieve this, we can rely on the options above and hence can assume that \({x_{K}}\in X\) for the solution output. We note that in our computational experiments, we never needed to employ these options to achieve feasibility with respect to X.

For \({x_{K}}\in X\), the subdifferential of the penalty term \(P_X({x_{K}})\) is contained in the normal cone of X at \({x_{K}}\), which we use in the following and which we denote by

$$\begin{aligned} N(X, {x_{K}}) = \{z\in \mathbb {R}^{n_x}: z^T(x-{x_{K}})\le 0\quad \forall x\in X\}. \end{aligned}$$

As we assume \({x_{K}}\in X\), our results thus hold for \(\partial P_X({x_{K}})\) replaced by \(N(X, {x_{K}})\).

5 Inexactness in Function Values and Subgradients

In the previous section, we have seen that inexact worst-case evaluations lead to the following situation: for every iterate \(({x_{K}},{y_{K}})\), an \(\epsilon _G^{K}\)-optimal solution to the adversarial problem with a known tolerance \(\epsilon _G^{K}\) is available. Denoting the approximation of the function value \(G({x_{K}}, {y_{K}})\) by \(\tilde{G}({x_{K}}, {y_{K}})\), we thus have

$$\begin{aligned} \tilde{G}({x_{K}},{y_{K}}) = V({x_{K}}, {y_{K}}, \tilde{u}) \ge \max _{u\in \mathcal {U}} V({x_{K}}, {y_{K}}, u) - \epsilon _G^{K}. \end{aligned}$$

Having access to the approximate worst case \(\tilde{u}\), one has natural access to a subgradient \(\xi \in \partial _x V({x_{K}}, {y_{K}}, \tilde{u})\), which fulfills

$$\begin{aligned} \tilde{G}({x_{K}},{y_{K}}) + \xi ^T (z-{x_{K}})\le G(z, {y_{K}}) \quad \forall z\in X. \end{aligned}$$

Such an approximate subgradient then lies in the convex \(\epsilon _G^{p}\)-subdifferential of G at \(x_K\), where \(\epsilon _G^{p}\) denotes the exact error in the evaluation of \(G\). It will be shown later in this section that any such subgradient can be used to generate a cutting plane, which cuts off a point only if it is infeasible or if it does not improve the current best objective value. However, in order to guarantee that our OA algorithm converges in a finite number of iterations, it is also required that every integer assignment should be visited only once. For this, we need the following stronger assumption.

Assumption 5.1

At an arbitrary iteration \(K\), the problems (\(NLP(y_{K})\)) and (\(F(y_{K})\)) can be solved with output \(\big ({x_{K}}, C({x_{K}}, {y_{K}}), \epsilon _G^{K}, \tilde{G}({x_{K}}, {y_{K}}), \alpha _{K}, \tilde{\xi }_{K}, \zeta _{K}\big )\), such that \({x_{K}}\in X\),

$$\begin{aligned} \qquad&\exists 0\le \epsilon _G^p \le \epsilon _G^{K}{:} ~ \tilde{G}({x_{K}},{y_{K}}) = G({x_{K}}, {y_{K}}) - \epsilon ^p_G, \end{aligned}$$
(35a)
$$\begin{aligned} \qquad&\alpha _{K} \in \partial _x C({x_{K}}, {y_{K}}), ~ \tilde{\xi }_{K} \in \partial ^{[\epsilon _G^{p}]}_xG({x_{K}}, {y_{K}}), ~ \zeta _{K} \in N(X, {x_{K}}), \qquad \qquad \qquad \ \end{aligned}$$
(35b)
$$\begin{aligned} \qquad&\exists \psi , \psi _{X}{:}~0 = {\alpha }_{K} + \psi \tilde{\xi }_{K} + \psi _{X} \zeta _{K}. \end{aligned}$$
(35c)

For the feasibility problem (\(F(y_{K})\)), we simply set \(C\equiv 0\) in (35b) and \(\psi =1\) in (35c). Further, if (\(NLP(y_{K})\)) is feasible, then it can be solved with \(\tilde{G}({x_{K}}, {y_{K}})=0\).

In Sect. 4, we have shown that Assumption 5.1 is satisfied when applying the adaptive bundle method from [23] with the modifications outlined in Algorithm 2 to the subproblems (\(NLP(y_{K})\)) and (\(F(y_{K})\)). In this case, Assumption 5.1 does not need to be checked. Nevertheless, the OA method we develop also allows the integration of any other method, as long as it fulfills Assumption 5.1.

To generate the linearized constraints of the master problem, we also need suitable subgradients with respect to the integer variables. More precisely, when we have subgradients \(\alpha _{K} \in \partial _x C({x_{K}}, {y_{K}}), \tilde{\xi }_{K} \in \partial ^{[\epsilon _G^{p}]}_x{G}({x_{K}}, {y_{K}})\) at hand, we use subgradients \(\beta _K\) and \(\tilde{\eta }_{K}\) with respect to the integer variables, such that

$$\begin{aligned} \begin{aligned}&C({x_{K}}, {y_{K}}) + \begin{pmatrix} \alpha _{K}\\ \beta _K\end{pmatrix}^T \begin{pmatrix} {\bar{x}} - {x_{K}}\\ {\bar{y}} - {y_{K}}\end{pmatrix} \le C({\bar{x}}, {\bar{y}})\quad&\forall ({\bar{x}}, {\bar{y}}) \in X \times Y \cap \mathbb {Z}^{n_y}, \end{aligned} \qquad \end{aligned}$$
(36)
$$\begin{aligned} \begin{aligned}&G({x_{K}}, {y_{K}}) + \begin{pmatrix} \tilde{\xi }_{K} \\ \tilde{\eta }_{K} \end{pmatrix}^T \begin{pmatrix} {\bar{x}} - {x_{K}}\\ {\bar{y}} - {y_{K}}\end{pmatrix} \le G({\bar{x}}, {\bar{y}}) + \epsilon _G^p \quad&\forall ({\bar{x}}, {\bar{y}}) \in X \times Y \cap \mathbb {Z}^{n_y}. \end{aligned}\nonumber \\ \end{aligned}$$
(37)

We have detailed in Sect. 4, how such subgradients \(\beta _{K}\) and \(\tilde{\eta }_{K}\) can also be generated in the course of the adaptive bundle method.

As we evaluate \(G\) only inexactly, we need an according notion of inexactness for the sets \(S^K\) and \(T^K\), which are in an exact setting subsets of S and T, respectively (see Sect. 3). At an integer point that we label as infeasible, we underestimate the minimum value of \(G\) (see Assumption 5.1). These integer points are hence indeed infeasible and we collect them in a set \(\tilde{S}^K\subseteq S\) with

$$\begin{aligned} \tilde{S}^K:=\{ y_L \mid L\le K, \text { Assumption} 5.1 \hbox { is fulfilled for } (F(y_{K})) \hbox { with } \tilde{G}({x_{K}}, {y_{K}}) > 0 \}. \end{aligned}$$

In contrast, integer points we label as feasible may in reality be infeasible. We collect them in the following set, which is an inexact version of visited feasible integer assignments.

$$\begin{aligned} \tilde{T}^K:=\{ y_J \mid J\le K, \text { Assumption } 5.1\hbox { is fulfilled for }(NLP(y_{K}))\hbox { with } \tilde{G}({x_{K}}, {y_{K}}) = 0 \}. \end{aligned}$$

If \(\tilde{G}({x_{K}}, {y_{K}}) = 0\) for the obtained solution to (\(NLP(y_{K})\)), then we set \({y_{K}}\in \tilde{T}^{K}\). In this case, it holds that \(\tilde{G}({x_{K}}, {y_{K}}) = 0\) with \(\tilde{G}({x_{K}},{y_{K}})\ge G({x_{K}}, {y_{K}}) - \epsilon _G^{K}\) and we say that \(({y_{K}}, {x_{K}})\) is \(\epsilon _G^{K}\)-feasible.

In an iteration \(K\), we obtain as inexact master problem (i.e., an inexact version of (\(MP^{K}\))), with approximate function values \(\tilde{G}(\cdot , \cdot )\) and subgradients \(\tilde{\xi }, \tilde{\eta }\),

figure i

5.1 Algorithm

With these algorithmic concepts at hand, we now state the OA method for mixed-integer nonlinear robust optimization with the notion of inexactness formalized in Assumption 5.1. We use the adaptive bundle method from Sect. 4 for the solution of the continuous subproblems. The corresponding steps in the outer approximation algorithm outlined below are marked by “bundle.” Moreover, if the bundle method is used, the computations in line 6 and line 12 can be realized as detailed in the paragraph on subgradients w.r.t. integer variables and the condition in line 16 can be realized by the strategies in the paragraph on inexactness in the solution output, both at the end of Sect. 4. However, we note that the OA method does not rely on a specific method for these steps and is thus not restricted to the bundle method suggested here. For the subproblems, any method that leads to solutions fulfilling Assumption 5.1 can be used instead.

figure j

5.2 Inexact Cutting Planes

We now prove correctness and finite convergence of the proposed OA method. Therefore, we closer examine the cutting planes generated by the two types of continuous problems.

Cutting Planes Generated by the Continuous Subproblem We show that the linear constraints with respect to \(\tilde{T}^K\) in (\({\widetilde{MP}}\) \(^{K}\)) are valid and cut off the current integer solution. In an iteration \(K\), let \({x_{K}}\) be an approximate solution to the continuous subproblem (\(NLP(y_{K})\)) that fulfills Assumption 5.1. We consider the following inexact cutting planes:

$$\begin{aligned} \tilde{G}({x_{K}}, {y_{K}}) + \tilde{\xi }_{K}^T(x - {x_{K}}) + \tilde{\eta }_{K}^T(y - {y_{K}})&\le 0 \end{aligned}$$
(38a)
$$\begin{aligned} C({x_{K}}, {y_{K}}) + {\alpha }_K^T(x - {x_{K}}) + \beta _K^T(y - {y_{K}})&\le \theta \end{aligned}$$
(38b)
$$\begin{aligned} \theta&\le \Theta ^{K} - \epsilon _{oa} \end{aligned}$$
(38c)
$$\begin{aligned} \Theta ^{K}&= \min \{\Theta _{K-1}, C({x_{K}}, {y_{K}})\}. \end{aligned}$$
(38d)

The constraints are valid in the sense that they cut off infeasible solutions, and feasible solutions only if they do not improve the current best objective value by more than \(\epsilon _{oa}\). We prove this and further show that (38) cuts off the current integer solution:

Lemma 5.1

If \(({\bar{x}}, {\bar{y}})\in \mathbb {R}^{n_x+n_y}\) is feasible for (P) and infeasible for (38), then \(C({\bar{x}}, {\bar{y}}) > \Theta ^{K}-\epsilon _{oa}\). Furthermore, for any \({\bar{x}}\in X\), \(({\bar{x}}, {y_{K}})\) is infeasible for (38).

Proof

We prove the first claim: Let \(({\bar{x}}, {\bar{y}}) \in {\mathbb {R}}^{n_x+n_y}\) be feasible for (P) and infeasible for (38). We show feasibility of \(({\bar{x}}, {\bar{y}})\) for (38a). There exists an \(\epsilon _G^{p}>0\) with \(\tilde{G}({x_{K}}, {y_{K}}) = G({x_{K}}, {y_{K}})-\epsilon _G^{p}\) and with (37), we have

$$\begin{aligned} \tilde{G}({x_{K}}, {y_{K}}) + \tilde{\xi }_{K}^T({\bar{x}} - {x_{K}}) + \tilde{\eta }_{K}^T({\bar{y}} - {y_{K}}) \le G({\bar{x}}, {\bar{y}}). \end{aligned}$$

As \(G({\bar{x}}, {\bar{y}})\le 0\) due to feasibility of \(({\bar{x}}, {\bar{y}})\) for (P), it follows that \(({\bar{x}}, {\bar{y}})\) fulfills (38a). It hence violates (38b)–(38c). This implies that \(C({\bar{x}}, {\bar{y}}) > \Theta ^{K}-\epsilon _{oa}\).

We prove the second claim by contradiction: We assume that there exists an \({\bar{x}}\in X\) such that \(({\bar{x}}, {y_{K}})\) is feasible for (38). Then,

$$\begin{aligned} \tilde{G}({x_{K}}, {y_{K}}) + \tilde{\xi }_{K}^T ({\bar{x}} - {x_{K}})&\le 0 \end{aligned}$$
(39a)
$$\begin{aligned} C({x_{K}}, {y_{K}}) + {\alpha }_K^T ({\bar{x}} - {x_{K}})&\le \theta \end{aligned}$$
(39b)
$$\begin{aligned} \theta&\le \Theta ^{K} - \epsilon _{oa} \end{aligned}$$
(39c)
$$\begin{aligned} \Theta ^{K}&= \min \{\Theta ^{K-1}, C({x_{K}}, {y_{K}})\}. \end{aligned}$$
(39d)

As \(\tilde{G}({x_{K}}, {y_{K}}) = 0\), we have \(\tilde{\xi }_{K}^T({\bar{x}} - {x_{K}}) \le 0\). It follows from Assumption 5.1, (35b), (35c), that \({\alpha }_K^T({\bar{x}}-{x_{K}}) \ge 0\). Hence, due to (39b), \(C({x_{K}}, {y_{K}})\le \theta \), which contradicts (39c),(39d). \(\square \)

Cutting Planes Generated by the Feasibility Problem Let \({x_{K}}\) be an approximate solution to the feasibility problem (\(F(y_{K})\)) fulfilling Assumption 5.1. We consider the cutting plane

$$\begin{aligned} \tilde{G}({x_{K}}, {y_{K}}) + \tilde{\xi }_{K}^T(x - {x_{K}}) + \tilde{\eta }_K^T(y - {y_{K}}) \le 0. \end{aligned}$$
(40)

We note that we have no inexactness with respect to the claim that the nonlinear subproblem is infeasible: if the underestimated optimal value of the feasibility problem indicates infeasibility, the subproblem is indeed infeasible. We now prove that the cutting plane (40) cuts off the current integer solution without cutting off any feasible solution.

Lemma 5.2

If \(({\bar{x}}, {\bar{y}})\in \mathbb {R}^{n_x+n_y}\) is feasible for (P), then it is feasible for (40). Furthermore, for any \({\bar{x}}\in X\), \(({\bar{x}}, {y_{K}})\) is infeasible for (40).

Proof

From feasibility of \(({\bar{x}}, {\bar{y}})\) for (P), it follows that \(G({\bar{x}}, {\bar{y}})\le 0\). As there is an \(\epsilon _G^{p}>0\) such that \(\tilde{G}({x_{K}}, {y_{K}}) = G({x_{K}}, {y_{K}})-\epsilon _G^{p}\) and by (37), it holds that

$$\begin{aligned} \tilde{G}({x_{K}}, {y_{K}}) + \tilde{\xi }_{K}^T({\bar{x}} - {x_{K}}) + \tilde{\eta }_{K}^T({\bar{y}} - {y_{K}}) \le G({\bar{x}}, {\bar{y}}), \end{aligned}$$

so that \(({\bar{x}}, {\bar{y}})\) fulfills the constraint (40).

We prove the second claim by contradiction: We assume that there exists an \({\bar{x}}\in X\) with

$$\begin{aligned} \tilde{G}({x_{K}}, {y_{K}}) + \tilde{\xi }_{K}^T({\bar{x}} - {x_{K}}) + \tilde{\eta }_{K}^T({y_{K}}- {y_{K}}) \le 0. \end{aligned}$$

From Assumption 5.1, (35b), (35c), it follows that \(\tilde{\xi }_{K}^T({\bar{x}}-{x_{K}}) \ge 0\). As \(\tilde{\eta }_{K}^T({y_{K}}- {y_{K}}) = 0\), this is is a contradiction to \(\tilde{G}({x_{K}}, {y_{K}}) > 0\). \(\square \)

5.3 Finite Convergence of the Outer Approximation Method

We now combine the results from the preceding section to show that Algorithm 1 terminates after finitely many steps and that a solution \((x_{K^*}, y_{K^*})\) found by the algorithm is \(\epsilon _G^{K^*}\)-feasible and \(\epsilon _{oa}\)-optimal. The proof uses similar arguments as, e.g., [35] and [14].

Theorem 5.1

If (P) is feasible, then Algorithm 1 terminates after finitely many iterations with a solution \((x_{K^*}, y_{K^*})\) that is \(\epsilon _G^{K^*}\)-feasible and \(\epsilon _{oa}\)-optimal for (P). If (P) is infeasible, Algorithm 1 either outputs a solution \((x_{K^*}, y_{K^*})\) that is \(\epsilon _G^{K^*}\)-feasible and \(\epsilon _{oa}\)-optimal for (P) or detects infeasibility, after finitely many iterations.

Proof

It follows from Lemma 5.1 and Lemma 5.2 that, if (\({\widetilde{MP}}\) \(^{K}\)) is infeasible, then Algorithm 1 either correctly detects infeasibility of (P) or outputs an \(\epsilon _{oa}\)-optimal solution. Further, any candidate solution \(({x_{K}}, {y_{K}})\) with feasibility tolerance \(\epsilon _G^{K}\) is \(\epsilon _G^{K}\)-feasible. Finite convergence follows from the fact that, by Lemma 5.1 and Lemma 5.2, each integer point in Y is visited only once. \(\square \)

The OA method thus is applicable to mixed-integer nonlinear robust optimization with the notion of inexactness specified in Assumption 5.1. We use inexact worst-case evaluations with precision \(\epsilon _G^{K}\) and therefore may accept solutions that are only \(\epsilon _G^{K}\)-feasible. Consequently, we cannot achieve a better result than the approximate feasibility in Theorem 5.1.

In an iteration \(K\) of the OA method, the feasibility tolerance \(\epsilon _G^{K}\) is not specified before the subproblem is solved. Whether or not this can be specified in advance depends on the method used for the subproblem. In any case, if the subproblem’s solution happens to be the final solution of the OA method, the algorithm outputs this solution, which is \(\epsilon _G^{K}\)-feasible.

6 Numerical Results for the Gas Transport Problem

We implemented the OA approach with the adaptive bundle method in MATLAB and Python with Gurobi 8.1 [18]. We approximated the adversarial maximization problem via piecewise linear relaxation, for which we used the delta method [15]. This was implemented in Python with Gurobi 8.1. The experiments were done on a machine with an Intel Core i7-8550U (4 cores) and 16GB of RAM.

We used instances from the GasLib library, which contains realistic gas network instances [31]. We slightly modified the instances such that they fulfill our assumptions. The modified instances are publicly available as online supplement to this paper. We evaluated our methods for networks with up to 103 nodes. The two smallest GasLib instances are defined on networks with 11 and 24 nodes, respectively, and the robust gas transport problem is solved by our method within only a few seconds. The computational results get more interesting for the larger GasLib instances with 40 and with 103 nodes, on which we focus here. These networks are of the sizes of real networks.

In the adaptive bundle method, we used the stopping criterion \({g^*_{k}}\le 10^{-7}\) along with heuristic stopping criteria from [23, Section 4.3]. Nevertheless, as it can be seen from the following tables, the required precision for the aggregate subgradient is met in almost all cases. In the tables, we list the computational times spent within the bundle method as ‘runtime bundle.’ The main part of the OA method’s running time is spent for the subproblems. For the OA iterations in which no approximate feasible solution could be found, we list the accumulated running times for the runs of the bundle method working on (\(F(y_{K})\)) and (\(NLP(y_{K})\)). We did not need to resolve (\(NLP(y_{K})\)) (line 16 in Algorithm 1) in our experiments. The bundle method’s running time is mainly spent for solving the adversarial problems up to the required precisions. In order to reach a solution within reasonable running time, we bounded the required precision by \(10^{-3}\) for the 40-node instance, i.e., \( {\epsilon _f^{k}}\ge 10^{-3}\), and by \(10^{-1}\) for the 103-node instance, i.e., \( {\epsilon _f^{k}}\ge 10^{-1}\). As it can be seen from the tables, where \({\bar{\epsilon }}_G^p\) denotes an upper bound on the exact a posteriori error, this did not prevent this error from becoming small. As cost function w in (\(P_{gas}\)), we used compressor costs, determined by the achieved difference of squared pressures. We internally scaled these costs by a factor of \(10^{-2}\). For the use of valves, we did not charge any costs.

Table 1 GasLib-40 with uncertain parameters in \([0.975 \cdot d, 1.025\cdot d]\) and \([\lambda , 1.05\cdot \lambda ]\) and 7 binary decision variables
Full size table

In Tables 1 and 2, results are presented for a slightly modified version of GasLib-40 with 40 nodes, 5 compressors and 2 valves. In detail, we removed a compressor on a cycle in the original instance in order to fulfill the assumption of Lemma 2.1. We replaced it by a valve and added another valve on a cycle. As a benchmark result, we first applied our method to the nominal problem, for which we obtained—within a few seconds—optimal compressor costs of 1148. Then, we solved the robust problems with different uncertainty sets, namely once with 5% and once with 10% deviation from the nominal value : \([0.975 \cdot d, 1.025\cdot d]\), \([\lambda , 1.05\cdot \lambda ]\) and \([0.95 \cdot d, 1.05\cdot d]\), \([\lambda , 1.1\cdot \lambda ]\). These sets yield a robust protection against a reasonable amount of parameter deviation. The corresponding results are presented in Table 1 and 2, respectively. From these results, we compute the price of robustness, which is the relative increase of compressor costs caused by the robust treatment of uncertainties. For the first uncertainty set, it amounts to \(45\%\) and for the second to \(93\%\). The larger uncertainty set thus leads to almost twice the nominal compressor costs.

Table 2 GasLib-40 with uncertain parameters in \([0.95 \cdot d, 1.05\cdot d]\) and \([\lambda , 1.1\cdot \lambda ]\) and 7 binary decision variables
Full size table
Table 3 103-nodes instance with uncertain parameters in \([0.975 \cdot d, 1.025\cdot d]\) and \([\lambda , 1.05\cdot \lambda ]\) and 24 binary decision variables
Full size table

In Table 3, we present results for a modified version of GasLib-135 that has 103 nodes, 21 compressors, which are not on cycles, and 3 valves. As uncertainty sets for the demand and for pressure loss coefficients d and \(\lambda \), we used the set of balanced demands in \([0.975 \cdot d, 1.025\cdot d]\) and the set \([\lambda , 1.05\cdot \lambda ]\), respectively. Typically, the running time for the adversarial problems, and thus for the whole method, increases when we enlarge the uncertainty set. In order to keep the adversarial problems solvable within a reasonable amount of time, we restricted ourselves to an uncertainty set of \(5\%\) deviation for this network.

For the nominal problem, we encountered—within less than one minute—an optimal objective value of 704.2, so that the price of robustness amounted to \(30\%\) for the chosen uncertainty sets, which is in the same order of magnitude as in the case of the smaller instance.

We care to mention that the considered robust setting that allows for discrete-continuous decisions has not been solved in the literature so far. The case of only continuous decisions is roughly comparable to one iteration within our OA method. This simpler case has been treated by a decomposition approach specifically designed for robust gas networks in [3]. There, the instance GasLib-40 could be solved within a few seconds or a few minutes—depending on an error in the relaxation of non-convex constraints. We have observed that the discrete-continuous robust gas transport problem on instances of size 40-nodes and 103-nodes are solvable within a few minutes by our method where we obtained—up to a small tolerance in the last case—robust feasible solutions. Thus, although our method is a general approach for mixed-integer robust optimization that is applicable in wider contexts as [3], it solves a challenging and more complex robust optimization task within a similar order of running time as could be obtained in [3].

7 Conclusion

We proposed an outer approximation approach for nonlinear robust optimization with mixed-integer decisions and inexact worst-case evaluations. In the core of this, an adaptive bundle method was used to solve the continuous subproblems. In general, the method can be applied to robust problems, in which uncertain parameters enter the problem in a non-concave way and in which only approximate worst cases are computationally accessible. This setting is extremely challenging, and no general solution approach exists. According to our numerical results, it performs very well on an example application in robust gas transport and can solve relevant real-world problems.

There are possibilities to improve the performance of the method. As proposed in [9], the bundle method in an iteration of the OA method could be initialized by the use of cutting planes from earlier runs. One could thereby think of an appropriate downshift mechanism of recycled cutting planes, as used in bundle methods to recycle cutting planes from former outer loops. Another idea would be to exchange cutting planes between the bundle method’s cutting plane model and the master problem in the OA approach. Also, to accelerate the master problems’ solution, one could employ a so-called single-tree approach, as proposed in [32], where the branch-and-bound tree for the MIP’s solution is not re-built in every iteration. Further, one could employ regularization strategies in order to avoid large step-sizes between the master problems’ solutions [1, 9, 22, 30].

Apart from accelerating the proposed approach, there are possibilities of extending the scope of applicability of our method. Probably the most interesting case would be a relaxation of the convexity assumption. One possible avenue here would be to resort to concepts of pseudo- and quasi-convexity, as has been done for the related extended cutting plane methods [11] and extended supporting hyperplane methods [36]. As pointed out in [13], a suitable framework for the OA method could be the one by [19], which requires only quasi-convexity. Such an integration could be a challenging subject of future research and requires a substantial extension of our results.