Asymmetric Information in a Capital Accumulation Differential Game with Spillover and Learning Effects

Abstract

This paper considers a capital accumulation game where the installation costs of investments are lowered by the firm’s own capital stock because of learning and by the competitor’s capital stock because of spillover effects. To properly understand the impact of the two capital stocks, we consider six information structures which differ in whether a firm takes into account that their competitor’s strategy depends only on time or on one or both capital stocks. We find that if firms are aware that their own capital stock makes investments of the competitor more efficient, a firm would invest less. Due to this effect, information only pays off if it is taken into account by both competitors, because otherwise the less informed and therefore less cautious player invests more and has a higher capital stock and revenues in the long run.

1 Introduction

A major problem within the differential game literature is the multiplicity of equilibrium concepts. There are quite a number of papers deriving Markov-perfect Nash equilibria of linear quadratic differential games (see, e.g. [13], section 7.1.) where, starting out from postulating a quadratic value function, the controls linearly depend on the states. In the case of a capital accumulation game, [24] obtains a feedback Nash equilibrium in this way. For the same model, [14] obtain a different feedback Nash equilibrium strategy due to a slightly different specification of the quadratic value function. Moreover, the value function resulting in a feedback Nash equilibrium does not have to be quadratic. So, one wonders how many more equilibria there would be if the assumption of the value function being quadratic, implying that strategies need no longer be linear, would be relaxed.

This paper explores a different route. In a two-player differential-game framework, where each firm has one state and one control, we employ an approach relying on Pontryagin’s maximum principle, i.e., open-loop (OL) and closed-loop memoryless (CL) Nash equilibrium (see, e.g., [5, 13] or [19] for details), and some mixes between them.¹² We subsequently analyze cases where either the player’s control is a function of just time, of the player’s own state, of the state of the other player, or of both the own state and the other player’s state variable. Combining all possible cases of both controls gives sixteen different scenarios. If we leave out the symmetric ones, we end up with six different cases. The resulting equilibria are analyzed and compared.

We perform the analysis by considering a duopolistic capital accumulation framework with symmetric firms, where each firm can build up capital stock by investing. The relatively new feature is that the installation costs experience a learning effect, i.e., the more the firms have installed capital goods in the past, the larger their current capital stock, and the lower the adjustment cost of investment. Besides being negatively dependent on the own capital stock, there is also a spillover effect in the sense that the competitor’s capital stock lowers the firm’s installation cost.

The literature has paid lots of attention to capital accumulation games. Dockner and Nishimura [9] consider a differential game with two players and a single stock where the production function is convex–concave . The pre-commitment equilibrium exhibits a Skiba threshold. On the other hand, also a Markov-perfect equilibrium is derived that has a unique stable steady state. A discrete time version is studied in [11]. Two Markov-perfect equilibria are derived. In one of them, the stock always converges to a steady state, while in the other one, complicated dynamics may arise. Further, it is shown that by applying a trigger strategy the efficient cooperative outcome can be reached.

In an n-player setting, but still with a single stock, [10] design an auxiliary system of ordinary differential equations to identify local and global Markov equilibria. Dockner et al. [12] study a two player capital accumulation game where each player has its own stock and the framework is discrete time. Profit functions are assumed to be additively separable in the capital stocks. So-called indifferent Markov-perfect equilibria are derived that exhibit complicated dynamics in the form of period-3 cycles and existence of chaos. A more numerical approach is applied in [8]. The model has n players, each having their own capital stock and the framework is again discrete time. It is found that firms over-invest to deter the rival from expanding. Feichtinger and Dockner [15] combines capital accumulation with endogenous population growth. Steady state behavior is studied where it is shown that stable limit cycles might exist.

We find that two effects play a dominant role in our results. The first effect is the investment-spillover effect. It arises because a large capital stock of the competitor gives a lot of experience in investing. This knowledge spills over to the firm and reduces its investment cost. Therefore, the firm will invest more, which increases its capital stock. Consequently, its production is increased, which reduces output price, and this in turn reduces the competitor’s payoff. For this reason, the competitor has an incentive to reduce the accumulation of its own capital stock, which can be achieved by investing less.

The second effect is the investment-spillover-enlargement effect. Due to learning, a larger capital stock reduces the adjustment cost of the firm, which makes it a stronger competitor to the other firm. This makes the negative spillover effect of the previous paragraph stronger. Especially the first effect causes a non-monotonic effect of the firms’ payoffs with respect to the spillover parameter. When the parameter is small, the payoff is increasing. This is the cost effect, i.e., investment costs are smaller because the firm benefits from knowledge spilling over from the other firm. When the parameter gets larger, the payoff is decreasing. This is caused by underinvesting due to the investment-spillover effect.

In the present paper, we compare the impact of different information structure, i.e., the firms do or do not take into account that their competitor’s capital stock depends on one or both capital stocks. To gain information on the opponent’s capital stock works like a prisoner’s dilemma: the symmetric outcome where both players have gained information (“not confessing”) gives a better outcome than if both players do not have information (“confessing”) about the other player’s capital stock. However, in principle, given that the opponent has information, it would be better for you to “confess,” i.e., to refrain from obtaining information. The reason for this outcome in the present paper is that the player who takes into account more information acts more cautiously (investment-spillover and investment-spillover-enlargement effects). Acting cautiously would pay off if the other player also acts cautiously, but not if the other player acts more aggressive in terms of investing. Then, the aggressive behavior leads the more cautious player to act even more cautiously due to the information he takes into account.

Note that effect of a different information/commitment structure (studying the effect of state variables on optimal strategies) is similar but different to the effect followed in the differential game literature on myopia and foresight, where the impact of own decisions on the dynamics of the state variables is studied (i.e., myopic players ignore the impact, farsighted players take the impact into account). Applications of theory are marketing (see [1, 2, 18, 23]), management (see [7, 22]) and environmental economics (see [6]). In particular, [6, 7, 22] proved (in different contexts) that foresight may be profit reducing for the player that acquires it.

The paper is organized as follows. Section 2 presents the model, whereas Sect. 3 contains the analysis. The numerical results are presented in Sect. 4. Section 5 concludes.

2 Model

We consider a capital accumulation model where two firms produce identical products on the same market. While acquisition costs are linear and independent of the other firm’s capital stock, adjustment costs are convex and subject to a learning effect. The larger the firm’s capital stock is, the lower the adjustment costs are. The learning effect is enlarged by the capital stock of the opponent. Experiences with installing capital goods of the other firm spill over to the focal firm, where the parameter $\theta \in [0,1 ]$ measures the strength of the spillover effect ($\theta =0$ means no spillover, $\theta =1$ means full spillover). Parameters b and c reflect investment costs, while parameter $\alpha$ weights the influence of the learning and the spillover effect on the investment installation costs.

Let $K_i(t)$ and $I_i(t)$ denote the capital stock (state variable) and investment rate (control variable) of firm i, $i=1,2$, at time t. We assume that firms operate at full capacity (therefore, the output is proportional to the capital stock) and postulate a linear demand function, i.e., $p(t)=A-K_{1}(t)-K_{2}(t)$. The market price of capital is denoted by p(t), while A is the market size. Installation costs are quadratic in the investment rate. Let us suppress the time argument t in the following. Then, the objective function of firm i ($i,j=1,2$, $j \ne i$) read

$$\begin{aligned} \max _{I_{i} \ge 0} \int _{0}^{\infty } e^{-r_{i}t} \Big [(A-K_{i}-K_{j})K_{i}-bI_{i}-cI_{i}^{2}(K_{i}+ \theta K_{j})^{- \alpha } \Big ]\,\mathrm{d}t, \end{aligned}$$

(1)

where $r_i$ is the discount rate of player i. With $\delta$ denoting the depreciation rate, the state dynamics are

$$\begin{aligned} {\dot{K}}_{i} = I_{i}- \delta K_{i}, \quad K_{i}(0)=K_{i,0}, \,\, i=1,2. \end{aligned}$$

(2)

Furthermore, we assume irreversibility of investment of both firms, i.e.,

$$\begin{aligned} I_{i} \ge 0, \quad i=1,2. \end{aligned}$$

(3)

This is a common assumption in capital accumulation games. Moreover, in our model the capital stock works as a proxy for learning effects that reduce the installation costs (depreciation in this context means forgetting). If we would allow negative investments, this assumption could not be used.

Note that in all cases below the optimal investments depend on the initial conditions $K_{i}(0)=K_{i,0}$, $i=1,2$, which suppressed in the following. In the following, we consider the following information/commitment structures of the corresponding Nash equilibrium which are defined by the dependence of the optimal strategies as follows:³

• OL: $I_{1}(t)= \phi _{1} (t)$, $I_{2}(t)= \phi _{2} (t)$,

• M1: $I_{1}(t)= \phi _{1} (t,K_{1})$, $I_{2}(t)= \phi _{2} (t)$,

• M2: $I_{1}(t)= \phi _{1} (t,K_{1})$, $I_{2}(t)= \phi _{2} (t,K_{2})$,

• M3: $I_{1}(t)= \phi _{1} (t,K_{1},K_{2})$, $I_{2}(t)= \phi _{2} (t)$,

• M4: $I_{1}(t)= \phi _{1} (t,K_{1},K_{2})$, $I_{2}(t)= \phi _{2} (t,K_{2})$,

• CL: $I_{1}(t)= \phi _{1} (t,K_{1},K_{2})$, $I_{2}(t)= \phi _{2} (t,K_{1},K_{2})$,

where “Mi” denote strategies corresponding to a mixed information/commitment structure to the capital stocks of both players (i.e., mix of open- and closed-loop information structure). In the OL case, each firm assumes that their competitor’s strategy is just a function of time and therefore, does not account for changes of the state value, see, e.g., [5, 13] or [19]. In the CL case, each firm is aware that the state variables influence their competitor’s strategy, i.e., optimal strategies are a function of time, both capital stocks and the initial conditions. The latter dependence implies that CL strategies are not Markov perfect, as carefully discussed in [19]. In the mixed cases, the different possibilities are considered which occur if the firms assume that their competitor’s strategy depends on one, both, or none of the state variables. In general, in such a game the problem of informational non-uniqueness arises as discussed, e.g., in [3, 4]. However, if $\phi _{i}( \cdot )$ is defined by firm i’s first-order condition (in the course of solving firm j’s optimal control problem), as used in [13,  example 4.1, pages 87–92] or [19], CL strategies are fixed and this issue resolves. The same method has been successfully applied in a number of interesting papers to obtain mixed-open and closed-loop Nash equilibria, e.g., [17, 20] or [26]. Note that when deriving the optimal strategies, i.e., the best responses to the competitor’s strategy, it must be assumed that the players commit to a certain information structure and cannot adapt their strategy over time by taking more or less information into account. Further note, that the CL Nash equilibrium encompasses as special cases all other cases if the dependence on (a) certain state variable(s) is (are) trivial. A similar property holds for other Nash equilibria as well (e.g., M3 encompasses M1 and OL as special cases).

Please note that there exist four mixed information/commitment structures more that are not listed above. These assume that investments of a firm depend on the capital stock of the other firm and not on its own. Since they are rather unrealistic they are not explored in the paper.

3 Analysis

The Hamiltonian and the Lagrangian of firm i are defined as

$$\begin{aligned} {\mathcal {H}}_i&= (A-K_{i}-K_{j})K_{i}-bI_{i}-cI_{i}^{2}(K_{i}+ \theta K_{j})^{- \alpha } \nonumber \\&\quad + \lambda _{ii} (I_{i}- \delta K_{i})+ \lambda _{ij} (I_{j}- \delta K_{j}), \end{aligned}$$

(4)

and

$$\begin{aligned} {\mathcal {L}}_i ={\mathcal {H}}_i+\mu _{i}I_{i}. \end{aligned}$$

(5)

3.1 Necessary Optimality Conditions

The first-order conditions are for all information structures:

$$\begin{aligned} \frac{\partial {\mathcal {L}}_{i}}{\partial I_{i}}&= -b-2cI_{i}(K_{i}+ \theta K_{j})^{- \alpha }+ \lambda _{ii} + \mu _{i} =0 \nonumber \\&\Longrightarrow I_{i}= \frac{\lambda _{ii} + \mu _{i} -b}{2c} (K_{i}+ \theta K_{j})^{\alpha }. \end{aligned}$$

(6)

Note that the adjoint variable $\lambda _{ii}$ is the marginal value of player i’s own capital stock, $i=1,2$, while $\lambda _{ij}$ with $j=3-i$ is the value firm i assigns to its competitor’s capital stock. $\lambda _{ii}$ differs with respect to the information/commitment structure (see Sect. 3.2), meaning that optimal investments are in general different. In case the constraint $I_i\ge 0$ becomes active, the non-negative Lagrange multiplier can be determined by means of the first-order necessary conditions, i.e.,

$$\begin{aligned} \mu _i= b-\lambda _{ii},\quad i=1,2. \end{aligned}$$

(7)

As usual, the complementary slackness conditions have to hold which are

$$\begin{aligned} \mu _i I_i=0,\quad i=1,2. \end{aligned}$$

(8)

3.2 Adjoint Equations

The adjoint equations (as derived by Pontryagin’s maximum principle, see, e.g., [5, 16] or [13]) of all 6 cases are defined by the following equations

$$\begin{aligned} {\dot{\lambda }}_{11}&= (r_{1}+ \delta ) \lambda _{11} -(A-2K_{1}-K_{2}) \nonumber \\&\quad -c \alpha I_{1}^{2}(K_{1}+ \theta K_{2})^{- \alpha -1} - \eta _{11} \theta \varGamma _{12}, \nonumber \\ {\dot{\lambda }}_{12}&= (r_{1}+ \delta ) \lambda _{12} +K_{1}-c \alpha \theta I_{1}^{2}(K_{1}+ \theta K_{2})^{- \alpha -1} - \eta _{12} \varGamma _{12}, \nonumber \\ {\dot{\lambda }}_{21}&= (r_{2}+ \delta ) \lambda _{21} +K_{2}-c \alpha \theta I_{2}^{2}(K_{1}+ \theta K_{1})^{- \alpha -1} - \eta _{21} \varGamma _{21},\nonumber \\ {\dot{\lambda }}_{22}&= (r_{2}+ \delta ) \lambda _{22} -(A-2K_{2}-K_{1}) \nonumber \\&\quad -c \alpha I_{2}^{2}(K_{2}+ \theta K_{1})^{- \alpha -1} - \eta _{22} \theta \varGamma _{21}, \end{aligned}$$

(9)

where for $i=1,2$ and $k =3-i$,

$$\begin{aligned} \varGamma _{ik} := \left( \alpha \frac{\lambda _{kk} -b}{2c} (K_{k}+ \theta K_{i})^{\alpha -1} \right) \lambda _{ik}. \end{aligned}$$

The $\eta _{ij}$, $i,j=1,2$, determine whether the additional term $\varGamma _{ik}:=\frac{\partial {\mathcal {H}}_{i}}{\partial I_{k}} \frac{\partial \phi _{k} ( \cdot )}{\partial K_{j}}$ ($k =3-i$) is present in the adjoint equation or not. They are different for all cases and are defined in Table 1.

Table 1 Values of $\eta _{ij}$, $i,j=1,2$, for all information/commitment structures

Hence, in a compact way this notation covers all 6 different subcases depending on the information structure.

Among the 6 information/commitment structures introduced in Sect. 2, OL and the CL (memoryless) case (explicitly discussed in Sects. 3.2.1 and 3.2.2, respectively) are standard in the literature on differential game (see [13] or [19]). In case of the OL Nash equilibrium, the adjoint equations (9) reduce to ($\eta _{ij} =0$ for all i, j, see first column in Table 1), i.e.,

$$\begin{aligned} {\dot{\lambda }}_{11}&= (r_{1}+ \delta ) \lambda _{11} -(A-2K_{1}-K_{2})-c \alpha I_{1}^{2}(K_{1}+ \theta K_{2})^{- \alpha -1} , \nonumber \\ {\dot{\lambda }}_{12}&= (r_{1}+ \delta ) \lambda _{12} +K_{1}-c \alpha \theta I_{1}^{2}(K_{1}+ \theta K_{2})^{- \alpha -1} , \nonumber \\ {\dot{\lambda }}_{21}&= (r_{2}+ \delta ) \lambda _{21} +K_{2}-c \alpha \theta I_{2}^{2}(K_{1}+ \theta K_{1})^{- \alpha -1} ,\nonumber \\ {\dot{\lambda }}_{22}&= (r_{2}+ \delta ) \lambda _{22} -(A-2K_{2}-K_{1})-c \alpha I_{2}^{2}(K_{2}+ \theta K_{1})^{- \alpha -1}, \end{aligned}$$

(10)

whereas in the CL memoryless Nash equilibrium they read ($\eta _{ij} =1$ for all i, j, see last column in Table 1), i.e.,

$$\begin{aligned} {\dot{\lambda }}_{11}= & {} (r_{1}+ \delta ) \lambda _{11} -(A-2K_{1}-K_{2})-c \alpha I_{1}^{2}(K_{1}+ \theta K_{2})^{- \alpha -1} - \theta \varGamma _{12}, \nonumber \\ {\dot{\lambda }}_{12}= & {} (r_{1}+ \delta ) \lambda _{12} +K_{1}-c \alpha \theta I_{1}^{2}(K_{1}+ \theta K_{2})^{- \alpha -1} - \varGamma _{12}, \nonumber \\ {\dot{\lambda }}_{21}= & {} (r_{2}+ \delta ) \lambda _{21} +K_{2}-c \alpha \theta I_{2}^{2}(K_{1}+ \theta K_{1})^{- \alpha -1} - \varGamma _{21},\nonumber \\ {\dot{\lambda }}_{22}= & {} (r_{2}+ \delta ) \lambda _{22} -(A-2K_{2}-K_{1}) -c \alpha I_{2}^{2}(K_{2}+ \theta K_{1})^{- \alpha -1} - \theta \varGamma _{21}. \end{aligned}$$

(11)

The usual transversality conditions for infinite time horizon (see [16]) have to hold for all adjoint variables in all cases, i.e.,

$$\begin{aligned} \lim _{t \rightarrow \infty } e^{-r_{i}t} \lambda _{ij} (t)=0, \quad i,j=1,2. \end{aligned}$$

(12)

3.2.1 Open-Loop

In the OL Nash equilibrium, both firms assume that their opponent’s investment strategy is just a function of time. Therefore, they do not take into account the actual effect of the capital stocks on the investment strategy when determining the shadow prices of the state variables [see (10)]. This is the reason why OL (and the mixed cases) are usually considered as not being realistic as by means of the problem formulation: the players have sufficient information to derive that their opponent’s strategy is actually a function of the capital stocks. Note, however, that OL can be considered as the foundation of the other cases and therefore can give some insights about the impact of the capital stocks and their marginal value on the optimal strategy.

It makes sense, as long as the capital stock is not too large, that a firm assigns a positive shadow price to its own capital stock as capital leads to output which generates revenues and to learning effects, i.e., a high capital stock reduces investment installation costs. The capital stock, however, negatively affects the price, which also needs to be taken into account.

It is interesting how a firm appreciates the capital stock of the other firm. Consider, without loss of generality, the appreciation of firm 2’s capital stock, $K_{2},$ by firm 1. This is measured by the adjoint variable, $\lambda _{12},$ which is firm 1’s shadow price of firm 2’s capital stock. A positive value of $\lambda _{12}$ means that $K_{2}$ is a good stock for firm 1. This is because an increased value of $K_{2}$ reduces the adjustment costs by the term $\theta K_{2},$ which makes investment cheaper for firm 1. The term $-c\alpha \theta I_{i}^{2}\left( K_{i}+\theta K_{j}\right) ^{-\alpha -1}$ in the ${\dot{\lambda }}_{ij}$-equation reflects this effect. A negative value of $\lambda _{12}$ implies that a large value of $K_{2}$ is negatively appreciated by firm 1. The economic reason for this is that increased production by firm 2 reduces the output price on the market, which reduces firm 1’s revenue. This is reflected by the term $K_{i}$ (a one-unit increase of $K_{j}$ reduces the output price with one unit, resulting in a revenue decrease by firm 1’s quantity $K_{i})$ in the ${\dot{\lambda }}_{ij}$-equation. In the numerical experiments in Sect. 4, it turns out that the steady-state value of $\lambda _{12}$ is negative so that in steady state the positive adjustment cost effect is always dominated by the negative price effect.

3.2.2 Closed-Loop Memoryless

In the CL, which is considered as more realistic, firm 2 takes into account that firm 1’s investment is, not only a function of time, but it is also influenced by the capital stock of both firms, i.e., $I_{1}=\phi \left( t,K_{1},K_{2} \right)$. By its own capital stock, $K_{2},$ firm 2 influences firm 1’s investment $I_{1}$. This generates the term $\varGamma _{21} = \left( \alpha \theta \frac{\lambda _{11}-b }{2c}\left( K_{1}+\theta K_{2}\right) ^{\alpha -1}\right) \left( -\lambda _{21}\right)$ in the ${\dot{\lambda }}_{22}$-equation [see (11)], as explained, e.g., in [19]. The economic interpretation is that when $K_{2}$ increases, through the spillover effect the adjustment costs of firm 1’s investment decrease. This will, ceteris paribus, enlarge firm 1’s investment and thus, firm 1’s capital stock, which in turn reduces the output price and thus, firm 2’s revenue. Hence, this gives an incentive for firm 2 to reduce the accumulation of its own capital stock $K_{2}$ and thus, reduce investment $I_{2}$. Note that firm 2’s investment $I_{2}$ is directly influenced by the shadow price for $K_{2},$ $\lambda _{22},$ see expression (6). We denote this effect as the investment-spillover effect.

Firm 1’s investment is also influenced by its own capital stock, $K_{1}.$ An additional unit of $K_{1}$ reduces firm 1’s adjustment costs by the term $\alpha \frac{\lambda _{11}-b}{2c}\left( K_{1}+\theta K_{2}\right) ^{\alpha -1}.$ This affects firm 2’s appreciation of firm 1’s capital stock,$\ \lambda _{21},$ by the amount of $\alpha \frac{\lambda _{11}-b}{2c}\left( K_{1}+\theta K_{2}\right) ^{\alpha -1}\left( -\lambda _{21}\right) ,$ which explains why this term occurs in the ${\dot{\lambda }}_{21}$-equation. In fact, since a larger $K_{1}$ will reduce firm 1’s adjustment costs, it makes firm 1 a stronger competitor for firm 2. This implies that a larger $K_{1}$ is more damaging for firm 2, and therefore, this effect will make $\lambda _{21}$ more negative. This enlarges, in absolute terms, the term $\left( \alpha \theta \frac{\lambda _{11}-b}{2c}\left( K_{1}+\theta K_{2}\right) ^{\alpha -1}\right) \left( -\lambda _{21}\right)$ in the ${\dot{\lambda }}_{22}$-equation, which makes the negative spillover effect of the previous paragraph stronger. We denote this effect as the investment-spillover-enlargement effect.

In the CL case, both firms are affected by the double negative effect of the investment-spillover-enlargement effect enlarging the investment-spillover effect for both firms.

3.2.3 Mixed Open- and Closed-Loop Information Structures

Mixed 1 Concerning Mixed 1 (M1), investment develops in the same way as under OL. Since firm 1’s investment is a function of its own capital stock, there is an investment-spillover-enlargement effect, but this does not affect firm 2’s investment due to the absence of the investment-spillover effect.

Mixed 2 In the Mixed 2 case (M2), the investments of both firms are functions of the own capital stock but not by the capital stock of the competitor. This implies that the investment-spillover-enlargement effect is present, but it will have no effect because the investment-spillover effect is absent.

Mixed 3 Firm 1’s investment is assumed to be a function of the own and firm 2’s capital stock. Therefore, firm 2 takes account of the fact that increasing its capital stock will reduce the adjustment costs of firm 1. The resulting investment-spillover effect reduces firm 2’s investments. This is enlarged by the investment-spillover-enlargement effect. The latter is caused by the fact that $I_{1}$ is also a function of $K_{1}.$ This causes an additional reduction in firm 2’s investments.

Mixed 4 In Mixed 4, firm 1’s investment is assumed to be like in the CL case (and in M3), i.e., a function of the two capital stocks and time. Firm 2’s investment, on the other hand, is affected by $K_{2}$ and t, but, unlike $I_{1},$ not by the capital stock, $K_{1},$ of the other firm. The latter leads to the absence of the investment-spillover effect. Since $I_{2}$ is not a function of $K_{1},$ the resulting reduction in the adjustment costs of Firm 2’s investment due to an enlargement of $K_{1}$ will not lead to more investment by Firm 2. The investment-spillover-enlargement effect is there, because $I_{2}$ still depends on $K_{2}.$ However, this will have no effect on $I_{1},$ because the investment-spillover-enlargement effect enlarges an effect, the investment-spillover effect, that is absent.

Technically, the point is that $I_{1}$ is influenced by $\lambda _{11},$ which is influenced by the investment-spillover effect, but not directly by $\lambda _{12}$, which is influenced by the investment-spillover-enlargement effect. If there is no investment-spillover effect, then $\lambda _{12}$ does not occur in the ${\dot{\lambda }}_{11}$-equation, and therefore, in such a case the investment-spillover-enlargement effect does not affect $I_{1}$.

4 Numerical Results

For the above model (1), (2) and (3) together with the information structures, the solution as well as the steady state values cannot be obtained analytically. Therefore, we have to rely on numerical calculations. For the used boundary value as well as for the appropriate asymptotic boundary condition, we approach we refer to [16]. For the steady states, we (numerically) obtain unique values (together with saddle path stability).

The parameters used in the base case (for comparability taken from the seminal paper [24]) are

$$\begin{aligned}&c=10;\quad b=100;\quad \delta =0.1;\quad \alpha =1;\quad r_{1} =r_{2} =0.05; \nonumber \\&A=60;\quad \theta =0.8. \end{aligned}$$

The corresponding steady state values are shown in Table 2. It makes sense that, in the long run, firms appreciate their own capital stock positively, $\lambda _{ii}>0$, and the opponent’s capital stock negatively, $\lambda _{ij}<0$. The presence of both, the investment-spillover effect and the investment-spillover-enlargement effect, in the CL equilibrium generate lower values for the capital stocks in equilibrium compared to OL, while the payoffs for both firms (represented in Table 2 by the instant utility $IU_i$, $i=1,2$) are higher. This would imply that information pays off. That this is not completely true is shown by the asymmetric cases (M3, M4) where the more informed firm actually has a lower payoff. In these cases, firm 2 takes into account that its own capital stock is advantageous for its competitor and acts more cautiously (investment-spillover effect). Firm 1 does not incorporate this information and therefore, acts more aggressively than firm 2 leading to a higher long run capital stock and higher profits. Due to the higher capital stock of its opponent firm 1 acts even more cautiously to prevent the price getting too low. Furthermore, in M3 and in M4 the investment-spillover-enlargement effect is present, i.e., firm 1 is aware that firm 2 learns from its capital stock. If, however, both firms invest much, because they do not take account of this information, the total capital stock of both firms together is the largest and therefore, the price is the lowest. Therefore, profits are lower compared to the case, where both firms act more cautiously.

Table 2 Steady state values for $\theta =0.8$

Fig. 1

Optimal trajectories for the initial state values $K_{1,0}=0$ and $K_{2,0}=10$ (left panel) and corresponding objective value (right panel; $\blacksquare$ represents player 1, $\bullet$ player 2)

Figure 1 shows the solution paths for the different information structures if firm 2 has a competitive advantage against firm 1 in the sense that it has an positive initial capital stock $K_{2,0}=10$, while the capital stock of firm 1 is zero ($K_{1,0}=0$). The control constraint $I_2\ge 0$ can become active. In particular, in cases M3, M4 and CL the second firm does not invest anything in the beginning. In these cases, the investment-spillover effect is present, i.e., firm 2 is aware that its capital stock affects the competitor’s investment strategy and acts more cautiously.

It becomes evident in the right panel of Fig. 1 that firm 2 has a competitive advantage from its higher initial capital stock as for the given solution paths its objective value $V_2$ is larger for most of the cases, but not for all of them. In cases M3 and M4, firm 1 acts more aggressively than firm 2 as it does not incorporate that its capital stock affects the investment strategy of the competitor and firm 2 acts more cautiously to prevent spillovers.

For a comparison on how the different capital stocks affect the optimal solution for the different cases, Figs. 2 and 3 show the time paths for OL, CL and M4, which are the two mixed cases which differ most. Depending on the information structure, a different player might choose a higher control. In the CL case, where all information is included, the second player initially invests nothing, only after some time he starts to increase the output. The first player invests more in the beginning to compensate for the lower capital stock. As its initial capital stock is zero, firm 1 needs to invest to make some profits. A small capital stock means that spillovers are small. As the capital stock grows, firm 1 reduces its investments because of the investment-spillover effect and to prevent the price to further decrease due to the size of its own capital stock.

Fig. 2

Timepaths for OL (left panel) and CL (right panel)

Fig. 3

Timepath M4

In Figs. 2 and 4, it can be seen that in the CL case the firm with a lower capital stock increases its capital stock very fast until the other firm’s capital stock level is reached, while the latter remains more or less unchanged. Then, both capital stocks approach the steady states slowly. This is in contrast to the OL case, where the approach to the steady state is smoother. There are two reasons for this. First, the steady states in case of CL are lower so that firm 1 catches up faster. Second, firm 2 starts investing later, because its adjustment costs are lower when $K_{1}$ is larger. So firm 2 first lets firm 1 build up its capital stock before it starts investing itself.

Fig. 4

Phase portrait for OL (left panel) and CL (right panel)

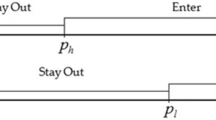
Effect of Initial Conditions $K_{1,0}$ and $K_{2,0}$ Note that there are solution paths in the CL case where control constraints become active and inactive several times. E.g., for the case with $K_{1,0}=0$ and $K_{2,0}=17.8$, which is depicted in Fig. 5, the solution path consists of four arcs, on the first $I_1>0$, $I_2=0$, on the second $I_1=0$, $I_2=0$, on the third again $I_1>0$, $I_2=0$ and finally on the fourth we have $I_1>0$, $I_2>0$. Similar to the case with $K_{1,0}=0$ and $K_{2,0}=10$, firm 1 needs to invest first to get its capital stock close to the capital stock of firm 2. Meanwhile, firm 2 invests nothing to increase the price, so its capital stock just depreciates. After some time, capital stock of firm 1 is so large that it stops investing. Capital depreciates, and after some time it reaches a level—first for firm 1, but then also for firm 2—that it pays off to invest again to support output. However, investments are smaller than capital depreciation as firms are still interested in lowering the price. Similarly if $K_{1,0}$ is larger than $K_{2,0}$, it can happen that first $I_1=0$, $I_2>0$, then $I_1=0$, $I_2=0$, then again $I_1=0$, $I_2>0$ and finally $I_1>0$, $I_2>0$.

Fig. 5

Time path CL for $K_{1,0}=0$ and $K_{2,0}=17.8$

Fig. 6

Optimal trajectories for the initial state values $K_{1,0}=0.1$ and $K_{2,0}=0.1$ (left panel) and corresponding objective value (right panel; $\blacksquare$ represents player 1, $\bullet$ player 2)

The optimal trajectories for small initial state values $K_{1,0}=0.1$ and $K_{2,0}=0.1$ are shown in Fig. 6 as well as the corresponding objective value. Here, no control constraints are active for the cases OL, M1, M2 and, CL. The constraint $I_2\ge 0$ is active in the beginning for M3 and M4. Therefore, the investment-spillover effect is present again as the firm, which takes into account that its capital stock affects the competitor’s investment strategy, acts more cautiously again.

Figure 6 shows that the OL payoff is larger than the CL payoff in most cases. The reason is that for CL the investment-spillover effect, augmented by the investment-spillover-enlargement effect, reduces the investment by both firms. If one firm invests a lot, it reduces the adjustment costs of its competitor considerably. Therefore, in the CL equilibrium the firms underinvest to be a tough competitor.

Effect of Spillover Parameter $\theta$ We now investigate the effect of the spillover parameter $\theta$. To do so, we decrease $\theta$ to 0.01 and keep $K_{1,0}=0$ and $K_{2,0}=10$. The resulting trajectories can be seen in Fig. 7 along with the corresponding objective value. The corresponding time paths for the OL and the CL case are shown in Fig. 8. The control constraint $I_2=0$ is active in the beginning of M3, M4 and CL. Unlike before, player 2 now always has an advantage in terms of always having a higher objective value than the first player because of the higher initial capital stock. The reason for this is that if spillovers are not present, firm 1 cannot exploit the capital stock of the competitor and the only incentive for firm 2 not to invest too much into its own capital stock is the negative impact of the capital stock on the price. Therefore, firm 2 would not act as cautiously as for a high value of $\theta$.

Fig. 7

Optimal trajectories for the initial state values $K_{1,0}=0$ and $K_{2,0}=10$ for $\theta =0.01$ and corresponding objective value ($\blacksquare$ represents player 1, $\bullet$ player 2)

In the left panel of Fig. 7, we clearly see that whenever $I_{1}=\phi \left( K_{1},K_{2},t\right) ,$ which holds in M3, M4 and CL, the combined effect of investment-spillover and investment-spillover-enlargement causes that firm 1 catches up quite early with firm 2 with respect to the level of their capital stocks. However, in the end the considered trajectories end up in a similar steady state as they do in the other cases. This is because the low spillover parameter $\theta$ reduces the strategic underinvestment effect of the CL equilibrium in such a way that the payoffs of the firms are almost the same as in the OL case, see the right panel of Fig. 7.

Fig. 8

Time paths for the initial state values $K_{1,0}=0$ and $K_{2,0}=10$ for $\theta =0.01$ for OL (left panel) and CL (right panel)

The impact of parameter $\theta$ on the steady state values is shown in Fig. 9 for the OL and the CL case. Interestingly, the effect of $\theta$ on the OL and the CL steady state is the opposite. The reason is that in the OL case the cost effect is the only effect, while in the CL case the firms start to act more strategically if $\theta$ is larger. Note, however, that the difference in the state values and controls is particularly small for OL, while the difference for the solution paths is significant, compare Figs. 2 and 8. While for a high $\theta$ firm 2 would initially invest nothing, and firm 1 would exploit the spillovers, for a low $\theta$ the strategy is the opposite: firm 2 invests much as due to the learning effects investments are efficient. Firm 1 only affords low investments in the beginning, but increases them over time. Firm 2 has to decrease investments so to prevent the price getting too low, which is also the case for firm 1 after some time.

Fig. 9

Dependency of the steady state values on $\theta$ for OL (left panel) and CL (right panel)

Figure 9 clearly shows the strategic underinvestment effect in the CL case. A larger $\theta$ implies that the firms benefit more from the increased capital stock of their competitor in the sense that adjustment costs are reduced more. This indeed leads in the OL case to the fact that firm investments are increasing in $\theta$. However, a larger $\theta$ in the CL case implies that firms increase underinvestment in order not to let the other firm benefit from their large capital stock.

Effect of Learning and Spillover Parameter $\alpha$ The impact of parameter $\alpha$ is shown in Fig. 10. Since a high $\alpha$ means that the impact of the capital stocks on the investment adaption costs get larger, in the OL case it makes sense that a higher value of $\alpha$ lead to higher investments and higher steady state values. However, in the CL case it is opposite, because there both firms are affected by the double negative effect of the investment-spillover-enlargement effect enlarging the investment-spillover effect for both firms. This double negative effect becomes bigger when $\alpha$ increases.

Fig. 10

Dependency of the steady state values on $\alpha$ for OL (left panel) and CL (right panel)

5 Conclusion

When determining the optimal strategy in a capital accumulation game, a firm not only has to take into account how the long-run outcome is affected by its own investments and capital stock but also by the investments and the capital stock of its opponent particularly in the presence of spillover effects. Different information structures account for the extent to which a firm includes information about the opponent’s investment strategy in its valuation of the capital stocks and therefore in its strategy.

To properly understand the impact of spillover and learning effects, it is helpful to not only consider a CL information structure, where the firms are aware that their competitor’s strategy depends on both capital stocks, but also to look at what happens if this is not the case. There are two particular effects of information: the investment-spillover effect which makes firms invest less in order to keep spillovers to the competitor low and investment-spillover-enlargement effect which makes firms invest even less to prevent the competitor from taking advantage of the spillovers by means of the learning effects caused by a high capital stock.

One would expect that incorporating more information about how the competitor determines his strategy would lead to higher payoffs, but this is not entirely true. If a firm takes into account that its own capital stock is advantageous for the competitor, it would act more cautiously than if it does not. If, however, only one of the firms considers the investment strategy of the other firm to depend on its own capital stock, but the other one does not, then the firm with less information has the higher payoff as it acts more aggressively and has a higher capital stock in the long run. If both firms invest much, however, by not taking the impact of their capital stock on the investment installation costs of the other firm into account, the total output is very high. This means that the market price is low, and the payoffs are smaller than if both firms incorporate the spillover effects in their valuation of their own capital stocks.

The outcome, that taking certain information into account only leads to a higher payoff if the other player does the same, is reminiscent of the prisoners’ dilemma: if both players do not confess (which corresponds to taking information into account in the capital accumulation problem), the payoff is higher than if both players confess (i.e., do not take the impact of the capital stocks into account). If only one of the players confesses, then this player has a higher payoff as long as the other player does not confess.

It is not surprising that the extent of the spillover effects affect the optimal strategy. The steady state is, however, stronger affected by spillover effects if at least one of the firms is aware that their opponents strategy is affected by their own capital stock. Then, this firm would invest less to prevent spillovers. If the other firm’s capital does not have much impact on the investment installation costs, investments are less efficient and a firm would invest slightly less.

In the present paper, we saw that the used information structure substantially affects the outcome, but not always as expected. While certainly for good reasons OL and mixed strategies are often considered to be not particularly realistic, it becomes evident that the perception of the competitor’s strategy is as important for the outcome as what the competitor actually does. It would be interesting to compare the impact of different information structures in problems where the optimal long-run solution is history-dependent, i.e., where depending on the initial state value it is optimal to approach different long-run steady states.