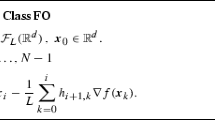1 Introduction

An L-smooth and \(\mu \)-strongly convex function \(f :{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is characterized by the two properties

$$\begin{aligned} \Vert \nabla f(x) - \nabla f(y) \Vert \le L\Vert x - y \Vert \end{aligned}$$

and

$$\begin{aligned} f(x) \ge f(y) + \langle \nabla f(y), x - y \rangle + \frac{\mu }{2} \Vert x - y \Vert ^2 \end{aligned}$$

for some constants \(0 < \mu \le L\) and all \(x,y \in {\mathbb {R}}^n\). Here, \(\langle \ , \ \rangle \) can be any inner product on \({\mathbb {R}}^n\) with corresponding norm \(\Vert \cdot \Vert \), and \(\nabla f\) denotes the gradient with respect to this inner product. Note that the constants \(\mu \) and L depend on the chosen inner product. The class of such functions plays a main role in the convergence theory of the gradient method and related descent methods for finding the unique global minimum \(x^*\) of a given f. The update rule of the gradient method is

$$\begin{aligned} x^+ = x - h \nabla f(x), \end{aligned}$$

where \(h > 0\) is a step size which may depend on the current point x. It is well known that the fixed step size

$$\begin{aligned} h = \frac{2}{L + \mu } \end{aligned}$$

achieves the optimal error reduction

$$\begin{aligned} \Vert x^+ - x^* \Vert ^2 \le \left( \frac{\kappa _f - 1}{\kappa _f + 1} \right) ^2 \Vert x - x^* \Vert ^2, \quad \kappa _f = \frac{L}{\mu }, \end{aligned}$$
(1.1)

per step, which inductively implies the convergence of the method to \(x^*\). We refer to [6, Theorem 2.1.15] for details.

In a more general setting of proximal gradient methods, it has recently been shown by Taylor et al. [9, Theorem 3.3 with \(h=0\)] that the same rate is also valid for the error in function value. Specifically, for any

$$\begin{aligned} 0 \le h \le \frac{2}{L + \mu } \end{aligned}$$
(1.2)

it holds that

$$\begin{aligned} f(x^+) - f(x^*) \le (1 - h\mu )^2 (f(x) - f(x^*)). \end{aligned}$$
(1.3)

Moreover, for \(\frac{2}{L+\mu } \le h < \frac{2}{L}\) one has \(f(x^+) - f(x^*) \le (hL - 1)^2 (f(x) - f(x^*))\). This automatically follows from (1.2) and (1.3) by using a weaker strong convexity bound \(0 < \mu ' \le \mu \) satisfying \(h = \frac{2}{L + \mu '}\) and noting that \(1 - h \mu ' = hL - 1\). The optimal choice in the estimates is \(h = 2/(L + \mu )\) and leads to

$$\begin{aligned} f(x^+) - f(x^*) \le \left( \frac{\kappa _f - 1}{\kappa _f + 1} \right) ^2 (f(x) - f(x^*)). \end{aligned}$$
(1.4)

This estimate for one step of the method is highly nontrivial. Obviously, it implies the same inequality for the gradient descent method with exact line search (when the left side is minimized over all h), which has been obtained earlier in [2]. Moreover, this estimate is known to be optimal in the class of L-smooth and \(\mu \)-strongly convex functions. In fact, it is already optimal for quadratic functions in that class; see, e.g., [2, Example 1.3].

Of course, in many applications the difference \(f(x) - f(x^*)\) is a natural error measure by itself. For example, for strongly convex quadratic functions it is proportional to the squared energy norm of the quadratic form. In general, for an L-smooth and \(\mu \)-convex function we always have

$$\begin{aligned} \frac{\mu }{2} \Vert x - x^* \Vert ^2 \le f(x) - f(x^*) \le \frac{L}{2} \Vert x - x^* \Vert ^2, \end{aligned}$$

which clearly shows that \(f(x_{\ell }) - f(x^*) \rightarrow 0\) for an iterative method implies \(\Vert x_\ell - x^* \Vert \rightarrow 0\) for \(\ell \rightarrow \infty \). Moreover, both error measures will exhibit the same R-linear convergence rate. The novelty of the estimate (1.4) is that one also has an optimal Q-linear rate for the function values, both for fixed step sizes and exact line search. (We refer to [8] for the definitions of R- and Q-linear rate.) However, compared to (1.1) an estimate like (1.4) is “more intrinsic,” because the chosen inner product in \({\mathbb {R}}^n\) enters only via the constants \(\mu \) and L. In this short note, we illustrate this advantage by showing that (1.4) allows for a rather clean analysis of general variable metric methods, as well as gradient-related methods subject to angle and scaling conditions. In addition, in Theorem 4.2 we show how (1.4) already implies the sharp rates for inexact gradient methods under relative error bounds with fixed step sizes, based on a suitable change of the metric, thereby improving and simplifying a similar result in [3].

2 Variable Metric Method

We first consider the variable metric method. Here the update rule reads

$$\begin{aligned} x^+ = x - h A^{-1} \nabla f(x), \end{aligned}$$
(2.1)

where A is a symmetric (with respect to the given inner product) and positive definite matrix. It is well known that such an update step can also be interpreted as a gradient step with respect to a modified inner product. This leads to the following result that will be the basis for our further considerations.

Theorem 2.1

Assume the eigenvalues of A are in the positive interval \([\lambda ,\varLambda ]\) and define

$$\begin{aligned} {\bar{h}} = \frac{2}{L/\lambda + \mu /\varLambda }. \end{aligned}$$

Then, \(x^+\) in (2.1) with \(0 \le h \le {\bar{h}}\) satisfies

$$\begin{aligned} f(x^+) - f(x^*) \le \left( 1 - \frac{h \mu }{\varLambda } \right) ^2 (f(x) - f(x^*)). \end{aligned}$$

In particular, the step size \(h = {\bar{h}}\) yields

$$\begin{aligned} f(x^+) - f(x^*) \le \left( \frac{\kappa _{f,A} - 1}{\kappa _{f,A} + 1} \right) ^2 (f(x) - f(x^*)), \quad \kappa _{f,A} = \frac{L }{\mu } \, \frac{\varLambda }{\lambda }. \end{aligned}$$
(2.2)

Proof

The result is obtained from (1.3) by noting that \(\nabla _A f(x) = A^{-1}\nabla f(x)\) is the gradient of f with respect to the A-inner product \(\langle x, y \rangle _A = \langle x, Ay \rangle \). We have

$$\begin{aligned} \langle \nabla _A f(x) - \nabla _A f(y), x - y \rangle _A \le L \Vert x - y \Vert ^2 \le \frac{L}{\lambda } \Vert x - y \Vert _A^2, \end{aligned}$$

as well as

$$\begin{aligned} \langle \nabla _A f(x) - \nabla _A f(y), x - y \rangle _A \ge \mu \Vert x - y \Vert ^2 \ge \frac{\mu }{\varLambda } \Vert x - y \Vert _A^2 \end{aligned}$$

for all x, y. These two conditions are equivalent to f being \((L/\lambda )\)-smooth and \((\mu /\varLambda )\)-strongly convex in that A-inner product; see, e.g., [6, Theorems 2.1.5  & 2.1.9]. Thus, in (1.2) and (1.3), we can replace \(\mu \) with \(\mu /\varLambda \) and L by \(L/\lambda \), which is exactly the statement of the theorem. \(\square \)

An alternative, and somewhat more direct proof of Theorem 2.1 that does not require changing the inner product, can be given by applying the result (1.3) directly to the function \(g(y) = f(A^{-1/2}y)\) at \(y = A^{1/2}x\).

Observe that \(\kappa _{f,A} = \kappa _f \cdot \kappa _A\) with \(\kappa _A = \varLambda / \lambda \ge 1\) the condition number of A. The contraction factor in (2.2) will therefore always be worse than the original factor in (1.4), which corresponds to \(A=I\). This might seem suboptimal since in Newton’s method, and under additional regularity conditions, the contraction factor improves when choosing \(A = \nabla ^2 f(x)\). However, for the general class of methods (2.1), the result in Theorem 2.1 is optimal. This can already be seen for the function \(f(x) = \frac{1}{2} \Vert x\Vert ^2\), in which case (2.1) becomes the linear iteration \(x^+ = (I - hA^{-1})x\). Its contraction factor as predicted by (2.2) is bounded by \((\kappa _A - 1)^2/(\kappa _A + 1)^2\), which is indeed a tight bound: as in [2, Example 1.3], take \(A = {{\,\mathrm{diag}\,}}(\lambda , \ldots , \varLambda )\) and \(x = (x_1, 0, \ldots , 0, x_n)\). Then, an exact line search yields \(x^+ = (\kappa _A - 1)/(\kappa _A + 1) \cdot (-x_1, 0, \ldots , 0, x_n)\), and clearly there cannot be a better contraction factor with fixed step size. Note that the step size \({\bar{h}}\) in Theorem 2.1 also leads to equality in (2.2) when x is an eigenvector corresponding to \(\lambda \) or \(\varLambda \). For a less trivial example, consider \(f(x) = \frac{1}{2} \langle x, A^{-1} x \rangle \). Then, (2.1) becomes \(x^+ = (I - hA^{-2})x\) and the same x from above now leads to a contraction with the factor \((\kappa _{A^2} - 1)^2/(\kappa _{A^2}+ 1)^2\) where indeed \(\kappa _{A^2} = \kappa _f \kappa _A\), as predicted by Theorem 2.1.

3 Gradient-Related Methods

Next, we provide error estimates for gradient-related descent methods under angle and scaling conditions. Specifically, we consider the update rule

$$\begin{aligned} x^+ = x - h d, \end{aligned}$$
(3.1)

where \(-d\) is a descent direction, that is, d satisfies

$$\begin{aligned} \langle \nabla f(x), d \rangle = \cos \theta \Vert \nabla f(x) \Vert \Vert d \Vert , \quad \cos \theta > 0, \end{aligned}$$
(3.2)

for some \(\theta \in [0, \pi /2)\). This condition is very natural since it guarantees the convergence of (3.1); see, e.g., [7, Chapter 3.2]. In particular, for the case of exact line search, it has been shown in [2, Theorem 5.1] that

$$\begin{aligned} f(x^+) - f(x^*) \le \left( \frac{\kappa _{f,\theta } - 1}{\kappa _{f,\theta } + 1} \right) ^2 (f(x) - f(x^*)), \quad \kappa _{f,\theta } = \frac{L}{\mu } \left( \frac{1 + \sin \theta }{1 - \sin \theta }\right) , \end{aligned}$$
(3.3)

and that this Q-linear rate is optimal. For the case of quadratic functions, this has been known before; see, e.g., [5]. We also mention the result of [1, Theorem 3.3], which identifies the rate in (3.3) as optimal R-linear rate for exact line search when f is twice continuously differentiable.

Here, we aim to generalize this result to fixed step sizes. The extent to which this is possible depends on the available information about the quantities \(\Vert \nabla f(x) \Vert \), \(\Vert d \Vert \), and \(\langle \nabla f(x), d \rangle \). The basic idea is to interpret (3.1) as a variable metric method in order to apply Theorem 2.1. For this, we need to find a symmetric and positive definite matrix A satisfying

$$\begin{aligned} A d = \nabla f(x) \end{aligned}$$

and estimate its condition number. Such a matrix can be found explicitly using the following lemma, which originates from the SR1 update rule; see, e.g., [7].

Lemma 3.1

Let \(u, v \in {\mathbb {R}}^n\) such that \(\Vert u \Vert = \Vert v \Vert = 1\) and \(\langle u, v \rangle = \cos \theta \). Then, the matrix

$$\begin{aligned} B = \frac{1}{\alpha } \left( I - \frac{r r^*}{\langle r, u \rangle } \right) , \quad r = u - \alpha v, \quad \alpha = \frac{1 - \sin \theta }{\cos \theta } = \frac{\cos \theta }{1+\sin \theta } \end{aligned}$$

is symmetric (for the given inner product), satisfies \(Bu=v\), and has

$$\begin{aligned} \lambda _{\min }(B) = \frac{\cos \theta }{1 + \sin \theta }, \quad \lambda _{\max }(B) = \frac{\cos \theta }{1 - \sin \theta }, \end{aligned}$$

as its smallest and largest eigenvalues, respectively. Here, \(rr^*\) denotes the rank-one matrix satisfying \(rr^* x = r \langle r,x\rangle \) for all \(x \in {\mathbb {R}}^n\).

Proof

This is checked by a straightforward calculation. Obviously, the matrix \(I - \frac{\ r^{} r^*}{\langle r, u \rangle }\) equals the identity on the orthogonal complement of r. Its eigenvalue belonging to the eigenvector r is

$$\begin{aligned} 1 - \frac{\Vert r \Vert ^2}{\langle r, u \rangle } = 1 - \frac{1 - 2 \alpha \cos \theta + \alpha ^2}{1 - \alpha \cos \theta } = \frac{1 - \sin \theta - \alpha ^2}{\sin \theta } = \alpha ^2, \end{aligned}$$

where one uses \(1 - \alpha \cos \theta = \sin \theta \) and \(\alpha ^2 = (1 - \sin \theta )/(1 + \sin \theta )\). Therefore, the largest eigenvalue of B is \(1/\alpha \) (with multiplicity \(n-1\)), and the smallest eigenvalue is \(\alpha \). \(\square \)

With Lemma 3.1 and Theorem 2.1 at our disposal, we can state our main result.

Theorem 3.2

Assume (3.2) and

$$\begin{aligned} \Vert d \Vert = c \Vert \nabla f(x) \Vert \end{aligned}$$
(3.4)

for some \(c > 0\). Define

$$\begin{aligned} {\bar{h}} = \frac{2 \cos \theta }{L c (1 + \sin \theta ) + \mu c (1 - \sin \theta )}. \end{aligned}$$

Then, \(x^+\) in (3.1) with \(0 \le h \le {\bar{h}}\) satisfies

$$\begin{aligned} f(x^+) - f(x^*) \le \left( 1 - \frac{h \mu c (1-\sin \theta )}{ \cos \theta } \right) ^2 (f(x) - f(x^*)). \end{aligned}$$

In particular, the step size \(h={\bar{h}}\) yields

$$\begin{aligned} f(x^+) - f(x^*) \le \left( \frac{\kappa _{f,\theta } - 1}{\kappa _{f,\theta } + 1} \right) ^2 (f(x) - f(x^*)). \end{aligned}$$

Proof

If \(d = 0\), the assertion is trivially true. Let \(d \ne 0\). By Lemma 3.1, there exists a symmetric and positive definite matrix of the form \(A = \frac{\Vert \nabla f(x) \Vert }{\Vert d \Vert }B = \frac{1}{c}B\) such that \(Ad = \nabla f(x)\) and

$$\begin{aligned} \lambda _{\min }(A) = \frac{1}{c} \left( \frac{\cos \theta }{1 + \sin \theta } \right) , \quad \lambda _{\max }(A) = \frac{1}{c} \left( \frac{\cos \theta }{1 - \sin \theta } \right) . \end{aligned}$$

The assertion follows therefore directly from Theorem 2.1. \(\square \)

Remark 3.3

The condition (3.4) can be replaced with equivalent conditions such as

$$\begin{aligned} \langle \nabla f(x), d \rangle = \sigma \Vert d \Vert ^2 \end{aligned}$$

for some \(\sigma > 0\). An equivalent version of Theorem 3.2 is obtained by observing that \(\cos \theta = \sigma c\).

To achieve the optimal rate in Theorem 3.2, the exact values of \(\theta \) and c need to be known in order to compute the optimal step size \({\bar{h}}\). In practice, this is almost never the case and only bounds are available. We therefore formulate another, more practical result of (3.2) under the following relaxed angle and scaling conditions: there exists \(0 < c_1 \le c_2\) and \(\theta ' \in [0,\pi /2)\) such that

$$\begin{aligned} \theta \le \theta ', \quad c_1 \Vert \nabla f(x) \Vert \le \Vert d \Vert \le c_2 \Vert \nabla f(x) \Vert . \end{aligned}$$
(3.5)

Under these conditions, the eigenvalues of the matrix \(A = \frac{\Vert \nabla f(x) \Vert }{\Vert d \Vert }B\) in the proof of Theorem 3.2 can be bounded as

$$\begin{aligned} \lambda _{\min }(A) \ge \frac{1}{c_2} \left( \frac{\cos \theta '}{1 + \sin \theta '} \right) , \quad \lambda _{\max }(A) \le \frac{1}{c_1} \left( \frac{\cos \theta '}{1 - \sin \theta '}\right) , \end{aligned}$$

since \(\cos \theta /(1 \pm \sin \theta )\) is monotonically decreasing/increasing in \(\theta \in [0, \pi /2)\). The following result is then again immediately obtained from Theorem 2.1.

Theorem 3.4

Assume (3.5) and define

$$\begin{aligned} {\bar{h}} = \frac{2 \cos \theta ' }{L c_2 (1 + \sin \theta ') + \mu c_1 (1 - \sin \theta ')}. \end{aligned}$$

Then, \(x^+\) in (3.1) with \(0 \le h \le {\bar{h}}\) satisfies

$$\begin{aligned} f(x^+) - f(x^*) \le \left( 1 - \frac{h \mu c_1 ( 1 - \sin \theta ')}{ \cos \theta '} \right) ^2 (f(x) - f(x^*)). \end{aligned}$$

In particular, the step size \(h={\bar{h}}\) yields

$$\begin{aligned} f(x^+) - f(x^*) \le \left( \frac{\kappa ' - 1}{\kappa ' + 1} \right) ^2 (f(x) - f(x^*)), \quad \kappa ' = \frac{L}{\mu } \frac{c_2}{c_1} \left( \frac{1 + \sin \theta '}{1 - \sin \theta '} \right) . \end{aligned}$$

We remark again that if \(c_1 = c_2 = \Vert d \Vert / \Vert \nabla f(x) \Vert \) and \(\theta ' = \theta \) are known, the resulting statements from Theorem 3.4 coincide with those in Theorem 3.2.

Remark 3.5

We conclude the section with a side remark. When just looking at the proofs of Theorem 3.2 or 3.4, it would be natural to ask if there exists a symmetric and positive definite matrix B (and thus A) with a smaller condition number than the one from Lemma 3.1. As for the SR1 update rule, when matrix \(B = B_\alpha \) in the lemma is regarded as a function of \(\alpha \ne 0\), then it is well known that the stated \(\alpha \) is one of the minimizers for the condition number in the class of all positive definite \(B_\alpha \) (another is \(\cos \theta / (1 - \sin \theta )\)); see, e.g., [10]. Indeed, any B with a smaller condition number would lead to a faster rate in Theorem 3.2 (via Theorem 2.1), which is not possible since the rate is known to be optimal when exact line search is used. This reasoning therefore provides a (rather indirect) proof for the following general statement.

Theorem 3.6

Let \(u, v \in {\mathbb {R}}^n\) such that \(\Vert u \Vert = \Vert v \Vert = 1\) and \(\cos \theta = \langle u, v \rangle > 0\) with \(\theta \in [0,\pi /2)\). Then, \((1 + \sin \theta )/(1 - \sin \theta )\) is the minimum possible (spectral) condition number among all symmetric and positive definite matrices B satisfying \(Bu = v\).

While probably well known in the field, we did not find this fact explicitly stated in the literature. It is, of course, not very difficult to prove this result directly by an elementary calculation on \(2 \times 2\) matrices.

4 Inexact Gradient Method

We now discuss the important case of an inexact gradient method, where instead of the angle and scaling conditions (3.5), it is assumed that

$$\begin{aligned} \Vert d - \nabla f(x) \Vert \le \varepsilon \Vert \nabla f(x) \Vert \end{aligned}$$
(4.1)

for some \(\varepsilon \in [0,1)\). This model is also considered in [2,3,4]. Our aim is again deriving convergence rates for a fixed step size rule from the variable metric approach. Since the matrix A in the proof of Theorem 3.2 no longer provides the optimal rates in this case, we use a different construction.

Lemma 4.1

Let \(u,v \in {\mathbb {R}}^n\) such that \(v \ne 0\) and \(\Vert u - v \Vert < \Vert v \Vert \). There exists a positive definite matrix A that satisfies \(Au = v\) and has eigenvalues \(\left( 1 \pm \frac{\Vert u -v \Vert }{\Vert v \Vert } \right) ^{-1}\).

Proof

Define \( A^{-1} = I + \frac{\Vert u - v \Vert }{\Vert v \Vert } Q \) with \(Q = I - 2 \frac{w w^*}{\Vert w\Vert ^2}\) and \(w = \frac{v}{\Vert v\Vert } - \frac{u-v}{\Vert u - v \Vert }\). Observe that Q is the orthogonal reflection matrix that sends \(\frac{v}{\Vert v \Vert }\) to \(\frac{u - v}{\Vert u - v \Vert }\), which implies \(A^{-1}v = u\). Since Q is symmetric with eigenvalues \(\pm 1\), the result follows. \(\square \)

Applying the lemma to \(u = d\) and \(v = \nabla f(x)\), the following theorem on the inexact gradient model (4.1) is an immediate consequence of Theorem 2.1.

Theorem 4.2

Assume \(\nabla f(x) \ne 0\) and (4.1) for some \(\varepsilon \in [0,1)\) and define

$$\begin{aligned} {\bar{h}} = \frac{2 }{L (1 + \varepsilon ) + \mu (1 - \varepsilon )}. \end{aligned}$$

Then, \(x^+ = x - hd\) with \(0 \le h \le {\bar{h}}\) satisfies

$$\begin{aligned} f(x^+) - f(x^*)&\le \left( 1 - h \mu \left( 1 - \frac{\Vert d - \nabla f(x) \Vert }{ \Vert \nabla f(x) \Vert } \right) \right) ^2 (f(x) - f(x^*)) \\&\le \left( 1 - h \mu ( 1 - \varepsilon ) \right) ^2 (f(x) - f(x^*)). \end{aligned}$$

In particular, the step size \(h={\bar{h}}\) yields

$$\begin{aligned} f(x^+) - f(x^*) \le \left( \frac{\kappa _\varepsilon - 1}{\kappa _\varepsilon + 1} \right) ^2 (f(x) - f(x^*)), \quad \kappa _\varepsilon = \frac{L}{\mu } \left( \frac{1 + \varepsilon }{1 - \varepsilon } \right) . \end{aligned}$$
(4.2)

The rate in (4.2) is optimal under the general assumption (4.1), in particular for quadratic f and d satisfying \(\langle \nabla f(x), d \rangle = \cos \theta \Vert d \Vert \Vert \nabla f(x) \Vert \) with \(\sin \theta = \varepsilon \). Trivially, for \(f(x) = \frac{1}{2}\Vert x \Vert ^2\) the estimate (4.2) is sharp for all d satisfying (4.1).

The result in Theorem 4.2 is not new. In [4, Proposition 1.5], it has been shown that \(\left( \frac{\kappa _\varepsilon - 1}{\kappa _\varepsilon + 1} \right) ^2\) is an upper bound for the R-linear convergence rate of the inexact gradient method with fixed step size \({\bar{h}}\). According to [4, Remark 1.6], the estimate (4.2) per step is implicitly contained in the proof of [3, Theorem 5.3], which, however, is rather technical. In addition, the statement of [3, Theorem 5.3] itself covers the rate (4.2) only for a range \(\varepsilon \in [0, \bar{\varepsilon }]\) with some \(\bar{\varepsilon } < \frac{2\mu }{L+\mu }\). Our proof via Lemma 4.1 provides a simple alternative for obtaining the result for all \(\varepsilon \in [0, 1)\) directly from the estimate (1.4) for the gradient method (which coincides with [3, Theorem 5.3] when \(\varepsilon =0\)).

5 Conclusions

Based on the result (1.4) due to [9], we have derived optimal convergence rates for the function values in gradient-related descent methods and inexact gradient methods with fixed step sizes for smooth and strongly convex functions. The results are obtained using an elementary variable metric approach, in which a single step is interpreted as a standard gradient step. This is possible since function values are a metric independent error measure. Compared to the existing results, our proofs offer a more direct way for obtaining the convergence rate estimates of perturbed gradient methods given the rates of their exact counterpart.