A Weighted Mirror Descent Algorithm for Nonsmooth Convex Optimization Problem

Abstract

Large-scale nonsmooth convex optimization is a common problem for a range of computational areas including machine learning and computer vision. Problems in these areas contain special domain structures and characteristics. Special treatment of such problem domains, exploiting their structures, can significantly reduce the computational burden. In this paper, we consider a Mirror Descent method with a special choice of distance function for solving nonsmooth optimization problems over a Cartesian product of convex sets. We propose to use a nonlinear weighted distance in the projection step. The convergence analysis identifies optimal weighting parameters that, eventually, lead to the optimally weighted step-size strategy for every projection on a corresponding convex set. We show that the optimality bound of the Mirror Descent algorithm using the weighted distance is either an improvement to, or in the worst case as good as, the optimality bound of the Mirror Descent using unweighted distances. We demonstrate the efficiency of the algorithm by solving the Markov Random Fields optimization problem. In order to exploit the domain of the problem, we use a weighted log-entropy distance and a weighted Euclidean distance. Promising experimental results demonstrate the effectiveness of the proposed method.

1 Introduction

It is well known that convex optimization problems can be solved in polynomial time at a low iteration count using interior point methods. However, most of these methods do not scale well with the dimension of the optimization problem. A single iteration cost of an interior point method grows nonlinearly with the problem size. As a result, low iteration count becomes expensive in terms of computational performance. Since what matters most in practice is the overall computational time to solve the problem, first-order methods with computationally low-cost iterations become a viable choice for large-scale optimization problems. In this paper, we present an efficient first-order method to solve a general large-scale nonsmooth optimization problem over a Cartesian product of convex sets. The proposed method is the Mirror Descent (MD) algorithm [1–4], an iterative first-order approach for nonsmooth optimization problems, with a special choice of distance function. The main idea of MD is to utilize a suitable Bregman distance [5] and identify the optimal step-size for the projection step over the feasible domain. In the case where the domain is a Cartesian product of convex sets, we propose to use optimal step-size strategy for each projection on the corresponding subset instead of using a common step-size for the projection on the entire domain. In order to achieve this, we employ a weighted distance function for the projection scheme. The weighted distance function exploits the ‘disjoint’ property of the problem’s domain by considering suitable weights for every subset. By assessing the optimality bound for the proposed algorithm, we establish the optimal weighting parameters for each distance function of the corresponding subset. These weighting parameters influence the projection step as scaling factors of the common step-size. Thus, the step-size is scaled appropriately for the corresponding subset projection.

As an illustration, we demonstrate the performance of the proposed algorithm, hereafter referred to as the weighted MD, by solving the Markov Random Fields (MRF) optimization problem [6, 7]. This problem often arises from the areas of image analysis and machine learning [8]. We employ the weighted MD with log-entropy distances and optimal subset-dependent step-sizes to initialize the starting point. Subsequently, we use the weighted MD with Euclidean distances and incorporate the duality gap in the step-size computation. Experimental results confirm the superiority of the weighted MD over the MD algorithm with unweighted distance.

The remainder of this paper focuses on analyzing and describing the proposed weighted MD algorithm and its application to the MRF optimization problem. In the next section, we review the MD algorithm with a general distance function. Section 3 derives the optimality bound for solving a nonsmooth convex optimization problem over a Cartesian product of convex sets using MD. In addition, Sect. 3 introduces required definitions for developing the weighted MD algorithm. In Sect. 3.3, we derive the optimality bound of the proposed weighted MD algorithm and show that it is either an improvement to, or in the worst case as good as, the MD algorithm as described in Sect. 2. In Sect. 4, we consider the dual of the MRF optimization problem. The MRF dual belongs to the class of large-scale nonsmooth optimization problem over a Cartesian product of convex sets. We can therefore employ the weighted MD to solve it. We report very promising computational results in the online supplementary material provided.

2 Mirror Descent Algorithm

Consider the following nonsmooth convex optimization problem:

$$\begin{aligned} \max _{x \in \mathcal {X}} f(x), \end{aligned}$$

(1)

where $\mathcal {X} = \mathcal {X}_1 \times \mathcal {X}_2 \times \cdots \times \mathcal {X}_N$ is the Cartesian product of N closed and convex sets; and $\mathcal {X} \subset \mathbb {R}^{n}$. In this problem, the decision variable x can be decomposed into N disjoint blocks, where each block $x_i \in \mathcal {X}_i$. In addition, we assume the following for (1):

• The objective function $f:\mathcal X \rightarrow \mathbb {R}$ is concave and Lipschitz continuous.

• $f^*:= f(x^*)$ denotes optimal objective value, where $x^* \in \mathcal X$.

Problem (1) can be solved by the Mirror Descent algorithm. MD algorithm [1–4] is a generalization of the projected subgradient method. The standard subgradient approach employs the Euclidean distance function with a suitable step-size in the projection step. Mirror Descent extends the standard projected subgradient method by employing a nonlinear distance function with an optimal step-size in the nonlinear projection step. In this section, we review the Mirror Descent algorithm for solving problem (1) without considering the domain geometry.

Let ${{\mathrm{D}}}(.,.)$ denote the distance between any two points in the set $\mathcal X$, and MD algorithm employs a sequence of nonlinear projection:

$$\begin{aligned} x^{k+1} = \underset{x \in \mathcal {X}}{{{\mathrm{argmax}}}} \left\langle f'_{x^k}, x \right\rangle - \frac{1}{\mu } {{\mathrm{D}}}(x,x^k), \end{aligned}$$

(2)

where $f'_{x^k}$ is a subgradient at the point $x^k$, $\mu$ is the optimal step-size. The set up of Mirror Descent requires ${{\mathrm{D}}}(.,.)$ compatible with the norm:

• $\Vert .\Vert$ on the space embedding $\mathcal {X}$ and its dual norm:

• $\Vert \xi \Vert _* = \max _{x\in \mathcal X} \{{{\mathrm{\langle }}}x,\xi {{\mathrm{\rangle }}}: \Vert x\Vert \le 1\}$.

The maximum distance is given by ${{\mathrm{\Omega }}}= \max _{x,y\in \mathcal {X}} {{\mathrm{D}}}(x,y)$. Suppose f(x) is Lipschitz continuous on $\mathcal {X}$ with the Lipschitz constant ${{{\mathrm{\mathcal L}}}= \max _{x \in \mathcal X} \Vert f'_x\Vert _* < \infty }$, we have the following convergence property for MD algorithm.

Theorem 2.1

Let $f^*$ denotes the global optimal objective function and $\bar{x} = {{\mathrm{argmax}}}_{x = \{x^1,\ldots ,x^K\}} \, f(x)$. Then, using the optimal step-size:

$$\begin{aligned} \mu = \frac{\sqrt{2{{\mathrm{\Omega }}}}}{{{\mathrm{\mathcal L}}}\sqrt{K}}, \end{aligned}$$

(3)

we have the following optimality bound after K iterations:

$$\begin{aligned} f^* - f(\bar{x}) \le \frac{{{\mathrm{\mathcal L}}}\sqrt{2 {{\mathrm{\Omega }}}}}{\sqrt{K}}. \end{aligned}$$

(4)

Theorem 2.1 is a well-known result, and its proof can be found in [2, 4]. In the following section, we derive explicitly the optimality bound where the domain $\mathcal X$ is the Cartesian product of subsets ${{\mathrm{\mathcal X_i}}}, i = 1,2,\ldots ,N$. After that, we introduce a new distance function that will improve the derived optimality bound. The proposed parameterised distance naturally assigns weighting parameters to the projection step (2) on each subset $\mathcal X_i$.

3 Mirror Descent Algorithm with Weighted Distance

We consider a distance measurement on the given domain (the Cartesian product of many subsets) as a sum of weighted subset distances. In this setting, each subset is equipped with a specific distance function and a weighting parameter. We subsequently utilize this weighted distance in the projection step to develop a weighted Mirror Descent algorithm.

3.1 Weighted Distance Function

The distance function ${{\mathrm{D}}}(x,y)$ is defined as the Bregman distance:

$$\begin{aligned} {{\mathrm{D}}}(x,y) = \psi (x) - \psi (y) - {{\mathrm{\langle }}}\nabla \psi (y), x-y {{\mathrm{\rangle }}}, \end{aligned}$$

where $\psi (.)$ is $\sigma$-strongly convex over a compatible norm $\Vert .\Vert$, i.e.,

$$\begin{aligned} \langle \nabla \psi (x) - \nabla \psi (y), x - y \rangle \ge \sigma \Vert x - y\Vert ^2 , \quad \forall x,y \in \mathcal X . \end{aligned}$$

(5)

Without any loss of generality, we assume¹ $\sigma = 1$ throughout the paper. A compatible norm $\Vert .\Vert$ is dependent of the choice of distance function. For example, $l_1$-norm is chosen for log-entropy distance [4], $l_2$-norm for Euclidean distance. Instead of using one distance function over the entire domain, let us consider separate choices of Bregman distance ${{\mathrm{D_i}}}$ for each subset ${{\mathrm{\mathcal X_i}}}, i \in \{1,2,\ldots ,N\}$:

$$\begin{aligned} {{\mathrm{D_i}}}(x_i,y_i) = \psi ^i(x_i) - \psi ^i(y_i) - {{\mathrm{\langle }}}\nabla \psi ^i(y_i) , x_i-y_i {{\mathrm{\rangle }}}, \forall x_i,y_i \in {{\mathrm{\mathcal X_i}}}. \end{aligned}$$

(6)

Each subset distance ${{\mathrm{D_i}}}(x_i,y_i)$ is equipped with a compatible norm $\Vert .\Vert _i$. Various choices of distance functions and compatible norms are discussed in [5, 9, 10]. Two examples that are relevant to the MRF application we consider later are:

• Euclidean distance: ${{\mathrm{D_i}}}(x_i,y_i) = \frac{1}{2}\Vert x_i - y_i\Vert ^2_2$. In this case, $\psi ^i(x_i) = \frac{1}{2}\Vert x_i\Vert ^2_2$ and it is straightforward to show $\psi ^i(.)$ is 1-strongly convex w.r.t $\Vert .\Vert _2$.

• Log-entropy distance: ${{\mathrm{D_i}}}(x_i,y_i) = \sum _j x^j_i \log (x^j_i / y^j_i) + y^j_i - x^j_i$. In this case, $\psi ^i(x_i) = \sum _j x^j_i \log x^j_i - x^j_i$ is shown to be 1-strongly convex w.r.t. $\Vert .\Vert _1$ [4].

When $x,y \in \mathcal X$ and the domain $\mathcal {X} = \mathcal {X}_1 \times \mathcal {X}_2 \times \cdots \times \mathcal {X}_N$, the distance between x and y is equivalent to the sum of distances ${{\mathrm{D_i}}}(x_i,y_i)$. Using this definition, we can now state a corollary to Theorem 2.1.

Corollary 3.1

Let ${{\mathrm{\Omega _i}}}$ denote the maximum distance of a subset $\mathcal X_i$, i.e., ${{\mathrm{\Omega _i}}}= \max _{x_i,y_i \in \mathcal X_i} {{\mathrm{D_i}}}(x_i,y_i)$, and let ${{\mathrm{\mathcal L_i}}}= \max _{x_i \in {{\mathrm{\mathcal X_i}}}} \Vert f'_{x_i}\Vert _*$ denotes the local Lipschitz constant w.r.t. to a subset ${{\mathrm{\mathcal X_i}}}$. The optimality bound (4) for solving problem (1) by the Mirror Descent algorithm is given by:

$$\begin{aligned} f^* - f(\bar{x}) \le \frac{\sqrt{\sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}^2} \sqrt{2 \sum ^N_{i=1} {{\mathrm{\Omega _i}}}}}{\sqrt{K}}. \end{aligned}$$

(7)

Proof

When $\mathcal X$ is the Cartesian product of N convex sets $\mathcal X_i, i \in \{1,2,\ldots ,N\}$, the distance between two vectors $x,y \in \mathcal X$ is the sum of distances between any two blocks $x_i,y_i \in {{\mathrm{\mathcal X_i}}}$. As a result, the maximum distance ${{\mathrm{\Omega }}}$ is also the sum of maximum distances on subset $\mathcal X_i$:

$$\begin{aligned} {{\mathrm{\Omega }}}= \sum ^N_{i=1} {{\mathrm{\Omega _i}}}. \end{aligned}$$

(8)

Since the subsets $\mathcal X_i$ and $\mathcal X_j$ are independent, $i\ne j; i,j \in \{1,2,\ldots ,N\}$, we have:

$$\begin{aligned} {{\mathrm{\mathcal L}}}= \max _{x \in \mathcal X} \Vert f'_x\Vert _* = \max _{x\in \mathcal X} \sqrt{\sum ^N_{i=1} \Vert f'_{x_i}\Vert ^2_*} = \sqrt{\sum ^N_{i=1} \max _{x_i\in \mathcal X_i} \Vert f'_{x_i}\Vert ^2_*} = \sqrt{\sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}^2} . \end{aligned}$$

(9)

Substituting ${{\mathrm{\Omega }}}$ and ${{\mathrm{\mathcal L}}}$ in the optimality bound (4) yields (7). $\square$

We now propose a weighted distance function in order to improve the optimality bound (7). For each subset distance ${{\mathrm{D_i}}}$, let us introduce a weighting parameter ${{\mathrm{\alpha _i}}}>0$. The new distance function is then defined as a weighted combination of subset distances:

$$\begin{aligned} {{\mathrm{D}}}(x,y) := \sum ^N_{i=1} {{\mathrm{\alpha _i}}}{{\mathrm{D_i}}}(x_i,y_i) = \sum ^N_{i=1} {{\mathrm{\alpha _i}}}\psi ^i(x_i) - {{\mathrm{\alpha _i}}}\psi ^i(y_i) - {{\mathrm{\alpha _i}}}{{\mathrm{\langle }}}\nabla \psi ^i(y_i) , x_i-y_i {{\mathrm{\rangle }}}. \end{aligned}$$

(10)

This yields the definition for ${{\mathrm{\psi }}}(x)$ as a weighted sum of convex function $\psi ^i(x_i)$:

$$\begin{aligned} {{\mathrm{\psi }}}(x) = \sum ^N_{i=1} {{\mathrm{\alpha _i}}}\psi ^i(x_i). \end{aligned}$$

(11)

Substituting (10) in the projection step (2) naturally yields:

$$\begin{aligned} x^{k+1} = \underset{x \in \mathcal {X}}{{{\mathrm{argmax}}}} \left\langle f'_{x^k}, x \right\rangle - \frac{1}{\mu } \sum ^N_{i=1} {{\mathrm{\alpha _i}}}{{\mathrm{D_i}}}(x_i,x_i^k). \end{aligned}$$

(12)

Essentially, the property of $\mathcal X$ triggers an ability to independently compute the projection (12) on each subset ${{\mathrm{\mathcal X_i}}}$. In other words, if we consider the optimality condition of the optimization problem (12) w.r.t. each block $x_i \in {{\mathrm{\mathcal X_i}}}$, then (12) is separable and is equivalent to:

$$\begin{aligned} \forall i \in \{1,\ldots ,N\}: \quad x^{k+1}_i = \underset{x_i \in {{\mathrm{\mathcal X_i}}}}{{{\mathrm{argmax}}}} \left\langle f'_{x^k_i}, x_i \right\rangle - \frac{{{\mathrm{\alpha _i}}}}{\mu } {{\mathrm{D_i}}}(x_i,y_i). \end{aligned}$$

(13)

As a result, we hope to achieve better performance by using suitable (or optimal) weighting parameters ${{\mathrm{\alpha _i}}}$ for the corresponding subset ${{\mathrm{\mathcal X_i}}}$.

3.2 Compatible Norm, Dual Norm, Weighted Lipschitz Constant and Maximum Weighted Distance

In order to analyze the convergence of the sequence generated by (12), we need to establish the Lipschitz constant. This can be computed as the upper bound of the dual norm of the subgradients. To this end, we propose a compatible norm $\Vert .\Vert$ associated with the weighted distance.

Lemma 3.1

For all $i \in \{1,\ldots ,N\}$, let ${{\mathrm{\alpha _i}}}>0, \psi ^i(x_i)$ is 1-strongly convex w.r.t. $\Vert x_i\Vert _i$, and then, the weighted function, ${{\mathrm{\psi }}}(x) = \sum ^N_{i=1} {{\mathrm{\alpha _i}}}\psi ^i(x_i)$, is 1-strongly convex w.r.t. the weighted norm:

$$\begin{aligned} \Vert x\Vert := \sqrt{\sum ^N_{i=1} \alpha ^i \Vert x_i\Vert ^2_i} . \end{aligned}$$

(14)

Proof

We have, $\forall x,y \in \mathcal X$:

$$\begin{aligned} \langle \nabla {{\mathrm{\psi }}}(x) - \nabla {{\mathrm{\psi }}}(y), x - y \rangle \ge \sum ^N_{i=1} \alpha ^i \Vert x_i - y_i \Vert ^2_i = \Vert x - y\Vert ^2. \end{aligned}$$

$\square$

The dual norm $\Vert .\Vert _*$ of the proposed weighted norm (14) can be derived using the definition of dual norm (see Sect. 2 and [11]):

$$\begin{aligned} \Vert \xi \Vert _* = \sqrt{\sum ^N_{i=1} \frac{\Vert \xi _i \Vert ^2_{i*}}{{{\mathrm{\alpha _i}}}}} , \end{aligned}$$

(15)

where $\Vert .\Vert _{i*}$ is a dual norm of $\Vert .\Vert _i$ over the subset ${{\mathrm{\mathcal X_i}}}$. Let ${{{\mathrm{\mathcal L_i}}}= \max _{x_i \in {{\mathrm{\mathcal X_i}}}} \Vert f'_{x_i}\Vert _{i*}}$ denote the local Lipschitz constant w.r.t. to a subset ${{\mathrm{\mathcal X_i}}}$; then, the weighed Lipschitz constant is given by:

$$\begin{aligned} {{\mathrm{\mathcal L}}}= \max _{x \in \mathcal X} \Vert f'_x\Vert _* = \sqrt{\sum ^N_{i=1} \frac{{{\mathrm{\mathcal L_i}}}^2}{{{\mathrm{\alpha _i}}}}} . \end{aligned}$$

(16)

In addition, the maximum weighted distance ${{\mathrm{\Omega }}}$ becomes:

$$\begin{aligned} {{\mathrm{\Omega }}}= \max _{x,y \in \mathcal X} {{\mathrm{D}}}(x,y) = \sum ^N_{i=1} {{\mathrm{\alpha _i}}}{{\mathrm{\Omega _i}}}, \end{aligned}$$

(17)

where ${{\mathrm{\Omega _i}}}= \max _{x_i,y_i \in \mathcal {X}_i} {{\mathrm{D_i}}}(x_i,y_i)$.

Remark 3.1

The unweighted functions (8) and (9) in Sect. 2 can be viewed as a special case of the above-weighted functions where ${{\mathrm{\alpha _i}}}= 1 \; , \; \forall i = 1,2,\ldots ,N$.

3.3 Convergence Properties

We show the first result for optimality bound of the weighted MD algorithm.

Lemma 3.2

Let $f^*$ denote the global optimal objective function and $\bar{x} = {{{\mathrm{argmax}}}}_{x = \{x^1,\ldots ,x^K\}} \, f(x)$ and $\mu$ be the step-size. We have the following optimality bound after K iterations:

$$\begin{aligned} f^* - f(\bar{x}) \le \frac{{{\mathrm{\Omega }}}}{K\mu } + \frac{\mu {{\mathrm{\mathcal L}}}^2}{2} . \end{aligned}$$

(18)

Similar results can be found in [1, 2, 4]. The initial bound (18) depends on three terms $\mu$, ${{\mathrm{\mathcal L}}}$ and ${{\mathrm{\Omega }}}$, where the last two terms are themselves functions of the weighting parameters ${{\mathrm{\alpha _i}}}$. Therefore, we can tighten the bound (18) by considering its minimization w.r.t. $\mu$ and ${{\mathrm{\alpha _i}}}$.

Theorem 3.1

For each subset ${{\mathrm{\mathcal X_i}}}$, let ${{\mathrm{\mathcal L_i}}}= \max _{x_i \in {{\mathrm{\mathcal X_i}}}} \Vert f'_{x_i}\Vert _{i*}$ be the local Lipschitz constant and ${{\mathrm{\Omega _i}}}= \max _{x_i,y_i \in \mathcal {X}_i} {{\mathrm{D_i}}}(x_i,y_i)$ be the maximum subset distance. Then, the optimal weighting parameters are given by:

$$\begin{aligned} {{\mathrm{\alpha _i}}}= \frac{{{\mathrm{\mathcal L_i}}}}{\sqrt{{{\mathrm{\Omega _i}}}}\left( \sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}} \right) }, \quad \forall i = 1,2,\ldots ,N . \end{aligned}$$

(19)

In addition, these parameters yield the optimal step-size:

$$\begin{aligned} \mu = \frac{\sqrt{2}}{\sqrt{K}\left( \sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}}\right) }. \end{aligned}$$

(20)

Proof

Minimizing the RHS of (18) w.r.t. $\mu$ yields the result of Theorem 2.1, ${f^* - f(\bar{x}) \le \frac{{{\mathrm{\mathcal L}}}\sqrt{2 {{\mathrm{\Omega }}}}}{\sqrt{K}}}$. This optimality bound is a function of $\alpha := [\alpha ^1,\alpha ^2,\ldots ,\alpha ^N]^\top$. The best optimality bound can be achieved by considering a minimization of:

$$\begin{aligned} \phi (\alpha ) = {{\mathrm{\mathcal L}}}^2(\alpha ) {{\mathrm{\Omega }}}(\alpha ) = \sum ^N_{i=1} \frac{{{\mathrm{\mathcal L_i}}}^2}{{{\mathrm{\alpha _i}}}}\sum ^N_{i=1} {{\mathrm{\alpha _i}}}{{\mathrm{\Omega _i}}}. \end{aligned}$$

The optimizer of $\phi (\alpha )$ needs to satisfy the following optimality condition:

$$\begin{aligned} \frac{{{\mathrm{\alpha _i}}}^2{{\mathrm{\Omega _i}}}}{{{\mathrm{\mathcal L_i}}}^2} \sum ^N_{j=1,j \ne i} \frac{{\mathcal L_j}^2}{\alpha _j} = \sum ^N_{j=1,j \ne i} \alpha _j\mathrm \Omega _j , \quad \forall i = 1,2,\ldots ,N. \end{aligned}$$

(21)

Now, let us rewrite the optimality bound $\frac{{{\mathrm{\Omega }}}}{K\mu } + \frac{\mu {{\mathrm{\mathcal L}}}^2}{2}$ in (18) as:

$$\begin{aligned} \frac{{{\mathrm{\Omega }}}}{K\mu } + \frac{\mu {{\mathrm{\mathcal L}}}^2}{2} = \frac{\sum ^N_{i=1} {{\mathrm{\alpha _i}}}{{\mathrm{\Omega _i}}}}{K\mu } + \frac{\mu }{2} \sum ^N_{i=1} \frac{{{\mathrm{\mathcal L_i}}}^2}{{{\mathrm{\alpha _i}}}} . \end{aligned}$$

Minimizing the RHS of the above equality w.r.t. ${{\mathrm{\alpha _i}}}$ and substituting $\mu = \frac{\sqrt{2{{\mathrm{\Omega }}}}}{{{\mathrm{\mathcal L}}}\sqrt{K}}$ (Theorem 2.1) in the minimizer give ${{\mathrm{\alpha _i}}}= \frac{{{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega }}}}}{{{\mathrm{\mathcal L}}}\sqrt{{{\mathrm{\Omega _i}}}}} , \forall i = 1,2,\ldots ,N$. Substituting these weighting parameters into the maximum distance, ${{\mathrm{\Omega }}}= \sum ^N_{i=1} {{\mathrm{\alpha _i}}}{{\mathrm{\Omega _i}}}$, yields $\sqrt{{{\mathrm{\Omega }}}} = \frac{\sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}}}{{{\mathrm{\mathcal L}}}}$. Suppose the weighted distance is normalized by the weighting parameters, i.e., ${{\mathrm{\Omega }}}= 1$, then the weighted Lipschitz is given by:

$$\begin{aligned} {{\mathrm{\mathcal L}}}= \sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}} . \end{aligned}$$

(22)

Using the above-weighted Lipschitz constant and the normalized maximum distance, ${{\mathrm{\Omega }}}=1$, yields the optimal weighting parameters (19). We can verify that the optimal ${{\mathrm{\alpha _i}}}$ normalizes the maximum distance, i.e., ${{\mathrm{\Omega }}}= 1$, generates the weighted Lipschitz constant (22) using the definition (16) and satisfies the optimality condition (21) of the optimality bound function $\phi (\alpha )$. $\square$

Theorem 3.2

Let $f^*$ denotes the global optimal objective function and $\bar{x} = {{{\mathrm{argmax}}}}_{x = \{x^1,..,x^K\}} \, f(x)$. The weighted MD algorithm with the optimal step-size (20) and the optimal weighting parameters (19) has the following optimality bound after K iterations:

$$\begin{aligned} f^* - f(\bar{x}) \le \frac{\sqrt{2}\sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}}}{\sqrt{K}} . \end{aligned}$$

(23)

Proof

Substituting the optimal step-size (20) and the optimal weighting parameters (19) into (18) directly yields the result. $\square$

The following result establishes the relative performance of the proposed weighted MD algorithm compared to the MD algorithm with unweighted distance. The proposed algorithm with weighted distance is an improvement over the algorithm with unweighted distance. Numerical experiments discussed in the next section and the supplementary material underline this promising result.

Corollary 3.2

The optimality bound (23) of the proposed weighted MD algorithm is either an improvement to, or in the worst case as good as, the optimality bound (7) of the MD algorithm with unweighted distance:

$$\begin{aligned} \frac{\sqrt{2}\sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}}}{\sqrt{K}} \le \frac{\sqrt{\sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}^2} \sqrt{2 \sum ^N_{i=1} {{\mathrm{\Omega _i}}}}}{\sqrt{K}} . \end{aligned}$$

(24)

Proof

By the Cauchy–Schwarz inequality, we have:

$$\begin{aligned} \left( \sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}\sqrt{{{\mathrm{\Omega _i}}}}\right) ^2\le \left( \sum ^N_{i=1} {{\mathrm{\mathcal L_i}}}^2\right) \left( \sum ^N_{i=1} {{\mathrm{\Omega _i}}}\right) . \end{aligned}$$

The above inequality directly yields (24).$\square$

4 Weighted Mirror Descent Algorithm for MRF Optimization

Markov Random Fields [8] are an important class of graph-structured models in image processing and machine learning. In general, the MRF model aims to reveal hidden quantities $\xi$ based on some observations of available input data. Various discussion about MRF modeling and MRF optimization methods in image analysis and machine learning can be found in [6, 8, 12, 13]. In this paper, we focus on the dual of the linear programming (LP) relaxation for the MRF optimization problem. The detailed description of the MRF model and the construction of the dual problem can be found in the supplementary material provided (see also [6]). Let us consider the LP relaxation of the MRF problem:

$$\begin{aligned} \min _{\xi \in \Xi ^G} \langle \theta , \xi \rangle . \end{aligned}$$

(25)

Applying the dual decomposition technique yields the dual objective function:

$$\begin{aligned} \sum _{t \in T} \min _{\xi ^t \in \Xi ^t} {{\mathrm{\langle }}}\theta ^t + \lambda ^t, \xi ^t {{\mathrm{\rangle }}}. \end{aligned}$$

In this setting, the sum of data cost $\theta ^t$ must equal to the original $\theta$ (see [6] or the supplementary material):

$$\begin{aligned} \sum _{t \in T} \theta ^t = \theta , \end{aligned}$$

(26)

and the Lagrangian vector $\lambda$ becomes the decision variables of the dual optimization problem:

$$\begin{aligned} \max _{\lambda \in \Lambda } \sum _{t \in T} \min _{\xi ^t \in \Xi ^t} {{\mathrm{\langle }}}\theta ^t + \lambda ^t, \xi ^t {{\mathrm{\rangle }}}, \end{aligned}$$

(27)

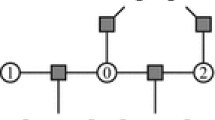
where $\Lambda := \left\{ \sum _{t \in T} \lambda ^t = \mathbf {0}\right\}$. The domain $\Lambda$ is a Cartesian product of subsets $\{\Lambda _i\}_{\forall i \in I}$, where ${I := \left\{ (a,l)\right\} _{\forall a \in V, \forall l \in L} \bigcup \left\{ (ab,lk)\right\} _{\forall ab \in E, \forall l,k \in L}}$. Each subset is defined as $\Lambda _i := \left\{ \sum _{t \in T} \lambda ^t_i = 0 \right\} , \forall i \in I$. As a result, ${\Lambda = \Lambda _1 \times \Lambda _2 \times \cdots \times \Lambda _{{{\mathrm{\mathcal I}}}}}$, where ${{\mathrm{\mathcal I}}}$ is the cardinality of I. It is well known that the solution of (27) is the lower bound of the LP problem (25). By strong duality, the solution of (27) becomes the solution of the LP (25). Problem (27) is a nonsmooth convex optimization problem over the Cartesian product of convex subsets (1).

There have been several approaches for solving the nonsmooth problem (27). One approach is by Savchynskyy et al. [7] using Nesterov’s smoothing technique. Their method relaxes the nonsmooth objective function by a smoothing parameter. As a result, the algorithm only computes a suboptimal solution of the dual problem and does not yield the optimal solution for the LP problem (25). In addition, this algorithm requires computations for all dual variables at every iteration, while the weighted MD requires fewer dual updates as the algorithm converges (as we will see in Remark 4.1). Schmidt et al. [14] proposed a primal-dual method for solving the LP (25); however, their paper shows that the primal-dual method is inferior to the dual decomposition technique for large-scale problem. The weighted MD algorithm is a generalization of the projected subgradient algorithm which was also proposed for solving the dual (27) by Komodakis et al. [6] and Jancsary et al. [15].

4.1 Weighted MD for the MRF Problem

Problem (27) requires an initialization of $\theta ^t$ that satisfies (26). The standard initialization $\theta ^t = \frac{\theta }{{{\mathrm{\mathcal T}}}}$ might not give a good starting point for subgradient-typed methods. A better initialization is an initialization such that the objective function value is closer to the optimal objective value. Suppose we have a better initialization $\theta ^{t*}$, we can reduce the computational efforts for solving $\lambda$ significantly. To this end, let us introduce the following optimization problem:

$$\begin{aligned} \max _{\rho \in \Delta } f(\rho ) := \max _{\rho \in \Delta } \sum _{t \in T} \min _{\xi ^t \in \Xi ^t} {{\mathrm{\langle }}}\rho ^t\circ \theta \, , \, \xi ^t {{\mathrm{\rangle }}}, \end{aligned}$$

(28)

where $\circ$ is a Hadamard product notation, $\Delta = \Delta _1 \times \Delta _2 \times \cdots \times \Delta _{{{\mathrm{\mathcal I}}}}$ is the product set of simplices:

$$\begin{aligned} \Delta _i := \left\{ \rho _i : \sum _{t \in T} \rho ^t_i = 1 \; ; \; \rho ^t_i \ge 0 \, , \, \forall t \in T \right\} , \quad \forall i \in I . \end{aligned}$$

(29)

Problem (28) also has the same form as (1) and can be solved using the weighted MD algorithm. After obtaining the optimal initialization ${\{\rho ^{t*}\circ \theta \,,\,\forall t \in T\}}$, where $\rho ^* = {{\mathrm{argmax}}}_{\rho \in \Delta } f(\rho )$, we can proceed to solve for $\lambda$:

$$\begin{aligned} \max _{\lambda \in \Lambda } f(\lambda ) := \max _{\lambda \in \Lambda } \sum _{t \in T} \min _{\xi ^t \in \Xi ^t} {{\mathrm{\langle }}}\rho ^{t*}\circ \theta + \lambda ^t, \xi ^t {{\mathrm{\rangle }}}, \end{aligned}$$

(30)

where $\Lambda = \Lambda \times \Lambda \times \cdots \times \Lambda _{{{\mathrm{\mathcal I}}}}$ is the product set of linear subsets:

$$\begin{aligned} \Lambda _i := \left\{ \lambda _i : \sum _{t \in T} \lambda ^t_i = 0 \right\} , \quad \forall i \in I . \end{aligned}$$

(31)

The two problems (28) and (30) can be combined into one problem:

$$\begin{aligned} \max _{\rho \in \Delta , \lambda \in \Lambda } f(\rho ,\lambda ) := \max _{\rho \in \Delta , \lambda \in \Lambda } \sum _{t \in T} \min _{\xi ^t \in \Xi ^t} {{\mathrm{\langle }}}\rho ^t\circ \theta + \lambda ^t, \xi ^t {{\mathrm{\rangle }}}. \end{aligned}$$

(32)

By setting $\lambda = 0$, we have (32) $\equiv$ (28). Similarly, if we set ${\rho ^{t*} = {{\mathrm{argmax}}}_{\rho \in \Delta } f(\rho )}$, then we have (32) $\equiv$ (30). The weighted MD algorithm for solving the MRF problem is described in Algorithm 1. As we will see later (equation (40)), exact and optimal step-size $\tau$ can be computed while the exact $\eta$ is not available. A heuristic based on the difference between the current objective value and the optimal solution will be used to approximate $\eta$. The smaller this difference is, the less error accumulates in approximating $\lambda$. Therefore, the solution to problem (28) yields a starting point for $\lambda$ such that its objective value is closer to the optimal solution compared to an objective value corresponding to a random starting point. We clarify the various aspects of the vector $\rho$ (similar for $\lambda$):

• $\rho \in \Delta$ denotes a full vector corresponding to all subgraphs of the set T.

• With superscript t, $\rho ^t$ denotes a vector corresponding to subgraph $t \in T$.

• With subscript i, $\rho _i$ denotes a collection of scalars $\rho ^t_i$ across all subgraphs that cover the index i, and $\rho _i \in \Delta _i$.

• With numeric superscripts, $\rho ^1,\rho ^2,..,\rho ^K$, or $\rho ^k, \rho ^k_i$ denote the corresponding iterate of the vector.

• When superscripts t and k are used together, we separate them by a comma: $\rho ^{t,k}$ is a vector, or $\rho ^{t,k}_i$ is a scalar.

The two weighted distances ${{\mathrm{D_{\Delta }}}}$ and ${{\mathrm{D_{\Lambda }}}}$ yield the corresponding subset projections for (33):

$$\begin{aligned} \forall i \in I: \quad \rho ^{k+1}_i= & {} \underset{\rho _i \in \Delta _i}{{{\mathrm{argmax}}}} \left\langle f'_{\rho ^k_i}, \rho _i \right\rangle - \frac{{{\mathrm{\alpha _{\Delta _i}}}}}{\tau } {{\mathrm{D_{\Delta _i}}}}(\rho _i,\rho ^k_i). \end{aligned}$$

(34a)

$$\begin{aligned} \forall i \in I: \quad \lambda ^{k+1}_i= & {} \underset{\lambda _i \in \Lambda _i}{{{\mathrm{argmax}}}} \left\langle f'_{\lambda ^k_i}, \lambda _i \right\rangle - \frac{{{\mathrm{\alpha _{\Lambda _i}}}}}{\eta } {{\mathrm{D_{\Lambda _i}}}}(\lambda _i,\lambda ^k_i). \end{aligned}$$

(34b)

To this end, we choose the log-entropy distance function for each subset $\Delta _i$ and the Euclidean distance function for each subset $\Lambda _i$. Let us consider:

• For each $\Delta _i$: Let ${\psi ^i_\Delta (\rho _i) = \sum _{t \in T} \rho ^t_i \log {\rho ^t_i}, \; \mathrm {if} \; \rho _i \in \Delta _i; \; else, +\infty }$. Then, $\psi ^i_\Delta$ is 1-strongly convex [4, Proposition5.1] w.r.t. $\Vert .\Vert _1$. The dual norm of $\Vert .\Vert _1$ is $\Vert .\Vert _\infty$ [11].

• For each $\Lambda _i$: Let ${\psi ^i_\Lambda (\lambda _i) = \frac{1}{2}\sum _{t \in T} (\lambda ^t_i)^2, \; \mathrm {if} \; \lambda _i \in \Lambda _i; \; else, +\infty }$. Then, $\psi ^i_\Lambda$ is 1-strongly convex w.r.t. $\Vert .\Vert _2$. The dual norm of $\Vert .\Vert _2$ is itself.

By using the Bregman distance, we can obtain the log-entropy distance function and the Euclidean distance function for the corresponding subset. As a result, each iteration of the recurrences (34) can be solved in a closed form:

$$\begin{aligned} \forall i \in I: \quad \rho ^{t,k+1}_i= & {} \frac{ \rho ^{t,k}_i \times \exp {\left( \frac{\tau }{{{\mathrm{\alpha _{\Delta _i}}}}}\times f'_{\rho ^{t,k}_i}\right) }}{ \sum _{t\in T} \left( \rho ^{t,k}_i\times \exp {\left( \frac{\tau }{{{\mathrm{\alpha _{\Delta _i}}}}}\times f'_{\rho ^{t,k}_i} \right) }\right) } . \end{aligned}$$

(35a)

$$\begin{aligned} \forall i \in I: \quad \lambda ^{t,k+1}_i= & {} \frac{\eta }{{{\mathrm{\alpha _{\Lambda _i}}}}} \left( f'_{\lambda ^{t,k}_i} - \frac{\sum _{t \in T} f'_{\lambda ^{t,k}_i} }{{{\mathrm{\mathcal T}}}} \right) . \end{aligned}$$

(35b)

We note that MD algorithm with unweighted distance also uses the above recurrences with the constant choice ${{\mathrm{\alpha _{\Delta _i}}}}={{\mathrm{\alpha _{\Lambda _i}}}}=1,\forall i \in I$. Using the definitions of optimal step-size (20) and weighting pararmeters (19), the two subset-dependent step-sizes $\frac{\tau }{{{\mathrm{\alpha _{\Delta _i}}}}}$ and $\frac{\eta }{{{\mathrm{\alpha _{\Lambda _i}}}}}$ can be written as:

$$\begin{aligned} \frac{\tau }{{{\mathrm{\alpha _{\Delta _i}}}}} = \frac{\sqrt{2{{\mathrm{\Omega _{\Delta _i}}}}}}{{{\mathrm{\mathcal L_{\Delta _i}}}}\sqrt{k}} \quad \text{ and } \quad \frac{\eta }{{{\mathrm{\alpha _{\Lambda _i}}}}} = \frac{\sqrt{2{{\mathrm{\Omega _{\Lambda _i}}}}}}{{{\mathrm{\mathcal L_{\Lambda _i}}}}\sqrt{k}}. \end{aligned}$$

(36)

The above subset-dependent step-sizes improve the performance of the weighted MD because they use optimal values of ${{\mathrm{\alpha _{\Delta _i}}}}$ and ${{\mathrm{\alpha _{\Lambda _i}}}}$ instead of the constant 1. It thus remains to show how to compute the subgradients $f'_{\rho }$ and $f'_{\lambda }$ at any feasible $\rho \in \Delta$ and $\lambda \in \Lambda$.

Lemma 4.1

Let $\bar{\xi }^t = {{\mathrm{argmin}}}_{\xi ^t \in \Xi ^t} \langle \rho ^t \circ \theta + \lambda ^t , \xi ^t \rangle$ be the optimal solution for the MRF subproblem of the corresponding subgraph $t \in T$. Then, the subgradients of $f(\rho ,\lambda )$ w.r.t. the corresponding decision vector are given by:

$$\begin{aligned} f_{\rho ^t}' = \theta \circ \bar{\xi }^t \quad \mathrm{{and}} \quad f'_{\lambda ^t} = \bar{\xi }^t . \end{aligned}$$

Proof

Let x, y be arbitrary vectors such that $x \in \Delta$ and $y \in \Lambda$. By definition, $\bar{\xi }^t$ is not necessarily optimal for $\min _{\xi ^t \in \Xi ^t} \langle x^t \circ \theta + y^t, \xi ^t \rangle$, i.e.,

$$\begin{aligned} \forall t \in T: \quad \min _{\xi ^t \in \Xi ^t} \langle x^t \circ \theta + y^t, \xi ^t \rangle \le {{\mathrm{\langle }}}x^t \circ \theta + y^t, \bar{\xi }^t {{\mathrm{\rangle }}}. \end{aligned}$$

In addition,

$$\begin{aligned} f(x,y)&= \sum _{t \in T} \min _{\xi ^t \in \Xi ^t} \langle x^t \circ \theta + y^t, \xi ^t \rangle \le \sum _{t \in T} \langle x^t \circ \theta + y^t, \bar{\xi }^t \rangle \\&= F(\rho ,\lambda ) + \langle \theta \circ \bar{\xi } , x - \rho \rangle + \langle \bar{\xi } , y - \lambda \rangle . \end{aligned}$$

$\square$

Remark 4.1

The above choices of subgradient rely on the exact solution ${\bar{\xi }^t \in \Xi ^{{{\mathrm{\mathcal I}}}}}$ for each subgraph t (that can be computed very efficiently by a dynamic programming algorithm, e.g., max-product belief propagation or graph cut). Using these subgradients, we can verify that updates (35) are only needed at disagreement nodes.² As a result, we can utilize this property to define a stopping criterion by counting the number of disagreement nodes. Let $L_k$ be the number of disagreement nodes at iteration k. Essentially, as $L_k \rightarrow 0$, the algorithm converges to a stationary point, i.e., the optimal solution.

By using the above subgradients and the fact that $\bar{\xi }^t_i \in [0,1]$, we can derive the local Lipschitz constants corresponding to their subsets, $\forall i \in I$:

$$\begin{aligned} {{\mathrm{\mathcal L_{\Delta _i}}}}= \sup _{\rho _i \in \Delta _i} \Vert f'_{\rho _i}\Vert _\infty = |\theta _i| \quad \text{ and } \quad {{\mathrm{\mathcal L_{\Lambda _i}}}}= \sup _{\lambda _i \in \Lambda _i} \Vert f'_{\lambda _i}\Vert _2 = \sqrt{{{\mathrm{\mathcal T}}}} . \end{aligned}$$

(37)

To specify the maximum subset distances, we need to find an upper bound for the distance between any feasible point to starting points $\rho ^{1}_i$ and $\lambda ^{1}_i$.

Lemma 4.2

Let all elements of starting point $\rho ^{t,1}_i = \frac{1}{{{\mathrm{\mathcal T}}}}$, and the upper bound of the distance between any feasible vector and $\rho ^1_i$ is given by:

$$\begin{aligned} {{\mathrm{\Omega _{\Delta _i}}}}= \log {{{\mathrm{\mathcal T}}}} . \end{aligned}$$

(38)

Proof

Using the Bregman distance (6) with log-entropy function $\psi ^i_\Delta (\rho _i) = \sum _{t \in T} \rho ^t_i \log {\rho ^t_i}$ for every subset $\Delta _i$, $i \in \mathcal {I}$, we have:

${{{\mathrm{D_{\Delta _i}}}}(\rho _i,\rho ^1_i) = \sum _{t \in T} \rho ^{t}_i \log {\rho ^{t}_i} + \left( \sum _{t \in T} \rho ^{t}_i\right) \log {{{\mathrm{\mathcal T}}}}\le \left( \sum _{t \in T} \rho ^{t}_i\right) \log {{{\mathrm{\mathcal T}}}}\le \log {{{\mathrm{\mathcal T}}}}}$.

The last two inequalities follow from the facts that $0\le \rho ^t_i \le 1$; therefore, $\log {\rho ^t_i} \le 0$, and $\sum _{t \in T} \rho ^t_i = 1$. $\square$

Similar to the above, the Bregman distance with $\psi ^i_\Lambda (\lambda _i) = \frac{1}{2}\sum _{t \in T} (\lambda ^t_i)^2$ yields the Euclidean distance corresponding to subset $\Lambda _i$; thus, the quantity ${{\mathrm{\Omega _{\Lambda _i}}}}$ is given by (with $\lambda ^1_i = \mathbf {0}$) ${{{\mathrm{\Omega _{\Lambda _i}}}}= \max _{\lambda _i \in \Lambda _i} \frac{1}{2}\Vert \lambda _i - \lambda _i^1\Vert ^2_2 = \max _{\lambda _i \in \Lambda _i} \frac{1}{2} \Vert \lambda _i\Vert ^2_2}$. The subset $\Lambda _i$ defined in (31) does not allow exact computation for ${{\mathrm{\Omega _{\Lambda _i}}}}$. For example, assume the index $i \in I$ is covered by two subgraphs $t_1,t_2 \in T$, then

$$\begin{aligned} 2{{\mathrm{\Omega _{\Lambda _i}}}}= \max _{\lambda _i^{t_1} + \lambda _i^{t_2} = 0} \Vert \lambda _i\Vert ^2_2= \max _{\lambda _i^{t_1} + \lambda _i^{t_2} = 0} (\lambda _i^{t_1})^2 + (\lambda _i^{t_2})^2. \end{aligned}$$

The quantity $2{{\mathrm{\Omega _{\Lambda _i}}}}$ can be infinitely large. Thus, the step-size $\frac{\eta }{{{\mathrm{\alpha _{\Lambda _i}}}}}$ also becomes infinitely large. In this problem, we assume subset $\Lambda _i$ to be bounded and nonempty. Therefore, we estimate ${{\mathrm{\Omega _{\Lambda _i}}}}$ by a quantity that is proportional to the distance between the solution $\lambda _i^*$ and the starting point $\lambda _i^1 = \mathbf {0}$. Given the primal problem (25) and dual problem (32), we use the approximate duality gap (since the primal solutions cannot always be computed exactly using the dual solutions) as a heuristic estimation of the distance between the current iterate and the optimal solution.

In order to estimate the duality gap at iteration k, we need to compute (approximately) the primal value $P(\xi ^k) = {{\mathrm{\langle }}}\theta , \xi ^k{{\mathrm{\rangle }}}$. Several approaches to estimate the primal variables are discussed in [6]. We employ the ergodic sequence of dual subgradients $f'_{\lambda ^k}$ to estimate the primal variables. Ergodic convergence analysis [16] has been used by many authors to bridge the primal-dual gap in convex optimization. In the approach, primal variables $\xi ^k$ are estimated by considering the weighted average of the dual subgradients over all iterations:

$$\begin{aligned} \xi ^K = \frac{\sum ^K_{k=1} \sum _{t \in T} f'_{\lambda ^{t,k}}}{K} = \frac{\sum ^K_{k=1}\sum _{t \in T} \bar{\xi }^{t,k}}{K} . \end{aligned}$$

The approximate duality gap is given by ${|P(\xi ^K) - f(\bar{\rho },\lambda ^K)|}$, which can be used as a heuristic to estimate ${{\mathrm{\Omega _{\Lambda _i}}}}$ at iteration k:

$$\begin{aligned} {{\mathrm{\Omega _{\Lambda _i}}}}= \frac{|P(\xi ^k) - f(\bar{\rho },\lambda ^k)|}{2L_k}, \end{aligned}$$

(39)

where $L_k$ is the number of disagreement nodes (see Remark 4.1). Substituting local Lipschitz constants (37) and subset distances (38), (39) into the subset-dependent step-sizes (36) yields:

$$\begin{aligned} \frac{\tau }{{{\mathrm{\alpha _{\Delta _i}}}}} = \frac{\sqrt{2\log ({{\mathrm{\mathcal T}}})}}{|\theta _i|\sqrt{k}} \quad \text{ and } \quad \frac{\eta }{{{\mathrm{\alpha _{\Lambda _i}}}}} = \sqrt{\frac{|P(\xi ^k) - f(\bar{\rho },\lambda ^k)|}{L_k {{\mathrm{\mathcal T}}}k}}. \end{aligned}$$

(40)

Relating the step-size $\frac{\eta }{{{\mathrm{\alpha _{\Lambda _i}}}}}$ to the duality gap allows the algorithm to admit large step-sizes when the duality gap is large (far from the optimum). As the duality gap reduces, so does the step-size. This choice of step-size is consistent with the diminishing step-size approach that guarantees convergence for subgradient methods [17].

4.2 Numerical Experiments

Experimental results are discussed in the supplementary material provided and published online along with this paper.

5 Conclusions

An efficient algorithm is presented for solving a large-scale nonsmooth convex problem. The method is based on the Mirror Descent algorithm employing a suitable weighted distance function. By assessing the optimality bound of the proposed algorithm, we are able to compute the optimal subset-dependent step-sizes. This yields a convergence rate that is not worse than the MD algorithm with unweighted distance. The experimental results for MRF optimization problems confirm the improved performance.