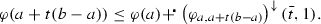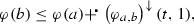Variational Inequalities Characterizing Weak Minimality in Set Optimization

Abstract

We introduce the notion of weak minimizer in set optimization. Necessary and sufficient conditions in terms of scalarized variational inequalities of Stampacchia and Minty type, respectively, are proved. As an application, we obtain necessary and sufficient optimality conditions for weak efficiency of vector optimization in infinite-dimensional spaces. A Minty variational principle in this framework is proved as a corollary of our main result.

Appendix

For the readers convenience, we include the proofs of those results quoted from [23, 33].

Addition and subtraction are extended from real to extended real numbers as follows, compare [41]:

Proposition 2.2 ([23, Proposition 2.11]) Let $A,B\in \mathcal {P}(Y)$ be given such that $B+C$ is convex. Then $A\ll B$ implies

$$\begin{aligned} \forall w^*\in W^*:\quad \inf \limits _{a\in A}w^*(a)=-\infty \;\vee \;\inf \limits _{a\in A}w^*(a)<\inf \limits _{b\in B}w^*(b), \end{aligned}$$

which in turn implies that $A<B$ if $A+C$ is convex.

Proof

Indeed, $A\ll B$ by definition implies $B+U\subseteq A+C$ for some $U\in \mathcal U_Y(0)$, thus

$$\begin{aligned} \forall w^*\in W^*:\inf \limits _{a\in A}w^*(a)\le \inf \limits _{\begin{array}{c} b\in B,\\ u\in U \end{array}}w^*(b+u)=\inf \limits _{b\in B}w^*(b)+\inf \limits _{u\in U}w^*(u). \end{aligned}$$

But as $\inf \limits _{u\in U}w^*(u)<0$ is true for all $w^*\in W^*$, this is the first implication. As for the second implication, assume $B\nsubseteq \mathrm{int\,}(A+C)$ and $A+C$ convex. Then by a separation theorem,

$$\begin{aligned} \exists w^*\in W^*:\inf \limits _{b\in B}w^*(b)\le \inf \limits _{a\in A}w^*(a)\ne -\infty , \end{aligned}$$

as $\mathrm{int\,}(A+C)\ne \emptyset$ is assumed. $\square$

Proposition 2.3 ([33, Proposition 4.13]) Let $\varphi :{\mathrm {I}}\!{\mathrm {R}}\rightarrow \overline{{\mathrm {I}}\!{\mathrm {R}}}$ be semistrictly quasiconvex and l.s.c. with $\mathrm{dom \,}\varphi \subseteq \left[ 0,1 \right]$. Then there exist $s_0 \le t_0 \in \left[ 0,1 \right]$ such that $\varphi$ is strictly decreasing on $\left] 0, s_0 \right[$, strictly increasing on $\left] t_0,1 \right[$ and constantly equal to $\inf \left\{ \varphi (x)\,|\;x\in {\mathrm {I}}\!{\mathrm {R}} \right\}$ on $\left[ s_0, t_0 \right]$.

Proof

Let $\varphi (0)=\varphi (1)$ be given, $t\in \left[ 0,1 \right]$. If $\varphi (t)>\varphi (0)$, then $\varphi (s)<\varphi (t)$ and thus also $\varphi (s)=\varphi (0)$ is true for all $s\in \left[ 0,1 \right] \setminus \left\{ t \right\}$ by semistrict quasiconvexity of $\varphi$. Lower semicontinuity of $\varphi$ thus implies $\varphi (t)\le \varphi (0)$, a contradiction. Define the level sets of $\varphi$ w.r.t. $k\in \overline{{\mathrm {I}}\!{\mathrm {R}}}$ as

$$\begin{aligned} L^\le _\varphi (k)= \left\{ x\in \left[ 0,1 \right] \,|\;\varphi (x)\le t \right\} . \end{aligned}$$

By the above $L^\le _\varphi (k)$ is convex and $L^\le _\varphi (k)$ is closed by lower semicontinuity of $\varphi$ for all $k\in \overline{{\mathrm {I}}\!{\mathrm {R}}}$. Especially,

$$\begin{aligned} L^\le _\varphi \left( \inf \limits _{x\in \left[ 0,1 \right] }\varphi (x)\right) =\bigcap \limits _{x\in \left[ 0,1 \right] }L^\le _\varphi (\varphi (x))= \left[ s_0,t_0 \right] \end{aligned}$$

is a closed convex set, and hence either $-\infty$ is attained in some $x\in \left[ 0,1 \right]$, trivially implying $L^\le _\varphi (\inf \limits _{x\in \left[ 0,1 \right] }\varphi (x))\ne \emptyset$, or the Weierstrass Theorem implies that the infimum of the lower semicontinuous function $\varphi$ is attained on the compact set $\left[ 0,1 \right]$.

Under the assumption of $0<s<t\le s_0$, semistrict quasiconvexity of $\varphi$ implies $\varphi (0)>\varphi (s)>\varphi (s_0)$ and $\varphi (s)>\varphi (t)>\varphi (s_0)$, as $\varphi (s_0)=\inf \limits _{x\in \left[ 0,1 \right] }\varphi (x)$. But thus $\varphi$ is strictly decreasing on $\left[ 0,s_0 \right]$ and the same arguments prove strict monotonicity on the interval $\left[ t_0,1 \right]$. $\square$

The following result is Diewert’s Mean Value Theorem [42].

Proposition 7.1

Let $\varphi :X \rightarrow \overline{{\mathrm {I}}\!{\mathrm {R}}}$ and $a, b\in X$ be such that $\varphi _{a,b} : \left[ 0,1 \right] \rightarrow {\mathrm {I}}\!{\mathrm {R}}$ is lower semicontinuous and real-valued. Then, there exist $0 \le t < 1$ and $0 < s \le 1$ such that

$$\begin{aligned} \varphi (b) - \varphi (a)&\le ( \varphi _{a,b})^\downarrow (t,1) \; \text {and} \\ \varphi (a) - \varphi (b)&\le ( \varphi _{a,b})^\downarrow (s,-1). \end{aligned}$$

By a careful case study, we extend this classical result to the case when $\varphi _{a,b} : \left[ 0,1 \right] \rightarrow \overline{{\mathrm {I}}\!{\mathrm {R}}}$ is extended real-valued and not necessarily proper. Then, the difference has to be replaced by the inf-residual in $\overline{{\mathrm {I}}\!{\mathrm {R}}}$

Especially,

Theorem 7.1

([33, Theorem 4.2]) Let $\varphi :X \rightarrow \overline{{\mathrm {I}}\!{\mathrm {R}}}$ and $a, b \in X$ be given such that $a \ne b$ and $\varphi _{a,b} :{\mathrm {I}}\!{\mathrm {R}}\rightarrow \overline{{\mathrm {I}}\!{\mathrm {R}}}$ is lower semicontinuous. Then

• (a) If either $\varphi (a) = +\infty$, or $\left\{ a,b \right\} \subseteq \mathrm{dom \,}\varphi$, then there exists $0\le t< 1$ such that

  

• (b) If either $\varphi (b)=+\infty$, or $\left\{ a,b \right\} \subseteq \mathrm{dom \,}\varphi$, then there exists $0< s \le 1$ such that

  

Proof

• (a) The proof of the first inequality is given via a case study. If $\varphi (a)=+\infty$ or $\varphi (b)=-\infty$, then

  

  so the first inequality is trivially satisfied. Next, assume $\left\{ a,b \right\} \subseteq \mathrm{dom \,}\varphi$ and $\varphi (b)\ne -\infty$. If $\varphi _{a,b}(t)=-\infty$ for some $0\le t<1$, then by lower semicontinuity $\varphi _{a,b}(t_0)=-\infty$, setting

  $$\begin{aligned} t_0=\sup \left\{ t\in \left[ 0,1 \right] \,|\;\varphi _{a,b}(t)=-\infty \right\} \end{aligned}$$

  and by assumption $t_0<1$. Hence, $\left( \varphi _{a,b} \right) ^\downarrow (t_0,1)=+\infty$, satisfying the first inequality. Finally, let $\left\{ a,b \right\} \subseteq \mathrm{dom \,}\varphi$, $\varphi (a+t(b-a))\ne -\infty$ be assumed for all $0\le t\le 1$ and $\varphi _{a,b}(t)=+\infty$ for some $0<t<1$ and set

  $$\begin{aligned} t_0=\inf \left\{ t\in \left] 0,1 \right[ \,|\;\varphi _{a,b}(t)=+\infty \right\} . \end{aligned}$$

  If $t_0=0$, then we are finished, as in this case $\left( \varphi _{a,b} \right) ^\downarrow (0,1)=+\infty$ is true, and hence assume $0<t_0$. In this case, $\varphi _{a,b} \left[ 0,t \right] \subseteq {\mathrm {I}}\!{\mathrm {R}}$ is true for all $t\in \left] 0,t_0 \right[$, and the above result combined with Proposition 7.1 applied to $b_t=a+t(b-a)$ gives that for all $0 < t < t_0$ there exists a $0\le \bar{t}<1$ such that

  

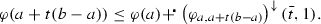
  But as $\left( \varphi _{a,a+t(b-a)} \right) ^\downarrow (\bar{t},1)=t\left( \varphi _{a,b} \right) ^\downarrow (\bar{t},1)$ is true and by lower semicontinuity of $\varphi _{a,b}$ the value $\varphi (a+t(b-a))$ converges to $+\infty$ as $t$ converges to $t_0$, this implies that $\left( \varphi _{a,b} \right) ^\downarrow (\bar{t},1)$ converges to $+\infty$ and eventually satisfies the desired inequality,

  

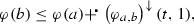
  as $\varphi (b)$ and $\varphi (a)\in {\mathrm {I}}\!{\mathrm {R}}$ was assumed. The real-valued case is Proposition 7.1.

• (b) Notice that $\varphi _{a,b}(s)=\varphi _{b,a}(1-s)$ and

  $$\begin{aligned} \left( \varphi _{a,b} \right) ^\downarrow (s,-1)=\left( \varphi _{b,a} \right) ^\downarrow ((1-s),1), \end{aligned}$$

and hence the result is immediate from the above. $\square$

Proposition 7.2

([33, Proposition 4.14]) If $\mathrm{dom \,}\varphi$ is star shaped at $x_0$ and $\varphi$ is radially pseudoconvex and l.s.c. w.r.t. $x_0$, then it is radially semistrictly quasiconvex w.r.t. $x_0$.

Proof

Assume that for some $b\in \mathrm{dom \,}\varphi$, the function $\varphi _{a,b}$ is not semistrictly quasiconvex. Then there are $r, s, t \in {\mathrm {I}}\!{\mathrm {R}}$ such that $0 \le r < s < t \le 1$ and $\varphi _{a,b}\left( r \right) \ne \varphi _{a,b}(t)$ and

$$\begin{aligned} \max \left\{ \varphi _{a,b}\left( r \right) , \varphi _{a,b}(t) \right\} \le \varphi _{a,b}(s). \end{aligned}$$

We assume $\varphi _{a,b}\left( r \right) < \max \left\{ \varphi _{a,b}\left( r \right) , \varphi _{a,b}\left( t \right) \right\} = \varphi _{a,b}\left( t \right)$. The other case can be dealt with by symmetric arguments.

Fix $\delta > 0$ such that $\varphi _{a,b}\left( r \right) < \varphi _{a,b}\left( t \right) - \delta$. Since $\varphi _{a,b}$ is l.s.c., the set

$$\begin{aligned} \left\{ s' \in {\mathrm {I}}\!{\mathrm {R}}\mid \varphi _{a,b}\left( s' \right) > \varphi _{a,b}\left( t \right) - \delta \right\} \end{aligned}$$

is open. Hence, there is $\varepsilon > 0$ such that $[s - \varepsilon , s + \varepsilon ] \subseteq \left( r, t \right)$ and

$$\begin{aligned} \forall s' \in [s - \varepsilon , s + \varepsilon ] :\varphi _{a,b}\left( t \right) - \delta < \varphi _{a,b}\left( s' \right) \in {\mathrm {I}}\!{\mathrm {R}}. \end{aligned}$$

Take $s' \in [s, s+\varepsilon [$, $s'' \in ]s', s+\varepsilon ]$ and assume $\varphi _{a,b}\left( s'' \right) < \varphi _{a,b}\left( s' \right)$. By Diewerts Mean Value Theorem, there exists an $\hat{s} \in ]s' , s'']$ satisfying

$$\begin{aligned} 0 < \varphi _{a,b}\left( s' \right) - \varphi _{a,b}\left( s'' \right) \le \left( \varphi _{a,b} \right) ^\downarrow \left( \hat{s}, s' - s'' \right) . \end{aligned}$$

Indeed, setting $a' = a+s'(b-a)$ and $b' = a+s''(b-a)$, one obtains by Diewerts Mean Value Theorem at $\alpha \in ]0, 1]$ satisfying $\varphi \left( a' \right) - \varphi \left( b' \right) \le \left( \varphi _{a',b'} \right) ^\downarrow \left( \alpha , -1 \right)$. Defining

$$\begin{aligned} \hat{s} = s' + \alpha (s''-s') \in ]s', s''], \end{aligned}$$

one obtains above inequality by observing $\varphi \left( a' \right) = \varphi _{a,b}\left( s' \right)$, $\varphi \left( b' \right) = \varphi _{a,b}\left( s'' \right)$ and ultimately $\left( \varphi _{a',b'} \right) ^\downarrow \left( \alpha , -1 \right) = \left( \varphi _{a,b} \right) ^\downarrow \left( \hat{s}, s' - s'' \right)$.

Using the positive homogeneity of the directional derivative, we can multiply the inequality $0 < \left( \varphi _{a,b} \right) ^\downarrow \left( \hat{s}, s' - s'' \right)$ by $\frac{r - \hat{s}}{s' - s''} > 0$ and thus obtain $0 < \left( \varphi _{a,b} \right) ^\downarrow \left( \hat{s}, r - \hat{s} \right)$. The pseudoconvexity of $\varphi _{a,b}$ yields $\varphi _{a,b}\left( r \right) \ge \varphi _{a,b}\left( \hat{s} \right)$ in contradiction to the assumption that $\varphi _{a,b}\left( r \right) < \varphi _{a,b}\left( t \right) - \delta < \varphi _{a,b}\left( \hat{s} \right)$ (observe $\hat{s} \in [s, s+\varepsilon ]$). Hence, $\varphi _{a,b}\left( s'' \right) \ge \varphi _{a,b}\left( s' \right)$ whenever $s', s'' \in [s, s+\varepsilon ]$ and $s' < s''$. This implies

$$\begin{aligned} \forall s' \in [s, s+\varepsilon ) :\left( \varphi _{a,b} \right) ^\downarrow \left( s', 1 \right) \ge 0, \end{aligned}$$

and positive homogeneity of the directional derivative implies

$$\begin{aligned} \left( \varphi _{a,b} \right) ^\downarrow \left( s', t-s' \right) \ge 0 \end{aligned}$$

and this by pseudoconvexity of $\varphi _{a,b}$

$$\begin{aligned} \varphi _{a,b}\left( t \right) \ge \varphi _{a,b}\left( s' \right) \ge \varphi _{a,b}\left( s \right) \ge \varphi _{a,b}\left( t \right) . \end{aligned}$$

This means $\varphi _{a,b}\left( s' \right) = \varphi _{a,b}\left( t \right)$ for all $s' \in [s, s+\varepsilon )$. In turn, this implies that for $s' \in \left] s, s+\varepsilon \right[$ we have $\left( \varphi _{a,b} \right) ^\downarrow \left( s', -1 \right) \ge 0$, and hence $\left( \varphi _{a,b} \right) ^\downarrow \left( s', r- s' \right) \ge 0$ and by pseudoconvexity $\varphi _{a,b}\left( s' \right) \le \varphi _{a,b}\left( r \right)$. This contradicts the assumption $\varphi _{a,b}\left( r \right) < \varphi _{a,b}\left( t \right)$, and hence (together with the symmetric case) the function $\varphi _{a,b}$ is semistrictly quasiconvex for all $b \in \mathrm{dom \,}\varphi$. $\square$

Proposition 4.1 ([23, Proposition 4.5]) Let $F:X\rightrightarrows Y$ be a $C$ -map, $x_0\in \mathrm{dom \,}F$. If $x_0$ solves the scalarized Stampacchia variational inequality (4.1), then it is a scalarized weak minimizer.

$$\begin{aligned} F(x_0)+C=Y\quad \vee \quad \forall x\in X\, \exists w^*\in W^*:\quad \left( \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle } \right) ^\downarrow (x_0,x-x_0)\ge 0 \end{aligned}$$

(4.1)

Proof

Assume to the contrary that $F(x_0)+C\ne Y$ and it exists $x\in X$ such that

$$\begin{aligned} \forall w^*\in W^*:\quad \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x)<\left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x_0). \end{aligned}$$

As all scalarizations are convex by assumption, this contradicts (4.1). $\square$

Proposition 4.2 ([23, Lemma 4.9]) Let $F:X\rightrightarrows Y$ be a $C$ -map with $x_0\in \mathrm{dom \,}F$. If $x_0$ is a scalarized weak minimizer, then it satisfies (4.2).

$$\begin{aligned} \begin{array}{cl} &{}F(x_0)+C=Y\;\vee \\ &{}\forall x\in X\, \exists w^*\in W^*:\quad \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x)\ne -\infty \wedge \left( \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle } \right) ^\downarrow (x,x_0-x)\le 0. \end{array} \end{aligned}$$

(4.2)

Proof

If $x_0$ satisfies (w-sc-Min), then either $F(x_0)+C=Y$ or for every $x\in X$ there exists a $w^*\in W^*$ such that $\left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x_0)\le \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x)\ne -\infty$ and thus

$$\begin{aligned} \left( \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle } \right) ^\downarrow (x,x_0-x)\le \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x_0)- \left( \varphi _{F,w^*} \right) ^\mathrm{\vartriangle }(x)\le 0. \end{aligned}$$

$\square$