Time-Optimal Control Problem for a Special Class of Control Systems: Optimal Controls and Approximation in the Sense of Time Optimality

Abstract

We consider the time-optimal control problem to the origin for a class of nonlinear systems, called dual-to-linear systems. We obtain the general description of possible optimal controls. In particular, we show that optimal controls take the values $-1$, $0$, and $+1$ only and have a finite number of points of discontinuity. We describe a class of nonlinear affine control systems which can be approximated by dual-to-linear systems in the sense of time optimality.

1 Introduction

One of the most powerful and well-investigated tools of the nonlinear control theory is the method of linearization, that is, finding the precise mapping that transforms given initial system to a linear one. A pioneer result in this direction was obtained in 1973 by Korobov [1], who introduced and studied the so-called class of triangular systems in connection with the controllability and stabilizability problems for nonlinear systems. Later on, the class of triangular systems was considered in many works, in particular, in connection with the problem of linearizability, i.e., the possibility to transform a nonlinear system to a linear one. A way using “Lie brackets technique” was proposed in 1973 by Krener [2] and developed in numerous works. However, the class of nonlinear linearizable systems is rather small. So, the next step was to develop methods of approximation (in some sense) of a given nonlinear system by a linear one. In [3] the approximation was considered for nonlinear affine systems with real analytic right-hand side, and a concept of approximation in the sense of time optimality was introduced. Moreover, necessary and sufficient conditions were obtained, under which the system is approximated by a certain linear system.

If these conditions are not satisfied, the question arises, how to approximate the original system by another nonlinear affine system of a simpler form. Further progress was achieved by developing the algebraic approach [4–10]. As a result, it was shown that the approximating system can be constructed with the use of some special structures in the algebra of nonlinear power moments.

In the present paper, we consider the time-optimal control problem for affine systems with real analytic right-hand side including control and the first coordinate only. It turns out that optimal controls take values $-1$, $0$, $+1$ and have a finite number of points of discontinuity. We study the question of approximation in the sense of time optimality, following the approach proposed in [3, 5]. We find conditions under which a system of the considered class approximates an affine control system. These conditions are “dual” to the corresponding conditions for systems approximated by linear ones [3]. That gives a certain reason to interpret such systems as dual-to-linear systems.

The paper is organized as follows. In Sect. 2, we consider the time-optimal control problem for dual-to-linear systems and show that optimal controls take values $-1$, $0$, and $+1$ only and have a finite number of points of discontinuity, and describe possible optimal controls. Section 3 contains the three-dimensional example. Finally, in Sect. 4 we describe the structure of right ideals induced by dual-to-linear systems in the algebra of nonlinear power moments and consider the question of approximation in the sense of time optimality.

2 Time-Optimal Control Problem for Dual-to-Linear Systems

In this section, we consider the time-optimal control problem

$$\begin{aligned}&\dot{x}_1=u, \quad \dot{x}_i = P_i(x_1), \quad i = 2,\ldots , n, \quad P_i(0)=0,\end{aligned}$$

(1)

$$\begin{aligned}&|u(t)| \le 1, \ t\in [0,\theta ],\ \quad \ x(0) = x^0, \quad \ x(\theta ) = 0, \quad \theta \rightarrow \min , \end{aligned}$$

(2)

where $P_2(z), \ldots , P_n(z)$ are real analytic functions for $z\in [-\alpha ,\alpha ]$, $\alpha >0$; below we suppose that they are linearly independent. As follows from Fillippov’s Theorem [11], if the point $x^0$ from a neighborhood of the origin can be steered to the origin, then there exists a solution of the time-optimal control problem (1), (2). Our nearest goal is to prove that any optimal control takes values $-1$, $0$, and $+1$ only and has a finite number of discontinuity points (that is, for such systems the chattering [12] is impossible).

Let us fix an initial point $x^0\not =0$ from a neighborhood of the origin and suppose that $\widehat{\theta }>0$ is the optimal time, and $\widehat{u}(t)$, $t\in [0,\widehat{\theta }]$ is an optimal control for (1), (2); let $\widehat{x}(t)=(\widehat{x}_1(t),\ldots ,\widehat{x}_n(t))$ be the corresponding optimal trajectory and $\widehat{x}_1(t)\in [-\alpha ,\alpha ]$, $t\in [0,\widehat{\theta }]$. Let us apply the Pontryagin Maximum Principle. Define $H:=\psi _1 u+\sum _{i=2}^n\psi _i P_i(x_1)$ and consider the dual system

$$\begin{aligned} \dot{\psi }_1 = -\sum _{i=2}^n\psi _i P'_i(\widehat{x}_1(t)),\qquad \dot{\psi }_2 = 0,\quad \ldots ,\quad \dot{\psi }_n =0. \end{aligned}$$

(3)

Hence, $\psi _2(t),\ldots ,\psi _n(t)$ are constant, i.e., $\psi _k(t)=\psi _k$, $k=2,\ldots ,n$. Due to the Pontryagin Maximum Principle, there exists a number $\psi _0\le 0$ and a nontrivial solution of the dual system (3) such that

$$\begin{aligned}&\widehat{u}(t)=\mathop {\mathrm {sign}}\nolimits (\psi _1(t))~ \mathrm{a.e.}~\mathrm{for}\,\mathrm{all}~t\ \text{ such } \text{ that }\ \psi _1(t)\ne 0,\end{aligned}$$

(4)

$$\begin{aligned}&\psi _0+\psi _1(t) \widehat{u}(t)+\sum _{i=2}^n\psi _i P_i(\widehat{x}_1(t))=0,\quad t\in [0,\widehat{\theta }]. \end{aligned}$$

(5)

Since $(\psi _1(t),\psi _2,\ldots ,\psi _n)$ is nontrivial, (4) and (5) imply

$$\begin{aligned} \psi _0^2+\psi _2^2+\ldots +\psi _n^2>0. \end{aligned}$$

(6)

Definition 2.1

We say that

$$\begin{aligned} P(z):=-\psi _0-\sum _{i=2}^n \psi _i P_i(z),\quad z\in [-\alpha ,\alpha ], \end{aligned}$$

is a characteristic function of the problem (1), (2).

We emphasize that the coefficients $\psi _0, \psi _2,\ldots ,\psi _n$ are defined by the optimal control $\widehat{u}(t)$ via the Pontryagin Maximum Principle. Thus, (4), (5) imply

$$\begin{aligned} |\psi _1(t)|=P(\widehat{x}_1(t)),\quad t\in [0,\widehat{\theta }]. \end{aligned}$$

(7)

Since $P_2(z), \ldots , P_n(z)$ are linearly independent and $P_2(0)=\cdots =P_n(0)=0$, inequality (6) implies that $P(z)$ is not identically zero. We suppose that there exists $\overline{t}\in [0,\widehat{\theta }]$ such that $\psi _1(\overline{t})=0$; due to (7), in this case $P(z)$ is not identically constant, i.e., its derivative $P'(z)$ is not identically zero. Let us denote by $\{z^1,\ldots ,z^p\}$ the set of all different roots of the function $P(z)$ on the segment $[-\alpha ,\alpha ]$ (if any). Analogously, we denote by $\{z_0^1,\ldots ,z_0^q\}$ the set of all different roots of the function $P'(z)$ on the segment $[-\alpha ,\alpha ]$ (if any). If $p\ge 2$, $q\ge 2$, then we put

$$\begin{aligned} d&:= \min \{|z^i-z^j|:1\le i<j\le p\}>0, \\ d_0&:= \min \{|z_0^i-z_0^j|:1\le i<j\le q\}>0. \end{aligned}$$

Lemma 2.1

Suppose $\psi _1(t)=0$ for all $t\in [t_2,t_1]$, where $0\le t_2<t_1\le \widehat{\theta }$. Then $\widehat{u}(t)=0$ for all $t\in [t_2,t_1]$.

Proof

The equality (7) implies that $\widehat{x}_1(t)$ is a root of the function $P(z)$ for any $t\in [t_2,t_1]$. Since $\widehat{x}_1(t)$ is continuous, it equals one of these roots identically on $[t_2,t_1]$, i.e., $\widehat{x}_1(t)=\mathrm {const}$. Therefore, $\widehat{u}(t)=\dot{\widehat{x}}_1(t)=0$ for all $t\in [t_2,t_1]$. $\square$

Lemma 2.2

Let $\psi _1(t_1)=\psi _1(t_2)=0$ and $\psi _1(t)\not =0$ for all $t\in ]t_2,t_1[$, where $0<t_2<t_1\le \widehat{\theta }$. Suppose there exists a strongly increasing sequence $\{\tau _k\}_{k=1}^\infty$ such that $\tau _k\rightarrow t_2$ as $k\rightarrow \infty$ and $\psi _1(\tau _k)=0$, $k\ge 1$. Then $P'(z)$ has at least two different roots and $t_1-t_2>d_0$.

Proof

Due to Rolle’s Theorem, there exists a strongly increasing sequence $\{\tau '_k\}_{k=1}^\infty$ such that $\tau _k'\rightarrow t_2$ and $\dot{\psi }_1(\tau _k')=0$, $k\ge 1$. Due to (3), $P'(\widehat{x}_1(\tau _k'))=0$. Since $P'(z)$ and $\widehat{x}_1(t)$ are continuous, $P'(\widehat{x}_1(t_2))=0$. Analogously, due to Rolle’s Theorem, there exists $t_2<t'<t_1$ such that $\dot{\psi }_1(t')=0$; hence, $P'(\widehat{x}_1(t'))=0$. Therefore, $\widehat{x}_1(t_2)$ and $\widehat{x}_1(t')$ are roots of the function $P'(z)$. However, $\psi _1(t)\not =0$ for all $t\in ]t_2,t'[$; hence, $\widehat{u}(t)$ equals $1$ or $-1$ on $]t_2,t'[$. Since $\dot{\widehat{x}}_1(t)=\widehat{u}(t)$, we get $\widehat{x}_1(t_2)\not =\widehat{x}_1(t')$, i.e., $\widehat{x}_1(t_2)$ and $\widehat{x}_1(t')$ are different roots of $P'(z)$. Moreover, $t_1-t_2>t'-t_2=|\widehat{x}_1(t')-\widehat{x}_1(t_2)|\ge d_0$. $\square$

Below we use the notation $\mathop {\mathrm {sign}}\nolimits (0):=0$.

Lemma 2.3

For any $\overline{t}\in [0,\widehat{\theta }]$ there exists $\varepsilon >0$ such that $\mathop {\mathrm {sign}}\nolimits (\psi _1(t))=\mathrm {const}$ for all $t\in \ ]\,\overline{t}-\varepsilon ,\overline{t}\,[$ (except of $\overline{t}=0$) and for all $t\in \ ]\,\overline{t},\overline{t}+\varepsilon \,[$ (except of $\overline{t}=\widehat{\theta }$).

Proof

If $\psi _1(\overline{t})\not =0$, the proof is trivial. Assume that $\psi _1(\overline{t})=0$, where $\overline{t}\in \, [0,\widehat{\theta }[$, and suppose that for any $\varepsilon >0$, the function $\psi _1(t)$ changes its sign on $]\overline{t},\overline{t}+\varepsilon [$ (the other cases are considered analogously). Then, for any $\varepsilon >0$ there exist $t_1,t_2 \in \ ]\overline{t},\overline{t}+\varepsilon [$ such that $\psi _1(t_1)=0$ and $\psi _1(t_2)\ne 0$.

We put $t^*:=\min \{\overline{t}+d_0,\widehat{\theta }\}$, provided $P'(z)$ has at least two different roots, and $t^*:=\widehat{\theta }$ otherwise. Then, the above-mentioned property implies that there exist $\overline{t}<t'_2<\tau '<t'_1<t^*$ such that $\psi _1(t'_1)=\psi _1(t'_2)=0$ and $\psi _1(\tau ')\not =0$. We denote $t_1:=\inf \{t>\tau ':\psi _1(t)=0\}$ and $t_2:=\sup \{t<\tau ':\psi _1(t)=0\}$, then $\overline{t}<t_2<\tau '<t_1<t^*$, $\psi _1(t_1)=\psi _1(t_2)=0$, and $\psi _1(t)\not =0$ for all $t\in ]t_2,t_1[$.

Due to Lemma 2.2, there exists $\varepsilon >0$ such that $\psi _1(t)\not =0$ for all $t\in ]t_2-\varepsilon ,t_2[$. We denote $t_3:=\sup \{t<t_2:\psi _1(t)=0\}$, then, due to our supposition, $\overline{t}<t_3<t_2$. Repeating this procedure, we put $t_{k+1}:=\sup \{t<t_k:\psi _1(t)=0\}$ for $k\ge 3$, hence, $\overline{t}<\cdots <t_{k+1}<t_k<\cdots <t_1$. Then $\psi _1(t_k)=0$, hence, $\widehat{x}_1(t_k)$ are roots of $P(z)$. However, $\psi _1(t)\not =0$ for all $t\in ]t_{k+1},t_k[$, hence, $\widehat{u}(t)\equiv 1$ or $\widehat{u}(t)\equiv -1$, $t\in ]t_{k+1},t_k[$. Since $\dot{\widehat{x}}_1(t)=\widehat{u}(t)$, we get $\widehat{x}_1(t_{k+1})\not =\widehat{x}_1(t_k)$, i.e., $\widehat{x}_1(t_{k+1})$ and $\widehat{x}_1(t_k)$ are different roots of $P(z)$. We have $t_k-t_{k+1}=|\widehat{x}_1(t_k)-\widehat{x}_1(t_{k+1})|\ge d>0$, $k\ge 1$; this contradicts the inequalities $\overline{t}<\cdots <t_{k+1}<t_k<\cdots <t_1$. $\square$

Lemmas 2.1 and 2.3 lead to the following theorem.

Theorem 2.1

Let $\widehat{u}(t)$, $t\in [0,\widehat{\theta }]$, be an optimal control for (1), (2). Then

$$\begin{aligned} \widehat{u}(t)=\mathop {\mathrm {sign}}\nolimits (\psi _1(t)),\quad t\in [0,\widehat{\theta }]\ \mathrm {a.e.}, \end{aligned}$$

(8)

and therefore, $\widehat{u}(t)$ is piecewise constant, takes the values $-1$, $0$ and $+1$ only and has a finite number of switching points.

Our next goal is to estimate the possible number of switching points and specify the character of optimal trajectories.

Lemma 2.4

If $\overline{t}$ is a switching point of the optimal control $\widehat{u}(t)$, then $\widehat{x}_1(\overline{t})$ is a root of $P(z)$. If $\widehat{u}(t)=0$ for all $t\in ]t_2,t_1[$ where $t_2<t_1$, then $\widehat{x}_1(t)\equiv c$, $t\in [t_2,t_1]$, and $c$ is a multiple root of the function $P(z)$.

Proof

The first statement follows from (8) and (7). Let us turn to the second statement. If $\widehat{u}(t)=0$, $t\in ]t_2,t_1[$, then (8) implies $\psi _1(t)=0$, hence, $P(\widehat{x}_1(t))=0$ for all $t\in ]t_2,t_1[$ due to equality (7). Moreover, $\dot{\psi }_1(t)=0$, therefore, (3) implies $P'(\widehat{x}_1(t))=0$. Thus, $P(\widehat{x}_1(t))=P'(\widehat{x}_1(t))=0$, i.e., $\widehat{x}_1(t)$ is a multiple root of the function $P(z)$ for any $t\in ]t_2,t_1[$. Since the function $\widehat{x}_1(t)$ is continuous, it equals one of such roots identically for $t\in [t_2,t_1]$. $\square$

Let us explain the meaning of Lemma 2.4. Suppose that $z^1,\ldots ,z^m \in [-\alpha ,\alpha ]$ are multiple roots of $P(z)$, and $z^{m+1},\ldots ,z^p\in [-\alpha ,\alpha ]$ are simple roots. Let us consider the graph of the function $P(z)$ and suppose that the point $z=\widehat{x}_1(t)$ moves along the axis $z$ when $t$ runs through the time interval $[0,\widehat{\theta }]$. Relation (7) means that $\widehat{x}_1(t)$ belongs to the connected component of the set $\{z:P(z)\ge 0\}$ containing the point $z=0$. Moreover, $\widehat{x}_1(t)$ can change the direction of its movement at the points $z^1,\ldots ,z^p$ only, and $\widehat{x}_1(t)$ can “stay” at the points $z^1,\ldots ,z^m$ only.

Below, we denote by $\varphi ^1\circ \varphi ^2$ the concatenation of functions $\varphi ^1(t)$, $t\in [0,t_1]$, and $\varphi ^2(t)$, $t\in [0,t_2]$, defined by

$$\begin{aligned} (\varphi ^{1}\circ \varphi ^{2})(t):=\left\{ \begin{array}{l} \varphi ^{1}(t)~\text{ for }~t\in [0,t_1], \\ \varphi ^{2}(t-t_1)\, \text{ for }\, t\in ]t_1,t_1+t_2]. \end{array}\right. \end{aligned}$$

Definition 2.2

Let $\varphi (t)$, $t\in [0,\theta ]$, be a continuous piecewise linear function and the points $0<\tau _1<\tau _2<\tau _3<\theta$ be such that $\varphi (\tau _1)= \varphi (\tau _2)=\varphi (\tau _3)$. Denote

$$\begin{aligned} \begin{array}{ll} \varphi ^1(t):=\varphi (t),\ t\in [0,\tau _1], &{}\qquad \varphi ^2(t):=\varphi (t+\tau _1),\ t\in [0,\tau _2-\tau _1], \\ \varphi ^3(t):=\varphi (t+\tau _2),\ t\in [0,\tau _3-\tau _2], &{}\qquad \varphi ^4(t):=\varphi (t+\tau _3),\ t\in [0,\theta -\tau _3]. \end{array} \end{aligned}$$

We say that the function $\widetilde{\varphi }(t):=(\varphi ^1\circ \varphi ^3\circ \varphi ^2\circ \varphi ^4)(t)$, $t\in [0,\theta ]$, is obtained from $\varphi (t)$ by a transposition w.r.t. the points $\tau _1$, $\tau _2$, $\tau _3$. We note that $\widetilde{\varphi }(t)$ is continuous and piecewise linear.

Definition 2.3

Let $u(t)$, $t\in [0,\theta ]$, be a piecewise constant control steering the initial point $x^0$ to the origin in the time $\theta$, and $x(t)$ be the corresponding trajectory. Let the points $0<\tau _1<\tau _2<\tau _3<\theta$ be such that $x_1(\tau _1)= x_1(\tau _2)=x_1(\tau _3)$. Let the function $\widetilde{x}_1(t)$ be obtained from $x_1(t)$ by a transposition w.r.t. the points $\tau _1$, $\tau _2$, $\tau _3$, and $\widetilde{u}(t)=\dot{\widetilde{x}}_1(t)$. Then we say that the control $\widetilde{u}(t)$ is obtained from $u(t)$ by an admissible transposition.

The next lemma follows from the form of the system (1).

Lemma 2.5

Let $u(t)$, $t\in [0,\theta ]$, be a control that steers the point $x^0$ to the origin in the time $\theta$. Suppose the control $\widetilde{u}(t)$ is obtained from $u(t)$ by an admissible transposition; then $\widetilde{u}(t)$ steers $x^0$ to the origin in the same time $\theta$.

Definition 2.4

Let $\varphi (t)$, $t\in [0,\theta ]$, be a continuous piecewise linear function and $\eta \in {\mathbb R}$. We say that the function $\varphi (t)$ takes the value $\eta$ $\ k$ times iff the pre-image $\varphi ^{-1}(\eta )\subset [0,\theta ]$ has $k$ connected components (points or segments).

Lemma 2.6

Suppose a continuous piecewise linear function $\varphi (t)$, $t\in [0,\theta ]$, such that $\varphi (\theta )=0$, takes a certain nonzero value at least three times; then, for any $k\ge 1$ there exists a function $\widetilde{\varphi }(t)$, which is obtained from $\varphi (t)$ by a finite number of transpositions and has at least $k$ pairwise different local extreme values.

Proof

By supposition, for a certain number $\eta \not =0$ the pre-image $\varphi ^{-1}(\eta )$ has at least three connected components and $\varphi (\theta )=0$. Then, there exist three disjoint intervals $]t_1,t_2[$, $]t_3,t_4[$, $]t_5,\theta [$, where $0\le t_1<t_2\le t_3<t_4\le t_5<\theta$, such that $\varphi (t_1)=\varphi (t_2)=\varphi (t_3)=\varphi (t_4)=\varphi (t_5)=\eta$, and $\mathop {\mathrm {sign}}\nolimits (\varphi (t)-\eta )$ is nonzero on each of them. Hence, it is the same at least on two of these intervals.

Let us assume that $\mathop {\mathrm {sign}}\nolimits (\varphi (t)-\eta )=1$ for $t\in ]t_1,t_2[\cup ]t_5,\theta [$ (the other cases are considered analogously). Then there exist a nonzero number $\eta '>\eta$ and three points $\tau _1$, $\tau _2$, $\tau _3$ such that $t_1<\tau _1<\tau _2<t_2<t_5<\tau _3<\theta$ and $\varphi (\tau _1)=\varphi (\tau _2)=\varphi (\tau _3)=\eta '$, $\dot{\varphi }(\tau _1)>0$, $\dot{\varphi }(\tau _2)<0$, $\dot{\varphi }(\tau _3)>0$. Moreover, $\eta '$ can be chosen so that it is not a local extreme value of the function $\varphi (t)$.

Let us denote by $\widetilde{\varphi }(t)$ the function which is obtained from $\varphi (t)$ by a transposition w.r.t. the points $\tau _1$, $\tau _2$, $\tau _3$. Then $\dot{\widetilde{\varphi }}(\tau _1-0)=\dot{\varphi }(\tau _1)>0$ and $\dot{\widetilde{\varphi }}(\tau _1+0)=\dot{\varphi }(\tau _2)<0$, hence, $\tau _1$ is a local maximum point of the function $\widetilde{\varphi }(t)$. Analogously, $\tau _3$ is a local minimum point of $\widetilde{\varphi }(t)$. Hence, $\eta '$ is a local extreme value of $\widetilde{\varphi }(t)$. Moreover, all local extreme values of $\varphi (t)$ (if any) are also local extreme values of $\widetilde{\varphi }(t)$ (maybe, corresponding to other extreme points). Hence, $\widetilde{\varphi }(t)$ has at least one local extreme value more than $\varphi (t)$.

We note that $\widetilde{\varphi }(t)$ takes the (nonzero) value $\eta '$ at least three times, so, we may repeat the described procedure, applying it to $\widetilde{\varphi }(t)$. Applying this procedure $k$ times, we obtain a function described in the statement of the lemma. $\square$

Lemma 2.7

Consider real analytic functions $f_1(z),\ldots ,f_n(z)$, $z\in [-\alpha ,\alpha ]$, and suppose they are linearly independent on $[-\alpha ,\alpha ]$. There exists a constant $N$ such that any function $F(z)=c_1f_1(z)+\cdots +c_nf_n(z)$, where $c_1^2+\cdots +c_n^2>0$, has no more than $N$ roots on $[-\alpha ,\alpha ]$.

Proof

Assume the converse. Then there exists a sequence $\{(c_{1,k},\ldots ,c_{n,k})\}_{k=1}^{\infty }$ such that $\sum _{i=1}^n c_{i,k}^2=1$ and the function $F_k(z)=\sum _{i=1}^n c_{i,k} f_i(z)$ has more than $k$ roots on $[-\alpha ,\alpha ]$, $k\ge 1$. We may assume $\lim _{k\rightarrow \infty }c_{i,k}=\widetilde{c}_i$, $i=1,\ldots ,n$, so $\sum _{i=1}^n\widetilde{c}_i^2=1$. We consider the function $\widetilde{F}(z)=\sum _{i=1}^n\widetilde{c}_if_i(z)$. Let us extend $f_1(z),\ldots ,f_n(z)$ to an open domain $D\subset {\mathbb C}$ such that $[-\alpha ,\alpha ]\subset D$, where $f_1(z),\ldots ,f_n(z)$ are holomorphic; then $F_k(z)$ and $\widetilde{F}(z)$ are also holomorphic. Then, $\widetilde{F}(z)$ has a finite number of roots in $D$. Due to Rouché’s Theorem for complex-valued functions, there exists a number $r$ such that the functions $\widetilde{F}(z)$ and $F_k(z)$ have the same number of roots in $D$ for $k\ge r$; this contradicts the assumption. $\square$

Corollary 2.1

For the set of real analytic functions $P_2(z), \ldots , P_n(z)$, $z\in [-\alpha ,\alpha ]$, there exists a number $N$ and a neighborhood of the origin $V$ satisfying the following property: suppose that $\widehat{u}(t)$ is an optimal control for (1), (2) with $x^0\in V$, $\{t_i\}_{i=1}^m$ are different switching points of $\widehat{u}(t)$, and $\widehat{x}(t)$ is the corresponding optimal trajectory; then the set $\{\widehat{x}_1(t_i)\}_{i=1}^m$ has no more than $N$ different elements.

Lemma 2.8

Let $u(t)$, $t\in [0,\theta ]$, be a piecewise constant control steering $x^0$ to the origin in the time $\theta$, and $x(t)$ be the corresponding trajectory. If $x_1(t)$ takes a certain nonzero value at least three times, then $u(t)$ is not time-optimal.

Proof

Assuming the converse, we suppose $\theta$ is the optimal time, $u(t)$ is an optimal control, and $x(t)$ is an optimal trajectory. Let $N$ be a constant from Corollary 2.1. Applying Lemma 2.6 to $x_1(t)$, we obtain a function $\widetilde{x}_1(t)$ having at least $N+1$ (different) local extreme values $\{\widetilde{x}_1(t_i)\}_{i=1}^{N+1}$. We put $\widetilde{u}(t)=\dot{\widetilde{x}}_1(t)$, then $\{t_i\}_{i=1}^{N+1}$ are switching points for $\widetilde{u}(t)$. Lemma 2.5 implies that $\widetilde{u}(t)$ steers $x^0$ to the origin in the optimal time $\theta$, hence, $\widetilde{u}(t)$ is optimal. This contradicts Corollary 2.1. $\square$

Roughly speaking, the previous results mean that the first coordinate of the optimal trajectory, $\widehat{x}_1(t)$, does not take the same value more than twice; the unique exception is the case $x_1^0=0$, when the value $\widehat{x}_1(t)=0$ can be taken three times. In particular, this implies that $\widehat{x}_1(t)$ has no more than one strong local maximum and one strong local minimum on the interval $]0,\widehat{\theta }[$ (and each of these values can be taken only once). Note that all “zero pieces” of $\widehat{x}_1(t)$ (corresponding to the intervals where $\widehat{u}(t)=0$) can be put between these extreme points by admissible transpositions.

Thus, let us describe possible optimal controls. We introduce the following notation for three constant functions

$$\begin{aligned} p_a(t):=1,\quad m_a(t):=-1,\quad n_a(t):=0,\quad t\in [0,a]. \end{aligned}$$

Theorem 2.2

If $x_1^0\ge 0$, then an optimal control can be chosen in the following “stair-step form”:

$$\begin{aligned} \widehat{u}(t)=(p_{a_1}\circ n_{\sigma _1}\circ m_{b_1}\circ \cdots \circ n_{\sigma _k}\circ m_{b_k}\circ n_{\sigma _{k+1}}\circ p_{a_2})(t), \end{aligned}$$

where $k\ge 1$ and

$$\begin{aligned}&a_1\ge 0 ,\quad \sigma _1\ge 0,\quad b_1,\ldots ,b_k>0,\ \sigma _2,\ldots ,\sigma _{k}>0,\quad \sigma _{k+1}\ge 0,\quad a_2\ge 0, \\&\text{ if } \ a_2=0,\ \text{ then } \ \sigma _{k+1}=0, \qquad x_1^0+a_1+a_2=b_1+\cdots +b_k, \\&x_1^0+a_1\not =b_1+\cdots +b_j,\ j=1,\ldots ,k-1. \end{aligned}$$

Moreover, any other optimal control can be reduced to this form by a finite number of admissible transpositions.

For $x_1^0\le 0$, the analogous result holds with the substitution of $m$ instead of $p$ and vice versa.

Corollary 2.1 implies that there exists a finite upper bound for $k$ for all initial points $x^0$ from a neighborhood of the origin. The additional information about the switching points $t_i$ of an optimal control can be obtained from the fact that the numbers $\widehat{x}_1(t_i)$ are roots of a function $P(z)=-\psi _0-\sum _{i=2}^n \psi _i P_i(z)$ for some $\psi _0,\psi _2,\ldots ,\psi _n$. In next section, we use this observation to specify the possible optimal controls for a concrete example.

3 Example

Consider the time-optimal control problem of the form

$$\begin{aligned}&\dot{x}_1=u, \quad \dot{x}_2 = x_1, \quad \dot{x}_3 = x_1^3,\nonumber \\&|u(t)| \le 1, \ t\in [0,\theta ],\ \quad \ x(0) = x^0, \quad \ x(\theta ) = 0, \quad \theta \rightarrow \min . \end{aligned}$$

(9)

The characteristic function of this system has the form $P(z)=-\psi _0-\psi _1z-\psi _3z^3$. Hence, it has no more than three simple different real roots or one multiple root and no more than one simple root. Suppose $x^0_1>0$ and consider “typical” cases for $P(z)$ when $\psi _3\not =0$ (Fig. 1).

Fig. 1

Graphics of $P(z)$, cases (i), (ii), (iii), (iv)

Let us ignore the controls having no more than one switching point (they obviously are optimal, since they are optimal for the linear sub-system $\dot{x}_1=u$, $\dot{x}_2=x_1$). Then we get the following possible forms of optimal controls (Figs. 2, 3, 4).

Case (i). Let $z_1<0<z_2<z_3$ be the roots of $P(z)$, then $z_1+z_2+z_3=0$ and $x_1^0<z_2$. Then $\widehat{u}(t)=(p_{a_1}\circ m_{b_1}\circ p_{a_2})(t)$, $a_1=z_2-x_1^0$, $b_1=z_2-z_1$, $a_2=-z_1$. Since $z_2<\frac{1}{2}(z_2+z_3)=\frac{1}{2}|z_1|$, we get $\widehat{x}_1(a_1)=z_2<\frac{1}{2}|z_1|=\frac{1}{2}|\widehat{x}_1(a_1+b_1)|$.

Case (ii). Let $z_1<z_2<0<z_3$ be the roots of $P(z)$, then $z_1+z_2+z_3=0$ and $x_1^0<z_3$. Then $\widehat{u}(t)=(p_{a_1}\circ m_{b_1}\circ p_{a_2})(t)$, $a_1=z_3-x_1^0$, $b_1=z_3-z_2$, $a_2=-z_2$. Since $z_3=|z_1|+|z_2|>2|z_2|$, we get $\widehat{x}_1(a_1)=z_3>2|z_2|=2|\widehat{x}_1(a_1+b_1)|$.

Fig. 2

Graphics of $\widehat{x}_1(t)$. Cases (i) and (ii)

Case (iii). Let $z_1<0$ be a simple root and $z_2>0$ be a multiple root of $P(z)$, then $z_1+2z_2=0$. If $x_1^0\ge z_2$, then two cases are possible:

$$\begin{aligned} \begin{array}{ll} \widehat{u}(t)=(m_{b_1}\circ n_{\sigma _2}\circ m_{b_2})(t), &{} b_1=x_1^0-z_2, \ \sigma _2\ge 0,\ b_2=z_2,\\ \widehat{u}(t)=(m_{b_1}\circ n_{\sigma _2}\circ m_{b_2}\circ p_{a_2})(t), &{} b_1=x_1^0-z_2, \sigma _2\ge 0, b_2=z_2-z_1, a_2=-z_1. \end{array} \end{aligned}$$

Note that in the last case $\widehat{x}_1(b_1)=z_2=\frac{1}{2}|z_1|=\frac{1}{2}|\widehat{x}_1(b_1+\sigma _2+b_2)|$.

If $x_1^0< z_2$, then also two cases are possible:

$$\begin{aligned} \begin{array}{ll} \widehat{u}(t)=(p_{a_1}\circ n_{\sigma _1}\circ m_{b_1})(t),&{} a_1=z_2-x_1^0,\ \sigma _1\ge 0,\ b_1=z_2,\\ \widehat{u}(t)=(p_{a_1}\circ n_{\sigma _1}\circ m_{b_1}\circ p_{a_2})(t), &{} a_1=z_2-x_1^0, \sigma _1\ge 0, b_1=z_2-z_1, a_2=-z_1. \end{array} \end{aligned}$$

Note that in the last case $\widehat{x}_1(a_1)=z_2=\frac{1}{2}|z_1|=\frac{1}{2}|\widehat{x}_1(a_1+\sigma _1+b_1)|$.

Fig. 3

Graphics of $\widehat{x}_1(t)$. Case (iii)

Case (iv). Let $z_1<0$ be a multiple root and $z_2>0$ be a simple root of $P(z)$, then $2z_1+z_2=0$ and $x_1^0<z_2$. We get two possible cases

$$\begin{aligned} \begin{array}{ll} \widehat{u}(t)=(m_{b_1}\circ n_{\sigma _2}\circ p_{a_2})(t), &{} b_1=x_1^0-z_1,\ \sigma _2\ge 0,\ a_2=-z_1,\\ \widehat{u}(t)=(p_{a_1}\circ m_{b_1}\circ n_{\sigma _2}\circ p_{a_2})(t), &{} a_1=z_2-x_1^0, b_1=z_2-z_1, \sigma _2\ge 0, a_2=-z_1, \end{array} \end{aligned}$$

where $x_1^0<z_2=2|z_1|=2|\widehat{x}_1(b_1)|$ and $\widehat{x}_1(a_1)=z_2=2|z_1|=2|\widehat{x}_1(a_1+b_1)|$, respectively.

Fig. 4

Graphics of $\widehat{x}_1(t)$. Case (iv)

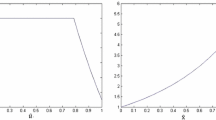
As an example, consider the initial point $x^0=(1,-0.5,-3)$. Checking all possible cases, we get that the optimal control corresponds to case (iv) and equals $\widehat{u}(t)= (p_{a_1}\circ m_{b_1}\circ n_{\sigma _2}\circ p_{a_2})(t)$, where $a_1=0.73$, $b_1=2.59$, $\sigma _2=1.43$, $a_2=0.86$, and the optimal time equals $\theta =5.62$. The components of the trajectory are given in Fig. 5 (left picture).

This initial point can be also steered to the origin by the bang-bang control with two switchings $u(t)=(p_{a_1}\circ m_{b_1}\circ p_{a_2})(t)$, where $a_1=0.94$, $b_1=3.60$, $a_2=1.66$. However, this control is not optimal, since it does not belong to the cases (i)–(iv) described above. In fact, we have $x_1(a_1)=1.94$ and $x_1(a_1+b_1)=-1.66$, and it is easy to check that $x_1(a_1)<2|x_1(a_1+b_1)|$ and $x_1(a_1)>\frac{1}{2}|x_1(a_1+b_1)|$. For this control, the time of motion equals $T=6.19$. The components of the trajectory are given in Fig. 5 (right picture).

Fig. 5

Components of two trajectories for the initial point $x^0=(1,-0.5,-3)$

4 Approximation in the Sense of Time Optimality

In this section, we describe the class of affine control systems that are equivalent to the ones of the form (1) in the sense of time optimality. Let us consider the time-optimal control problem for affine control systems of the form

$$\begin{aligned}&\dot{x} = a(t, x) + u b(t,x), \quad a(t,0)\equiv 0,\end{aligned}$$

(10)

$$\begin{aligned}&|u(t)| \le 1, t\in [0,\theta ], \quad x(0) = x^{0}, \quad x(\theta ) = 0, \quad \theta \rightarrow \min , \end{aligned}$$

(11)

where $a(t,x)$, $b(t,x)$ are real analytic on a neighborhood of the origin in $\mathbb {R}^{n+1}$. We introduce the operator $\mathrm{S}_{a,b}(\theta ,u)$ that maps a pair $(\theta ,u)$ to the initial point $x^0$, which is steered to the origin by the control $u=u(t)$ in the time $\theta$, i.e., $\mathrm{S}_{a,b}(\theta ,u)=x^0$. This operator admits the following series expansion [3, 5]:

$$\begin{aligned} \hbox {S}_{a,b}(\theta ,u)=\sum \limits _{m=1}^\infty \sum \limits _{\begin{array}{c} {m_1+\cdots +m_k+k=m}\\ {k\ge 1,\ m_j\ge 0} \end{array}} v_{m_1\ldots m_k} \xi _{m_1\ldots m_k}(\theta , u), \end{aligned}$$

(12)

where $\xi _{m_1\ldots m_k}(\theta , u)$ are nonlinear power moments of the function $u(t)$,

$$\begin{aligned} \xi _{m_1\ldots m_k}(\theta , u) = \int \limits _0 ^\theta \int \limits _0 ^{\tau _1} \cdots \int \limits _0 ^{\tau _{k-1}} \prod \limits _{j=1}^k \tau _j^{m_j}u(\tau _j) \mathrm{d}\tau _k \cdots \mathrm{d}\tau _2\mathrm{d}\tau _1, \end{aligned}$$

(13)

and $v_{m_1\ldots m_k}$ are constant vector coefficients defined via $a(t,x)$ and $b(t,x)$ by the following formulas. We introduce the operators $\mathrm{R}_a$ and $\mathrm{R}_b$ acting as

$$\begin{aligned} \mathrm{R}_a f(t,x)=f_t(t,x)+f_x(t,x)\cdot a(t,x), \quad \mathrm{R}_b f(t,x)= f_x(t,x)\cdot b(t,x) \end{aligned}$$

for any real analytic vector function $f(t,x)$. We use the notation $\mathrm {ad}^{0}_{\mathrm{R}_a} {\mathrm{R}_b}={\mathrm{R}_b}$, $\mathrm {ad}^{m+1}_{\mathrm{R}_a} {\mathrm{R}_b}= [{\mathrm{R}_a},\mathrm {ad}^m_{\mathrm{R}_a} {\mathrm{R}_b}]$, $m\ge 0$, where brackets $[\cdot ,\cdot ]$ denote the operator commutator. Then

$$\begin{aligned} v_{m_1\ldots m_k}=\frac{(-1)^k}{m_1!\cdots m_k!} \mathrm {ad}^{m_1}_{\mathrm{R}_a} {\mathrm{R}_b} \circ \cdots \circ \mathrm {ad}^{m_k}_{\mathrm{R}_a} {\mathrm{R}_b} {E}(x)_{\bigl |_{\begin{array}{c} {x=0} \\ {t=0} \end{array}}}, \end{aligned}$$

(14)

where $E(x)\equiv x$. Now, we recall some concepts and results concerning the application of the free algebras technique proposed and developed in [4–10]. Different approaches based on series representations close to (12) can be found in [13–19].

We consider nonlinear power moments $\xi _{m_1 \cdots m_k}(\theta ,u)$ as words generated by the letters $\xi _i(\theta , u)$, i.e., assume that the word $\xi _{m_1\ldots m_k}(\theta ,u)$ is a concatenation of the letters $\xi _{m_1}(\theta ,u),\ldots ,\xi _{m_k}(\theta ,u)$. Then the linear span of nonlinear power moments becomes an associative non-commutative algebra. It can be shown that nonlinear power moments are linearly independent as functionals on $L_\infty [0,\theta ]$ (for $\theta >0$); therefore, the above-mentioned algebra is free. Hence, it is isomorphic to an abstract free algebra generated by abstract elements $\{\xi _i\}_{i=0}^\infty$ (over ${\mathbb R}$) with the multiplication $\xi _{m_1\cdots m_k}:= \xi _{m_1}\vee \cdots \vee \xi _{m_k}$. We denote this algebra by $\mathcal {A}$ and call it the algebra of nonlinear power moments. We introduce the free Lie algebra $\mathcal {L}$ generated by $\{\xi _i\}_{i=0}^\infty$ with the Lie bracket operation $[\ell _1,\ell _2]:=\ell _1\vee \ell _2-\ell _2 \vee \ell _1$, $\ell _1,\ell _2 \in \mathcal {L}$. Then $\mathcal {A}$ is a universal enveloping algebra for $\mathcal {L}$. Finally, we introduce the inner product $\langle \cdot ,\cdot \rangle$ such that $\{\xi _{m_1\ldots m_k}:k\ge 1,\ m_1,\ldots ,m_k\ge 0\}$ is an orthonormal basis of $\mathcal {A}$. We note that the algebra $\mathcal {A}$ admits the natural grading, $\mathcal {A}=\sum _{m=1}^\infty \mathcal {A}^m$, where $\mathcal {A}^m:=\mathrm {Lin}\{\xi _{m_1 \ldots m_k} : m_1+ \cdots + m_k+k=m\}$. We denote $\mathcal {L}^m:=\mathcal {L} \cap \mathcal {A}^m$.

We note that the series (12) defines the linear mapping $v : \mathcal {A} \rightarrow \mathbb {R}^n$ by the rule $v(\xi _{m_1\ldots m_k}) = v_{m_1\ldots m_k}$. Thus, one can consider an abstract analog of the series (12), i.e., the series of elements of $\mathcal {A}$ with constant vector coefficients of the form

$$\begin{aligned} \mathrm{S}_{a,b}=\sum \limits _{m=1}^\infty \sum \limits _{\begin{array}{c} {m_1+\cdots +m_k+k=m}\\ {k\ge 1,\ m_j\ge 0} \end{array}} v(\xi _{m_1\ldots m_k})\,\xi _{m_1\ldots m_k}. \end{aligned}$$

Below, we assume that $v$ satisfies the Rashevsky–Chow condition [20, 21]

$$\begin{aligned} v(\mathcal {L})=\mathbb {R}^n. \end{aligned}$$

(15)

We recall that (15) is an accessibility condition for the system (10), i.e., it guarantees that the set of those $x^0$, that can be steered to the origin, has a nonempty interior, and the origin belongs to the closure of this interior.

For a given system (10), we consider its core Lie subalgebra $\mathcal {L}_{a,b}$ defined by $\mathcal {L}_{a,b}:=\sum _{m=1}^\infty \mathcal {P}^m$, where $\mathcal {P}^m:=\{\ell \in \mathcal {L}^m : v(\ell )\in v(\mathcal {L}^1+\cdots +\mathcal {L}^{m-1}) \}$, $m \ge 1$. We introduce also the right ideal $\mathcal {J}_{a,b}:=\mathrm {Lin}\{\ell \vee z : \ell \in \mathcal {L}_{a,b},\ z\in \mathcal {A}+\mathbb {R}\}$ and denote by $\mathcal {J}_{a,b}^{\perp }$ the orthogonal complement of $\mathcal {J}_{a,b}$ in $\mathcal {A}$. Let the Rashevsky–Chow condition (15) be satisfied; then $\mathcal {L}_{a,b}$ is of codimension $n$. Suppose $\ell _1,\ldots ,\ell _n\in \mathcal {L}$ are such that

$$\begin{aligned} \mathcal {L}=\mathcal {L}_{a,b}+\mathrm {Lin}\{\ell _1,\ldots ,\ell _n\}, \end{aligned}$$

(16)

and $\ell _i\in {\mathcal A}^{w_i}$, $i=1,\ldots ,n$. For any element $a\in \mathcal {A}$, we denote by $\widetilde{a}$ the orthoprojection of $a$ on the subspace $\mathcal {J}_{a,b}^{\perp }$. One can show [5] that there exists a nonsingular analytic transformation $z=\Phi (x)$ of a neighborhood of the origin such that

$$\begin{aligned} (\Phi (\mathrm{S}_{a,b}))_i = \widetilde{\ell }_i+\rho _i,\quad i = 1,\ldots , n, \end{aligned}$$

(17)

and $\rho _i\in \sum _{j=w_i+1}^\infty \mathcal {A}^j$, $i=1,\ldots ,n$. In other words, $(\widetilde{\ell }_1,\ldots ,\widetilde{\ell }_n)$ is the main part of the series $\mathrm{S}_{a,b}$. One can show that there exists a system

$$\begin{aligned} \dot{x} =a^*(t,x)+ u b^*(t,x), \quad a^*(t,0)\equiv 0, \end{aligned}$$

(18)

such that

$$\begin{aligned} (\mathrm{S}_{a^*,b^*})_i = \widetilde{\ell }_i,\quad i = 1,\ldots , n. \end{aligned}$$

(19)

Moreover, one can achieve $a^*(t,x)\equiv 0$. Such a system can be interpreted as an algebraic approximation of the initial system.

Let us consider the time-optimal control problem

$$\begin{aligned}&\dot{x} = a^*(t, x) + u b^*(t, x), \quad a^*(t,0)\equiv 0,\end{aligned}$$

(20)

$$\begin{aligned}&x(0) = x^0 , \ x(\theta )=0,\ |u(t)| \le 1,\ t\in [0,\theta ],\quad \theta \rightarrow \min , \end{aligned}$$

(21)

where (20) is an algebraic approximation of (10). The question is whether the time-optimal control problem (20), (21) approximates the initial time-optimal control problem (10), (11). Below, we recall the corresponding definition and result [5].

We suppose $\Omega \subset \mathbb {R}^n\backslash \{0\}$, $0\in \overline{\Omega }$, is an open domain such that, for any $x^0\in \overline{\Omega }$, there exists the unique solution $(\theta ^*_{x^0},u^*_{x^0})$ of (20), (21). By $U_{x^0}^{a,b}(\theta )$ we denote the set of all admissible controls which transfer the point $x^0$ to the origin by virtue of the system (10) in the time $\theta$, and by $\theta _{x^0}$ we denote the optimal time for (10), (11). Then $\theta _{x^0}=\min \{\theta : U_{x^0}^{a,b}(\theta )\ne \varnothing \}$.

Definition 4.1

We say that the nonlinear time-optimal control problem (20), (21) approximates the time-optimal control problem (10), (11) in the domain $\Omega$ iff there exists a nonsingular real analytic transformation $\Phi$ of a neighborhood of the origin, $\Phi (0)=0$, and a set of pairs $(\widetilde{\theta }_{x^0},\widetilde{u}_{x^0})$, $x^0\in \Omega$, such that $\widetilde{u}_{x^0}\in U_{\Phi (x^0)}^{a,b}(\widetilde{\theta }_{x^0})$ and

$$\begin{aligned} \frac{\theta _{\Phi (x^0)}}{\theta ^*_{x^0}}\rightarrow 1,\quad \frac{\widetilde{\theta }_{x^0}}{\theta ^*_{x^0}}\rightarrow 1,\quad \frac{1}{\theta } \int \limits _0^\theta |u^*_{x^0}(t)-\widetilde{u}_{x^0}(t)|\mathrm{d}t\rightarrow 0\ \text{ as } \ x^0\rightarrow 0, \ x^0 \in \Omega , \end{aligned}$$

(22)

where $\theta =\min \{\widetilde{\theta }_{x^0},\theta ^*_{x^0}\}$.

Now we recall the main result of [5].

Theorem 4.1

Let the system (10) satisfy the Rashevsky–Chow condition (15). We assume that the elements $\ell _1,\ldots ,\ell _n$ are chosen by (16) and consider the system (20), whose series has the form (19). Let us suppose that there exists an open domain $\Omega \subset {\mathbb R}^n\backslash \{0\}$, $0\in \overline{\Omega }$, such that

• (i) the time-optimal control problem (20), (21) has a unique solution $(\theta ^*_{x^0},u^*_{x^0})$ for any $x^0\in {\Omega }$;

• (ii) the function $\theta ^*_{x^0}$ is continuous for $x^0\in {\Omega }$;

• (iii) when considering the set $K = \{u^*_{x^0}(t\theta ^*_{x^0}) : x^0\in {\Omega }\}$ as a set in the space $L_2(0, 1)$, the weak convergence of a sequence of elements from $K$ implies the strong convergence.

Then, for any $\delta >0$ there exists a domain $\Omega _\delta \subset {\mathbb R}^n$ such that $0\in \overline{\Omega }_\delta$ and $\Omega =\cup _{\delta >0}\Omega _\delta$, and the time-optimal control problem (20), (21) approximates the time-optimal control problem (10), (11) in any domain $\Omega _\delta$.

Moreover, if the set $\widehat{K}= \{u_{x^0}(t\theta _{x^0}) : x^0\in {\Omega }\}$ also satisfies condition (iii), where $(\theta _{x^0},u_{x^0})$ is a solution of the time-optimal control problem (10), (11), then in (22) one can choose $\widetilde{\theta }_{x^0}=\theta _{\Phi (x^0)}$ and $\widetilde{u}_{x^0}(t)=u_{\Phi (x^0)}(t)$.

We consider the condition (iii) in a separate way. It is, obviously, satisfied if the system (20) is linear, because in this case $K$ includes only piecewise constant functions having no more than $n-1$ switchings. However, in the general case this is an open question about a class of systems satisfying this condition [6]. The results of Sect. 2 allow us to conclude that systems of the form (1) satisfy condition (iii) automatically. Let us describe the form of the approximating series (19) for systems (1) more specifically and obtain the corresponding corollary of Theorem 4.1. We denote $D^m(x_1):=(0, P_2^{(m)}(x_1),\cdots ,P^{(m)}_n(x_1))^{T}$, $m\ge 0$, and $e_1:=\left( 1,0,\cdots ,0\right) ^{T}$, where $P_k^{(m)}(x_1)$ means the $m$-th derivative of $P_k(x_1)$. Then $a(t,x)=D^0(x_1)$ and $b(t,x)=e_1$. Therefore, $\mathrm{R}_b^2E(x)\equiv 0$, $\mathrm{R}_a\mathrm{R}_bE(x)\equiv 0$, $\mathrm{R}_b^m\mathrm{R}_aE(x)=D^m(x_1)$ and $\mathrm{R}_a\mathrm{R}_b^m\mathrm{R}_aE(x)\equiv 0$ for $m\ge 0$. We denote $\xi _0^k:=\xi _0\vee \cdots \vee \xi _0$ ($k$ times). Then

$$\begin{aligned} \mathrm{S}_{a,b}= -e_1\xi _0+\sum \limits _{k=0}^\infty (-1)^{k}D^{k+1}(0)\xi _0^k\vee \xi _1. \end{aligned}$$

(23)

Since the functions $P_2(x_1),\ldots ,P_n(x_1)$ are linearly independent, the Rashevsky–Chow condition (15) holds. Suppose $q_2<\cdots <q_n$ are the indices of the first $n-1$ linearly independent elements in the sequence $\{D^k(0)\}_{k=1}^\infty$. Then, there exists a system (18) of the form

$$\begin{aligned} \dot{x}_1=u,\quad \dot{x}_i =x_1^{q_i},\ i=2,\ldots ,n,\quad 1\le q_2 < \ldots < q_n, \end{aligned}$$

(24)

such that $\mathcal {J}_{a,b}=\mathcal {J}_{a^*,b^*}$. Therefore, (24) is an algebraic approximation of (1).

In general, we say that a system of the form (10) is essentially dual-to-linear iff there exists a dual-to-linear system (1) whose ideal coincides with the ideal of (10). The discussion above implies that a system of the form (10) is essentially dual-to-linear if and only if

(25)

and

(26)

Thus, a system of the form (24) satisfies condition (iii) of Theorem 4.1. Moreover, as follows from [22], if all numbers $q_2,\ldots ,q_n$ are odd, then condition (ii) holds. As a result, we obtain the following corollary.

Corollary 4.1

Suppose a system of the form (10) is essentially dual-to-linear, i.e., satisfies conditions (25), (26). Let $0=q_1<q_2<\cdots < q_n$ be the indices of the first $n$ linearly independent elements in the sequence $\{y_j\}_{j=0}^\infty$, where $y_0=b(0,0)$ and $y_j=\mathrm {ad}^j_{\mathrm{R}_b}\mathrm{R}_a E(x)_{\bigl |_{\begin{array}{c} {x=0}\\ {t=0} \end{array}}}$, $j\ge 1$. We suppose that there exists an open domain $\Omega \subset {\mathbb R}^n\backslash \{0\}$, $0\in \overline{\Omega }$, such that

• (i) the time-optimal control problem for the system (24) has a unique solution $(\theta ^*_{x^0},u^*_{x^0})$ for any $x^0\in {\Omega }$;

• (ii) the function $\theta ^*_{x^0}$ is continuous for $x^0\in {\Omega }$;

Then, for any $\delta >0$ there exists a domain $\Omega _\delta \subset {\mathbb R}^n$ such that $0\in \overline{\Omega }_\delta$ and $\Omega =\cup _{\delta >0}\Omega _\delta$, and the time-optimal control problem (20), (21) approximates the time-optimal control problem (10), (11) in any domain $\Omega _\delta$.

Moreover, in the case when the initial system is of the form (1), one can choose $\widetilde{\theta }_{x^0}=\theta _{\Phi (x^0)}$ and $\widetilde{u}_{x^0}(t)=u_{\Phi (x^0)}(t)$. Finally, if $q_2,\ldots ,q_n$ are odd, then condition (ii) holds automatically.

Now, we are ready to explain, why systems (1) are called “dual-to-linear.” In [3], we considered systems of the form (10), which are approximated, in the sense of time optimality, by linear systems $\dot{x} = A(t)x + u b(t)$. We found out that the result analogous to Corollary 4.1 holds, where, instead of (26), the following condition appears

$$\begin{aligned}&[\mathrm {ad}^{m_1}_{\mathrm{R}_a}\mathrm{R}_b,\cdots [\mathrm {ad}^{m_{k-1}}_{\mathrm{R}_a}\mathrm{R}_b,\mathrm {ad}^{m_k}_{\mathrm{R}_a}\mathrm{R}_b]\cdots ]E(x)_{{\bigl |}_{\begin{array}{c} {x=0}\\ {t=0} \end{array}}} \in \mathrm {Lin}\{\mathrm {ad}^j_{\mathrm{R}_a}\mathrm{R}_b E(x)_{{\bigl |}_{\begin{array}{c} {x=0}\\ {t=0} \end{array}}}\}_{j=0}^{m-2},\nonumber \\&\quad \text{ where } \ m=m_1+\cdots +m_k+k,\quad k\ge 2,\quad m_1,\ldots ,m_k\ge 0.\quad \end{aligned}$$

(27)

We note that (26) is obtained as a result of partial replacing of $\mathrm {ad}^j_{\mathrm{R}_a}\mathrm{R}_b$ by $\mathrm {ad}^j_{\mathrm{R}_b}\mathrm{R}_a$ in (27). Such a “duality” of conditions (26) and (27) justifies our term “dual-to-linear systems.”

5 Conclusions

In the paper, we have considered one special class of nonlinear control systems, called dual-to-linear systems. For these systems, we studied the time-optimal control problem and gave the explicit description of the possible character of optimal controls. The three-dimensional example was given to illustrate these results. We described the class of nonlinear affine control systems, which can be approximated by dual-to-linear systems in the sense of time optimality. Our analysis gave reason to conclude that dual-to-linear systems are, in a certain sense, close to linear systems.

It is well known that the time-optimal control problem for a linear system admits an interpretation in terms of the Markov moment problem [23, 24]. The results of the present paper open the following direction of the further research: find a moment interpretation for dual-to-linear systems. The explicit form of optimal controls can be considered as a starting point of such an investigation.