1 Introduction

Evolutionary multiobjective optimization (EMO) algorithms [1–3] derive finite approximations of Pareto fronts (i.e. sets of efficient solutions, as defined below). They can be regarded, conventionally, as lower approximations (we assume that all objectives are to be maximized), because all their elements are feasible solutions. Yet, with the exception of test problems, Pareto fronts are generally not known. Hence the exact accuracy of such approximations is not known either.

To rectify this, we propose to work with elements outside the feasible solution set (infeasible solutions), with the objective to provide upper approximations of Pareto fronts. A pair consisting of a lower and an upper approximation forms an approximation of the Pareto front, whose accuracy can be controlled by distance between the lower and the upper approximation. Thus, the approach proposed herein effectuates the idea of two-sided Pareto front approximations, which is as yet absent from the literature on EMO. Exploiting explicitly infeasible solutions to provide two-sided approximations of Pareto fronts offers a new turn in research in the field.

Our research has been motivated by the absence, to our best knowledge, of papers pertaining to EMO or multiobjective optimization, in which active use of infeasible elements would be harnessed to approximate the Pareto front. The only exception is perhaps paper [4]; however, in that work, infeasible solutions were not generated intentionally, as it is done in our work.

The outline of the paper is as follows. In Sect. 2, necessary definitions are provided; in particular; lower and upper shells, which yield specific lower and upper approximations of Pareto fronts, are defined. In Sect. 3, an approximation accuracy measure is set, and a relaxation of the definition of upper shell is proposed with the purpose to have a construct more suitable for computations than upper shell itself.

In Sect. 4, a rudimentary evolutionary algorithm for approximating Pareto fronts within given accuracy is presented. The algorithm has been run on five test problems taken from literature and the results are reported in Sect. 5. Directions for further research are proposed in Sect. 6, whereas Sect. 7 contains the concluding remarks.

2 Definitions and Notation

Multicriteria Optimization (MO) problem is formulated as

$$ \begin{aligned} &\max f(x) \\ &x \in X_0 \subseteq\mathbb{R}^n, \end{aligned} $$
(1)

where \(f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{k}; \ f=(f_{1},\ldots ,f_{k}), \ f_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R}, \ i=1, \ldots,k, \ k \geq2\), are objective (criteria) functions; max denotes the operator of deriving all efficient elements (see the definition below). We assume that X 0 has an interior.

The dominance relation ≺ is defined on \(\mathbb{R}^{n}\) as

$$x' \prec x \quad \Leftrightarrow\quad f(x') \ll f(x), $$

where ≪ denotes f i (x′)≤f i (x), i=1,…,k, and f i (x′)<f i (x) for at least one i.

If x≺x′ then x is dominated by x′ and x′ is dominating x.

An element x of X 0 is called efficient iff

$$\nexists\, x' \in X_0 \quad \ x \prec x' . $$

We denote the set of efficient elements by N and the set f(N) (the Pareto front) by P, P⊆f(X 0).

Lower shell is a finite nonempty set S L ⊆X 0, elements of which satisfy

$$ \forall\, x \in S_L \ \nexists\, x' \in S_L \quad x \prec x' $$
(2)

(thus no element of S L is dominated by another element of S L ).

We define the nadir point y nad as

$$y^{\mathrm{nad}}_i := \min_{x \in N} f_i(x), \quad i=1,\ldots,k. $$

Upper shell is a finite nonempty set \(S_{U} \subseteq \mathbb{R}^{n} \setminus X_{0}\), elements of which satisfyFootnote 1

$$\begin{aligned} &\forall\, x \in S_U \ \nexists\, x' \in S_U \quad x' \prec x, \end{aligned}$$
(3)
$$\begin{aligned} &\forall\, x \in S_U \ \nexists\, x' \in N \quad x \prec x', \end{aligned}$$
(4)
$$\begin{aligned} &\forall\, x \in S_U \quad y^{\mathrm{nad}} \ll f(x). \end{aligned}$$
(5)

3 Approximations of P

We aim at constructing numerically viable two-sided approximations of P.

To derive S L for which f(S L ) is “close” to P, any EMO algorithm can be used (cf. [1, 2, 6–9]).

Since the definition of an upper shell involves N, this construct is not a suitable approximation of N. A more suitable construct, referring to S L instead of N, namely an upper approximation A U , is obtained by replacing:

condition (3) by

$$ \forall\, x \in A_U \ \nexists\, x' \in A_U \quad x' \prec x, $$
(6)

condition (4) by

$$ \forall\, x \in A_U \ \nexists\, x' \in S_L \quad x \prec x' \,, $$
(7)

condition (5) by

$$ \forall\, x \in A_U \quad y^{\mathrm{nad}}(S_L) \ll f(x), $$
(8)

where y nad(S L ) denotes an element of \(\mathbb{R}^{k}\) such that

$$y^{\mathrm{nad}}_i(S_L) := \min_{x \in S_L} \, f_i(x), \ i=1,\ldots,k $$

(y nad(S L ) varies with S L ).

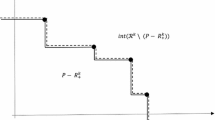
By definition, an upper approximation A U can contain elements which are dominated by some elements of N, as shown in Fig. 1, and certainly such elements are undesirable for the purpose. Condition (8) is meant to limit the domain for such elements. However, as S L gets “closer” to N and y nad(S L ) gets “closer” to y nad, the chance for such elements being included in A U decreases.

Fig. 1
figure 1

An example when an element x, dominated by some element of N, belongs to A U

Full size image

With S L and A U derived, the accuracy of the approximation of P by f(S L ) and f(A U ) can be measured as

$$\overline{\mathit{acc}}_P := \frac{1}{|S_L|} \sum_{x \in S_L} \min_{x' \in A_U} \big\| f(x) - f(x')\big\| , $$

or

$$\mathit{acc}_P := \max_{x \in S_L} \min_{x' \in A_U} \big\| f(x) - f(x')\big\| , $$

where ∥⋅∥ is a norm and |⋅| is cardinality of a set. In numerical experiments and applications, a form of normalization of \(\overline{\mathit{acc}}_{P}\) and acc P with respect to ranges of values of objective functions over e.g. S L is advisable (cf. Sect. 5).

Those two indices measure only “closeness” of f(S L ), f(A U ). “Goodness” or “fairness” of the approximation of P by such constructs has to be ensured by standard EMO mechanisms.

In next section, we propose an algorithm for deriving two-sided approximations of P.

4 An Algorithm for Two-sided Approximations of P

The algorithm we propose below derives two-sided approximations of P, thus providing a way for approximation accuracy monitoring.

Let α P denote the desired value of acc P .

We limit the domain of searching in \(\mathbb{R}^{n} \setminus X_{0}\) to some set

$$X_{\mathrm{DEC}} := \bigl\{ x \in\mathbb{R}^n \, | \, X^L_i \leq x_i \leq X^U_i, i=1,\ldots,n \bigr\} \quad \mbox{such that}\quad X_0 \subseteq \mathrm{int}(X_{\mathrm{DEC}}). $$

By assumption, X 0 has an interior, hence elements of X DEC, generated randomly, belong to X 0 with positive probability.

Algorithm EMO-APPROX

  1. 1.

    \(j :=0, \ S^{j}_{L} := \emptyset, \ A^{j}_{U} := \emptyset\).

  2. 2.

    Select randomly η elements of X 0 and derive \(S^{j}_{L}\).

  3. 3.

    Select randomly an element x of \(S^{j}_{L}\) and:

    1. 3.1.

      derive an element x′∈X DEC such that x′⊀x,

    2. 3.2.

      if x′∈X 0 then update \(S_{L}^{j}\) and \(A_{U}^{j}\) with \(S' = S_{L}^{j} \cup\{ x' \}\), go to 3.4,

    3. 3.3.

      update \(A_{U}^{j}\) with \(A' = A_{U}^{j} \cup\{ x' \}\),

    4. 3.4.

      if acc P ≤α P or j=j max then STOP,

    5. 3.5.

      j:=j+1, go to 3.

In step 2, η is a parameter and derivation of S L means that selected elements which do not satisfy condition (2) are to be removed.

In substep 3.1, to derive an element x′ of the required properties, components of x are mutated until x∈X DEC and x′⊀x holds. Mutations can increase or decrease with probability 0.5 the value of a randomly selected component. The range of mutations decreases with the increasing j. If a mutation increases the ith component of x, then the value of this component after mutation is

$$x_i + \bigl(X^U_i - x_i\bigr)\times\Bigl(1-\mathrm{rnd}(0,1)^{2(1-\frac{j}{j^{\max}})}\Bigr), $$

and if this mutation decreases the component, then the value of this component after mutation is

$$x_i - \bigl(x_i - X^L_i\bigr) \times\Bigl(1-\mathrm{rnd}(0,1)^{2(1-\frac{j}{j^{\max}})}\Bigr). $$

Function rnd(0,1) returns a random number from the range [0,1] with uniform probability. The presented method of mutation and the strategy of decreasing mutation range have been taken from the literature (cf. e.g. [6]).

In substep 3.2, the update of \(S^{j}_{L}\) means that elements of \(S' = S^{j}_{L} \cup\{ x' \}\) which do not satisfy condition (2) are to be removed from S′, and only then \(S^{j}_{L} := S'\). The update of \(A^{j}_{U}\) means that elements of \(A^{j}_{U}\) which do not satisfy condition (7) with respect to updated \(S^{j}_{L}\) are to be removed.

In substep 3.3, the update of \(A^{j}_{U}\) means that elements of \(A'= A^{j}_{U} \cup\{ x' \}\) which do not satisfy conditions (6), (7) and (8) are to be removed from A′, and only then \(A^{j}_{U} := A'\).

In substep 3.4, j max is the maximal number of iterations in the algorithm.

There is no guarantee that the approximation accuracy monotonously improves by each iteration of EMO-APPROX (i.e. on (i+1)-th iteration acc P takes a smaller value than on iteration i). The phenomenon is illustrated in Fig. 2. Indeed, suppose that S L ={a,b}, A U ={c,d}. Clearly, \(\mathit{acc}_{P}^{1} = \max\{ \|f(a) - f(c)\|, \|f(b) - f(d)\| \} \) (the superscript indicates the iteration). Including e into S L causes b to be eliminated from S L (for e dominates b—condition (2)). Now we have \(\mathit{acc}_{P}^{2} = \max\{ \|f(a) - f(c)\|, \|f(e) - f(d)\| \} \) and clearly \(\mathit{acc}_{P}^{2} \geq \mathit{acc}_{P}^{1}\), which means that the approximation accuracy has deteriorated. However, it can be expected that in successive iterations mutations of e or d can recover this local loss of accuracy.

Fig. 2
figure 2

Possible non-monotonous behavior of the algorithm

Full size image

As the algorithm is founded on genetic-type heuristics, no formal proof is offered that in general the algorithm is able to derive a two-sided approximation of P within a given accuracy. However, by means of two-sided approximations at least the behavior of such heuristics is put under control.

5 Numerical Experiments

We illustrate the behavior of EMO-APPROX on four test problems taken from [8], denoted DTLZ2a, DTLZ4a, DTLZ7a, Selri, and one taken from [10, 11], denoted Kita.

We normalized the accuracies \(\overline{\mathit{acc}}_{P}\) and acc P as follows:

$$\begin{aligned} \overline{\mathit{acc}}_P :=& \frac{1}{|S_L|} \sum_{x \in S_L} \min_{x' \in A_U} \left( \sum^k_{i=1} \left(\frac{f_i(x) - f_i(x')}{s^f_i} \right)^2 \right)^{\frac{1}{2}}, \\ \mathit{acc}_P :=& \max_{x \in S_L} \min_{x' \in A_U} \left( \sum^k_{i=1} \left(\frac{f_i(x) - f_i(x')}{s^f_i} \right)^2 \right)^{\frac{1}{2}}, \end{aligned}$$

where \(s^{f}_{i} := \max_{x \in S_{L}} f_{i}(x) - \min_{x \in S_{L}} f_{i}(x), \ i = 1,\ldots,k\) (the normalization factor varies with S L ).

We ran EMO-APPROX on the test problems with j max=9000, η=100 in each case, taking three shots of the algorithm behavior and the results it provided at j=3000, j=6000 and finally at j=9000. Since it was not certain what values of the parameter α P should be used, we set it to zero and we stopped the algorithm after the iteration count reached j max. In each case, X DEC was assumed to be [−0.2,1.2]×[−0.2,1.2]×…×[−0.2,1.2] for all four DTLZ problems and [−2.0,9.0]×[−2.0,9.0] for the Kita problem.

Table 1 Footnote 2 shows the values of \(\overline{\mathit{acc}}_{P}\) and acc P for each problem and shot, where n, m, b and k are, respectively, the number of variables, the number of general constraints, the number of box constraints and the number of criteria; #f is the number of function f evaluations; ∥A U ∥, ∥S L ∥ and ∥A U ∥+∥S L ∥ are the cardinality of, respectively, A U , S L and A U ∪S L .

Table 1 Test results—EMO-APPROX
Full size table

Figures 3 and 4 present, respectively, the elements of S L , A U and f(S L ), f(A U ) for the Kita problem.

Fig. 3
figure 3

Elements of S L and A U for the Kita problem

Full size image
Fig. 4
figure 4

Elements of f(S L ) and f(A U ) for the Kita problem

Full size image

These test results constitute a rather limited base for drawing general conclusions. It is, nevertheless, possible to point to some regularities, which seem to be in line with the expected behavior of the algorithm.

Both accuracies improve monotonously for 3000, 6000 and 9000 iterations only in two instances (DTLZ7a and Kita), whereas for other problems improvements are not monotonous due to a phenomenon explained in previous section. In the remaining instances, there was no significant gain in increasing the number of iterations from 6000 to 9000, for at 9000 the accuracies are either worse or only slightly better.

In all instances, S L has more elements then A U . This is caused by the order in which the algorithm attempts to produce new elements of those sets—first in S L and then in A U . By interchanging this order, more balanced sets can be produced.

For the Kita, DTLZ2a and DTLZ4a problems, for which analytic forms of N are known, we have generated a number of elements of N (1852 elements for Kita, 2001 elements for DTLZ2a and DTLZ4a). In none of those problems is an element of A U dominated by a generated element of N, which could be attributed to the strength of condition (8) (we have inspected only A U derived in 9000 iterations).

6 Further Directions

To demonstrate the potential in further fine tuning of the approach, we have coupled EMO-APPROX with the algorithm NSGA-II ([7]); the latter has proved itself a very effective in producing well distributed and accurate lower approximations (S L ) of P. In this experiment, NSGA-II has been instructed to derive, for each problem considered, a lower approximation of P with 200 elements in 200 generations (’generation’ is NSGA-II parlance) to serve as a starting S L for EMO-APPROX.

Next, EMO-APPROX has been run for each problem with the respective S L . Because EMO-APPROX has been building successive S L and A U not from scratch, but from the results provided by NSGA-II, we have decreased j max to 3000. And as we did not know how to account in EMO-APPROX for NSGA-II impact on mutating factor \((1-\mathrm{rnd}(0,1)^{2(1-\frac{j}{j^{\max}})})\), for each problem we run the tandem NSGA-II + EMO–APPROX with four different scalings of the starting mutating factor values, namely with 1.0,0.1,0.01,0.001.

For each problem, at least one scaling produced lower or equal acc P than algorithm EMO-APPROX run alone for 9000 iterations. From all such cases, we have selected those with the highest ∥S L ∥+∥A U ∥. Results for runs selected in that manner are presented in Table 2.Footnote 3

Table 2 Test results—NSGA-II + EMO-APPROX
Full size table

Comparing Tables 1 and 2, it is evident that EMO-APPROX, producing two-sided approximations of the Pareto front, has benefited significantly from the preprocessing provided by NSGA-II—the tandem NSGA-II + EMO-APPROX has produced results comparable to, and in some cases distinctly better than those produced by EMO-APPROX alone, within three times less iterations. This strengthens our claim that, in the future, embedding the full range of EMO mechanisms into EMO-APPROX is worthwhile.

7 Conclusions

In this work, we limited ourselves to showing the viability of the idea to approximate Pareto fronts by pairs of lower and upper approximations. We also demonstrated how to improve interactively “closeness” between them. “Goodness” or “fairness” of approximations of P by such constructs constitutes the topic for further research. Another further topic is to provide means to derive pairs of S L and S U -like (A U -like) constructs for cases where S U does not exist. Some preliminary results pertaining to that issue have been already obtained and are reported in [5].

In the future experiments, to ensure even more uniform layouts of pairs f(A U ), f(S L ) along P, other genetic operators should be also exploited, whereas here we have confined ourselves only to the operator of mutation. We have done this deliberately to ensure clarity of the presentation and to demonstrate the viability of the concept of two-sided approximations of P.

The problem of providing accurate two-sided approximations with uniform layouts along Pareto fronts, being of interest in itself, has an immediate application in Multiple Criteria Decision Making, where a decision process can be enhanced if it is started with a not necessarily very accurate but uniform two-sided approximation of the Pareto set to roughly represent it. Next, in the course of the decision process, such approximations can be improved locally as directed by the decision maker’s preferences [12, 13].