Abstract
Mobile devices (smartphones or tablets) as experimental tools (METs) offer inspiring possibilities for science education, but until now, there has been little research studying this approach. Previous research indicated that METs have positive effects on students’ interest and curiosity. The present investigation focuses on potential cognitive effects of METs using video analyses on tablets to investigate pendulum movements and an instruction that has been used before to study effects of smartphones’ acceleration sensors. In a quasi-experimental repeated-measurement design, a treatment group uses METs (TG, NTG = 23) and a control group works with traditional experimental tools (CG, NCG = 28) to study the effects on interest, curiosity, and learning achievement. Moreover, various control variables were taken into account. We suppose that pupils in the TG have a lower extraneous cognitive load and higher learning achievement than those in the CG working with traditional experimental tools. ANCOVAs showed significantly higher levels of learning achievement in the TG (medium effect size). No differences were found for interest, curiosity, or cognitive load. This might be due to a smaller material context provided by tablets, in comparison to smartphones, as more pupils possess and are familiar with smartphones than with tablets. Another reason for the unchanged interest might be the composition of the sample: While previous research showed that especially originally less-interested students profited most from using METs, the current sample contained only specialized courses, i.e., students with a high original interest, for whom the effect of METs on their interest is presumably smaller.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Nowadays, most pupils cannot imagine life without mobile devices as smartphones or tablets. These devices create new possibilities for teaching and learning, especially in science education. They cannot only be used for communication or browsing the internet but also as mobile pocket-labs, as they come with a multitude of built-in sensors. The advantage of using smartphones or tablets as experimental tools does not lie in the ability to take more accurate measurements than with traditional means, but in the ability to do a variety of experiments and combine experimental procedure with analyzing measuring data with only one device. With the internal sensors of mobile devices, it is possible to investigate phenomena in mechanics, acoustics, electromagnetism, optics, and even radioactivity. Interpretation of the sensor data is quickly and easily possible, as applications (apps) generate tables, graphs, or other forms of data representation automatically on the device’s screen. Furthermore, the portability and versatility of smartphones and tablets allow for experiments inside as well as outside the classroom and also as homework (as almost every pupil possesses their own smartphone). Thus, experiment-oriented seamless learning can be generated. Numerous experimental concepts for the use of mobile devices as experimental tools (METs) in science education have appeared in the last years (for an overview, see Hochberg et al. 2018). The Physics Teacher journal has established a column about METs since 2012 (Kuhn and Vogt 2015). Despite the seeming “boom” of METs due to favorable theoretical and practical arguments, there have been few empirical studies regarding the learning effects of METs in science education in high school (see, e.g., Kuhn and Vogt 2015; Mazzella and Testa 2016; Becker et al. 2018a; Hochberg et al. 2018; for reviews, see, e.g., Bano et al. 2018; Oliveira et al. 2019).
In 2018, the Journal of Science Education and Technology published a study (Hochberg et al. 2018) which reported an empirical investigation of METs in science education regarding mechanical oscillations. The present study is a follow-up to that research addressing open questions mentioned in its limitations and outlook chapter. Briefly, Hochberg et al. (2018) used a quasi-experimental repeated-measurement design, consisting of an experimental group using a smartphones’ acceleration sensor to investigate pendulum movements (smartphone group, SG, NSG = 87) and a control group working with traditional experimental tools (CG, NCG = 67). Effects on interest, curiosity, and learning achievement were investigated with multiple-regression analyses and ANCOVA, taking into account various control variables. The study found significantly higher levels of interest in the SG (small to medium effect size). Pupils that were less interested at the beginning of the study profited most from implementing METs. Moreover, the SG showed higher levels of topic-specific curiosity (small effect size).
Inspired by the success of context-based science education (CBSE) interventions on the level of instructional episodes (see, e.g., Kuhn and Müller 2014; Bahtaji 2015), the previous study was focused only on the effects of potential “material contexts” of METs. A “material context” is defined as the “connection of the experimental medium itself, based on its material basis, to pupils’ everyday life” (Hochberg et al. 2018). This focus meant a concentration on affective rather than cognitive effects. As both groups were working with almost identical tasks, involving the same variables and forms of representations, cognitive activities were almost identical and no or only small differences could be expected from them. Indeed, no differences were found for learning achievement.
In the current follow-up study, we focus on potential cognitive effects of METs using video analyses instead of the acceleration sensor following the same instruction, namely to investigate pendulum movements. So, this study has two aims: first, we want to replicate the results of the prior study described in Hochberg et al. (2018), and second, we want to adapt the intervention by presenting multiple external representation (MER; see “Learning with Multiple External Representations”) using mobile video analysis in the treatment group (see Table 1).
Based on the research results of Becker et al. (2019) and Becker et al. (2018a), we suppose that pupils in the treatment group have higher cognitive activation by learning with multiple external representations and smaller extraneous cognitive load by using video analysis methods which present an integrated learning format to the pupils. So we assume that treatment group has a higher learning achievement compared with the control group working with traditional experimental tools.
Current Research Status and Theoretical Background
As the current follow-up study is concentrating on the potential cognitive effects of using METs for video analyses in science education, the current research status and theoretical background are only related to these effects. A rationale for using METs in science education to foster interest and curiosity can be found in the previous paper (Hochberg et al. 2018).
Current Research Status
Current work points out that little is known about integrating multimedia learning in inquiry-based learning processes with physical experiments in real classroom settings (Oliveira et al. 2019). Through a meta-analysis of 80 primary studies published between 2000 and 2016, Hillmayr et al. (2017) demonstrated that the overall use of digital media in teaching has a moderately strong impact on students’ learning performance, across all subjects studied (biology, chemistry, physics, and mathematics) as well as across all grade levels. In a meta-analysis for the teaching of mobile digital media (laptops, tablets, smartphones, etc.), Sung et al. (2016) found a positive medium effect (g = 0.52) on students’ learning performance; for the teaching use of only tablets, the effect was g = 0.62. The research findings prove the potential of digital media to effectively support the teaching process. However, the authors of the meta-studies agree that a blanket statement on how digital media can be meaningfully used in the classroom is also not possible due to the variety of teaching and learning scenarios as well as the media and learning programs used. Rather, each newly developed digitally supported learning process must be tested for the fit of medium and learning program, as well as for learning effectiveness. Using mobile devices as smartphones and tablets as experimental tools in physics was first investigated by Kuhn and Vogt (2015) in the field of acoustics in lower secondary education. A positive learning effect on achievement and motivation could be proven. Mazzella and Testa (2016) used smartphones to increase students’ conceptual understanding of acceleration. In higher secondary instruction, they showed that students who followed smartphone activities regarding the motion on an inclined plane and pendulum oscillations were more able to design an experiment to measure acceleration and to correctly describe acceleration in a free fall motion than their peers following traditional instruction.
Against this background, it can be stated that modern technologies offer a variety of possible applications to support the experiment-based learning process, especially in the subject area of mechanics, which represents an essential field of classical physics and is therefore treated very intensely in physics teaching, as well as in physics studies. One possibility for technology support is provided by video motion analysis, a method for non-contact measurement of time and location of moving objects, which means that the position of a moving object with respect to a two-dimensional coordinate system is stored in each frame of a recorded video, from which velocity and the acceleration of the object can be calculated. The learning effectiveness of video analysis has been empirically studied in education research since the 1990s. Thus, a positive learning effect could be empirically proven with regard to different forms of representation (for diagrams: Beichner 1998; for strobe pictures: Boyd and Rubin 1996; for tables: Pappas et al. 2002; for vectors: Kanim and Subero 2010) as well as conceptual understanding in the field of mechanics (Hockicko et al. 2014; Wee et al. 2015). Regarding affective effects of video analysis, qualitative studies indicated possible advantageous effects on motivation, interest, and curiosity (for example, Zollman and Escalada 1996; Rodrigues et al. 2010; Wee et al. 2012). It should be noted that, to date, when using video analysis in teaching-learning scenarios, the recording (usually with conventional digital camera) and the analysis of the movement (usually on the PC) are separated and take place one after the other. The transfer to the PC can also be associated with technical hurdles such as a necessary conversion of the video format. The resulting disruption of the learning process can reduce the learning-promoting effect of the video motion analysis by the temporal separation of corresponding sources of information (temporal contiguity principle; Mayer and Moreno 2003) and thus complicate an effective learning implementation in regular lessons. Tablets today have technically advanced cameras that can record videos in outstanding quality. Specially developed video analysis applications open up the possibility of combining the single video motion analysis process steps on only one mobile device, from the recording of the moving object in an experiment to the analysis of the movement to the visualization of the relevant physical quantities by providing multiple representations such as tables, strobe pictures, and diagrams (see Fig. 1), between which the learner can switch as needed and view them in combination. Thus, learners can use this digital learning tool to record movements of arbitrary bodies and investigate their physical relationships and laws independently almost in real time by interpreting multiple forms of representation. In this way, the advantages of using mobile devices in teaching-learning scenarios are combined with the possibilities of physical video motion analysis as a measurement method. This opens up new creative possibilities for learning processes (Becker et al. 2016, 2018b, 2018c; Thees et al. 2018; Klein et al. 2013), which can help to foster the learning with multiple representations.
In this regard, Klein et al. (2018) designed a learning scenario for task-oriented learning with (mobile) video analysis using tablets for introductory physics courses in universities and could diagnose positive effects on conceptual understanding and representational competence. In a quasi-experimental study with a pre-post-test design involving high school physics courses, Becker et al. (2019) and Becker et al. (2018a) could show for two essential topics of mechanics, uniform and accelerated motion, that using mobile video analysis in regular teaching leads to better conceptual understanding than traditional lessons, especially for the more complex topic of accelerated motion. Furthermore, Becker et al. (2019a) conceived an application for task-oriented learning with mobile video analysis using tablet computers and were able to determine positive effects on intervention-induced extraneous cognitive load and conceptual understanding for high school physics courses.
Theoretical Background
Learning with Multiple External Representations
For scientific learning, multiple external representations (MERs) play a beneficial role, which is well documented for the natural sciences, in general (Tytler et al. 2013), and for physics, in particular (Treagust et al. 2017). It is of especially great importance for conceptual understanding (Verschaffel et al. 2010) and is discussed as a necessary condition for in-depth understanding (DiSessa 2004). Ainsworth (2006, 2008) created a conceptual framework that provides an overview of the prerequisites for the effective use of MERs in teaching–learning situations and the unique benefits for learning complex or new scientific content. According to her, in the design, functions, and tasks (DeFT) taxonomy, learning with MERs means two or more external representations (e.g., diagrams, formulas, and data tables) are used simultaneously. Specifically, there are three key functions that MERs can fulfill (even simultaneously) to support the learning process. According to the first function, MERs can complement one another either by providing complementary information or by allowing for complementary approaches to process information. The presentation of MERs with complementary information content may be advantageous if the presentation of all relevant information in a single form of representation would lead to cognitive overload of the learner. However, even if different representations contain the same information, they can support the learning process by allowing learners to select the most appropriate form of representation to accomplish the given learning task in the particular learning situation. The second function is that simultaneously presented representations can constrain one another’s interpretation in two ways: the more familiar representation can constrain the interpretation of the less-familiar one, or the inherent properties of one representation can trigger the usage of the other representation, which is considered helpful for the learning process. According to the third function, the construction of a deeper understanding is fostered if learners integrate information from different forms of representation to gain insights that could not have been obtained with just one form of representation. Although MERs demonstrably have the potential to support learning processes, their use in learning situations is also associated with learner demands that can overwhelm learners and even negatively affect the learning process (De Jong et al. 1998). Indeed, many studies point toward student difficulties with MERs (e.g., Ainsworth 2006; Nieminen et al. 2010). Consequently, the difficulty of the learning environment must be considered and managed carefully. In this context, technology support can facilitate the learning-promoting effect of MERs (e.g., Horz et al. 2009) by helping to reduce learning irrelevant parts of the so-called cognitive load when learning with MERs.
Cognitive Load Theory
The basic assumption of the Cognitive Load Theory (CLT) (Sweller 1988; van Merriënboer and Sweller 2005) is the limited capacity of working memory in terms of the amount of information that can be processed simultaneously, but also in terms of the time at which information is available for processing. In the relevant literature (Leppink and van den Heuvel 2015; Sweller et al. 1998; Sweller et al. 2019), the cognitive load is composed of three types: intrinsic cognitive load (ICL), extraneous cognitive load (ECL), and germane cognitive load (GCL). ICL refers to the complexity of information that the learner has to process during the learning process and is therefore determined by the learning task and the foreknowledge of the learner regarding the learning content. ECL refers to learning irrelevant cognitive processes, which occupy the working memory but do not lead to a relevant learning gain and can be influenced by the design of the learning procedure, such as how the information is presented to the learner. GCL refers to the amount of cognitive resources needed while processing the information in a learning process. Principles can be derived from CLT to enable instructors to design (short) instructional units that are conducive to learning (Sweller et al. 2019). One fundamental principle is to keep the learning-irrelevant ECL as low as possible during the learning process (Leppink 2017; Leppink and van den Heuvel 2015; Sweller et al. 1998). Sweller et al. (1998) reported seven effects that can influence the cognitive load. One of them is the split-attention effect (Mayer and Pilegard 2014; Sweller and Chandler 1994; Sweller et al. 2019). This (negative) effect implies that the spatial or temporal separation of related information sources requires mental integration processes, thus increasing ECL and therefore inhibiting the learning process by occupying mental resources that are no longer available for learning-related processing.
Cognitive Theory of Multimedia Learning
The Cognitive Theory of Multimedia Learning (CTML; Mayer 1999, 2003, 2005) builds on the principle of CLT of limited working memory. In addition, the CTML postulates two separate channels of limited-capacity working memory in which visual-pictorial and verbalized information is processed. Learning environments should be designed so that both learning channels (visual and auditory) are addressed during the learning process. The CTML is based on the principle of active knowledge construction, which assumes that an active engagement with the subject of learning is required to form a coherent, mental representation. Furthermore, one feature of an effective multimedia instruction should be to “reduce extraneous processing, manage essential processing, and fostering generative processing” (Mayer 2009, p.57). The principle of contiguity (Mayer 2009; Mayer and Moreno 2003) aimed at reducing extraneous processing by avoiding split-attention effects (Mayer 2009; Mayer and Moreno 2003). With the principle of contiguity, the CTML provides an explanatory approach for avoiding/specifying the split-attention effect (Moreno and Mayer 1999). On the one hand, corresponding information should not be presented spatially separated from each other (spatial contiguity principle). Spatial proximity helps to avoid visual search processes that contribute to an increase in extraneous cognitive load. On the other hand, a temporal separation should also be avoided (temporal contiguity principle). This is justified by the additional cognitive load that arises when mental representations have to be maintained over a longer period of time (Mayer and Moreno 2003; Clark and Mayer 2011). In addition, the segmentation or interactivity principle is assumed in the context of dynamic visualizations (Mayer and Chandler 2001; Mayer and Pilegard 2014), which postulates a learning-conducive effect when learners themselves can determine the sequence or tempo of the information presentation. This self-control of the learning process avoids cognitive overload.
Research Questions
As reported in the current research status, a promising method to support the learning process in the subject area of mechanics is video analysis. This is especially true for tablet-supported video analysis, as the latest research findings prove that the use of this digital learning tool can effectively reduce ECL in experiment-based learning processes (Becker et al. 2019a). This learning-enhancing effect can be theoretically substantiated on the basis of the previously described fundamental learning theories. In particular, elementary functions of the video analysis application that can contribute to a learning-conducive use of MERs in learning environments will be explained.
Fulfillment of the Key Functions of the DeFT Framework
The video analysis application automatically provides learners with multiple forms of representation that include complementary information regarding the investigated motion, the real and stroboscopic image, and the associated motion diagrams (the first key function). The learners in this study are much more familiar with the diagram representation form than with the stroboscopic image representation form because of the experienced teaching (in accordance with their curriculum). The interpretation of the less-familiar stroboscopic image representation form could thus be triggered by the automatic display together with the familiar motion diagram representation form (the second key function). In addition, the automatic multicoding of the movement process makes it easier for the learner to integrate the information from the different MERs into a coherent mental model of the movement process, which would not be possible if only one form of representation were presented (the third key function).
Fulfillment of the Principle of Contiguity
By simultaneously displaying corresponding sources of information (real motion sequence and the stroboscopic image, as well as the time-position and time-velocity diagram), the use of the video analysis application fulfills the spatial contiguity principle. In addition, the learner is allowed to switch between the individual forms of representation quasi-simultaneously, which is understood here as the absence of a noticeable time delay, by means of a swipe movement. This also fulfills the temporal contiguity principle.
Fulfillment of the Interactivity Principle
During the video analysis, the students themselves can control the transition between the individual segments (forms of representation) of the data evaluation (real motion sequence, motion diagrams, and the stroboscopic image). For example, to improve the understanding of the motion diagrams, the students can again call up the stroboscopic image or vice versa. The use of the video analysis application fulfills the interactivity principle by allowing this self-control of the learning process. The interactivity of the application also promotes the active engagement of the learners with the subject of learning itself. For example, the origin and spatial orientation of the coordinate system can be manipulated by the learner at any point in the learning process, and the effects of this variation on the motion diagrams can be observed quasi-simultaneously.
In summary, we assume that the presentation features of the video analysis application regarding MERs meet the design principles for multimedia learning environments and thereby reduce ECL (especially via the avoidance of the split-attention effect) in multi-representational learning environments; in turn, this fosters the effective use of MERs in the study’s learning scenarios. From this theoretically founded learning-enhancing effect on the learning process and the rationale for using METs in science education to foster interest and curiosity that can be found in the previous paper (Hochberg et al. 2018), we derive the following research questions:
RQ1: Does using METs for video motion analysis lead to higher learning achievement than using conventional experimental tools?
RQ2: Can the advantages of METs for interest and curiosity found in the previous study be reproduced by using METs for video motion analysis?
The Intervention
The intervention was comprised of experiments and associated instruction material, largely based on those of the previous study (Hochberg et al. 2018). For the treatment group (TG), experiments and materials were adapted to video motion analysis (see Online Resource “Instruction Material”). For the control group (CG), exactly the same experiments and materials as in Hochberg et al. (2018) were used.
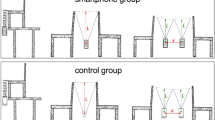
As in Hochberg et al. (2018), during the intervention, each pupil conducted three experiments on the periodicity of a spring pendulum, a simple pendulum, and a coupled pendulum (see Fig. 2; for more details about the embedment of the intervention into the regular classes, see Hochberg et al. 2018). The experimental setups of both groups were almost identical; different were only the measurement tools: While the CG used a ruler and a stopwatch to measure the oscillations’ period, the TG recorded a video of the pendulum movement and performed a video motion analysis with the tablet using the apps Viana and Graphical Analysis.Footnote 1 These apps showed measurement data as position markers within the video and as acceleration-time, velocity-time, and position-time graphs.
Pupils were provided with all necessary materials for conducting the experiments. All pupils in the TG were given the same devices, regardless of whether they owned a tablet. Where possible, everyday material was used to realize the experimental setups.
The instruction material was designed to be almost identical for both groups; e.g., both groups were provided with worksheets showing idealized graphs of the oscillation. The CG compared the given, idealized graphs on the worksheets with their observation of the experiment and measured the oscillations’ period with a stopwatch. The TG produced several measurement graphs of different oscillations on the tablet and used them to investigate the period of the oscillation. They compared different graphs on the tablet with each other and with the given idealized graphs on the worksheets.
Methods
Study Design
The study design also was mostly adopted from Hochberg et al. (2018). Again, we conducted a quasi-experimental treatment group–control group study (see Fig. 3), which took place during pupils’ regular physics lessons: Before the intervention, all pupils were tested for 45 min. In the following four lessons (spread over 1 or 2 weeks), the intervention took place as described above. In the next lesson, a post-test of 45 min was conducted. In addition, the treatment group got an introduction of 45 min, in which pupils were taught how to conduct a video motion analysis on the tablet with an example video regarding a projectile motion. The control group did not get any special introduction. The treatment groups’ introduction took place before the pre-test so that any learning differences caused by the introduction can be controlled by using the pre-test as control variable.
Sample
The sample of this pilot study consists of 52 pupils in specialized physics courses of grade 12 from 5 secondary schools in Rhineland-Palatinate, Germany (age range 16–19 years). In agreement with the participating teachers, 3 courses were assigned to the treatment group (N (TG) = 23) and 2 to the control group (N (CG) = 28). In both groups, the majority of pupils were male (TG, 26% girls; CG, 7% girls). Each group was taught by the same tutor.
Test Instruments
All test items were adopted exactly from Hochberg et al. (2018).
Affective Variables
All items except learning achievement and curiosity as a trait were assessed using 6-point Likert-type scales (for examples, see Table 2). For the items concerning curiosity as a trait (CT), according to the original instrument, a 4-point Likert-type scale was used. For conducting statistical analyses, the mean score of every item was transformed into a percentage, where 0% meant no affirmation of the statement and 100% meant a full affirmation of the statement. For negated items, the scale was inverted, so that 100% always stood for the highest evidence of the underlying variable. To put it clearly, all ratings were linearly transformed to a [0, 100%] scale where 0% represents the lower bound of the Likert-type scale, meaning the lowest affirmation to the individual statement, and 100% represents the upper bound of the Likert-type scale, meaning the highest affirmation to the individual statement.
Learning Achievement
As in the previous study, the free text and drawing items were categorized, rated, and accordingly scored as 0, 0.25, 0.5, 0.75, or 1 point (for item examples, see Table 3). The total score was calculated as the sum of points divided by number of items; hence, it was always a percentage between 0 and 100%. There were in sum 23 items in the pre-test and 29 items in the post-test. This was due to the fact that pupils were already acquainted with the questionnaires in the post-test and able to answer more items in the same time and that they had more knowledge and could be asked additional questions especially about coupled pendula.
Cognitive Load and Further Control Items
As in Hochberg et al. (2018), the intervention-induced general cognitive load (GCL) was measured with 10 items (CLE) adapted from Kuhn (2010), Paas et al. (1994), and Chandler and Sweller (1991) and with the 5 items of the NASA TLX instrument (Hart 2007, 2019; Hart and Staveland 1988), which is one of the most used, multi-dimensional rating scale for workload (Hart 2006). As in the other instruments, 6-point Likert-type scales were used (bipolar scales in case of the NASA TLX instrument), the scales of negated items were inverted, and the mean scores transformed into percentages, so that 100% correlated the highest evidence of cognitive load (for item examples, see Table 4). Further control variables that were measured can be found in Table 4.
Data Analyses
Analyses of Test Instruments
As all test instruments were exactly adopted from Hochberg et al. (2018), and the sample was considerably smaller than the original sample, item and scale characteristics were not reassessed. Subscales were adopted from the original instruments and reliability analyses performed for a comparison with the original reliability.
Analyses of Cognitive and Affective Effects
As a first step, predispositions in TG and CG were compared by t tests, or Mann-Whitney U tests, if the normal distribution assumption was not met. For all significantly different predispositions, correlations with the dependant variables were calculated to check for a sampling bias. As we collected a wide range of possible covariates for our analyses and our sample is too small to meet the assumptions for structural equation modeling or multiple regression analysis, t tests and analyses of covariance (ANCOVA) were used to analyze cognitive and affective effects. For these analyses, the following assumptions were tested: independence and normal distribution of residuals and homogeneity of residuals’ variances, and additionally, for analyses of covariance homogeneity of regression slopes, adequate correlation between the covariate and the dependant variable (r > 0.3), sufficient reliability of the covariate, and measurement of the covariate prior to the intervention. Of all covariates that met the assumptions, we only included those in the ANCOVA that explained a significant amount of additional variance (tested with a stepwise regression analysis).
Results
Analyses of Test Instruments
The reliability (Cronbach’s α) of all scales used in the analyses below and the respective original scales from Hochberg et al. (2018) can be found in Table 5. The reliability exceeded α = 0.7 for all subscales and did not differ largely from the original values except for the general cognitive load. To keep the data comparable with the previous study, the scale for cognitive load was not altered despite the low reliability. Of all scales and subscales, means and standard errors for both groups can be found in Table 6.
Analyses of Cognitive and Affective Effects
Learning Achievement (RQ1)
The assumptions for calculating ANCOVA (see “Data Analyses” above) were met. The ANCOVA showed a significant mid-sized effect between groups: F (1, 47) = 5.22, p = 0.027, d = 0.66 (group means and standard errors; see Fig. 4 and Table 7).
Interest and Curiosity (RQ2)
The assumptions for calculating ANCOVA (see “Data Analyses” above) were met. The ANCOVA did not show an effect between groups, neither for interest (F (1, 49) < 0.01, p = 0.960) nor for curiosity (F (1, 49) = 0.02, p = 0.889) (for group means and standard errors, see Table 8).
Control Variables
Regarding personal assessment of tutor in the post-test, self-concept in the post-test, and cognitive load, no significant effects between treatment groups were found (see Table 9).
Discussion
Learning Achievement (RQ1)
Results of the analysis of the cognitive effects prove that the intervention led for both control and treatment group to a learning gain. By comparing both groups, the assumed higher learning achievement of the use of METs for video analysis could be statistically confirmed with a significant mid-sized effect. This reproduces and extends the research findings from Becker et al. (2019), Becker et al. (2018a), Hockicko et al. (2014), and Wee et al. (2015), which have already been able to prove empirically a positive effect of the video motion analysis on the understanding of physical concepts for other topics of mechanics. We assume that the positive effect is on the one hand based on the automatic recording and visualization of measurement data. In this way, repetitive activities, which do not lead to an increase in the understanding of the physical concept, can be avoided for the learner. According to the CLT, this results in a reduction of learning-irrelevant cognitive load, which enables the learners to use the becoming free cognitive resources for an active preoccupation with the learning subject. According to CTML, this is essential for forming of a coherent mental representation and thus for the active construction of knowledge structures. On the other hand, we assume that the simultaneous presentation of multiple representations by the video analysis application has a positive effect on the representational competence of the learners. Being based on the CTML, this can be explained by avoiding the split-attention effect which reduces the learning-irrelevant cognitive load furthermore. As one of the main aims of this study is to replicate effects of the original study and to optimize its shortcoming concerning the lack of increasing learning achievement by a change in the intervention (see “Introduction”), we used the same materials and methods as the original study (Hochberg et al. 2018). This included a cognitive load scale which does not allow differing between the three dimensions of cognitive load (Ayres 2006). It was hence not possible to investigate the reduction of the learning-irrelevant extraneous load through the use of mobile video analysis within the scope of this work. We did not measure a significant difference regarding cognitive load between the treatment and the control group. This is not surprising, as based on results of corresponding work (Becker et al. 2019a) we have evidence to assume that the effects of ECL and GCL have neutralized each other within the treatment and the control group (Wouters et al. 2009). In other words, learning with traditional experiments in the control group may have imposed rather high extraneous cognitive load and low germane cognitive load, whereas learning with video analysis in the treatment group may have imposed rather low extraneous cognitive load and high germane cognitive load, leading in sum to approximately the same amount of general cognitive load.
Interest and Curiosity (RQ2)
Positive effects of METs regarding interest and curiosity, which were found in the previous study, could not be found. There are different reasons which might explain this finding: First, in the current study, there was a change of the mobile device. Out of practical reasons (bigger screen), pupils were working with tablets instead of smartphones. In the previous study, Hochberg et al. supposed that the effect on pupils’ interest was generated by the “material context” of the smartphones that were used as experimental tools. It is possible that this material context, i.e., the “connection of the experimental medium itself, based on its material basis, to pupils’ everyday life” (Hochberg et al. 2018), is weaker for tablets than for smartphones, because they are less present in pupils’ lives. In the current study, 98% of the pupils reported possessing their own smartphone and using it very frequently (M = 90.2%), only 52% reported the possession of a tablet and they were using it less frequently (M = 61.5%). The lower everyday occurrence of tablets might also affect the effect on curiosity: In the previous study, the rationale behind the effect on curiosity was that pupils were provided with a new way of accessing information by performing experiments with their own everyday devices, that was said to raise their confidence in being able to find a satisfactory resolution, thereby increasing their curiosity. Not possessing an own tablet might lower that confidence. All experiments performed in the current intervention could also be done with smartphones, but this was not explicitly taught to pupils. Another possible reason for the absence of an effect on pupils’ interest is a difference of the samples in the current and the previous study. In the previous study, pupils with less original interest (INpre ≤ 0.40) profited most from the intervention. In the current study, only specialized courses were part of the sample, i.e., pupils, that specifically chose physics to be one of their main courses. As expected, the original interest is higher in this sample (INpre: M = 0.66, only one case with INpre ≤ 0.40). It is possible that, in an originally less interested sample, effects on interest might be found even though pupils were working with tablets instead of smartphones. Another reason why no effect on interest or curiosity was found might be the size of the current sample: In the previous study in a sample of N = 154, a small to midsize effect on curiosity was found (d = 0.40). To find an effect of this size with a test power of 0.80, a similar sample size would be needed. For curiosity, the effect was small (d = 0.25) and could only be detected with a multiple regression analysis. To find an effect of this size with a test power of 0.80 with an ANCOVA, a sample size of N = 505 would be needed.
Conclusions, Limitations, and Outlook
We first aimed at replicating a study about using METs in an attempt to generate relevant material context in the sense of a relation to pupils’ everyday life and like this increase their interest and curiosity (Hochberg et al. 2018). Second, we focused on potential cognitive effects of METs using video analyses instead of the acceleration sensor to investigate pendulum movements in the current study. As before, the devices were used within standard, well-tried experimental setups involving pendulum movements in regular physics classes of the upper secondary level; the video analyses provided pupils with multiple representations of their data which we assume reduced their extraneous cognitive load. Besides the already known practical and experimental advantages of METs and mobile video analysis, we can conclude the following statements from our findings: (a) The use of METs significantly raised pupils’ learning achievement compared with the control group. Even after a relatively short intervention (3 h), we found mid-sized effects. (b) There were no effects found regarding interest or curiosity as in the previous study. The reason for this might be that tablets, which were used in this study for practical reasons, are less familiar to pupils than smartphones as fewer pupils possess them. This might lead to a reduction of the material context in comparison to smartphones and hence in a smaller potential of tablets to increase interest or curiosity. Another reason why students’ interest has not been increased by METs might be the composition of the sample: Hochberg et al. (2018) showed that especially originally less interested students profited most from using METs in their physics classes. The current sample contained only specialized courses, i.e., students with a high original interest, for whom the effect of METs on their interest is presumably smaller.
The current study provided evidence for the research question, if a higher learning efficacy can be achieved by using video analysis with tablets in comparison with traditional physics classes. These findings are limited to the specific learning situation concerning pendulum movements in a specific sample (specialized courses of the German “Gymnasium”). Furthermore, the test instrument used to measure cognitive load did not allow a differentiation of the three different categories of cognitive load. This was caused by the aim of replicating effects of the original study and so using the same measures as before. Like this, the expected reduction of extraneous cognitive load by relieving learners of tasks which are irrelevant for learning by using video analysis could not be measured. The dependence of the efficiency of using video analysis from the amount of intrinsic cognitive load could neither be investigated. This methodological deficit will be resolved in follow-up studies by using an instrument after Leppink et al. (2013), with which Becker et al. (2019a) were already able to prove the reduction of ECL for the use of mobile video analysis in another physical context. Nevertheless, this study shows the vast potential of using tablets as experimental tools. Further research might concern different topics of mechanics or other areas of physics and different target groups. As Hochberg et al. (2018) showed that METs have the potential to promote especially the interest of originally less interested students, it may be advantageous to study mobile video analysis with tablets in samples of lower academic levels. Furthermore, the full potential of METs has not been used to full capacity in this study: The fact that they are mobile. Knowing that there are advantageous effects of using METs for mobile video analysis in the classroom of regular physics classes, subsequent studies may investigate the effects of analyzing movements in everyday life in their authentic context on interest, curiosity, and learning achievement.
Notes
The newest version of Viana can be found under the following link: https://itunes.apple.com/de/app/viana-videoanalyse/id1031084428?mt=8 (FU Berlin 2017); a detailed description of the application is available from Becker et al. (2018a); the newest version of Graphical Analysis can be found under the following link: https://itunes.apple.com/us/app/vernier-graphical-analysis/id522996341?ls=1&mt=8 (Vernier 2018).
References
Ainsworth, S. (2006). DeFT: a conceptual framework for considering learning with multiple representations. Learning and Instruction, 16, 183–198. https://doi.org/10.1016/j.learninstruc.2006.03.001.
Ainsworth, S. (2008). The educational value of multiple representations when learning complex scientific concepts. In J. K. Gilbert, M. Reiner, & M. Nakhleh (Eds.), Visualization: theory and practice in science education (pp. 191–208). Dordrecht: Springer Netherlands.
Ayres, P. (2006). Using subjective measures to detect variations of intrinsic cognitive load within problems. Learning and Instruction, 16, 389–400.
Bahtaji, M. A. A. (2015). Improving transfer of learning through designed context-based instructional materials. European Journal of Science and Mathematics Education, 3(3), 265–274.
Bano, M., Zowghi, D., Kearney, M., Schuck, S., & Aubusson, P. (2018). Mobile learning for science and mathematics school education: a systematic review of empirical evidence. Computers in Education, 121, 30–58.
Becker, S., Klein, P., & Kuhn, J. (2016). Video analysis on tablet computers to investigate effects of air resistance. Physics Teacher, 54(7), 440–441.
Becker, S., Klein, P., & Kuhn, J. (2018a). Promoting students’ conceptual knowledge using video analysis on tablet computers (pp. 1–4). Presented at the PERC. https://doi.org/10.1119/perc.2018.pr.Becker.
Becker, S., Thees, M., & Kuhn, J. (2018b). The dynamics of the magnetic linear accelerator examined by video motion analysis. Physics Teacher, 56(7), 484–485.
Becker, S., Klein, P., Kuhn, J., & Wilhelm, T. (2018c). Viana analysiert Bewegungen. Physik in Unserer Zeit, 49(1), 46–47.
Becker, S., Klein, P., Gößling, A., & Kuhn, J. (2019). Förderung von Konzeptverständnis und Repräsentationskompetenz durch Tablet-PC-gestützte Videoanalyse: Empirische Untersuchung der Lernwirksamkeit eines digitalen Lernwerkzeugs im Mechanikunterricht der Sekundarstufe 2. Zeitschrift für Didaktik der Naturwissenschaften, 25(1), 1–24. https://doi.org/10.1007/s40573-019-00089-4.
Becker, S., Klein, P., Gößling, A., & Kuhn, J. (2019a). Using mobile devices to augment inquiry-based learning processes with multiple representations. arXiv preprint, arXiv:1908.11281[physics.ed-ph].
Beichner, R. J. (1998). The impact of video motion analysis on kinematics graph interpretation skills. American Journal of Physics, 64, 1272–1277.
Boyd, A., & Rubin, A. (1996). Interactive video: a bridge between motion and math. International Journal of Computers for Mathematical Learning, 1(1), 57–93.
Chandler, P., & Sweller, J. (1991). Cognitive load theory and the format of instruction. Cognition and instruction, 8(4), 293–332.
Clark, R. C., & Mayer, R. E. (2011). E-learning and the science of instruction, Proven guidelines for consumers and designers of multimedia learning (3rd ed.). San Francisco: John Wiley & Sons.
De Jong, T., Ainsworth, S., Dobson, M., van der Hulst, A., Levonen, J., Reimann, P., et al. (1998). Acquiring knowledge in science and mathematics: the use of multiple representations in technology based learning environments. In M. Van Someren, P. Reimann, H. Boshuisen, & T. De Jong (Eds.), Learning with multiple representations (pp. 9–40). Amsterdam: Pergamon.
DiSessa, A. A. (2004). Metarepresentation: native competence and targets for instruction. Cognition and Instruction, 22(3), 293–331.
FU Berlin. (2017). Viana (Version 1.2). Freie Universitaet Berlin. https://itunes.apple.com/de/app/viana-videoanalyse/id1031084428?mt=8. Accessed 12 January 2019.
Hart, S. (2006). NASA- task load index [NASA-TLX]; 20 years later. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 50(2006), 904–908.
Hart, S. (2007). Proceeding of the human factors and ergonomic society 50th annual meeting NASA-task load index (NASA TLX).
Hart, S. (2019). Proceedings of the human factors and ergonomics society annual meeting NASA-task load index (NASA-TLX); 20 years later. Proceedings of the Human Factors and Ergonomics Society Annual Meeting, 50(9), 904–908.
Hart, S., & Staveland, L. (1988). Development of NASA-TLX (task load index): results of empirical and theoretical research. Human Mental Workload, 52, 139–183.
Hillmayr, D., Reinhold, F., Ziernwald, L., & Reiss, K. (2017). Digitale Medien im mathematisch-naturwissenschaftlichen Unterricht der Sekundarstufe. Münster: Waxmann Verlag GmbH.
Hochberg, K., Kuhn, J., & Müller, A. (2018). Using smartphones as experimental tools—effects on interest, curiosity, and learning in physics education. Journal of Science Education and Technology, 27(5), 385–403.
Hockicko, P., Trpisova, B., & Ondrus, J. (2014). Correcting students’ misconceptions about automobile braking distances and video analysis using interactive program tracker. Journal of Science Education and Technology, 23(6), 763–776.
Horz, H., Schnotz, W., Plass, J. L., Moreno, R., & Brünken, R. (2009). Cognitive load in learning with multiple representations. In J. Plass, R. Moreno, & R. Brünken (Eds.), Cognitive load theory (pp. 229–252). Cambridge: Cambridge University Press.
Kanim, S. E., & Subero, K. (2010). Introductory labs on the vector nature of force and acceleration. American Journal of Physics, 78(5), 461–466.
Klein, P., Gröber, S., Kuhn, J., & Müller, A. (2013). Video analysis of projectile motion using tablet computers as experimental tools. Physics Education, 49(1), 37–40.
Klein, P., Kuhn, J., & Müller, A. (2018). Förderung von Repräsentationskompetenz und Experimentbezug in den vorlesungsbegleitenden Übungen zur Experimentalphysik. Zeitschrift für Didaktik der Naturwissenschaften, 24(1), 17–34.
Kuhn, J. (2010). Authentische Aufgaben im theoretischen Rahmen von Instruktions- und Lehr-Lern-Forschung: Effektivität und Optimierung von Ankermedien für eine neue Aufgabenkultur im Physikunterricht. Vieweg+Teubner, Wiesbaden.
Kuhn, J., & Müller, A. (2014). Context-based science education by newspaper story problems: a study on motivation and learning effects. Perspectives in Science, 2(1–4), 5–21.
Kuhn, J., & Vogt, P. (2015). Smartphones & co. in physics education: effects of learning with new media experimental tools in acoustics. In W. Schnotz, A. Kauertz, H. Ludwig, A. Müller, & J. Pretsch (Eds.), Multidisciplinary research on teaching and learning (pp. 253–269). Basingstoke: Palgrave Macmillan UK.
Leppink, J. (2017). Cognitive load theory: practical implications and an important challenge. Journal of Taibah University Medical Sciences, 12(1), 1–7. https://doi.org/10.1016/j.jtumed.2016.08.007.
Leppink, J., & van den Heuvel, A. (2015). The evolution of cognitive load theory and its application to medical education. Perspectives on Medical Education, 4(3), 119–127. https://doi.org/10.1007/s40037-015-0192-x.
Leppink, J., Paas, F., van der Vleuten, C. P. M., van Gog, T., & van Merriënboer, J. J. G. (2013). Development of an instrument for measuring different types of cognitive load. Behavior Research Methods, 45(4), 1058–1072. https://doi.org/10.3758/s13428-013-0334-1.
Mayer, R. (1999). Multimedia aids to problem-solving transfer. International Journal of Educational Research, 31, 611–624.
Mayer, R. (2003). The promise of multimedia learning: using the same instructional design methods across different media. Learning and Instruction, 13, 125–139.
Mayer, R. (2005). Cognitive theory of multimedia learning (Vol. 31). Cambridge: Cambridge University Press.
Mayer, R. E. (2009). Multimedia learning (2nd ed.). Ney York: Cambridge University Press.
Mayer, R. E., & Chandler, P. (2001). When learning is just a click away: does simple user interaction foster deeper understanding of multimedia messages? Journal of Education & Psychology, 93(2), 390–397.
Mayer, R. E., & Moreno, R. (2003). Nine ways to reduce cognitive load in multimedia learning. Educational Psychologist, 38(1), 43–52.
Mayer, R. E., & Pilegard, C. (2014). Cambridge handbooks in psychology (pp. 316–344). Cambridge: Cambridge University Press.
Mazzella, A., & Testa, I. (2016). An investigation into the effectiveness of smartphone experiments on students’ conceptual knowledge about acceleration. Physics Education, 51(5), 055010.
Moreno, R., & Mayer, R. E. (1999). Cognitive Principles of Multimedia Learning: The Role of Modality and Contiguity. Journal of Educational Psychology, 91, 358–368.
Nieminen, P., Savinainen, A., & Viiri, J. (2010). Force concept inventory-based multiple-choice test for investigating students’ representational consistency. Physical Review Physics Education Research, 6, 020109. https://doi.org/10.1103/PhysRevSTPER.6.020109.
Oliveira, A., Behnagh, R. F., Ni, L., Mohsinah, A. A., Burgess, K. J., & Guo, L. (2019). Emerging technologies as pedagogical tools for teaching and learning science: a literature review. [Special issue]. Human Behavior and Emerging Technologies, 1(2), 149–160. https://doi.org/10.1002/hbe2.141.
Pappas, J., Koleza, E., Rizos, J., & Skordoulis, C. (2002). Using interactive digital video and motion analysis to bridge abstract mathematical notions with concrete everyday experience. In: Second international conference on the teaching of mathematics, Hersonissos, pp 1–9.
Paas, F. G. W. C., van Merriënboer, J. J. G., & Adam, J. J. (1994). Measurement of Cognitive Load in Instructional Research. Perceptual and Motor Skills, 79(1), 419–430.
Rodrigues, S., Pearce, J., & Livett, M. (2010). Using video analysis or data loggers during practical work in first year physics. Educational Studies, 27(1), 31–43.
Sung, Y. T., Chang, K. E., & Liu, T. C. (2016). The effects of integrating mobile devices with teaching and learning on students’ learning performance: a meta-analysis and research synthesis. Computers in Education, 94, 252–275.
Sweller, J. (1988). Cognitive load during problem solving: effects on learning. Cognitive Science, 12, 257–285.
Sweller, J., & Chandler, P. (1994). Why some material is difficult to learn. Cognition and Instruction, 12(3), 185–233.
Sweller, J., van Merriënboer, J. J. G., & Paas, F. (1998). Cognitive architecture and instructional design. Educational Psychology Review, 10, 251–296. https://doi.org/10.1023/A:1022193728205.
Sweller, J., van Merriënboer, J. J. G., & Paas, F. (2019). Cognitive architecture and instructional design: 20 years later. Educational Psychology Review, 31(2), 261–292. https://doi.org/10.1007/s10648-019-09465-5.
Thees, M., Becker, S., Rexigel, E., Cullman, N., & Kuhn, J. (2018). Coupled pendulums on a clothesline, 56(6), 404–405.
Treagust, D., Duit, R., & Fischer, H. (Eds.). (2017). Multiple representations in physics education. Dordrecht: Springer.
Tytler, R., Prain, V., Hubber, P., & Waldrip, B. (Eds.). (2013). Constructing representations to learn in science. Rotterdam: Sense.
van Merriënboer, J. J. G., & Sweller, J. (2005). Cognitive load theory and complex learning: recent developments and future directions. Educational Psychology Review, 17(2), 147–177.
Vernier (2018). Graphical Analysis (Version 4.0.5). Vernier Sofware and Technology. https://itunes.apple.com/us/app/vernier-graphical-analysis/id522996341?ls=1&mt=8. Accessed 11 January 2019.
Verschaffel, L., De Corte, E., de Jong, T., & Elen, J. (2010). Use of external representations in reasoning and problem solving. New York: Routledge.
Wee, L. K., Chew, C., Goh, G. H., Tan, S., & Lee, T. L. (2012). Using tracker as a pedagogical tool for understanding projectile motion. Physics Education, 47(4), 448–455.
Wee, L. K., Tan, K. K., Leong, T. K., & Tan, C. (2015). Using tracker to understand ‘toss up’ and free fall motion: a case study. Physics Education, 436–442.
Wouters, P., Paas, F., & van Merriënboer, J. J. G. (2009). Observational learning from animated models: effects of modality and reflection on transfer. Contemporary Educational Psychology, 34, 1–8.
Zollman, D., & Escalada, L. (1996). Applications of interactive digital video in a physics classroom. Journal of Educational Multimedia and Hypermedia, 5(1), 73–97.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
The authors declare that they have no conflict of rest. All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards. Informed consent was obtained from all individual participants included in the study.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic Supplementary Material
ESM 1
(PDF 4846 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hochberg, K., Becker, S., Louis, M. et al. Using Smartphones as Experimental Tools—a Follow-up: Cognitive Effects by Video Analysis and Reduction of Cognitive Load by Multiple Representations. J Sci Educ Technol 29, 303–317 (2020). https://doi.org/10.1007/s10956-020-09816-w
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10956-020-09816-w