Introduction

Many students experience difficulties in solving applied physics problems. These difficulties can be the result of deficiencies in the different kinds of knowledge needed to solve science problems: declarative knowledge (facts and concepts), procedural knowledge (how to use these facts and concepts in methods or procedures) and strategic knowledge (knowledge needed to organize the process of solving new problems) (De Jong and Ferguson-Hessler 1996). The question is what kind of knowledge can best be developed to support problem-solving skills, and how can these skills be supported effectively? There is discussion about which type of knowledge to improve first. Moreno (2006) indicates that in the introductory stage of a new domain, worked examples with decreasing instruction will be effective (fading). However, once students have gained basic content knowledge and are asked to apply their knowledge to new problems, worked examples is no longer an effective instructional method. Other researchers claim that it is often not content knowledge that students lack when they try to solve new problems but strategic knowledge (Mathan and Koedinger 2005; Taconis 1995). Strategic knowledge allows students to analyse the problem, find relevant content knowledge, make a plan and solve the problem (De Jong and Ferguson-Hessler 1996).

In the last decade many new computer programs for mathematics or science problems have been developed and tested (Aleven et al. 2003). These programs aim at different types of knowledge: some focus more on declarative and procedural knowledge and others more on strategic knowledge. In this study, we describe several types of programs and we discuss why the program we have chosen has so much promise. The program we propose makes declarative and procedural knowledge available in such a way that it emphasizes the development of strategic knowledge. It gives the student a scaffold when solving problems by offering declarative and procedural hints within structured episodes. Students are free to use the hints and the program does not dictate one way of solving problems, thus giving students the possibility to develop their own problem-solving strategies. We will investigate the way students solve new problems and observe their use of hints during the process of problem solving and, afterwards, how they deal with worked examples. We will also attempt to find out how these forms of embedded scaffolding instruction improve students’ strategic knowledge.

Types of Computer-Supported Problem-Solving Programs

The study by Aleven et al. (2003) reviews how programs that support the learning of problem solving can be designed. Intelligent tutoring systems and Computer-assisted instruction are aimed at developing strategic knowledge by providing standard solution procedures that can be used to solve certain types of problems. In computer-assisted instruction, worked examples are often used for instruction, with fading of support during practice on analogous problems. Students receive feedback on their answers based on the solution procedures in the worked example. In both intelligent tutoring and computer-assisted instruction students are supported before and during problem solving. Intelligent tutor programs often allow for more than one standard solution and estimate from the student’s actions which solution path the student seems to be following. However, Aleven et al. (2004) indicate that intelligent tutoring programs often fail to induce the intended use of extra help by the students.

On the other hand, educational hypermedia systems and computer simulations aim at developing strategic knowledge that will enable students to apply general problem-solving skills to analyse complex problem situations and apply their content knowledge of a domain. For novice problem solvers, these types of programs are often too open and ill-structured. There is little instruction to show how problems can be analysed, or solutions planned and executed (Aleven et al. 2003).

In the first group of programs, the system gives instruction. The programs decide when to support the student. The last group of programs, as indicated by Aleven et al. (2003), give control of the support to the student—they assume the skilled student knows when he or she needs help. At first sight, strategic knowledge seems best supported by a student-controlled system which allows students to work on their own individual solving strategies. However, in implementing student-controlled learning environments one needs to consider the disadvantages of this form of instruction—students need a certain level of declarative knowledge and procedural knowledge to take control of the solving process. If the necessary knowledge is not present then the student needs to be supported in gaining this knowledge. This may take some form of system control because a novice finds it hard to tell what knowledge is needed when working on new problems (Clark and Mayer 2002).

We assume that a combination of system and student-controlled instruction will be the most effective. On the one hand, the student should be able to follow a well-structured line of problems using the instruction available, thus preventing failure. On the other hand, in order to develop strategic knowledge a program needs to be open enough to create space for students to choose their own problem-solving strategies. An example of using a blend of open tasks on the one hand, and supporting students in cases where they cannot work out a problem on the other, can be found in the work of the Modeling across the Curriculum project. In this project students work in a modelling environment, but are guided in cases where they cannot work out a problem themselves (Buckley et al. 2004). A blend of student and system-controlled instruction is also proposed by some of the proponents of instruction by worked examples. Instruction with worked examples is too limited and needs further improvement in order to support diverse problem solving. One way of doing this is by not providing worked examples at the beginning of the problem-solving process but offering hints during the process (Reif 1995) and worked examples (model answers) as feedback afterwards so that the student can reflect on the solution he has chosen (Moreno 2006).

The issue for the design of a physics problem-solving program is how this blend of student and system control can be shaped into an effective learning environment. Although many students fail to solve physics problems because they have too small a basis of declarative knowledge and procedural knowledge, the main reason for difficulties in problem solving seems to be the lack of strategic knowledge (inter alia, Taconis 1995). Inexperienced students often spend little time on analysing a physics problem, instead choosing a solution method immediately, which may turn out to be only partly applicable or not applicable at all (Chi et al. 1981; Sherin 2001). This is why the design of problem-solving programs is best directed at strengthening the base of strategic knowledge.

Schoenfeld (1992) is an important proponent of the approach to problem solving where students take the initiative in building up their strategic knowledge. He investigated expert and novice problem-solving behaviour and on the basis of this research distinguished five ‘episodes’ in the process of problem solving:

  1. 1.

    survey the problem (read, analyse)

  2. 2.

    activate student’s prior knowledge (explore)

  3. 3.

    make a plan (plan)

  4. 4.

    carry out the plan (implement)

  5. 5.

    check the answer (verify)

Harskamp and Suhre (2007), for example, have specified how the Schoenfeld episodes could be implemented with regard to mathematics.

Experts and novices differ in their approach to solving problems. Novices almost immediately start work with a poorly defined plan, whereas experts take the time to analyse the problem and gather information before making and implementing a plan. Schoenfeld (1992) argued that novices need to learn to work through the different episodes more effectively and he demonstrated how it was possible to teach students to use the episodes through questions and hints.

An important question is whether all students can be instructed the way Schoenfeld suggests regardless of their prior knowledge, or whether students with different prior knowledge have to be offered different ‘just-in-time’ instruction. Anzai and Yokoyama (1984) and Maccini et al. (1999) indicated that students can use and comprehend one hint, and at the same time not understand and thus ignore another. For novices in particular, in giving a heuristic hint or instruction one needs to clarify how to use this hint in solving the problem. For example, if you tell a student to make a drawing of the problem concerned, you need to provide first-hand help in drawing techniques. The study of the effect of a program on electric circuits by Van Gog et al. (2006) with procedural and content-related just-in-time instruction should be seen in this light. Comparable effects have been found by, for example, Lehrer and Schauble (2000) who wanted students to model a situation, and in questioning one situation they obtained correct answers, while in a similar situation found that the students went completely wrong.

Choice of a Program Type and Question for Research

From the review of literature above one may assume that a student-controlled problem-solving program is effective when it contains embedded scaffolding instruction that enables students to develop a more systematic approach to problem solving. Moreno (2006) suggests that for most students just-in-time instruction during problem solving may be more effective than instruction by worked examples prior to problem solving. In practice this means that programs should contain just-in-time instruction during problem solving and worked examples after the solving process. The embedded instruction and worked examples should present the student with a choice of different solution methods. The student should be free to choose the help but should be given advice on how to use it when providing a wrong answer. In this way, the student is offered structured help and feedback without being forced to follow a standardized solution procedure. Such an adaptive problem-solving program may improve students’ strategic knowledge in solving diverse problems.

Inspired by Schoenfeld’s episodes (1992), Pol et al. (2005) constructed a web-based computer program which supports novices when solving physics problems on forces. The aim of the program is to enhance the further development of problem-solving skills by offering tasks that can be completed with the help of the program. The help is structured according to Schoenfeld’s five episodes of systematic problem solving listed above, with our program providing hints for all five episodes. The hints show students how applied problems can be analysed and allows them to choose between informal and formal solution strategies (Maccini et al. 1999).

Instead of dictating specific solution methods, each episode gives students the space to select a hint on the recommended method. The program is based on embedded scaffolding instruction with students controlling the learning pace, the problems worked on and the hints selected. The rationale is that the best way to develop the problem-solving skills of novices is to support them with a system that gives sufficient room to develop strategic knowledge that fits their way of learning. Students need to acquire a flexible problem-solving strategy to enable them to tackle different types of problems (Reif 1995).

With regard to the level of the tasks, Joshua and Dupin (1991) have shown that the teacher will often find the problems easy to solve, whereas the students are quite unable to do so. In fitting the level of the tasks to the prior knowledge of the students, one should be conscious of not making the tasks, including the use of help, too difficult. At the same time, one should try not to make the level of the tasks too easy. Problem solving can only be learned in a situation where students indirectly have all the required information at their disposal, but still need to be challenged (see, for example, Van Heuvelen 1991a, b). The necessary level of complexity of the problems and the hints, that is, neither too complicated nor too simple, was tested in an exploratory study by Pol et al. (2005). They showed that the program was effective: the students in the experimental group provided with hints during problem solving and model answers afterwards were more competent problem solvers on a transfer test than those of the control group. Declarative and procedural knowledge about the subject was also measured before and after the experiment. No significant differences were found between the three groups. In the study, it was hypothesized that the experimental group was able to score significantly higher on the transfer test because it developed a more systematic approach to problem solving than the control group. This would mean that scaffolded instruction—offering hints during the solving of problems as well as offering worked examples afterwards—can have a positive effect on the development of strategic knowledge.

Our present general research question therefore is:

How does a student-controlled problem-solving program that provides embedded scaffolding instruction during problem-solving and afterwards improve students’ strategic knowledge?

The next section presents a problem-solving program that offers an ordered group of physics problems for students in secondary education. The aim of this article is to analyse how students use the hints in the program and develop their strategic knowledge and how this improves their problem-solving skills as measured by a problem-solving post-test.

There may be two ways of achieving more strategic knowledge: (1) by practising a large number of problems in a certain domain (Chi et al. 1981) and (2) by increasing the systematic use of problem-solving episodes (Schoenfeld 1992), thereby enhancing students’ strategic knowledge. Clark and Mayer (2002) state that skill development and expertise are strongly related to time and efficiency of deliberate practice. The more a person practices, the better he or she becomes regardless of initial talent or skills. One important factor for strategic knowledge with respect to practice is that the tasks should not be too complex so that students are able to provide many correct answers. This is known as learning for mastery (Bloom 1980). In the present study we wish to discover whether an increase in strategic knowledge is brought about by finishing more of the tasks correctly in the program (practice effect) and/or by learning to make strategic use of hints and problem-solving episodes in the program (systematic hint-use effect).

The Physhint Program

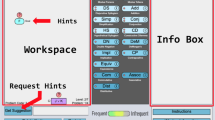
Figure 1 shows the computer screen as seen by the students. The problem (original taken from Middelink et al. 1998) is on the left of the screen. The hints menu is on the right.

Fig. 1
figure 1

Task 74 from the Physhint computer program (original from Middelink et al. 1998)

Full size image

The hints are provided under the headings of Survey (Schoenfeld’s episodes: ‘read’ and ‘analyse’), Tools (‘explore’) and Plan (‘plan’). After answering, students are allowed to check and reflect on their solution (‘verify’). Students are given three opportunities to check their solution against the model answer, during which time they can continue to consult hints. The hints given for Task 74 are shown in Fig. 2.

Fig. 2
figure 2

Hints for Task 74 using the episodes Survey, Tools and Plan

Full size image

Hints given in the first episode discuss the problem situation, mostly using informal methods such as a scheme, table or simple numerical calculation. The intention of these hints is not only to give help, but also to demonstrate the usefulness of these informal methods and to stimulate their use. However, hints in the computer program not only offer common descriptions of a certain action, but are almost always linked to a specific domain of declarative and procedural knowledge needed for the task. Several researchers have emphasized the need to link strategic knowledge to declarative and procedural knowledge, which are always domain specific (Maccini et al. 1999; Wood and Wood 1999).

In Tools the student needs to choose which domain-specific declarative and procedural knowledge is needed to solve the problem. The use of certain definitions is discussed under this menu. Declarative hints are especially important because in this phase of the problem-solving process students may need to be led away from possibly wrong physical representations of the problem to the correct one. Heuristic hints are needed for this guidance, but there can also be a simple lack of domain-specific declarative and procedural knowledge.

If the help offered under the Survey and Tools episodes is insufficient, a hint in the Plan episode is called for. Plan hints are focused on the different ways of solving the problem and on helping the student when they are about halfway through the solution process. Very often students can choose from various solution methods. In this case there are two.

In the program, students can give an answer up to three times, with the computer comparing their answer to the correct one. After the last try, students are given access to a menu with short descriptions of the model answers. They can consult one or more of these. The different model answers may cover informal solution methods (table, numerical calculation, etc.) or formal solution methods (formula, algebraic equation, etc.). The function of the model answer is to support reflection on the solution process. Figure 3 gives possible formal solutions for Task 74.

Fig. 3
figure 3

Model answers for Task 74

Full size image

Methodology

Our study of the Physhint program asked the following research questions: first, in general, how does the Physhint program improve students’ strategic knowledge?; and second, more specifically, if the program is effective, is this due to a practice effect and/or to an effect caused by the students’ systematic use of the help (hints)? To find answers, the following methodology was used.

Embedding the Computer Program in the Lesson Plan

One of our starting points is that our computer program should be a natural part of typical lessons in physics as taught in Dutch secondary schools. Since the most recent curriculum reform in 1998 of upper secondary school (Stuurgroep Profiel Tweede Fase 1994), lessons in physics characteristically:

  • concentrate on the active and independent role of students

  • accommodate differences among students

  • stimulate students’ thinking skills

In typical school practice there is a combination of brief instruction for the whole group, independent work, practical work and discussion of some of the completed problems. The lesson plan on the subject of forces can be found in Table 1, which shows the different activities as experienced by students. In Lessons 1–3 (Tasks 1–21) the topic of vectors is taught, Lessons 4–8 (Tasks 22–51) deal with Newton’s laws, and in Lessons 9–14 (Tasks 52–80) the concept of torque is introduced and combined with the other two topics. The tasks in the lessons on torque are more complicated than the tasks in the lessons on vectors or Newton’s laws.

Table 1 Lesson plan
Full size table

During independent work, the teacher acts as a mentor and is available to answer students’ questions. However, if students do not manage to solve a problem themselves, they often prefer to consult the freely available answers in their textbook and model answers in the answer book instead of asking the teacher for feedback on their solution process—they think they have understood the problem and its solution and move on to the next task.

Physhint can play an important role in the independent work sessions of the students. When students are stumped, the program does not directly offer a model answer. Students can instead choose from hints with just-in-time instruction, after which they can continue the problem-solving process. As the program takes on the role of teacher, the student no longer needs to ask a person but can click on a hint for the episode that could not be solved without help.

Design of the Study

For this study, a group of 16-year-olds with average exam results was selected from two classes at a typical pre-university school in the north of the Netherlands. To prevent negative influences on the experiment due to a lack of sufficient computer skills, the students were selected on the basis of the availability of a broadband Internet connection at home. Representation was checked by pre-testing. A quasi-experimental procedure was used, with the students assigned to the research conditions according to whether they had a fast Internet connection rather than at random. We checked whether there were systematic differences in pre-test scores between the experimental group and the control group. As this was not the case (see Sect. 4.1) we assumed there was no systematic difference between the experimental and the control group.

There were 11 students in the experimental group and 26 in the control group. The treatment consisted of lessons wherein the students of both groups were taught the subject of ‘Forces’ using the same project and the same textbook. Both groups received all the classroom tuition together but were separated for their independent work, with the experimental group moving to the computer room and the control group staying in the classroom. The teacher and a researcher supervised the students at work. All students were given the same 80 tasks. The students from the experimental group received short instructions on how to access and use the program and then worked on the tasks on the computer. Students in the control group were not given any special instructions on problem solving and worked on the same tasks from their textbook. They had an answer book with model answers. Data on the number of tasks as worked out correctly during the project by the students of the control group were logged by the students themselves and were checked by the teacher.

Log Files

During the solution process the use of episodes and hints by the 11 students in the experimental group was analysed by means of the log file created by the Physhint program. All tasks, hints and solutions were incorporated as separate files which could be accessed individually by the student. Each time a student clicked on and accessed a task, a hint or a model answer, this act was logged on the server computer together with the identity of the student and the time of the act. In addition, any check of a completed answer was also logged by the program. In order to find possible relationships between program-use behaviour and post-test gains, a qualitative analysis of individual program use was undertaken, then grouped and compared with post-test scores (corrected for pre-test scores) (see, for example, Buckley et al. 2006). For the students in the control group, the teacher checked the number of tasks worked out by the students and kept a record of the tasks solved correctly during the project. The students kept a record of the time they spent working on the tasks.

Pre- and Post-tests

All 37 students of both groups took a pre-test and a post-test consisting of applied problems. Their scores were used to analyse the differences between the three conditions with respect to their problem-solving skills. At the end of the experiment, a content-knowledge test to find out the level of domain-specific declarative and procedural knowledge was also administered. The pre-test consisted of six applied problems about topics which had been taught during the previous 2 years. The problems were set in situations not previously encountered by the students. The subjects of the pre-test were distance, velocity and acceleration. Examples of tasks assigned in the pre-test can be found in Fig. 4.

Fig. 4
figure 4

A task from the problem-solving pre-test

Full size image

When solving the problems in the pre-test and the post-test the students of both groups were asked to state explicitly how they analysed the problem, came up with a solution plan, and how they checked their solution. A pre-flight task was discussed before testing which showed the students which information they should write down and how this should be related to the problem-solving process. The various episodes were graded with maximums of two, six and two points, respectively, making a possible total of 60 points for the pre-test.

The post-test consisted of five applied tasks on the subjects of forces and torque in situations not previously encountered by the students. An example of the post-test tasks can be found in Fig. 5. As in the pre-test, the students had the opportunity to demonstrate their skill in filling in the episodes ‘analyse,’ ‘plan’ and ‘verify the solution’. Both the experimental and control group students had the same experience in writing about their solution process. Again, marks were given with maximums of two, six and two points, respectively, with a possible total of 50 points.

Fig. 5
figure 5

A problem from the problem-solving post-test

Full size image

The reliability (internal consistency) of the problem-solving pre-test as shown by Cronbach’s α is 0.76 and that for the problem-solving post-test is 0.69. The correlation between both problem-solving tests is r = 0.48 (p < 0.05).

The pre-test and post-test were rated by one observer using a very specific rating protocol. A random check of the tests of 20 students by a second observer using a more general rating protocol resulted in correlations of between 0.60 and 0.95 for the different items, with an average of 0.82. This means the scoring procedure for the test has sufficient inter-rater reliability. The overall reliability of the two tests was sufficient to use the tests to compare group means.

Results

The question of the present study is: How does a student-controlled problem-solving program that provides hints during problem solving and model answers afterwards improve students’ strategic knowledge? If the program was effective we would expect to find explanations from two sources: a practice effect and a systematic hint-use effect (see Sect. 1).

In order to analyse the different possible effects, we will first present data on the program implementation. This data might provide insight into the presence of differences encountered in practice, as it compares the number of tasks finished by the experimental and the control groups and the possibility of a practice effect. We will then analyse data on the systematic use of hints by the experimental group. In the last part of this section, we will analyse the pre-tests and post-tests of the two groups looking for evidence of the two effects mentioned above.

Use of the Tasks and the Students’ Results

First we analysed the general use of the program to find possible signs of a practice effect. All students received 14 lessons of 45 min in which classroom teaching, practical work and demonstrations were alternated with independent work. Classroom teaching and practical work were the same for both the experimental and the control group. These activities were undertaken together and according to the lesson scheme given in Table 1. During independent work, the control group worked in the classroom or at home on the 80 tasks in the textbook. The control group could check their solutions in the answer book available to every student. The experimental group carried out the same 80 tasks, using Physhint in the computer room and making use of the hints in the program. The time spent working on problems independently was also comparable for the control and experimental groups. The number of tasks undertaken by the students of the different groups during the project is given in Table 2.

Table 2 Number of the 80 tasks undertaken during the project and percentage of correct answers for both groups
Full size table

The table shows that the average number of tasks undertaken by the students of both groups did not differ greatly. Analysis of variance showed no difference (F = 0.058; p = 0.81, ns) but there is a significant difference in the percentage of tasks answered correctly during the project. In the experimental group more tasks were solved correctly during the project than in the control group (F = 8.8; p < 0.01). This result does not come as a surprise as the students in the experimental group could use hints during problem solving and check model answers afterwards, while the students working with the textbook could only check their answers after they had finished a problem.

In order to relate the results on the tasks to the post-test results, in Table 3 we present the results of the students’ pre-tests and post-tests.

Table 3 Students’ test scores: means and standard deviations (Data: Pol et al. 2005)
Full size table

An analysis of variance showed that the average pre-test results of both groups did not differ significantly. An analysis of covariance with the post-test scores as the dependent variables and the pre-test scores as the covariate was conducted. First, we checked that there was no significant interaction effect between the pre-test and research condition on the post-test results. The covariance analyses showed that the average score on the problem-solving post-test of the experimental group was significantly higher than the average score of the control group (F = 8.54, p = 0.006).

The information in Tables 2 and 3 shows that students in the experimental group clearly scored higher on the problem-solving post-test than the control group and that they also answered more tasks correctly during the project, although both groups worked out about the same number of tasks during the project. The higher post-test score of the experimental group could partly be due to the fact that these students solved more tasks correctly during the project than those in the control group. We therefore investigated with an ANOVA whether there was evidence of a positive covariate of the percentage of correct answers during the project on the post-test scores (corrected for pre-test scores) in both groups. In the experimental group, we expected the covariate percentage of tasks finished correctly during the project to have more effect on the post-test than the effect of this covariate in the control group, since in the experimental group students were allowed up to three attempts at giving a correct answer. They also received corrective feedback (and help if they wanted). In the control group, students had a textbook but received no feedback until they believed they had completed a task and were then free to check the answer. These students could only use the instructions and worked examples in their textbook to help them solve the tasks. The covariate for the experimental group was F = 3.71 (p < 0.05, one-tailed test) and for the control group F = 0.002 (ns). This indicates that completing tasks correctly during the project helped students in the experimental group to score higher on their post-test, whereas in the control group the percentage of correctly answered problems during the project did not have an effect on their post-test scores.

We shall now further explore the ways students in the experimental group used the program and whether the way in which they used the hints contributed to their problem-solving skills.

Use of Hints by the Experimental Group During Problem-Solving

To provide statistical data on the students’ use of hints, we counted the number of tasks undertaken within two distinct periods of the project and during which help was consulted. The two periods were divided according to the topics: the first period (Tasks 1–51) dealt with vectors and Newton’s laws and the second period (Tasks 52–80) dealt with torque.

Table 4 starts with the average percentage of tasks completed and solved correctly in both periods and then shows the average percentages of tasks for which the students used hints pertaining to the Survey, Tools and Plan episodes. Finally, the table shows the percentage of model answers consulted.

Table 4 Use of the program
Full size table

The percentage of tasks undertaken is lower in the second period than in the first. This may be due to differences between both periods in the actual time available to students and the time they needed to solve the problems. In the second period, the students had to solve more complex problems in the same amount of time as in the first period: on average, six tasks per lesson (see previous section). Table 4 suggests that in the second period fewer problems were solved correctly than in the first period. However, the difference between the two periods is not significant (t = 1.691; ns).

Overall, the use of hints during the solving of tasks decreased over the two periods for almost all students. Statistical analysis showed a significant difference for percentages of tasks in which Survey, Tools or Plan were consulted (t = 2.604; p < 0.05). Although the tasks were more complex in the second period, the students in the experimental group used fewer hints in trying to solve the tasks. This can be seen in the light of developing strategic knowledge. Students learn by doing: they still have to cope with the tasks, but better know and understand the function of the hints. Perhaps that is why they used hints on fewer of the later tasks. The use of model answers, on the other hand, increased. Statistical analysis showed a nearly significant difference for the percentage of problems for which the model was consulted (t = −1.851; p < 0.10). It is thus apparent that over the course of the project, students from the experimental group checked more model answers. This may be an indication of the development of strategic knowledge, as checking and evaluating a solution after finishing a problem is an indication of strategic knowledge. We will explore these hypotheses further in the next section when analysing the use of the program by the individual students.

To gain more insight into the effect of the use of hints in general, we checked whether there was a relationship between the experimental group’s use of the different kinds of help and the percentage of the tasks in the program answered correctly during the project. We assumed that the help provided during problem solving had a positive effect on solving a task. However, it is probable that students checked the model answer more often when they did not succeed in solving a task than when they did solve the task correctly. The results can be found in Table 5.

Table 5 Relationship (Pearson correlation) between percentage of tasks answered during the project and the use of the different kinds of help (n = 11)
Full size table

The table shows positive correlations for the use of all three kinds of hints during the solving of tasks in the project. This means that the hints help students to solve tasks. Only model use shows a negative but not significant correlation: students who solve fewer tasks correctly during the project tend to check model answers more often. These results indicate that the use of hints during problem solving has a positive effect on solving a task. However, the results do not provide evidence that the use of help actually enhances the systematic use of problem-solving episodes and thus improves strategic knowledge. For this reason, we will study individual profiles in the development of hint use in the next section.

Individual Profiles

In the program, students were allowed to use the hints at will when they experienced difficulties. We expected that students would profit from using these hints especially if they used them systematically to support effective problem solving. The individual scores of students were scrutinized to obtain more detail on the way the hints were used. The graph shown in Fig. 5 indicates the systematic use of hints during the project for each student in the experimental group.

How did we analyse the systematic use of hints? In our definition of systematic hint use, a student should use the episode-related hints according to the sequence of episodes an expert would follow (see Sect. 1): clicking from Survey to Tools and finally Plan, but also on Model answer after finishing a task. If the expert problem solver already knew how to work through the first two episodes, then we would expect him to start with a hint for the Plan episode. If hints were used in the expected order then we classified this as ‘systematic use’ of hints. If one or more hints were used out of sequence then we classified this as ‘unsystematic use’.

All of the tasks undertaken by the students were analysed according to the sequence of hint use. If no hints or model answers were used, or hints were used in an unexpected order, then the task was classified as ‘no systematic use of help’. Consultation of the model answer was thus also taken as an indication of systematic use. However, high scores on our scale of systematic use could be attained not only by students with little prior knowledge and much need of hints, but also by students with much prior knowledge and little need of hints. In any event, students were advised to check their answers against the model answer in order to reflect on their solution method in comparison with other ways of solving a problem.

Figure 6 shows the percentage of tasks for which help was used systematically by the 11 students in the experimental group, thus demonstrating the development from the first to the second period.

Fig. 6
figure 6

Percentages of tasks for which the students systematically used help

Full size image

As the graph indicates, five individuals increased their systematic use of help during the project: (from the top) students 11, 4, 8, 3 and 1. The remaining students did not increase their systematic use of help: students 2, 10, 7, 6, 5 and 9. We will now discuss their individual profiles. We will describe the number of tasks a student completed, the number of correct answers and the use of hints and model answers when solving tasks.

Student 1: This student completed 61 of 80 tasks, a little less than average, but with 56 problems answered correctly (92% of the completed tasks) he solved more tasks correctly than the average. In the first period he was a regular but unsystematic user of hints, especially Tools and Plan, and the model answer was rarely used. In the second period he became a more frequent and systematic user of hints and model answers, especially when he had answered a task correctly. We can conclude a ‘more systematic use’ of the program during the course of the project.

Student 2: This student correctly solved 54 of his 63 completed tasks. He was a frequent user of hints for all episodes, including the model answer, starting with an unsystematic use of hints. He used an above-average number of attempts to answer the tasks correctly. Between attempts he viewed many hints. We did not find any development in the systematic use of hints. This student can be described as a ‘less systematic’ problem solver showing no improvement during the project.

Student 3: The student solved 61 of 74 tasks attempted, using lots of hints for all three episodes in problem solving, as well as the model answers. During the first period, this student showed an irregular use of hints, which gives the impression of a non-systematic hint user, mostly rushing through the tasks. During the second period, the student showed a systematic use of model answers on more tasks. The student also used hints more systematically than in the first period. This individual can be described as a ‘not very systematic’ problem solver, but shows clear development from little to some systematic use of the help in the program.

Student 4: This student correctly solved 62 of the 79 tasks he completed. He used a more than average number of hints. The positive development shown by this student from the first to second period is reflected in the sequence of hints used. It became more systematic. Model answers were also consulted more frequently in the second period, especially after answering correctly. We will elaborate on some of his work. Table 6 gives the sequence of actions as registered in the log file for this student, where for every ten tasks, the one showing the most action is taken (student is using hints, trial answers or model answers).

Table 6 Sequences of the use of help and answers given for a selected number of tasks undertaken by student 4
Full size table

The sequences show that in the beginning (Task 9 to Task 31) the student consulted many hints, and sometimes then immediately filled in the correct answer (Task 18). Over the course of the project the student chose hints more selectively. In the last four tasks shown in this overview, he first took hints from Survey, then from Tools, after which he consulted Plan. He did not return to Survey or Tools again, as he did with the first tasks; furthermore, he answered the last three tasks correctly and consulted one or more model answers. This is in contrast to the start of the project where he only checked a model answer after not solving the task (Task 31). In short, this student showed development in the systematic use of the program.

Student 5: Of an above-average number of 75 tasks completed, this student answered an average number of tasks correctly (60). From the beginning, he was not an intensive user of hints and as the project progressed he used the hints even less. He rarely used model answers and then only when he gave an incorrect final answer. We characterize this student as a ‘weak systematic’ problem solver, who showed no development in the systematic use of the program.

Student 6: With 45 of 62 tasks completed correctly this student scored relatively low for correct answers. The student also completed fewer tasks than average. The student was a sparing user of hints and model answers. If hints were used, they were used erratically. It seems that the choice of which hint to use first (out of the three episodes) was made randomly. This student used model answers only after he had given a wrong final answer. We characterize this student as a ‘weak systematic’ problem solver showing no development in the systematic solving of problems.

Student 7: The student did not give many correct answers, only 60 out of 80 and thus was below the average of the group. However, he did work through all the tasks of the project. He used relatively few hints but used model answers more than average. For some tasks, the student used more hints and then succeeded in submitting the correct answer. Although he occasionally used hints systematically there was no development in systematic use from one period to the other.

Student 8: The student completed all 80 tasks of the project, and was above average in the number of correct answers (70 = 88% of the tasks carried out). The student was a regular user of hints and an average user of model answers. From the beginning, the student showed a systematic use of hints. During the project, the frequency of the use of model answers increased.

Student 9: This student began well but later on seemed less motivated to finish tasks. He started many tasks but did not finish them. Ultimately, he completed 24 tasks with 22 answered correctly. In the first three lessons, the student had an above-average use of hints. He first tried to solve a task without help and viewed hints only when he did not succeed. Sometimes he could solve a task without help. Other times he kept trying and after three trials finished the task and looked at the model answer. This student did not show a systematic use of hints, nor positive development in the systematic use of the program.

Student 10: With only 44 correct out of 63 tasks attempted this student also completed less than the average amount of tasks. Sometimes he started tasks but did not finish them. For these tasks, he occasionally viewed hints or submitted a trial answer, but ultimately gave no correct solution (the student gave three incorrect answers). The use of hints is low compared with the rest of the group. The frequency of use of the model answers by this student was above average. This student can be characterized as a less systematic user and is clearly not showing positive development in the systematic use of help from the program.

Student 11: With 55 correct out of 65 completed tasks (85%) this student was above average in the number of tasks solved correctly, many of them in only one attempt. The student used many hints, including model answers. For more than half of the tasks we found a systematic sequence in the hints used. This was far above average. He used model answers usually after solving a task correctly, especially in the second period of the project. We describe this student as an ‘above average systematic’ user showing development in the systematic use of help.

Effects of Systematic Use of Hints on the Problem-Solving Skills of Students

The question that now remains to be answered is whether the group of students showing an increase in the systematic use of the program also showed an improvement in strategic knowledge as tested by the problem-solving post-test. The group not showing an increase in the systematic use of help consists of students 2, 5, 6, 7, 9 and 10. Of the other students 4, 8 and 11 show an increase in the systematic use of help despite an already high starting level. Students 1 and 3 did not start systematically, but they clearly developed from a low level of systematic use to more frequent systematic use of the help in the second period of the project. Table 7 shows a difference between the groups in the average score in the post-test.

Table 7 Scores on the problem-solving post-test of students with no development in the systematic use of help versus students with a development in the systematic use of help
Full size table

We investigated whether there were significant differences in the scores on the post-test between the group of students with an increase in the systematic use of hints and the group with no increase in the systematic use of hints. On the problem-solving pre-test, the groups do not score significantly differently (t = 0.17; p = 0.69, two-tailed test). However, at first sight we see a difference between the groups’ averages on the problem-solving post-test. The means and standard deviations of the groups are 25.4 (std. 4.3) for the group of systematic users versus 20.5 (std. 3.7) for the group of unsystematic users. In order to find out if the increase in the systematic use of the program is a predictor in post-test scores, a regression analysis was conducted with post-test scores as the independent variable and the pre-test scores and the increase in systematic use as the covariates. An increase in systematic use was shown to be a significant factor (Beta = 0.48; p < 0.05, two-tailed). This reveals that students profit most from the program when there is an increase in the systematic use of the available hints.

However, is development of systematic use of the programme independent of the effectiveness of practice? We explored the answer to this question with non-parametric correlational analysis. First we studied the relationship between the development in systematic use (yes or no) and the number of exercises the students solved correctly. The Spearman’s rank coefficient showed a significant relationship (Spearman’s rho = 0.63, p < 0.05). Although the number of students is very small (n = 11) we tested if there was a relationship between the number of tasks solved correctly during the project and their post-test scores, controlling for their pre-test scores and development in the systematic use of hints. The partial correlation coefficient was 0.35 (p < 0.10). Thus, the present study did not find a strong relationship between the practice effect and post-test gain scores when controlling for differences between students in the growth of a systematic use of hints. The same holds true for the relationship between systematic use of hints and post-test gain scores if we control for the number of tasks solved correctly during the project.

The effect of development in systematic use cannot be disentangled from the practice effect. Both effects will play a role in acquiring problem-solving skills, but they are not independent.

Conclusions, Discussion and Implications

Conclusions

This is a small-scale study into students’ problem-solving behaviour while working with tasks and hints in a computer program. The main purpose of this study was to find indications of how the use of hints and model answers by students can help them improve their strategic knowledge. We undertook this research because there are few studies on the effectiveness of problem-solving programs on student behaviour. The teacher first taught the students the basic knowledge needed to solve problems, and then the students were assigned to one of two groups: an experimental group which learned to solve problems with the help of a student-controlled computer program with embedded instruction, and a control group which learned to solve the same problems using a textbook and model answers. By incorporating the program into the school curriculum we not only tried to improve strategic knowledge, but also wished to take into account conceptual knowledge and understanding, as well as the experience and interests of students (see, for example, National Research Council 1995).

This study asked: How does a student-controlled problem-solving program that provides embedded scaffolding instruction during problem solving and afterwards improve students’ strategic knowledge?

We assumed that there are two possible ways in which students can use a program to improve their problem-solving skills: through much practice, or by systematic use of the hints in the program. The hints in the program were linked to different episodes in problem solving. By using hints according to an expert’s chain of solution episodes, students may acquire more strategic knowledge. Within the experimental group, we distinguished a subgroup that worked more systematically with the program over the course of the project and a subgroup that showed no development. Our evidence is based on a small sample. Nonetheless, it is important that our working hypothesis finds support in our analyses. The conclusions we have drawn in this study should be regarded as hypotheses to be tested by further research.

At the end of the project, the experimental group showed a significantly higher score on the problem-solving post-test. Teaching students with the assistance of the program proved to be more effective than with the textbook. The tasks undertaken in the project required students to apply the content knowledge (declarative as well as procedural knowledge) taught in the lessons. The tasks consisted of applied physics problems that invited students to analyse the problem context, think of schemes or knowledge that could help solve the problem, make a plan and verify the outcome. Students could train themselves in all these problem-solving episodes by using the hints in the computer program, whereas the students using the textbook could not.

We expected a practice effect due to the availability of hints relevant to each problem-solving episode, thus creating more efficient use of problem-solving time. Clark and Mayer (2002) point out that the time allotted to practice always plays an important role in learning. They state that often it is not the specific type of training, but the amount of practice that explains the effect. Others claim that, especially for higher-level tasks, the amount of practice can play a role, but also other effects can interact with the amount of practice, or even overrule the effect of practice. Grote (1995) and Ross and Maynes (1985), for example, showed that the spread of instruction is as important for the effect of practice as is the amount of practice. With our program we wanted to research the influence of just-in-time instruction during practice. In the program in our study, students could use the help of hints. In this way they could find a solution path for a problem more readily and with little waste of time. Students working with the textbook had to solve the tasks without help. After finishing a task, they were allowed to check their solution in the answer book. We expected that students working with the program would process more tasks correctly during the project.

There are indications that the program has a practice effect. Students using the program indeed solved more tasks correctly during the project in comparison with the control group who used the textbook. In the experimental group there was a positive (partial) correlation between the tasks solved correctly during the project and the results in the problem-solving post-test. This was not the case in the control group. The results thus indicate a practice effect: the more tasks that are finished correctly with the computer program the more problem-solving skills students develop.

The second effect we expected was a systematic hints-use effect. According to Schoenfeld (1992) students confronted with systematic support guided by problem-solving episodes may improve their strategic knowledge of how to solve diverse problems in a domain. In working with Physhint we expected the students, as novice problem solvers, not to begin using hints according to the sequence most experts would follow. Instead we expected them to choose hints at random in several tasks, or to start directly with a hint containing a plan. However, we considered that these students might learn to first consult hints which help in surveying and analysing the problem, after which they would consult the necessary resources, find help with a plan and finally check for alternative solutions using model answers.

During the experiment, we found that some students showed an increase in the systematic use of hints in accordance with Schoenfeld’s theory. We found 5 out of 11 students improved in their use of hints, showing an increase in the percentage of tasks for which the hints were consulted systematically from period one to period two of the project. The group not only used hints systematically during the process of solving problems, but also used model answers after correctly solving a problem. This means that some students grasped the correct way of working with the program while others did not.

A correlational analysis showed that there is an overlap between students who make more systematic use of the hints in the program and students who solve more problems correctly in the program. As we have no data about the systematic use of episodes in the control group we cannot disentangle the effect of systematic use and the percentage of tasks answered correctly on the post-test scores. What can be said is that we found a significant difference in problem-solving post-test scores between the group of students who increased their systematic use of hints and the group that showed no increase in systematic hint use. This result indicates that a more systematic use of the episodes in the program may lead to an improvement in strategic knowledge. However, to a certain degree this effect overlaps with the practice effect, the latter being the consequence of solving more tasks correctly during the project.

Discussion and Implications

If the practice effect and the systematic hint-use effect cannot be disentangled, the question that must be considered is how these different aspects can be analysed. Due to the small size of the experiment and the fact that there is no data about a development in the systematic use of the problem-solving episodes in the control group it is not possible to say more at this stage. Further research needs to be done on a larger scale. We consider that the effects should be studied in both the experimental group and the control group. Therefore, the control group’s problem-solving process during the project needs to be studied. This could be done by asking the students in the control group to explain how they went about some of the tasks in the program (e.g. Schoenfeld 1992, describes such a procedure). The students’ answers could be scored according to the episodes outlined in this article. If such information from the control group is available with respect to the different stages of the project, a comparison of the ‘practice effect’ and the ‘systematic use of episodes effect’ on the post-test scores in the experimental versus the control group could be made.

A second question to consider is why in the experimental group one student’s strategic knowledge improved more than another, and having analysed the influence of the development of systematic use, the question as to why some students seem to learn more from the support of the program than other students also arises.

Third, the question of how to support this other group of students who apparently seem to learn less from the program needs to be addressed. It may be that these students learn less about the way this program is designed and they need direct instruction in the use of the program when they do not develop a systematic approach to the problems (e.g. Maccini et al. 1999). Many researchers agree that the degree of help should be dependent on the need of the student. However, the needs of the students should determine whether the scaffolding should be provided before, during or after the solution process. Moreno (2006) points out that we know very little about what makes students into more systematic problem solvers and how the instructional design of computer programs can help students with this task. She discusses the various studies in which scaffolding is provided before, during or after problem solving with experienced and novice students and also discusses the possible conclusions from these studies. One conclusion is that the strategic knowledge of novice students could best be enhanced by scaffolding during and after the process in order to allow the transfer of knowledge. A hypothesis for further research might be that the effect of hints during problem solving, together with model answers afterwards, is stronger in combination than the effect of either hints during problem solving or model answers afterwards.

The issue of what kind of scaffolding to offer weak problem solvers also concerns the control of feedback. Researchers such as Wood and Wood (1999) and Mathan and Koedinger (2005) believe that an intelligent tutoring program can deliver the just-in-time instruction needed for a student. Others such as Reif (1995) and Harskamp and Suhre (2006) believe that the student should be in control of instruction and feedback. The latter point of view is supported by this study. In allowing students to choose the help they require, we expect them to become aware of what help they need and where they encounter difficulties in the problem-solving process. Further research might create an extra condition in which students in the experimental group are first given feedback on whether their answer is right or wrong, and if their answer is incorrect they can choose from a series of systematic hints that correspond to two different solution paths that can help them find a solution. For weak problem solvers in particular this may be more effective in evoking strategic knowledge than feedback offered by an intelligent computer program. The experimental condition we suggest would be in line with Corbett and Anderson (2001), who state that the locus of feedback control is an important factor in learning to solve problems.