Redundant Basis Interpretation of Doi–Peliti Method and an Application

Abstract

The Doi–Peliti method is effective for investigating classical stochastic processes, and it has wide applications, including field theoretic approaches. Furthermore, it is applicable not only to master equations but also to stochastic differential equations; one can derive a kind of discrete process from stochastic differential equations. A remarkable fact is that the Doi–Peliti method is related to a different analytical approach, i.e., generating function. The connection with the generating function approach helps to understand the derivation of discrete processes from stochastic differential equations. Here, a redundant basis interpretation for the Doi–Peliti method is proposed, which enables us to derive different types of discrete processes. The conventional correspondence with the generating function approach is also extended. The proposed extensions give us a new tool to study stochastic differential equations. As an application of the proposed interpretation, we perform numerical experiments for a finite-state approximation of the derived discrete process from the noisy van der Pol system; the redundant basis yields reasonable results compared with the conventional discrete process with the same number of states.

Appendix A: Numerical Details

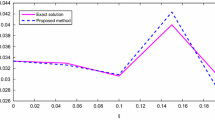
For the noisy van der Pol equation, we here use the parameters $\epsilon = 1.0$ and $\nu _{11} = \nu _{22} = 0.5$. The initial state is $\varvec{x}_\textrm{ini} = (-0.1, 0.9)^\textrm{T}$, and the statistics at $T=0.8$ are evaluated.

In the Monte Carlo simulations, we take the averages of 200 samples to evaluate the mean values of the statistics. We repeat this procedure 200 times to obtain the standard deviation of the means. The time-discretization with $\Delta t = 10^{-3}$ is used in the Euler-Maruyama approximation [33].

For the conventional basis, the number of basis (states) is 15, as denoted in Sect. 4. We must specify the center positions $\{\varvec{c}_d | d = 1, \ldots , 9\}$ for the redundant basis $| \zeta _{0,d}\rangle$. First, we solve the van der Pol equation without noise, i.e., $\nu _{11} = \nu _{22} = 0$. Second, we use equally-spaced $25\times 25 = 625$ grid points in the range $[-2,2]$ on each dimension. Then, we tentatively set the center position $\varvec{c}_d$ on each grid points, and the values of $\exp (-\beta \Vert \varvec{x}(T)-{c}_d\Vert ^2)$ are numerically evaluated. Third, we select 9 grid points with the largest values; the selected points consist of the set $\mathcal {S}_\textrm{r}$. Table 1 shows the selected center points. In the time-evolution of the derived discrete-state process, we use $\beta = 4$ in $| \zeta _{0,d}\rangle$.

Table 1 The center points used as $\varvec{c}_d$ in $| \zeta _{0,d}\rangle$