Energy-Constrained Random Walk with Boundary Replenishment

Abstract

We study an energy-constrained random walker on a length-N interval of the one-dimensional integer lattice, with boundary reflection. The walker consumes one unit of energy for every step taken in the interior, and energy is replenished up to a capacity of M on each boundary visit. We establish large N, M distributional asymptotics for the lifetime of the walker, i.e., the first time at which the walker runs out of energy while in the interior. Three phases are exhibited. When $M \ll N^2$ (energy is scarce), we show that there is an M-scale limit distribution related to a Darling–Mandelbrot law, while when $M \gg N^2$ (energy is plentiful) we show that there is an exponential limit distribution on a stretched-exponential scale. In the critical case where $M / N^2 \rightarrow \rho \in (0,\infty )$, we show that there is an M-scale limit in terms of an infinitely-divisible distribution expressed via certain theta functions.

1 Introduction

This paper is motivated by a number of problems in mathematical ecology. The motion of individual animals and the space-time statistics of animal populations are of central interest in ecology, crucial to the understanding of population structure and dynamics, dispersion patterns, foraging, herding, territoriality, and other aspects of the behaviour of animals and their interactions with and responses to their environment and broader ecosystem [22, 26, 33, 35, 40]. Movement ultimately bears on large-scale (in space and time) phenomena, such as biological fitness, genetic variability, and inter-species dynamics.

Random walks, diffusions, and related processes have been used for over a century to model animal movement: see e.g. [15, 27, 40] for an introduction to the extensive literature on these topics. Assuming Fickian diffusion leads to reaction–diffusion models in which dynamics is driven by smooth gradients of resource or habitat, such as chemotactic or haptotactic dynamics in microbiology [37], but fails in several important respects to reflect the real-world behaviour of animals [21, 27]. Various modelling paradigms attempt to incorporate more realistic aspects of animal behaviour, such as memory and persistence [24], intermittent rest periods [39], or anomalous diffusion [27].

A basic aspect of population dynamics is the flow of energy: individuals consume resource and subsequently expend energy in somatic growth, maintenance, reproduction, foraging, and so on; penguins must balance feeding and swimming, for example [11]. The distribution of scarce food or water in the environment imposes constraints on animal movement, as is seen, for instance, in flights of butterflies between flowers, elk movements between feeding craters, and elephants moving between water sources in the dry season [24, 41]. An important modelling challenge is to incorporate resource heterogeneity in space and time, to model the distribution of food and shelter, consumption of resources, and seasonality; in bounded domains, one must provide a well-motivated choice of boundary conditions.

Traditionally, mathematical ecology modelling of spatially distributed processes in bounded domains employs Dirichlet or Neumann boundary conditions, which do not do justice to the wealth of behaviour that can be exhibited at the boundary of a domain occupied by an animal population. Clearly, availability of resources can be different in the interior of the domain and at the boundary, as can the nature of interactions among members of the population. It is not impossible that an animal may want to spend some time staying at, or diffusing along the boundary. An example of the differences in behaviours, this time of a population of molecules, is provided in the pregnancy-test model of [32], where the species only diffuse in the bulk of the sample, but participate in reactions with the coating of the vessel where the test takes place. Another area in which reaction–diffusion systems are applied and in which boundary conditions enter in a crucial way is porous-medium transport [13, 38].

There have been proposed random walk models where arrival on the boundary results in the termination of the walk; see [6] for a review. In the present paper we take a “dual” view, in which staying in the interior of the domain leads ultimately to the demise of the walker, while arrival at the boundary provides viaticum to replenish the walker’s energy and allows the walk to continue. For example, an island in a lake may support animals that roam the interior but must return to shore to drink. Adjacent models include the “mortal random walks” of [7] and the “starving random walks” of [42], but in neither of these does the walker carry an internal energy state. Our model differs from models that incorporate resource depletion by feeding [8,9,10, 14, 23] in that, for us, energy replenishment only occurs on the boundary and the resource is inexhaustible. Comparison of our results to those for models including resource depletion, in which the domain in which the walk is in danger of extinction grows over time, is a topic we hope to address in future work.

Section 2 describes our mathematical set-up and our main results, starting, in Sect. 2.1 with an introduction of a class of Markov models of energy-constrained random walks with boundary replenishment.

2 Model and Main Results

2.1 Energy-Constrained Random Walk

For $N \in \mathbb {N}:= \{1,2,3,\ldots \}$, denote the finite discrete interval $I_N:= \{ x \in \mathbb {Z}: 0 \le x \le N \}$. Also define the semi-infinite interval by $I_\infty := {\mathbb {Z}}_+:= \{ x \in \mathbb {Z}: x \ge 0 \}$. We write ${\overline{\mathbb {N}}}:= \mathbb {N}\cup \{ \infty \}$ and then $I_N, N \in {\overline{\mathbb {N}}}$ includes both finite and infinite cases. The boundary $\partial I_N$ of $I_N$ is defined as $\partial I_N:= \{0,N\}$ for $N \in \mathbb {N}$, and $\partial I_\infty := \{0\}$ for $N = \infty$; the interior is $I^{{{{\circ }}}}_N:= I_N {\setminus } \partial I_N$. We suppose $N \ge 2$, so that $I^{{{{\circ }}}}_N$ is non-empty. Over ${\overline{\mathbb {N}}}$ we define simple arithmetic and function evaluations in the way consistent with taking limits over $\mathbb {N}$, e.g., $1/\infty := 0$, $\exp \{ -\infty \}:= 0$, and so on.

We define a class of discrete-time Markov chains $\zeta := (\zeta _0, \zeta _1, \ldots )$, where $\zeta _n:= (X_n,\eta _n) \in I_N \times {\mathbb {Z}}_+$, whose transition law is determined by an energy update (stochastic) matrix P over ${\mathbb {Z}}_+$, i.e., a function $P: {\mathbb {Z}}_+^2 \rightarrow [0,1]$ with $\sum _{j \in {\mathbb {Z}}_+} P(i,j) = 1$ for all $i \in {\mathbb {Z}}_+$. The coordinate $X_n$ represents the location of a random walker, and $\eta _n$ its current energy level. Informally, the dynamics of the process are as follows. As long as it has positive energy and is in the interior, the walker performs simple random walk steps; each step uses one unit of energy. If the walker runs out of energy while in the interior, the walk terminates. If the process is at the boundary $\partial I_N$ with current energy level i, P(i, j) is the probability that the energy changes to level j; the walk reflects into the interior.

Formally, the transition law is as follows.

• Energy-consuming random walk in the interior: If $i \in \mathbb {N}$ and $x \in I^{{{{\circ }}}}_N$, then

  $$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( X_{n+1} = X_n + e, \, \eta _{n+1} = \eta _n - 1 \mid X_n = x, \eta _n = i ) = \frac{1}{2}, e \in \{-1,+1\}.\end{aligned}$$

  (2.1)

• Extinction through exhaustion: If $x \in I^{{{{\circ }}}}_N$, then

  $$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( X_{n+1} = x, \, \eta _{n+1} = 0 \mid X_n = x, \eta _n = 0 ) = 1.\end{aligned}$$

  (2.2)

• Boundary reflection and energy transition: If $i \in {\mathbb {Z}}_+$, $x \in \partial I_N$, and $y \in I^{{{{\circ }}}}_N$ is the unique y such that $|y-x| = 1$, then

  $$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( X_{n+1} = y, \, \eta _{n+1} = j \mid X_n = x, \eta _n =i ) = P ( i, j). \end{aligned}$$

  (2.3)

In the present paper, we focus on a model with finite energy capacity and maximal energy replenishment at the boundary. This corresponds to a specific choice of P, namely $P(i, M)=1$, as described in the next section. Other choices of the update matrix P are left for future work.

2.2 Finite Energy Capacity

Our finite-capacity model has a parameter $M \in \mathbb {N}$, representing the maximum energy capacity of the walker. The boundary energy update rule that we take is that energy is always replenished up to the maximal level M. Here is the definition.

Definition 2.1

For $N \in {\overline{\mathbb {N}}}, M \in \mathbb {N}$, and $z \in I_N \times I_M$, the finite-capacity (N, M, z)-model is the Markov chain $\zeta$ with initial state $\zeta _0 = z$ and with transition law defined through (2.1)–(2.3) with energy update matrix P given by $P(i,M) =1$ for all $i \in {\mathbb {Z}}_+$.

For the (N, M, z) model from Definition 2.1, with $z = (x,y) \in I_N \times I_M$, we write ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z$ and ${{{\,\mathrm{\mathbb {E}}\,}}}^{N,M}_z$ for probability and expectation under the law of the corresponding Markov chain $\zeta$ with spatial domain $I_N$, energy capacity M, initial location $X_0=x \in I_N$, and initial energy $\eta _0=y \in I_M$. The main quantity of interest for us here is the total lifetime (i.e., time before extinction) of the process, defined by

$$\begin{aligned} \lambda := \min \{ n \in {\mathbb {Z}}_+: X_n \in I^{{{{\circ }}}}_N, \, \eta _n = 0 \}, \end{aligned}$$

(2.4)

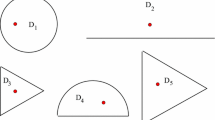
where we adopt the usual convention that $\min \emptyset :=+\infty$. The process $\zeta \in I_N \times I_M$ can be viewed as a two-dimensional random walk with a reflecting/absorbing boundary, in which the interior drift (negative in the energy component) competes against the (positive in energy) boundary reflection: see Fig. 1 for a schematic.

Fig. 1

Schematic of the transitions for the reflecting random walk $\zeta _n = (X_n, \eta _n)$ in the rectangle $I_N \times I_M$. The arrows indicate some possible transitions: in the interior, energy decreases and the particle executes a nearest-neighbour random walk, while the boundary states provide energy replenishment. The larger (red-filled) circles indicate the absorbing states (zero energy, but not at the boundary)

If for initial state $z = (x,y) \in I_N \times I_M$ it holds that $N > M+x$ (including $N = \infty$), then the energy constraint and the fact that $X_0 =x$ ensures that $X_n$ can never exceed $M+x$, so $X_n$ is constrained to the finite interval $I_{M+1+x}$. In other words, every (N, M, z) model with $N > M+x$ is equivalent to the $(\infty ,M,z)$ model, for any $y \in I_M$. Since we start with $\eta _0 = y$ and energy decreases by at most one unit per unit time, ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \lambda \ge y ) = 1$. The following ‘irreducibility’ result, proved in Sect. 4.1, shows that extinction is certain, i.e., ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z(\lambda < \infty ) =1$, provided there are at least two sites in $I^{{{{\circ }}}}_N$.

Lemma 2.2

Suppose that $N \in {\overline{\mathbb {N}}}$ with $N \ge 3$, that $M \in \mathbb {N}$, and that $\zeta _0 = z = (x,y)$. Under ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z$, the process $\zeta$ is a time-homogeneous Markov chain on the finite state space $\Lambda _{N,M}:= I_{N \wedge (M+x)} \times I_M$. Moreover, there exists $\delta >0$ (depending only on M) such that $\sup _{z \in I_N \times I_M} {{{\,\mathrm{\mathbb {E}}\,}}}^{N,M}_z[ \textrm{e}^{\delta \lambda } ] < \infty$.

Our main results concern distributional asymptotics for the random variable $\lambda$ as $N, M \rightarrow \infty$. We will demonstrate a phase transition depending on the relative growth of M and N. Roughly speaking, since in time M a simple random walk typically travels distance of order $\sqrt{M}$, it turns out that if $M \gg N^2$ the random walk will visit the boundary many times, and $\lambda$ grows exponentially in $M/N^2$, while if $M \ll N^2$ then there are relatively few (in fact, of order $\sqrt{M}$) visits to the boundary before extinction, and $\lambda$ is of order M. The case $M \ll N^2$, where the capacity constraint dominates, we call the meagre-capacity limit, and we treat this case first; in the limit law appears the relatively unusual Darling–Mandelbrot distribution (see Sect. 2.3). The case $M \gg N^2$, where energy is plentiful, we call the confined-space limit, and (see Sect. 2.4) the limit law is exponential, as might be expected due to the small rate of extinction in that case. The critical case, where $M /N^2 \rightarrow \rho \in (0,\infty )$ is dealt with in Sect. 2.5. Section 2.6 gives an outline, at the level of heuristics, of the proofs.

2.3 The Meagre-Capacity Limit

Our first result looks at the case where N, M are both large but $M \in \mathbb {N}$ is small (in a sense we quantify) with respect to $N \in {\overline{\mathbb {N}}}$. This will include all the $(\infty ,M,z)$ models, which, as remarked above, coincide with the (N, M, z) models for $N > M+x$. However, it turns out that the $(\infty ,M,z)$ behaviour is also asymptotically replicated in (N, M, z) models for $N \gg \sqrt{M}$. The formal statement is Theorem 2.3 below.

To describe the limit distribution in the theorem, we define, for $t \in \mathbb {R}$,

$$\begin{aligned} \mathcal {I}(t):= t \int _0^1 u^{-1/2} \textrm{e}^{u t} \textrm{d}u, \text { and } t_0:= \inf \{ t \in \mathbb {R}: \textrm{e}^t - \mathcal {I}(t) \le 0 \}. \end{aligned}$$

(2.5)

Then $t_0 \approx 0.8540326566$ (see Lemma A.1 below), and

$$\begin{aligned} \varphi _{\textrm{DM}}(t):= \frac{1}{\textrm{e}^{t} - \mathcal {I}(t)}, \text { for } t < t_0, \end{aligned}$$

(2.6)

defines the moment generating function of a distribution on ${\mathbb {R}}_+$ known as the Darling–Mandelbrot distribution with parameter 1/2. We write $\xi \sim \textrm{DM}(1/2)$ to mean that $\xi$ is an ${\mathbb {R}}_+$-valued random variable with ${{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{t \xi } ] = \varphi _{\textrm{DM}}(t)$, $t < t_0$. We refer to Sect. 2.6 for an heuristic explanation behind the appearance in our Theorem 2.3 below of the $\textrm{DM}(1/2)$ distribution, based on its role in the theory of heavy-tailed random sums. We also refer to Lemma A.3 for the moments of $\textrm{DM}(1/2)$, the first of which is ${{\,\mathrm{\mathbb {E}}\,}}\xi = 1$.

The result in this section is stated for a sequence of $(N_M,M,z_M)$ models, indexed by $M \in \mathbb {N}$, with $z_M = (x_M,y_M) \in I_{N_M} \times I_M$ and $N_M \in {\overline{\mathbb {N}}}$ satisfying the meagre-capacity assumption that, for some $a \in [0,\infty ]$ and $u \in (0,1]$,

$$\begin{aligned} \lim _{M \rightarrow \infty } \frac{ x^2_M \wedge (N_M - x_M)^2 }{M} = a, ~~\lim _{M \rightarrow \infty } \frac{y_M}{M} = u, ~\text { and } \lim _{M \rightarrow \infty } \frac{M}{N^2_M} = 0. \end{aligned}$$

(2.7)

Included in (2.7) is any sequence $N_M$ for which $N_M = \infty$ eventually.

For $b = (b_t, t\in {\mathbb {R}}_+)$ a standard Brownian motion on $\mathbb {R}$ started from $b_0=0$, define $\tau ^{{\tiny BM }}_1:= \inf \{ t \in {\mathbb {R}}_+: b_t = 1\}$. Then (see Remarks 2.4(d) below) $\tau ^{{\tiny BM }}_1$ has a positive (1/2)-stable (Lévy) distribution:

$$\begin{aligned} \tau ^{{\tiny BM }}_1\sim \textrm{S}_+(1/2), \text { i.e., } \tau ^{{\tiny BM }}_1\,\text {has density} f(t) = (2\pi t^3)^{-1/2} \textrm{e}^{-1/(2t)}, t>0. \end{aligned}$$

(2.8)

Write $\Phi (s):= {{\,\mathrm{\mathbb {P}}\,}}( b_1 \le s)$ and ${\overline{\Phi }}(s):= 1 - \Phi (s) = {{\,\mathrm{\mathbb {P}}\,}}( b_1 > s)$, $s \in \mathbb {R}$, for the standard normal distribution and tail functions. Define

$$\begin{aligned} g (a,u):= u + (4-2u-2a ) {\overline{\Phi }}( \sqrt{a/u} ) + \sqrt{\frac{2a u}{\pi } } \textrm{e}^{-a/(2u)}. \end{aligned}$$

(2.9)

Here is the limit theorem in the meagre-capacity case. The case $N_M=\infty$, $a=0$ of (2.10) can be read off from results of [6] (see Sect. 2.6); the other cases, we believe, are new. We use ‘$\overset{\textrm{d}}{\longrightarrow }$’ to denote convergence in distribution under the implicit probability measure (in the following theorem, namely ${{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{z_M}$).

Theorem 2.3

Consider the $(N_M,M,z_M)$ model with $M \in \mathbb {N}$, $N_M \in {\overline{\mathbb {N}}}$ and $z_M \in I_{N_M} \times I_M$ such that (2.7) holds. Then, if $\xi \sim \textrm{DM}(1/2)$ and $\tau ^{{\tiny BM }}_1\sim \textrm{S}_+(1/2)$ are independent with distributions given by (2.6) and (2.8) respectively, it holds that

$$\begin{aligned}&\frac{\lambda }{M} \overset{\textrm{d}}{\longrightarrow }\min ( u, a \tau ^{{\tiny BM }}_1) + (1+ \xi ) {\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1< u\}}, \text { as } M \rightarrow \infty ; \text { and} \end{aligned}$$

(2.10)

$$\begin{aligned}&\lim _{M \rightarrow \infty } \frac{{{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}\lambda }{M} = g (a,u) , \end{aligned}$$

(2.11)

where g is defined at (2.9). In particular, if $a=0$, then the limits in (2.10) and (2.11) are equal to $1+\xi$ and $2 = 1 + {{\,\mathrm{\mathbb {E}}\,}}\xi$, respectively, while for $a=\infty$ they are both u.

Remarks 2.4

• (a) For every $0 < u \le 1$, the function $a \mapsto g(a,u)$ on the right-hand side of (2.9) is strictly decreasing: see Lemma 4.4 below.

• (b) If $a >0$, then the distribution of the limit in (2.10) has an atom at value u of mass ${{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1\ge u ) = 2 \Phi ( \sqrt{a /u} ) -1$, as given by (2.12) below; on the other hand, if $a=0$, it has a density (since $\xi$ does, as explained in the next remark). The atom at u represents the possibility that the random walk runs out of energy before ever reaching the boundary.

• (c) The $\textrm{DM}(1/2)$ distribution specified by (2.6) appears in a classical result of Darling [17] on maxima and sums of positive $\alpha$-stable random variables in the case $\alpha =1/2$, and more recently in the analysis of anticipated rejection algorithms [6, 29, 31], where it has become known as the Darling–Mandelbrot distribution with parameter 1/2. Darling [17, p. 103] works with the characteristic function (Fourier transform); Feller [20, p. 465] gives the $t<0$ Laplace transform (2.6). The $\textrm{DM}(1/2)$ distribution has a probability density which is continuous on $(0,\infty )$, is non-analytic at integer points, and has no elementary closed form, but has an infinite series representation, can be efficiently approximated, and its asymptotic properties are known: see [6, 29, 30].

• (d) To justify (2.8), recall that, by the reflection principle, for $t \in (0,\infty )$,

  $$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( \tau ^{{\tiny BM }}_1> t ) = {{\,\mathrm{\mathbb {P}}\,}}\biggl ( \sup _{0 \le s \le t} b_s< 1 \biggr )= 2 {{\,\mathrm{\mathbb {P}}\,}}( b_t < 1 ) -1 = 2 \Phi ( t^{-1/2} ) -1; \end{aligned}$$

  (2.12)

  this gives (2.8), cf. [20, pp. 173–175].

2.4 The Confined-Space Limit

We now turn to the second limiting regime. The result in this section is stated for a sequence of $(N_M,M,z_M)$ models, indexed by $M \in \mathbb {N}$, with $z_M = (x_M, y_M) \in I_{N_M} \times I_M$ and $N_M \in \mathbb {N}$ (note $N_M < \infty$ now) satisfying the confined-space assumption

$$\begin{aligned} \lim _{M \rightarrow \infty } N_M = \infty , ~~ \lim _{M \rightarrow \infty } \frac{M}{N^2_M} = \infty , \text { and } \liminf _{M \rightarrow \infty } \frac{y_M}{M} >0. \end{aligned}$$

(2.13)

Let ${\mathcal {E}_1}$ denote a unit-mean exponential random variable. Here is the limit theorem in this case; in contrast to Theorem 2.3, the initial location $x_M$ is unimportant for the limit in (2.14), and the initial energy $y_M$ only enters through the lower bound in (2.13).

Theorem 2.5

Consider the $(N_M,M,z_M)$ model with $M \in \mathbb {N}$, $N_M \in \mathbb {N}$ and $z_M \in I_{N_M} \times I_M$ such that (2.13) holds. Then, as $M \rightarrow \infty$,

$$\begin{aligned} \frac{4 \lambda }{N_M^2} \cos ^M ( \pi / N_M)&\overset{\textrm{d}}{\longrightarrow }{\mathcal {E}_1}. \end{aligned}$$

(2.14)

Remarks 2.6

• (a) The appearance of the exponential distribution in the limit (2.14) is a consequence of the fact that it is a rare event for the random walk to spend time $\gg N^2$ in the interior of the interval $I_N$, and can be viewed as a manifestation of the Poisson clumping heuristic for Markov chain hitting times [1, §B] or metastability of the system that arises from the fact extinction is certain but unlikely on any individual excursion.

• (b) Since $\log \cos \theta = - (\theta ^2/2) + O (\theta ^4)$ as $\theta \rightarrow 0$, we can re-write (2.14), in the case where M does not grow too fast compared to $N_M^2$, as

  $$\begin{aligned} \frac{4\lambda }{N_M^2} \exp \left\{ - \frac{\pi ^2 M}{2N_M^2} \right\} \overset{\textrm{d}}{\longrightarrow }{\mathcal {E}_1}, \text { if } \lim _{M \rightarrow \infty } \frac{M}{N_M^4} = 0.\end{aligned}$$

2.5 The Critical Case

Finally, we treat the critical case in which there exists $\rho \in (0,\infty )$ such that

$$\begin{aligned} \lim _{M \rightarrow \infty } N_M = \infty , \text { and } \lim _{M \rightarrow \infty } \frac{M}{N^2_M} = \rho . \end{aligned}$$

(2.15)

Define the decreasing function $H: (0,\infty ) \rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} H (y):= \sum _{k=1}^\infty h_k(y), \text { where } h_k (y):= \exp \left\{ - \frac{\pi ^2 (2k-1)^2 y}{2} \right\} .\end{aligned}$$

(2.16)

Since $H(y) \sim 1/\sqrt{8\pi y}$ as $y \downarrow 0$ (see Lemma 4.8 below), for every $\rho >0$ and $s \in \mathbb {R}$,

$$\begin{aligned} G(\rho , s):= \frac{s}{H(\rho )} \int _0^1 \textrm{e}^{s v} \bigl ( H (v \rho ) - H(\rho ) \bigr ) \textrm{d}v, \end{aligned}$$

(2.17)

is finite. For fixed $\rho >0$, $s \mapsto G(\rho ,s)$ is strictly increasing for $s \in \mathbb {R}$, and $G (\rho , 0 ) = 0$. For $\rho >0$, define $s_\rho := \sup \{ s > 0: G(\rho , s) < 1 \}$, and then set

$$\begin{aligned} \phi _\rho (s):= \frac{1}{1-G(\rho , s)}, \text { for } s < s_\rho .\end{aligned}$$

(2.18)

Finally, define $\mu : (0, \infty ) \rightarrow {\mathbb {R}}_+$ by

$$\begin{aligned} \mu (\rho ):= \frac{1}{\rho H(\rho )} \int _0^\rho H(y) \textrm{d}y -1. \end{aligned}$$

(2.19)

Here is our result in the critical case. For simplicity of presentation, we restrict to the case where $\zeta _0 = (1,M)$; one could permit initial conditions similar to those in (2.7), but this would complicate the statement and lengthen the proofs (see Remarks 2.8(d) below).

Theorem 2.7

Consider the $(N_M,M,z_M)$ model with $M \in \mathbb {N}$, $N_M \in \mathbb {N}$ and $z_M = (1,M)$ such that (2.15) holds. Then, as $M \rightarrow \infty$,

$$\begin{aligned} \frac{\lambda }{M}&\overset{\textrm{d}}{\longrightarrow }1 + \xi _\rho , \text { and } \frac{{{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\lambda }{M} \rightarrow 1 + \mu (\rho ), \end{aligned}$$

(2.20)

where $\xi _\rho$ has moment generating function ${{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{s \xi _\rho } ] = \phi _\rho (s)$, $s < s_\rho$, and expectation ${{\,\mathrm{\mathbb {E}}\,}}\xi _\rho = \mu (\rho )$. Moreover,

$$\begin{aligned} \lim _{\rho \downarrow 0} \mu (\rho ) = 1, \text { and } \mu (\rho ) = \frac{\textrm{e}^{\pi ^2 \rho /2}}{4 \rho } (1+o(1)), \text { as } \rho \rightarrow \infty .\end{aligned}$$

(2.21)

Remarks 2.8

• (a) The function H defined at (2.16) is in the family of theta functions, which arise throughout the distributional theory of one-dimensional Brownian motion on an interval, which is the origin of the appearance here: see e.g. [20, pp. 340–343] or Appendix 1 of [12], and Sect. 3.3 below.

• (b) The $\rho \rightarrow \infty$ asymptotics in (2.21) are consistent with Remark 2.6(b), in the sense that both are consistent with, loosely speaking, the claim that

  $$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\lambda \sim \frac{N_M^2}{4} \exp \left\{ - \frac{\pi ^2 M}{2N_M^2} \right\} , \text { when } N_M^2 \ll M \ll N_M^4, \end{aligned}$$

  although neither of those results formally establishes this.

• (c) An integration by parts shows that G defined at (2.17) has the representation

  $$\begin{aligned} G(\rho , s)= & {} \int _0^\infty ( \textrm{e}^{sx} -1) \frac{m_\rho (x)}{x} \textrm{d}x, \text { where }\\{} & {} \quad m_\rho (x)\\ m_{\rho }(x):= & {} \frac{\pi ^2 \rho x}{2 H(\rho )} \mathbbm {1}_{[0,1]} (x) \sum _{k=1}^\infty (2k-1)^2 h_k (\rho x), \end{aligned}$$

  which shows that $\phi _\rho$ corresponds to an infinitely divisible distribution (see e.g. [36, p. 91]); since $m_\rho$ is compactly supported, however, the distribution is not compound exponential [36, p. 100].

• (d) It is possible to extend Theorem 2.7 to initial states $z_M = (x_M, y_M)$ satisfying $y_M/M \rightarrow u \in (0,1]$ and $x_M^2/M \rightarrow a \in [0,\infty ]$, and the limit statement (2.20) would need to be modified to include additional terms similar to in Theorem 2.3, but with $\tau ^{{\tiny BM }}_1$ replaced by a two-sided exit time. We do not pursue this extension here.

2.6 Organization and Heuristics Behind the Proofs

The rest of the paper presents proofs of Theorems 2.3, 2.5, and 2.7. The basic ingredients are provided by some results on excursions of simple symmetric random walk on $\mathbb {Z}$, given in Sect. 3; some of this material is classical, but the core estimates that we need are, in parts, quite intricate and we were unable to find them in the literature. The main body of the proofs is presented in Sect. 4. First, we establish a renewal framework that provides the structure for the proofs, which, together with a generating-function analysis involving the excursion estimates from Sect. 3, yields the results. In Sect. 5 we comment on some possible future directions. Appendix A briefly presents some necessary facts about the Darling–Mandelbrot distribution appearing in Theorem 2.3. Here we outline the main ideas behind the proofs, and make some links to the literature.

It is helpful to first imagine a walker that is “immortal”, i.e., has an unlimited supply of energy. The energy-constrained walker is indistinguishable from the immortal walker until the first moment that the time since its most recent visit to the boundary exceeds $M+1$, at which point the energy-constrained walker becomes extinct. Let $s_1< s_2 < \cdots$ denote the successive times of visits to $\partial I_N$ by the immortal walker, and let $u_k = s_k - s_{k-1}$ denote the duration of the kth excursion ($k \in \mathbb {N}$, with $s_0:=0$). The energy-constrained walker starts $\kappa \in \mathbb {N}$ excursions before becoming extinct, where $\kappa = \inf \{ k \in \mathbb {N}: u_k > M+1\}$. At every boundary visit at which the energy-constrained walk is still active, there is a probability $\theta (N, M) = {{\,\mathrm{{\textbf{P}}}\,}}_1 ( \tau _{0,N} > M+1 )$ that the walk will run out of energy on the next excursion, where $\tau _{0,N}$ is the hitting time of $\partial I_N$ by the random walk, and ${{\,\mathrm{{\textbf{P}}}\,}}_1$ indicates we start from site 1 (equivalently, site $N-1$). Each time the walker visits $\partial I_N$ there is a “renewal”, because energy is topped up to level M and the next excursion begins, started from one step away from the boundary. If the walk starts at time 0 in a state other than at full energy, next to the boundary, then the very first excursion has a different distribution from the rest, and this plays a role in some of our results, but is a second-order consideration for the present heuristics. The key consequence of the renewal structure is that the excursions have a (conditional) independence property, and the number $\kappa$ of excursions has a geometric distribution with parameter given by the extinction probability $\theta (N,M)$ (see Lemma 4.1 below for a formal statement).

Suppose first that $N = \infty$, the simplest case of the meagre-capacity limit. We indicate the relevance of Darling’s result on the maxima of stable variables [17, Theorem 5.1] to this model, which gives some intuition for the appearance of the $\textrm{DM}(1/2)$ distribution in Theorem 2.3. First we describe Darling’s result. Suppose that $Z_1, Z_2, \ldots$ are i.i.d. ${\mathbb {R}}_+$-valued random variables in the domain of attraction of a (positive) stable law with index $\alpha \in (0,1)$, and let $S_n:= \sum _{i=1}^n Z_i$ and $T_n:= \max _{1 \le i \le n} Z_i$. Darling’s theorem says that $S_n / T_n$ converges in distribution to $1 +\xi _\alpha$, as $n \rightarrow \infty$, where $\xi _\alpha \sim \textrm{DM} (\alpha )$. A generalization to other order statistics is [3, Corollary 4].

In the case where $N = \infty$, the durations $u_1, u_2, \ldots$ of excursions of simple symmetric random walk on ${\mathbb {Z}}_+$ away from 0 satisfy the $\alpha =1/2$ case of Darling’s result, so that $T_n:= \sum _{i=1}^n u_i$ and $M_n:= \max _{1 \le i \le n} u_i$ satisfy $T_n / M_n \overset{\textrm{d}}{\longrightarrow }1 + \xi$ where $\xi \sim \textrm{DM}(1/2)$. Replacing n by $\kappa$, the number of excursions up to extinction, for which $\kappa \rightarrow \infty$ in probability as $M, N \rightarrow \infty$, it is plausible that $T_\kappa / M_\kappa \overset{\textrm{d}}{\longrightarrow }1 + \xi$ also. But $T_\kappa$ is essentially $\lambda$, while $M_\kappa$ will be very close to M, the upper bound on $u_i$, $i < \kappa$. This heuristic argument is not far from a proof of the case $N = \infty$ of Theorem 2.3. More precisely, one can express $\lambda$ in terms of the threshold sum process [6], and then the $N=\infty$, $a=0$ case of Theorem 2.3 is a consequence of Theorem 1 of [6]. Another way to access intuition behind the M-scale result for $\lambda$ is that in this case $\theta (N, M)$ is of order $M^{-1/2}$ (see Proposition 4.2 below), so there are of order $M^{1/2}$ completed excursions before extinction, while the expected duration of an excursion of length less than M is of order $M^{1/2}$ (due to the 1/2-stable tail). Our proof below (Sect. 4.2) covers the full regime $M \ll N^2$. That this is the relevant scale is due to the fact that simple random walk travels distance about $\sqrt{M}$ in time M, so if $N^2 \gg M$ it is rare for the random walk to encounter the opposite end of the boundary from which it started.

Consider now the confined-space regime, where $M \gg N^2$. Now it is very likely that the random walk will traverse the whole of $I_N$ many times before it runs out of energy, and so there will be many excursions before extinction. Indeed, the key quantitative result in this case, Proposition 4.5 below, shows that $\theta (N, M) \sim (4/N) \cos ^M (\pi /N)$, which is small. Each excursion has mean duration about N (${{\,\mathrm{{\textbf{E}}}\,}}_1 \tau _{0,N} = N-1$; see Lemma 3.3). Roughly speaking, the law of large numbers ensures that $\lambda \approx \kappa N$, and then

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( \lambda \ge n ) \approx {{\,\mathrm{\mathbb {P}}\,}}( \kappa \ge n/N ) \approx (1 -\theta (N,M) )^{n/N} \approx \exp \left\{ - \frac{4n}{N^2} \cos ^M \left( \frac{\pi }{N} \right) \right\} ,\end{aligned}$$

which is essentially the exponential convergence result in Theorem 2.5.

The case that is most delicate is the critical case where $M \sim \rho N^2$. The extinction probability estimate, given in Proposition 4.7 below, is now $\theta (N, M) \sim (4/N) H(\rho )$, where H is given by (2.16); the delicate nature is because, on the critical scale, the two-boundary nature of the problem has an impact (unlike the meagre-capacity regime), while extinction is sufficiently likely that the largest individual excursion fluctuations are on the same scale as the total lifetime (unlike the confined-space regime). Since $\theta (N, M)$ is of order 1/N, both the number of excursions before extinction, and the duration of a typical excursion, are of order N (i.e., $M^{1/2}$), similarly to the meagre-capacity case, and so again there is an M-scale limit for $\lambda$, but the (universal) Darling–Mandelbrot distribution is replaced by the curious distribution exhibited in Theorem 2.7, which we have not seen elsewhere.

3 Excursions of Simple Random Walks

3.1 Notation and Preliminaries

For $x \in \mathbb {Z}$, let ${{\,\mathrm{{\textbf{P}}}\,}}_x$ denote the law of a simple symmetric random walk on $\mathbb {Z}$ with initial state x. We denote by $S_0, S_1, S_2, \ldots$ the trajectory of the random walk with law ${{\,\mathrm{{\textbf{P}}}\,}}_x$, realised on a suitable probability space, so that ${{\,\mathrm{{\textbf{P}}}\,}}_x (S_0 = x) =1$ and ${{\,\mathrm{{\textbf{P}}}\,}}_x ( S_{n+1} - S_n = + 1 \mid S_0, \ldots , S_n ) = {{\,\mathrm{{\textbf{P}}}\,}}_x ( S_{n+1} - S_n = - 1 \mid S_0, \ldots , S_n) = 1/2$ for all $n \in {\mathbb {Z}}_+$. Let ${{\,\mathrm{{\textbf{E}}}\,}}_x$ denote the expectation corresponding to ${{\,\mathrm{{\textbf{P}}}\,}}_x$. We sometimes write simply ${{\,\mathrm{{\textbf{P}}}\,}}$ and ${{\,\mathrm{{\textbf{E}}}\,}}$ in the case where the initial state plays no role.

For $y \in \mathbb {Z}$, let $\tau _y:= \inf \{ n \in {\mathbb {Z}}_+: S_n = y \}$, the hitting time of y. As usual, we set $\inf \emptyset := +\infty$; the recurrence of the random walk says that ${{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _y < \infty ) = 1$ for all $x, y \in \mathbb {Z}$. Also define $\tau _{0,\infty }:= \tau _0$ and, for $N \in \mathbb {N}$, $\tau _{0,N}:= \tau _0 \wedge \tau _N = \inf \{ n \in {\mathbb {Z}}_+: S_n \in \{0,N\}\}$.

The number of $(2n+1)$-step simple random walk paths that start at 1 and visit 0 for the first time at time $2n+1$ is the same as the number of $(2n+1)$-step paths that start at 0, finish at 1, and never return to 0, which, by the classical ballot theorem [19, p. 73], is $\frac{1}{2n+1} \left( {\begin{array}{c}2n+1\\ n+1\end{array}}\right) = \frac{1}{n+1} \left( {\begin{array}{c}2n\\ n\end{array}}\right)$. Hence, by Stirling’s formula (cf. [19, p. 90]),

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _0 = 2n + 1) = \frac{2^{-1-2n}}{n+1} \left( {\begin{array}{c}2n\\ n\end{array}}\right) \sim \frac{1}{2 \sqrt{ \pi }} n^{-3/2}, \text { as } n \rightarrow \infty .\end{aligned}$$

(3.1)

Similarly, since ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _0 \ge 2n+1 ) = {{\,\mathrm{{\textbf{P}}}\,}}_1( S_1>0, \ldots , S_{2n-1}> 0 ) = 2{{\,\mathrm{{\textbf{P}}}\,}}_0 ( S_1> 0, \ldots , S_{2n} > 0)$ (cf. [19, pp. 75–77]) we have that

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _0 \ge 2n + 1) = 2^{-2n} \left( {\begin{array}{c}2n\\ n\end{array}}\right) \sim \frac{1}{\sqrt{\pi n}}, \text { as } n \rightarrow \infty .\end{aligned}$$

(3.2)

The distribution of $\tau _{0,N}$ is more complicated; there’s an exact formula (see e.g. [19, p. 369]) that will be needed when we look at larger time-scales (see Theorem 3.4 below), but for shorter time-scales, it will suffice to approximate the two-sided exit time $\tau _{0,N}$ in terms of the (simpler) one-sided exit time $\tau _0$. This is the subject of the next subsection.

3.2 Short-Time Approximation by One-Sided Exit Times

The next lemma studies the duration of excursions that are constrained to be short.

Lemma 3.1

• (i) For all $N \in {\overline{\mathbb {N}}}$, all $x \in I_N$, and all $n \in {\mathbb {Z}}_+$,

  $$\begin{aligned} \left| {{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _{0,N}> n ) - {{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _{0} > n ) \right| \le \frac{x}{N}.\end{aligned}$$

  (3.3)

• (ii) Let $\varepsilon >0$. Then there exists $n_\varepsilon \in \mathbb {N}$, depending only on $\varepsilon$, such that, for all $N \in {\overline{\mathbb {N}}}$,

  $$\begin{aligned} \left| {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n ) - n^{-1/2} \sqrt{ {2} / {\pi }} \right| \le \varepsilon n^{-1/2} + \frac{1}{N}, \text { for all } n \ge n_\varepsilon .\end{aligned}$$

  (3.4)

• (iii) Fix $\varepsilon >0$. Then there exist $n_\varepsilon \in \mathbb {N}$ and $\delta _\varepsilon \in (0,\infty )$ such that

  $$\begin{aligned} \sup _{n_\varepsilon \le n < \delta _\varepsilon N^2 } \left| n^{1/2} {{\,\mathrm{{\textbf{P}}}\,}}_1 ( \tau _{0,N} > n ) - \sqrt{ {2} / {\pi }} \right| \le \varepsilon , \text { for all } N \in {\overline{\mathbb {N}}}. \end{aligned}$$

  (3.5)

Proof

Suppose that $N \in \mathbb {N}$ and $x \in I_N$. Since $\tau _0 \ne \tau _{0,N}$ if and only if $\tau _N < \tau _0$,

$$\begin{aligned} \sup _{n \in {\mathbb {Z}}_+} \left| {{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _{0,N}> n ) - {{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _0 > n ) \right| \le {{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _N < \tau _0 ) = \frac{x}{N}, \text { for all } x \in I_N,\end{aligned}$$

by the classical gambler’s ruin result for symmetric random walk; if $N = \infty$ then ${{\,\mathrm{{\textbf{P}}}\,}}_x ( \tau _{0,N}> n) = {{\,\mathrm{{\textbf{P}}}\,}}_x (\tau _0 > n)$ by definition. This verifies (3.3). Then (3.4) follows from the $x=1$ case of (3.3) together with (3.2). Finally, for a given $\varepsilon >0$, the bound (3.4) implies that there exists $n_\varepsilon \in \mathbb {N}$ such that, for all $n_\varepsilon \le n \le \delta N^2$,

$$\begin{aligned} \left| {{\,\mathrm{{\textbf{P}}}\,}}_1 ( \tau _{0,N} > n ) - n^{-1/2} \sqrt{{2}/{\pi }} \right| \le ( \varepsilon + \delta ^{1/2} ) n^{-1/2} \le 2 \varepsilon n^{1/2}, \end{aligned}$$

if $\delta = \varepsilon ^2$, say. This yields (3.5) (suitably adjusting $\varepsilon$). $\square$

Lemma 3.2 gives a limit result for the duration of a simple random walk excursion started with initial condition $x_M$ of order $\sqrt{M}$; we will apply this to study the initial excursion of the energy-constrained walker. Recall that $b = (b_t, t\in {\mathbb {R}}_+)$ denotes standard Brownian motion started at $b_0 =0$, and $\tau ^{{\tiny BM }}_1$ its first time of hitting level 1.

Lemma 3.2

Let $a \in [0,\infty ]$. Suppose that $M, N_M \in \mathbb {N}$ and $x_M \in I_{N_M}$ are such that $x^2_M / M \rightarrow a$ and $x_M / N_M \rightarrow 0$ as $M \rightarrow \infty$. Then for every $y \in {\mathbb {R}}_+$,

$$\begin{aligned} \frac{\tau _{0,N_M}}{M} {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N_M} \le y M \}} \overset{\textrm{d}}{\longrightarrow }a \tau ^{{\tiny BM }}_1{\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1\le y \}},\end{aligned}$$

(3.6)

where the right-hand side of (3.6) is to be interpreted as 0 whenever $a \in \{0,\infty \}$. In particular, for every $\beta \in {\mathbb {R}}_+$ and all $y \in {\mathbb {R}}_+$,

$$\begin{aligned} \lim _{M \rightarrow \infty } M^{-\beta } {{\,\mathrm{{\textbf{E}}}\,}}_{x_M} [ \tau ^\beta _{0,N_M} {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N_M} \le y M \}} ] = a^\beta {{\,\mathrm{\mathbb {E}}\,}}[ (\tau ^{{\tiny BM }}_1)^\beta {\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1\le y \}} ]. \end{aligned}$$

(3.7)

Proof

Suppose that $0 \le a < \infty$. Let $\mathcal {C}$ denote the space of continuous functions $f: {\mathbb {R}}_+\rightarrow \mathbb {R}$, endowed with the uniform metric $\Vert f - g \Vert _\infty := \sup _{t \in {\mathbb {R}}_+} | f(t) - g(t) |$. Define the re-scaled and interpolated random walk trajectory $z_M \in \mathcal {C}$ by

$$\begin{aligned} z_M (t) = M^{-1/2} \left( S_{\lfloor M t \rfloor } - S_0 + (Mt - \lfloor M t \rfloor ) ( S_{\lfloor M t \rfloor +1} - S_{\lfloor M t \rfloor } ) \right) , \text { for } t \in {\mathbb {R}}_+. \end{aligned}$$

Then $S_0 / M^{1/2} \rightarrow \sqrt{a}$, and, by Donsker’s theorem (see e.g. Theorem 8.1.4 of [18]), $z_M$ converges weakly in $\mathcal {C}$ to $(b_t)_{t \in {\mathbb {R}}_+}$, where b is standard Brownian motion started from 0. For $f \in \mathcal {C}$, let $T_a (f):= \inf \{ t \in {\mathbb {R}}_+: f(t) \le -\sqrt{a} \}$. By Brownian scaling, $T_a (b)$ has the same distribution as $a \tau ^{{\tiny BM }}_1$. With probability 1, $T_a(b)< \infty$ and b has no intervals of constancy. Hence (cf. [18, p. 395]) the set $\mathcal {C}':= \{ f \in \mathcal {C}: T_a \text { is finite and continuous at } f \}$ has ${{\,\mathrm{\mathbb {P}}\,}}( b \in \mathcal {C}' ) = 1$ and hence, by the continuous mapping theorem, $T_a ( z_M) \rightarrow T_a (b)$ in distribution. If $a = \infty$ this says $T_\infty (z_M) \rightarrow \infty$ in probability, and if $a=0$ it says $T_0 (z_M) \rightarrow 0$ in probability; otherwise, ${{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1> y )$ is continuous for all $y \in {\mathbb {R}}_+$ and $\tau _0 / M = T_a ( z_M + M^{-1/2} S_0 - \sqrt{a} )$ has the same limit as $T_a (z_M)$. Hence we conclude that

$$\begin{aligned} \lim _{M \rightarrow \infty } {{\,\mathrm{{\textbf{P}}}\,}}_{x_M} ( \tau _0> y M) = {{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1> y ), \text { for all } y \in {\mathbb {R}}_+,\end{aligned}$$

(3.8)

where the right-hand side is equal to 0 if $a=0$ and 1 if $a=\infty$. It follows from (3.3) that (3.8) also holds for $\tau _{0,N_M}$ in place of $\tau _0$, provided that $x_M / N_M \rightarrow 0$. Hence, under the conditions of the lemma, we have

$$\begin{aligned} \frac{\tau _{0,N_M}}{M} \overset{\textrm{d}}{\longrightarrow }a \tau ^{{\tiny BM }}_1, \text { as } M \rightarrow \infty .\end{aligned}$$

(3.9)

If random variables $X, X_n$ satisfy $X_n \overset{\textrm{d}}{\longrightarrow }X$, then, for every $y \in {\mathbb {R}}_+$, $X_n {\mathbbm {1}\hspace{-0.83328pt}}{\{ X_n \le y \}} \overset{\textrm{d}}{\longrightarrow }X {\mathbbm {1}\hspace{-0.83328pt}}{\{ X \le y \}}$; this follows from the fact that

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( X_n {\mathbbm {1}\hspace{-0.83328pt}}{\{ X_n \le y \}} \le x ) = {\left\{ \begin{array}{ll} 1 &{} \text {if } x \ge y,\\ {{\,\mathrm{\mathbb {P}}\,}}(X_n \le x) &{} \text {if } x < y, \end{array}\right. } \end{aligned}$$

and $x <y$ is a continuity point of ${{\,\mathrm{\mathbb {P}}\,}}( X {\mathbbm {1}\hspace{-0.83328pt}}{\{ X \le y \}} \le x)$ if and only if it is a continuity point of ${{\,\mathrm{\mathbb {P}}\,}}(X \le x)$. Hence (3.9) implies (3.6). The bounded convergence theorem then yields (3.7).

$\square$

3.3 Long Time-Scale Asymptotics for Two-Sided Exit Times

The following result gives the expectation and variance of the duration of the classical gambler’s ruin game; the expectation can be found, for example, in [19, pp. 348–349], while the variance is computed in [2, 5].

Lemma 3.3

For every $N \in \mathbb {N}$ and every $x \in I_N$, we have

$$\begin{aligned} {{\,\mathrm{{\textbf{E}}}\,}}_x \tau _{0,N} = x (N -x), \text { and } {{\,\mathrm{{\textbf{V}\!ar}}\,}}_x \tau _{0,N} = \frac{x (N-x)}{3} \left[ x^2 + (N-x)^2 -2 \right] .\end{aligned}$$

Note that although ${{\,\mathrm{{\textbf{E}}}\,}}_1\tau _{0,N} = N-1$, ${{\,\mathrm{{\textbf{V}\!ar}}\,}}_1 \tau _{0,N} \sim N^3/3$ is much greater than the square of the mean, which reflects the fact that while (under ${{\,\mathrm{{\textbf{P}}}\,}}_1$) $\tau _{0,N}$ is frequently very small, with probability about 1/N it exceeds $N^2$ (consider reaching around N/2 before 0). Theorem 3.4 below gives asymptotic estimates for the tails ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n )$. These estimates are informative when n is at least of order $N^2$, i.e., at least the scale for $\tau _{0,N}$ that contributes to most of the variance.

Define the trigonometric sum

$$\begin{aligned} \mathcal {S}_0 (N, m, n):= \sum _{k=1}^{m} \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) . \end{aligned}$$

(3.10)

Theorem 3.4

Suppose that $k_0 \in \mathbb {N}$. Then, there exists $N_0 \in \mathbb {N}$ (depending only on $k_0$) such that, for all $N \ge N_0$ and all $n \in {\mathbb {Z}}_+$,

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n ) = \frac{4}{N} \bigl [ 1 + \Delta (N, k_0, n) \bigr ] \mathcal {S}_0 ( N, k_0, n), \end{aligned}$$

(3.11)

where the function $\Delta$ satisfies

$$\begin{aligned} | \Delta (N, k_0, n ) |&\le \frac{4 \pi ^2 k_0^2}{N^2} + 2 \left( 1 + \frac{N^2}{4 \pi ^2 n k_0 } \right) \exp \left\{ - \frac{2 \pi ^2 n k_0^2}{N^2} \right\} .\end{aligned}$$

(3.12)

Before giving the proof of Theorem 3.4, we state two important consequences. Part (i) of Corollary 3.5 will be our key estimate in studying the confined space regime ($M \gg N^2$), while part (ii) is required for the critical regime ($M \sim \rho N^2$).

Corollary 3.5

• (i) If $n / N^2 \rightarrow \infty$ as $n \rightarrow \infty$, then

  $$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n ) = \frac{4}{N} (1 + o(1) ) \cos ^n ( \pi / N). \end{aligned}$$

  (3.13)

  Moreover, for every $\beta \in {\mathbb {R}}_+$,

  $$\begin{aligned} \lim _{n \rightarrow \infty } \frac{{{\,\mathrm{{\textbf{E}}}\,}}_1[ \tau ^\beta _{0,N} \mid \tau _{0,N} \le n ]}{{{\,\mathrm{{\textbf{E}}}\,}}_1[ \tau ^\beta _{0,N} ]} = 1.\end{aligned}$$

  (3.14)

• (ii) Let $y_0 \in (0,\infty )$. Then, with H defined in (2.16),

  $$\begin{aligned} \lim _{N \rightarrow \infty } \sup _{y \ge y_0} \left| \frac{N}{4} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > y N^2 ) - H(y) \right| = 0.\end{aligned}$$

Remark 3.6

We are not able to obtain the conclusions of Corollary 3.5 directly from Brownian scaling arguments. Indeed, an appealing approximation is to say ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N}> n ) \approx {{\,\mathrm{\mathbb {P}}\,}}_{1/N} ( \tau ^{{\tiny BM }}_{0,1}> n/N^2)$, where $\tau ^{{\tiny BM }}_{0,1}$ is the first hitting time of $\{0,1\}$ for Brownian motion started at 1/N. This approximation does not, however, achieve the correct asymptotics for the full range of n, N, even if the error is quantified. In particular (see e.g. [20, p. 342] or [12, p. 126]) we have

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}_{1/N} ( \tau ^{{\tiny BM }}_{0,1}> n/N^2) = \frac{4}{\pi } \sum _{m=0}^\infty \frac{\sin \bigl ( \frac{(2m+1) \pi }{N} \bigr )}{2m+1} \exp \left\{ - \frac{ (2m+1)^2 \pi ^2 n }{2 N^2} \right\} ,\end{aligned}$$

which for $n \gg N^2$ leads to the conclusion that

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}_{1/N} ( \tau ^{{\tiny BM }}_{0,1}> n/N^2) = \frac{4}{N} (1 + o(1)) \exp \left\{ -\frac{ \pi ^2 n}{2 N^2 } \right\} .\end{aligned}$$

This agrees with asymptotically with (3.13) only when $N^2 \ll n \ll N^4$; cf. Remark 2.6(b). Hence we develop the quantitative estimates in Theorem 3.4.

To end this section, we complete the proofs of Theorem 3.4 and Corollary 3.5.

Proof of Theorem 3.4

A classical result, whose origins Feller traces to Laplace [19, p. 353], yields

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} = n )&= \frac{1}{N} \sum _{k=1}^{N-1} \cos ^{n-1} \left( \frac{\pi k}{N} \right) \sin \left( \frac{\pi k}{N} \right) \left[ \sin \left( \frac{\pi k}{N} \right) + \sin \left( \frac{\pi (N-1) k}{N} \right) \right] \nonumber \\&= \frac{2}{N} \sum _{k=1}^{N-1} \sin ^2 \left( \frac{\pi k}{2} \right) \cos ^{n-1} \left( \frac{\pi k}{N} \right) \sin ^2 \left( \frac{\pi k}{N} \right) \nonumber \\&= \frac{2}{N} \sum _{k=1}^{\big \lceil \frac{N-1}{2} \big \rceil } \cos ^{n-1} \left( \frac{\pi (2k-1)}{N} \right) \sin ^2 \left( \frac{\pi (2k-1)}{N} \right) . \end{aligned}$$

(3.15)

(The expression in (3.15) is 0 if N and n are both even.) Define $m_N:= \big \lceil \frac{N-1}{2} \big \rceil$ and note that $N - 2m_N = \delta _N \in \{0,1\}$, where

$$\begin{aligned} \delta _N:= {\left\{ \begin{array}{ll} 0 &{}\text {if } N \text { is even}, \\ 1 &{} \text {if } N \text { is odd.} \end{array}\right. } \end{aligned}$$

(3.16)

Also define

$$\begin{aligned} \mathcal {S}_1 (N, m, n):= \sum _{k=1}^{m} \cos ^{n} \left( \frac{\pi (\delta _N+2k-1)}{N} \right) . \end{aligned}$$

(3.17)

Then, from (3.15), and the notation introduced in (3.10), we have

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n )&= \frac{2}{N} \sum _{k=1}^{m_N} \frac{\cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) \sin ^2 \left( \frac{\pi (2k-1)}{N} \right) }{1 -\cos \left( \frac{\pi (2k-1)}{N} \right) } \nonumber \\&= \frac{2}{N} \sum _{k=1}^{m_N} \left\{ 1 + \cos \left( \frac{\pi (2k-1)}{N} \right) \right\} \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) \nonumber \\&= \frac{2}{N} \mathcal {S}_0 ( N, m_N, n) + \frac{2}{N} \mathcal {S}_0 (N, m_N , n+1). \end{aligned}$$

(3.18)

The proof of the theorem requires several key estimates. The first claim is that

$$\begin{aligned} \mathcal {S}_0 ( N , m_N , n )&= \mathcal {S}_0 ( N , k_0, n) + (-1)^n \mathcal {S}_1 ( N, k_0 , n ) + \Delta _1 ( N, k_0, n ),\end{aligned}$$

(3.19)

for all $m_N > k_0 \in \mathbb {N}$, where $\mathcal {S}_1$ is defined at (3.17), and

$$\begin{aligned} | \Delta _1 ( N, k_0, n ) | \le 2 \left( 1 + \frac{N^2}{4 \pi ^2 n k_0 } \right) \exp \left\{ - \frac{\pi ^2 n (2k_0+1)^2}{2N^2} \right\} .\end{aligned}$$

The second claim is that, for every $k_0 \in \mathbb {N}$,

$$\begin{aligned} \begin{aligned} \left| \mathcal {S}_0 ( N, k_0, n+1)- \mathcal {S}_0 ( N, k_0, n) \right|&\le \frac{4 \pi ^2 k_0^2}{N^2} \mathcal {S}_0 ( N, k_0, n);\\ \left| \mathcal {S}_1 ( N, k_0, n+1)- \mathcal {S}_1 ( N, k_0, n) \right|&\le \frac{4 \pi ^2 k_0^2}{N^2} \mathcal {S}_0 ( N, k_0, n). \end{aligned} \end{aligned}$$

(3.20)

Take the bounds in (3.19) and (3.20) as given, for now; then from (3.18) and (3.19),

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n )&= \frac{2}{N} \bigl [ \mathcal {S}_0 ( N , k_0, n) + \mathcal {S}_0 ( N , k_0, n+1) \bigr ] \\&{} \qquad {} + \frac{2}{N} (-1)^n \bigl [ \mathcal {S}_1 ( N, k_0 , n ) - \mathcal {S}_1 ( N, k_0 , n+1 ) \bigr ] \\&{} \qquad {} + \frac{2}{N} \bigl [ \Delta _1 ( N, k_0, n )+ \Delta _1 ( N, k_0, n+1 ) \bigr ], \end{aligned}$$

and then applying (3.20) we obtain

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n ) = \frac{4}{N} \bigl [ ( 1 + \Delta _2 (N, k_0, n) ) \mathcal {S}_0 ( N, k_0, n) + \Delta _3 ( N, k_0, n) \bigr ], \end{aligned}$$

(3.21)

where the terms $\Delta _2, \Delta _3$ satisfy

$$\begin{aligned} | \Delta _2 ( N, k_0, n ) |&\le \frac{4 \pi ^2 k_0^2}{N^2} ; \end{aligned}$$

(3.22)

$$\begin{aligned} | \Delta _3 (N, k_0, n ) |&\le 2 \left( 1 + \frac{N^2}{4 \pi ^2 n k_0 } \right) \exp \left\{ - \frac{ \pi ^2 n (2k_0+1)^2}{2N^2} \right\} .\end{aligned}$$

(3.23)

Now, there exists $\theta _0 > 0$ ($\theta _0=1$ will do) for which $\log \cos \theta \ge - \theta ^2$ for all $| \theta | \le \theta _0$. Hence

$$\begin{aligned} \mathcal {S}_0 (N, k_0, n) \ge \cos ^n ( \pi /N) \ge \exp \left\{ -\frac{\pi ^2 n}{N^2} \right\} , \end{aligned}$$

for all N sufficiently large (as a function of $k_0 \in \mathbb {N}$), and all $n \in \mathbb {N}$. Hence, by (3.23),

$$\begin{aligned} \frac{| \Delta _3 ( N, k_0, n)|}{\mathcal {S}_0 (N, k_0, n) } \le 2 \left( 1 + \frac{N^2}{4 \pi ^2 n k_0 } \right) \exp \left\{ - \frac{\pi ^2 n ( ( 2 k_0+1)^2 -2 )}{2N^2} \right\} ,\end{aligned}$$

and, together with (3.21) and (3.22), this implies (3.11).

It remains to verify (3.19) and (3.20). For the former, write

$$\begin{aligned} \mathcal {S}_0 (N , m , n)&= \sum _{k=1}^{\lfloor m/2 \rfloor } \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) + \sum _{k=\lfloor m/2 \rfloor +1}^{m} \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) \\&= \sum _{k=1}^{\lfloor m/2 \rfloor } \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) + (-1)^n \sum _{\ell =1}^{\lceil m/2 \rceil } \cos ^{n} \left( \frac{\pi (N - 2m + 2\ell -1)}{N} \right) ,\end{aligned}$$

using the change of variable $\ell = m-k+1$ and the fact that $\cos ( \pi - \theta ) = -\cos \theta$. Since $\log \cos \theta \le - \theta ^2/2$ for $| \theta | < \pi /2$, we have

$$\begin{aligned} 0 \le \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) \le \exp \left\{ - \frac{\pi ^2 n (2k-1)^2}{2N^2} \right\} , \text { for } 1 \le k \le N/4,\end{aligned}$$

(3.24)

and, similarly, since $N - 2m_N = \delta _N \in \{0,1\}$,

$$\begin{aligned} 0 \le \cos ^{n} \left( \frac{\pi (\delta _N + 2\ell -1)}{N} \right) \le \exp \left\{ - \frac{\pi ^2 n (2\ell -1)^2}{2N^2} \right\} , \text { for } 1 \le \ell \le N/4.\end{aligned}$$

(3.25)

From (3.24), we obtain that, for any $k_0 \in \mathbb {N}$, since $\lfloor m_N /2 \rfloor \le N/4$,

$$\begin{aligned} \sum _{k=k_0+1}^{\lfloor m_N/2 \rfloor } \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right)&\le \sum _{k=k_0+1}^{\lfloor m_N/2 \rfloor } \exp \left\{ - \frac{\pi ^2 n (2k-1)^2}{2N^2} \right\} \\&\le \sum _{\ell = 0}^{\infty } \exp \left\{ - \frac{\pi ^2 n (2\ell + 2k_0 +1)^2}{2N^2} \right\} \\&\le \exp \left\{ - \frac{\pi ^2 n (2k_0+1)^2}{2N^2} \right\} \sum _{\ell = 0}^{\infty } \exp \left\{ - \frac{4 (1+k_0) \pi ^2 n \ell }{N^2} \right\} , \end{aligned}$$

using the inequality $(2\ell + 2k_0 + 1)^2 \ge 8 (1+k_0) \ell + (2k_0 +1)^2$. Since

$$\begin{aligned} \sum _{\ell =0}^\infty \textrm{e}^{-\alpha \ell } \le 1 + \int _0^\infty \textrm{e}^{-\alpha x} \textrm{d}x = 1 + \frac{1}{\alpha }, \text { for } \alpha > 0,\end{aligned}$$

we get

$$\begin{aligned} 0 \le \sum _{k=k_0+1}^{\lfloor m_N/2 \rfloor } \cos ^{n} \left( \frac{\pi (2k-1)}{N} \right) \le \left( 1 + \frac{N^2}{4 \pi ^2 n k_0 } \right) \exp \left\{ - \frac{\pi ^2 n (2k_0+1)^2}{2N^2} \right\} .\end{aligned}$$

Similarly, from (3.25), we get

$$\begin{aligned} 0 \le \sum _{\ell =k_0+1}^{\lceil m_N/2 \rceil } \cos ^{n} \left( \frac{\pi (N - 2m_N + 2\ell -1)}{N} \right) \le \left( 1 + \frac{N^2}{4 \pi ^2 n k_0 } \right) \exp \left\{ - \frac{\pi ^2 n (2k_0+1)^2}{2N^2} \right\} .\end{aligned}$$

This verifies (3.19). Finally, we have from (3.10) that

$$\begin{aligned} \left| \mathcal {S}_0 ( N , k_0, n+1)- \mathcal {S}_0 ( N , k_0, n) \right|&\le \mathcal {S}_0 ( N , k_0, n) \sup _{1 \le k \le k_0} \left| 1 - \cos \left( \frac{\pi (2k -1)}{N} \right) \right| \\&\le \frac{4 \pi ^2 k_0^2}{N^2} \mathcal {S}_0 ( N , k_0, n) , \end{aligned}$$

for all N sufficiently large (depending only on $k_0$), since $| 1 - \cos \theta | \le \theta ^2$ for all $\theta \in \mathbb {R}$. Similarly,

$$\begin{aligned} \left| \mathcal {S}_1 ( N , k_0, n+1)- \mathcal {S}_1 ( N , k_0, n) \right|&\le \mathcal {S}_1 ( N , k_0, n) \sup _{1 \le k \le k_0} \left| 1 - \cos \left( \frac{\pi (\delta _N + 2k -1)}{N} \right) \right| \\&\le \frac{4 \pi ^2 k_0^2}{N^2} \mathcal {S}_1 ( N , k_0, n) \le \frac{4 \pi ^2 k_0^2}{N^2} \mathcal {S}_0 ( N , k_0, n) , \end{aligned}$$

where, again, N must be large enough. This verifies (3.20). $\square$

Proof of Corollary 3.5

First, suppose that $n / N^2 \rightarrow \infty$. Then we can take $k_0 =1$ in Theorem 3.4 to see that ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n ) = (4/N) (1+ \Delta (N, 1, n) ) \cos ^n ( \pi /N)$, where, by (3.12), $| \Delta (N,1,n) | = o(1)$. This proves (3.13). Since $\log \cos \theta \le - \theta ^2/2$ for $|\theta | < \pi /2$, it follows from (3.13) that

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > n) \le \frac{5}{N} \exp \left\{ - \frac{\pi ^2 n}{2N^2} \right\} , \text { for all } n \text { large enough.} \end{aligned}$$

(3.26)

For any random variable $X \ge 0$, and $\beta \in {\mathbb {R}}_+$, and any $r \in {\mathbb {R}}_+$, one has

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ X^\beta {\mathbbm {1}\hspace{-0.83328pt}}{\{ X \ge r \}} ]&= \int _0^\infty {{\,\mathrm{\mathbb {P}}\,}}( X^\beta {\mathbbm {1}\hspace{-0.83328pt}}{\{ X \ge r \}}> y ) \textrm{d}y \\&\le r^\beta {{\,\mathrm{\mathbb {P}}\,}}( X \ge r) + \int _{r^\beta }^\infty {{\,\mathrm{\mathbb {P}}\,}}( X^\beta> y ) \textrm{d}y\\&= r^\beta {{\,\mathrm{\mathbb {P}}\,}}( X \ge r) + \beta \int _{r}^\infty s^{\beta -1} {{\,\mathrm{\mathbb {P}}\,}}( X > s ) \textrm{d}s . \end{aligned}$$

Hence (3.26) shows that there is a constant $C_\beta \in {\mathbb {R}}_+$ such that, for all n sufficiently large,

$$\begin{aligned} {{\,\mathrm{{\textbf{E}}}\,}}_1[ \tau ^\beta _{0,N} {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N} \ge n+1 \}} ]&\le \frac{C_\beta n^\beta }{N} \exp \left\{ - \frac{\pi ^2 n}{2 N^2} \right\} + \frac{C_\beta }{N} \int _{n}^\infty s^{\beta -1} \exp \left\{ - \frac{\pi ^2 s}{4 N^2} \right\} \textrm{d}s \\&= C_\beta N^{2\beta -1} \left[ \left( \frac{n}{N^2} \right) ^\beta \exp \left\{ - \frac{\pi ^2 n}{2 N^2} \right\} + \int _{n/N^2}^\infty t^{\beta -1} \exp \left\{ - \frac{\pi ^2 t}{4} \right\} \textrm{d}t \right] , \end{aligned}$$

using the change of variable $t = s/N^2$. Since $n /N^2 \rightarrow \infty$, this means that

$$\begin{aligned} {{\,\mathrm{{\textbf{E}}}\,}}_1[ \tau ^\beta _{0,N} {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N} \ge n+1 \}} ] = o ( N^{2\beta -1}). \end{aligned}$$

(3.27)

In particular, the $\beta =0$ case of (3.27) shows that $\lim _{n \rightarrow \infty } {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} \le n ) =1$. A consequence of (3.5) is that ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} > \delta N^2 ) \ge \delta /N$ for some $\delta >0$, and hence ${{\,\mathrm{{\textbf{E}}}\,}}_1[ \tau ^\beta _{0,N} ] \ge c_\beta N^{2\beta -1}$ for some $c_\beta >0$; the conclusion in (3.14) then follows from (3.27). The proves part (i)

Finally, fix $y \ge y_0 > 0$ and suppose that $n / N^2 \rightarrow y$. Then, uniformly in $k \le N^{1/2}$,

$$\begin{aligned} \cos ^n \left( \frac{\pi (2k-1)}{N} \right)= & {} \exp \left\{ - \frac{\pi ^2 n (2k-1)^2}{2N^2} (1+O(k^2/N^2)) \right\} \nonumber \\= & {} (1+o(1)) h_k (y),\nonumber \\\end{aligned}$$

(3.28)

as $n \rightarrow \infty$, where $h_k$ is defined at (2.16) and $\sum _{k=1}^\infty h_k (y) = H(y)$ satisfies $\sup _{y \ge y_0} H(y) < \infty$. In particular, for any $\varepsilon >0$ we can choose $k_0 \in \mathbb {N}$ large enough so that $\sup _{y \ge y_0} |\sum _{k=1}^{k_0} h_k (y) - H(y) | < \varepsilon$. From (3.28) it follows that, for any $\varepsilon >0$,

$$\begin{aligned} \left| {\sum _{k= 1}^{k_0} \cos ^n \left( \frac{\pi (2k-1)}{N} \right) } - {\sum _{k=1}^{k_0} h_k (y) } \right| \le \varepsilon , \end{aligned}$$

for all n sufficiently large. Hence, for every $\varepsilon >0$,

$$\begin{aligned} \sup _{y \ge y_0} \left| \mathcal {S}_0 ( N, k_0, n ) - H(y) \right| \le \varepsilon ,\end{aligned}$$

(3.29)

for all n sufficiently large. By (3.12), there exist $k_0, n_0 \in \mathbb {N}$ such that, for every $y \ge y_0$,

$$\begin{aligned} | \Delta (N, k_0, n ) | \le \frac{4 \pi ^2 k_0^2}{N^2} + 2 \left( 1 + \frac{1}{3 \pi ^2 y k_0 } \right) \exp \left\{ - \pi ^2 k_0^2 y \right\} \le \varepsilon , \end{aligned}$$

(3.30)

for all $n \ge n_0$ (given $\varepsilon$ and $y_0$, first take $k_0$ large, and then N large). From (3.11) with (3.29), (3.30), and the fact that $\sup _{y \ge y_0} H(y) < \infty$, we verify part (ii). $\square$

4 Proofs of Main Results

4.1 Excursions, Renewals, and Extinction

We start by giving the proof of the irreducibility result, Lemma 2.2, stated in Sect. 2.2.

Proof of Lemma 2.2

Let $\mathcal {F}_n:= \sigma ( \zeta _0, \ldots , \zeta _n)$, the $\sigma$-algebra generated by the first $n \in {\mathbb {Z}}_+$ steps of the Markov chain $\zeta$. Then, given $\mathcal {F}_n$, at least one of the two neighbouring sites of $\mathbb {Z}$ to $X_n$ is in $I^{{{{\circ }}}}_N$; take $y \in I^{{{{\circ }}}}_N$ to be any site such that $| y - X_n | = 1$. If $X_n \in \partial I_N$, then the walker will move to y with probability 1, and the energy level will be refreshed to M:

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( X_{n+1} \in I^{{{{\circ }}}}_N, \, \eta _{n+1} = M \mid \mathcal {F}_n ) = 1, \text { on } \{ X_n \in \partial I_N \}. \end{aligned}$$

(4.1)

Otherwise, $X_n \in I^{{{{\circ }}}}_N$. If $\eta _n \ge 1$, then the walker can, with probability 1/2, take a step to y on the next move, which uses 1 unit of energy. On the other hand, if $\eta _n = 0$, then $X_{n+1} = X_n$ must remain in $I^{{{{\circ }}}}_N$. Thus, writing $x^+:= x {\mathbbm {1}\hspace{-0.83328pt}}{\{ x > 0\}}$,

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( X_{n+1} \in I^{{{{\circ }}}}_N, \, \eta _{n+1} = (\eta _n -1)^+ \mid \mathcal {F}_n ) \ge \frac{1}{2}, \text { on } \{ X_n \in I^{{{{\circ }}}}_N \}. \end{aligned}$$

(4.2)

In particular, since $\eta _n \le M$, we can combine (4.1) and (4.2) (applied M times) to get

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( \eta _{(k+1)(M+1)} = 0, \, X_{(k+1)(M+1) } \in I^{{{{\circ }}}}_N \mid \mathcal {F}_{k(M+1)} ) \ge 2^{-M}, \ \text {a.s.}, \text { for all } k \in {\mathbb {Z}}_+.\end{aligned}$$

Thus

$$\begin{aligned} {{\,\mathrm{\mathbb {P}}\,}}( \lambda> (k+1) (M+1) \mid \mathcal {F}_{k(M+1)} ) \le (1 - 2^{-M}) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \lambda > k (M+1) \}}, \ \text {a.s.}, \end{aligned}$$

repeated application of which implies that

$$\begin{aligned} \sup _{z \in I_N \times I_M} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \lambda > k (M+1) ) \le (1-2^{-M} )^k \le \exp \left\{ - k 2^{-M} \right\} , \end{aligned}$$

uniformly over $N \in {\overline{\mathbb {N}}}$. Every $n \in {\mathbb {Z}}_+$ has $k (M+1) \le n < (k+1)(M+1)$ for some $k = k(n) \in {\mathbb {Z}}_+$, and so

$$\begin{aligned} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z(\lambda> n ) \le {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z(\lambda > k (M+1)) \le \exp \left\{ - \left( \frac{2^{-M}}{M+1}\right) n \right\} , \text { for all } n \in {\mathbb {Z}}_+.\end{aligned}$$

The verifies that $\sup _{z \in I_N \times I_M} {{{\,\mathrm{\mathbb {E}}\,}}}^{N,M}_z[ \textrm{e}^{\delta \lambda } ] < \infty$ for any $\delta \in (0, \frac{2^{-M}}{M+1} )$. $\square$

We denote by $\sigma _1< \sigma _2< \cdots < \sigma _\kappa$ the successive times of visiting the boundary before time $\lambda$; formally, set $\sigma _0:= 0$ and

$$\begin{aligned} \sigma _k:= \inf \{ n > \sigma _{k-1}: X_n \in \partial I_N \}, \text { for } k \in \mathbb {N}, \end{aligned}$$

with the usual convention that $\inf \emptyset := \infty$. Then $\sigma _k < \infty$ if and only if $\sigma _k < \lambda$. The number of complete excursions is then

$$\begin{aligned} \kappa := \max \{ k \in {\mathbb {Z}}_+: \sigma _k < \lambda \}, \end{aligned}$$

(4.3)

i.e., the number of visits to $\partial I_N$ before extinction. Since $\lambda < \infty$, a.s. (by Lemma 2.2), $\kappa \in {\mathbb {Z}}_+$ is a.s. finite.

For $k \in \mathbb {N}$, define the excursion duration $\nu _k:= \sigma _k - \sigma _{k-1}$ as long as $\sigma _k <\infty$; otherwise, set $\nu _k = \infty$. We claim that

$$\begin{aligned} \text {for every } k \in \mathbb {N}, ~ \nu _k \in I_{M+1} \cup \{ \infty \}, \text { and } \nu _k< \infty \text { if and only if } \sigma _k < \lambda . \end{aligned}$$

(4.4)

To see (4.4), observe that, if $\sigma _{k-1} < \lambda$ then $\eta _{\sigma _{k-1}+1} = M$ and $X_n \in I^{{{{\circ }}}}_N$ for all $\sigma _{k-1}< n < \sigma _k$. Hence $\eta _{\sigma _{k-1} + i} = M+1 -i$ for all $1 \le i \le \nu _k$ if $\nu _k < \infty$. In particular, if $\nu _k < \infty$, then $0 \le \eta _{\sigma _k} = M + 1 - \nu _k$, which implies that $\nu _k \le M+1$. This verifies (4.4).

For simplicity, we write $\nu := \nu _1$. By the strong Markov property, for all $k, n \in {\mathbb {Z}}_+$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu _{k+1} = n \mid \mathcal {F}_{\sigma _k} ) = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_{(1,M)}( \nu = n), \text { on } \{ \sigma _k < \lambda \}, \end{aligned}$$

(4.5)

meaning that excursions subsequent to the first are identically distributed. On the other hand, ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu _1 = n ) = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu = n)$ for $n \in {\mathbb {Z}}_+$, so that if $z \ne (1,M)$ the first excursion may have a different distribution.

After the final visit to the boundary at time $\sigma _\kappa$, the energy $\eta _{\sigma _\kappa +1} =M$ decreases one unit at a time until $\eta _{\sigma _\kappa + M + 1} = 0$ achieves extinction. Thus, by (4.4),

$$\begin{aligned} \lambda = M+1 + \sigma _\kappa = M + 1 + \sum _{k=1}^{\kappa } \nu _k. \end{aligned}$$

(4.6)

In the terminology of renewal theory, $\nu _1, \nu _2, \ldots$ is a renewal sequence that is delayed (since $\nu _1$ may have a different distribution from the subsequent terms) and terminating, since ${{\,\mathrm{\mathbb {P}}\,}}(\nu _k = \infty ) >0$. A key quantity is the per-excursion extinction probability

$$\begin{aligned} \theta _z ( N, M ):= {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \lambda < \sigma _1 ) = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu _1 = \infty ),\end{aligned}$$

(4.7)

the probability that the process started in state z terminates before reaching the boundary. Set $\theta (N,M):= \theta _{(1,M)} (N,M)$ for the case where $z=(1,M)$, which plays a special role, due to (4.5). The following basic result exhibits the probabilistic structure associated with the renewal set-up. Recall the definitions of the number of completed excursions $\kappa$ and extinction probability $\theta _z(N,M)$ from (4.3) and (4.7), respectively.

Lemma 4.1

Let $N \in {\overline{\mathbb {N}}}$ and $M \in \mathbb {N}$. Then, for all $k \in \mathbb {N}$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \kappa \ge k ) = (1- \theta _z (N,M) ) (1 - \theta (N, M) )^{k-1}, \end{aligned}$$

(4.8)

and

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N,M}_z[ \kappa ] = \frac{1- \theta _z (N,M)}{\theta (N,M)}.\end{aligned}$$

Moreover, given that $\kappa =k \in \mathbb {N}$, the random variables $\nu _1, \ldots \nu _k$ are (conditionally) independent, and satisfy, for every $n_1, \ldots , n_k \in I_{M+1}$,

$$\begin{aligned}&{} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu _1 = n_1, \ldots , \nu _k = n_k \mid \kappa = k ) \nonumber \\&{} \quad {} = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu = n_1 \mid \nu< \infty ) \prod _{i=2}^k {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_{(1,M)}( \nu = n_i \mid \nu < \infty ) . \end{aligned}$$

(4.9)

Proof

By definition, $\sigma _0 = 0$. Let $k \in \mathbb {N}$. From (4.3), we have that $\kappa \ge k$ if and only if $\sigma _k < \lambda$. If $\sigma _k < \lambda$, then $|X_{\sigma _k+1} - y | = 1$ for some $y \in \partial I_N$, and $\eta _{\sigma _k+1} = M$. Hence, by (4.7) and the strong Markov property applied at the stopping time $\sigma _k+1$, for $k \in \mathbb {N}$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \kappa \ge k+1 \mid \mathcal {F}_{\sigma _k} ) = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \sigma _{k+1} < \lambda \mid \mathcal {F}_{\sigma _k} ) = 1- \theta (N, M), \text { on } \{ \lambda > \sigma _k \}.\end{aligned}$$

Hence ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \kappa \ge k+1 \mid \kappa \ge k ) = 1 - \theta (N,M)$ for $k \in \mathbb {N}$, and, since ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \kappa \ge 1) = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \sigma _1 < \lambda ) = 1 - \theta _z (N,M)$, we obtain (4.8). Moreover, for $n_1, \ldots , n_k \le M+1$,

$$\begin{aligned}&{} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z\left( \{ \kappa = k \} \cap ( \cap _{i=1}^k \{ \nu _i = n_i \} ) \right) \nonumber \\&{} \quad {} = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z\left( \{ \nu _{k+1} = \infty \} \cap ( \cap _{i=1}^k \{ \nu _i = n_i \} ) \right) \nonumber \\&{} \quad {} = {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z(\nu = n_1) {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_{(1,M)}( \nu = \infty ) \prod _{i=2}^k {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_{(1,M)}( \nu = n_i ) ,\end{aligned}$$

(4.10)

by repeated application of (4.5). Similarly,

$$\begin{aligned} {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \kappa = k )&= {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z\left( \{ \nu _{k+1} = \infty \} \cap ( \cap _{i=1}^k \{ \nu _i< \infty \} ) \right) \nonumber \\&= {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z(\nu< \infty ) {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_{(1,M)}( \nu = \infty ) \prod _{i=2}^k {{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_{(1,M)}( \nu < \infty ) . \end{aligned}$$

(4.11)

Dividing the expression in (4.10) by that in (4.11) gives (4.9), since, by (4.7), ${{{\,\mathrm{\mathbb {P}}\,}}}^{N,M}_z( \nu < \infty ) = 1 - \theta _z (N,M)$. $\square$

4.2 The Meagre-Capacity Limit

In this section we present the proof of Theorem 2.3; at several points we appeal to the results from Sect. 3 on simple random walk. Consider the generating function

$$\begin{aligned} \psi _M(s):= \sum _{n=1}^{M+1} \textrm{e}^{sn} {{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( \nu = n \mid \nu < \infty ), \text { for } s \in \mathbb {R}.\end{aligned}$$

(4.12)

Define for $t \in \mathbb {R}$,

$$\begin{aligned} K(t):= 1 - \sum _{\ell =1}^\infty \frac{t^\ell }{(2\ell -1) \cdot \ell !}, \text { and } \mathcal {T}:= \{ t \in \mathbb {R}: K(t) > 0 \}. \end{aligned}$$

(4.13)

For each $t \in \mathbb {R}$, the series in (4.13) converges absolutely, and, indeed, $| 1 - K(t) | \le \textrm{e}^{|t|}$ for all $t \in \mathbb {R}$. The series for K defined by (4.13) compared to equation (13.1.2) in [4] identifies K as the Kummer (confluent hypergeometric) function $K(t) = M\big (-\frac{1}{2}, \frac{1}{2}, t \big )$; see Appendix A for some of its properties.

The following result gives asymptotics for $\theta (N_M, M) = \theta _{(1,M)} (N_M, M)$ as defined at (4.7), and for the generating function $\psi _M$ as defined at (4.12).

Proposition 4.2

Consider the $(N_M,M,z_M)$ model with $M \in \mathbb {N}$ and $N_M \in {\overline{\mathbb {N}}}$ such that $\lim _{M \rightarrow \infty } (M / N_M^2 ) = 0$. Then

$$\begin{aligned} \theta (N_M, M ) = \sqrt{\frac{2}{\pi }} (1+o(1)) M^{-1/2}, \text { as } M \rightarrow \infty . \end{aligned}$$

(4.14)

Moreover,

$$\begin{aligned} \lim _{M \rightarrow \infty } \left[ \left( \psi _M(t / M) -1 \right) {M^{1/2}} \right] = \sqrt{ \frac{2}{\pi } } (1 - K(t)),\end{aligned}$$

(4.15)

uniformly over $t \in R$, for any compact $R \subset \mathbb {R}$.

In the proof of this result, and later, we will use the following integration by parts formula for restricted expectations, which is a slight generalization of Theorem 2.12.3 of [25, p. 76].

Lemma 4.3

For any real-valued random variable X and every $a, b \in \mathbb {R}$ with $a \le b$, and any monotone and differentiable $g: \mathbb {R}\rightarrow \mathbb {R}$,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ g (X) {\mathbbm {1}\hspace{-0.83328pt}}{\{ a < X \le b\}} ]&= g(a) {{\,\mathrm{\mathbb {P}}\,}}(X> a ) - g(b) {{\,\mathrm{\mathbb {P}}\,}}(X> b) + \int _a^b g' (y) {{\,\mathrm{\mathbb {P}}\,}}(X > y) \textrm{d}y . \end{aligned}$$

(4.16)

Proof

Suppose that $g: \mathbb {R}\rightarrow \mathbb {R}$ is differentiable. Write $F_X (y):={{\,\mathrm{\mathbb {P}}\,}}( X \le y)$ for the distribution function of X. If g is monotone non-decreasing, then

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ g (X) {\mathbbm {1}\hspace{-0.83328pt}}{\{ a < X \le b\}} ]&= \int _a^b g (y) \textrm{d}F_X (y)\\ {}&= g(b) F_X(b) - g(a) F_X (a) - \int _a^b F_X (y ) g' (y) \textrm{d}y, \end{aligned}$$

where the first equality is e.g. Theorem 2.7.1 of [25, p. 60] and the second follows from Theorem 2.9.3 of [25, p. 66]; this yields (4.16). If g is monotone non-increasing, then the same result follows by considering ${\tilde{g}} (y):= g(b) - g(y)$. $\square$

Proof of Proposition 4.2

For ease of notation, write $\tau := \tau _{0,N_M}$ throughout this proof. Apply Lemma 3.1 with $n = M+1$ to get

$$\begin{aligned} \theta (N_M, M ) = {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > M+1 ) = \sqrt{\frac{2}{\pi }} M^{-1/2} + O (1/N_M), \text { as } M \rightarrow \infty . \end{aligned}$$

Since $M = o( N_M^2 )$, the $O(1/N_M)$ term here can be neglected asymptotically; this verifies (4.14).

We apply (4.16) with $X = \tau /M$, $a=0$, $b=1$, and $g (y) = \textrm{e}^{ty} -1$, ($t \ne 0$) to get

$$\begin{aligned}&{{\,\mathrm{{\textbf{E}}}\,}}_1[ (\textrm{e}^{t \tau / M} - 1) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau \le M \}} ] \nonumber \\&{} \qquad {} = (1 - \textrm{e}^{t}) {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau> M ) + t \int _0^1 \textrm{e}^{tu} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > u M ) \textrm{d}u . \end{aligned}$$

(4.17)

Fix $\varepsilon >0$, and let $n_\varepsilon \in \mathbb {N}$ and $\delta _\varepsilon > 0$ be as in Lemma 3.1(iii). Since $M / N_M^2 \rightarrow 0$, we have $M < \delta _\varepsilon N_M^2$ for all M sufficiently large. Hence from (3.5) we have that

$$\begin{aligned} \sup _{n_\varepsilon /M \le u \le 1} \left| M^{1/2} u^{1/2} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > u M ) - \sqrt{2/\pi } \right| \le \varepsilon ,\end{aligned}$$

(4.18)

for all M sufficiently large. It follows from (4.18) that, as $M \rightarrow \infty$,

$$\begin{aligned} t \int _0^1 \textrm{e}^{tu} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > u M ) \textrm{d}u&\ge \bigl ( \sqrt{2/\pi } - \varepsilon \bigr ) M^{-1/2} t \int _{n_\varepsilon /M}^1 \textrm{e}^{tu} u^{-1/2} \textrm{d}u \nonumber \\&= \bigl ( \sqrt{2/\pi } - \varepsilon \bigr ) M^{-1/2} ( \mathcal {I}( t) + o(1) ) ,\end{aligned}$$

(4.19)

using the definition of $\mathcal {I}$ from (2.5); here the o(1) is uniform for $t \in R$ for a given compact $R \subset \mathbb {R}$. Similarly, from (4.18) again, uniformly for $t \in R$ (compact),

$$\begin{aligned} t \int _0^1 \textrm{e}^{tu} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > u M ) \textrm{d}u&\le \bigl ( \sqrt{2/\pi } + \varepsilon \bigr ) M^{-1/2} ( \mathcal {I}( t) + o(1) ). \end{aligned}$$

(4.20)

Combining (4.19) and (4.20), since $\varepsilon >0$ was arbitrary, we obtain

$$\begin{aligned} t \int _0^1 \textrm{e}^{tu} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > u M ) \textrm{d}u = \bigl ( \sqrt{2/\pi } +o(1) \bigr ) M^{-1/2} \mathcal {I}( t),\end{aligned}$$

as $M \rightarrow \infty$, uniformly for $t \in R$, R compact. Together with the asymptotics for ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau > M+1 ) = \theta (N_M, M )$ from (4.14), we thus conclude from (4.17) that

$$\begin{aligned} {{\,\mathrm{{\textbf{E}}}\,}}_1[ (\textrm{e}^{t \tau / M} - 1) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau \le M+1 \}} ] = \bigl ( \sqrt{2/\pi } +o(1) \bigr ) M^{-1/2} \left( 1 - \textrm{e}^t + \mathcal {I}( t) \right) , \end{aligned}$$

uniformly for $t \in R$, R compact, from which (4.15) follows, since $1 - \textrm{e}^t + \mathcal {I}( t) = 1-K(t)$ by (A.1), and, from (4.12),

$$\begin{aligned} \psi _M(t / M) = 1 + {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \textrm{e}^{t \nu / M} - 1 \mid \nu < \infty ] = \frac{{{\,\mathrm{{\textbf{E}}}\,}}_1[ (\textrm{e}^{t \tau / M} - 1) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau \le M+1 \}} ]}{{{\,\mathrm{{\textbf{P}}}\,}}_1( \tau \le M+1) },\end{aligned}$$

where ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau \le M+1) = 1 - \theta (N_M, M ) \rightarrow 1$, by (4.14). $\square$

To avoid burdening notation with conditioning, let $Y_M$ denote a random variable taking values in $I_{M+1}$ (enriching the underlying probability space if necessary) such that

$$\begin{aligned} {{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( Y_M = n ) = {{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( \nu = n \mid \nu < \infty ), \text { for } n \in I_{M+1}.\end{aligned}$$

(4.21)

Given $Y_n$ as constructed through (4.21), it is the case that $\psi _M$ as defined at (4.12) can be represented via $\psi _M(s) = {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \textrm{e}^{s Y_M} ]$, $s \in \mathbb {R}$.

The next lemma proves that the limit distribution in Theorem 2.3 has expectation given by the function g defined at (2.9), and establishes some of the key properties of g.

Lemma 4.4

Suppose that $\xi \sim \textrm{DM}(1/2)$ and $\tau ^{{\tiny BM }}_1\sim \textrm{S}_+(1/2)$ are independent with distributions given by (2.6) and (2.8) respectively. Let $a \in {\mathbb {R}}_+$ and $u \in (0,\infty )$. The random variable $\zeta _{a,u}:= \min ( u, a \tau ^{{\tiny BM }}_1) + (1+ \xi ) {\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1< u\}}$ has mean given by ${{\,\mathrm{\mathbb {E}}\,}}\zeta _{a,u} = g(a,u)$, where g is defined at (2.9). Moreover, for every $u\in (0,1]$, the function $a \mapsto g(a,u)$ is strictly decreasing and infinitely differentiable on $(0,\infty )$, with $g(0,u)=2$ and $\lim _{a \rightarrow \infty } g(a,u)=u$.

Proof

If $a=0 <u$, then $\zeta _0 = 1 +\xi$, a.s., and the result is true because $g(0,u) = 2 = 1 +{{\,\mathrm{\mathbb {E}}\,}}\xi$. Suppose that $a, u \in (0,\infty )$. From (2.8), we have that

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ u \wedge a \tau ^{{\tiny BM }}_1]&= \int _0^{u/a} \frac{a}{\sqrt{2\pi t}} \textrm{e}^{-1/(2t)} \textrm{d}t + u \int _{u/a}^\infty \frac{1}{\sqrt{2\pi t^3}} \textrm{e}^{-1/(2t)} \textrm{d}t \\&= \sqrt{\frac{au}{2\pi }} \int _{1}^\infty y^{-3/2} \textrm{e}^{-ay/(2u)} \textrm{d}y + \frac{2u}{\sqrt{2\pi }} \int _0^{\sqrt{a/u}} \textrm{e}^{-s^2 /2} \textrm{d}s , \end{aligned}$$

using the substitutions $y = u/(at)$ in the first integral and $s^2 = 1/t$ in the second. Here

$$\begin{aligned} \frac{2}{\sqrt{2\pi }} \int _0^{\sqrt{a/u}} \textrm{e}^{-s^2 /2} \textrm{d}s = 2 \bigl [ \Phi ( \sqrt{a/u} ) - \Phi (0) \bigr ] = 2 \Phi ( \sqrt{a/u} ) - 1.\end{aligned}$$

Moreover, an integration by parts followed by the substitution $s^2 = ry$ gives

$$\begin{aligned} \int _{1}^\infty y^{-3/2} \textrm{e}^{-r y/2} \textrm{d}y&= 2 \textrm{e}^{-r/2} - r \int _1^\infty y^{-1/2} \textrm{e}^{-ry/2} \textrm{d}y \\&= 2 \textrm{e}^{-r/2} - 2 \sqrt{r} \int _{\sqrt{r}}^\infty \textrm{e}^{-s^2/2} \textrm{d}s , \text { for } r > 0 . \end{aligned}$$

Hence

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ u \wedge a \tau ^{{\tiny BM }}_1] = u + \sqrt{\frac{2au}{\pi }} \textrm{e}^{-a/(2u)} - 2 (a+u) {\overline{\Phi }}( \sqrt{a/u} ).\end{aligned}$$

Finally, by (2.12), ${{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1< u ) = {{\,\mathrm{\mathbb {P}}\,}}( \tau ^{{\tiny BM }}_1< u/a) = 2 {\overline{\Phi }}(\sqrt{a/u} )$, and then using the independence of $\xi$ and $\tau ^{{\tiny BM }}_1$, and the fact that ${{\,\mathrm{\mathbb {E}}\,}}\xi = 1$, gives

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}\zeta _{a,u} =u + \sqrt{\frac{2au}{\pi }} \textrm{e}^{-a/(2u)} - 2 (a+u) {\overline{\Phi }}( \sqrt{a/u} ) + 4 {\overline{\Phi }}( \sqrt{a/u} ), \end{aligned}$$

which is equal to g(a, u) as defined at (2.9).

Write $\phi (z):= (2\pi )^{-1/2} \textrm{e}^{-z^2/2}$ for the standard normal density, so that ${\overline{\Phi }}' ( z) = - \phi (z)$ and $\phi '(z) = - z \phi (z)$. The formula (2.9) can then be expressed as

$$\begin{aligned} g(a) = u + (4-2u-2a) {\overline{\Phi }}(\sqrt{a/u} ) + 2 \sqrt{au} \phi (\sqrt{a/u}), \end{aligned}$$

which, on differentiation, yields, for $u >0$,

$$\begin{aligned} g' (a,u)&:= \frac{\partial }{\partial a} g (a,u) = -\frac{2(1-u)}{\sqrt{au}} \phi (\sqrt{au} ) - 2 {\overline{\Phi }}(\sqrt{a/u} ) .\end{aligned}$$

(4.22)

Thus $g'(a,u) < 0$ for all $a \in (0,\infty )$ and all $u \in (0,1]$, with $\lim _{a \rightarrow 0} g'(a,u) = -\infty$ for $u \in (0,1)$ and $\lim _{a \rightarrow 0} g'(a,1) = -1$. In particular, $a \mapsto g(a,u)$ is strictly decreasing. $\square$

Proof of Theorem 2.3

To simplify notation, set $\theta _M:= \theta (N_M, M)$. First suppose that $X_0 = 1$ and $\eta _0 =M$. Then in the representation $\sigma _\kappa = \sum _{i=1}^\kappa \nu _i$, Lemma 4.1 shows that, given $\kappa = k \in \mathbb {N}$, $\nu _1, \ldots , \nu _k$ are i.i.d. with the law of $Y_M$ as given by (4.21), and the law of $\kappa$ is ${{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( \kappa = k ) = (1-\theta _M)^k \theta _M$, for $k \in {\mathbb {Z}}_+$. In particular, for $| r (1-\theta _M ) | < 1$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ r^{\kappa } ] =\sum _{k=0}^\infty r^k (1-\theta _M)^k \theta _M = \frac{\theta _M}{1-(1-\theta _M)r}.\end{aligned}$$

Hence, by (conditional) independence,

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ {\textrm{e}^{s \sigma _\kappa }} \right]&= {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ {{\,\mathrm{\mathbb {E}}\,}}\biggl [ \prod _{i=1}^{\kappa } \textrm{e}^{s \nu _i} \; \biggl | \;\kappa \biggr ] \right] \nonumber \\&= {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ \left( \psi _M(s) \right) ^{\kappa } \right] \nonumber \\&= \frac{\theta _M}{1-(1-\theta _M) \psi _M(s)} , \text { if } (1 -\theta _M) \psi _M(s) < 1. \end{aligned}$$

(4.23)

For $s=t/M$, we have from Proposition 4.2 that, for $t \in \mathbb {R}$,

$$\begin{aligned} ( 1 - \theta _M ) \psi _M( t / M ) = 1 - M^{-1/2} \sqrt{\frac{2}{\pi }} K(t) + o (M^{-1/2} ),\end{aligned}$$

(4.24)

as $M \rightarrow \infty$. In particular, for $t \in \mathcal {T}$, with $\mathcal {T}$ defined at (4.13), the asymptotics in (4.24) show that $( 1 - \theta _M ) \psi _M( t / M ) < 1$ for all M sufficiently large. Hence from (4.23) applied at $s = t/M$, $t \in \mathcal {T}$, with (4.24) and another application of (4.14), we get

$$\begin{aligned} \lim _{M \rightarrow \infty } {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ {\textrm{e}^{t \sigma _\kappa /M}} \right]&= \lim _{M \rightarrow \infty } \left[ M^{1/2} \sqrt{\frac{\pi }{2}} \frac{\theta _M}{K(t) +o(1)} \right] = \frac{1}{K(t)}, \text { for } t \in \mathcal {T}. \end{aligned}$$

(4.25)

Since $\lambda = M +1 + \sigma _\kappa$, by (4.6), it follows from (4.25), and the fact that convergence of moment generating functions in a neighbourhood of 0 implies convergence in distribution, and convergence of all moments (see e.g. [25, p. 242]), that $\lambda /M \overset{\textrm{d}}{\longrightarrow }1+\xi$ where ${{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{t \xi } ] = 1 / K(t)$ for $t \in \mathcal {T}$, and $M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \sigma _\kappa ] \rightarrow {{\,\mathrm{\mathbb {E}}\,}}\xi = 1$. The form for ${{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{t \xi }]$ given in (2.6) is obtained using the relation (A.1). This establishes both (2.10) and (2.11) in the case $X_0 = x_M \equiv 1$ and $\eta _0 = y_M \equiv M$, where (2.7) is satisfied for $a=0$ and $u=1$.

More generally, suppose that $(X_0,\eta _0) = ( x_M,y_M)$ satisfying (2.7). Then

$$\begin{aligned} \lambda \overset{d}{=}M + 1 + (\nu _1 + Z ) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu _1 < \infty \}},\end{aligned}$$

(4.26)

by the strong Markov property, where the $Z, \nu _1$ on the right are independent, and Z has the distribution of $\sigma _\kappa$ under ${{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}$. Here $\sigma _\kappa / M \overset{\textrm{d}}{\longrightarrow }\xi$ and, by Lemma 3.2,

$$\begin{aligned} \lim _{M \rightarrow \infty } {{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{z_M}( \nu _1 < \infty ) = \lim _{M \rightarrow \infty } M^{-1} {{\,\mathrm{{\textbf{P}}}\,}}_{x_M} ( \tau _{0,N_M} \le y_M + 1 ) = {{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1\le u ), \end{aligned}$$

and $M^{-1} \nu _1 {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu _1 < \infty \}}$ converges in distribution to $a \tau ^{{\tiny BM }}_1{\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1\le u \}}$. This completes the proof of (2.10). Taking expectations in (4.26), and using the stated independence, we get

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}\lambda&= M + 1 + {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}[ \nu {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu< \infty \}} ] +{{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{z_M}( \nu < \infty ) {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \sigma _\kappa ] , \end{aligned}$$

where ${{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{z_M}( \nu < \infty ) = \theta _{z_M} (N_M, M) = {{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1\le u) + o(1)$, by the $\beta =0$ case of (3.7) and hypothesis (2.7). It follows that

$$\begin{aligned} M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}\lambda&= 1 + M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}[ \nu {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu < \infty \}} ] + {{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1\le u ) + o(1),\end{aligned}$$

using the fact that $\lim _{M \rightarrow \infty } M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \sigma _\kappa ] = 1$, as established via (4.25) above. Moreover, using (2.7), we have from Lemma 3.2 that

$$\begin{aligned} \lim _{M \rightarrow \infty } M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}[ \nu {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu < \infty \}} ]&= \lim _{M \rightarrow \infty } M^{-1} {{\,\mathrm{{\textbf{E}}}\,}}_{x_M} [ \tau _{0,N_M} {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N_M} \le y_M+1 \}} ] \\&= {{\,\mathrm{\mathbb {E}}\,}}[ a \tau ^{{\tiny BM }}_1{\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1\le u\}} ].\end{aligned}$$

Thus we conclude that, as $M \rightarrow \infty$,

$$\begin{aligned} \lim _{M \rightarrow \infty } M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}\lambda = 1 + a {{\,\mathrm{\mathbb {E}}\,}}[ \tau ^{{\tiny BM }}_1{\mathbbm {1}\hspace{-0.83328pt}}{\{ a \tau ^{{\tiny BM }}_1\le u\}} ] + {{\,\mathrm{\mathbb {P}}\,}}( a \tau ^{{\tiny BM }}_1\le u ) = {{\,\mathrm{\mathbb {E}}\,}}\zeta _{a,u}, \end{aligned}$$

where $\zeta _{a,u}$ is as defined in Lemma 4.4. This establishes (2.11), and completes the proof of the theorem. $\square$

4.3 The Confined-Space Limit

In this section we present the proof of Theorem 2.5. As in the previous section, we start with an asymptotic estimate on $\theta (N_M, M):= \theta _{(1,M)} (N_M, M)$ as defined at (4.7).

Proposition 4.5

Suppose that (2.13) holds. Then, as $M \rightarrow \infty$,

$$\begin{aligned} \theta ( N_M, M) = \frac{4}{N_M} (1 + o(1)) \cos ^M \left( \frac{\pi }{N_M} \right) . \end{aligned}$$

(4.27)

Moreover, as $M \rightarrow \infty$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \nu \mid \nu< \infty ] \sim N_M, \text { and } {{{\,\mathrm{\mathbb {V}ar}\,}}}^{N_M,M}_{(1,M)}[ \nu \mid \nu < \infty ] \sim \frac{N_M^3}{3}. \end{aligned}$$

(4.28)

Proof

This follows from Corollary 3.5(i) Indeed (4.27) is (3.13) applied to $\theta (N_M, M ) = {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} > M+1 )$. Similarly (4.28) is a consequence of (3.14) together with the facts that ${{\,\mathrm{{\textbf{E}}}\,}}_1\tau _{0,N} = N-1$ and ${{\,\mathrm{{\textbf{V}\!ar}}\,}}\tau _{0,N} = N (N-1)(N-2)/3$, given in Lemma 3.3. $\square$

We will use the following exponential convergence result for triangular arrays.

Lemma 4.6

Let $K_M \in {\mathbb {Z}}_+$ satisfy ${{\,\mathrm{\mathbb {P}}\,}}( K_M = k) = (1-p_M)^{k} p_M$ for $k \in {\mathbb {Z}}_+$, where $p_M \in (0,1)$, and $\lim _{M \rightarrow \infty } p_M = 0$. Suppose also that $Y_M,Y_{M,1}, Y_{M,2}, \ldots$ are i.i.d., ${\mathbb {R}}_+$-valued, and independent of $K_M$, with ${{\,\mathrm{\mathbb {E}}\,}}[ Y_M^2 ] = \sigma _M^2 < \infty$ and ${{\,\mathrm{\mathbb {E}}\,}}Y_M = \mu _M >0$. Let $Z_M:= \sum _{i=1}^{K_M} Y_{M,i}$. Assuming that

$$\begin{aligned} \lim _{M \rightarrow \infty } \frac{\sigma _M^2 p_M}{\mu _M^2} = 0,\end{aligned}$$

(4.29)

it is the case that, as $M \rightarrow \infty$,

$$\begin{aligned} \frac{p_M Z_M}{\mu _M} \overset{\textrm{d}}{\longrightarrow }{\mathcal {E}_1}.\end{aligned}$$

Lemma 4.6 can be deduced from e.g. Theorem 3.2.4 of [28, p. 85], by verifying that the condition (4.29) implies the ‘uniformly weighted family’ condition from [28, p. 44]. For convenience, we include a direct proof here.

Proof of Lemma 4.6

Let $r_M:= 1/p_M \in (0,\infty )$. For $s \in (0,\infty )$, we have

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ s^{K_M} ] = \frac{p_M}{1-(1-p_M) s}.\end{aligned}$$

Write $\psi _M (t):= {{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{ i t Y_M} ]$, the characteristic function of $Y_M$. Then, for $t \in \mathbb {R}$,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{ i tZ_M} ]&= {{\,\mathrm{\mathbb {E}}\,}}\left[ {{\,\mathrm{\mathbb {E}}\,}}\biggl [ \exp \biggl \{ \sum _{j=1}^{K_M} i t Y_{M,j} \biggr \} \; \biggl | \;K_M \biggr ] \right] = {{\,\mathrm{\mathbb {E}}\,}}\left[ (\psi _M (t) )^{K_M} \right] = \frac{p_M}{1-(1-p_M) \psi _M (t) } .\end{aligned}$$

Set $a_M:= r_M \mu _M$. Thus, for $t \in \mathbb {R}$,

$$\begin{aligned} {{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{i t Z_M/a_M} ] = \frac{1}{1 - (r_M-1) (\psi _M (t/a_M) -1) }.\end{aligned}$$

(4.30)

Fix $t_0 \in (0,\infty )$. The $n=1$ case of (3.3.3) in [18, p. 135], together with the facts that ${{\,\mathrm{\mathbb {E}}\,}}[ Y_M^2 ] = \sigma _M^2 < \infty$ and ${{\,\mathrm{\mathbb {E}}\,}}Y_M = \mu _M$, yields

$$\begin{aligned} r_M \sup _{t \in [-t_0, t_0]} \left| \psi _M ( t / a_M ) - 1 - \frac{ i t}{r_M} \right| \le | t_0 | \frac{\sigma _M^2}{\mu _M^2 r_M},\end{aligned}$$

which tends to zero as $M \rightarrow \infty$, by (4.29). Since $r_M \rightarrow \infty$, it follows that $1 - (r_M-1) ( \psi _M (t/a_M) - 1) = 1 - i t + o(1)$, uniformly in $| t | \le t_0$, and so, by (4.30)

$$\begin{aligned} \lim _{M \rightarrow \infty } {{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{i t Z_M/a_M} ] = \frac{1}{1 - i t}, \end{aligned}$$

for all t in an open interval containing 0, and since ${{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{i t {\mathcal {E}_1}} ] = (1-it)^{-1}$ is the characteristic function of the unit-mean exponential distribution, this completes the proof. $\square$

Proof of Theorem 2.5

To simplify notation, we write $\theta _M:= \theta (N_M, M)$. First suppose that $X_0 = 1$. Then in the representation $\sigma _\kappa = \sum _{i=1}^\kappa \nu _i$, Lemma 4.1 shows that, given $\kappa = k \in \mathbb {N}$, $\nu _1, \ldots , \nu _k$ are i.i.d. with the law of $Y_M$ as given by (4.21), and the law of $\kappa$ is ${{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( \kappa = k ) = (1-\theta _M)^k \theta _M$, for $k \in {\mathbb {Z}}_+$. Thus Lemma 4.6 applies to show that $\sigma _\kappa \rightarrow {\mathcal {E}_1}$ in distribution, provided that (4.29) holds, where $p_M = \theta _M$ satisfies (4.27), and, by (4.28), $\mu _M = {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \nu \mid \nu < \infty ] \sim N_M$ and $\sigma ^2_M = {{{\,\mathrm{\mathbb {V}ar}\,}}}^{N_M,M}_{(1,M)}[ \nu \mid \nu < \infty ] \sim N_M^3/3$. Hence the quantity in (4.29) satisfies

$$\begin{aligned} \frac{\sigma _M^2 p_M}{\mu _M^2 } = \frac{4}{3} (1+o(1)) \cos ^M \left( \frac{\pi }{N_M} \right) \le \frac{4}{3} (1+o(1)) \exp \left\{ - \frac{\pi ^2 M}{2 N_M^2} \right\} ,\end{aligned}$$

which tends to 0 provided that (2.13) holds. Lemma 4.6 then establishes (2.14) in the case where $\zeta _0 = (1,M)$. For general $z_M$ we have (by Lemma 3.3) that ${{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{z_M}[ \nu \mid \nu < \infty ] = O ( N_M^2)$, and, since, by (2.13), $M /N_M^2 \rightarrow \infty$ and $y_M \ge \varepsilon M$ for some $\varepsilon >0$ and all M large enough, it follows from the $a=0$, $y = \varepsilon$ case of (3.8) that $\theta _{z_M} (N_M, M) \rightarrow 0$ as $M \rightarrow \infty$. Hence the first excursion does not change the limit behaviour. $\square$

4.4 The Critical Case

Recall the definition of H from (2.16).

Proposition 4.7

Suppose that (2.15) holds. Then,

$$\begin{aligned} \theta ( N_M, M) = (4/N_M) (1+o(1)) H (\rho ), \text { as } M \rightarrow \infty . \end{aligned}$$

(4.31)

Moreover, for any $s_0 \in (0,\infty )$, as $M \rightarrow \infty$, uniformly for $s \in (0,s_0]$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \textrm{e}^{s \nu / N_M^2} \mid \nu < \infty ] = 1 + \frac{4 s}{N_M} (1+o(1)) \int _0^\rho \textrm{e}^{s y} \bigl ( H (y) - H(\rho ) \bigr ) \textrm{d}y. \end{aligned}$$

(4.32)

Proof

We have from Corollary 3.5(ii) that ${{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N}/N^2 > y ) = (4/N) (1+o(1)) H (y)$, as $N \rightarrow \infty$, uniformly in $y \ge y_0 >0$, where H is defined at (2.16). In particular, under condition (2.15), it follows from continuity of H that $\theta (N_M,M) = {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M}/N_M^2> (M +1)/N_M^2 ) = (1+o(1)) {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M}/N_M^2 > \rho )$ satisfies (4.31).

Let $\varepsilon \in (0,\rho )$. Note that, for every $s \in {\mathbb {R}}_+$,

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ \left( \textrm{e}^{s \nu / N_M^2} -1 \right) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu< \infty \}} \right]&= {{\,\mathrm{{\textbf{E}}}\,}}_1\left[ \left( \textrm{e}^{s \tau _{0,N_M} / N_M^2} -1 \right) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \varepsilon N_M^2 \le \tau _{0,N_M} \le M+1 \}} \right] \nonumber \\&{} \quad {} + {{\,\mathrm{{\textbf{E}}}\,}}_1\left[ \left( \textrm{e}^{s \tau _{0,N_M} / N_M^2} -1 \right) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N_M} < \varepsilon N_M^2 \}} \right] .\nonumber \\\end{aligned}$$

(4.33)

To estimate the second term on the right-hand side of (4.33), we apply (4.16) with $X = \tau _{0,N_M} / N_M^2$, $g(y) = \textrm{e}^{sy} - 1$, $a = 0$, and $b = \varepsilon$ to obtain, for every $s \in (0,\infty )$,

$$\begin{aligned} {{\,\mathrm{{\textbf{E}}}\,}}_1\left[ \left| \textrm{e}^{s \tau _{0,N_M} / N_M^2} -1 \right| {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N_M} < \varepsilon N_M^2 \}} \right] \le s \int _0^{\varepsilon } \textrm{e}^{sy} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} > y N_M^2 ) \textrm{d}y.\end{aligned}$$

Here, it follows from (3.4) that there exists $C < \infty$ such that, for all $N \in \mathbb {N}$,

$$\begin{aligned} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N} \ge y N^2 ) \le \frac{C}{N} (1+y^{-1/2}), \text { for all } y >0.\end{aligned}$$

(4.34)

Thus, for $0 \le s \le s_0 < \infty$ and all $\varepsilon \in (0,1)$,

$$\begin{aligned} {{\,\mathrm{{\textbf{E}}}\,}}_1\left[ \left| \textrm{e}^{s \tau _{0,N_M} / N_M^2} -1 \right| {\mathbbm {1}\hspace{-0.83328pt}}{\{ \tau _{0,N_M} < \varepsilon N_M^2 \}} \right]{} & {} \le \frac{C s_0 \textrm{e}^{s_0}}{N_M} \int _0^{\varepsilon } (1+ y^{-1/2}) \textrm{d}y\nonumber \\ {}{} & {} \le \frac{C(s_0) \varepsilon ^{1/2}}{N_M},\end{aligned}$$

(4.35)

where $C(s_0) < \infty$ depends on $s_0$ only. To estimate the first term on the right-hand side of (4.33), we apply (4.16) with $X = \tau _{0,N_M} / N_M^2$, $g(y) = \textrm{e}^{sy} - 1$, $a = \varepsilon$, and $b = \rho _M:= (M+1)/N_M^2 = \rho + o(1)$ to obtain

$$\begin{aligned}&{} {{\,\mathrm{{\textbf{E}}}\,}}_1\left[ \left( \textrm{e}^{s \tau _{0,N_M} / N_M^2} -1 \right) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \varepsilon N_M^2 \le \tau _{0,N_M} \le M+1 \}} \right] = (\textrm{e}^{s\varepsilon }-1) {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} \ge \varepsilon N_M^2 ) \nonumber \\&\quad {} - (\textrm{e}^{s\rho _M}-1) {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M}> \rho _M N_M^2 ) + s \int _\varepsilon ^{\rho _M} \textrm{e}^{sy} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} > y N_M^2 ) \textrm{d}y ; \end{aligned}$$

(4.36)

note that $\rho _M > \varepsilon$ for all M sufficiently large, since $\varepsilon < \rho$. Since there is some $C < \infty$ for which $\textrm{e}^{s\varepsilon }-1 \le C s_0 \varepsilon$ for all $s \le s_0$ and all $\varepsilon \in (0,1)$, we have from (4.34) that the first term on the right-hand side of (4.36) satisfies

$$\begin{aligned} 0 \le (\textrm{e}^{s\varepsilon }-1){{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} \ge \varepsilon N_M^2 ) \le \frac{C(s_0) \varepsilon ^{1/2}}{N_M}, \end{aligned}$$

where, again, $C(s_0) < \infty$ depends on $s_0$ only. Corollary 3.5(ii) implies that, for any fixed $\varepsilon \in (0,1)$,

$$\begin{aligned} \int _\varepsilon ^{\rho _M} \textrm{e}^{sy} {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} > y N_M^2 ) \textrm{d}y = \frac{4}{N_M} (1+o(1)) \int _\varepsilon ^\rho \textrm{e}^{sy} H (y) \textrm{d}y,\end{aligned}$$

and

$$\begin{aligned} (\textrm{e}^{s\rho _M}-1) {{\,\mathrm{{\textbf{P}}}\,}}_1( \tau _{0,N_M} > \rho _M N_M^2 ) = \frac{4}{N_M} (1+o(1)) (\textrm{e}^{s\rho }-1) H(\rho ).\end{aligned}$$

Hence, combining (4.33) with (4.35) and (4.36), and taking $\varepsilon \downarrow 0$, we obtain

$$\begin{aligned} \lim _{M \rightarrow \infty } \sup _{0<s \le s_0} \left| \frac{N_M}{4} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ \left( \textrm{e}^{s \nu / N_M^2} -1 \right) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu < \infty \}} \right] - s \int _0^\rho \textrm{e}^{sy} \bigl ( H (y) - H(\rho ) \bigr ) \textrm{d}y \right| = 0.\end{aligned}$$

Finally, we observe that

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \textrm{e}^{s \nu / N_M^2} - 1 \mid \nu< \infty ] = \frac{ {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\left[ \left( \textrm{e}^{s \nu / N_M^2} -1 \right) {\mathbbm {1}\hspace{-0.83328pt}}{\{ \nu< \infty \}} \right] }{{{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( \nu < \infty )},\end{aligned}$$

and ${{{\,\mathrm{\mathbb {P}}\,}}}^{N_M,M}_{(1,M)}( \nu < \infty ) = 1- \theta (N_M,M) \rightarrow 1$, by (4.7) and (4.31). Now (4.32) follows. $\square$

Lemma 4.8

The function H from (2.16) satisfies the following.

• (i) As $y \downarrow 0$, $2\,H(y) \sqrt{2 \pi y} \rightarrow 1$.

• (ii) As $y \rightarrow \infty$, $H(y) = (1+o(1)) \textrm{e}^{-\pi ^2 y /2}$.

Proof

Write $c:= \pi ^2 /2$, so that (2.16) reads $H(y) = \sum _{k=1}^\infty \textrm{e}^{-c (2k-1)^2 y}$. Then,

$$\begin{aligned} 0 \le H(y) - \textrm{e}^{-cy} \le \textrm{e}^{-9cy} \sum _{k=0}^\infty \textrm{e}^{-c [ (2k+3)^2 -9 ] y} \le \textrm{e}^{-9cy} \sum _{k=0}^\infty \textrm{e}^{-16c k y},\end{aligned}$$

and hence $0 \le H(y) - \textrm{e}^{-\pi ^2 y /2} \le \textrm{e}^{- 4 \pi ^2 y}$ for all y sufficiently large. This yields part (ii). On the other hand, since $k \mapsto h_k (y)$ is strictly decreasing for fixed $y >0$,

$$\begin{aligned} \int _1^\infty \textrm{e}^{- c (2 t -1)^2 y} \textrm{d}t \le H (y) \le 1 + \int _1^\infty \textrm{e}^{- c (2 t -1)^2 y} \textrm{d}t,\end{aligned}$$

where, by the change of variable $z = (2t-1) \sqrt{2 cy}$,

$$\begin{aligned} \int _1^\infty \textrm{e}^{- c (2 t -1)^2 y} \textrm{d}t = \frac{1}{2 \pi \sqrt{y}} \int _{\sqrt{2cy}}^\infty \textrm{e}^{- z^2 /2} \textrm{d}z = \frac{1+o(1)}{2 \sqrt{2\pi y}}, \end{aligned}$$

as $y \downarrow 0$, which gives part (i). $\square$

Proof of Theorem 2.7

Let $s > 0$, and recall the definition of $\psi _M(s)= {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}[ \textrm{e}^{s \nu } \mid \nu < \infty ]$ from (4.12). Then, as at (4.23),

$$\begin{aligned} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\bigl [ \textrm{e}^{s \sigma _\kappa / M} \bigr ] = \frac{\theta _M}{1-(1-\theta _M) \psi _M ( s / M ) }, \text { provided } (1-\theta _M) \psi _M ( s / M ) < 1, \end{aligned}$$

where $\theta _M:= \theta (N_M, M)$. Combining (4.31) and (4.32), with the fact that $M \sim \rho N_M^2$, by (2.15), we conclude that

$$\begin{aligned} \lim _{M \rightarrow \infty } {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\bigl [ \textrm{e}^{s \sigma _\kappa / M} \bigr ] = \frac{1}{1 - G (\rho , s)}, \text { provided } G (\rho , s) < 1, \end{aligned}$$

(4.37)

where G is defined at (2.17). Since $\lambda = M +1 + \sigma _\kappa$, by (4.6), it follows from (4.37) that $\lambda / M$ converges in distribution to $1 + \xi _\rho$, where ${{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{s\xi _\rho } ] = \phi _\rho (s)$ as defined at (2.18).

From (2.17), we have that, for fixed $\rho >0$, $s \mapsto G(\rho , s)$ is differentiable on $s \in (0,\infty )$, with derivative $G' ( \rho , s):= \frac{\textrm{d}}{\textrm{d}s} G (\rho , s)$ satisfying

$$\begin{aligned} G' (\rho , 0^+):= \lim _{s \downarrow 0} G' (\rho , s ) = \frac{1}{H ( \rho )} \int _0^1 \bigl ( H ( v \rho ) - H(\rho ) \bigr ) \textrm{d}v = \mu ( \rho ),\end{aligned}$$

as given by (2.19), as we see from the change of variable $y = \rho v$. Hence $\phi _\rho$ is differentiable for $s \in (0,s_\rho )$, with derivative $\phi '_\rho (s) = \frac{G'(\rho ,s)}{(1-G(\rho ,s))^2}$, and

$$\begin{aligned} \phi '_\rho (0^+):= \lim _{s \downarrow 0} \phi '_\rho (s) = G' (\rho , 0^+) = \mu (\rho ). \end{aligned}$$

The convergence of the moment generating function in (4.37) in the region $s \in (0,s_0)$ implies convergence also of the mean, $\lim _{M \rightarrow \infty } M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\sigma _\kappa = \phi _\rho (0^+) = \mu (\rho )$, and hence $\lim _{M \rightarrow \infty } M^{-1} {{{\,\mathrm{\mathbb {E}}\,}}}^{N_M,M}_{(1,M)}\lambda = 1 + \mu (\rho )$. The asymptotics for $\mu$ stated in (2.21) follow from (2.19) with the asymptotics for H in Lemma 4.8, together with the observation that

$$\begin{aligned} \int _0^\infty H(y) \textrm{d}y = \sum _{k=1}^\infty \int _0^\infty h_k (y)\textrm{d}y = \frac{2}{\pi ^2} \sum _{k=1}^\infty \frac{1}{(2k-1)^2} = \frac{1}{4},\end{aligned}$$

using Fubini’s theorem. This completes the proof. $\square$

5 Concluding Remarks

To conclude, we identify a number of potentially interesting open problems.

• Staying in the context of the M-capacity models, we expect that at least the non-critical results of the present paper are rather universal, and should extend to more general domains, and to more general diffusion dynamics within a suitable class. For example, we expect that for a large class of energy-constrained random walk models in a domain of diameter N with energy capacity M, the regimes $M \ll N^2$ (meagre capacity) and $M \gg N^2$ (confined space) should lead to Darling–Mandelbrot and exponential limits, respectively, for the total lifetime.

• The total lifetime is just one statistic associated with the model: other quantities that it would be of interest to study include the location of the walker on extinction.

• The model presented in Sect. 2.1 includes several other natural models, in addition to the particular finite-capacity model with total replenishment that we study here. For example, one could consider a model of infinite capacity and a random replenishment distribution. In models with unbounded energy, there may be positive probability that the walker survives for ever (i.e., transience).

Appendix A: Darling–Mandelbrot Distribution

Recall the definition of the function $K: \mathbb {R}\rightarrow \mathbb {R}$ and the set $\mathcal {T}$ from (4.13). Write M(a, b, t) for the Kummer function defined for $a, b \notin -\mathbb {N}$ by the convergent series

$$\begin{aligned} M(a,b,t):= \frac{\Gamma (b)}{\Gamma (a)} \sum _{\ell =0}^\infty \frac{\Gamma (a+\ell )}{\Gamma (b+\ell )} \frac{t^\ell }{\ell !}, \text { for } t \in \mathbb {R}; \end{aligned}$$

see [4, Chapter 13] or [12, pp. 647–8]. Then, by (4.13), $K (t) = M (-\frac{1}{2}, \frac{1}{2}, t)$. This identification is the basis for the following facts.

Lemma A.1

• (a) As $t \rightarrow \infty$, we have $K(-t) \sim \sqrt{\pi t}$ and $K(t) \sim - \textrm{e}^t/(2t)$.

• (b) The function K is infinitely differentiable, with $K^{(\ell )} (t):= (\textrm{d}^\ell / \textrm{d}t^\ell ) K (t) < 0$ for every $\ell \in \mathbb {N}$ and all $t \in \mathbb {R}$, and $K^{(\ell )} (0) = -1/(2\ell -1)$.

• (c) We have that $\mathcal {T}= (-\infty , t_0)$ where $t_0$ is uniquely determined by $\sum _{\ell =1}^\infty \frac{t_0^\ell }{(2\ell -1) \cdot \ell !} =1$; numerically, $t_0 \approx 0.8540326566$.

• (d) With $\mathcal {I}$ as defined at (2.5), it is the case that

  $$\begin{aligned} K(t) = \textrm{e}^t - \mathcal {I}( t ), \text { for all } t \in \mathbb {R}. \end{aligned}$$

  (A.1)

Remark A.2

The constant $t_0$ in Lemma A.1(c) also appears in relation to asymptotics of $T_n$, the maximum excursion duration over the first n steps of a simple symmetric random walk on $\mathbb {Z}$. It was shown by Csáki, Erdős and Révész [16, Thm. 1] that

$$\begin{aligned} \liminf _{n \rightarrow \infty } \left[ \frac{\log \log n}{n} T_n \right] = t_0, \ \text {a.s.}\end{aligned}$$

See also [30, 34] for some neighbouring results.

Proof of Lemma A.1

The $t \rightarrow \pm \infty$ asymptotics can be read off from (13.1.4) and (13.1.5) in [4]. The derivatives of K are obtained from equation (13.4.9) in [4] as

$$\begin{aligned} \frac{\textrm{d}^\ell }{\textrm{d}t^\ell } K(t) = \frac{\Gamma \left( \tfrac{1}{2} \right) \Gamma \left( \ell - \tfrac{1}{2} \right) }{\Gamma \left( -\tfrac{1}{2} \right) \Gamma \left( \ell + \tfrac{1}{2} \right) } M \left( \ell - \frac{1}{2}, \ell + \frac{1}{2}, t \right) = - \frac{1}{2\ell -1 } M \left( \ell - \frac{1}{2}, \ell + \frac{1}{2}, t \right) .\end{aligned}$$

Thus $K^{(\ell )} (0) = -1/(2\ell -1)$. For $b> a > 0$, the integral representation (13.2.1) in [4] shows that $M (a,b,t) > 0$ for all $t \in \mathbb {R}$, and hence $(\textrm{d}^\ell / \textrm{d}t^\ell ) K (t) < 0$ for all $\ell \in \mathbb {N}$, as claimed. In particular, K is monotone decreasing, with $K(0) = 1$, so there is a unique $t_0 \in \mathbb {R}$ with $K(t_0) = 0$, one has $t_0 > 0$, and $K(t) > 0$ if and only if $t < t_0$. Finally, equations (13.4.4) and (13.6.12) in [4] show that

$$\begin{aligned} K (t) = M \left( -\frac{1}{2}, \frac{1}{2}, t \right) = M \left( \frac{1}{2}, \frac{1}{2}, t \right) - 2 t M \left( \frac{1}{2}, \frac{3}{2}, t \right) = \textrm{e}^t - 2 t M \left( \frac{1}{2}, \frac{3}{2}, t \right) .\end{aligned}$$

Moreover, since $\frac{3}{2}> \frac{1}{2} >0$, equation (13.2.1) in [4] shows that $\mathcal {I}(t) = 2 t M( \frac{1}{2}, \frac{3}{2}, t )$. This verifies (A.1). $\square$

Lemma A.3

The moments $\upsilon _k:= {{\,\mathrm{\mathbb {E}}\,}}[ \xi ^k ]$ $(k\in \mathbb {N})$ of the random variable $\xi$ defined by (2.6) are determined uniquely by the recursion

$$\begin{aligned} \upsilon _k = \sum _{j=1}^k \left( {\begin{array}{c}k\\ j\end{array}}\right) \frac{\upsilon _{k-j}}{2j-1}, \text { for } k \in \mathbb {N}, \end{aligned}$$

(A.2)

with the initial condition $\upsilon _0 = 1$. In particular, the first few moments are as follows:

k	1	2	3	4	5	6
$\upsilon _k$	1	$\frac{7}{3}$	$\frac{41}{5}$	$\frac{4033}{105}$	$\frac{14167}{63}$	$\frac{1824719}{1155}$

Proof

From (2.6) and (A.1), we have that $\varphi _{\textrm{DM}}(t) = {{\,\mathrm{\mathbb {E}}\,}}[ \textrm{e}^{t\xi } ] = 1 / K(t)$, where, for $\ell \in \mathbb {N}$, $K^{(\ell )} (0) = - 1/(2\ell -1)$, as shown in Lemma A.1(b). Differentiating $k \in \mathbb {N}$ times the equality $K(t) \varphi _{\textrm{DM}}(t) = 1$, we obtain

$$\begin{aligned} \sum _{j=0}^k \left( {\begin{array}{c}k\\ j\end{array}}\right) K^{(j)} (t) \varphi _{\textrm{DM}}^{(k-j)} (t) = 0, \text { for } k \in \mathbb {N}. \end{aligned}$$

Taking $t=0$ and noting that $\nu _k = \varphi _{\textrm{DM}}^{(k)} (0)$ and $K^{(0)} (0) = K(0) = 1$ gives the result. $\square$