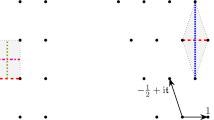Extensions of Exact and K-Mixing Dynamical Systems

Abstract

We consider extensions of non-singular maps which are exact, respectively K-mixing, or at least have a decomposition into positive-measure exact, respectively K-mixing, components. The fibers of the extension spaces have countable (finite or infinite) cardinality and the action on them is assumed surjective or bijective. We call these systems, respectively, fiber-surjective and fiber-bijective extensions. Technically, they are skew products, though the point of view we take here is not the one generally associated with skew products. Our main results are an Exact and a K-mixing Decomposition Theorem. The latter can be used to show that a large number of periodic Lorentz gases (the term denoting here general group extensions of Sinai billiards, including Lorentz tubes and slabs, in any dimension) are K-mixing.

1 Introduction

A non-invertible map $T: \mathcal {M}\longrightarrow \mathcal {M}$, which is two-sided non-singular for the $\sigma$-finite measure space $(\mathcal {M}, \mathscr {A}, \mu )$, is called exact if

$$\begin{aligned} \bigcap _{n \in \mathbb {N}} T^{-n} \mathscr {A}= \mathscr {N}, \end{aligned}$$

(1)

where $\mathscr {N}$ is the null, or trivial $\sigma$-algebra on $\mathcal {M}$, containing only the zero-measure sets and their complements. Its significance is that the dynamical system $(\mathcal {M}, \mathscr {A}, \mu , T)$ carries vanishing information about its initial conditions into the far future; equivalently, it retains vanishing information about the state of the system in the remote past. In fact, if an observer makes a finite-precision measurement of the state of the system at present time and $\mathscr {O}$ is the (necessarily finite) $\sigma$-algebra representing the resolution of the measurement, the resolution that the observer obtains on the state of the system at time $-n$ is given by $T^{-n} \mathscr {O} \subseteq T^{-n} \mathscr {A}$, which becomes trivially coarse as $n \rightarrow \infty$.

If T is an invertible map the above definition cannot work, in general, because $T^{-n} \mathscr {A}= \mathscr {A}$ for all n. One uses instead the definition of K-mixing, a.k.a. K-property (after Kolmogorov), which means that there exists a $\sigma$-algebra $\mathscr {B}\subset \mathscr {A}$ such that

$$\begin{aligned} T \mathscr {B}\supset \mathscr {B}, \qquad \sigma \! \left( \bigcup _{n\in \mathbb {N}} T^n \mathscr {B}\right) = \mathscr {A}\mod \mu , \qquad \bigcap _{n \in \mathbb {N}} T^{-n} \mathscr {B}= \mathscr {N}, \end{aligned}$$

(2)

where $\sigma ( \cdot )$ means the $\sigma$-algebra generated by a family of subsets. In this case, the $\sigma$-algebra $\mathscr {O}$ of the present-time observation, being finite, can be approximated to any degree by a $\sigma$-algebra $\mathscr {O}' \subseteq T^N \mathscr {B}$, for some N. This implies that $\bigcap _n T^{-n} \mathscr {O}' = \mathscr {N}$, leading to the same interpretation as before.

In this paper we study the exact, respectively K-mixing, components of extensions of exact, respectively K-mixing, dynamical systems, or at least dynamical systems whose exact/K-mixing components have positive measure. If $T_o$ is an endomorphism of the Lebesgue space $(\mathcal {M}_0, \mathscr {A}_o, \mu _o)$, we consider the system $(\mathcal {M}, \mathscr {A}, \mu , T)$, where $\mathcal {M}:= \mathcal {M}_o \times \mathcal {I}$ and $\mathcal {I}$ is a countable (finite or infinite) set. The map $T: \mathcal {M}\longrightarrow \mathcal {M}$ acts as

$$\begin{aligned} T(x,i) := (T_o(x), \Psi (x,i)), \end{aligned}$$

(3)

where the functions $\Psi (x, \cdot ): \mathcal {I}\longrightarrow \mathcal {I}$ are surjective or bijective, depending on the sought result (of course the two assumptions coincide when $\mathcal {I}$ is finite). As for $\mathscr {A}$ and $\mu$, they are the natural lifts of $\mathscr {A}_o$ and $\mu _o$, respectively, to $\mathcal {M}_o \times \mathcal {I}$ (see Sect. 2 for details). If the functions $\Psi (x, \cdot )$ are surjective, respectively bijective, we say that T is a fiber-surjective, respectively fiber-bijective, extension of $T_o$. These two classes of dynamical systems are quite general. For example, every group extension, that is, a case where $\mathcal {I}$ is an abelian group and $\Psi (x,i) = i + \psi (x)$, for some $\psi : \mathcal {M}_o \longrightarrow \mathcal {I}$, is fiber-bijective. Notable examples are periodic Lorentz gases, which are $\mathbb {Z}^d$-extensions of Sinai billiards. The recent paper [17] studies the exact components of certain Markov maps of $\mathbb {R}$, including $\mathbb {Z}$-extensions of expanding circle maps.

A term that is often used for systems similar to fiber-surjective maps is skew products, but when one speaks of a skew product, one usually means the case where $\mathcal {I}$ is an uncountable space with some structure (measure-theoretic, topological, differentiable, etc.) and $T_o$ is an automorphism of a measure space (typically a probability space). More importantly, the focus tends to be on the action of the maps $\Psi (T_o^{n-1}(x), \cdot ) \circ \cdots \circ \Psi (T_o(x), \cdot ) \circ \Psi (x, \cdot )$ on $\mathcal {I}$, rather than the dynamics of T on the whole $\mathcal {M}_o \times \mathcal {I}$, as is the case here. (See [5, 12] for results on the exactness of certain families of skew products.)

We describe our main results in some detail. If $(\mathcal {M}_0, \mathscr {A}_o, \mu _o, T_o)$ is exact and T is fiber-surjective, there are at most countably many ergodic components of T. Each of them is partitioned into $m \in \mathbb {Z}^+ \cup \{ \infty \}$ positive-measure sets, which we call atoms, and T maps atoms onto atoms. If $m \in \mathbb {Z}^+$, T acts as an m-cycle between the atoms and $T^m$ is exact on each of them. If $m = \infty$, T acts as a shift between the atoms. A completely analogous theorem is proved for the case where $(\mathcal {M}_0, \mathscr {A}_o, \mu _o, T_o)$ is K-mixing and T is fiber-bijective (subject to a natural technical condition). In this case, for $m \in \mathbb {Z}^+$, $T^m$ is K-mixing on the atoms of an m-cycle. Theorems of this kind are sometimes called Spectral Decomposition Theorems [11, 18], a phrase we choose to avoid in the context of infinite ergodic theory. Here we refer to them, respectively, as the Exact and the K-mixing Decomposition Theorem. In addition, assuming that T is fiber-bijective (even for the case of $T_o$ exact), we are able to provide extra information on the structure of the ergodic components and of the atoms within cycles. This implies in particular that, if T is conservative (i.e., recurrent), it is isomorphic to another map $T_1$ on $(\mathcal {M}, \mathscr {A}, \mu )$ whose atoms are made up of sets $\mathcal {M}_o \times \{i\}$.

Finally, as an application of the K-mixing Decomposition Theorem, we show that, rather generally, a periodic Lorentz gas is K-mixing if and only if it is conservative. In particular, this establishes the K-property for a large number of periodic Lorentz tubes and slabs (see Sect. 4).

The paper is organized as follows. In Sect. 2 we present the mathematical setup, establish the notation that is used throughout the paper, and state our main results, which are proved in Sect. 3. In Sect. 4, which is designed to be read independently of Sect. 3, we show how to apply the K-mixing Decomposition Theorem to periodic Lorentz gases.

2 Setup and Results

Given a dynamical system $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$, with $(\mathcal {M}_o, \mathscr {A}_o, \mu _o)$ a Lebesgue measure space and $T_o: \mathcal {M}_o \longrightarrow \mathcal {M}_o$ bimeasurable and two-sided non-singular (i.e., $\mu _o(A)=0$ $\Leftrightarrow$ $\mu _o(T_o^{-1} A)=0$), we consider its extension $(\mathcal {M}, \mathscr {A}, \mu , T)$, where:

• $\mathcal {M}:= \mathcal {M}_o \times \mathcal {I}$, for some countable (finite or infinite) $\mathcal {I}$;

• $\mathscr {A}$ is the lift of $\mathscr {A}_o$ to $\mathcal {M}$, i.e., $\mathscr {A}:= \sigma ( \left\{ A \times \{i\} \, \left| \, A \in \mathscr {A}_o,\, i\in \mathcal {I} \right. \! \right\} )$;

• $\mu$ is the lift of $\mu _o$ to $\mathcal {M}$, i.e., $\mu$ is the measure on $\mathscr {A}$ uniquely defined by $\mu ( A \times \{i\} ) = \mu _o(A)$, for all $A \in \mathscr {A}_o$ and $i\in \mathcal {I}$;

• T is a bimeasurable self-map of $\mathcal {M}$ given by $T(x,i) = (T_o(x), \Psi (x,i))$. Depending on the context, we assume that, for $\mu _o$-a.a. $x \in \mathcal {M}_o$,

  $$\begin{aligned} \Psi _x := \Psi (x, \cdot ) : \mathcal {I}\longrightarrow \mathcal {I}\ \text{ is } \text{ surjective } \text{ or } \text{ bijective }. \end{aligned}$$

  (4)

  In the first case we call T a fiber-surjective extension of $T_o$; in the second case, we call it a fiber-bijective extension of $T_o$. Clearly, the two conditions are equivalent if $\# \mathcal {I}< \infty$.

Observe that, since $T_o$ is bimeasurable, the bimeasurability of T is equivalent to the condition that the level sets of $\Psi ( \cdot , i)$ are measurable, that is, for all $i,j \in \mathcal {I}$, $\left\{ x\in \mathcal {M}_o \, \left| \, \Psi (x,i)=j \right. \! \right\} \in \mathscr {A}_o$. This is in turn equivalent to the measurability and bimeasurability of $\Psi$ w.r.t. the power set of $\mathcal {I}$.

We denote by $\pi : \mathcal {M}\longrightarrow \mathcal {M}_o$ the natural projection $\pi (x,i) := x$. By construction, $\pi \circ T = T_o \circ \pi$. The main purpose of assumption (4) is to also have $\pi \circ T^{-1} = T_o^{-1} \circ \pi$, in the sense of a relation between sets, as follows.

Lemma 2.1

If T is a fiber-surjective extension of $T_o$ then, for all $A \in \mathscr {A}$,

$$\begin{aligned} \pi \, T^{-1} A = T_o^{-1} \, \pi A \mod \mu . \end{aligned}$$

Proof

It is enough to show that $\pi (T^{-1}(y,j)) = T_o^{-1}(\pi (y,j)) = T_o^{-1}(y)$, for $\mu$-a.e. $(y,j) \in \mathcal {M}$. By fiber-surjectivity, for $\mu _o$-a.e. $x \in T_o^{-1}(y)$, there exists $i \in \mathcal {I}$ such that $T(x,i) = (y,j)$. Also, clearly, no $x \not \in T_o^{-1}(y)$ can be such that $T(x,i) = (y,j)$ for some i. Thus, $\mu$-a.s. in (y, j), which implies $\mu _o$-a.s. in y and thus $\mu _o$-a.s. in x (by the non-singularity of $T_o$),

$$\begin{aligned} \pi (T^{-1}(y,j)) = \pi ( \left\{ (x,i) \in \mathcal {M} \, \left| \, T(x,i) = (y,j) \right. \! \right\} ) = T_o^{-1}(y), \end{aligned}$$

(5)

which is equivalent to the desired claim. $\square$

Proposition 2.2

If T is fiber-surjective, T is two-sided non-singular if and only if $T_o$ is. If T is fiber-bijective, T preserves $\mu$ if and only if $T_o$ preserves $\mu _o$.

Proof

The two-sided non-singularity is an immediate consequence of Lemma 2.1, since, for all $A \in \mathscr {A}$, $\mu (A) = 0$ $\Leftrightarrow$ $\mu _o(\pi A) = 0$.

As for the second statement, it suffices to check the preservation of $\mu$ on all sets of the type $B \times \{j\}$. By the injectivity of a.a. $\Psi _x$, cf. (4), the sets

$$\begin{aligned} B_i := \left\{ x \in \mathcal {M}_o \, \left| \, T(x,i) \in B \times \{j\} \right. \! \right\} \end{aligned}$$

(6)

are disjoint mod $\mu _o$ in $\mathcal {M}_o$. In other words, $\pi$ is injective mod $\mu$ on $T^{-1}(B \times \{j\})$, giving

$$\begin{aligned} \mu ( T^{-1}(B \times \{j\}) ) = \sum _{i \in \mathcal {I}} \mu (B_i \times \{i\}) = \mu _o \! \left( \bigsqcup _{i \in \mathcal {I}} B_i \right) = \mu _o ( T_o^{-1} B ), \end{aligned}$$

(7)

where the last equality follows from the surjectivity of a.a. $\Psi _x$. Since $\mu (B \times \{j\}) = \mu _o(B)$, this concludes the proof of the second statement. $\square$

Convention From now on, all statements about sets are intended modulo null sets, w.r.t. the relevant measure. For example, if $A,B \in \mathcal {M}$, the equality $A=B$ means $\mu (A \triangle B) = 0$; the inclusion $A \subseteq B$ means $\mu (A\setminus B) = 0$; with $A \subset B$ implying in addition that $\mu (B\setminus A) > 0$. The convention includes $\sigma$-algebras. For instance, $\mathscr {A}\subseteq \mathscr {B}$ is intended in the sense that the inclusion holds for the respective completions.

We now present our decomposition theorems and corollaries. In order to do so, we recall that, for any non-singular dynamical system $(\mathcal {M}, \mathscr {A}, \mu , T)$, $\mathcal {M}$ can be decomposed into a conservative part $\mathcal {C}$ and a dissipative part $\mathcal {D}$ [1, Sect. 1.1]. $\mathcal {C}$ is the part where Poincaré recurrence holds, $\mathcal {D}$ is the measurable union of all wandering sets. This is called the Hopf decomposition of T and is such that $T^{-1} \mathcal {C} \supseteq \mathcal {C}$ and $T^{-1} \mathcal {D} \subseteq \mathcal {D}$. It T is measure-preserving, these inclusions become equalities. It is easy to see that $T^m$, $m\ge 2$, has the same Hopf decomposition as T. The proofs of all the following results are given in Sect. 3.

Theorem 2.3

Let $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$ be exact with $(\mathcal {M}, \mathscr {A}, \mu , T)$ a fiber-surjective extension, as defined earlier. Then the tail $\sigma$-algebra

$$\begin{aligned} \mathscr {T}(T) := \bigcap _{n\in \mathbb {N}} T^{-n} \mathscr {A}\end{aligned}$$

is atomic, in the sense that it is generated by a partition $\mathscr {P}$ of $\mathcal {M}$, with the following properties:

• (i) Every $P \in \mathscr {P}$ (henceforth called an atom of $\mathscr {P}$ or $\mathscr {T}(T)$) has positive (possibly infinite) measure. In particular, $\mathscr {P}$ is countable.

• (ii) For all $P \in \mathscr {P}$ and $n \in \mathbb {Z}$, $T^n P \in \mathscr {P}$.

• (iii) All ergodic components are of the form $\mathcal {E}= \mathcal {E}_P := \bigcup _{n \in \mathbb {Z}} T^n P$, for some $P \in \mathscr {P}$. An ergodic component can comprise a finite number m of atoms, in which case we call it an m-cycle, or an infinite number of atoms, in which case we call it a chain.

• (iv) If $P \in \mathscr {P}$ and $m \in \mathbb {Z}^+$ are such that $T^m P = P$, then $T^m|_P : P \longrightarrow P$ is exact. If in addition $\mu (P) < \infty$, then $\mathcal {E}_P$ belongs to the conservative part of the system.

If T is also fiber-bijective then:

• (v) Given an ergodic component $\mathcal {E}$, $\# \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in \mathcal {E} \right. \! \right\}$ is constant for $\mu _o$-a.e. $x \in \mathcal {M}_o$. Denoting it $N_\mathcal {E}\in \mathbb {Z}^+ \cup \{\infty \}$, it follows that $\pi |_\mathcal {E}: \mathcal {E}\longrightarrow \mathcal {M}_o$ is $N_\mathcal {E}$-to-1 and onto, whence $\mu (\mathcal {E}) = N_\mathcal {E}\, \mu _o(\mathcal {M}_o)$.

• (vi) If $\mathcal {E}= \mathcal {E}_P$ is an m-cycle, then also $\# \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in P \right. \! \right\}$ is constant for $\mu _o$-a.e. $x \in \mathcal {M}_o$. Denoting it $N_P \in \mathbb {Z}^+ \cup \{\infty \}$, it follows that $\pi |_P: P \longrightarrow \mathcal {M}_o$ is $N_P$-to-1 and onto, whence $\mu (P) = N_P \, \mu _o(\mathcal {M}_o)$. Furthermore, $N_P = N_{P'}$ for all atoms $P'$ of $\mathcal {E}_P$. Thus, $\mu (P) = \mu (P')$ and $\mu (\mathcal {E}_P) = m \mu (P)$.

• (vii) If T is conservative, T is isomorphic to another fiber-bijective extension $T_1$, defined again on $(\mathcal {M}, \mathscr {A}, \mu )$, the atoms of whose $\sigma$-algebra are made up of entire levels $\mathcal {M}_o \times \{i\}$.

One need not assume the exactness of the base system to ensure that a fiber-bijective extension has an atomic tail $\sigma$-algebra. If the base system itself has an atomic tail $\sigma$-algebra, this property carries over to the extension.

Corollary 2.4

Assertions (i)–(iv) of Theorem 2.3 also hold in the case where the tail $\sigma$-algebra of $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$ is atomic, i.e., $\mathscr {T}(T_o)$ is generated by a partition with positive-measure elements. Moreover, if P is an atom of $\mathscr {T}(T)$, then $\pi P$ is an atom of $\mathscr {T}(T_o)$.

Analogous results hold for the case where $T_o$ is K-mixing. The familiar reader will see how the extra assumption on the $\mathscr {B}$-measurability of $\Psi ( \cdot , i)$ is obvious if T is to exploit the K-property of $T_o$.

Theorem 2.5

Let $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$ be K-mixing w.r.t. the $\sigma$-algebra $\mathscr {B}_o \subset \mathscr {A}_o$, with $(\mathcal {M}, \mathscr {A}, \mu , T)$ a fiber-bijective extension, as defined earlier. Denote by $\mathscr {B}$ the lift of $\mathscr {B}_o$ to $\mathcal {M}$. Assume that $\Psi$ is measurable w.r.t. $\mathscr {B}$ (equivalently, $\Psi ( \cdot , i): \mathcal {M}_o \longrightarrow \mathcal {I}$ is $\mathscr {B}_o$-measurable for all i; equivalently, the level sets of $\Psi ( \cdot , i )$ are $\mathscr {B}_o$-measurable). Then the $\sigma$-algebra

$$\begin{aligned} \mathscr {T}_\mathscr {B}(T) := \bigcap _{n\in \mathbb {N}} T^{-n} \mathscr {B}\end{aligned}$$

is atomic, being generated by a partition $\mathscr {P}$ of $\mathcal {M}$ with the following properties:

• (i) Every $P \in \mathscr {P}$ (again called an atom of $\mathscr {P}$ or $\mathscr {T}_\mathscr {B}(T)$) has positive (possibly infinite) measure. In particular, $\mathscr {P}$ is countable.

• (ii) For all $P \in \mathscr {P}$ and $n \in \mathbb {Z}$, $T^n P \in \mathscr {P}$.

• (iii) All ergodic components are of the form $\mathcal {E}= \mathcal {E}_P := \bigcup _{n \in \mathbb {Z}} T^n P$, for some $P \in \mathscr {P}$.

• (iv) If $P \in \mathscr {P}$ and $m \in \mathbb {Z}^+$ are such that $T^m P = P$, then $T^m|_P : P \longrightarrow P$ is K-mixing w.r.t. the $\sigma$-algebra $\mathscr {B}\cap P := \left\{ A \cap P \, \left| \, A \in \mathscr {B} \right. \! \right\}$. In particular, if $\mu (P) < \infty$, then $\mathcal {E}_P$ belongs to the conservative part of the system.

• (v) Given an ergodic component $\mathcal {E}$, $\# \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in \mathcal {E} \right. \! \right\}$ is constant for $\mu _o$-a.e. $x \in \mathcal {M}_o$. Denoting it $N_\mathcal {E}\in \mathbb {Z}^+ \cup \{\infty \}$, it follows that $\pi |_\mathcal {E}: \mathcal {E}\longrightarrow \mathcal {M}_o$ is $N_\mathcal {E}$-to-1 and onto, whence $\mu (\mathcal {E}) = N_\mathcal {E}\, \mu _o(\mathcal {M}_o)$.

• (vi) If $\mathcal {E}= \mathcal {E}_P$ is an m-cycle, then also $\# \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in P \right. \! \right\}$ is constant for $\mu _o$-a.e. $x \in \mathcal {M}_o$. Denoting it $N_P \in \mathbb {Z}^+ \cup \{\infty \}$, it follows that $\pi |_P: P \longrightarrow \mathcal {M}_o$ is $N_P$-to-1 and onto, whence $\mu (P) = N_P \, \mu _o(\mathcal {M}_o)$. Furthermore, $N_P = N_{P'}$ for all atoms $P'$ of $\mathcal {E}_P$. Thus, $\mu (P) = \mu (P')$ and $\mu (\mathcal {E}_P) = m \mu (P)$.

• (vii) If T is conservative, there is an isomorphism of dynamical systems that takes T to another fiber-bijective extension $T_1$ on $(\mathcal {M}, \mathscr {A}, \mu )$, and maps $\mathscr {T}_\mathscr {B}(T)$ to a $\sigma$-algebra whose atoms are made up of entire levels $\mathcal {M}_o \times \{i\}$.

Corollary 2.6

Assertions (i)–(iv) above also hold in the case where $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$ has an atomic K-mixing decomposition relative to $\mathscr {B}_o$, that is,

$$\begin{aligned} T_o \mathscr {B}_o \supset \mathscr {B}_o, \qquad \sigma \! \left( \bigcup _{n\in \mathbb {N}} T_o^n \mathscr {B}_o \right) = \mathscr {A}_o \mod \mu , \qquad \mathscr {T}_{\mathscr {B}_o}(T_o) \text{ is } \text{ atomic. } \end{aligned}$$

Moreover, if P is an atom of $\mathscr {T}_\mathscr {B}(T)$, then $\pi P$ is an atom of $\mathscr {T}_{\mathscr {B}_o}(T_o)$.

3 Proofs

Proof of Theorem 2.3

It is a general simple fact that $A \in \mathscr {T}(T)$ if and only if $A = T^{-n} \, T^n A$, for all $n \in \mathbb {N}$. For any such A, Lemma 2.1 gives

$$\begin{aligned} \pi A = \pi \, T^{-n} \, T^n A = T_o^{-n} \, T_o^n \, \pi A, \end{aligned}$$

(8)

and so $\pi A \in \mathscr {T}(T_o) = \mathscr {N}_o$, by the exactness of $T_o$, where $\mathscr {N}_o$ is the trivial $\sigma$-algebra of $\mathcal {M}_o$. This implies that if $\mu (A) > 0$ (and so $\mu _o(\pi A) > 0$), then

$$\begin{aligned} \mu (A) \ge \mu _o(\pi A) = \mu _o(\mathcal {M}_o). \end{aligned}$$

(9)

Since $(\mathcal {M}_o, \mathscr {A}_o, \mu _o)$ is a Lebesgue space and $\mathcal {I}$ is countable, $(\mathcal {M}, \mathscr {A}, \mu )$ is also a Lebesgue space. Therefore, there exists a unique measurable partition $\mathscr {P}$ that generates $\mathscr {T}:= \mathscr {T}(T)$ (the uniqueness is intended mod $\mu$, according to our convention) [19]. Let D be the union of all the zero-measure elements of $\mathscr {P}$: $D \in \mathscr {T}$ because it is the complement of the (necessarily countable) union of all the positive-measure elements of $\mathscr {P}$.

We claim that $\mu (D)=0$. If not, by construction, D is infinitely divisible in $\mathscr {T}$, in the sense that any of its positive-measure subsets can be split into two positive-measure subsets belonging to $\mathscr {T}$. In particular, there exist $D_1, D_2 \in \mathscr {T}$, with $\mu (D_1), \mu (D_2) >0$ and $D = D_1 \sqcup D_2$. Recursively, for every $n \ge 2$ and $i_1, \ldots , i_{n-1}, i_n \in \{1,2\}$, there exists a set $D_{i_1, \ldots , i_{n-1}, i_n} \in \mathscr {T}$ such that

$$\begin{aligned} D_{i_1, \ldots , i_{n-1}, i_n} \subset D_{i_1, \ldots , i_{n-1}}, \qquad \mu ( D_{i_1, \ldots , i_{n-1}, i_n} ) > 0. \end{aligned}$$

(10)

By (9), then, $\mu ( D_{i_1, \ldots , i_{n-1}, i_n} ) \ge \mu _o(\mathcal {M}_o)$. For every $\bar{\imath }= (i_1, \ldots , i_n, \ldots ) \in \{1,2\}^{\mathbb {Z}^+}$, define

$$\begin{aligned} D_{\bar{\imath }} := \bigcap _{n=1}^\infty D_{i_1, \ldots , i_n} \in \mathscr {T}. \end{aligned}$$

(11)

Clearly, $\mu ( D_{\bar{\imath }} ) \ge \mu _o(\mathcal {M}_o)$, but the sets $\{ D_{\bar{\imath }} \}$ are uncountably many and disjoint, in contradiction with the fact that $(\mathcal {M}, \mathscr {A}, \mu )$ is $\sigma$-finite (being Lebesgue). This proves our claim and assertion (i) of Theorem 2.3.

Now, recall that $\mathscr {T}$ is invariant for both T and $T^{-1}$. If $P, P' \in \mathscr {P}$ and $n \in \mathbb {Z}$, the case $0< \mu ( T^n P \cap P' ) < \mu (P')$ cannot occur, otherwise $T^n P \cap P'$ would be a strict subset of the atom $P'$. Also $T^n P \supset P'$ is excluded, otherwise, since T is two-sided non-singular, $T^{-n} P'$ would be a strict subset of the atom P. (Notice that, if $n>0$, we must also use the identity $T^{-n} T^n P = P$.) It follows that $T^n P$ is either $P'$ or disjoint from $P'$, mod $\mu$, yielding (ii).

Assertion (iii) is a simple consequence of the fact that any invariant set $A = T^{-1} A$ belongs to $\mathscr {T}$ and thus must be a union of atoms.

As for (iv), it suffices to observe that, for a general T, $\mathscr {T}(T^m) = \mathscr {T}(T)$ for all $m>0$; and $\mathscr {T}(T|_A) = \mathscr {T}(T) \cap A$, for any invariant set A. Under our hypotheses, this implies that

$$\begin{aligned} \mathscr {T}(T^m|_P) = \mathscr {T}(T^m) \cap P = \mathscr {T}(T) \cap P = \mathscr {N}\cap P, \end{aligned}$$

(12)

the trivial $\sigma$-algebra on P. Hence $T^m|_P$ is exact. For the second assertion of (iv), we first observe that, by the Poincaré Recurrence Theorem applied to $T^m |_{\mathcal {E}_P}$, P belongs to the conservative part of $T^m$, which coincides with $\mathcal {C}$, the conservative part of T. Secondly, any other atom $P'$ of $\mathcal {E}_P$ can be rewritten as $P' = T^n P$, for some $n>0$. Since $T \mathcal {C} \subseteq \mathcal {C}$, we have that $P' \subseteq \mathcal {C}$, ending the proof of (iv).

For the rest of the proof we assume that T is fiber-bijective. For $x \in \mathcal {M}_o$, set $f_\mathcal {E}(x) := \# \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in \mathcal {E} \right. \! \right\}$. Since $\mathcal {E}$ is T-invariant and T is fiber-bijective, $f_{\mathcal {E}}$ is a $T_o$-invariant observable of $\mathcal {M}_o$, taking values in $\mathbb {N}\cup \{ \infty \}$. By the ergodicity of $T_o$, $f_{\mathcal {E}}$ is a.e. equal to a constant value $N_\mathcal {E}$, which cannot be zero because $\mu (\mathcal {E})>0$. This proves (v).

The first part of (vi) is proved by the above argument applied to P, $T^m$ and $T_o^m$. The fact that $N_P = N_{P'}$, whenever $P'$ is an atom of $\mathcal {E}_P$, comes from the fiber-bijectivity of $T^n$, for $n \in \mathbb {Z}^+$ such that $T^n P= P'$.

Lastly, we prove (vii). We will construct an isomorphism of measure spaces $\phi : \mathcal {M}\longrightarrow \mathcal {M}$ by defining it separately on each atom $P \in \mathscr {P}$. So fix any such P and consider $N_P \in \mathbb {Z}^+ \cup \{\infty \}$ as given by (vi). For $x \in \mathcal {M}_o$, set $P_x := \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in P \right. \! \right\}$. Since $\mathcal {I}$ is countable, we endow it with a well-order whereby, for $\mu _o$-a.e. x, $P_x$ can be enumerated as $\{ i_j(x) \}_{j=1}^{N_P}$, where $i_j: \mathcal {M}_o \longrightarrow \mathcal {I}$ is recursively defined by

$$\begin{aligned} i_1(x)&:= \min \left\{ i \in \mathcal {I} \, \left| \, (x,i) \in P \right. \! \right\} , \end{aligned}$$

(13)

$$\begin{aligned} i_{j+1}(x)&:= \min \left\{ i \in \mathcal {I} \, \left| \, i > i_j(x), \, (x,i) \in P \right. \! \right\} . \end{aligned}$$

(14)

These expressions prove that the functions $i_j$ are measurable. Now, if $N_P \in \mathbb {Z}^+$, set $\mathbb {Z}_{N_P} := \{ 1, 2, \ldots , N_P \}$; if $N_P = \infty$, set $\mathbb {Z}_{N_P} := \mathbb {Z}^+$. For x such that $\# P_x = N_P$, set

$$\begin{aligned} \phi _P(x,i_j(x)) := (x,j). \end{aligned}$$

(15)

This defines a bijection $\phi _P : P \longrightarrow \mathcal {M}_o \times \mathbb {Z}_{N_P}$ mod $\mu$. The expression $\phi _P^{-1} (x,j) = (x,i_j(x))$ shows that $\phi _P^{-1}$ is measurable, whereas the fact that, for all $B \in \mathscr {A}_o$ and $j \in \mathbb {Z}_{N_P}$,

$$\begin{aligned} \phi _P^{-1}(B \times \{j\}) := \left\{ (x,i_j(x)) \, \left| \, x \in B \right. \! \right\} = \bigsqcup _{k \in \mathcal {I}} (B \cap i_j^{-1}(k)) \times \{k\}. \end{aligned}$$

(16)

proves that $\phi _P$ is measurable and carries the measure $\mu |_P$ to the measure $\mu _o \times \#$ on $\mathcal {M}_o \times \mathbb {Z}_{N_P}$, where $\#$ is the counting measure.

We aggregate all bijections $\phi _P$ to construct a bijection $\phi : \mathcal {M}\longrightarrow \bigsqcup _{P \in \mathscr {P}} \mathcal {M}_o \times \mathbb {Z}_{N_P}$ (all bijections are intended mod $\mu$ and $\mu _o \times \#$, respectively). We do so, with a slight abuse of notation on the codomain, by defining $\phi (x,i) := \phi _P(x,i)$ whenever $(x,i) \in P$. Evidently, $\sum _{P \in \mathscr {P}} N_P = \# \mathcal {I}$ and this cardinality can be finite or countably infinite. In either case, there exists a bijection $\gamma : \bigsqcup _{P \in \mathscr {P}} \mathbb {Z}_{N_P} \longrightarrow \mathcal {I}$. Defining $\Phi : \mathcal {M}\longrightarrow \mathcal {M}$ via $\Phi := (\textrm{id}, \gamma ) \circ \phi$ results in an automorphism of the measure space $(\mathcal {M}, \mathscr {A}, \mu )$ which, by construction, acts on the factor $\mathcal {M}_o$ as the identity. In other words, it commutes with the projection $\pi$. Setting $T_1 := \Phi \circ T \circ \Phi ^{-1}$ gives the sought isomorphism, because $T_1 \circ \pi = \pi \circ T_1$ and the atoms of the tail $\sigma$-algebra of $T_1$ are the sets $\Phi P = \mathcal {M}_o \times \gamma \!\left( \mathbb {Z}_{N_P} \right)$, for all $P \in \mathscr {P}$. $\square$

Proof of corollary 2.4

This corollary is in fact a porism, in that its proof derives not from the statement of Theorem 2.3, but from its proof, which we refer the reader to.

Let D be the union of all the null elements of $\mathscr {T}:= \mathscr {T}(T)$. Proving the absurdity of the claim $\mu (D)>0$ is slightly more involved that in the proof of Theorem 2.3, because $A \in \mathscr {T}$ no longer implies (9). On the other hand, for any atom $P_o$ of $\mathscr {T}(T_o)$, $P_o \times \mathcal {I}\in \mathscr {T}$ (because $T^{-n} T^n (P_o \times \mathcal {I}) = (T_o^{-n} T_o^n P_o) \times \mathcal {I}= P_o \times \mathcal {I}$). So, for some $P_o$, $D' := D \cap (P_o \times \mathcal {I})$ must have positive measure. But $D'$ is infinitely divisible by construction and, for all $A \in \mathscr {T}$ with $A \subseteq D'$ and $\mu (A)>0$, the inequality $\mu (A) \ge \mu _o(\pi A) = \mu _o(P_o)$ holds for the same reasons as for (9). This leads to a contradiction as in (10)–(11). Assertion (i) is proved. As for (ii)–(iv), the proof of Theorem 2.3 works as is.

Regarding the last assertion of Corollary 2.4, we already know that $\pi P \in \mathscr {T}(T_o)$. Given an atom $P_o$ of $\mathscr {T}(T_o)$, it cannot be $\pi P \cap P_o \subset P_o$, otherwise $P_o$ would not be an atom; and neither can be that $P_o \subset \pi P$, for in that case $(P_o \times \mathcal {I}) \cap P \in \mathscr {T}(T)$, with $\mu ( (P_o \times \mathcal {I}) \cap P) > 0$. Since P is an atom, this would imply $P \subseteq P_o \times \mathcal {I}$ and thus $\pi P \subseteq P_o$, a contradiction. Therefore $\pi P$ must either coincide with or be disjoint from $P_o$ (mod $\mu _o$). $\square$

Proof of Theorem 2.5

The idea here is to reduce the invertible dynamical system $(\mathcal {M}, \mathscr {A}, \mu , T)$ to a non-invertible system whose base dynamics is exact, cf. [16, Rmk 3.3], and then apply Theorem 2.3.

Let $\mathscr {Q}_o$ denote the partition of $\mathcal {M}_o$ associated to $\mathscr {B}_o$ and [x] the element of $\mathscr {Q}_o$ containing a given $x \in \mathcal {M}_o$. For $B \subseteq \mathcal {M}_o$, denote $[B] := \left\{ [x] \in \mathscr {Q}_o \, \left| \, x \in B \right. \! \right\}$. Observe that this transformation of sets is invertible mod $\mu _o$ on $\mathscr {B}_o$, in the sense that, if $B, B' \in \mathscr {B}_o$ and $[B] = [B']$, then $B=B'$ mod $\mu _o$ (this is one of the properties of the correspondence between $\sigma$-algebras and measurable partitions in Lebesgue spaces [19]). This shows that the collection $[\mathscr {B}_o] := \left\{ [B] \, \left| \, B \in \mathscr {B}_o \right. \! \right\}$ is a $\sigma$-algebra for $\mathscr {Q}_o$ and the measure $\mu _{[\mathscr {B}_o]}([B]) := \mu _o(B)$ is well-defined on it. Finally define $T_{\mathscr {B}_o}: \mathscr {Q}_o \longrightarrow \mathscr {Q}_o$ via $T_{\mathscr {B}_o}([x]) = [T_o(x)]$. This definition is well-posed since $T_o$ is K-mixing w.r.t. $\mathscr {B}_o$, implying that $T_o \mathscr {Q}_o$ is a finer partition than $\mathscr {Q}_o$. Clearly $(\mathscr {Q}_o, [\mathscr {B}_o], \mu _{[\mathscr {B}_o]}, T_{\mathscr {B}_o})$ is a two-sided non-singular factor of $(\mathcal {M}_o, \mathscr {B}_o, \mu _o, T_o)$, which is non-invertible because $T_o \mathscr {Q}_o$ is strictly finer than $\mathscr {Q}_o$. The factor property shows that $\mathscr {T}( T_{\mathscr {B}_o} ) = [ \mathscr {T}_{\mathscr {B}_o} (T_o) ] = [\mathscr {N}]$. that is, $T_{\mathscr {B}_o}$ is exact.

We make the analogous construction for $\mathscr {Q}:= \mathscr {Q}_o \times \mathcal {I}$, which is evidently the partition of $\mathcal {M}$ corresponding to $\mathscr {B}$. We end up with the system $(\mathscr {Q}, [\mathscr {B}], \mu _{[\mathscr {B}]}, T_\mathscr {B})$, which is thus a fiber-bijective $\mathcal {I}$-extension of $(\mathscr {Q}_o, [\mathscr {B}_o], \mu _{[\mathscr {B}_o]}, T_{\mathscr {B}_o})$. A very important remark here is that $T_\mathscr {B}$ is well-defined if and only if $\Psi$ is $\mathscr {B}$-measurable.

Theorem 2.3 can be applied to $T_\mathscr {B}$, implying properties (i)–(vii) for the dynamics of $T_\mathscr {B}$ on $\mathscr {T}(T_\mathscr {B})$. But the transformation $\mathscr {B}\ni A \mapsto [A]$ is invertible mod $\mu$, in the sense explained earlier, so P is an atom of $\mathscr {T}_\mathscr {B}(T)$ if and only if [P] is an atom of $\mathscr {T}(T_\mathscr {B})$, and they have the same measure, respectively w.r.t. $\mu$ and $\mu _{[\mathscr {B}]}$. This proves all the assertions of Theorem 2.5, except for the K-mixing of $T^m|_P$ w.r.t. $\mathscr {B}\cap P$, when P is part of an m-cycle.

The triviality of $\mathscr {T}_{\mathscr {B}\cap P}(T^m)$ is equivalent to the triviality of $\mathscr {T}_\mathscr {B}(T) \cap P$, which is equivalent to the triviality of $\mathscr {T}(T_\mathscr {B}) \cap [P]$, which we have proved. For the two remaining conditions of (2) we state the following lemma, which will be proved at the end of Sect. 3.

Lemma 3.1

With the notation $\mathscr {B}_o \times \mathcal {I}:= \left\{ B \times \{i\} \, \left| \, B \in \mathscr {B}_o,\, i \in \mathcal {I} \right. \! \right\}$, the following hold:

• (i) For all $n \in \mathbb {N}$, $T^n ( \sigma (\mathscr {B}_o \times \mathcal {I}) ) \supseteq \sigma (T_o^n \mathscr {B}_o \times \mathcal {I})$;

• (ii) $\displaystyle \sigma \!\left( \bigcup _{n \in \mathbb {N}} \sigma (T_o^n\mathscr {B}_o\times \mathcal {I}) \right) = \sigma \!\left( \sigma \!\left( \bigcup _{n \in \mathbb {N}} T_o^n \mathscr {B}_o \right) \times \mathcal {I}\right)$.

Lemma 3.1(i), with $n=1$, gives

$$\begin{aligned} T \mathscr {B}= T(\sigma (\mathscr {B}_o \times \mathcal {I})) \supseteq \sigma (T_o \mathscr {B}_o \times \mathcal {I}) \supset \sigma (\mathscr {B}_o \times \mathcal {I}) = \mathscr {B}, \end{aligned}$$

(17)

which in turn implies $T^m (\mathscr {B}\cap P) = (T^m \mathscr {B}) \cap P \supset \mathscr {B}\cap P$. Furthermore,

$$\begin{aligned} \begin{aligned} \sigma \!\left( \bigcup _{n\in \mathbb {N}} T^n \mathscr {B}\right)&= \sigma \! \left( \bigcup _{n\in \mathbb {N}} T^n \sigma \!\left( \mathscr {B}_o \times \mathcal {I}\right) \right) \\&\supseteq \sigma \! \left( \bigcup _{n\in \mathbb {N}} \sigma \!\left( T_o^n \mathscr {B}_o \times \mathcal {I}\right) \right) \\&= \sigma \!\left( \sigma \!\left( \bigcup _{n\in \mathbb {N}}T_o^n \mathscr {B}_o \right) \times \mathcal {I}\right) \\&= \sigma \!\left( \mathscr {A}_o \times \mathcal {I}\right) = \mathscr {A}, \end{aligned} \end{aligned}$$

(18)

where the second line comes from Lemma 3.1(i), the third line comes from Lemma 3.1(ii), and the fourth line comes from the hypothesis $\sigma \!\left( \bigcup _{n\in \mathbb {N}} T_o^n \mathscr {B}_o \right) = \mathscr {A}_o$. But (18) must be a chain of equalities because its leftmost term cannot exceed $\mathscr {A}$. The K-property of $T^m|_P$ is proved. $\square$

Proof of Corollary 2.6

This proof employs a combination of arguments explained in the two preceding proofs.

One constructs the systems $(\mathscr {Q}_o, [\mathscr {B}_o], \mu _{[\mathscr {B}_o]}, T_{\mathscr {B}_o})$ and $(\mathscr {Q}, [\mathscr {B}], \mu _{[\mathscr {B}]}, T_\mathscr {B})$ as in the proof of Theorem 2.5, and reasons as in the proof of Corollary 2.4 to show that $\mathscr {T}(T_\mathscr {B})$, and therefore $\mathscr {T}_\mathscr {B}(T)$, is atomic with the properties (i)–(iii) and part of (iv). The K-property of $T^m|_P$, when P is an atom of an m-chain, was already established in the previous proof. The last claim of Corollary 2.6 is proved as in the proof of Corollary 2.4. $\square$

Proof of Lemma 3.1

We start with inclusion (i). Since $T^n$ is invertible, $T^n ( \sigma (\mathscr {B}_o \times \mathcal {I}) )$ is a $\sigma$-algebra, so it suffices to show that $T_o^n \mathscr {B}_o \times \mathcal {I}\subseteq T^n( \sigma ( \mathscr {B}_o \times \mathcal {I}))$. We may assume $n=1$ (otherwise we use $T_o^n, T^n$ in lieu of $T_o, T$). For all $B \in \mathscr {B}_o$ and $j \in \mathcal {I}$, we need to prove that $T_o B \times \{j\} \in T(\sigma (\mathscr {B}_o \times \mathcal {I}))$. For $i \in \mathcal {I}$, set $B_i := B \cap \left\{ x \in \mathcal {M}_o \, \left| \, \Psi (x,i) = j \right. \! \right\}$. Since $\Psi (\cdot , i)$ is $\mathscr {B}_o$-measurable, $B_i \in \mathscr {B}_o$. By fiber-bijectivity, $B = \bigsqcup _{i \in \mathcal {I}} B_i$. Therefore

$$\begin{aligned} T_o B \times \{j\} = \left( T_o \bigsqcup _{i \in \mathcal {I}} B_i \right) \! \times \{j\} = T \!\left( \bigsqcup _{i \in \mathcal {I}} B_i \times \{i\} \right) \in T \!\left( \sigma ( \mathscr {B}_o \times \mathcal {I}) \right) , \end{aligned}$$

(19)

where the second equality comes from the definition of $B_i$.

As for (ii), clearly, for all $n \in \mathbb {N}$,

$$\begin{aligned} T_o^n \mathscr {B}_o \times \mathcal {I}\subseteq \sigma \!\left( \sigma \!\left( \bigcup _{n\in \mathbb {N}} T_o^n \mathscr {B}_o \right) \times \mathcal {I}\right) , \end{aligned}$$

(20)

which readily implies the left-to-right inclusion of (ii). On the other hand, take $B \times \{i\} \in \sigma (\bigcup _{n\in \mathbb {N}} T_o^n \mathscr {B}_o) \times \mathcal {I}$. Then

$$\begin{aligned} B \times \{i\} \in \sigma \!\left( \bigcup _{n\in \mathbb {N}} (T_o^n \mathscr {B}_o \times \mathcal {I}) \right) \subseteq \sigma \!\left( \bigcup _{n\in \mathbb {N}} \sigma (T_o^n \mathscr {B}_o \times \mathcal {I}) \right) . \end{aligned}$$

(21)

Since the above r.h.s. is a $\sigma$-algebra, the right-to-left inclusion of (ii) follows. $\square$

4 Application to Periodic Lorentz Gases

In this section we use Theorem 2.5, or rather Corollary 2.6, to show that, under general hypotheses, a periodic Lorentz gas is K-mixing if and only if it is conservative. This will readily imply that many 2-dimensional periodic Lorentz gases and d-dimensional periodic Lorentz tubes and slabs are K-mixing. In what follows we use the term ‘Lorentz gas’ in its most general meaning of a billiard system defined by infinitely many convex scatterers in an unbounded space.

We consider a periodic Lorentz gas in the space $E^d := \mathbb {R}^{d_1} \times \mathcal {T}^{d_2}$, where $d_1 \in \mathbb {Z}^+, d_2 \in \mathbb {N}$, $d_1 + d_2 = d$, and $\mathcal {T}^{d_2}$ is a $d_2$-dimensional torus (not necessarily the standard one). So, for $d_1=d$ and $d_2=0$, $E^d$ coincides with $\mathbb {R}^d$. See Figs. 1, 2 and 3 for examples.

Fig. 1

A (proper) periodic Lorentz gas in $\mathbb {R}^2$

Fig. 2

A Lorentz tube in the space $E^2 = \mathbb {R}\times \mathcal {T}^1$

Fig. 3

A Lorentz slab in the space $E^3 = \mathbb {R}^2 \times \mathcal {T}^1$

More in detail, we study the system $(\mathcal {M}, \mathscr {A}, \mu , T)$ given by a $\Gamma$-extension of the billiard map $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$ of a d-dimensional Sinai billiard, where:

• $\Gamma$ is a co-compact lattice of $\mathbb {R}^{d_1}$, naturally acting on $E^d$.

• The Sinai billiard is defined by a finite number of scatterers $\mathcal {O}^\ell$, $\ell \in \mathcal {L}$, on $E^d / \Gamma$. The $\mathcal {O}^\ell$ are pairwise disjoint, regular, strictly convex closed sets of $E^d$. (It is not important to prescribe the degree of regularity at this stage, but do observe that $\partial \mathcal {O}^\ell$ is assumed to be regular and not just piecewise regular. See however Remark 4.4.)

• $\mathcal {M}_o := \bigsqcup _{\ell \in \mathcal {L}} \mathcal {M}_o^\ell$, where

  $$\begin{aligned} \mathcal {M}_o^\ell := \left\{ (q,v) \in \partial \mathcal {O}^\ell \times \mathbb {R}^d \, \left| \, v \cdot n_q \ge 0, \ |v|=1 \right. \! \right\} \end{aligned}$$

  (22)

  and $n_q$ is the outer unit normal to $\mathcal {O}^\ell$ in q. Any such pair (q, v) is also called a line element of $\mathcal {O}^\ell$, and we refer to

  $$\begin{aligned} \Omega _o := (E^d / \Gamma ) \setminus \bigsqcup _{\ell \in \mathcal {L}} \mathcal {O}^\ell \end{aligned}$$

  (23)

  as the billiard table of the Sinai billiard.

• $\mathscr {A}_o$ is the natural Borel $\sigma$-algebra on $\mathcal {M}_o$ and $\mu _o$ is the usual invariant measure for billiard maps, defined on each $\mathcal {M}_o^\ell$ by $d \mu _o(q,v) = (v \cdot n_q) dq dv$, where dq is the (hyper)surface element of $\partial \mathcal {O}^\ell$ at q, and dv is the (hyper)surface element of $\mathbb {S}^{d-1} := \left\{ v \in \mathbb {R}^d \, \left| \, |v|=1 \right. \! \right\}$ at v.

• $T_o: \mathcal {M}_o \longrightarrow \mathcal {M}_o$ is defined so that $T_o(q,v) = (q',v')$ is the line element that the forward trajectory of (q, v) in $\Omega _o$ takes on right after its first collision with some scatterer $\mathcal {O}^\ell$.

• $\mathcal {M}= \mathcal {M}_o \times \Gamma$ and, for $x = (q,v) \in \mathcal {M}_o$ and $i \in \Gamma$, $\Psi (x,i) = i + \psi (x)$ (cf. beginning of Sect. 2), where $\psi$ is the discrete displacement function, defined as follows. We consider the periodic Lorentz gas, that is, the billiard in

  $$\begin{aligned} \Omega := E^d \setminus \bigsqcup _{\ell \in \mathcal {L}} \bigsqcup _{i \in \Gamma } \mathcal {O}_i^\ell , \end{aligned}$$

  (24)

  where $\mathcal {O}_i^\ell$ is the copy of $\mathcal {O}^\ell$ in the $i^\textrm{th}$ copy of the fundamental domain of $\Gamma$ within $E^d$. (In other words, if we tile $E^d$ by means of $\Gamma$ and draw all the scatterers $\mathcal {O}^\ell$ in the $0^\textrm{th}$ tile, then $\mathcal {O}_i^\ell := \mathcal {O}^\ell + i$, a subset of the $i^\textrm{th}$ tile.) So, $\psi (x) = j$ if and only if the forward trajectory in $\Omega$ of $x = (q,v)$, with $q \in \partial \mathcal {O}_0^\ell$, for some $\ell$, has its first collision with a scatterer $\mathcal {O}_j^{\ell '}$, for some $\ell '$. (In other words, the forward trajectory of (q, v) in the periodic Lorentz gas, with q interpreted as a point in the $0^\textrm{th}$ tile, has its first collision in the $j^\textrm{th}$ tile.) This completely defines T. $\mathscr {A}$ and $\mu$ are then defined out of $\mathscr {A}_o$ and $\mu _o$ as in Sect. 2. Finally, we refer to $\Omega$ as the billiard table of the Lorentz gas, or simply the billiard table.

A simple but important observation here is that one could also define $(\mathcal {M}, \mathscr {A}, \mu , T)$ as the scatterer-to-scatterer billiard map for the table $\Omega$. In this case $\mathcal {M}$ would be given as $\bigsqcup _{\ell \in \mathcal {L}} \bigsqcup _{i \in \Gamma } \mathcal {M}_i^\ell$, where $\mathcal {M}_i^\ell$ is the set of all line elements for the scatterer $\mathcal {O}_i^\ell$; and T would be the first-return map to $\mathcal {M}$ of the billiard flow in $\Omega$. Finally, $\mu$ would be the billiard measure on the Borel $\sigma$-algebra $\mathscr {A}$ of $\mathcal {M}$. This dynamical system is evidently isomorphic to the extension system introduced earlier, so much so that we use the same notation for both.

When $d_1=1$ and $d \ge 2$, these Lorentz gases are also referred to as Lorentz tubes, see Fig. 2; when $d_1=2$ and $d \ge 3$, they are also called Lorentz slabs, see Fig. 3.

In the interest of generality, the next proposition is formulated in a relatively abstract manner, but we will see below that it can be applied easily to many examples of periodic Lorentz gases.

Proposition 4.1

Let $(\mathcal {M}, \mathscr {A}, \mu , T)$ be a periodic Lorentz gas corresponding to a Sinai billiard $(\mathcal {M}_o, \mathscr {A}_o, \mu _o, T_o)$, as described above. Assume the following:

• (a) $T_o$ has an atomic K-mixing decomposition in the sense of Corollary 2.6, relative to some $\sigma$-algebra $\mathscr {B}_o$.

• (b) T is conservative.

• (c) For all $m \in \mathbb {Z}^+$, $\ell \in \mathcal {L}$ and $i \in \Gamma$, the first-return map of $T^m$ to $\mathcal {M}_i^\ell$, denoted $(T^m)_{\mathcal {M}_i^\ell }$, is ergodic. (Observe that $(T^m)_{\mathcal {M}_i^\ell }$ is well-defined $\mu$-almost everywhere because $T^m$ is conservative by (b).)

Then T is K-mixing relative to $\mathscr {B}$, the lift of $\mathscr {B}_o$.

Remark 4.2

Viceversa, any K-mixing Lorentz gas, with no extra assumptions, is conservative. This is because any measure-preserving, invertible, ergodic dynamical system is conservative. In fact, for a measure-preserving system, $\mathcal {C}$ and $\mathcal {D}$ are invariant [1, Prop. 1.1.6]. If the system is also ergodic, then either $\mathcal {M}= \mathcal {C}$ or $\mathcal {M}= \mathcal {D}$. In the latter case, it is easy to find a wandering set W such that $\bigsqcup _{n\in \mathbb {Z}} T^n W$, which is invariant because T is invertible, has positive but not full measure.

Proof of Proposition 4.1

By Corollary 2.6, $\mathscr {T}_\mathscr {B}(T)$, the tail $\sigma$-algebra of $\mathscr {B}$ w.r.t. T, is atomic, with generating partition $\mathscr {P}$.

We first claim that $\mathscr {P}$ is coarser than $\{ \mathcal {M}_i^\ell \}_{\ell \in \mathcal {L}, i \in \Gamma }$, that is, every $\mathcal {M}_i^\ell$ is contained in an atom of $\mathscr {P}$. By (b), every atom of $\mathscr {P}$ is part of an m-cycle, for some $m \in \mathbb {Z}^+$. Thus, if $\mathcal {M}_i^\ell$ intersects (in a positive-measure set) some atom P of order m, then $\mathcal {M}_i^\ell \cap P$ is invariant for $(T^m)_{\mathcal {M}_i^\ell }$. By (c), then, $\mathcal {M}_i^\ell \subseteq P$, which proves the claim. Using an imprecise but understandable expression, we describe the inclusion $\mathcal {M}_i^\ell \subseteq P$ by saying that the scatterer $\mathcal {O}_i^\ell$ of the Lorentz gas is contained in P.

Let us now prove that T is ergodic. If it were not, $\mathcal {M}$ could be split into two disjoint invariant sets A and B with $\mu (A), \mu (B) > 0$. In the imprecise language just introduced, every scatterer of the Lorentz gas is contained in either A or B. Take two scatterers $\mathcal {O}_1$ and $\mathcal {O}_2$ which are contained in A and B, respectively, and realize the minimum distance between all such pairs of scatterers. The existence of $\mathcal {O}_1$ and $\mathcal {O}_2$ is guaranteed by the facts that neither A nor B is empty and the configuration of scatterers is periodic and locally finite. Now, clearly there exists a segment connecting $\mathcal {O}_1$ and $\mathcal {O}_2$ that is tangent to no scatterer of the Lorentz gas. This is then a portion of a billiard trajectory (called non-singular in jargon) whose perturbations still connect $\mathcal {O}_1$ to $\mathcal {O}_2$, implying that T takes a positive-measure set from A to B, a contradiction. So, T is ergodic and $\mathcal {M}$ is an m-cycle.

By Theorem 2.5(iv), it only remains to prove that $m=1$. Assume by contradiction that $m\ge 2$. Given an atom P, set $P_j := T^j P$, for all $0 \le j \le m-1$. Take a scatterer $\mathcal {O}_0$ contained in $P_0$. Varying a line element (q, v) with $q \in \partial \mathcal {O}_0$ and v directed outwardly w.r.t. $\mathcal {O}_0$, we are bound to find a segment $\overline{qq_2}$, with $q_2$ on the boundary of some scatterer $\mathcal {O}_2$, such that the interior of $\overline{qq_2}$ contains exactly one point of intersection $q_1$ with a scatterer $\mathcal {O}_1$, as in Fig. 4. The segment is then tangent to $\mathcal {O}_1$ in $q_1$ and is part of a billiard trajectory which is called singular precisely because of that tangency. The existence of this segment is a consequence of the facts that all scatterers are convex (so $\mathcal {O}_0$ cannot be entirely “surrounded” by a unique scatterer) and that, for $\mu$-a.e. (q, v), the half-line defined by (q, v) intersects a scatterer of the Lorentz gas in a point different from q (otherwise the base system, the Sinai billiard, would not be well-defined). Observe that, since the ambient space $E^d$ may have a toroidal factor, $\mathcal {O}_1$ and $\mathcal {O}_2$ may in principle coincide with $\mathcal {O}_0$, although we will soon see that this is not the case. In any event, the three segments $\overline{qq_1}$, $\overline{qq_2}$, and $\overline{q_1 q_2}$ can be independently perturbed into non-singular trajectory segments connecting, respectively, $\mathcal {O}_0$ to $\mathcal {O}_1$, $\mathcal {O}_0$ to $\mathcal {O}_2$, and $\mathcal {O}_1$ to $\mathcal {O}_2$, cf. Fig. 4. Since $\mathcal {O}_0$ is contained in $P_0$, the properties of the m-cycle imply that both $\mathcal {O}_1$ and $\mathcal {O}_2$ are contained in $P_1$ and, at the same time, $\mathcal {O}_2$ is contained in $P_2$ (or $P_0$, if $m=2$), which is a contradiction. $\square$

Fig. 4

Illustration of an argument for the proof of Proposition 4.1

The researcher with a basic familiarity with hyperbolic billiards will see how to use Proposition 4.1 to prove that a given Lorentz gas is K-mixing. First of all, the vast majority of Sinai billiards that have been studied (a very partial list of references includes [3, 4, 6, 11, 22,23,24]; see also [7, 8]) are known to be K-mixing w.r.t. the $\sigma$-algebra $\mathscr {B}_o$ generated by a suitable family of local stable manifolds (LSMs), so ascertaining (a) likely boils down to a verification in the literature. The lifts to $\mathcal {M}$ of the LSMs for the base system are thus LSMs for the extension and generate $\mathscr {B}$ by definition. The first ingredient in the proof of any ergodic property for a hyperbolic billiard is the so-called fundamental theorem, a.k.a. local ergodic theorem, which in our case reduces to the following property: for all $\ell \in \mathcal {L}$, $\mu _o$-a.e. pair of points $x,y \in \mathcal {M}_o^\ell$ is connected via a chain of alternating local stable and unstable manifolds (LSUMs), with the property that all intersection points between successive LSUMs can be chosen in a pre-determined full-measure subset of $\mathcal {M}_o^\ell$. Now, if T is conservative, the LSUMs for T in $\mathcal {M}_i^\ell$ are also LSUMs for $(T^m)_{\mathcal {M}_i^\ell }$, for all $m \ge 1$, because, by definition, all points in the same LSM have the same itinerary in terms of the scatterers hit by the forward trajectories, and analogously for LUMs and backward trajectories. Finally, the usual zig-zag argument for LSUMs (in the terminology of [13]) shows that $(T^m)_{\mathcal {M}_i^\ell }$ is ergodic, yielding (c).

This method applies easily to all d-dimensional Lorentz tubes whose base system is K-mixing because of a hyperbolic structure as described above. In fact, the conservativity of T comes from a known result by Atkinson [2], whereby a $\mathbb {Z}$-valued (or $\mathbb {R}$-valued) cocycle over an ergodic dynamical system is recurrent if and only if its displacement function (assumed to be integrable) has zero average; see also [10, 21]. As for Lorentz slabs and 2-dimensional proper Lorentz gases, independent results by Schmidt [20] and Conze [9] show that recurrence (thus conservativity) is implied by the CLT for the displacement function; see also [15]. So, if the base Sinai billiard is K-mixing by way of the standard hyperbolic structure, and satisfies a CLT for observables that are locally constant outside its singularity set, the corresponding Lorentz slab (or Lorentz gas, in the 2D case) is K-mixing.

Remark 4.3

For the sake of exposition, we have chosen to discuss only Lorentz gases in $E^d$, which is practically a Euclidean space, but the same ideas and arguments apply to more general ambient spaces, as in the example of Fig. 5. In fact, $\mathcal {T}^{d_2}$ can be replaced by a polyhedron with $d_1$ pairs of identified parallel facets, with the other facets regarded as hard walls for the billiard dynamics. Proposition 4.1 still holds in many cases: one need only check that the scatterers of the Lorentz gas cannot be divided into invariant families (of scatterers) or m-cycles with $m \ge 2$ (whose atoms are made up of whole scatterers). The method of application of Proposition 4.1 is then the same as described above, showing for example that the Lorentz tube of Fig. 5 is K-mixing.

Fig. 5

A Lorentz tube with hard walls (cf. Remark 4.3)

Remark 4.4

One could also extend the above technique to certain Lorentz gases whose scatterers are only piecewise regular. An analogue of Proposition 4.1 can be proved in some cases, with the difference that, in place of $\mathcal {M}_i^\ell$, one uses $\mathcal {M}_i^{\ell ,j}$, the part of phase space associated to the $j^\textrm{th}$ regular component of $\partial \mathcal {O}_i^\ell$. (The proof might be cumbersome in this case, and depends on which regular boundary components of other scatterers are “seen” by each regular boundary component of each scatterer.) It is not hard to see that the whole procedure works for the Lorentz tube of Fig. 6, which is therefore K-mixing.

Fig. 6

A Lorentz tube with (hard walls and) piecewise regular scatterers (cf. Remark 4.4)