Sparse Hard-Disk Packings and Local Markov Chains

Abstract

We propose locally stable sparse hard-disk packings, as introduced by Böröczky, as a model for the analysis and benchmarking of Markov-chain Monte Carlo (MCMC) algorithms. We first generate such Böröczky packings in a square box with periodic boundary conditions and analyze their properties. We then study how local MCMC algorithms, namely the Metropolis algorithm and several versions of event-chain Monte Carlo (ECMC), escape from configurations that are obtained from the packings by slightly reducing all disk radii by a relaxation parameter. We obtain two classes of ECMC, one in which the escape time varies algebraically with the relaxation parameter (as for the local Metropolis algorithm) and another in which the escape time scales as the logarithm of the relaxation parameter. A scaling analysis is confirmed by simulation results. We discuss the connectivity of the hard-disk sample space, the ergodicity of local MCMC algorithms, as well as the meaning of packings in the context of the NPT ensemble. Our work is accompanied by open-source, arbitrary-precision software for Böröczky packings (in Python) and for straight, reflective, forward, and Newtonian ECMC (in Go).

1 Introduction

The hard-disk system is a fundamental statistical-physics model that has been intensely studied since 1953. Numerical simulations, notably Markov-chain Monte Carlo [1] (MCMC) and event-driven molecular dynamics [2], have played a particular role in its study. The existence of hard-disk phase transitions [3] was asserted as early as 1962. The recent identification of the actual transition scenario [4] required the use of a modern event-chain Monte Carlo (ECMC) algorithm [5, 6].

The hard-disk model has been much studied in mathematics. Even today, the existence of a phase transition has not been proven [7, 8]. A fundamental rigorous result is that the densest packing of N equal hard disks (for $N\rightarrow \infty$) arranges them in a hexagonal lattice [9]. This densest packing is locally stable, which means that no single disk can move infinitesimally in the two-dimensional plane. The densest packing is furthermore collectively stable, which means that no subset of disks can move at once, except if the collective infinitesimal move corresponds to symmetries, as for example uniform translations in the presence of periodic boundary conditions [10,11,12]. In 1964, Böröczky [13] constructed two-dimensional disk packings that are sparse, that is, have vanishing density in the limit $N \rightarrow \infty$. The properties of these Böröczky packings are very different from those of the densest hexagonal lattice. Infinitesimal motion of just a single disk remains impossible, so that Böröczky packings are locally stable. However, coherent infinitesimal motion of more than one disk does allow escape from Böröczky packings so that they are not collectively stable.

In this work, we construct finite-N Böröczky packings in a fixed periodic box and use them to build initial configurations for local Markov-chain Monte Carlo (MCMC) algorithms, namely the reversible Metropolis algorithm [1, 14] and several variants [5, 15, 16] of non-reversible ECMC. In the Metropolis algorithm, single disks are moved one by one within a given range $\delta$. A Böröczky packing traps the local Metropolis algorithm if $\delta$ is small enough, because all single-disk moves are rejected. ECMC is by definition local. It features individual infinitesimal displacements of single disks, and it also cannot escape from a Böröczky packing. We thus consider $\varepsilon$-relaxed Böröczky configurations that have the same disk positions as the Böröczky packings but with disk radii reduced by a factor $(1-\varepsilon )$. Here, $\varepsilon \gtrsim 0$ is the relaxation parameter. Our scaling theory for the escape times from $\varepsilon$-relaxed Böröczky configurations predicts the existence of two classes of local Markov-chain algorithms. In one class, escape times grow as a power of the relaxation parameter $\varepsilon$, whereas the other class features only logarithmic growth. Numerical simulations confirm our scaling theory, whose power-law exponents we conjecture to be exact. The $\varepsilon$-relaxed Böröczky configurations are representative of a finite portion of sample space. For a fixed number of disks, the growth of the escape times thus leads to the existence of a small but finite fraction of sample space that cannot be escaped from or even accessed by local MCMC in a given upper limit of CPU time. More generally, we discuss the apparent paradox that the lacking proof for the connectedness of the hard-disk sample space, on the one hand, might render local MCMC non-irreducible (that is, “non-ergodic”) but, on the other hand, does not invalidate their practical use. We resolve this paradox by considering the NPT ensemble (where the pressure is conserved instead of the volume). We moreover advocate the usefulness of $\varepsilon$-relaxed Böröczky configurations for modeling bottlenecks in MCMC and consider the comparison of escape times from these configurations as an interesting benchmark. We provide open-source arbitrary-precision software for Böröczky packings and for ECMC. Several of the ECMC algorithms can evolve towards numerical gridlock, that can be diagnosed and studied using our arbitrary-precision software.

This work is organized as follows. In Sect. 2, we construct Böröczky packings following the original proposal [13] and a variant due to Kahle [17], and we analyze their properties. In Sect. 3, we discuss local MCMC algorithms and present analytical and numerical results for the escape times from the $\varepsilon$-relaxed Böröczky configurations. In Sect. 4, we analyze algorithms and their escape times and discuss fundamental aspects, among them irreducibility, statistical ensembles, as well as the question of bottlenecks, and the difference between local and non-local MCMC methods. In the conclusion (Sect. 5), we point to several extensions and place our findings into the wider context of equilibrium statistical mechanics, the physics of glasses and the mechanics of granular materials. In Appendix A, we present further numerical analysis and, in Appendix B, we introduce our open-source arbitrary-precision software package BigBoro for Böröczky packings and for ECMC.

2 Böröczky Packings

In the present section, we discuss Böröczky packings of N disks of radius $\sigma =1$ in a periodic square box of sides L. The density $\eta$ is the ratio of the disk areas to that of the box:

$$\begin{aligned} \eta = N \pi \sigma ^2 / L^2 . \end{aligned}$$

(1)

For concreteness, the central simulation box ranges from $-L/2$ to L/2 in both the x and the y direction. The periodic boundary conditions map the central simulation box onto an infinite hard-disk system with periodically repeated boxes or, equivalently, onto a torus. A Böröczky packing is locally stable, and each of its N disks is blocked—at a distance $2 \sigma$—by at least three other disks (taking into account periodic boundary conditions), with the contacts not all in the same half-plane. The opening angle of a disk i, the largest angle formed by the contacts to its neighbors, is then always smaller than $\pi$. The maximum opening angle is the largest of the N opening angle of all disks. Clearly, a locally stable packing cannot be escaped from through the infinitesimal single-disk moves of ECMC or, in Metropolis MCMC, through steps of small enough range. Only collective infinitesimal moves of all disks may escape from the packing.

In a nutshell, Böröczky packings (see Sect. 2.1 for their construction) consist in cores and branches (as visible in Fig. 1). The original Ref. [13] mainly focused on Böröczky packings in an infinite plane, but also sketched how to generalize the packings to the periodic case. Böröczky packings can exist for different cores, and they depend on a bounding curve (more precisely: a convex polygonal chain) which encloses the branches, and which can be chosen more or less freely (see Sect. 2.2 for the properties of Böröczky packings, including the collective infinitesimal escape modes from them).

2.1 Construction of Böröczky Packings

In the central simulation box, a finite-N Böröczky packing is built on a central core placed around (0, 0) (see Sect. 2.1.1 for a discussion of cores). This core connects to four periodic copies of the core centered at (L, 0), (0, L), $(-L,0)$, and $(0,-L)$ by branches that have k separate layers (see Sects. 2.1.2 and 2.1.3 for a detailed discussion of branches). A Böröczky packing shares the symmetries of the central simulation box. Cores with different shapes, as for example that of a triangle, yield Böröczky packings in other geometries (see [13, 17] and [18, Sect. 9.3]).

2.1.1 Böröczky Core, Kahle Core

We consider Böröczky packings with two different cores, either the Böröczky core or the Kahle core. Both options are implemented in the BigBoro software package (see Appendix B). The Böröczky core [13] consists of 20 disks (see Fig. 1a). Using reflection symmetry about coordinate axes and diagonals, this core can be constructed from four disks at coordinates $(\sqrt{2}, 0)$, $(2 + \sqrt{2}, 0)$, $(2 + \sqrt{6} / 2 + 1 / \sqrt{2}, \sqrt{6} / 2 + 1 / \sqrt{2})$, and $(2 + \sqrt{6} / 2 + 1 / \sqrt{2}, 2 + \sqrt{6} / 2 + 1 / \sqrt{2})$ (see highlighted disks in Fig. 1a). The Kahle core [17], with a total of 8 disks, is constructed from two disks at coordinates (1, 1), and $(1 + \sqrt{3}, 0)$, using the same symmetries (see highlighted disks in Fig. 1b). The Böröczky core for $k=0$, that is without the branches included in Fig. 1a, is only locally stable if repeated periodically in a central simulation box that fully encloses the core disks, with $L/2= 3+ \sqrt{6}/2 + 1/\sqrt{2}$. The Kahle core, again without branches, can be embedded in two non-equivalent ways into a periodic structure. When the outer-disk centers are placed on the cell boundaries, with $L/2=1+\sqrt{3}$, it forms a collectively stable packing with no remaining degrees of freedom other than uniform translations. Alternatively, it only forms a locally stable packing, with the possibility of non-trivial collective deformations, if the outer disks are enclosed in a larger simulation cell, with $L/2=2+\sqrt{3}$. These two cores are the seeds from which larger and less dense Böröczky packings are now constructed and studied.

Fig. 1

Hard-disk Böröczky packings, composed of a core and of four branches with $k=5$ layers, with contact graphs and highlighted opening angles. a Packing with the Böröczky core [13]. b Packing with the Kahle core [17]. c Detail of a branch. d Convex polygonal chain $\mathcal {A}$, and horizontal lines $g_2^<$, $g_2$, and $g_3$. Two different classes of polygonal chains, called $\mathcal {A}^{\text {geo}}$ and $\mathcal {A}^{\text {circ}}$, are considered in this work

2.1.2 Branches—Infinite-Layer Case (Infinite N)

Following Ref. [13], we first construct infinite branches ($k=\infty$) that correspond to the $N \rightarrow \infty$ and $\eta \rightarrow 0$ limits, without periodic boundary conditions. One such branch is attached to each of the four sides of the central core so that all disks are locally stable. The horizontal branch that extends from the central core in the positive x-direction is symmetric about the x-axis. The half branch for $y \ge 0$ uses three sets of disks $\{A_1, A_2, \ldots \}$, $\{B_1, B_2, \ldots \}$, and $\{C_1, C_2, \ldots \}$, where $i= 1,2,\ldots$ is the layer index.

For the branch that is symmetric about the x-axis, the construction relies on four horizontal lines [13]:

$$\begin{aligned} \begin{array}{c|ccccc} \text {horizontal line} &{}\quad g\quad &{} \quad g_1 \quad &{} \quad g_2\quad &{} \quad g_3 \quad \\ \hline { y}\text {-value} &{} 0 &{} \sqrt{3} &{} 2\sqrt{3} &{} \sqrt{3} + 2\\ \end{array} \quad . \end{aligned}$$

(2)

The disks $A_1$ and $B_1$ are aligned in x at heights $g_3$ and $g_1$, respectively. All A disks lie on a given convex polygonal chain $\mathcal {A}$ between $g_2$ and $g_3$. The chain segments on $\mathcal {A}$ are of length 2 so that subsequent disks $A_i$ and $A_{i+1}$ block each other, and the position of $A_1$ fixes all other A disks. All C disks lie on g, and $C_i$ blocks $B_i$ from the right (in particular, $C_1$ is placed after $B_1$). The disk $B_i$, for $i>1$, lies between g and $g_1$ and it blocks disks $A_i$ and $C_{i-1}$ from the right. With the position of $g_2$, the branch approaches a hexagonal packing for $i\rightarrow \infty$. After reflection about the x-axis, all disks except $A_1$ and $B_1$ are locally stable in the infinite branch.

The Böröczky packing is completed by attaching the four branches along the four coordinate axes to a core. For the Böröczky core, both $A_1$ and $B_1$ are blocked by core disks (see Fig. 1a). For the Kahle core, $B_1$ is blocked by a core disk, and $A_1$ is locally stable as it also belongs to another branch (see Fig. 1b).

2.1.3 Branches—Finite-Layer Case (Finite N), Periodic Boundary Conditions

Branches can also be constructed for periodic simulation boxes, with a finite number k of layers and finite N (see [13]). The branch that connects the central core placed around (0, 0) with its periodic image around (L, 0) is then again symmetric about the x-axis but, in addition, also about the boundary of the central simulation box at $x=L/2$. We describe the construction of the half-branch (for $y \ge 0$) up to this boundary (see Fig. 1).

For half-branches with a finite number of layers k and a finite number of disks $\{A_1 ,\ldots ,A_k\}$, $\{B_1 ,\ldots ,B_k\}$, and $\{C_1 ,\ldots ,C_{k-1}\}$ (with their corresponding mirror images), the convex polygonal chain $\mathcal {A}$ lies between $g_2^<$ and $g_3$ where $g_2^<$ is an auxiliary horizontal line placed slightly below $g_2$. The horizontal lines g and $g_1$ and the algorithm for placing the disks are as in Sect. 2.1.2 (see Fig. 1c, d). By varying the distance between $g_2$ and $g_2^<$, one can make disk $B_k$ satisfy the additional requirement $x_{B_k} = x_{A_k} +1$ that allows for periodic boundary conditions. The position of $B_k$ then fixes the boundary of the square box ($x_{B_k} = L/2$) and $B_k$ blocks $A_k$ as well as the mirror image $A_{k+1}$ of $A_k$ (see Fig. 1c again).

2.2 Properties of Böröczky Packings

The local stability of Böröczky packings only relies on the fact that all A disks lie on a largely arbitrary convex polygonal chain $\mathcal {A}$ [13]. The choice of $\mathcal {A}$ influences the qualitative properties of the packing. The BigBoro software package (see Appendix B) implements two different classes of convex polygonal chains that we discuss in Sect. 2.2.1. Another computer program in the package explicitly determines the space of collective escape modes from a Böröczky packing, which we discuss in Sect. 2.2.2.

2.2.1 Convex Polygonal Chains (Geometric, Circular)

In the convex geometric chain $\mathcal {A}^{\text {geo}}$ (which is for instance used in Fig. 1), the disks $A_i$ approach the line $g_2^<$ exponentially in i. In contrast, in the convex circular chain $\mathcal {A}^{\text {circ}}$, all A disks lie on a circle (including their mirror images after reflection about $x = L/2$) so that their opening angles are all the same.

For the convex geometric chain $\mathcal {A}^{\text {geo}}$, the distance between $A_i$ and $g_2^<$ follows a geometric progression:

$$\begin{aligned} \text {dist}(A_{i + 1},g_2^<) = \phi \; \text {dist}(A_i,g_2^<), \quad \phi \in (0,1), \end{aligned}$$

(3)

with the attenuation parameter $\phi$. (For a horizontal branch, the distances in Eq. (3) are simply the difference between y-values.) The densities $\eta _{{\mathrm{B}}\ddot{\mathrm{o}}{\mathrm{r}}}$ and $\eta _{\text {Kahle}}$ of the Böröczky packings that either use the Böröczky or the Kahle core vary with $\phi$, and they decrease as $\sim 1/k$ for large k (see Table 1). The geometric sequence for $A_i$ induces that the maximum opening angle, usually the one between $A_{k-1},A_k$, and $A_{k+1}$, approaches the angle $\pi$ as $\theta _k =\phi ^{k-2}(1-\phi )(g_3 - g_2^<)/2 \sim \phi ^k$, that is, exponentially in k and in L. This implies that the Böröczky packing with the convex geometric chain $\mathcal {A}^{\text {geo}}$ is for large number of layers k exponentially close to losing its local stability (see fifth column of Table 1).

Table 1 Parameters of Böröczky packings for different numbers k of layers with $N \sim 20k$ given by Eq. (4)

The convex circular chain $\mathcal {A}^{\text {circ}}$ improves the local stability of the Böröczky packing, as the maximum opening angle on $\mathcal {A}$ approaches the critical angle $\pi$ only algebraically with the number of layers k. Here, all A disks lie on a circle of radius R. This includes $A_1$, which by construction lies on $g_3$ (see Sect. 2.1.2). The circle is tangent to $g_2^<$ at $x=L/2$. The center of the circle lies on the vertical line at $x = L/2$. It follows from elementary trigonometry that for large k, the radius of the circle R scales as $\sim k^2$ and that the maximum opening angle approaches the angle $\pi$ as $\sim k^{-2}$ (see fourth column of Table 1).

2.2.2 Contact Graphs: Local and Collective Stability

The contact graph of a Böröczky packing connects any two disks whose pair distance equals 2 (including periodic boundary conditions, see Fig. 1). In a Böröczky packing with $k \ge 1$ layers, the number N of disks and the number $N_{\text {contact}}$ of contacts are:

$$\begin{aligned} \begin{array}{l|ccc} &{} \quad N \quad &{} N_{\text {contact}} \quad \\ \hline \mathrm{Bp}{\ddot{\mathrm{o}}}\mathrm{r}{\ddot{\mathrm{o}}}\mathrm{czky}\, \mathrm{core} &{} \quad 20 k + 12 &{} \quad 32k+20 \\ \mathrm{{Kahle\, core}} &{} \quad 20 k -4 &{} \quad 32 k + 4 \end{array}. \end{aligned}$$

(4)

For all values of $k > 1$, the number of contacts is smaller than $2N-2$. This implies that collective infinitesimal two-dimensional displacements, with $2N-2$ degrees of freedom (the values of the displacements in x and in y for each disk avoiding trivial translations), can escape from a Böröczky packing, which is thus not collectively stable [17].

When all disks i, at positions $\mathbf {x}_i = (x_i, y_i)$, are moved to $\mathbf {x}_i + \varvec{\varDelta }_i$ with $\varvec{\varDelta }_i = (\varDelta _i^x, \varDelta _i^y)$, the squared separation between two touching disks from the contact graph i and j changes from $| \mathbf {x}_i - \mathbf {x}_j| ^2$ to

$$\begin{aligned} | \mathbf {x}_i + \varvec{\varDelta }_i - (\mathbf {x}_j + \varvec{\varDelta }_j) | ^2 = | \mathbf {x}_i - \mathbf {x}_j|^2 + \underbrace{2 (\mathbf {x}_i-\mathbf {x}_j)\cdot (\varvec{\varDelta }_i - \varvec{\varDelta }_j)}_{\text {first-order variation}} + |\varvec{\varDelta }_i - \varvec{\varDelta }_j | ^2 . \end{aligned}$$

(5)

If the first-order term in Eq. (5) vanishes for all contacts i and j, the separation between touching disks cannot decrease. It then increases to second order in the displacements, if $\varvec{\varDelta }_i \ne \varvec{\varDelta }_j$, so that contact is lost. Distances between disks that are not in contact need not be considered because the displacements $\varvec{\varDelta }_i$ are infinitesimal. The first-order variation in Eq. (5) can be written as a product of twice an “escape matrix” $\mathcal {M}^{\text {esc}}$ of dimensions $N_{\text {contacts}} \times 2N$ with a 2N-dimensional vector $\varvec{\varDelta } = ( \varDelta _1^x, \varDelta _1^y, \varDelta _2^x, \varDelta _2^y, \ldots )$. The row r of $\mathcal {M}^{\text {esc}}$ corresponding to the contact between i and j has four non-zero entries

$$\begin{aligned} \begin{aligned} \mathcal {M}^{\text {esc}}_{r, 2i-1}&= x_i - x_j, \\ \mathcal {M}^{\text {esc}}_{r, 2i}&= y_i - y_j, \\ \mathcal {M}^{\text {esc}}_{r, 2j-1}&=-(x_i - x_j), \\ \mathcal {M}^{\text {esc}}_{r, 2j}&=-(y_i - y_j) . \end{aligned} \end{aligned}$$

(6)

The BigBoro software package (see Appendix B) solves for

$$\begin{aligned} \mathcal {M}^{\text {esc}}\varvec{\varDelta }= 0 \end{aligned}$$

(7)

using singular-value decomposition. The solutions of Eq. (7) are the directions of the small displacements that break the contacts but do not introduce overlapping disks. For the $k=5$ Böröczky packing with the Kahle core, we find 28 vanishing singular values. It follows from Eq. (4) that, because of $28 = 2N - N_{\text {contact}}$, all contacts are linearly independent. We classify the 28 modes by studying the following cost function on the contact graph:

$$\begin{aligned} L= \sum _{i,j} (\varvec{\varDelta }_i-\varvec{\varDelta }_j)^2, \end{aligned}$$

(8)

where the sum is over all contact pairs i and j. This function, acting on the 2N displacements $\varvec{\varDelta }$, measures the non-uniformity of a deformation. It acts as a quadratic form within the 28-dimensional space of vanishing singular values, and can be diagonalized within this space. The resulting two lowest eigenmodes (with zero eigenvalue) of Eq. (8) describe rigid translation of the packing in the plane. Other low-lying eigenmodes give smooth large-scale deformations which collectively escape the contact constraints (see Fig. 2).

Fig. 2

Two orthogonal modes (represented as red arrows) out of the 28-dimensional space of all collective escape modes $\varvec{\varDelta }$ for the $k=5$ Böröczky packing with the Kahle core and the convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi =0.7$. Lines are drawn between pairs of disks which are in contact

For $k \ge 1$, the number of contacts in Eq. (4) is larger than $N-1$. Böröczky packings are thus collectively stable for displacements that are constrained to a single direction, as for example the x or y direction. This strongly constrains the dynamics of MCMC algorithms that for a certain time have only one degree of freedom per disk.

2.2.3 Dimension of the Space of Böröczky Packings

As discussed in Sect. 2.2.2, each Böröczky packing has a contact graph. Conversely, a given contact graph describes Böröczky packings for a continuous range of densities $\eta$. As an example, changing the attenuation parameter $\phi$ of the convex polygonal chain $\mathcal {A}^{\text {geo}}$ in Eq. (3) continuously moves all branch disks, and in particular disk $B_{k}$ and, therefore, the value of L and the density $\eta$ (see Table 1 for density windows that can be obtained in this way). We conjecture that locally stable packings exist for any density at large enough N. Sparse locally stable packings can also be part of dense hard-disk configurations where the majority of disks are free to move.

Moreover, the space $\mathcal {B}$ of locally stable packings of N disks of radius $\sigma$ in a given central simulation box is of lower dimension than the sample space $\varOmega$: For each contact graph, each independent edge decreases the dimensionality by one. In addition there is only a finite number of contact graphs for a given N. The low dimension of $\mathcal {B}$ also checks with the fact that any packing, and more generally, any configuration with contacts, has effectively infinite pressure (see the detailed discussion in Sect. 4.2.2). As the ensemble-averaged pressure is finite (except for the densest packing), the packings (and the configurations containing packings) must be of lower dimension. As the dimension of $\mathcal {B}$, for large N, is much lower than that of $\varOmega$, we conjecture $\varOmega \setminus \mathcal {B}$ to be connected for a given $\eta$ below the densest packing at large enough N although, in our understanding, this is proven only for $\eta \sim 1/\sqrt{N}$ (see [19, 20]).

3 MCMC Algorithms and $\varepsilon$-relaxed Böröczky configurations

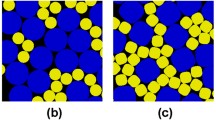
In this section, we first introduce to a number of local MCMC algorithms (see Sect. 3.1). In Sect. 3.2, we then determine the escape times (in the number of trials or events) after which these algorithms escape from $\varepsilon$-relaxed Böröczky configurations, that is, from Böröczky packings with disk radii multiplied by a factor $(1-\varepsilon )$ (see Fig. 3a, b). A scaling theory establishes the existence of two classes of MCMC algorithms, one in which the escape time from an $\varepsilon$-relaxed Böröczky configurations scales algebraically with $\varepsilon$, with exponents that are predicted exactly, and the other in which the scaling is logarithmic. Numerical simulations confirm the theory.

3.1 Local Hard-Disk MCMC Algorithms

We define the reversible Metropolis algorithm with two displacement sets, from which the trial moves are uniformly sampled (see Sect. 3.1.1). We also consider variants of the non-reversible ECMC algorithm that only differ in their treatment of events, that is, of disk collisions (see Sect. 3.1.2). An arbitrary-precision implementation of the discussed ECMC algorithms (in the Go programming language) is contained in the BigBoro software package (see Appendix B).

3.1.1 Local Metropolis Algorithm: Displacement Sets

The N disks are at positions $\mathbf {x} = ( \mathbf {x}_1, \ldots , \mathbf {x}_N )$. In the local Metropolis algorithm [1], at each time $t=1,2,\ldots$, a trial move is proposed for a randomly chosen disk i, from its position $\mathbf {x}_i$ to $\mathbf {x}_i + \varDelta \mathbf {x}_i$. If the trial produces an overlap, disk i stays put and $\mathbf {x}$ remains unchanged. We study two sets for the trial moves. For the cross-shaped displacement set, the trial moves are uniformly sampled within a range $\delta$ along the coordinate axes, that is, either along the x-axis ($\varDelta \mathbf {x}_i = (\texttt {ran}_{} \! \left( -\delta ,\delta \right) , 0)$) or along the y-axis ($\varDelta \mathbf {x}_i = (0, \texttt {ran}_{} \! \left( -\delta ,\delta \right) )$). Alternatively, for the square-shaped displacement set, the trial moves are uniformly sampled as $\varDelta \mathbf {x}_i = (\texttt {ran}_{} \! \left( -\delta ,\delta \right) , \texttt {ran}_{} \! \left( -\delta , \delta \right) )$. A Böröczky packing traps the local Metropolis algorithm if the range $\delta$ is smaller than a critical range $\delta _c$. This range is closely related to the maximum opening angle (see the discussion in Sect. 2.2.1 and Fig. 3c). For these packings, the critical range vanishes for $N \rightarrow \infty$ independently of the specific core or of the convex polygonal chain, simply because the maximum opening angle approaches $\pi$ in that limit. On the other hand, for large range $\delta$, the algorithm can readily escape from the stable configuration. For $\delta =L/2$, the Metropolis algorithm with a square-shaped displacement set proposes a random placement of the disk i inside the central simulation box. This displacement set leads to a very inefficient algorithm at the densities of physical interest, but it mixes very quickly at small finite densities (see Sect. 4.2.1). For the scaling theory of the escape of the Metropolis algorithm from $\varepsilon$-relaxed Böröczky configurations, we consider ranges $\delta$ smaller than the critical range $\delta _c$.

Fig. 3

Contact graphs, constraint graphs and minimal escape range. a Contact graph for a packing consisting solely of the Böröczky core. b Constraint graph in x-direction for an $\varepsilon$-relaxed Böröczky configurations derived from the same packing with $\varepsilon = 0.25$. The edges indicate all possible collisions of straight ECMC in x-direction. c Escape move $\varvec{\delta }$ and minimal escape range $\delta _c$ of the Metropolis algorithm with a square-shaped displacement set

3.1.2 Hard-Disk ECMC: Straight, Reflective, Forward, Newtonian

Straight ECMC [5] is one of the two original variants of event-chain Monte Carlo. This Markov chain evolves in (real-valued) continuous Monte-Carlo time $t_{\text {MCMC}}$, but its implementation is event-driven. The algorithm is organized in a sequence of “chains”, each with a chain time $\tau _{\text {chain}}$, its intrinsic parameter. In each chain, with Monte-Carlo time between $t_{\text {MCMC}}$ and $t_{\text {MCMC}}+ \tau _{\text {chain}}$, disks move with unit velocity in one given direction (alternatively in $+x$ or in $+y$). A randomly sampled initial disk thus moves either until the chain time $\tau _{\text {chain}}$ is used up, or until, at a collision event, it collides with another disk, which then moves in its turn, etc. This algorithm is highly efficient in some applications [4, 5, 21]. During each chain (in between changes of direction), any disk can collide only with three other disks or fewer [22, 23]. A constraint graph with directed edges may encode these relations. This constraint graph (defined for hard-disk configurations) takes on the role of the contact graph (that is defined for packings) (see Fig. 3a, b). As the moves in a chain are all in the same direction, straight ECMC has only $N -1$ degrees of freedom, fewer than there are edges in the constraint graph. It is for this reason that it may encounter the rigidity problems evoked in Sect. 2.2.2.

In reflective ECMC [5], in between events, disks move in straight lines with unit velocity just as in straight ECMC. At a collision event, the target disk does not continue in the same direction as the active disk. Rather, the target-disk direction is the original active-disk direction reflected from the line connecting the two disk centers at contact (see [5]). As all ECMC variants, reflective ECMC satisfies the global-balance condition. Irreducibility (for connected sample spaces) requires in principle resamplings of the active disk and its velocity in intervals of the chain time $\tau _{\text {chain}}$ [15, 24, 25]. However, this seems not always necessary [15, 25]. Numerical experiments indicate that reflective ECMC requires no resamplings in our case as well. It is also faster without them (see Appendix A.2). A variant of reflective ECMC, obtuse ECMC [16], has shown interesting behavior.

Forward ECMC [15] updates the normalized target-disk direction as follows after an event. The component orthogonal to the line connecting the disks at contact is uniformly sampled between 0 and 1 (reflecting the orthogonal orientation). Its parallel component is determined so that the direction vector (which is also the velocity vector) is of unit norm. The parallel orientation remains unchanged. In contrast to reflective ECMC, the event-based randomness renders forward ECMC practically irreducible for the considered two-dimensional hard-disk systems even without resamplings. Resamplings in intervals of the chain time $\tau _{\text {chain}}$ can still be considered but slow the algorithm down (see Appendix A.2). We thus consider forward ECMC without resampling.

Newtonian ECMC [16] mimics molecular dynamics in order to determine the velocity of the target disk in an event. It initially samples disk velocities from the two-dimensional Maxwell distribution with unit root-mean-square velocity. However, at each moment, only a single disk is actually moving with its constant velocity. At a collision event, the velocities of the colliding disks are updated according to Newton’s law of elastic collisions for hard disks of equal masses, but only the target disks actually moves after the event. In this algorithm, the velocity (which indexes the Monte-Carlo time) generally differs from unity. Similar to reflective ECMC, we tested that resamplings appear not to be required in our case (and again yield a slower performance, see Appendix A.2), although Newtonian ECMC manifestly violates irreducibility in highly symmetric models [25]. As in earlier studies for three-dimensional hard-sphere systems [16] and for two-dimensional dipoles [25], Newtonian ECMC is typically very fast for $\varepsilon$-relaxed Böröczky configurations. However, it suffers from frequent gridlocks (see Sect. 3.2.4).

3.2 Escape Times from $\varepsilon$-relaxed Böröczky configurations

The principal figure of merit for a Markov chain is its mixing time [26], the number of steps it takes from the worst-case initial condition to approach the stationary probability distribution to some precision level. Böröczky packings trap the local Metropolis dynamics (of sufficiently small range) as well as ECMC dynamics, so that the mixing time is, strictly speaking, infinite. Although they cannot be escaped from, the packings make up only a set of measure zero in sample space, and might thus be judged irrelevant.

However, as we will discuss in the present subsection, the situation is more complex. For every Böröczky packing, an associated $\varepsilon$-relaxed Böröczky configurations keeps the central simulation box and the disk positions, but reduces the disk radii from 1 to $1-\varepsilon$. An $\varepsilon$-relaxed Böröczky configurations effectively defines a finite portion of the sample space (the spheres of radius $\varepsilon$ around each disk position of the packing). All MCMC algorithms considered in this work escape from these configurations in an escape time that diverges as $\varepsilon \rightarrow 0$ (see Sect. 3.2.1 for a definition of escape times). Numerical results and a scaling theory for the escape times are discussed in Sects. 3.2.2  and 3.2.3, and a synopsis of our results is contained in Sect. 3.2.4. The divergent escape times as $\varepsilon \rightarrow 0$ are specific to the NVT ensemble (as we will discuss in Sect. 4.2.2).

3.2.1 Nearest-Neighbor Distances and Escape Times

In a Böröczky packing, disks are locally stable, and they all have a nearest-neighbor distance of 2. The packings are sparse, and the nearest-neighbor distance is thus smaller than its $\sim 1/ \sqrt{\eta }$ equilibrium value. To track the escape from an $\varepsilon$-relaxed Böröczky configurations, we monitor the maximum nearest-neighbor distance:

$$\begin{aligned} d(t) = \max _i \left[ \min _{j (\ne i)} |\mathbf {x}_{ij}(t)| \right] , \end{aligned}$$

(9)

where $|\mathbf {x}_{ij}(t)| = |\mathbf {x}_j(t) - \mathbf {x}_i(t)|$ is the distance between disks i and j (possibly corrected for periodic boundary conditions). The maximum nearest-neighbor distance signals when a single disk breaks loose from what corresponds to its contacts. In the further time evolution, the configuration then falls apart. For the Metropolis algorithm, we compute d(t) once every N trials, and t denotes the integer-valued number of individual trial moves. For ECMC, we sample d(t) and the number of events in intervals of the sampling Monte-Carlo time. In Eq. (9), t then denotes the integer-valued number of events. Both discrete times t increment by one with a computational effort $\mathcal {O}(1)$, corresponding to one trial in the Metropolis algorithm and to one event in ECMC. Starting from an $\varepsilon$-relaxed Böröczky configurations, d(t) typically remains at $d(t) \sim 2 + \mathcal {O}\left( \varepsilon \right)$ for a long time until it approaches the equilibrium value in a way that depends on the algorithm. We define the escape time $t_\mathrm {esc}$, an integer, as the time t at which d(t) has increased by ten percent:

$$\begin{aligned} t_\mathrm {esc}= \min ^{} \left[ t: d(t) > 2 (1+ \gamma ) \right] , \end{aligned}$$

(10)

with $\gamma =0.1$. All our results for the scaling of the escape time with the relaxation parameter $\varepsilon$ in the following subsections were reproduced for $\gamma =0.025$ (see Appendix A.1). The definition of the escape time based on the maximum nearest-neighbor distance d(t) is certainly not the only one to monitor the stability of $\varepsilon$-relaxed Böröczky configurations. It may not be equally well-suited for all considered algorithms. Still, our scaling theory suggests that the algorithms with an intrinsic parameter show a distinctly different behavior than the algorithms without them, which appears to be independent of the precise definition of the escape time.

3.2.2 Escape-Time Scaling for Metropolis and Straight ECMC

The local Metropolis algorithm and straight ECMC both have an intrinsic parameter, namely the range $\delta$ of the displacement set or the chain time $\tau _{\text {chain}}$. These two parameters play a similar role. We numerically measure the escape time $t_\mathrm {esc}$ of these algorithms for a wide range of their intrinsic parameters and for small relaxation parameters $\varepsilon$ (see Fig. 4, for the escape times from $\varepsilon$-relaxed Böröczky configurations with $k=5$ layers and the Kahle core). The escape time diverges for $\delta , \tau _{\text {chain}}\rightarrow 0$. For straight ECMC and small $\varepsilon$, $t_\mathrm {esc}$ also diverges for $\tau _{\text {chain}}\rightarrow \infty$ so that the function is “V”-shaped with an optimal chain time $\tau _{\text {chain}}^\text {min}$. For the Metropolis algorithm, $t_\mathrm {esc}$ increases until around the critical range $\delta _c$ so that there is an optimal range $\delta ^\text {min}<\delta _c$.

Fig. 4

Median escape times from the $k=5$ $\varepsilon$-relaxed Böröczky configurations (Kahle core and convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi =0.7$, $N=96$ disks) for different $\varepsilon$. a $t_\mathrm {esc}$ (in trials) vs. range $\delta$ for the Metropolis algorithm with the cross-shaped displacement set. b $t_\mathrm {esc}$ (in events) vs. chain time $\tau _{\text {chain}}$ for straight ECMC. Asymptotes are from Eqs. (11) and (12). Error bars are smaller than the marker sizes

Two limiting cases can be analyzed in terms of the intrinsic parameter $\delta < \delta _c$ or $\tau _{\text {chain}}$, and the internal length scales $\varepsilon$, and $\sigma$. For the Metropolis algorithm at small $\delta$, a trajectory spanning a constant distance is required to escape from an $\varepsilon$-relaxed Böröczky configurations. This constant distance can be thought of as the escape distance $\delta _c$ in Fig. 3, which is on a scale $\sigma$ and independent of $\varepsilon$ for small $\varepsilon$. As the Monte-Carlo dynamics is diffusive, this constant distance satisfies $\text {const}= \delta \sqrt{t_\mathrm {esc}}$. For straight ECMC with small chain times $\tau _{\text {chain}}$, the effective dynamics (after subtraction of the uniform displacement), is again diffusive. This leads to:

$$\begin{aligned} t_\mathrm {esc}\sim {\left\{ \begin{array}{ll} \text {const}/ \delta ^ 2 &{} \text {(Metropolis)},\\ \text {const}/ \tau _{\text {chain}}^ 2 &{} \text {(straight ECMC)}, \end{array}\right. }\quad (\text {for small} \, \delta < \delta _c, \tau _{\text {chain}}). \end{aligned}$$

(11)

The independence of $t_\mathrm {esc}$ of the relaxation parameter $\varepsilon$ for small intrinsic parameters is clearly brought out in the numerical simulations (see Fig. 4).

On the other hand, even for large $\delta < \delta _c$ or $\tau _{\text {chain}}$, the Markov chain must make a certain number of moves on a length scale $\varepsilon$ in order to escape from the $\varepsilon$-relaxed Böröczky configurations. In the Metropolis algorithm, the probability for a trial on this scale is $\varepsilon / \delta$ for the cross-shaped displacement set and $\varepsilon ^2 /\delta ^2$ for the square-shaped displacement set. For the straight ECMC with large $\tau _{\text {chain}}$, all displacements beyond a time $\sim \varepsilon$ (or, possibly, $\sim N \varepsilon$) effectively cancel each other, because the constraint graph is rigid. This leads to:

$$\begin{aligned} t_\mathrm {esc}\sim {\left\{ \begin{array}{ll} \delta ^2 / \varepsilon ^2 &{} \text {(Metropolis---square)},\\ \delta / \varepsilon &{} \text {(Metropolis---cross)},\\ \tau _{\text {chain}}/ \varepsilon &{} \text {(straight ECMC)},\\ \end{array}\right. } \quad (\text {for large}\, \delta < \delta _c, \tau _{\text {chain}}). \end{aligned}$$

(12)

The scaling of $t_\mathrm {esc}$ as $\sim 1/\varepsilon$ or $\sim 1/\varepsilon ^2$ for large intrinsic parameters is confirmed in the numerical simulations for small relaxation parameters $\varepsilon$ (see Fig. 4). For large $\varepsilon$, the critical range $\delta _c$ of the Metropolis algorithm (that slightly decreases with $\varepsilon$) falls below the region of large $\delta$. For large $\varepsilon$, the constraint graph of straight ECMC loses its rigidity, and $\tau _{\text {chain}}$ no longer appears as a relevant intrinsic parameter. The scaling theory no longer applies.

The two asymptotes of Eqs. (11) and (12) form a “V” with a base $\delta ^\text {min}$ (or $\tau _{\text {chain}}^\text {min}$) that is obtained by equating the two expressions for $t_\mathrm {esc}(\delta )$ (or $t_\mathrm {esc}(\tau _{\text {chain}})$). This yields $\delta ^\text {min} \sim \root 3 \of {\varepsilon }$ for the Metropolis algorithm with a cross-shaped displacement set, and likewise $\tau _{\text {chain}}^\text {min} \sim \root 3 \of {\varepsilon }$ for straight ECMC. For the Metropolis algorithm with a square-shaped move set, one obtains $\delta ^\text {min} \sim \sqrt{\varepsilon }$. The resulting optimum, the minimal escape time with respect to $\varepsilon$, is

$$\begin{aligned} t_\mathrm {esc}\sim {\left\{ \begin{array}{ll} \varepsilon ^{-1} &{} \text {(Metropolis---square)}, \\ \varepsilon ^{-2/3} &{} \text {(Metropolis---cross)},\\ \varepsilon ^{-2/3} &{} \text {(straight ECMC)}, \\ \end{array}\right. } \quad (\text {for optimal}\, \delta ^\text {min}, \tau _{\text {chain}}^\text {min}). \end{aligned}$$

(13)

These scalings balance two requirements: to move by a constant distance (which favors large $\delta$ or $\tau _{\text {chain}}$) and to move on the scale $\varepsilon$ (which favors small $\delta$ or $\tau _{\text {chain}}$).

3.2.3 Time Dependence of Free Path—Reflective, Forward, and Newtonian ECMC

The forward, reflective, and Newtonian variants of ECMC move in any direction, even in the absence of resamplings, so that their displacement sets are 2N-dimensional. This avoids the rigidity problem of straight ECMC (the fact that the number of constraints can be larger than the number of degrees of freedom). We consider these algorithms without resamplings, that is, for $\tau _{\text {chain}}= \infty$. Finite chain times yield larger escape times that approach the value at $\tau _{\text {chain}}=\infty$ (see Appendix A.2). Without an intrinsic parameter, the effective free path between events may thus adapt as the configuration gradually escapes from the $\varepsilon$-relaxed Böröczky configurations. The free path is initially on the scale $\varepsilon$, but then grows on average by a constant factor at each event, reaching a scale $\varepsilon ' > \varepsilon$ after a time (that is, after a number of events) that scales as $\sim \ln ( \varepsilon '/\varepsilon )$. The scale $\varepsilon '$ at which the algorithms break free is independent of the initial scale $\varepsilon$, and we expect a logarithmic scaling of the escape time (measured in events):

$$\begin{aligned} t_\mathrm {esc}\sim \ln (1 / \varepsilon )\quad \text {(reflective, forward, and Newtonian ECMC)}. \end{aligned}$$

(14)

The absence of an imposed scale for displacements manifests itself in the logarithmic growth with time of the average free path, that is, the averaged displacement between events over many simulations starting from the same $\varepsilon$-relaxed Böröczky configurations (see Fig. 5 for the example of the escape of forward ECMC from $\varepsilon$-relaxed Böröczky configurations with $k=5$ layers and the Kahle core). Individual evolutions as a function of time t for small relaxation parameters $\varepsilon$ and $\varepsilon '$ overlap when shifted by their escape times. Starting from an $\varepsilon$-relaxed Böröczky configurations with $\varepsilon = 10^{-30}$, as an example, the same time is on average required to move from an average free path of $\sim 10^{-30}$ to $10^{-25}$, as from an average free path $\sim 10^{-25}$ to $10^{-20}$. The time t in this discussion refers to the number of events and not to the Monte-Carlo time $t_{\text {MCMC}}$. As discussed, the velocity in reflective and forward ECMC, and the root-mean-square velocity in Newtonian ECMC, have unit value. The free path between subsequent events—which, as discussed, grows exponentially with t—then equals the difference of Monte-Carlo times $t_{\text {MCMC}}(t +1) - t_{\text {MCMC}}(t)$. The Monte-Carlo time $t_{\text {MCMC}}$ thus grows as a geometric series and depends exponentially on the number of events t. This emphasizes that the escape from an $\varepsilon$-relaxed Böröczky configurations is a non-equilibrium phenomenon.

Fig. 5

Free path (equivalently: Monte-Carlo time between events) for the forward ECMC algorithm started from three $k=5$ $\varepsilon$-relaxed Böröczky configurations (Kahle core and convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi = 0.7$, $N=96$ disks) with $\varepsilon = 10^{-30}$, $10^{-25}$ and $10^{-20}$. Integer time t (lower x-axis) counts events, while $t_{\text {MCMC}}$ (upper x-axis) is the real-valued continuous Monte-Carlo time. Event times are shifted. Expanded light curves show single simulations for each $\varepsilon$, dark lines average over 10,000 simulations

3.2.4 Escape Times: Synopsis of Numerical Results and Scaling Theory

Overall, escape times $t_\mathrm {esc}(\varepsilon )$ (with intrinsic parameters optimized through a systematic scan for the Metropolis algorithm and for straight ECMC) validate the algebraic scalings of Eq. (13), on the one hand, and the logarithmic scaling of Eq. (14), on the other (see Fig. 6 for the escape times from $\varepsilon$-relaxed Böröczky configurations with $k=5$ layers with either the Kahle core or the Böröczky core). Our arbitrary-precision implementation of reflective, forward, and Newtonian ECMC confirms their logarithmic scaling down to $\varepsilon =10^{-29}$. Newtonian ECMC appears a priori as the fastest variant of ECMC. However, it frequently gets gridlocked, i.e., trapped in circles of repeatedly active disks with a diverging event rate. Gridlocks also rarely appear in straight and reflective ECMC. In runs that end up in gridlock, escape times are very large, possibly diverging. (In Figs. 4 and 6, median escape times rather than the means are therefore displayed for all algorithms. Mean and median escape times are similar for the Metropolis algorithm and forward ECMC where gridlocks play no role.) The gridlock rate increases with $1/\varepsilon$. For the Kahle core, this effect is negligible for all $\varepsilon$. For the Böröczky core, the gridlock rate of Newtonian ECMC is $\sim 30 \%$ for $\varepsilon = 10^{-29}$ (see Fig. 6b, the logarithmic scaling is distorted even for the median). We observe no clear dependence of the gridlock rate on the floating-point precision of our arbitrary-precision ECMC implementation, and it thus appears unlikely that gridlocks are merely numerical artifacts (see Appendix A.3).

Fig. 6

Median escape time $t_\mathrm {esc}$ from $k=5$ $\varepsilon$-relaxed Böröczky configurations with different cores (with convex geometric chain $\mathcal {A}^{\text {geo}}$ and attenuation parameter $\phi = 0.7$) for local MCMC algorithms (where applicable: with optimized intrinsic parameters). a a $t_\mathrm {esc}$ for the Kahle core ($N = 96$ disks). The Metropolis algorithm and straight ECMC show an algebraic scaling. Inset: log–lin plots suggesting logarithmic scaling for the forward, reflective, and Newtonian ECMC. b $t_\mathrm {esc}$ for the Böröczky core ($N=112$ disks). Newtonian ECMC has frequent gridlocks for small $\varepsilon$ so that its logarithmic scaling is distorted. Error bars are smaller than the marker sizes.

Gridlock is the very essence of ECMC dynamics from a locally stable Böröczky packing, but it can also appear as a final state from an $\varepsilon$-relaxed Böröczky configurations. We observe gridlocks in all hard-disk ECMC variants that feature deterministic collision rules. They were previously observed for straight ECMC from tightly packed initial configurations [27, Sect. 4.2.3]. Only forward ECMC with its event-based randomness is free of them. In a gridlock, the event rate diverges at a given Monte-Carlo time, which then seems to stand still so that no finite amount of Monte-Carlo time is spent in a configuration with contacts. Because of the divergence of the event rate, gridlocks cannot be cured through resamplings at fixed Monte-Carlo-time intervals. To overcome them in Newtonian ECMC, which appears a priori as the fastest of our ECMC variants, one can probably introduce event-based randomness as is done in forward ECMC. Nevertheless, gridlocks play no role in large systems at reasonable densities. Also, ECMC algorithms for soft potentials introduce randomness at each event so that gridlocks should not appear.

4 Discussion

In the present section, we discuss our results for the escape times (Sect. 4.1), as well as a number of more fundamental aspects of Böröczky packings in the context of MCMC (Sect. 4.2). We in particular clarify why a packing effectively realizes an infinite-pressure configuration that in a constant-pressure Monte-Carlo simulation is instantly relaxed through a volume increase.

4.1 Escape Times: Speedups, Bottlenecks

ECMC is a continuous-time MCMC method, and its continuous Monte-Carlo time $t_{\text {MCMC}}$ takes the place of the usual count of discrete-time Monte-Carlo trials. However, ECMC is event-driven. The time t, and especially the escape time $t_\mathrm {esc}$, are integers, and they count events. The computational effort in hard-disk ECMC is $\mathcal {O}\left( 1 \right)$ per event, using a cell-occupancy system that is also implemented in the BigBoro software package. In several of our algorithms, the times t and $t_{\text {MCMC}}$ are not proportional to each other, because the free path (roughly equivalent to the Monte-Carlo time between events) evolves during each individual run.

4.1.1 Range of Speedups

The speedup realized by lifted Markov chains, of which ECMC is a representative, corresponds to the transition from diffusive to ballistic transport [6, 28, 29]. This speedup refers to what we call the “Monte-Carlo time” $t_{\text {MCMC}}$, that is the underlying time of the Markov process, and not to the time t that is measured in events. For Markov chains in a finite sample space $\varOmega$, the Monte-Carlo time for mixing of the lifted Markov chain cannot be smaller than the square root of the mixing time for the original (collapsed) chain. The remarkable power-law-to-logarithm speedup in $\varepsilon$ realized by some of the ECMC algorithms concerns escape times which measure the number of events. The Monte-Carlo escape times probably conform to the mathematical bounds, although it is unclear how to approximate hard-disk MCMC for $\varepsilon \rightarrow 0$ through a finite Markov chain. Mathematical results for the Monte-Carlo escape times from locally blocked configurations would be extremely interesting, even for models with a restricted number of disks.

4.1.2 Space of $\varepsilon$-Relaxed Böröczky Configurations

The definition of an $\varepsilon$-relaxed Böröczky configurations can be generalized. Equivalent legal hard-disk configurations are obtained by reducing the disk radii and choosing random disk positions in a circle of radius $\varepsilon$ around the original disk positions in the Böröczky packing. These configurations also feature the escape-time scalings given in Eqs. (13) and (14). Any $\varepsilon$-relaxed Böröczky configurations is thus merely a sample in a space $\mathcal {B}_\varepsilon$ of volume $\sim \varepsilon ^{2N}$. For a given upper limit $t_{\text {cpu}}$ of CPU time at fixed N, this corresponds to a volume of $\mathcal {B}_\varepsilon$ (that cannot be escaped from in $t_{\text {cpu}}$) scaling with the computer-time budget as $\sim t_{\text {cpu}}^{-3 N}$ for the straight ECMC and scaling as $\sim \exp \left( -2N t_{\text {cpu}} \right)$ for the forward ECMC. We expect $\mathcal {B}_\varepsilon$ to have a double role, as a space of configurations that the Monte-Carlo dynamics cannot practically escape from, but maybe also a space that it cannot even access. The volume of $\mathcal {B}_\varepsilon$ (with $\varepsilon$ chosen such that it cannot be escaped from in a reasonable CPU time) as well as the corresponding changes in the free energy per disk are probably unmeasurably small except, possibly, at very small N. The existence of a finite fraction of sample space that cannot be escaped from in any reasonable CPU time at finite N is however remarkable. In many MCMC algorithms for physical systems, as for example the Ising model, parts of sample space are practically excluded because of their low Boltzmann weight, but they feature diverging escape times only in the limit $N \rightarrow \infty$.

In this context, we note that Markov chains can be interpreted in terms of a single bottleneck partitioning the sample space into two pieces [26, Sect. 7.2]. The algorithmic stationary probability flow across the bottleneck sets the conductance of an algorithm, which again bounds mixing and correlation times. Ideally, MCMC algorithms would be benchmarked through their conductances. In the hard-disk model, the bottleneck has not been identified, so that the benchmarking and the analysis of MCMC algorithms must rely on empirical criteria. However, Böröczky packings and the related $\varepsilon$-relaxed Böröczky configurations may well model a bottleneck, from which the Markov chain has to escape in order to cross from one piece of the sample space into its complement. The benchmarks obtained by comparing escape times from an $\varepsilon$-relaxed Böröczky configurations may thus reflect the relative merits of sampling algorithms.

4.2 Böröczky Packings and Local MCMC: Fundamental Aspects

We now discuss fundamental aspects of the present work, namely the question of the irreducibility of local hard-sphere Markov chains and the connection with non-local MCMC algorithms (see Sect. 4.2.1), as well as regularization of Böröczky packings and $\varepsilon$-relaxed Böröczky configurations in the NPT ensemble (see Sect. 4.2.2).

4.2.1 Irreducibility of Local and Non-local Hard-Disk MCMC

Strictly speaking, ECMC can be irreducible only if $\varOmega \setminus \mathcal {B}$ is connected, where $\mathcal {B}$ is a suitably defined space of locally stable configurations. Packings in $\mathcal {B}$ (a space of low dimension) are certainly invariant under any version of the ECMC algorithm, so that they cannot evolve towards other samples in $\varOmega$. Connectivity in $\varOmega \setminus \mathcal {B}$ would at least assure that this space can be sampled. In addition it appears necessary to guarantee that a well-behaved initial configuration cannot evolve towards an $\varepsilon$-environment around $\mathcal {B}$ (e.g., the space $\mathcal {B}_\varepsilon$ of $\varepsilon$-relaxed Böröczky configurations that makes up a finite portion of $\varOmega$) or to gridlocks with diverging event rates. These properties appear not clearly established for finite densities $\eta$ and for large N. In other models, for example the Ising model of statistical physics, irreducibility can be proven for any N.

These unresolved mathematical questions concerning irreducibility do not shed doubt on the practical usefulness of MCMC for particle systems. First, the concept of local stability is restricted to hard disks and hard spheres (that is, to potentials that are either zero or infinite). The phase diagram of soft-disk models can be continuously connected to the hard-disk case [30]. For soft disks, irreducibility is trivial, but the sampling speed of algorithms remains crucial. Second, in applications, one may change the thermodynamic ensemble. In the NPT ensemble, the central simulation box fluctuates in size and can become arbitrarily large. In this ensemble, irreducibility follows from the fact that large enough simulation boxes are free of steric constraints. Again, the question of mixing and correlation time scales is primordial. Third, practical simulations that require some degree of irreducibility are always performed under conditions where the simulation box houses a number of effectively independent copies of the system. This excludes the crystalline or solid phases. Monte Carlo simulations of such phases are more empirical in nature. They require a careful choice of initial states, and are then not expected to visit the entire sample space during their time evolution. Fundamental quantitative results can nevertheless be obtained [31].

In this work, we concentrate on local MCMC algorithms, because global-move algorithms, as the cluster algorithms in spin systems, rely on a priori probabilities for many-particle moves that appear too complicated. Also, global single-particle moves are related to the single-particle insertion probabilities, in other words to fugacities (the exponential of the negative chemical potential) that are prohibitively small. At lower (finite) densities, however, placing at each time step a randomly chosen disk at a random position inside the box corresponds to the Metropolis algorithm of Sect. 3.1.1 with a square-shaped displacement set and a range $\delta =L/2$. This non-local algorithm easily escapes from a Böröczky packing. Moreover, it is proven to mix in $\mathcal {O}\left( N \log ^{}\! \,N \right)$ steps at densities $\eta < 1/6$ [8, 32] (see also [33]), a result that implies that the liquid phase in the hard-disk system extends at least to the density $\eta =1/6$ [8]. The density bound for the algorithm (which yields a bound for the stability of the liquid phase) is much smaller than the empirical density bound for the liquid phase, at $\eta \simeq 0.70$. At this higher density, the global-move Metropolis algorithm and the more general hard-disk cluster algorithm [34] are almost totally stuck. For applications, we imagine structures resembling $\varepsilon$-relaxed Böröczky configurations to be backbones of configurations at high density, where global moves cannot be used.

4.2.2 Böröczky Packings and the NPT Ensemble

The concepts of packings and of local and collective stability make sense only in the NVT ensemble, that is, for a constant number of particles and for a simulation box with fixed shape and volume (the temperature $T = 1/\beta$ that appears in NVT plays no role in hard-disk systems [14]). In the NPT ensemble, the pressure P is constant, and the size of the simulation box may vary. The equivalence of the two ensembles is proven [35] for large N, so that the choice of ensemble is more a question of convenience than of necessity. As we will see, in the NPT ensemble, tiny relaxation parameters (as $\varepsilon = 10 ^{-29}$ in Fig. 6) are instantly relaxed to $\varepsilon \sim 10^{-3}$ for normal pressures and system sizes.

To change the volume at constant pressure, one may, among others, proceed to “rift volume changes” (see [36, Sect. VI]) or else to homothetic transformations of the central simulation box. We discuss this second approach (see [14, Sect. 2.3.4]), where the disk positions (but not the radii) are rescaled by the box size L as:

$$\begin{aligned} \mathbf {x}= (\mathbf {x}_1 ,\ldots ,\mathbf {x}_N) \rightarrow \varvec{\alpha }= (\varvec{\alpha }_1 ,\ldots ,\varvec{\alpha }_N) \quad \text {with} ~\varvec{\alpha }_i = \mathbf {x}_i/L. \end{aligned}$$

(15)

Each configuration is then specified by an $\varvec{\alpha }$ vector in the 2N-dimensional periodic unit square and an associated volume $V = L^2$, which must satisfy $V \ge V_{\text {cut}}(\varvec{\alpha })$. A classic MCMC algorithm [37] directly samples the volume at fixed $\varvec{\alpha }$ from a gamma distribution above $V_{\text {cut}}(\varvec{\alpha })$, below which $(\varvec{\alpha }, V)$ ceases to represent a valid hard-disk configuration [14, Eq. (2.19)]. Typical sample volumes are characterized by $\beta P (V - V_{\text {cut}}) \sim 1$, and with $V = (L_{\text {cut}}+ \varDelta L) ^2$, it follows that

$$\begin{aligned} \frac{\varDelta L}{L} \sim \varepsilon \sim \frac{1}{\beta P V_{\text {cut}}} \quad (\text {at fixed} ~\varvec{\alpha }). \end{aligned}$$

(16)

This equation illustrates that a packing, with $\varepsilon \rightarrow 0$, is realized as a typical configuration only in the limit $\beta P \rightarrow \infty$. For the Böröczky packings of Fig. 1, we have $L\simeq 20$, and a typical value for the pressure for hard-disk systems is $\beta P \sim 1$, which results in $\varepsilon \sim 10^{-3}$. In the NPT ensemble, as a consequence, escape times from a packing naturally correspond to a relaxation parameter $\varepsilon \sim 1/ (\beta P V)$, in our example to $t_\mathrm {esc}(\varepsilon \sim 10^{-3})$, which is $\mathcal {O}\left( 1 \right)$.

The above NPT algorithm combines constant-volume NVT-type moves of $\varvec{\alpha }$ with the mentioned direct-sampling moves of V at fixed $\varvec{\alpha }$. In practice, however, NPT calculations are rarely performed in hard-disk systems [38, 39]. This is because, as discussed in Eq. (16), the expected single-move displacement in volume at fixed $\varvec{\alpha }$ is $\varDelta V \sim 1/( \beta P)$, so that $\varDelta V/V \sim 1 /N$ (because $N \sim V$ and $\beta P \sim 1$). The fluctuations of the equilibrium volume $V^{\text {eq}}$ (averaged over $\varvec{\alpha }$) scale as $\sqrt{V^{\text {eq}}}$, which implies $\varDelta V^{\text {eq}}/ V^{\text {eq}}\sim 1 /\sqrt{N}$. The volume-sampling algorithm requires $\sim N$ single updates of the volume to go from the 1/N scale of volume fluctuations at fixed $\varvec{\alpha }$ to the $1/\sqrt{N}$ scale of the fluctuations of $V^{\text {eq}}$ at equilibrium. This multiplies with the number of steps to decorrelate at a given volume. In practice, it has proven more successful to perform single NVT simulations, but to restrict them to physical parameters where the central simulation box houses a finite number of effectively independent systems mimicking constant-pressure configurations.

5 Conclusion

Building on an early breakthrough by Böröczky, we have studied in this work locally stable hard-disk packings. Böröczky packings are sparse, with arbitrarily small densities for large numbers N of disks. We constructed different types of these packings to arbitrary precision for finite N, namely Böröczky packings with the original Böröczky core [13] and those with the Kahle core [17]. In addition to the core and the number k of layers, Böröczky packings are defined by the convex polygonal chain which bounds their branches. We constructed Böröczky packings in a continuous range of densities, and made our software implementation of the construction openly accessible. Böröczky packings are locally, but not collectively stable. Using singular-value decomposition (in an implementation that is included in our open-source software) we explicitly exposed the unstable collective modes. We furthermore reduced the radius of Böröczky packings slightly, and determined the escape times from $\varepsilon$-relaxed Böröczky configurations as a function of the parameter $\varepsilon$ for a number of local MCMC algorithms, including several variants of ECMC, arbitrary-precision implementations of which are also made openly available. Although the algorithms depart from each other in seemingly insignificant details only, we witnessed widely different escape times, ranging from $1/\varepsilon$ to $\log (1/\varepsilon )$. Our theory suggested that the significant speedup of some of the algorithms is rooted in their event-driven nature coupled to their lack of an intrinsic scale. We noted that the space of $\varepsilon$-relaxed Böröczky configurations is a finite portion of the sample space, and that a given computer-time budget implies such a finite fraction of sample space that is practically excluded in local MCMC at finite N. Here, the excluded volume only vanishes in the limit of infinite CPU time. More generally, connectedness of the hard-disk sample space is not proven. We pointed to the importance of statistical ensembles to reconcile the possible loss of irreducibility with the proven practical usefulness of local hard-disk MCMC algorithms. Although Böröczky packings or $\varepsilon$-relaxed Böröczky configurations are sparse, they could form the locally stable (or almost locally stable) backbones of hard-disk configurations at the much higher density which are of practical interest.

We expect the observed differences in escape times to carry over to real-world ECMC implementations. Qualitatively similar performance differences were already observed in autocorrelation times of hard-disk dipoles [25]. In statistical mechanics, bottlenecks and escape times possibly play an important role in polymer physics and complex molecular systems and some of the algorithms studied here may find useful applications. Escape times may also play an important role in the study of glasses and in granular matter, where the high or even infinite pressures favor local configurations that resemble the mutually blocked disks in the $\varepsilon$-relaxed Böröczky configurations. We finally point out that the very concept of locally stable packings naturally extends to higher dimensions.

Appendices

A Escape Times, Resamplings and Gridlocks

In this appendix we collect a number of numerical results that support statements made in the main text.

1.1 A.1 Critical Maximum Nearest-Neighbor Distance

In the escape time $t_\mathrm {esc}$ of Eq. (10), the parameter $\gamma$ sets the critical maximum nearest-neighbor distance d(t) for the escape from an $\varepsilon$-relaxed Böröczky configurations. In Sect. 3.2, we use $\gamma =0.1$ which corresponds to a $10\,\%$-increase of the initial value $d(t=0) = 2$. Using the alternative value $\gamma =0.025$, we find that the escape time of straight ECMC again varies algebraically as $t_\mathrm {esc}\sim \varepsilon ^{-2/3}$ and, for forward, reflective, and Newtonian ECMC we again find $t_\mathrm {esc}\sim \ln (1/\varepsilon )$ (see Fig. 7). Our conclusions thus appear robust with respect to the value of $\gamma$.

Fig. 7

Median escape times $t_\mathrm {esc}$ from $k=5$ $\varepsilon$-relaxed Böröczky configurations (Kahle core and convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi = 0.7$, $N=96$ disks) for ECMC algorithms. Solid curves use $\gamma =0.1$ for the definition of $t_\mathrm {esc}$ (as in Sect. 3.2), dashed curves use $\gamma =0.025$ (see Eq. (10)). For both values of $\gamma$, straight ECMC with optimized chain time $\tau _{\text {chain}}$ shows algebraic scaling with identical exponents, whereas forward, reflective, and Newtonian ECMC scale logarithmically. Error bars are smaller than the marker sizes

1.2 A.2 Escape Times with Resamplings

The reflective, forward and Newtonian variants of ECMC, at a difference of straight ECMC, appear to not always require resampling. In the main text, we therefore use $\tau _{\text {chain}}= \infty$, which, given our discussion in Sect. 3.1, is appropriate. Moreover, resamplings after chain times $\tau _{\text {chain}}$ considerably deteriorate the escape time for all three variants (see Fig. 8). This again illustrates the power of lifted Markov chains, in which the proposed moves are correlated over long Monte-Carlo times.

Fig. 8

Median escape times $t_\mathrm {esc}$ from $k=5$ $\varepsilon$-relaxed Böröczky configurations (Kahle core and convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi =0.7$, $N=96$ disks) for forward, reflective, and Newtonian ECMC vs. chain time $\tau _{\text {chain}}$ for two different relaxation parameters $\varepsilon$. Horizontal lines indicate the escape times without any resamplings. Error bars are smaller than the marker sizes

1.3 A.3 Gridlock Rates with Different Numerical Precisions

The straight, reflective, and Newtonian variants of ECMC feature deterministic collision rules, and they may run into gridlocks if started from $\varepsilon$-relaxed Böröczky configurations for very small $\varepsilon$ (see Sect. 3.2.4). In a gridlock, the active-disk label loops through a subset of the N disks which are in contact. The event rate diverges, and so does the CPU time spent in the gridlock. The Monte-Carlo time, however, stands still. Newtonian ECMC starting from $k=5$ $\varepsilon$-relaxed Böröczky configurations with the Böröczky core appears particularly prone to gridlocks.

It remains an open question whether gridlocks are a numerical artifact related to the finite-precision computer arithmetic. In our arbitrary-precision BigBoro software, the number of mantissa bits (in base 2) can be set freely. We have studied the gridlock rate of Newtonian ECMC (the fraction of simulations that run into gridlock) for the problematic $k=5$ $\varepsilon$-relaxed Böröczky configurations (using the convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi =0.7$) with the Böröczky core, and observed no clear influence of the numerical precision. It thus appears unlikely that gridlocks are a precision issue (see Fig. 9).

Fig. 9

Gridlock rate of Newtonian ECMC simulations with different numerical precisions starting from a $k=5$ $\varepsilon$-relaxed Böröczky configurations (Böröczky core and convex geometric chain $\mathcal {A}^{\text {geo}}$ with attenuation parameter $\phi =0.7$, $N=112$ disks). The inset shows the gridlock rate as a function of $1/\varepsilon$ for the Newtonian ECMC simulations with 200 mantissa bits that were used to measure the escape times in Fig. 6b

B BigBoro Software Package: Outline, License, Access

The BigBoro software package is published as an open-source project under the GNU GPLv3 license. It is available on GitHub as part of the JeLLyFysh organization.¹ The software package consists of three parts: First, the arbitrary-precision Python script construct_packing.py constructs finite-N Böröczky packings of hard disks in a periodic square box. Second, the Python script collective_escape_modes.py computes collective infinitesimal displacements of hard disks in a packing that result in an escape. Third, the arbitrary-precision Go application go-hard-disks performs hard-disk ECMC simulations that may start from $\varepsilon$-relaxed Böröczky configurations derived from Böröczky packings.

1.1 B.1 Python Script construct_packing.py

The arbitrary-precision Python script construct_packing.py implements the construction of Böröczky packings. It allows for the Böröczky or Kahle cores (see Sect. 2.1.1), and connects them to branches with a finite number of layers (see Sect. 2.1.3). The convex geometric chain $\mathcal {A}^{\text {geo}}$ with different attenuation parameters $\phi$, and the convex circular chain $\mathcal {A}^{\text {circ}}$ are implemented (see Sect. 2.2.1). The core, the number of layers, and the convex polygonal chain are specified using command-line arguments. The construction of the Böröczky packings uses arbitrary-precision decimal floating-point arithmetic. Two additional command-line options specify the number of decimal digits, and the precision of the bisection search for the value $g_2^<$ that renders the Böröczky packing compatible with periodic boundary conditions (see Sect. 2.1.3). The final configuration and its parameters (as for example the system length) are stored in a human-readable format in a specified output file.

The example_packings directory of BigBoro contains several Böröczky packings in corresponding subdirectories (as for example kahle_geometric_5). The headers of these files contain the values of the command-line arguments for construct_packing.py. A plot of each example configuration is provided. The different packings in kahle_geometric_5 and boro_geometric_5 (see Fig. 1) were used in this work. Although the bisection search for the construction of the Böröczky packing usually requires an increased precision, the high-precision packings with small enough number of layers may be used as input for standard double-precision applications. For simplicity and improved readability, we provide packing_double.txt files that store the configurations in double precision, where applicable.

1.2 B.2 Python Script collective_escape_modes.py

The double-precision Python script collective_escape_modes.py identifies the orthonormal basis vectors of the escape matrix $\mathcal {M}^{\text {esc}}$ from a packing $\mathbf {x}$ (see Eq. (6)) that have zero singular values. Afterwards, these modes are classified using the cost function in Eq. (8). The resulting basis vectors $\varvec{\varDelta }_a$ form the solution space for 2N-dimensional displacements $\varvec{\varDelta }= \{\varDelta ^x_1, \varDelta ^y_1, \varDelta ^x_2, \varDelta ^y_2, \ldots \}$ that have a vanishing first-order term in Eq. (5) and thus for collective infinitesimal displacements $\varvec{\varDelta }$ of all disks that escape from the packing. The basis vectors $\varvec{\varDelta }_a$ are stored in a human-readable output file, and optionally represented as in Fig. 2. The input filename of the packing, and the output filename for the collective escape modes are specified in command-line arguments. Further optional arguments specify the filename for the plots of the escape modes, and the system length of the central simulation box (that is unnecessary for packings generated by the Python script construct_packing.py in which case the system length is parsed from the packing file).

1.3 B.3 Go Application go-hard-disks

The Go application go-hard-disks relies on a cell-occupancy system for the efficient simulations of large-N hard-disk systems using several variants of the ECMC algorithm. Straight, reflective, forward, and Newtonian ECMC are implemented. After each sampling interval, it samples the maximum nearest-neighbor distance d(t) (see Eq. (9)). All computations use a fixed number of mantissa bits (in base 2) that may exceed the usual 24 or 53 bits for single- or double-precision floating-point values. The ECMC variant, its parameters (as for example the sampling time or chain time), and further specifications (the number of mantissa bits, the cell specifications, the filename for the initial configuration, etc.) are again set using command-line arguments.