1 Introduction

Binary processes arise in natural and social sciences any time a phenomenon is dichotomized according to the occurrence or non-occurrence of a property of interest. Modeling, statistical inference from data, and generation of dependent binary sequences, both finite and infinite, have thus received a lot of attention in a number of disciplines, such as statistical physics [1], system biology [2], computational neuroscience [3], actuarial and financial sciences [4], and machine learning [5], among others. While finite sequences are generally associated with graphical models [6], infinite sequences are usually understood as time series.

Modeling and generating binary sequences with prescribed correlations is one of the major problems to be faced [1]. For finite sequences, the solution to the problem is in principle represented by the Ising model, which is an exponential family able to reproduce all inputs in (the interior of) the correlation polytope [6]. For infinite sequences, the problem of constructing binary variables with given correlations is more challenging since there is no universal framework to refer to. Indeed, finite-dimensional distributions structured according to the Ising model are generally not consistent under marginalization, so that they cannot be regarded as children of a common probability measure associated with a stochastic process. On the other hand, the Ising model is the only known parametric family that can cover all correlations of a finite number of binary variables. For this reason, in order to describe and generate infinite binary sequences, researchers have devised several approaches, each with its own advantages and disadvantages, which can be grouped in autoregressive models [7,8,9,10,11,12,13,14], latent factor models [15,16,17], and mixed models which combine autoregression with latent factors [7, 20]. Autoregressive models are Markov chains with the property that the current probability of a symbol conditional on the past history is determined by a linear function of the previous outcomes [7], in a number corresponding to the order of the chain, linearity being postulated to not have explosion of parameters. These type of models can produce any exponential decay of correlations, whereas subexponential decays are off limits due to Markovianity and finite state space [21]. Latent factor models rely on an underlying latent process, and the first proposal to generate an infinite dependent binary sequence was to clip a latent Gaussian process at a fixed level [15]. Different latent factor approaches are represented by mixture models whereby the binary symbols are drawn independently with law determined by the realization of an underlying process, such as a latent Gaussian process [16] or a latent binary process [17]. Latent factor approaches can introduce a long-range dependence between the binary variables and can thus describe both exponential and subexponential decays of correlations, such as polynomial decay. However, the analysis of clipping performed in [18] has revealed that there are serious restrictions to the type of correlations that can be produced. In fact, decay rates, in the case of exponential decay, and decay exponents, in the case of polynomial decay, cannot be smaller than a certain minimum threshold. Similar restrictions have been found in mixture models with latent binary inputs [17]. These restrictions have been weakened in [19] by means of an algorithm that by iterating the latent factor model of [17], which transforms the latent binary input in a binary output, adds dependence to an initial uncorrelated binary sequence step by step. Other algorithms to generate dependent binary sequences and their demonstration through numerical experiments are discussed in [22,23,24,25].

In this paper we suggest and investigate a new latent factor approach for infinite binary sequences that relies on renewal processes [26]. Our proposal is to associate one of the two symbols of the sequence with the renewal times of a discrete-time delayed renewal process, and the other symbol with all other times, thus defining a regenerative phenomenon a la Kingman [27]. Delay makes it possible to construct stationary binary sequences. This way, we can offer a flexible and powerful model that is under full mathematical control and that is able to implement a large variety of subexponential prescriptions for the correlations, from polynomial to stretched-exponential decays as we shall demonstrate. Furthermore, reflecting an underlying renewal structure, generation of the process in numerical experiments is immediate.

The paper is organized as follows. In Sect. 2 we introduce the model and discuss its Markovian limit. Section 3 is devoted to correlations. In this section we prove the fundamental property of the model that binary symbols that follows a renewal time are independent of previous symbols and we show that the autocovariance solves a renewal equation. Then we investigate the direct problem of determining the asymptotics of correlations from the waiting time distribution and the inverse problem of associating a renewal structure to a prescribed autocovariance for binary symbols. In Sect. 4 we prove limit theorems for the probability of typical sequences and for the time averages of general observables. In particular, we demonstrate an asymptotic equipartition property that naturally introduces the Shannon entropy of the waiting time distribution and leads to the maximum entropy principle for model selection [28, 29]. Then we provide a law of large numbers and a central limit theorem for the normal fluctuations of empirical means, and we apply them to estimation of the waiting time distribution and of the autocovariance from data. These results cannot be deduced from the standard limit theory of regenerative processes with independent cycles [26] and require new arguments. Conclusions are drawn in Sect. 5. The most technical mathematical proofs are reported in the appendices in order to not interrupt the flow of the presentation.

2 Definition of the Model

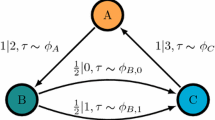
Let on a probability space \((\Omega ,{\mathscr {F}},{\mathbb {P}})\) be given positive integer-valued random variables \(S_1,S_2,\ldots \). We construct a binary stochastic sequence \(X:=\{X_t\}_{t\ge 1}\) with entries valued in \({\mathbb {N}}_2:=\{0,1\}\) by supposing that the variable \(S_n\) is the waiting time for the nth symbol 1 of the sequence, which occurs at the renewal time \(T_n:=S_1+\cdots +S_n\). Thus, \(X_t:=1\) if \(t\in \{T_n\}_{n\ge 1}\) and \(X_t:=0\) otherwise for each \(t\ge 1\). Our fundamental assumptions are (i) that waiting times are independent and (ii) that \(S_2,S_3,\ldots \) have the same distribution, which could differ from the distribution of \(S_1\). Under these assumptions, the sequence \(\{T_n\}_{n\ge 1}\) is a renewal process, delayed if \(S_1\) is not distributed as \(S_2\). We refer to [26] for basics of renewal theory. The reason for letting \(S_1\) behave differently from the other waiting times is that its distribution can be chosen in such a way that the sequence X is stationary, as explained by the following theorem which is proved in Appendix A. We recall that the process X is stationary if \(\{X_{t+1}\}_{t\ge 1}\) is distributed as \(\{X_t\}_{t\ge 1}\), where \(\{X_t\}_{t\ge 1}\) is understood as a random element in the set \({\mathbb {N}}_2^\infty \) of all binary sequences equipped with the cylinder \(\sigma \)-field \({\mathscr {B}}\). Hereafter, \({\mathbb {E}}\) denotes expectation with respect to \({\mathbb {P}}\).

Theorem 2.1

The binary sequence X is stationary if and only if \({\mathbb {E}}[S_2]<\infty \) and for every \(s\ge 1\)

$$\begin{aligned} {\mathbb {E}}[S_2]\,{\mathbb {P}}[S_1=s]={\mathbb {P}}[S_2\ge s]. \end{aligned}$$

Theorem 2.1 recovers well-known conditions for the delayed renewal chain \(\{T_n\}_{n\ge 1}\) to be stationary, that means that the statistical properties of the number of renewals in a given temporal window are invariant with respect to time shifts [26]. Under the hypothesis of stationarity, which is now made, the only input of the model X is the distribution of the waiting time \(S_2\). Depending on the need, we refer to its density \(p:={\mathbb {P}}[S_2=\cdot \,]\) or to its tail \(Q:={\mathbb {P}}[S_2>\cdot \,]\). Thus, according to Theorem 2.1, we suppose that \(\mu :={\mathbb {E}}[S_2]=\sum _{s\ge 1}sp(s)=\sum _{t\ge 0}Q(t)<\infty \) and that \({\mathbb {P}}[S_1=s]=(1/\mu )\sum _{n\ge s}p(n)\) for every \(s\ge 1\). We notice that \({\mathbb {E}}[X_1]={\mathbb {P}}[T_1=1]={\mathbb {P}}[S_1=1]=1/\mu \).

The analysis of the finite-dimensional distributions reveals that if the sequence X is stationary, then it is time-reversible in the sense that \((X_t,\ldots ,X_2,X_1)\) is distributed as \((X_1,X_2,\ldots ,X_t)\) for all t. The finite-dimensional distributions of X are provided by the next proposition, which is demonstrated in Appendix B. We make the usual conventions that an empty sum is assumed to be 0 and an empty product is assumed to be 1.

Proposition 2.1

For any integer \(t\ge 1\) and numbers \(x_1,x_2,\ldots ,x_t\) in \({\mathbb {N}}_2\)

$$\begin{aligned} \pi _t(x_1,x_2,\ldots ,x_t):&={\mathbb {P}}\big [X_1=x_1,X_2=x_2,\ldots ,X_t=x_t\big ]\\&=\frac{1}{\mu }\bigg [\sum _{s\ge t}Q(s)\bigg ]^{\prod _{n=1}^t(1-x_n)} \prod _{i=1}^t\big [Q(i-1)\big ]^{\prod _{n=1}^{i-1}(1-x_n)x_i}\\&\,\cdot \,\,\prod _{i=1}^{t-1}\prod _{j=i+1}^t\big [p(j-i)\big ]^{x_i\prod _{n=i+1}^{j-1}(1-x_n)x_j}\prod _{j=1}^t\big [Q(t-j)\big ]^{x_j\prod _{n=j+1}^t(1-x_n)}\\&=\pi _t(x_t,\ldots ,x_2,x_1) \end{aligned}$$

with \(0^0:=1\).

Proposition 2.1 can be used to compute the conditional probability of a symbol given the past and allows us to get some insight into the dependence structure of the stochastic sequence X. Let us denote by \(l_t(x_1,\ldots ,x_t)\) the position of the first symbol 1 in the binary string \((x_1,\ldots ,x_t)\): \(l_t(x_1,\ldots ,x_t):=l\) if \(x_l=1\) and \(x_1=\cdots =x_{l-1}=0\) for some \(l\le t\), and \(l_t(x_1,\ldots ,x_t):=\infty \) if \(x_1=\cdots =x_t=0\). Proposition 2.1 shows through easy manipulations that for any positive integer t and binary numbers \(x_1,\ldots ,x_t\)

$$\begin{aligned} {\mathbb {P}}\big [X_{t+1}=1\big |X_t=x_1,\ldots ,X_1=x_t\big ]= {\left\{ \begin{array}{ll} \displaystyle {\frac{Q(t)}{\sum _{s\ge t}Q(s)}} &{} \text{ if } l_t(x_1,\ldots ,x_t)=\infty ;\\ \displaystyle {\frac{p(l)}{Q(l-1)}} &{} \text{ if } l_t(x_1,\ldots ,x_t)=:l<\infty \end{array}\right. } \end{aligned}$$
(2.1)

provided that \({\mathbb {P}}[X_1=x_t,\ldots ,X_t=x_1]>0\). Pay attention to the inverse order of \(x_1,\ldots ,x_t\) in the conditioning event. Formula (2.1) draws a link between our model and the so-called “stochastic chains with memory of variable length” [30]. In this class of models, which can be built on a larger alphabet than \({\mathbb {N}}_2\), the number of variables involved in the conditioning event is determined by a “context length function”, which itself depends on the past variables. The context length function of our model is exactly the function \(l_t\) that maps any binary string \((x_1,\ldots ,x_t)\) in \(l_t(x_1,\ldots ,x_t)\). Since the function \(l_t\) is unbounded as the time t goes on, our model constitutes a stochastic chain having in general memory of unbounded variable length.

In spite of an unbounded context length, the process X is a Markov chain for certain particular waiting time distributions p. The sequence X is a Markov chain of order \(M\ge 1\) if the conditional probability of a symbol given the past depends only on the state of the last M variables. We can include sequences of i.i.d. random variables in this definition by letting M to take the value zero. The requirement that the conditional probability (2.1) is independent of \(x_{M+1},\ldots ,x_t\) for Markovianity of order \(M\ge 0\) results in the following corollary of Proposition 2.1, whose proof is reported in Appendix C.

Corollary 2.1

The binary sequence X is a Markov chain of order \(M\ge 0\) if and only if there exists a real number \(\lambda \in [0,1)\) such that \(p(M+s+1)=\lambda ^sp(M+1)\) for all \(s\ge 1\).

3 Correlations

The binary sequence \(X:=\{X_t\}_{t\ge 1}\) is a regenerative process with regeneration points \(\{T_n\}_{n\ge 1}\) and independent cycles [26]. This means that the past and the future of each renewal event, i.e. of each symbol 1, are independent. Such conditional independence is stated by the following proposition, whose proof is provided in Appendix D.

Proposition 3.1

For every positive integers \(s\le t\) and binary numbers \(x_1,\ldots ,x_t\)

$$\begin{aligned} {\mathbb {P}}\big [X_1=x_1,\ldots ,X_t=x_t\big |X_s=1\big ]=\,\,&{\mathbb {P}}\big [X_1=x_1,\ldots ,X_s=x_s\big |X_s=1\big ]\\ \cdot \,\,\,&{\mathbb {P}}\big [X_s=x_s,\ldots ,X_t=x_t\big |X_s=1\big ]. \end{aligned}$$

Conditional independence associated with renewals is exploited in this section to study correlations. The covariance of two random variables Y and Z on the probability space \((\Omega ,{\mathscr {F}},{\mathbb {P}})\) is denoted by \(\mathrm {cov}[Y,Z]\):

$$\begin{aligned} \mathrm {cov}[Y,Z]:={\mathbb {E}}\big [(Y-{\mathbb {E}}[Y])(Z-{\mathbb {E}}[Z])\big ]={\mathbb {E}}[YZ]-{\mathbb {E}}[Y]\,{\mathbb {E}}[Z]. \end{aligned}$$

For every \(t\ge 0\), the autocovariance \(\rho _t:=\mathrm {cov}[X_1,X_{t+1}]\) reads \(\rho _t=c_t-c_0^2\) with

$$\begin{aligned} c_t:={\mathbb {E}}[X_1X_{t+1}]. \end{aligned}$$

Notice that \(c_0={\mathbb {E}}[X_1]=1/\mu \). The next proposition, which is based on Proposition 3.1 and is proved in Appendix E, shows that the sequence \(c:=\{c_t\}_{t\ge 0}\) solves a renewal equation with waiting time distribution p. As a consequence, the renewal theorem [31] gives \(\lim _{t\uparrow \infty }c_t=c_0/\mu =c_0^2\), namely \(\lim _{t\uparrow \infty }\rho _t=0\), provided that p is aperiodic. The probability distribution p is aperiodic if there is no proper sublattice of \(\{1,2,\dots \}\) containing its support.

Proposition 3.2

For every integer \(t\ge 1\)

$$\begin{aligned} c_t=\sum _{s=1}^tp(s)\,c_{t-s}. \end{aligned}$$

By resorting to the literature on the renewal equation, we investigate the direct problem of determining the asymptotics of the sequence c, and hence of the autocovariance, from a given waiting time distribution p, as well as the inverse problem of finding conditions on a prescribed c such that c solves a renewal equation with some probability distribution p of finite mean. The latter aims to answer the question of which autocovariance structures can be reproduced by our model. Before that, we want to point out that the autocovariance of the binary sequence X describes the time dependence of any temporal correlations, as shown by the following technical lemma that explores temporal correlations of general observables. The lemma is proved in Appendix F and will be used in Sect. 4 to address the mixing properties of X.

Lemma 3.1

Fix positive integers m and n and let f and g be two real functions on \({\mathbb {N}}_2^m\) and \({\mathbb {N}}_2^n\), respectively, such that \(f(0,\ldots ,0)=g(0,\ldots ,0)=0\). Set \(Z_t:=g(X_t,\ldots ,X_{t+n-1})\) for \(t\ge 1\). Then, for all \(t\ge 1\)

$$\begin{aligned} \mathrm {cov}\big [f(X_1,\ldots ,X_m),Z_{m+t}\big ]&=\sum _{i=1}^m\sum _{j=1}^n C_{i,j}(t)\, \frac{{\mathbb {E}}[\mathbbm {1}_{\{S_1=i\}}f(X_m,\ldots ,X_1)]}{{\mathbb {P}}[S_1=i]}\,\frac{{\mathbb {E}}[\mathbbm {1}_{\{S_1=j\}}Z_1]}{{\mathbb {P}}[S_1=j]}, \end{aligned}$$

where for \(i\ge 1\) and \(j\ge 1\)

$$\begin{aligned} C_{i,j}(t):=\sum _{u=1}^i\sum _{v=1}^j p(i-u)\,\rho _{u+t+v-2}\,p(j-v) \end{aligned}$$

with \(p(0):=-1\).

3.1 Autocorrelation: Direct Problem

Let us study the asymptotics of the autocovariance for a given waiting time distribution. Pure exponential decay of correlations can be described by Markov chains as identified by Corollary 2.1 and is somehow trivial. We shall touch on the exponential behavior of the autocovariance when dealing with the inverse problem. Here we focus on subexponential decays that account for long-range dependence that cannot be explained by Markov processes. A natural setting for subexponentiality in renewal theory was given in [32]. Let the symbol \(\sim \) denotes asymptotic equivalence for sequences: \(a_t\sim b_t\) means \(\lim _{t\uparrow \infty }a_t/b_t=1\). Following [32], we say that a positive real sequence \(a:=\{a_t\}_{t\ge 0}\) belongs to the class \({\mathscr {S}}\) of subexponential sequences if \(A:=\sum _{t\ge 0}a_t<\infty \), \(a_{t+1}\sim a_t\), and \(\sum _{n=0}^ta_na_{t-n}\sim 2Aa_t\). The requirement \(a_{t+1}\sim a_t\) prevents a from growing exponentially, thus justifying the terminology “subexponential”. The asymptotic behavior of the autocovariance \(\rho _t\) can be characterized in general when there exists \(\lambda \in (0,1]\) such that \(\{\lambda ^{-t}Q(t)\}_{t\ge 0}\in {\mathscr {S}}\), namely when the tail probability Q has exponential rate \(\lambda \) and a subexponential correction that forms a sequence in \({\mathscr {S}}\). The case \(\lambda =1\) corresponds to a pure subexponential behavior. In fact, Theorem 3.2 of [33] for the rate of convergence of renewal sequences gives the following result.

Theorem 3.1

Assume that p is aperiodic and that \(\{\lambda ^{-t} Q(t)\}_{t\ge 0}\in {\mathscr {S}}\) for some \(\lambda \in (0,1]\). Then

$$\begin{aligned} \rho _t\sim \frac{\sum _{n>t}Q(n)}{\mu \big [\sum _{n\ge 0}\lambda ^{-n} Q(n)\big ]^2}. \end{aligned}$$

Subexponential behaviors that find wide application are polynomial decays, which fall under the umbrella of regular variation, and Weibull-type decays represented by stretched exponentials. We now suppose \(\lambda =1\) and discuss these decays in some detail. We stress that the necessary condition \(\sum _{t\ge 0}Q(t)<\infty \) for the sequence \(\{Q(t)\}_{t\ge 0}\) to belong to \({\mathscr {S}}\) is satisfied since \(\sum _{t\ge 0}Q(t)=\mu <\infty \) by the hypothesis of stationarity.

3.1.1 Polynomial Decay

A positive sequence \(a:=\{a_t\}_{t\ge 0}\) is regularly varying if there exists an index \(\alpha \in {\mathbb {R}}\) and a slowly varying function \(\ell \) such that \(a_t\sim t^\alpha \ell (t)\). A real measurable function \(\ell \) is slowly varying if it is positive on a neighborhood of infinity, say \((\tau ,\infty )\) with some \(\tau >0\), and satisfies the scale-invariance property \(\lim _{z\uparrow \infty }\ell (\eta z)/\ell (z)=1\) for any number \(\eta >0\). Trivially, a measurable function with a finite positive limit at infinity is slowly varying. The simplest non-trivial example is represented by the logarithm. We refer to [34] for the theory of slow and regular variation. We stress that a slowly varying function \(\ell \) is dominated by polynomials in the sense that \(\lim _{z\uparrow \infty }z^\gamma \ell (z)=\infty \) and \(\lim _{z\uparrow \infty }z^{-\gamma }\ell (z)=0\) for all \(\gamma >0\) according to Proposition 1.3.6 of [34]. The uniform convergence theorem [34] states that the scale-invariance property of slowly varying functions actually is uniform for \(\eta \) that belongs to each compact set in \((0,\infty )\). This fact can be used to show that \(a_{t+1}\sim a_t\) if a is a regularly varying sequence. Combined with the dominated convergence theorem, it also shows that \(\sum _{n=0}^ta_na_{t-n}\sim 2\sum _{n=0}^{\lfloor t/2\rfloor }a_na_{t-n}\sim 2Aa_t\) when \(A:=\sum _{t\ge 0}a_t<\infty \), \(\lfloor t/2\rfloor \) denoting the integer part of t/2. Thus, any summable regularly varying sequence is an element of \({\mathscr {S}}\). Summability imposes the restriction \(\alpha \le -1\) to the index.

These arguments show that if \(Q(t)\sim t^{-\gamma -1}\ell (t)\) with an exponent \(\gamma >0\) and an arbitrary slowly varying function \(\ell \), then \(\{Q(t)\}_{t\ge 0}\in {\mathscr {S}}\). In such case we have the asymptotic equivalence \(\sum _{n>t}Q(n)\sim (1/\gamma )t^{-\gamma }\ell (t)\) by Proposition 1.5.10 of [34]. Thus, we get the following corollary of Theorem 3.1.

Corollary 3.1

Assume that p is aperiodic and \(Q(t)\sim t^{-\gamma -1}\ell (t)\) with an exponent \(\gamma >0\) and a slowly varying function \(\ell \). Then

$$\begin{aligned} \rho _t\sim \frac{\ell (t)}{\gamma \mu ^3t^{\gamma }}. \end{aligned}$$

In contrast to the latent factor models analyzed in [17] and [18], which can account for polynomial decay of correlations but not for too small exponents, Corollary 3.1 of Theorem 3.1 shows that a renewal structure is able to describe polynomial decays of the autocovariance with any exponent \(\gamma >0\). Actually, the hypothesis \(\gamma >0\) is not necessary and we can also have \(\gamma =0\), so that the autocovariance decays slower than any polynomial, but in this case the asymptotic behavior of \(\{\sum _{n>t}Q(n)\}_{t\ge 0}\) cannot be resolved in general. Notice that summability of \(\{Q(t)\}_{t\ge 0}\) when \(\gamma =0\) imposes restrictions on \(\ell \). For instance, if \(Q(t)\sim t^{-1}(\ln t)^{-\beta -1}\) with a number \(\beta >0\), then \(\{Q(t)\}_{t\ge 0}\in {\mathscr {S}}\) and Theorem 3.1 gives \(\rho _t\sim (1/\mu ^3)\sum _{n>t}Q(n)\sim (1/\beta \mu ^3)(\ln t)^{-\beta }\).

3.1.2 Stretched-Exponential Decay

In [32] the following sufficient condition for subexponentiality was proposed. Let h be a continuously differentiable real function on a neighborhood of infinity, say \((\tau ,\infty )\) with some \(\tau >0\), such that its derivative \(h'\) enjoys the properties that \(-z^2h'(z)\) is increasing to infinity with respect to z and that \(\int _\tau ^\infty e^{\frac{1}{2}z^2h'(z)}dz<\infty \). Then, a positive sequence \(a:=\{a_t\}_{t\ge 0}\) such that \(A:=\sum _{t\ge 0}a_t<\infty \) and \(a_{t+1}\sim a_t\sim e^{-th(t)}\) satisfies \(\sum _{n=0}^ta_na_{t-n}\sim 2Aa_t\), and hence belongs to \({\mathscr {S}}\). We have used this criterion to investigate the asymptotic behavior of the autocovariance when \(Q(t)\sim e^{-t^\beta \ell (t)}\) with a stretching exponent \(\beta \in (0,1)\) and some function \(\ell \). The following corollary of Theorem 3.1, which is proved in Appendix G, gives sufficient conditions on \(\ell \) that imply \(\{Q(t)\}_{t\ge 0}\in {\mathscr {S}}\). We point out that \(\ell \) is slowly varying under those conditions.

Corollary 3.2

Assume that p is aperiodic and \(Q(t)\sim e^{-t^\beta \ell (t)}\) with a stretching exponent \(\beta \in (0,1)\) and a twice continuously differentiable positive function \(\ell \) on a neighborhood of infinity that satisfies \(\lim _{z\uparrow \infty }z\ell '(z)/\ell (z)=0\) and \(\lim _{z\uparrow \infty }z^2\ell ''(z)/\ell (z)\) exists. Then

$$\begin{aligned} \rho _t\sim \frac{t^{1-\beta }}{\mu ^3\beta \ell (t)} e^{-t^\beta \ell (t)}. \end{aligned}$$

To conclude, we observe that the hypothesis \(\beta <1\) can be relaxed in favor of \(\beta =1\) to come fairly close to exponential decay of correlations while staying in the framework of subexponential sequences. If for example \(Q(t)\sim e^{-t(\ln t)^{-\gamma }}\) with some number \(\gamma >0\), then \(Q(t+1)\sim Q(t)\sim e^{-th(t)}\) with \(h(z):=(\ln z)^{-\gamma }\). This function h satisfies the above sufficient condition for subexponentiality, so that \(\rho _t\sim (1/\mu ^3)\sum _{n>t}Q(n)\sim (1/\mu ^3)(\ln t)^\gamma e^{-t(\ln t)^{-\gamma }}\) by Theorem 3.1.

3.2 Autocorrelation: Inverse Problem

Let us now investigate the possibility to implement a prescribed autocovariance. Here the focus is on short time scales since Theorem 3.1 and its Corollaries 3.1 and 3.2 already settle the issue on long time scales, demonstrating that a large class of asymptotic prescriptions can be obtained. We want to understand conditions on a non-negative sequence \(c:=\{c_t\}_{t\ge 0}\) under which there exists a waiting time distribution p of finite mean whose associated stationary binary sequence \(X:=\{X_t\}_{t\ge 1}\) satisfies \(c_t={\mathbb {E}}[X_1X_{t+1}]\) for all \(t\ge 0\). For simplicity, we assume that \(c_t>0\) for every \(t\ge 0\). In the light of Theorem 2.1 and Proposition 3.2, this is tantamount to ask under which conditions on c there exists a probability distribution p with the properties \(\sum _{s\ge 1}sp(s)=1/c_0\) and \(\sum _{s=1}^tp(s)\,c_{t-s}=c_t\) for all \(t\ge 1\). Such a p, if any, is uniquely defined by the renewal equation and meets the requirement \(\sum _{s\ge 1}sp(s)=1/c_0\) if and only if \(\lim _{t\uparrow \infty }c_t=c_0^2\). In fact, if p is a probability distribution such that \(\sum _{s=1}^tp(s)\,c_{t-s}=c_t\) for all \(t\ge 1\), then it is aperiodic since \(p(1)=c_1/c_0>0\). This way, the renewal theorem [31] gives \(\lim _{t\uparrow \infty }c_t=c_0/\sum _{s\ge 1}sp(s)\) if \(\sum _{s\ge 1}sp(s)<\infty \) and \(\lim _{t\uparrow \infty }c_t=0\) if \(\sum _{s\ge 1}sp(s)=\infty \).

Finding the minimal conditions on the sequence c for the existence of an associated waiting time distribution p is a difficult task. We stress that the problem consists in determining whether or not the function p that solves the problem \(\sum _{s=1}^tp(s)\,c_{t-s}=c_t\) for every \(t\ge 1\) is non-negative and sums to 1. However, there is a sufficient condition that covers many applications. A sequence \(c:=\{c_t\}_{t\ge 0}\) is a Kaluza sequence [27] if \(c_t>0\) and \(c_{t-1}c_{t+1}\ge c_t^2\) for all \(t\ge 1\). It follows that \(c_0>0\). The following theorem states that the hypothesis that c is a Kaluza sequence such that \(\lim _{t\uparrow \infty }c_t=c_0^2\) guarantees the existence of an associated waiting time distribution of finite mean. The proof is provided in Appendix H.

Theorem 3.2

Let \(c:=\{c_t\}_{t\ge 0}\) be a Kaluza sequence such that \(\lim _{t\uparrow \infty }c_t=c_0^2\). Then, there exists a unique waiting time distribution p with the properties \(\sum _{s\ge 1}sp(s)=1/c_0\) and \(\sum _{s=1}^tp(s)\,c_{t-s}=c_t\) for all \(t\ge 1\). As a consequence, the stationary binary sequence \(X:=\{X_t\}_{t\ge 1}\) associated with p satisfies \(c_t={\mathbb {E}}[X_1X_{t+1}]\) for all \(t\ge 0\).

We point out that Theorem 3.2 of [33] offers an inverse of Theorem 3.1: if \(c:=\{c_t\}_{t\ge 0}\) is a Kaluza sequence such that \(\lim _{t\uparrow \infty }c_t=c_0^2\) and \(\{c_{t+1}-c_t\}_{t\ge 0}\in {\mathscr {S}}\), then there exists a unique associated waiting time distribution p whose tail Q enjoys the property \((1/\mu ^3)\sum _{n>t}Q(n)\sim \rho _t:=c_t-c_0^2\).

A practical criterion to recognize a Kaluza sequence that puts the emphasis on the autocovariance is the following. Consider a sequence \(c:=\{c_t\}_{t\ge 0}\) defined by \(c_0:=\xi \) and \(c_t:=\xi ^2+m e^{-\phi (t)}\) for \(t\ge 1\) with constants \(\xi \in (0,1]\) and \(m\in [0,\xi (1-\xi )]\) and a concave function \(\phi \) such that \(\phi (0)=0\) and \(\lim _{z\uparrow \infty }\phi (z)=\infty \). Then, c is a Kaluza sequence and \(\lim _{t\uparrow \infty }c_t=c_0^2\). Indeed, \(c_0=\xi ^2+\xi (1-\xi )\ge \xi ^2+me^{-\phi (0)}\), so that for each \(t\ge 1\)

$$\begin{aligned} c_{t-1}c_{t+1}-c_t^2&\ge [\xi ^2+m e^{-\phi (t-1)}][\xi ^2+m e^{-\phi (t+1)}]-[\xi ^2+m e^{-\phi (t)}]^2\\&=m\xi ^2[e^{-\phi (t-1)}+e^{-\phi (t+1)}-2e^{-\phi (t)}]\\&\quad +m^2e^{-2\phi (t)}[e^{2\phi (t)-\phi (t-1)-\phi (t+1)}-1]. \end{aligned}$$

This way, the concavity of \(\phi \) and the consequent convexity of \(e^{-\phi }\) give \(c_{t-1}c_{t+1}-c_t^2\ge 0\) for all \(t\ge 1\). We have thus proved the following corollary of Theorem 3.2.

Corollary 3.3

Let \(\xi \in (0,1]\) and \(m\in [0,\xi (1-\xi )]\) be two constants and let \(\phi \) be a concave function such that \(\phi (0)=0\) and \(\lim _{z\uparrow \infty }\phi (z)=\infty \). Then, there exists a unique waiting time distribution p of finite mean whose associated stationary binary sequence \(X:=\{X_t\}_{t\ge 1}\) satisfies \({\mathbb {E}}[X_1]=\xi \) and \(\rho _t:=\mathrm {cov}[X_1,X_{t+1}]=m e^{-\phi (t)}\) for all \(t\ge 1\).

Fig. 1
figure 1

Autocovariance \(\rho _t\) (red) and \((1/\mu ^3)\sum _{n>t}Q(n)\) (blue) versus t for the inverse problem with \(c_t=1/4+(1/4)(1+t)^{-\gamma }\) for \(t\ge 0\) with \(\gamma =2\) (left) and \(\gamma =4\) (right) (Color figure online)

Full size image
Fig. 2
figure 2

Autocovariance \(\rho _t\) (red) and \((1/\mu ^3)\sum _{n>t}Q(n)\) (blue) versus t for the inverse problem with \(c_t=1/4+(1/4)e^{-t^\beta }\) for \(t\ge 0\) with \(\beta =1/2\) (left) and \(\beta =1\) (right) (Color figure online)

Full size image

We appeal to Corollary 3.3 to draw some examples. Our model can implement the autocovariances \(\rho _t=m(1+t)^{-\gamma }\) and \(\rho _t=me^{-\kappa t^\beta }\) for \(t\ge 1\) with any real numbers \(\xi \in (0,1]\), \(m\in [0,\xi (1-\xi )]\), \(\gamma >0\), \(\kappa >0\), and \(\beta \in (0,1]\). Figure 1 compares \(\rho _t\) with \((1/\mu ^3)\sum _{n>t}Q(n)\) for the two inverse problems corresponding to the polynomial correlation structures \(c_t=1/4+(1/4)(1+t)^{-\gamma }\) for \(t\ge 0\) with exponents \(\gamma =2\) and \(\gamma =4\), respectively. We see that the earlier mentioned asymptotic equivalence \(\rho _t\sim (1/\mu ^3)\sum _{n>t}Q(n)\) is confirmed. Figure 2 shows the same comparison for the two stretched-exponential cases \(c_t=1/4+(1/4)e^{-t^\beta }\) for \(t\ge 0\) with exponents \(\beta =1/2\) and \(\beta =1\), respectively. This time, the asymptotic equivalence \(\rho _t\sim (1/\mu ^3)\sum _{n>t}Q(n)\) is confirmed only for the subexponential case \(\beta =1/2\). The exponential case \(\beta =1\) is solved explicitly by the formulas \(\rho _t=(1/4)e^{-t}\) and \((1/\mu ^3)\sum _{n>t}Q(n)=(1/8)(\frac{1+e^{-1}}{2})^t\) for all \(t\ge 0\), which shows that the decay rates of the autocovariance and of the associated waiting time distribution are different.

4 Limit Theorems

There are a number of limit theorems for the sequence \(X:=\{X_t\}_{t\ge 1}\) that follow from an underlying ergodic property. In this section we discuss some of these limit theorems, proving at first ergodicity of a related dynamical system. We refer to [35] for basics of ergodic theory. Recalling that \({\mathscr {B}}\) denotes the \(\sigma \)-field on \({\mathbb {N}}_2^\infty \) generated by the cylinder subsets, it is now convenient to introduce the probability measure \({\mathbb {P}}_o[\,\cdot \,]:={\mathbb {P}}[X\in \cdot \,]\) on \({\mathscr {B}}\) and the probability space \(({\mathbb {N}}_2^\infty ,{\mathscr {B}},{\mathbb {P}}_o)\). We can deduce almost sure convergence in \((\Omega ,{\mathscr {F}},{\mathbb {P}})\) from almost sure convergence in \(({\mathbb {N}}_2^\infty ,{\mathscr {B}},{\mathbb {P}}_o)\). In fact, since almost sure convergence is defined only in terms of probability distributions [36], if \(G,G_1,G_2,\ldots \) are real \({\mathscr {B}}\)-measurable functions on \({\mathbb {N}}_2^\infty \) such that \(\lim _{n\uparrow \infty }G_n(x)=G(x)\) for \({\mathbb {P}}_o\text{-a.e. } \ x\), then \(\lim _{t\uparrow \infty }G_t(X)=G(X)\) \({\mathbb {P}}\)-a.s. The same can be said for convergence in mean. The reason to deal with the new probability space \(({\mathbb {N}}_2^\infty ,{\mathscr {B}},{\mathbb {P}}_o)\) is that it can be endowed with a measure-preserving transformation. Such transformation is the left-shift operator \({\mathcal {T}}\) that maps any binary sequence \(x:=\{x_t\}_{t\ge 1}\in {\mathbb {N}}_2^\infty \) in \({\mathcal {T}}x:=\{x_{t+1}\}_{t\ge 1}\). The operator \({\mathcal {T}}\) is measurable and, due to stationary of X, preserves measures, namely \({\mathbb {P}}_o[{\mathcal {T}}^{-1}{\mathcal {B}}]={\mathbb {P}}_o[{\mathcal {B}}]\) for each \({\mathcal {B}}\in {\mathscr {B}}\). Indeed, if \({\mathcal {B}}\) is an element of \({\mathscr {B}}\), then \({\mathbb {P}}_o[{\mathcal {T}}^{-1}{\mathcal {B}}]={\mathbb {P}}[{\mathcal {T}}X\in {\mathcal {B}}]={\mathbb {P}}[\{X_{t+1}\}_{t\ge 1}\in {\mathcal {B}}]={\mathbb {P}}[\{X_t\}_{t\ge 1}\in {\mathcal {B}}]={\mathbb {P}}_o[{\mathcal {B}}]\). The transformation \({\mathcal {T}}\) is strong-mixing in the sense of ergodic theory, as stated by the following lemma that in proved in Appendix I. The proof relies on Lemma 3.1.

Lemma 4.1

Assume that p is aperiodic. Then, for all \({\mathcal {A}}\) and \({\mathcal {B}}\) in \({\mathscr {B}}\)

$$\begin{aligned} \lim _{t\uparrow \infty }{\mathbb {P}}_o[{\mathcal {A}}\cap {\mathcal {T}}^{-t}{\mathcal {B}}]={\mathbb {P}}_o[{\mathcal {A}}]\,{\mathbb {P}}_o[{\mathcal {B}}]. \end{aligned}$$

Due to strong-mixing, the transformation \({\mathcal {T}}\) is ergodic according to Corollary 1.14.2 of [35], which means that the only members \({\mathcal {B}}\) of \({\mathscr {B}}\) with \({\mathcal {T}}^{-1}{\mathcal {B}}={\mathcal {B}}\) satisfy \({\mathbb {P}}_o[{\mathcal {B}}]=0\) or \({\mathbb {P}}_o[{\mathcal {B}}]=1\). We use ergodicity to demonstrate an asymptotic equipartition property, which justifies the principle of maximum entropy for model selection, and to investigate the behavior of empirical means.

4.1 Asymptotic Equipartition Property

Description of data requires to select a statistical model, that is a waiting time distribution p once our framework is considered. One tool for model selection is the maximum entropy principle [28, 29], which would amount to pick the probability distribution p of finite mean that meets certain moment constraints representing the available information and that maximizes the Shannon entropy. The Shannon entropy \({\mathcal {H}}(p)\) of p is defined by

$$\begin{aligned} {\mathcal {H}}(p):=-\sum _{s\ge 1}p(s)\ln p(s) \end{aligned}$$

with \(0\ln 0:=0\). We point out that \({\mathcal {H}}(p)\le \mu \ln \mu +(1-\mu )\ln (\mu -1)<\infty \) whenever \(\mu :=\sum _{s\ge 1}sp(s)<\infty \) since \(-p(s)\ln p(s)\le \mu ^{-s}(\mu -1)^{s-1}-p(s)-p(s)\ln [\mu ^{-s}(\mu -1)^{s-1}]\) for all \(s\ge 1\) by concavity. Actually, the largest value of the entropy is \(\mu \ln \mu +(1-\mu )\ln (\mu -1)\), which is attained if and only if \(p(s)=\mu ^{-s}(\mu -1)^{s-1}\) for every s. The Shannon entropy can be derived axiomatically as a measure of uncertainty in the outcomes of a random variable. Instead, in this section we show that the entropy \({\mathcal {H}}(p)\) of p naturally arises as the answer to the question “how many typical sequences are there?”. In fact, we demonstrate that there are about \(e^{(t/\mu ){\mathcal {H}}(p)}\) typical sequences of length t, each with probability about \(e^{-(t/\mu ){\mathcal {H}}(p)}\). It follows that selecting the waiting time distribution that maximizes the entropy means not excluding possible sequences arbitrarily. If the only available information is the mean \(\mu \), then the maximum entropy prescription is the waiting time distribution p defined by \(p(s)=\mu ^{-s}(\mu -1)^{s-1}\) for all s. According to Corollary 2.1, the binary sequence X associated with such p is a sequence of i.i.d. binary random variables with mean \(1/\mu \).

Let us formalize and explain the above statements. Together with the Shannon entropy of the waiting time distribution, we consider for each \(t\ge 1\) the Shannon entropy \({\mathcal {H}}(\pi _t)\) of the finite-dimensional distribution \(\pi _t\) of X:

$$\begin{aligned} {\mathcal {H}}(\pi _t):=-\sum _{x_1\in {\mathbb {N}}_2}\cdots \sum _{x_t\in {\mathbb {N}}_2}\pi _t(x_1,\ldots ,x_t)\ln \pi _t(x_1,\ldots ,x_t). \end{aligned}$$

Proposition 2.1 and stationary and reversibility of X give

$$\begin{aligned} {\mathcal {H}}(\pi _t)&=\ln \mu -{\mathbb {E}}\Bigg [\prod _{n=1}^t(1-X_n)\Bigg ]\ln \sum _{s\ge t}Q(s)-2\sum _{s=1}^t{\mathbb {E}}\Bigg [\prod _{n=1}^{s-1}(1-X_n)X_s\Bigg ]\ln Q(s-1)\\&\quad -\sum _{s=1}^t(t-s)\,{\mathbb {E}}\Bigg [X_1\prod _{n=2}^s(1-X_n)X_{s+1}\Bigg ]\ln p(s)\\&=\ln \mu -\frac{1}{\mu }\sum _{s\ge t}Q(s)\ln \sum _{s\ge t}Q(s)-\frac{2}{\mu }\sum _{s=1}^t Q(s-1)\ln Q(s-1)\\&\quad -\frac{1}{\mu }\sum _{s=1}^t(t-s)\,p(s)\ln p(s), \end{aligned}$$

where we have used the facts that \({\mathbb {E}}[\prod _{n=1}^t(1-X_n)]={\mathbb {P}}[S_1>t]\), \({\mathbb {E}}[\prod _{n=1}^{s-1}(1-X_n)X_s]={\mathbb {P}}[S_1=s]\), and \({\mathbb {E}}[X_1\prod _{n=2}^s(1-X_n)X_{s+1}]={\mathbb {P}}[S_1=1,S_2=s]\) for all s. After invoking the properties of Cesáro means and the dominated converge theorem, this formula shows that the entropy rate of the sequence X is

$$\begin{aligned} \lim _{t\uparrow \infty }\frac{{\mathcal {H}}(\pi _t)}{t}=\frac{{\mathcal {H}}(p)}{\mu }. \end{aligned}$$
(4.1)

Then, under ergodicity of the left-shift operator \({\mathcal {T}}\), the Shannon–McMillan–Breiman theorem [37] yields for \({\mathbb {P}}_o\text{-a.e. } \ x\)

$$\begin{aligned} \lim _{t\uparrow \infty }-\frac{1}{t}\ln \pi _t(x_1,\ldots ,x_t)=\lim _{t\uparrow \infty }\frac{{\mathcal {H}}(\pi _t)}{t}=\frac{{\mathcal {H}}(p)}{\mu }. \end{aligned}$$

These considerations, in combination with Lemma 4.1 and the possibility to deduce almost sure convergence in \((\Omega ,{\mathscr {F}},{\mathbb {P}})\) from almost sure convergence in \(({\mathbb {N}}_2^\infty ,{\mathscr {B}},{\mathbb {P}}_o)\), prove the following asymptotic equipartition property, which states that all long typical sequences of length t have roughly the same probability \(e^{-(t/\mu ){\mathcal {H}}(p)}\).

Theorem 4.1

Assume that p is aperiodic. Then

$$\begin{aligned} \lim _{t\uparrow \infty }-\frac{\mu }{t}\ln \pi _t(X_1,\ldots ,X_t)={\mathcal {H}}(p)~~~~~{\mathbb {P}}\text{-a.s. }. \end{aligned}$$

Theorem 4.1 implies that there are about \(e^{(t/\mu ){\mathcal {H}}(p)}\) typical sequences of length t. This fact is illustrated by the following corollary, whose proof is reported in Appendix J. A formal notion of typical set is needed here. Given a real number \(\delta \in (0,1)\), according to [37] we say that \({\mathcal {X}}\subseteq {\mathbb {N}}_2^t\) is a typical set of length \(t\ge 1\) if \({\mathbb {P}}[(X_1,\ldots ,X_t)\in {\mathcal {X}}]\ge 1-\delta \). We denote by \(|{\mathcal {X}}|\) the cardinality of a set \({\mathcal {X}}\).

Corollary 4.1

Fix \(\epsilon >0\) and assume that p is aperiodic. The following conclusions hold for all sufficiently large t:

  1. (i)

    there exists a typical set \({\mathcal {X}}_o\) of length t such that \(|{\mathcal {X}}_o|\le e^{(t/\mu )[{\mathcal {H}}(p)+\epsilon ]}\);

  2. (ii)

    any typical set \({\mathcal {X}}\) of length t satisfies \(|{\mathcal {X}}|\ge e^{(t/\mu )[{\mathcal {H}}(p)-\epsilon ]}\).

4.2 Empirical Means

Applications to real data require to explain whether or not ensemble averages can be estimated by means of time averages, also known as empirical means. If G is a \({\mathscr {B}}\)-measurable function on \({\mathbb {N}}_2^\infty \), then its empirical mean up to time \(t\ge 1\) is the random variable

$$\begin{aligned} \frac{1}{t}\sum _{n=1}^t G(X_n,X_{n+1},\ldots )=\frac{1}{t}\sum _{n=0}^{t-1} G({\mathcal {T}}^nX). \end{aligned}$$

Birkhoff ergodic theorem [35] tells us that if the left-shift operator \({\mathcal {T}}\) is ergodic and the expectation \(\int _{{\mathbb {N}}_2^\infty } |G(x)|\,{\mathbb {P}}_o[dx]={\mathbb {E}}[|G(X)|]\) is finite, then for \({\mathbb {P}}_o\text{-a.e. } \ x\)

$$\begin{aligned} \lim _{t\uparrow \infty }\frac{1}{t}\sum _{n=0}^{t-1} G({\mathcal {T}}^nx)=\int _{{\mathbb {N}}_2^\infty } G(x)\,{\mathbb {P}}_o[dx]={\mathbb {E}}[G(X)]. \end{aligned}$$

The convergence also holds in mean by Corollary 1.14.1 of [35]. This way, Lemma 4.1 and the possibility to export convergences from \(({\mathbb {N}}_2^\infty ,{\mathscr {B}},{\mathbb {P}}_o)\) to \((\Omega ,{\mathscr {F}},{\mathbb {P}})\) result in the following law of large numbers, which gives a positive answer to the possibility of estimating ensemble averages with time averages. We stress that in most applications the observable G depends only on a finite number of variables, so that G is automatically \({\mathscr {B}}\)-measurable and bounded.

Theorem 4.2

Let G be a \({\mathscr {B}}\)-measurable function on \({\mathbb {N}}_2^\infty \) such that \({\mathbb {E}}[|G(X)|]<\infty \). If p is aperiodic, then

$$\begin{aligned} \lim _{t\uparrow \infty }\frac{1}{t}\sum _{n=0}^{t-1} G({\mathcal {T}}^nX)={\mathbb {E}}[G(X)]~~~~~{\mathbb {P}}\text{-a.s. } \text{ and } \text{ in } \text{ mean }. \end{aligned}$$

We deepen the study of empirical means investigating their normal fluctuations. Since X is a regenerative process with independent cycles [26], if G depends on exactly one binary variable, then the normal fluctuations of its empirical mean are described under the optimal hypothesis \({\mathbb {E}}[S_2^2]=\sum _{s\ge 1}s^2p(s)<\infty \) by the central limit theorem for cumulative processes with a regenerative structure [26]. It is worth noting that in such case the empirical mean of G up to time t is a linear function of the number of renewals by t, so that even its large fluctuations can be completely characterized through well-established large deviation principles for discrete-time renewal-reward processes [38, 39], which include the counting renewal process. To deal with functions G that involve more than one variable, and that cannot be tackled by the standard limit theory of regenerative processes with independent cycles, we resort to the theory of the central limit theorem for stationary sequences [40]. To begin with, we introduce the strong mixing coefficient \(\alpha _t\) of the sequence X, which measures the memory of the past on future events t time steps later. According to [21], the strong mixing coefficient \(\alpha _t\), or \(\alpha \)-mixing coefficient, of X is defined for each \(t\ge 1\) by

$$\begin{aligned} \alpha _t:=\sup _{m\ge 1}\,\sup _{{\mathcal {A}}\in {\mathscr {F}}_1^m}\sup _{{\mathcal {B}}\in {\mathscr {F}}_{m+t}^\infty } \bigg \{\Big |{\mathbb {P}}[{\mathcal {A}}\cap {\mathcal {B}}]-{\mathbb {P}}[{\mathcal {A}}]\,{\mathbb {P}}[{\mathcal {B}}]\Big |\bigg \}. \end{aligned}$$

Here \({\mathscr {F}}_a^b\) is the \(\sigma \)-algebra generated by \(X_a,\ldots ,X_b\) for \(1\le a\le b\le \infty \). The sequence X is strong mixing in the sense of probability theory if \(\lim _{t\uparrow \infty }\alpha _t=0\). The following proposition provides an estimate of the \(\alpha \)-mixing coefficient of our model. The proof is based on Lemma 3.1 and is proposed in Appendix K. Recall that \(\rho _t:=\mathrm {cov}[X_1,X_{t+1}]\).

Proposition 4.1

For each \(t\ge 1\)

$$\begin{aligned} \alpha _t\le 3\mu ^2\sum _{n\ge t}|\rho _{n+1}-\rho _n|+4\mu ^2\sum _{n\ge t}n\,|\rho _{n+1}-2\rho _n+\rho _{n-1}|. \end{aligned}$$

Empirical means display normal fluctuations when the strong mixing coefficient decays reasonably fast, and precisely when \(\sum _{t\ge 1}\alpha _t<\infty \). In fact, let us consider a bounded observable G and for each \(n\ge 0\) let us set \(Z_n:=G({\mathcal {T}}^nX)\) for brevity. Due to boundedness of G Theorem 4.2 tells us that \(\lim _{t\uparrow \infty }(1/t)\sum _{n=0}^{t-1}Z_n={\mathbb {E}}[Z_0]\) \({\mathbb {P}}\text{-a.s. }\) if p is aperiodic. The normal fluctuations of \((1/t)\sum _{n=0}^{t-1}Z_n\) around \({\mathbb {E}}[Z_0]\) are described as follows by Theorem 18.6.3 of [40], which states the central limit theorem for functionals of mixing sequences.

Theorem 4.3

Let G be a bounded \({\mathscr {B}}\)-measurable function on \({\mathbb {N}}_2^\infty \) and set \(Z_n:=G({\mathcal {T}}^nX)\) for \(n\ge 0\). Assume that \(\sum _{t\ge 1}\alpha _t<\infty \) and \(\sum _{m\ge 1}{\mathbb {E}}[|Z_0-{\mathbb {E}}[Z_0|{\mathscr {F}}_1^m]|]<\infty \). Then

$$\begin{aligned} v:=\mathrm {cov}[Z_0,Z_0]+2\sum _{n\ge 1}\mathrm {cov}[Z_0,Z_n] \end{aligned}$$

is finite and non-negative, and provided that \(v\ne 0\)

$$\begin{aligned} \lim _{t\uparrow \infty }{\mathbb {P}}\Bigg [\frac{1}{\sqrt{vt}}\sum _{n=0}^{t-1} \big (Z_n-{\mathbb {E}}[Z_0]\big )\le z\Bigg ]=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^ze^{-\frac{1}{2}\zeta ^2}d\zeta . \end{aligned}$$

We point out that the hypotheses of the theorem about G are automatically satisfied when G depends only on a finite number of variables, since in such case \({\mathbb {E}}[Z_0|{\mathscr {F}}_1^m]=Z_0\) for all sufficiently large m. The following lemma based on Proposition 4.1 shows that the finiteness of the second moment of the waiting time distribution suffices for \(\sum _{t\ge 1}\alpha _t<\infty \), thus implying the validity of the central limit theorem. The proof is provided in Appendix L.

Lemma 4.2

The two following statements are equivalent:

  1. (i)

    p is aperiodic and \(\sum _{s\ge 1}s^2p(s)<\infty \);

  2. (ii)

    \(\sum _{t\ge 1}t|\rho _t-\rho _{t-1}|<\infty \).

Either of them implies \(\sum _{t\ge 1}\alpha _t<\infty \) and \(\sum _{s\ge 1}s^2p(s)=\mu +2\mu ^3\sum _{t\ge 0}\rho _t\).

We stress that a coupling argument can show, without the need of an explicit estimate of the \(\alpha \)-mixing coefficient, that an aperiodic waiting time distribution satisfies \(\sum _{s\ge 1}s^\gamma p(s)<\infty \) for a real number \(\gamma >1\) if and only if \(\sum _{t\ge 1}t^{\gamma -2}\alpha _t<\infty \) (see [41], Theorem 6.1).

4.3 Empirical Analyses

Finally, we demonstrate the theory of empirical means through estimation of the waiting time distribution and of the autocovariance from data. The focus is on the possibility to identify their decay, that is on the possibility to estimate p(s) for large s and \(\rho _\tau \) for large \(\tau \). In order to avoid complications related to nonlinear functions of empirical means, we imagine that \(\mu \) is known in advance. Importantly, we suppose that either (i) or (ii) of Lemma 4.2 hold, so that if G is an observable that depends on a finite number of variables, then both the law of large numbers stated by Theorem 4.2 and the central limit theorem of Theorem 4.3 hold.

Fig. 3
figure 3

Empirical estimates of p(s) versus s with data sequences of length \(t=10^6\) (red) and \(t=10^8\) (blue) generated by the models defined by \(c_t=1/4+(1/4)(1+t)^{-\gamma }\) for \(t\ge 0\) with \(\gamma =2\) (left) and \(\gamma =4\) (right). Black curves are the theoretical limits p(s) (Color figure online)

Full size image

Fix an integer \(s\ge 1\) and take

$$\begin{aligned} G(x):=\mu x_1\prod _{k=2}^s(1-x_k)x_{s+1} \end{aligned}$$

for all \(x\in {\mathbb {N}}_2^\infty \). Recalling that \(Z_n:=G({\mathcal {T}}^nX)\) for \(n\ge 0\), we have \({\mathbb {E}}[Z_0]=\mu {\mathbb {P}}[S_1=1,S_2=s]=p(s)\), so that the empirical mean of G estimates the waiting time distribution at s. Simple applications of Proposition 3.1 show that \(\mathrm {cov}[Z_0,Z_n]=\mu p(s)-p^2(s)\) if \(n=0\), \(\mathrm {cov}[Z_0,Z_n]=-p^2(s)\) if \(1\le n<s\), and \(\mathrm {cov}[Z_0,Z_n]=\mu ^2p^2(s)\rho _{n-s}\) if \(n\ge s\). This way, the variance \(v_s:=\mathrm {cov}[Z_0,Z_0]+2\sum _{n\ge 1}\mathrm {cov}[Z_0,Z_n]\) introduced by Theorem 4.3 turns out to be

$$\begin{aligned} v_s&=\mu p(s)+(1-2s)p^2(s)+2\mu ^2p^2(s)\sum _{n\ge 0}\rho _n\\&=\mu p(s)-2sp^2(s)+\mu ^{-1}p^2(s)\sum _{n\ge 1}n^2p(n). \end{aligned}$$

We have made use of the identity \(\sum _{s\ge 1}s^2p(s)=\mu +2\mu ^3\sum _{t\ge 0}\rho _t\) provided by Lemma 4.2 to get at the second equality. If a data sequence of length t is given, then we expect to be able to estimate p(s) for values of s such that \(\sqrt{v_s/t}\ll p(s)\). At large s, this means values of s such that \(p(s)\gg \mu /t\) because \(v_s\sim \mu p(s)\). Figure 3 shows results of estimation for two data sequences of length \(t=10^6\) and \(t=10^8\), respectively, when data are generated by the models of Fig. 1, which correspond to \(c_t=1/4+(1/4)(1+t)^{-\gamma }\) for \(t\ge 0\) with exponents \(\gamma =2\) and \(\gamma =4\). In such cases, the condition \(p(s)\gg \mu /t\) for proper estimation reads \(s\ll 1.56\,t^{1/4}\) for \(\gamma =2\) and \(s\ll 1.65\,t^{1/6}\) for \(\gamma =4\). Figure 4 reports the same estimation for the models of Fig. 2 defined by \(c_t=1/4+(1/4)e^{-t^\beta }\) for \(t\ge 0\) with exponents \(\beta =1/2\) and \(\beta =1\). The condition \(p(s)\gg \mu /t\) now becomes \(s\ll \ln ^2t\) for \(\beta =1/2\) and \(s\ll 2.63\,\ln t\) for \(\beta =1\).

Fig. 4
figure 4

Empirical estimates of p(s) versus s with data sequences of length \(t=10^6\) (red) and \(t=10^8\) (blue) generated by the models defined by \(c_t=1/4+(1/4)e^{-t^\beta }\) for \(t\ge 0\) with \(\beta =1/2\) (left) and \(\beta =1\) (right). Black curves are the theoretical limits p(s) (Color figure online)

Full size image

Moving to the autocovariance, pick an integer \(\tau \ge 0\) and consider the function

$$\begin{aligned} G(x):=x_1x_{\tau +1}-1/\mu ^2 \end{aligned}$$
(4.2)

for all \(x\in {\mathbb {N}}_2^\infty \). As \({\mathbb {E}}[Z_0]=\rho _\tau \), the empirical mean of F estimates \(\rho _\tau \). Once again, simple applications of Proposition 3.1 yield \(\mathrm {cov}[Z_0,Z_n]=\mu ^2c_n^2c_{\tau -n}-c_\tau ^2\) if \(0\le n<\tau \) and \(\mathrm {cov}[Z_0,Z_n]=\mu ^2 c_\tau ^2\rho _{n-\tau }\) if \(n\ge \tau \). This way, the variance \(v_\tau :=\mathrm {cov}[Z_0,Z_0]+2\sum _{n\ge 1}\mathrm {cov}[Z_0,Z_n]\) reads

$$\begin{aligned} v_\tau&={\left\{ \begin{array}{ll} \rho _0+2\sum _{n\ge 1}\rho _n &{} \text{ if } \tau =0;\\ c_\tau -c_\tau ^2+2\sum _{n=1}^\tau (\mu ^2c_n^2c_{\tau -n}-c_\tau ^2)+2\mu ^2c_\tau ^2\sum _{n\ge 0}\rho _n &{} \text{ if } \tau \ge 1 \end{array}\right. }\nonumber \\&={\left\{ \begin{array}{ll} \mu ^{-3}\sum _{n\ge 1}n^2p(n)-\mu ^{-1} &{} \text{ if } \tau =0;\\ 2\sum _{n=0}^\tau (\mu ^2c_n^2c_{\tau -n}-c_\tau ^2)+\mu ^{-1}c_\tau ^2\sum _{n\ge 1}n^2p(n)-c_\tau &{} \text{ if } \tau \ge 1. \end{array}\right. } \end{aligned}$$
(4.3)

Since \(\lim _{\tau \uparrow \infty }v_\tau =c_0^2(1-4c_0+3c_0^2)+8c_0^2\sum _{t\ge 0}\rho _t+2\mu \sum _{t\ge 1}\rho _t^2=:\sigma ^2\) with \(\sigma >0\), we expect that \(\rho _\tau \) can be estimated with a data sequence of length t when \(\tau \) satisfies \(\rho _\tau \gg \sigma /\sqrt{t}\). Figure 5 illustrates results of estimation for two data sequences of length \(t=10^6\) and \(t=10^8\), respectively, when data are generated by the models of Figs. 1 and 3. The condition \(\rho _\tau \gg \sigma /\sqrt{t}\) explicitly is \(\tau \ll 0.54\, t^{1/4}\) for \(\gamma =2\) and \(\tau \ll 0.77\, t^{1/8}\) for \(\gamma =4\). Figure 6 provides the same results with reference to the models of Figs. 2 and 4. This time, the condition \(\rho _\tau \gg \sigma /\sqrt{t}\) is \(\tau \ll 0.25\,\ln ^2t\) for \(\beta =1/2\) and \(\tau \ll 0.5\,\ln t\) for \(\beta =1\). The comparison between the waiting time distribution and the autocovariance shows that the former is easier to estimate than the latter.

Fig. 5
figure 5

Empirical estimates of \(\rho _\tau \) versus \(\tau \) with data sequences of length \(t=10^6\) (red) and \(t=10^8\) (blue) generated by the models defined by \(c_t=1/4+(1/4)(1+t)^{-\gamma }\) for \(t\ge 0\) with \(\gamma =2\) (left) and \(\gamma =4\) (right). Black curves are the theoretical limits \(\rho _\tau \) (Color figure online)

Full size image
Fig. 6
figure 6

Empirical estimates of \(\rho _\tau \) versus \(\tau \) with data sequences of length \(t=10^6\) (red) and \(t=10^8\) (blue) generated by the models defined by \(c_t=1/4+(1/4)e^{-t^\beta }\) for \(t\ge 0\) with \(\beta =1/2\) (left) and \(\beta =1\) (right). Black curves are the theoretical limits \(\rho _\tau \) (Color figure online)

Full size image

A final remark is in order. If \(\mu \) is not known in advance, then its inverse can be estimated through the empirical mean of the observable \(G(x):=x_1\) for all \(x\in {\mathbb {N}}_2^\infty \). Apart from an additive constant, this observable is (4.2) with \(\tau =0\). Thus, the variance of its empirical mean exactly is \(v_0\) given by (4.3).

5 Conclusions

We have explored the use of renewal processes to generate binary sequences valued in \(\{0,1\}\), where the symbol 1 marks a renewal event. Focusing on stationary binary sequences corresponding to delayed renewal processes, we have demonstrated the ability of the model to account for subexponential autocovariances with special attention to polynomial and stretched-exponential decays. Our model performs at least as well as the algorithms proposed in [19] and [23, 24] that seem to represent the state of the art, but at variance with them, generating a binary sequence with our model is a trivial task. Furthermore, our model is under full mathematical control, and this fact allowed us to build a mathematical theory of its asymptotic properties. In fact, in addition to shedding light on the asymptotic behaviors of a large class of correlations and to demonstrating an asymptotic equipartition property, we have developed a theory for empirical means proving a law of large numbers and a central limit theorem. The latter describes the typical fluctuations of empirical means when the second moment of the waiting time distribution is finite. We leave for future work the study of typical fluctuations when the second moment of the waiting time distribution is infinite. In such case, empirical means are expected to be not in the Gaussian basin of attraction. We also leave for future work the investigation of their large fluctuations.