Abstract
Based on the theory of “snapshot/pullback attractors”, we show that important features of the climate change that we are observing can be understood by imagining many replicas of Earth that are not interacting with each other. Their climate systems evolve in parallel, but not in the same way, although they all obey the same physical laws, in harmony with the chaotic-like nature of the climate dynamics. These parallel climate realizations evolving in time can be considered as members of an ensemble. We argue that the contingency of our Earth’s climate system is characterized by the multiplicity of parallel climate realizations rather than by the variability that we experience in a time series of our observed past. The natural measure of the snapshot attractor enables one to determine averages and other statistical quantifiers of the climate at any instant of time. In this paper, we review the basic idea for climate changes associated with monotonic drifts, and illustrate the large number of possible applications. Examples are given in a low-dimensional model and in numerical climate models of different complexity. We recall that systems undergoing climate change are not ergodic, hence temporal averages are generically not appropriate for the instantaneous characterization of the climate. In particular, teleconnections, i.e. correlated phenomena of remote geographical locations are properly characterized only by correlation coefficients evaluated with respect to the natural measure of a given time instant, and may also change in time. Physics experiments dealing with turbulent-like phenomena in a changing environment are also worth being interpreted in view of the attractor-based ensemble approach. The possibility of the splitting of the snapshot attractor to two branches, near points where the corresponding time-independent system undergoes bifurcation as a function of the changing parameter, is briefly mentioned. This can lead in certain climate-change scenarios to the coexistence of two distinct sub-ensembles representing dramatically different climatic options. The problem of pollutant spreading during climate change is also discussed in the framework of parallel climate realizations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introductory Comments
The traditional theory of chaos in dissipative systems has taught us that on a chaotic attractor there is a plethora of states, all compatible with the single equation of motion of the problem belonging to a fixed set of parameters [1, 2]. The existence of these many different states can be understood in terms of time series. Let us consider a time evolution whose initial position in the phase space lies on the attractor itself, and another one emanated from a nearby point of the attractor. It is well-known that these time series considerably deviate and visit states lying far away from each other on the attractor. The extended size of a chaotic attractor and the sensitivity to initial conditions (unpredictability) are therefore two sides of the same coin. In traditional cases chaotic attractors are low-dimensional and do not depend on time, or can be made time-independent by a properly chosen sampling (stroboscopic mapping).
The dynamics of the atmosphere and the oceans is turbulent, weather, therefore, exhibits chaos-like properties, and is certainly unpredictable [3]. This is also true in the more general context of the climate system [4, 5], which incorporates sea ice and land surface processes including biology for the description of century-scale dynamics. The “chaotic attractor” of the climate system is, however, of very large dimensionality and is not easy to visualize. We are unable to plot this attractor and consider its size as a measure of unpredictability. For a qualitative view of this property, we can accept that there is a multitude of possible states, all governed by the same laws of physics and external forcing. In a stationary case, it is worth speaking of parallel states of the climate. This is a concept that helps in making the term “internal variability” [6] plausible: even if we observe only a single state at a given time instant, many others would also be plausible, simply due to the chaotic nature of the dynamics. It is important to note that the distribution of the parallel states is not arbitrary: an additional property of attractors with chaotic properties is the existence of a unique probability measure, the natural measure [7], which describes the distribution of the permitted states in the phase space [1, 2, 7]. In stationary climate, the external forcing is constant or periodic (with the longest considered period given by the annual cycle), and the dynamical system is autonomous when observed on the same day of the year. A forcing of general time dependence, leads to a changing climate, a fully nonautonomous dynamics. The main message of this work is that climate should then be characterized by a set of permitted “parallel climate realizations”.
The paper is organized as follows. In the next Section we show that a changing climate can be described by an extension of the traditional theory of chaotic attractors: in particular, the theory of snapshot/pullback attractors [8, 9] appears to be an appropriate tool to handle the problem. This necessitates investigating ensembles of “parallel climate realizations” to be discussed in detail in Sect. 3. The aim of the paper is to illustrate the broad range of applicability of this concept in several climate-change-related problems, and show that the underlying ensemble view enables one to explore a number of analogies with statistical physics. Particular emphasis is put on the natural measure on snapshot attractors with respect to which averages and other statistics can be evaluated providing a characterization of the climate at any instant of time. Section 4 is devoted to the illustration of the general ideas in a low-order, conceptual climate model where the time dependent snapshot attractor and its natural measure can be actually visualized, and in a high-dimensional intermediate-complexity climate model where only projections of the attractor can be illustrated, but spatial (geographical) features can also be studied. The remaining part of the paper treats additional problems and concepts. Section 5 is devoted to ergodicity (in the sense of coinciding ensemble and temporal averages) and its breakdown in changing climates, leading to the conclusion that temporal averages over individual time series do not provide an appropriate characterization in generic cases. As a particular example of spatial features, in Sect. 6, we turn to the problem of teleconnections, i.e. correlations between different properties at certain remote geographical locations. Via several examples we illustrate that teleconnections should be handled in the spirit of parallel climate realizations, e.g. by means of appropriately chosen correlation coefficients evaluated with respect to the instantaneous natural measure. A traditional approach based on empirical orthogonal functions is extended for the ensemble framework. The resulting quantities may essentially change in a changing climate. Section 7 shows that the ensemble approach provides an appropriate characterization of any experiments carried out in turbulence-like problems in which the external parameters undergo a temporal change. In problems where one of two coexisting traditional attractors disappears as a function of a changing parameter, the (temporally evolving) snapshot attractor may split into two qualitatively different branches of climate states (see Sect. 8). In this case, tipping is endowed with a probability. Section 9 is devoted to the problem of the dispersion of pollutants under climate change. In Sects. 10 and 11 we discuss open problems and give a short conclusion, respectively. Appendix A offers a didactic illustration of the concept of snapshot/pullback attractors by showing that in the class of dissipative linear differential equations this attractor is nothing but one of the particular solutions of the problem.
2 Changing Climates: Mathematical Tools
Our climate is changing, and it belongs to a class of systems in which parameters (e.g. the atmospheric \(\hbox {CO}_2\) concentration) are drifting monotonically in time. Even in elementary unpredictable models, an appropriate treatment of such a property is not obvious, since traditional methods like periodic orbit theories of chaos (e.g. [1]) cannot be used, as no strictly periodic orbits exist in such systems.
From the 1990s, nevertheless, there has been a progress in the understanding of nonautonomous dynamics subjected to forcings of general time dependence: the concept of snapshot attractors emerged. The first article written by Romeiras et al. [8] drew attention to an interesting difference: a single long “noisy” trajectory traces out a fuzzy shape, while an ensemble of motions starting from many different initial conditions, using the same noise realization along each track, creates a structured fractal pattern at any instant, which changes in time.Footnote 1 With the help of this concept, phenomena that were not interpretable in the traditional view could be explained as snapshot attractors, e.g. a fractal advection pattern in an irregular surface flow which also appeared on the cover of Science [11]. It is worth noting that the concept of snapshot attractors has been used to understand a variety of time-dependent physical systems (see e.g. [12,13,14,15,16,17]) including high-dimensional ones [18, 19], and laboratory experiments [20].
The spread of the concept of snapshot attractor in the field of dynamical systems was augmented by a development in the mathematics literature [21,22,23,24,25], and became accelerated by the fact that, in the context of climate dynamics, Ghil and his colleagues rediscovered and somewhat generalized this concept more than 10 years ago. They used the term pullback attractor [9, 26], and immediately referred to its important role in climate dynamics. It has become clear later [27,28,29] that in the context of climate change, not noisy excitations, rather a continuous drift of parameters (such as increasing \(\hbox {CO}_2\) concentration) is relevant, and therefore deterministic (noise-free) snapshot/pullback attractors capture the essence of the phenomenology of an unpredictable system under these changing conditions.
Qualitatively speaking, a snapshot or pullback attractor can be considered as a unique object of the phase space of a dissipative dynamical system with arbitrary forcing to which an ensemble of trajectories converges within a basin of attraction. A distinction from traditional attractors by means of the adjective snapshot/pullback is useful, since the former ones obey the property that they can be obtained from a single long time series. The equivalence of this “single trajectory” method and the instantaneous observation of an ensemble of trajectories emanating from many initial conditions (ergodic principle) does not hold with arbitrary forcing. One has to choose between the two approaches (see Sect. 5). It is the ensemble approach that is appropriate for a faithful statistical representation of a changing climate. The reason is that the ensemble also represents a natural measure which can be associated to any instant of time. Even if the concept of snapshot and pullback attractors is practically the same, it is useful to remark here that a pullback attractor is defined as an object that exists along the entire time axis (provided the dynamics remains well-defined back to the remote past), while a snapshot attractor is a slice of this at a given, finite instant of time (their union over all time instants thus constitutes the entire pullback attractor). Note, however, that if the dynamics is not defined back to the remote past, then the pullback attractor is also undefined, but from some time after initialization the snapshot attractors can be practically identified. This has to do with the fact that when ensembles are initiated at finite times, they quickly converge to a sequence of snapshot attractors, as demonstrated in Sec. 4.3. It might be illuminating to mention that in linear dissipative systems with time dependent forcings, well-known from elementary calculus classes, the particular solution of the linear system plays the role of the pullback attractor (nonchaotic in this case, as illustrated in Appendix A), which all trajectories converge to.
3 The Theory of Parallel Climate Realizations
In order to make the unusual concept of pullback/snapshot attractors plausible, which might appear too much mathematically-oriented, while the concept of observed time series is widely used, we proposed the term parallel climate realizationsFootnote 2 in [30]. Qualitatively speaking, we imagine many copies of the Earth system moving on different hydrodynamic paths, obeying the same physical laws and being subjected to the same time-dependent set of boundary conditions (forcing), e.g., in terms of irradiation. Parallel climate realizations constitute, in principle, an ensemble of an infinite number of members. At any given time instant, the snapshot taken over the ensemble, the snapshot attractor, represents the plethora of all permitted states in that instant, just like in a stationary climate. However, the ensemble, representing the natural measure of the snapshot attractor, undergoes a change in time due to the time-dependence of the forcing, and, as a consequence, both the “mean state” (average values) and the internal variability of the climate changes with time.
It is remarkable that the idea of parallel climate realizations came up as early as 1978 in a paper by Leith [31]. He also argued about the importance of parallel climate histories and claimed that the instantaneous state of the climate should be described in terms of the ensemble formed by these members, based on an analogy with classical statistical mechanics. He appears to have intuitively understood the central importance of time-dependent probability distributions under changing “external influences”. We feel that Leith should be strongly credited for these early illuminating ideas. However, he did not yet have the necessary methodological tools at hand to explore the full potential of this view and neither did it become widely adopted in the climate community.
The mathematical background discussed in the previous section was the one that has finally turned out to provide a strict and firm foundation for the practical applicability of the vision of parallel climate realizations. A basic element of this formulation is the existence of an instantaneous natural measure on the snapshot attractor which is the real source of the statistics that define climate.
It is worth recalling two essential properties known from chaos theory that remain valid in the snapshot/pullback approach, too:
-
The simultaneous presence of a wide variety of states is an inherent, objective feature of unpredictable systems, which cannot be reduced by external influences (e.g., more accurate measurement, or using a better numerical method). Internal variability is an inherent property of climate, too. This is expressed by the term “irreducible uncertainty” in the climate community [32].
-
These states may accumulate with a higher or lower density in certain regions of the phase space, thereby defining the natural measure on the time-dependent snapshot attractor (for an example, see Fig. 1). One of the important assertions of chaos is that, while following individual trajectories, predictability is lost quickly, chaos can be predicted with arbitrary precision at the level of distributions [1, 2].
The view of parallel climate realizations offers the opportunity of precisely answering classical questions raised by climate research. The “official” consensual assessment of the current climatic situation and its change can be found in the publications of the Intergovernmental Panel on Climate Change (IPCC, [6]). These texts refer to climate at various levels as “average weather”, implying a probabilistic view. Yet, they do not specify the probability distribution according to which the statistical quantifiers should be evaluated. The statistical description may rely on observations of the past, supported by the statement that “the classical period of averaging is 30 years.”Footnote 3 However, if the climate state itself is changing markedly within such a time interval, these averages unavoidably yield statistical artefacts that may be misinterpreted as they mix up events of the recent and more remote past.
The theory of parallel climate realizations claims that averages should be taken with respect to the natural measure\(\mu (t)\)on the snapshot attractor at time t. The average of an observable A over the ensemble of parallel climate realizations is the integral of A with respect to this measure:
The ensemble average in (1) belongs to a given time instant t, and this way temporal averaging can fully be avoided. Averages of observables with respect to the natural measure of the snapshot attractor provide information on the typical behavior, and the time evolution of such averages gives the temporal changes of this behavior.Footnote 4 From the variance or higher order moments about the average the statistics of fluctuations follows, which are different characteristics of the internal variability. We can say that the ensemble of parallel climate realizations is the generalization of the Gibbs distributions known from statistical physics for a non-equilibrium system whose parameters are drifting in time. The micro-states, at a given time instant t, are the permitted states of the climate system (the permitted positions in the phase space), while the macro-state is described by the full natural measure, \(\mu (t)\), including averages etc. taken with respect to this measure.Footnote 5
A general definition of climate change was given in this spirit as early as in 2012 by Bódai and Tél [27] who wrote: “climate change can be seen as the evolution of snapshot attractors”.
We illustrate the advantage of the existence of instantaneous probability measures on the snapshot attractor by the concept of climate sensitivity [34,35,36], which plays a central role in climate science [6] (for a recent review see [37]). In the most elementary formulation, one is interested in a quantity A characterizing climate at a fixed parameter value p and in how much this quantity changes when observed at another parameter value \(p+\varDelta p\). If all other parameters are also fixed, this is called “equilibrium climate sensitivity” [6], and can be obtained by evaluating an average of A over a long time interval. Time-dependence can be introduced in various ways, e.g. involving the parameter p itself (as usually done for \(\hbox {CO}_2\) concentration). We briefly discuss here the case when p is not changing in time, but the change of other parameters are responsible for a non-autonomous dynamics. In this case, we are in a position of defining instantaneous climate sensitivities over the ensemble as follows.
We determine first the ensemble average \(\langle A(t) \rangle _p\) of quantity A at time t with a fixed parameter p, and then the ensemble average with the shifted parameter \(\langle A(t) \rangle _{p+\varDelta p}\) at the same time. Denoting the difference by \(\varDelta \langle A(t) \rangle \), the sensitivity can be defined as
Given the full natural measure, of course, sensitivities beyond that of the average can also be defined, e.g. that of the standard deviation \(\sigma _A(t) =(\langle A^2(t) \rangle -\langle A(t) \rangle ^2)^{1/2}\) of quantity A as
This provides a measure of the change of internal variability under \(\varDelta p\), but any other cumulant can also be taken. One might also think of more advanced definitions, we only mention here the one based on an appropriate distance between the natural measures taken with p and \(p+\varDelta p\) at the same time t. An example of this distance can be the so-called Wasserstein distance [34], the evaluation of which is, however, rather computation-demanding in realistic climate models. As the formulas above suggest, the theory of parallel climate realizations opens the way towards a linear response theory of the climate [31, 35, 38] to be discussed in some detail in Sect. 4.3. Note that a response theory currently exists for infinitesimal changes only; finite-size changes as in (2)–(3) would require theoretical generalization.
After these conceptual considerations, let us briefly discuss the issue of numerical simulations, the application of the theory of parallel climate realizations to projections of the future of the climate, perhaps using cutting-edge Earth system models. Let us imagine that a simulation starts from an initial distribution of a large number N of points in the phase space. The range over which they are distributed is unlikely to lie exactly on the snapshot attractor belonging to the time instant \(t_0\) of initialization. Based on a general feature of dissipative systems (phase space contraction) and chaoticity, initial conditions are, however, forgotten after some time [1, 2]. As a consequence, the ensemble of any initial shape and distribution converges towards the pullback attractor (as schematically illustrated by Fig. 9 of the Appendix, and by Fig. 3). The convergence is found to be typically exponentially fast [29, 39].Footnote 6
After a characteristic convergence time, \(t_{\mathrm {c}}\), the numerical ensemble thus faithfully represents the natural measure of the snapshot/pullback attractor. Statistics of the climate can properly be determined from such numerics, but only for times \(t > t_0+t_{\mathrm {c}}\). The value of the convergence time will be given in the forthcoming examples (and shall be found surprisingly short on the time scales of interest).Footnote 7 In simulations carried out with a sufficiently large number N of ensemble members, the formula (1) of the average is replaced by a much simpler one. Denoting the numerically obtained value of an observable A at time t in the ith member as \(A_i(t)\), the average is an arithmetic mean:
Higher-order moments and multivariate quantifiers (e.g. correlation coefficients) can be determined analogously.
Although such a numerics formally provides N different time series, chaos theory teaches us that their individual meaning is lost after the predictability time (which might be on the order of \(t_{\mathrm {c}}\)). Individual time series are thus on the long run unavoidably ill-defined, and non-representative. It is only their union, the ensemble tracing out the snapshot/pullback attractor and the corresponding natural measure \(\mu (t)\) upon it, that carries reliable content.
4 Illustration of Parallel Climate Realizations
4.1 Illustration in a Conceptual Model
Since an explicit illustration of the snapshot attractors’ properties can be acquired in low-order models only, we turn to such an example. Lorenz formulated an elementary model of the mid-latitude atmosphere in just three first order differential equations [41]. He assigned a meteorological meaning to each variable: x represents the instantaneous average wind speed of the westerlies over one of the hemispheres, and y and z are the amplitudes of two modes of heat transfer towards the polar region via cyclonic activity. The forcing of the system stems, of course, from the insolation, specified by a quantity called F. This is proportional to the temperature contrast between the equator and the pole (and can also be related to the average carbon dioxide content of the atmosphere). The model has been studied in many papers (see e.g. [42,43,44]). The time unit corresponds to 5 days, and therefore it was natural for Lorenz to introduce seasonal oscillations by making F sinusoidally time-dependent with a period of \(T = 73 \, \text {time units} = 365 \, \mathrm {days}\) about a central value of \(F_0\) [45].
In today’s climate change, global warming is primarily due to the warming of the poles [46, 47], which means that the temperature contrast decreases in time. This can be taken into account in the Lorenz84 model by making the central \(F_0\) time-dependent [27]: we can write \(F_0(t)\) instead of \(F_0\). The time axis is chosen such that climate change sets in at \(t = 0\), and afterwards, for the sake of simplicity, \(F_0\) decreases linearly for 150 years, as shown in the last panel of Fig. 1.
Parallel climate realizations of this model are produced by taking \(N = 10^6\) randomly distributed initial points in a large cuboid of the phase space \((x, \ y, \ z)\) at \(t_0 = -\,250\,\mathrm {years}\), and by following the numerical trajectories emanating from them. The convergence to the attractor is found to occur in 5 years with at least an accuracy of one thousandth, so the convergence time is \(t_{\mathrm {c}} = 5\,\mathrm {years}\). We follow the N trajectories until time t when the simulation is stopped. By plotting the points of the ensemble at time \(t > t_0 + t_{\mathrm {c}}\) on a fine grid we obtain the snapshot attractor at t along with its natural measure. This is illustrated in the first panels of Fig. 1, where, for the sake of clarity, only (x, y) values to which \(z=0\) belongs (with \({\dot{z}} > 0\)) are plotted. The natural measure obtained shows how often the states represented by each pixel are occurring in the ensemble of parallel climate realizations. Figure 1 illustrates that this distribution might be rather irregular above its support, the snapshot attractor. Comparing different time instants t reveals that both the attractor and its natural measure change, and undergo quite substantial changes on the time scale of decades.
The numerically determined natural measure of the ensemble of parallel climate realization in the Lorenz84 model above the \((x,y,z=0)\), \({\dot{z}}>0\) plane in the 25th, 50th, and 88th years after the onset of climate change (December 22 of each year) in panels a–c, respectively. Results are given in bins whose linear size is chosen to be 0.01 in both directions. The support of the natural measure is the snapshot attractor belonging to these time instants. The last panel shows a single time series of x in one member of the ensemble (thin magenta line) and the ensemble average \(\langle x(t)\rangle \) (thick black line). The forcing scenario, i.e., the time dependence of the annual mean temperature contrast \(F_0\) is pictorially represented in the lower part of panel d (Color figure online)
Note that the size of the snapshot attractor is bounded, very high x or y values cannot occur. In other words, there are regions of the (x, y) plane at any time instant that correspond to forbidden states.
The fact that the convergence time \(t_{\mathrm {c}}\) is 5 years implies that the distributions of Fig. 1 are objective (do not depend on the details of their generation, since \(t > t_0 + t_{\mathrm {c}}\)). Averages taken with respect to the snapshot natural measure are thus also objective. Panel d) of Fig. 1 exhibits the ensemble average \(\langle x(t)\rangle \) of variable x (the strength of the westerlies) as a thick black line. This can be interpreted as the typical wind speed of westerlies over the parallel climate realizations. One sees indeed that this is constant up to the onset of the climate change at \(t=0\), after which a slightly increasing trend occurs with strong irregular vacillations superimposed on it.Footnote 8
The magenta curve is a single time series of x from one of the ensemble members. The vacillations here are so strong that hardly any trend can be extracted, but, as discussed earlier, such time series are ill-defined due to the unpredictability of the dynamics.
4.2 Ensemble View in Other Conceptual Models
Natural measures of snapshot attractors (also called sample measures [26]) were generated and investigated in several papers. Knowing them enables one to determine different statistical measures, or the aforementioned climate sensitivity [35], as well as, extreme value statistics [28].
Early publications focused on noisy systems, where the ensemble was based on a fixed realization of the random process. Chekroun et al. [26] determined the sample measure of intricate distribution and time dependence in the noisy Lorenz attractor, and in a stochastic model of El Niño–Southern Oscillation (ENSO), Bódai et al. [48, 49] studied the measure on the snapshot attractors arising in the context of noise-induced chaos. The Lorenz84 model subjected to chaotic signals, white and colored noise was investigated by Bódai et al. [28].
Special attention was devoted to periodically forced low-order climate models without external noise. An investigation of the Lorenz84 model with seasonal forcing [45] was carried out by Bódai et al. [27] from the point of view of an ensemble approach and led to the conclusion that the snapshot attractor of the forced system appears to be chaotic in spite of the fact that in extended regions of the forcing parameter F of the time-independent system the attractors are periodic. It is the underlying transient chaos what the periodic forcing converts into permanent chaos. Daron and Stainforth [50] investigated the Lorenz84 model coupled to an ocean box model under seasonal forcing. They compared the distributions based on the instantaneous snapshot attractors and an ensemble of finite-time statistics (30-year averages), and analysed the ensemble-size-dependence of the finite-size estimates. Both taking temporal statistics and a finite ensemble size have been pointed out there to yield biases in general; and the authors suggested that “ensembles of several hundred members may be required to characterize a model’s climate”. Daron and Stainforth [51] provided further evidence of the biases and discrepancies between temporal and ensemble-wise statistics, and demonstrated the initial-condition-dependence of “transient” convergence properties of ensembles. Pierini [52] and Pierini et al. [53] considered a periodically forced reduced double-gyre model described by four variables and determined sample measures, while Chekroun et al. [54] studied the pullback attractor and its measure in a delay differential model of ENSO.
The effect of a kind of temporally quasi-periodic forcing was investigated by Daron and Stainforth [51] who considered the classical Lorenz model as a model climate in which one of the parameters was made time-dependent.
It should be noted that periodically forced systems constitute a rather special case of the pullback/snapshot approach since in this class the use of this approach can be avoided. When such cases are considered on a stroboscopic map taken with the period of the driving, the dynamics turns out to be autonomous. Attractors in such systems are traditionally called [1] attractors without the adjective pullback/snapshot. These attactors are in fact ergodic as the classical paper by Eckmann and Ruelle [7] claims.
It appears to be worth reserving the term pullback/snapshot attractor for nonperiodically time-dependent systems since these are not ergodic as we shall see in Sect. 5. In this sense, perhaps the first sample measures determined for a deterministic pullback/snapshot attractors is the one found in [28] for the Lorenz84 model forced with the x component of the dynamics on the celebrated Lorenz attractor. Cases forced with other irregularly recurrent signals are treated in [40, 55] and in the last section of [53]. An interesting discovery of the previous paper is the identification of two disjoint basin boundaries, designating the coexistence of two pullback attractors (a chaotic and a nonchaotic one). The effect of a forcing related to a monotonic deterministic parameter drift was first investigated by Drótos et al. [29] in the context of the Lorenz84 model, results of which are sampled in Fig. 1, as discussed in the previous subsection.
4.3 Illustration in a General Circulation Model
The question naturally arises of how the aforementioned properties of snapshot/pullback attractors manifest themselves in more realistic climate models. The Planet Simulator (PlaSim) is an intermediate-complexity climate model developed at the University of Hamburg. It is a well-documented [56, 57] open source software, freely accessible.Footnote 9 Due to discretization, the degrees of freedom are on the order of \(10^5\). The temporal development of the output fields, such as temperature, wind in different air layers, or surface pressure and precipitation can be displayed on sequences of geographic maps. Therefore, a single climate realization results in such “movies” of different fields, and parallel climate realizations in several movies. Figure 2 illustrates that the maps corresponding to the same time instant, but taken from two different realizations differ considerably. One can see that, in contrast to the previous conceptual model, it is now possible to investigate also regional or local quantities and spatial correlations between them in the spirit of spatio-temporal chaos research [58].
The number of parallel climate realizations one can choose is, of course, limited by the running time, and in our example an ensemble of \(N=40\) members is used obtained by minor random perturbations of the initial surface pressure field. In this large model, we can only examine the projection of the natural distribution on some of the selected quantities.
The concentration of carbon dioxide can be prescribed, and the lower part of Figure 3 shows the scenario used for this example. Climate change begins in the 600th year, the concentration doubles in a period of 100 years, and after a plateau the concentration ultimately restores to its initial value in year 1150.
In [59] the local surface temperature T at the geographic location of the Carpathian Basin is determined in all 40 ensemble members until the end of year 1500. These are represented by the thin light gray lines in Fig. 3 to be compared with the ensemble average \(\langle T(t)\rangle \) given in the thick black line. The difference is strong again, individual time series are not representative.
The time evolution of the annual average surface temperature in the Carpathian Basin following the \(\hbox {CO}_2\) scenario (lower panel) is shown by thin gray lines in each member of the Planet Simulator ensemble, and their ensemble average \(\langle T(t)\rangle \) is marked by a thick black line. The initial condition of year \(t = 0\) resulting in a temperature of about \(5\,^{\circ }{\mathrm {C}}\) is forgotten by \(t_{\mathrm {c}} = 150\) years: after this a constant value (approximately 2 \({^{\circ }\mathrm {C}}\)) characterizes the stationary climate up to the onset of climate change in year 600. The ensemble averages in additional simulations launched in years 570 and 1020 (thick red and yellow lines) are also shown. The snapshot attractor is indicated by a dashed black line for t < 150 years. Before this time, the ensemble of simulations does not coincide yet with the snapshot attractor (Color figure online)
It is satisfying to see that within the first 600 years we find a constant average temperature since the climate is stationary. This is seen in the ensemble average only after approximately \(t_{\mathrm {c}}=150\,\mathrm {years}\). The decay leading to this constant is due to the fact that the initial condition was an artificial choice, which fell outside the attractor. Although our simulation started at \(t=0\), the existence of a constant climate can be assumed back in the remote past. In order to emphasize that a pullback attractor exists already at \(t=0\), we extended the black plateau with a dashed black line down to year 0. This helps visualize that the numerical simulation is attracted by an objective entity, the pullback attractor. In our figure this corresponds to the union of the dashed line and the continuous black line for \(t > t_{\mathrm {c}}\). For \(t > t_{\mathrm {c}}\) (\(=150\,\mathrm {years}\)) the average over the numerical ensemble faithfully represents the typical behavior of the surface temperature on the pullback attractor. Its shape is reminiscent of the graph of the \(\hbox {CO}_2\) concentration, occasionally with some delay. As a consequence, slices of the pullback attractor, i.e., the snapshot attractors are time-dependent in intervals when there is a strong \(\hbox {CO}_2\) change. We note again that what we see is the projection of the attractors of the high-dimensional phase space on a single variable, on the temperature of the Carpathian Basin.
As an additional proof of the objective existence of the pullback attractor, we launch additional ensembles of \(N=40\) members at \(t_0'=570\,\mathrm {years}\) and \(t_0''=1020\,\mathrm {years}\) (with the same type of initial condition as at \(t = 0\)). The ensemble averages are represented by the thick red and yellow lines, and it is apparent that they reach the average of the first ensemble simulation (the thick black line) relatively quickly. In addition, the time needed for this is approximately 150 years in both cases, that is, the convergence time \(t_{\mathrm {c}}\) is found to be practically independent of the time of initialization (\(t_0\), \(t_0'\) or \(t_0''\)). We see that whatever time \(t_\mathrm {in}\) an ensemble is initiated, for times \(t > t_\mathrm {in} + t_{\mathrm {c}}\) the ensemble correctly represents the pullback/snapshot attractor, and thus displays the internal variability of the climate.
Concerning a climate projection for year t, Fig. 3 suggests that from the ensemble of realizations a probability distribution of a given quantity, in our example the surface temperature T, can be generated. The probability P(T, t) possesses its mean as the ensemble average \(\langle T(t)\rangle \), has some width, but as our previous discussion on the non-permitted states implies, the support of P is bounded. This means that we can be sure that certain temperatures are impossible (within the particular model). For e.g. \(t=650\,\mathrm {years}\) the permitted temperatures are in the interval (2, 6) \({^{\circ }\mathrm {C}}\) (with \(\langle T\rangle =3.8\)\({^{\circ }\mathrm {C}}\)), we can thus predict that the chance to have a temperature \(T>6\) or \(T<2\)\({^{\circ }\mathrm {C}}\) is practically zero in this year.
The convergence to a “climatological distribution” (i.e. the natural measure on the snapshot attractor in our language) was foreseen by Branstator and Teng in 2010 [60], although neither a clear numerical demonstration, similar to that in Fig. 3, was given, nor a proper justification, referring to the theory of nonautonomous dynamical systems [9], was provided. Beyond reviving Leith’s basic idea about the existence of a time-dependent “climatological distribution” [31], the authors claimed that (i) it is traced out by a remotely-initialized ensemble, that (ii) a probability distribution emanating from nearby initial conditions differs from the “climatological distribution” during its early evolution, but (iii) this difference vanishes after a finite amount of time due to memory loss.Footnote 10
Beyond case-by-case direct numerical simulation for each different forcing scenario of interest, we mention here the application of Ruelle’s response theory [65], whereby one wishes to determine Green’s functions, i.e. the response functions of the system [31, 38], and then predict the response of the natural measure to any forcing scenario. An illustration of this idea in the aforementioned intermediate-complexity model PlaSim, was given by Ragone et al. [35], and an application of the technique to an Earth system model is presented in [66].
4.4 The Boom of “Large Ensembles” in State-of-the-Art Earth System Models
In the recent couple of years a naive interest in so-called “single-model initial-condition large ensembles” for Earth system models (ESMs) has abruptly risen. “Large” means a number of members on the order of 10 or 100 at most, and the attribute “initial-condition” indicates that the members differ in their initial conditions. At this time large ensemble data sets exist for about a dozen of coupled general circulation models or ESMs, and analyses of a few of such data sets have been already reported on.
Most of these ensembles are generated by branching a single run, introducing small or moderate perturbations to some or all model components, to obtain initial conditions for the different ensemble members. With this scheme, called nowadays the “micro” initialisation method [67], it takes some time that the ensemble converges to the natural measure (or, in the language of climate research, full ensemble spread is reached), and the output data have to be excluded from any climatological analysis before convergence becomes complete from some practical point of view. The treatment of various time scales present in the Earth system, including rather long ones, poses a theoretical problem with practical implications, see Sect. 10.2. We believe that a simple and useful approach is to concentrate on variables in the atmosphere and the upper ocean only (above the thermocline), including sea ice complemented with land, and investigate convergence properties in these variables, which have moderate time scales (up to a few decades at most). It may be important to include upper oceanic variables to the assessment of convergence, since the faster time scales of the atmosphere, the sea surface or the land may result in an apparent faster convergence which, however, does not involve layers of the upper ocean.Footnote 11 Earlier convergence might be facilitated by perturbing some oceanic variables besides or instead of atmospheric ones [33, 60], but we emphasize that any initialization scheme suffices in principle (unlike what is suggested by [33]).
Most large ensemble projects that are available to date are reviewed in [69]. With a great vision and effort, a set of these has been made available for public use by the “US CLIVAR Working Group on Large Ensembles” in a centralized data archive,Footnote 12 the content and utility of which is discussed by Deser et al. [67]. In all ensembles that we are aware of, the data belonging to the earliest time does not conform to the natural measure of the attractor but only at later times. The time interval to discard at the beginning of the simulations would ideally need case-by-case specific investigations, but it can generally be estimated to be a few decades. In a few works, concentrating on the atmosphere, the rapidity of atmospheric memory loss is emphasized [70, 71], even though this approach may be insufficient due to the dynamics of the upper ocean as discussed above. Works that pay attention to convergence in the upper ocean or the sea ice (either via memory loss, i.e., independence of initial conditions, or via concentrating on the increase in the ensemble spread) conclude about time scales of around a decade, which they discard before the beginning of their analyses [68, 72,73,74,75]. Unfortunately, several of the more recent works do not pay attention to the need of convergence (e.g. [76,77,78]), which may corrupt analyses that include the time interval of the convergence process.
After convergence takes place, any ensemble represents the natural measure of the model faithfully and can thus be regarded as a set of parallel climate realizations. The only complication may arise from the previously mentioned extremely long time scales in the deep ocean, for which see Sect. 10.2, and which may affect sea level [79] among the more commonly analyzed observables. Deep oceanic variability is sampled only in a single set of ensemble simulations, the Max Planck Institute Grand Ensemble (MPI-GE, [69]), all other ensembles are practically initialized in a single deep oceanic state.
The so-called “macro” initialization scheme in the MPI-GE is qualitatively different from that of the other ensembles. In this case, no perturbation is applied. Instead, an almost 4000-year-long control run, subject to a fixed forcing representing “preindustrial conditions” of 1850, is sampled in its last 2000 years, with the intention of fully sampling variability already at the beginning of the ensemble simulations [69]. The sampling is, however, too frequent for the statistical independence of the ensemble members: the initialization of certain members is separated by no more than 6 years, which is definitely less than the memory of even the upper ocean. Furthermore, constant 1850-conditions correspond to a different attractor than the one that evolves according to the preceding historical forcing including considerable volcanic activity [80]. For these reasons, discarding the first decades is desirable in the MPI-GE as well.
Additional issues about initialization may arise from the insufficient spinup time: drifts corresponding to the convergence process from some state off the attractor in deep oceanic variables may appear and are actually documented in the MPI-GE [69], while their importance is mostly unknown in the other ensembles. Numerical drift, like in CESM-LE [76], may also represent a technical problem.
Even with all the drawbacks and deficiencies, “single-model initial-condition large ensembles” of ESMs are expected to be essential for the determination of the forced response of certain observables, especially those to do with localized climate phenomena, when the relatively strong internal variability masks the possibly weak forced response signal [81,82,83,84,85,86,87,88].
One may also try to utilize the framework of single-model initial condition ensembles, beyond directly describing the complete internal variability of fully coupled global ESM simulations, for characterizing some kind of natural variability specifically associated to some given subsystem of Earth. However, if different subsystems are coupled, quantifying internal variability restricted to only one subsystem is not necessarily a well-defined problem. An example is provided by ensemble studies of the ocean subsystem published recently (see [89] and references therein) in the framework of the OCCIPUT project (OceaniC Chaos - ImPacts, strUcture, predicTability [90, 91]). Their 50-member ocean ensemble is forced by a single realization of the atmospheric dynamics (corresponding to historical instrumental records) and is claimed to represent the “intrinsically oceanic” contribution to the full variability (which includes that of the atmosphere). However, the atmospheric variability is influenced by the ocean in any realistic ESM configuration through a two-way coupling of the modules, and the full variability is described by an ensemble in which both atmospheric and oceanic variables have a nonzero ensemble spread. If one takes the time evolution of the atmospheric variables in different members of such a hypothetical full ensemble, and then constructs an ocean ensemble with each of these atmospheric realizations applied as a fixed forcing, the result will be an extended set of OCCIPUT-type ocean ensembles. Due to the very nature of two-way coupled nonlinear systems, the superposition of these ocean ensembles with prescribed atmospheric forcing are unlikely to be statistically identical to the full ensemble of the two-way coupled configuration. Oceanic processes in the latter will then not be described correctly by the oceanic processes in the individual OCCIPUT-type ocean ensembles in a statistical sense. Note that the inconsistency of the OCCIPUT-type approach (to quantify something called “intrinsic oceanic variability”) with the actual oceanic processes will appear within a single configuration (which can be any arbitrary realistic configuration that involves atmospheric variability). Although OCCIPUT-type ensembles are thus inconsistent with realistic assumptions about the ocean-atmosphere coupling and also with the spirit of parallel climate realizations, they might shed qualitative light to physical mechanisms relevant for inter-decadal oceanic variability, a concept discussed in [92]. For a quantitative description of internal variability if subsystems have substantially different time scales, when two-way coupling can be approximated by one-way coupling, see basic ideas in Sect. 10.2.
In a different approach, the manifestation of the full internal variability of the Earth system on spatial scales unresolved by global ESM simulations may be studied by downscaling such ensemble simulations by regional climate models, see [93] and references therein.
5 Nonergodicity and Its Quantification
The original observation of Romeiras et al. [8], according to which a single long trajectory traces out a pattern different from that of an ensemble stopped at a given instant, implies that ergodicity (in the sense of the coincidence of ensemble and temporal averages) is not met in nonautonomous systems. Traditional chaotic attractors are known to be ergodic [7]: sufficiently long temporal averages coincide with averages taken with respect to sufficiently large ensembles.
Daron and Stainforth [50, 51] have demonstrated discrepancies between temporal and ensemble-based averages, saying that what they call the “kairodic assumption” is not satisfied in nonautonomous systems.
A systematic investigation of such questions was carried out by Drótos et al. [94]. In order to characterize the difference between the two kinds of averages, the term nonergodic mismatch was coined. Consider an observable A. Its time average over a time window of length \(\tau \) (centered at time t) in a single realization is denoted as \(\overline{A_\tau (t)}\). This is compared with the average \(\langle A(t)\rangle \) of the same quantity taken over an asymptotically large ensemble at t. The nonergodic mismatch \(\delta _\tau (t)\) is defined as
and is a quantity that depends not only on the time instant t but also on the window length \(\tau \) over which the temporal average is taken. Ergodicity would be marked by the vanishing of this mismatch for \(\tau \rightarrow \infty \).
The nonergodic mismatch can be evaluated along each single realization of the climate ensemble and depends on the realization. For finite window length \(\tau \), different values of \(\delta _\tau (t)\) are expected, even in ergodic cases, since the window length \(\tau \) is not necessarily sufficient to visit the full phase space. We thus expect a distribution of \(\delta _\tau (t)\) in the ensemble of parallel climate realizations for any t and \(\tau \). From the numerical results a probability density function \(P(\delta _\tau (t))\) can be obtained, called the nonergodic mismatch probability density function (pdf). Here we summarize the results obtained in [94] qualitatively.
In an ergodic case, a stationary climate (panel a of Fig. 4), the distribution remains centered about zero, that is at least the ensemble average of this mismatch is zero. The width of the distribution, the spread, depends on the window length \(\tau \) and decreases with increasing \(\tau \). The decrease is, however, rather slow, decays according to the law of large numbers as \(1/\sqrt{\tau }\). To have a feeling, we mention that in the stationary case of the Lorenz84 model a one-hundredth agreement between the time average and the ensemble average of variable y requires a window length of about \(\tau =10{,}000\,\mathrm {years}\), while a 0.1 degree agreement in the surface temperature data of Fig. 3 of PlaSim can be expected with about \(\tau =200\,\mathrm {years}\).
In the case of a monotonic climate change (panel b of Fig. 4) the pdfs are not centered about zero, moreover, their maximum moves away from zero with increasing \(\tau \). The spread decreases with \(\tau \), and scales as \(1/\sqrt{\tau }\) again.Footnote 13 The fact that the ensemble average of \(\delta _\tau (t)\) increases means that the deviation from ergodicity is the stronger on average the larger the window length \(\tau \) is. It is therefore needless to hope for the validity of ergodicity in a changing climate. This provides an additional argument for avoiding the use of individual time series in climate simulations. Certainly, the quantity \(\langle |\delta _\tau (t)|\rangle \), called the ergodic deficit in [94], can be considered as a measure for the breakdown of ergodicity.
6 Teleconnections: Analyzing Spatial Correlations
Teleconnections are statistical correlations between the states of remote locations of the globe. These amazing links connect regions lying thousands of kilometers from each other and are manifestations of the structured nature of internal variability. One of the most important teleconnections is the relationship of the amount of the precipitation or the average temperature of the Indian summer monsoon with the temperature of the Central Pacific. If the Central Pacific gets warmer, then Southern India becomes wetter and colder.
All traditional methods quantifying teleconnections (evaluating correlations in some way) agree in that they are based on long-term temporal statistics. This naturally implies that these methods, in principle, cannot be used in a changing climate, since they bring certain subjectivity into the investigation (see Sect. 2). Furthermore, investigating the teleconnections through the temporal correlations between a so-called teleconnection index and another variable (e.g., temperature or precipitation) a single correlation coefficient can be obtained. This correlation coefficient characterizes the strength of the relationship for a given time interval, assuming that the climate is stationary for this given period. However, as climate is changing, there is no guarantee that the strength of the teleconnections remain the same.
The application of the parallel climate realizations provides a simple solution for the aforementioned problem, eliminating also any subjectivity. With a sufficiently large number (N) of realizations an ensemble-based instantaneous correlation coefficient can be defined which provides the appropriate characterization of the strength of teleconnections in the spirit of parallel climate realizations.
At a given time instant t, utilizing the whole ensemble, N values of two variables A and B (between which the relationship is studied) are available, and the ensemble-based correlation coefficient is obtained as
where \(\sigma _A(t)\) and \(\sigma _B(t)\) are the ensemble standard deviations of quantity A and B, as defined in relation with Eq. (3). The obtained correlation coefficient characterizes the chosen time instant t indeed. Therefore, during a changing climate the time-dependence of the strength of correlations, i.e., \(r_{A,B}(t)\), can be studied. In the context of teleconnections, one of the variables A and B is chosen typically as a teleconnection index, while the other is some common meteorological variable.
As a first example, we consider the North Atlantic Oscillation (NAO) [95,96,97], which is an oscillation observable in the difference of sea level pressure between the permanent low pressure system over Iceland and the permanent high pressure system over the Azores. Teleconnection indices typically characterize the phase of an oscillation in a meteorological quantity taken at remote locations. In particular, the NAO teleconnection index (NAOI) is based on the difference in the normalized sea level pressure between Iceland and the Azores. Since the pressure difference controls the direction and strength of the westerlies entering into the European region, a high (positive) NAOI, meaning large difference in the sea level pressure between Iceland and the Azores, implies stronger westerlies. These result in higher winter temperature in the Scandinavian region and in the eastern United States, and a lower temperature in the Mediterranean and Greenland [98,99,100]. Analogously, low (negative) NAOI goes together with above-than-average precipitation during winter in Scandinavia, and below-than-average precipitation over the Mediterranean.
At a given time instant, it is also possible to compute an instantaneous teleconnection index in the spirit of parallel climate realizations. For the NAO index, NAOI, the definition in the ensemble framework for the ith member reads as
where \(p_{\mathrm {A},i}(t)\) and \(p_{\mathrm {I},i}(t)\) are the sea level pressures in the ith ensemble member at the Azores and Iceland, respectively.
Figure 5 illustrates the time evolution of the correlation coefficient between the NAOI and the Mediterranean winter temperature and precipitation in PlaSim under the \(\hbox {CO}_2\) concentration change scenario given in Fig. 3, computed for a 40-member ensemble of climate realizations. Similarly to what is experienced nowadays, during the plateau of 360 ppm a negative correlation coefficient between the NAOI and both quantities can be found: larger NAOI (due to larger pressure difference between the Azores and Iceland) results in lower temperature and less precipitation in the Mediterranean region. However, as the \(\hbox {CO}_2\) concentration increases, the correlation of the NAOI and the temperature decreases and practically disappears on the plateau of 720 ppm \(\hbox {CO}_2\). We also emphasize that generally different quantities are affected in different ways: the right panel of Fig. 5 demonstrates that, e.g., the strength of the teleconnection with the Mediterranean precipitation does not change at all despite the change in the forcing [30]. We note that the large fluctuations in the curves are due to the relatively low number of climate realizations. The utilization of a larger ensemble would result in smoother curves, as the amplitude of these fluctuations, representing the sampling error of the correlation coefficient for a finite number of ensemble members, monotonically decreases with increasing ensemble size. These examples draw attention to the fact that remarkable changes in the typical strength of the teleconnections can be observed.
The time evolution of the ensemble-based correlation coefficient of the NAOI with the Mediterranean winter (December to February) surface mean temperature T (left) and precipitation P (right) in the PlaSim model. The \(\hbox {CO}_2\) scenario can be seen in Fig. 3
We turn now to a brief discussion of one of the most known teleconnections, the El Niño–Southern Oscillation phenomenon (ENSO). ENSO is manifested in the irregular variation of wind and sea surface temperatures over the tropical Pacific Ocean [92, 101,102,103,104]. ENSO has an impact locally and globally as well. It controls at least the half of the global climate system, therefore it is urgent to study its teleconnections.
One prominent ENSO teleconnection is the relationship with the Indian summer monsoon. In the framework of parallel climate realizations, ENSO indices similar to Eq. (7) can be defined. An increasing strength of the teleconnection between a particular ENSO index and the Indian summer precipitation has been detected in the MPI Grand Ensemble in the 20th century. No strong change was found, however, under future scenarios forced even more strongly either in the MPI Grand Ensemble or in the CESM Large Ensemble [87]. Very recently [88] a similar conclusion has been drawn regarding the observed strengthening of the Pacific Walker circulation, namely, that the forced response signal seen in the CESM-LE is very weak, and the apparent strengthening should be mostly due to internal variability.
Another phenomenon is the Arctic Oscillation (AO) which appears as a ring-like pattern of sea-level pressure anomalies over the Northern Hemisphere centered at the polar region [105, 106]. Since we experience the largest temperature changes in the Arctic region, where the surface temperature increase is twice that of the tropics [46, 47], it is also worth investigating correlations in the context of AO-related phenomena.
The AO phenomenon has the specific feature that its index (AOI) is defined solely by means of EOF (empirical orthogonal function) analysis (also known as principal component analysis in the physics literature) [107]. Traditionally it is also based on time series utilizing long-term statistics. In this context, it is worth emphasizing here that the theory of parallel climate realizations provides an opportunity for an ensemble-type extension of EOF analysis, too. In this spirit a novel, so-called snapshot EOF (SEOF) analysis method has been developed in [108]). It computes the characteristic pattern for the AO, represented by the leading mode of the EOF analysis over the ensemble for any given time instant. Hence it is capable of monitoring both the time dependence of the pattern and that of the AO amplitude. We note that a similar method (called EOF-E) has also been developed recently in Ref. [109], however, it differs from [108] as it washes together the variability of the monthly data and that of the ensemble.
The AOI teleconnection index is computed in this framework as the standardized principal component of the first EOF mode of the SEOF analysis. Particular features of the AO and its related phenomenon have been studied by means of two state-of-the-art climate models (CESM-LE and MPI-GE) in [108]. The results reveal that the AO pattern and the AO-related phenomena, usually treated to be stationary, are actually time-dependent. Furthermore, the AO’s amplitude, i.e., the fluctuation in the sea level pressure field, appears to be enhanced significantly. The AO-related phenomena also show a remarkable shift, especially in wintertime at the Eastern coast of the USA and Northern Europe between 1950 and 2100 in the investigated scenarios.
Finally, we mention that the SEOF method can also be used as a refined characterization of ENSO. Preliminary results [110] suggest that the influence of the ENSO on the Indian Monsoon increases in the 21st century: the anticorrelation becomes stronger, resulting in wetter summers in India in El Niño years. The Arctic and the tropics exhibit considerable connections with each other, therefore, studying ENSO and AO as a coupled system could be an interesting direction of future research.
7 Ensembles in Experiments
“Minimal modeling” of various components of the terrestrial climate system using laboratory-based experiments has a long history stretching back to the mid-20th century [111, 112]. Ever since, measurements investigating rotating, density-driven shallow-layer flows have provided remarkably useful insights to the basic underlying phenomena of atmospheric and ocean circulation, such as cyclogenesis via baroclinic instability [113], time-reversal asymmetry of temperature fluctuations in weather station records [114], excitation of internal gravity waves [115] just to name a few examples. Furthermore, laboratory models of the mid-latitude atmospheric circulation have been applied to test and validate numerical hydrodynamic solvers [116] and meteorological (ensemble) forecast techniques [117].
Such experimental investigations nicely complement research based on numerical general circulation models: the latter can, theoretically, access the full set of parameters but with a limited resolution which hides important subgrid-scale nonlinear phenomena that may affect multiple scales. Experiments, however, provide practically infinite spatio-temporal resolution (making the setting an ‘analogue computer’ in a sense) but are very limited in the number of parameters to be controlled.
It is indeed impossible to scale down the plethora of relevant effects of the actual climate system simultaneously to a typically tabletop-size laboratory tank. Yet, a careful order-of-magnitude analysis of the equations of motion enables experimenters to select the most relevant non-dimensional parameters the setting of which yields an approximate hydrodynamical similarity to the large-scale flows in question. For ‘sideways convective’ rotating flows – such as thermally driven ocean currents or atmospheric circulation cells powered by the Equator-to-pole gradient of solar heat flux – the most important similarity parameter is the thermal Rossby number \(\mathrm {Ro}_T\) which reads as
where g is the gravitational acceleration, \(\alpha \) represents the volumetric thermal expansion coefficient of the medium, \(\varOmega \) is the rotation rate (of the planet or experimental tank), \(\varDelta T\) denotes the lateral temperature contrast, and H and L are the vertical and horizontal scales, respectively.
\(\mathrm {Ro}_T\) is a measure of (geostrophic) turbulence in the system. When \(\mathrm {Ro}_T \ll 1\) holds, the flow is considered quasi-geostrophic, i.e. dominated by the Coriolis force; the planet-scale currents in the atmosphere and the ocean are in this regime, with \(\mathrm {Ro}_T\) values of ca. 0.1 and 0.01, respectively [118]. Typically, the smaller \(\mathrm {Ro}_T\) is, the more (geostrophically) turbulent and more irregular the flow patterns become. Thus, by setting different values of rotation rate \(\varOmega \) and lateral temperature contrast \(\varDelta T\) in a given laboratory tank, qualitatively different flow structures can be encountered.
This observation opens up the opportunity of modeling climate change scenarios experimentally via applying time-dependent thermal boundary conditions \(\varDelta T(t)\) as forcing that are expected to have a similar effect to the \(\hbox {CO}_2\) forcing used in the numerical models. As explained earlier, in the real Earth system the Equator-to-pole temperature difference tends to decrease in parallel to the rise of global mean temperature [46, 47].
An obvious advantage of experimental setups compared to observations of the real Earth system is the opportunity to reproduce experiments. Reproducing them with the same boundary conditions (forcing) most naturally provides an ensemble of different realizations of the same process, which represents the multitude of possibilities permitted by turbulence or chaotic-like phenomena, i.e., parallel realizations of the minimal climate system model.
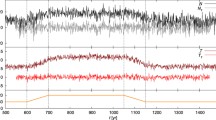
Results from a small ensemble, consisting of nine individual experimental members, of a climate-change-inspired setup described above were reported in [20]. Temperature time series were obtained from a rotating differentially heated annular wave tank mounted on a turntable and rotating about its axis of symmetry (Fig. 6a), yielding \(\mathrm {Ro}_T \sim 0.01\). From each ensemble member 10000s (3300 revolutions of the tank) of temperature data were evaluated, with the onset of ‘climate change’ (hereafter marked as time zero, \(t = 0\)) occurring exactly at half time. In this scenario the lateral temperature contrast \(\varDelta T\) was set to be constant at \(t<0\) followed by an exponential decay \(\varDelta T \sim e^{-t/\tau }\) for \(t>0\) (Fig. 6b).
The experimental set-up used in [20] for the ensemble modeling of mid-latitude atmospheric circulation (a). The dimensions are \(L= 12\) cm, \(H = 4.5\) cm, denoting the horizontal scale and fluid depth, respectively. Time-dependent temperature contrast \(\varDelta T\) was changing as shown in the bottom graph of panel b. (The practically indistinguishable green curves represent the forcing time series from all members and the black curve shows their mean.) The top panel of b shows the ensemble of temperature response in terms of spatially averaged temperature \(\langle T \rangle (t)\) as obtained from three temperature sensors whose locations are marked in panel a. Solid and dotted black curves represent the ensemble mean and the upper- and lower bounds of the instantaneous ensemble standard deviation interval, respectively. Coloring is also added to distinguish between the “stationary” (turquoise) and “changing” (yellow) sections, and one exemplary ensemble member (red), shifted by \(+2.5 ^\circ C\) for visibility. Panel c shows the histograms of ensemble standard deviations about the ensemble mean (determined for a large number of time instants) for the “stationary” (\(t<0\)) and “changing” (\(t > 0\)) sections. The color coding is as in panel b) (Color figure online)
Addressing spatio-temporal variability in the water surface temperature field, ‘traditional’ single-realization measures and their ensemble-based counterparts were compared, e.g. standard deviations, spatial and temporal spectra and characteristic timescales. As an example of a rather typical finding, we briefly discuss the case of standard deviations. When computing running standard deviations within \(501\mathrm {s}\) long windows of records of spatially averaged temperature from the ‘stationary’ (\(t<0\)) and ‘changing’ (\(t>0\)) sections of any given ensemble member (following appropriate detrending) the authors did not find significant differences in the distributions of the obtained running standard deviation values, thus no clear evidence was found that the nature of thermal fluctuations in a changing model climate would differ from that in the stationary part of the same run. However, when the ensemble standard deviations were considered about the ensemble mean (calculated at each time instant t) it was found that the histograms of these values differed markedly in the \(t<0\) and \(t>0\) intervals both in terms of their mean and their skewness (Fig. 6c). This observation can be interpreted as a manifest difference between probability density functions of the (snapshot) attractors corresponding to the ‘stationary’ and ‘changing’ sections of the dynamics.
Besides climate-related aspects it is worth noting that the ensemble approach may be the proper way to conduct fluid dynamics experiments in which non-equilibrium (non-ergodic) processes and turbulence are involved, i.e. phenomena characterized by inherent internal variability. The saying ‘one experiment is no experiment’ is of course probably just as old as physics itself, but what experimenters usually mean by it is the separation of measurement errors (noise) from significant data. However, in non-stationary fluid dynamics problems fluctuations are inherent, even dominant features of the investigated nonlinear processes and the aim of repeated experiments can be the exploration of internal variability. A well-known example – and a research area where ensemble statistics are already widely accepted and used – is the case of laminar-to-turbulent transition in pipe flows [119,120,121]. Perturbing a laminar background flow with a small standardized injection of matter yields the formation of transient turbulent structures (so-called puffs and slugs) with a finite lifespan. This lifespan can vary largely in different experimental runs due to the nonlinear nature of the processes involved. Thus, only an ensemble statistics of these lifespans from a multitude of experiments (that are initiated identically within measurement precision) can provide meaningful information of these interesting intermittent phenomena, as demonstrated in e.g. [121]. In this example, the external parameters are fixed; a particularly wide range of applications of ensemble experiments is expected in the future in cases characterized by drifting parameters.
8 Splitting of the Snapshot Attractor
It is a general feature of multistable dynamical systems [122], where multiple stable asymptotic states coexist in some range of the parameters (or forcing) that a parameter drift may result in drastic changes in the system’s behaviour. It was demonstrated in various studies that a sharp transition between the possible asymptotic states may take place. This behavior is referred to as a tipping transition, or critical transition. In terms of climate dynamics, the stopping of the thermohaline ocean circulation [123] or the occurrence of “snowball Earth events” [124,125,126] are important examples.
Multistability of the Earth’s climate was first found using conceptual, energy balance models (e.g. the one-dimensional diffusive, Ghil–Sellers [127] model), and later in intermediate complexity models, like PlaSim [128]. Multistability comes from the fact that a type of instability appears in these models [129,130,131], which is referred to as a saddle state, or Melancholia state. This unstable equilibrium is embedded in the boundary between the basins of attraction of the two stable climates. Unlike the attracting climate regimes, the Melancholia state is characterized in [130] by a planet that is ice-covered up to the midlatitudes. It was also demonstrated that the Melancholia state plays an important role in noise-induced transitions between the stable climate regimes [132].
In low-dimensional systems that lack any kind of internal variability, Ashwin and coworkers [133, 134] used the framework of pullback attractors to investigate tipping phenomena. They were able to formulate conditions under which tipping may happen. However, not much is known about such transitions in systems with rich internal variability (e.g. the climate system). Since in these systems a single simulated trajectory does not necessarily carry any predictive meaning, we argue that in general, the theory of parallel climate realizations should be applied to these problems, too [135].
An important property of the climate system is that for some range of fixed parameter values, it also allows two coexisting usual (stationary) attractors. The main difference from regular multistability is that both of these attractors are chaotic-like, given the complexity of the system. Let us now consider a scenario during which a parameter S drifts through a region where one of the coexisting chaotic attractors loses stability. After passing the bifurcation point, the parameter S returns abruptly to the initial value. Even when initializing the ensemble entirely inside one of the basins of attraction (that belongs to the initial parameter value), only a fraction of the ensemble may end up on the usual attractor on which the ensemble was started. During the returning part of the parameter drift, at the point when this usual attractor reappears, the snapshot attractor (as an extended object) may overlap with the basin of attraction of both of the coexisting usual attractors. The ensemble’s subset that overlaps with the (time evolving) basin is then captured by the given attractor. Through this mechanism it is possible for snapshot attractors to split into two unconnected parts. Strictly speaking, the snapshot (and the pullback) attractor remains a single object, but for some practical purposes, it is reasonable to treat the two parts as separate entities. In particular, for initializations taking place after the splitting event, they are two snapshot attractors, with their own basin of attraction, since it is no longer possible for trajectories to cross from one part to the other.
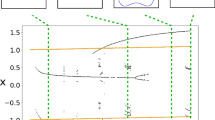
Left panel: Schematic diagram in a bistable system showing two coexisting chaotic-like attractors in the projection to an arbitrary variable, A (for visualization), as a function of the stationary parameter value, S. Right panel: Schematic illustration of the time dependence of the variable A over the ensemble subjected to the S(t) parameter drift scenario (shown in the lower part of the panel). Internal variability is represented by the gray band, the variance of the ensemble. The ensemble average is indicated by the thick black curve. The ensemble splits at about year 300. After this time, a red (blue) stripe illustrates the distribution of the realizations ending up on the red (blue) colored usual attractors in the left panel. The average of these subensembles is marked by a dark line (Color figure online)
This phenomenon is depicted schematically in Fig. 7. In the left panel, the two coexisting usual chaotic-like attractors, with internal variability (red and blue colors) are shown by projecting them onto a single variable, A. This may stand for e.g. surface temperature or any other relevant quantity. The right panel illustrates the time dependence of A in an ensemble subjected to a drift in parameter S by the scenario given in the lower panel. The red and blue bands encompass those members of the ensemble that end up on the corresponding chaotic attractors by the end of the scenario. Initially, these coincide and make up a single connected part of the snapshot attractor (grey band). After a certain time the snapshot attractor splits and two unconnected parts (colored red and blue in Fig. 7) appear, and the transition becomes impossible between them.
In this view, it is not useful to talk about a single average/typical behaviour, after the splitting at least. Simply averaging the variable over the full ensemble (the full snapshot attractor) yields a value which is far from any realization, and would not reflect any of the possible states permitted by the system (the average would fall into a forbidden region in the terminology of Sect. 4).
Once the two branches have separated, it makes more sense to consider the two subensembles, and characterizing the corresponding climate regimes by their own parts of the natural measure. For example, one can define an average within each of the separated ensemble’s disjoint components.
The separation of the snapshot attractor to two unconnected branches, between which transition of trajectories is not possible, stems from the fact that the corresponding stationary system is not ergodic in the sense of the existence of a unique global asymptotic probability measure [136]. As a consequence, the time-dependent system remains inergodic [22], even if the ensemble starts within the basin of one of the attractors since the ultimate outcomes are described in practice by two distinct distributions, see Fig. 7. The uniqueness of the full measure associates a well-defined probability of ending up on each climate regime.
The probabilistic nature of the outcomes was investigated in a similarly bistable system, which also contains noise [132]. Lately, the limiting case was also discussed, where the strength of the noise goes to 0, which results in a deterministic system. In this limit it was found that the probabilities associated to ending up on the stable attractors is either 1 or 0, and this can be exchanged between the attractors by tuning a parameter [137].
The mechanism described provides an example applicable to a snowball Earth transition [138] when the realization of tipping might have a nonzero probability in a deterministic system, which is dependent on the particular forcing scenario.
9 Spreading of Pollutants in a Changing Climate
As an additional utilization of an ensemble of parallel climate realizations, the change in the intensity of atmospheric large-scale spreading of pollutants can also be investigated in a changing climate. Due to the chaotic nature of the spreading of pollutants in three-dimensional flows, pollutant clouds in the atmosphere expand in an exponential manner in time. This phenomenon is illustrated in the left panel of Fig. 8 in which the time evolution of a filament of initial length of 660 km (thick straight red line) is tracked for 10 days. The inset shows that the increase of the length L of the filament is indeed exponential in time t after some days: \(L(t) \sim \exp (ht)\). The rate of this exponential stretching, i.e. the quantity h, is called the stretching rate [139, 140]. In this case the stretching rate is \(h = 0.41\hbox { day}^{-1}\) which implies that in \(t = 10\) days the length grows by a factor of \(\exp (ht) = 60.3\) and the filament becomes almost \(40\,000\hbox { km}\) long.
Left: Advection image of an initially \(6^{\circ }\)-long filament on the 10th day after the initialization (thin red curve) using meteorological data from a PlaSim climate realizations. Initial conditions: \(n_0 = 1000\) ideal particles (corresponding to inert gas) initiated on December 1, yr 64 at 00 UTC at \(30^{\circ }\hbox { E}\), \(30^{\circ }\hbox { N}\), 500 hPa, \(50^{\circ }\hbox { N}\) (vertical thick red line segment). For precise length calculation, new particles are inserted between subsequent particles if their distance becomes larger than 10 km. The inset illustrates the time-dependence of the length of the filament and the exponential function fitted from day 3 to 10 (dashed line). The stretching rate of the filament is \(h = 0.41\)\(\hbox {day}^{-1}\). Bottom right: PlaSim \(\hbox {CO}_2\) forcing for the investigation of the stretching rate due to climate change. Top right: Time-dependence, in 110 climate realizations (gray), of the December–January–February seasonal mean stretching rate h averaged over a set of different filaments. These different filaments are initialized as short meridional line segments distributed evenly along the latitude \(30^{\circ }\hbox { S}\). The ensemble mean is indicated by black color. The systematic trend is due to the indicated \(\hbox {CO}_2\) forcing. Data source: [141] (Color figure online)
The intensity of the spreading can be characterized in general by such stretching rates [139,140,141]. This quantity corresponds to a measure of chaotic systems, the topological entropy (see, e.g., [142]), in the atmospheric context. In [141] in order to explore what the typical spreading behavior is in a changing climate, ensemble simulations of the PlaSim and CESM climate models were used. In these ensembles the global mean surface temperature increased by \(6\,^{\circ }\hbox {C}\) and \(3.5\,^{\circ }\hbox {C}\) in a hundred years, respectively. Results showed that the stretching rate has a typical zonal distribution: the smallest values can be found in the tropical belt, while the largest ones are typical for the mid- and high latitudes due to the more enhanced cyclonic activity in this region.
As a consequence of climate change, spreading simulations showed an overall decreasing trend in the the stretching rate in the ensembles of both climate models. The right panel of Fig. 8 illustrates how the December–January–February seasonal mean stretching rate changes due to the prescribed \(\hbox {CO}_2\) forcing in the PlaSim simulations at \(30^{\circ }\hbox { S}\). It is worth mentioning that even the obtained decrease of approximately \(0.02\hbox { day}^{-1}\) in the ensemble mean (thick black curve) during the investigated climate change period results in the fact that on average the length of 10-day-old filaments becomes 82% of that of the typical filament lengths in the stationary climate before year 50. This seemingly small decrease in h might cause larger pollutant concentration for several regions, resulting in higher environmental risk.
Furthermore, in [141] strong correlation was found between the time series of the ensemble mean values of the stretching rate and of the absolute value of the relative vorticity. This relationship is useful for the estimation of the changes in the intensity of spreading as computationally costly dispersion simulations can be avoided since vorticity fields are operationally generated by climate models.
10 Temporal Aspects: An Emerging Research Direction
10.1 Temporal Statistics
The traditional characterization of a multitude of climate-related phenomena is based on analyses of power spectra. However, Fourier transformation is defined only for stationary time series, so that power spectra do not exist in a monotonically drifting climate in a strict sense. This is actually rather intuitive, since the statistical or dynamical relationship between two time instants separated by a given time is not temporally invariant any more: it depends on when within the climate change either of these instants is chosen.
To characterize the relationship between temporally separated values of a given variable, a “workaround” is to compute the correlation coefficient between two time instants with respect to the time-dependent natural probability measure (with respect to temporally evolving ensemble members in practice). By fixing one of the time instants and scanning through the time axis with the other time instant we obtain an analogue of an autocorrelation function. However, this new function has an extra parameter, the choice of the reference time instant. Or it might be better to simply say that this generalization of the autocorrelation function is defined on two time variables.
For stationary time series, the power spectrum and the autocorrelation function are each other’s Fourier transform according to the Wiener-Khinchin theorem [143]. While only one of the two concepts exists in nonautonomous systems with a monotonic drift, this theorem suggests that characterizing the system by an autocorrelation function in place of a power spectrum is an appropriate approach. Further research is needed, however, to unfold how the generalized autocorrelation function can be utilized for characterizing particular climate-related phenomena and their change.
Statistical quantifiers of time intervals of nonzero length can be interesting in themselves, too. For example, it is meaningful to compute the temporal average or standard deviation of some variable for e.g. a given decade, but then this average or standard deviation will have its own probabilistic description as defined via the time-dependent natural measure. The probabilistic description of such interval-wise taken temporal statistics [29] will depend, of course, on which decade is chosen. The ensemble average of this interval-wise taken quantifier should not be confused with the corresponding ensemble quantifier of a time instant within the given time interval: while these two characterizations coincide in a stationary climate, biases are introduced if the climate is changing. For more details see Sect. 5 about nonergodicity.
A motivation for temporal averaging can be to improve the quality of the ensemble estimation. On the one hand, fluctuations tend to be smoothed out in a given range of time windows (from 5–10 days to 10–30 years) which is termed ‘macroweather’ in [144], so that e.g. expectation values of interval-wise taken temporal statistics with interval lengths in this regime can be estimated with increasing precision. On the other hand, one may consider the ensemble estimation of a given time instant, and then try to improve its quality by temporally averaging the ensemble estimation in a neighborhood of the given time instant. Of course, this introduces bias to the estimation via the temporal evolution of the given ensemble quantifier, but the gain in precision can be more important up to some neighborhood size (cf. again with Sect. 5). In particular, the situation is rather favorable in the sense that the temporal evolution is generally expected to be linear in a small neighborhood, and the bias only appears for nonlinear trends, when the size of the neighborhood exceeds the linearizable regime.
10.2 Long Timescales in the System
The practical relevance and accessibility of the snapshot attractor and its natural measure relies on the exponential convergence with a short time scale relative to the targeted time span of the investigation. For example, for 21st-century climate projections, the time range of interest is around 100 years, and the time scale of the atmosphere with a realistic depth of the mixed-layer ocean in PlaSim is a few decades at most [39, 59]. Similarly, the atmosphere and the upper ocean (complemented with sea ice and land) have decadal time scales and convergence times in any Earth system model, see Sect. 4.4.
However, the deep ocean has time scales of thousands of years. Taking into account the full variability (the full extension of the attractor) in these oceanic variables might prove to be unfavorable for century-long climate projections. If considerable amount of variability nevertheless emerges within a century, then neglecting it would also be erroneous, and the snapshot attractor approach might prove to be of limited suitability for such analyses.
There are two possibilities that would nevertheless make the snapshot attractor approach appropriate. First, deep oceanic variability may prove to be uncorrelated with the rest of the system. Second, if the separation of long and short time scales is sufficiently large, one may treat the variables of the deep ocean as “frozen-in” and speak about a conditional natural measure corresponding to given values of the deep oceanic variables. Even if the variation of these variables is not completely negligible, a nonautonomous analogue of the singular perturbation theory of slow-fast systems [25] may help.Footnote 14 Preliminary analyses of the MPI-ESM suggest that both an uncorrelated nature of fluctuations and time-scale separation might actually be realized, but careful further research will be crucial for drawing conclusions.
11 Conclusion
We have shown that the diversity of our Earth’s climate is characterized by the difference between parallel climate realizations rather than the variability that we experience in our own past. An appropriate mathematical tool is the concept of snapshot/pullback attractors. These are objective entities reflecting the internal variability of the climate. Fortunately, they can be well reproduced numerically in models of the climate system: the convergence time \(t_{\mathrm {c}}\) is short, and typical properties, e.g. spatial correlations to characterize teleconnections can be investigated even in large numerical models.
The concepts of the average and the deviation from it also appear in the IPCC report [6], but it also considers averages taken over different climate models relevant. The report uses multimodel ensembles without dealing with large ensembles in the individual models. The different models, however, describe climates of “different physics”, the differences of which do not reflect the internal variability of the climate, rather the perhaps significant inaccuracies of the models. In the spirit of the article, it seems more appropriate to evaluate projections within single models based on parallel climate histories.
Finally, we wish to briefly address the characterization of model uncertainties within a single climate model. This can account e.g. for uncertainties in the parametrizations of unresolved processes (e.g. convection or different diffusive processes): the parameters appearing here are not physical constants and may originate from a restricted set of observations or simulations of a given process. Let us assume that a model parameter p is uncertain, that is \(p= p_0 + \eta \), with the random variable \(\eta \) following a probability distribution which we have access to. For simplicity, the value of the random variable \(\eta \) is assumed to be constant in time, which is reasonable if p represents (possibly unresolved) model physics.Footnote 15 We then construct a parameter ensemble, by carrying out an ensemble simulation with a fixed parameter p corresponding to a particular realization of \(\eta \), and repeating this with other realizations of \(\eta \).Footnote 16 A measure of model uncertainty can be the standard deviation (with respect to the realizations of \(\eta \)) of an observable quantity’s ensemble average (with respect to the parallel climate realizations). That is, for a general observable quantity A we carry out parallel climate simulations with a fixed parameter \(p_0+\eta \), evaluate the ensemble average, and then compute the standard deviation with respect to \(\eta \). This can be defined for any instant of time:
We also note that in this framework, the best estimate of the mean value of the observable quantity A is obtained through the double average \(\langle \langle A(t) \rangle \rangle _{\eta }\). More generally, the notion of internal variability can also be extended by its best estimate: for example, the best estimate of its strength is (with the notation used previously) \(\langle \sigma _A \rangle _{\eta }\). Dividing (9) with this quantity, a dimensionless measure of model uncertainty is obtained. A detailed investigation of these and similar quantities is beyond the scope of our paper, and might be the subject of future studies.
Notes
A precursor of this idea for simple snapshot attractors was the discovery of synchronization by common noise by Pikovsky [10].
or parallel climate histories.
This is augmented in the Glossary of [6] by defining climate, “more rigorously, as the statistical description in terms of the mean and variability of relevant quantities over a period of time”.
This is often called the “forced response” in climate research [6], which is often trend-like when parameters are drifting.
This analogy is not to be confused with the terminology of [33] where micro- and macro-states refer to local variables and those characterizing spatially extended parts of the system (possessing shorter and longer time scales, respectively).
Even if the initial distribution falls on the attractor at \(t_0\), it need not coincide with the natural measure, and some time is needed in this case, too, until the distribution converges to the natural measure.
The situation is more complicated if more than one local pullback attractors (each with its own basin of attraction) coexist. In most known cases this is not so, but examples have already been found and studied with two such coexisting attractors [40]. Another source of complication might be a broad spectrum of internal time scales to be discussed in Sect. 10.
These strong vacillations appear to be consequences of the low dimensionality of this model. In high-dimensional cases the ensemble average appears to change smoothly, see Fig. 3.
The view of Branstator and Teng has been completely adopted (illustrating convergence in a stochastic conceptual model) by DelSole and Tippett in 2018 [61], whose motivating problem was predictability [62, 63]: the decay of “initial-value predictability” (chaotic memory loss) calls for an inherent probabilistic description of climate, which has already been recognized by Lorenz [64], and has served as basis for Leith’s statistical mechanical analogy [31].
In practice, one might try to assess convergence separately for each variable studied in a particular analysis — however, it carries a risk of overlooking slower time scales in the convergence process. Notwithstanding, uncorrelated fluctuations of different parts of the system may result in factually different convergence times and time scales, cf. Sect. 10.2. This is conjectured e.g. in [68] for the sea ice extent in relation with the ocean.
Note that this process in window length \(\tau \) is much slower than the convergence to the snapshot/pullback attractor in time t.
In an even “softer” framework, one might, in principle, just take a conditional distribution with respect to certain initial conditions [61], but objectivity is practically lost with this choice.
In principle, the unresolved processes, which are taken into account in parametrizations, may vary during climate change. Such variation are, however, never taken into account in Earth system models.
Note that if the dynamics is defined only for \(t>0\), no pullback attractor can be defined, because the limit \(t_0 \rightarrow -\infty \) is not defined either. Any particular solution nevertheless converges to a unique object, \(x_{\mathrm {p}}(t) = \frac{c}{a} t +\frac{d}{a} - \frac{bc}{a^2}\). The snapshot attractor can thus be regarded as \(x^*(t')=x_{\mathrm {p}}(t')\) for any \(t' \gg \tau =-1/Re(\lambda _1)\).
References
Ott, E.: Chaos in Dynamical Systems. Cambridge University Press, Cambridge (1993)
Gruiz, M., Tél, T.: Chaotic Dynamics. Cambridge University Press, Cambridge (2006)
Kalnay, E.: Atmospheric Modeling, Data Assimilation and Predictability. Cambridge University Press, Cambridge (2002)
Dijkstra, H.A.: Nonlinear Climate Dynamics. Cambridge University Press, Cambridge (2013)
Flato, G.M.: Earth system models: an overview. Wiley Interdiscip. Rev. 2(6), 783 (2011)
Stocker, T., Qin, D., Plattner, G.K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.: IPCC, Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge (2013)
Eckmann, J.P., Ruelle, D.: Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57(3), 617 (1985)
Romeiras, F.J., Grebogi, C., Ott, E.: Multifractal properties of snapshot attractors of random maps. Phys. Rev. A 41(2), 784 (1990)
Ghil, M., Chekroun, M.D., Simonnet, E.: Climate dynamics and fluid mechanics: natural variability and related uncertainties. Physica D 237(14–17), 2111 (2008)
Pikovsky, A.S.: Synchronization and stochastization of the ensamble of autogenerators by external noise. Radiophys. Quantum Electron. 27, 390 (1984)
Sommerer, J.C., Ott, E.: Particles floating on a moving fluid: a dynamically comprehensible physical fractal. Science 259(5093), 335 (1993)
Yu, L., Ott, E., Chen, Q.: Transition to chaos for random dynamical systems. Phys. Rev. Lett. 65(24), 2935 (1990)
Lai, Y.C., Feudel, U., Grebogi, C.: Scaling behavior of transition to chaos in quasiperiodically driven dynamical systems. Phys. Rev. E 54(6), 6070 (1996)
Jacobs, J., Ott, E., Antonsen, T., Yorke, J.: Modeling fractal entrainment sets of tracers advected by chaotic temporally irregular fluid flows using random maps. Physica D 110(1), 1 (1997)
Neufeld, Z., Tél, T.: Advection in chaotically time-dependent open flows. Phys. Rev. E 57(3), 2832 (1998)
Károlyi, G., Tél, T., De Moura, A.P.S., Grebogi, C.: Reactive particles in random flows. Phys. Rev. Lett. 92(17), 174101 (2004)
Serquina, R., Lai, Y.C., Chen, Q.: Characterization of nonstationary chaotic systems. Phys. Rev. E 77(2), 26208 (2008)
Hansen, J.L., Bohr, T.: Fractal tracer distributions in turbulent field theories. Physica D 118(1–2), 40 (1998)
Ku, W.L., Girvan, M., Ott, E.: Dynamical transitions in large systems of mean field-coupled Landau-Stuart oscillators: extensive chaos and cluster states. Chaos 25(12), 123122 (2015)
Vincze, M., Borcia, I.D., Harlander, U.: Temperature fluctuations in a changing climate: an ensemble-based experimental approach. Sci. Rep. 7(1), 254 (2017)
Crauel, H., Flandoli, F.: Attractors for Random Dynamical Systems. Probab. Theory Relat. Fields 100, 365 (1994)
Arnold, L.: Random Dynamical Systems. Springer, Berlin (1998)
Kloeden, P.E., Rasmussen, M.: Nonautonomous Dynamical Systems, vol. 176. American Mathematical Society, Providence, RI (2011)
Carvalho, A.N., Langa, J.A., Robinson, J.C.: Attractors for Infinite-Dimensional Nonautonomous Dynamical Systems. Applied Mathematical Sciences. Springer, New York (2013)
Kuehn, C.: Multiple Time Scale Dynamics. Springer, New York (2015)
Chekroun, M.D., Simonnet, E., Ghil, M.: Stochastic climate dynamics: random attractors and time-dependent invariant measures. Physica D 240(21), 1685 (2011)
Bódai, T., Tél, T.: Annual variability in a conceptual climate model: snapshot attractors, hysteresis in extreme events, and climate sensitivity. Chaos 22(2), 023110 (2012)
Bódai, T., Károlyi, G., Tél, T.: A chaotically driven model climate: extreme events and snapshot attractors. Nonlin. Processes Geophys. 18, 573 (2011)
Drótos, G., Bódai, T., Tél, T.: Probabilistic concepts in a changing climate: a anapshot attractor picture. J. Clim. 28(8), 3275 (2015)
Herein, M., Drótos, G., Haszpra, T., Márfy, J., Tél, T.: The theory of parallel climate realizations as a new framework for teleconnection analysis. Sci. Rep. 7(January), 44529 (2017)
Leith, C.: Predictability of climate. Nature 276(5686), 352 (1978)
Hawkins, E., Sutton, R.: The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 90(8), 1095 (2009)
Hawkins, E., Smith, R.S., Gregory, J.M., Stainforth, D.A.: Irreducible uncertainty in near-term climate projections. Clim. Dyn. 46(11), 3807 (2016)
Ghil, M.: Climate Change: Multidecadal and Beyond, Chap. 2, pp. 31–51. World Scientific, Singapore (2015)
Ragone, F., Lucarini, V., Lunkeit, F.: A new framework for climate sensitivity and prediction: a modelling perspective. Clim. Dyn. 46(5), 1459 (2016)
Crauel, H., Flandoli, F.: Extreme sensitivity and climate tipping points. J. Stat. Phys. (this issue) (2019)
Ghil, M., Lucarini, V.: The physics of climate variability and climate change (2019)
Leith, C.E.: Climate response and fluctuation dissipation. J. Atmos. Sci. 32(10), 2022 (1975)
Drótos, G., Bódai, T., Tél, T.: On the importance of the convergence to climate attractors. Eur. Phys. J. 226(9), 2031 (2017)
Pierini, S., Ghil, M., Chekroun, M.D.: Exploring the pullback attractors of a low-order quasigeostrophic ocean model: the deterministic case. J. Clim. 29(11), 4185 (2016)
Lorenz, E.N.: Irregularity: a fundamental property of the atmosphere. Tellus A 36 A(2), 98 (1984)
Nicolis, C., Vannitsem, S., Royer, J.F.: Short-range predictability of the atmosphere: mechanisms for superexponential error growth. Q. J. R. Meteorol. Soc. 121(523), 705 (1995)
Provenzale, A., Balmforth, N.J.: Chaos and Structures in Geophysics and Astrophysics (Woods Hole Lecture Notes). Proceedings of GFD (Geophysical Fluid Dynamics of Woods Hole Oceanographic Institution). https://www.whoi.edu/fileserver.do?id=21476&pt=10&p=17353 (1999)
Freire, J.G., Bonatto, C., Dacamara, C.C., Gallas, J.A.: Multistability, phase diagrams, and intransitivity in the Lorenz-84 low-order atmospheric circulation model. Chaos 18(3), (2008)
Lorenz, E.N.: Can chaos and intransivity lead to interannual variability? Tellus A 42A, 378 (1990)
Blunden, J., Arndt, D.S.: Supplement: State of the Climate in 2013 supplemental figures. Bull. Am. Meteorol. Soc. 95(7), ES1 (2014)
Serreze, M.C., Francis, J.A.: The arctic amplification debate. Clim. Chang. 76(3–4), 241 (2006)
Bódai, T., Károlyi, G., Tél, T.: Fractal snapshot components in chaos induced by strong noise. Phys. Rev. E 83, 046201 (2011)
Bódai, T., Altmann, E.G., Endler, A.: Stochastic perturbations in open chaotic systems: random versus noisy maps. Phys. Rev. E 87, 042902 (2013)
Daron, J.D., Stainforth, D.A.: On predicting climate under climate change. Environ. Res. Lett. 8(3), 034021 (2013)
Daron, J.D., Stainforth, D.A.: On quantifying the climate of the nonautonomous Lorenz-63 model. Chaos 25(4), 043103 (2015)
Pierini, S.: Ensemble simulations and pullback attractors of a periodically forced double-gyre system. J. Phys. Oceanogr. 44, 3245 (2014)
Pierini, S., Chekroun, M.D., Ghil, M.: The onset of chaos in nonautonomous dissipative dynamical systems: a low-order ocean-model case study. Nonlinear Process. Geophys. 25(3), 671 (2018)
Chekroun, M.D., Ghil, M., Neelin, J.D.: Advances in Nonlinear Geosciences, pp. 1–33. Springer, New York (2018)
Pierini, S.: Statistical significance of small ensembles of simulations and detection of the internal climate variability: an excitable ocean system case study. J. Stat. Phys. (2019)
Fraedrich, K., Jansen, H., Kirk, E., Luksch, U., Lunkeit, F.: The planet simulator: towards a user friendly model. Meteorol. Z. 14(3), 299 (2005)
Lunkeit, F., Blessing, S., Fraedrich, K., Jansen, H., Kirk, E., Luksch, U., Sielmann, F.: Planet simulator user’s guide version 16.0. https://www.mi.uni-hamburg.de/en/arbeitsgruppen/theoretische-meteorologie/modelle/sources/psusersguide.pdf (2011)
Cross, M.C., Hohenberg, P.C.: Spatiotemporal chaos. Science 263(5153), 1569 (1994)
Herein, M., Márfy, J., Drótos, G., Tél, T.: Probabilistic concepts in intermediate-complexity climate models: a snapshot attractor picture. J. Clim. 29(1), 259 (2016)
Branstator, G., Teng, H.: Two limits of initial-value decadal predictability in a CGCM. J. Clim. 23, 6292 (2010)
DelSole, T., Tippett, M.K.: Predictability in a changing climate. Clim. Dyn. 51(1), 531 (2018)
Palmer, T.N., Hagedorn, R.: Predictability of Weather and Climate. Cambridge University Press, Cambridge (2006)
Vannitsem, S., Solé-Pomies, R., De Cruz, L.: Routes to long-term atmospheric predictability in coupled ocean-atmosphere systems–impact of the ocean basin boundary conditions. arXiv:1901.06203 (2019)
Lorenz, E.N.: Climatic change as a mathematical problem. J. Appl. Meteorol. 9(3), 325 (1970)
Ruelle, D.: A review of linear response theory for general differentiable dynamical systems. Nonlinearity 22(4), 855 (2009)
Liu, F., Lu, J., Garuba, O., Leung, L.R., Luo, Y., Wan, X.: Sensitivity of surface temperature to oceanic forcing via q-flux Green’s function experiments. part i: linear response function. J. Clim. 31(9), 3625 (2018)
Deser, C., Lehner, F., Rodgers, K., Ault, T., Delworth, T., DiNezio, P., Fiore, A., Frankignoul, C., Fyfe, J.C., Horton, D., Kay, J., Knutti, R., Lovenduski, N., Marotzke, J., McKinnon, K., Minobe, S., Randerson, J., Screen, J., Simpson, I., Ting, M.: Strength in numbers: the utility of large ensembles with multiple Earth system models (2019)
Kirchmeier-Young, M.C., Zwiers, F.W., Gillett, N.P.: Attribution of extreme events in arctic sea ice extent. J. Clim. 30(2), 553 (2017)
Maher, N., Milinski, S., Suarez-Gutierrez, L., Botzet, M., Kornblueh, L., Takano, Y., Kröger, J., Ghosh, R., Hedemann, C., Li, C., et al.: The Max Planck Institute grand ensemble-enabling the exploration of climate system variability. J. Adv. Model. Earth Syst. 11, 2050 (2019)
Selten, F.M., Branstator, G.W., Dijkstra, H.A., Kliphuis, M.: Tropical origins for recent and future northern hemisphere climate change. Geophys. Res. Lett. 31(21), L21205 (2004)
Zelle, H., Jan van Oldenborgh, G., Burgers, G., Dijkstra, H.: El Niño and greenhouse warming: results from ensemble simulations with the NCAR CESM. J. Clim. 18(22), 4669 (2005)
Deser, C., Phillips, A., Bourdette, V., Teng, H.: Uncertainty in climate change projections: the role of internal variability. Clim. Dyn. 38(3), 527 (2012)
Mudryk, L.R., Kushner, P.J., Derksen, C.: Interpreting observed northern hemisphere snow trends with large ensembles of climate simulations. Clim. Dyn. 43(1), 345 (2014)
von Känel, L., Frölicher, T.L., Gruber, N.: Hiatus-like decades in the absence of equatorial pacific cooling and accelerated global ocean heat uptake. Geophys. Res. Lett. 44(15), 7909 (2017)
Li, H., Ilyina, T.: Current and future decadal trends in the oceanic carbon uptake are dominated by internal variability. Geophys. Res. Lett. 45(2), 916 (2018)
Kay, J.E., Deser, C., Phillips, A., Mai, A., Hannay, C., Strand, G., Arblaster, J.M., Bates, S.C., Danabasoglu, G., Edwards, J., Holland, M., Kushner, P., Lamarque, J.F., Lawrence, D., Lindsay, K., Middleton, A., Munoz, E., Neale, R., Oleson, K., Polvani, L., Vertenstein, M.: The Community Earth System model (CESM) large ensemble project: a community resource for studying climate change in the presence of internal climate variability. Bull. Am. Meteorol. Soc. 96(8), 1333 (2015)
Hedemann, C., Mauritsen, T., Jungclaus, J., Marotzke, J.: The subtle origins of surface-warming hiatuses. Nat. Clim. Chang. 7, 336 EP (2017)
Yettella, V., Weiss, J.B., Kay, J.E., Pendergrass, A.G.: An ensemble covariance framework for quantifying forced climate variability and its time of emergence. J. Clim. 31(10), 4117 (2018)
Hu, A., Meehl, G.A., Stammer, D., Han, W., Strand, W.G.: Role of perturbing ocean initial condition in simulated regional sea level change. Water 9(6), 213 (2017)
Meinshausen, M., Smith, S.J., Calvin, K., Daniel, J.S., Kainuma, M.L.T., Lamarque, J.F., Matsumoto, K., Montzka, S.A., Raper, S.C.B., Riahi, K., Thomson, A., Velders, G.J.M., van Vuuren, D.P.: The rcp greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 109(1), 213 (2011)
Deser, C., Knutti, R., Solomon, S., Phillips, A.S.: Communication of the role of natural variability in future North American climate. Nat. Clim. Chang. 2, 775 (2012)
Dai, A.: The influence of the inter-decadal pacific oscillation on us precipitation during 1923–2010. Clim. Dyn. 41(3), 633 (2013)
Dai, A., Fyfe, J.C., Xie, S.P., Dai, X.: Decadal modulation of global surface temperature by internal climate variability. Nat. Clim. Chang. 5, 555 (2015)
Hegerl, G.C., Black, E., Allan, R.P., Ingram, W.J., Polson, D., Trenberth, K.E., Chadwick, R.S., Arkin, P.A., Sarojini, B.B., Becker, A., Dai, A., Durack, P.J., Easterling, D., Fowler, H.J., Kendon, E.J., Huffman, G.J., Liu, C., Marsh, R., New, M., Osborn, T.J., Skliris, N., Stott, P.A., Vidale, P.L., Wijffels, S.E., Wilcox, L.J., Willett, K.M., Zhang, X.: Challenges in quantifying changes in the global water cycle. Bull. Am. Meteorol. Soc. 96(7), 1097 (2015)
Hua, W., Dai, A., Qin, M.: Contributions of internal variability and external forcing to the recent pacific decadal variations. Geophys. Res. Lett. 45(14), 7084 (2018)
Dai, A., Bloecker, C.E.: Impacts of internal variability on temperature and precipitation trends in large ensemble simulations by two climate models. Clim. Dyn. 52(1), 289 (2019)
Bódai T., Drótos, G., Herein M., Lunkeit F., Lucarini, V.: The forced response of the El Niño–Southern Oscillation–Indian monsoon teleconnection in ensembles of Earth System Models. J. Clim. (2019). https://doi.org/10.1175/JCLID-19-0341.1
Chung, E.S., Timmermann, A., Soden, B.J., Ha, K.J., Shi, L., John, V.O.: Reconciling opposing walker circulation trends in observations and model projections. Nat. Clim. Chang. 9(5), 405 (2019)
Penduff, T., Llovel, W., Close, S., Garcia-Gomez, I., Leroux, S.: Trends of coastal sea level between 1993 and 2015: imprints of atmospheric forcing and oceanic chaos. Surv. Geophys. 40(6), 1543 (2019)
Penduff, T., Barnier, B., Terray, L., Bessières, L., Sérazin, G., Grégorio, S., Brankart, J.-M., Moine, M.-P., Molines, J.-M., Brasseur, P.: Ensembles of eddying ocean simulations for climate. CLIVAR Exch. Spec. Issue High Resolut. Ocean Clim. Model. 19(2), 65 (2014)
Bessières, L., Leroux, S., Brankart, J.M., Molines, J.M., Moine, M.P., Bouttier, P.A., Penduff, T., Terray, L., Barnier, B., Sérazin, G.: Development of a probabilistic ocean modelling system based on nemo 3.5: application at eddying resolution. Geosci. Model Dev. 10(3), 1091 (2017)
Timmermann, A., An, S.I., Kug, J.S., Jin, F.F., Cai, W., Capotondi, A., Cobb, K., Lengaigne, M., McPhaden, M.J., Stuecker, M.F., Stein, K., Wittenberg, A.T., Yun, K.S., Bayr, T., Chen, H.C., Chikamoto, Y., Dewitte, B., Dommenget, D., Grothe, P., Guilyardi, E., Ham, Y.G., Hayashi, M., Ineson, S., Kang, D., Kim, S., Kim, W.M., Lee, J.Y., Li, T., Luo, J.J., McGregor, S., Planton, Y., Power, S., Rashid, H., Ren, H.L., Santoso, A., Takahashi, K., Todd, A., Wang, G., Wang, G., Xie, R., Yang, W.H., Yeh, S.W., Yoon, J., Zeller, E., Zhang, X.: El Niño-Southern oscillation complexity. Nature 559(7715), 535 (2018)
Leduc, M., Mailhot, A., Frigon, A., Martel, J.L., Ludwig, R., Brietzke, G.B., Giguère, M., Brissette, F., Turcotte, R., Braun, M., Scinocca, J.: The climex project: a 50-member ensemble of climate change projections at 12-km resolution over Europe and northeastern North America with the Canadian regional climate model (crcm5). J. Appl. Meteorol. Clim. 58(4), 663 (2019)
Drótos, G., Bódai, T., Tél, T.: Quantifying nonergodicity in nonautonomous dissipative dynamical systems: an application to climate change. Phys. Rev. E 94(2), 1 (2016)
Hurrell, J.W.: Decadal trends in the north atlantic oscillation: regional temperatures and precipitation. Science 269(5224), 676 (1995)
Wanner, H., Brönnimann, S., Casty, C., Luterbacher, J., Schmutz, C., David, B.: NAO—concepts and studies. Surv. Geophys. 22(1984), 321 (2001)
Hurrell, J.W., Kushnir, Y., Ottersen, G., Visbeck, M.: The North Atlantic Oscillation: Climate Significance and Environmental Impact. American Geophysical Union, Washington, DC (2003)
Walker, G.T., Bliss, E.W., World Weather V.: Memoirs of the Royal Meteorological Society. Q. J. R. Meteorol. Soc. 4(36), 53 (1932)
Van Loon, H., Rogers, J.C.: The seesaw in winter temperatures between Greenland and Northern Europe: part I. Mon. Weather Rev. 106, 296–310 (1978)
Rogers, J.C., Van Loon, H.: The seesaw in winter temperatures between Greenland and Northern Europe. Part II: some oceanic and atmospheric effects in middle and high latitudes. Mon. Weather Rev. 107(5), 509 (1979)
Bjerknes, J.: Atmospheric teleconnections from the equatorial Pacific. Mon. Weather Rev. 97(3), 163 (1959)
Neelin, J.D., Battisti, D.S., Hirst, A.C., Jin, F.F., Wakata, Y., Yamagata, T., Zebiak, S.E.: ENSO theory. J. Geophys. Res. 103(C7), 14261 (1998)
Runge, J., Petoukhov, V., Donges, J.F., Hlinka, J., Jajcay, N., Vejmelka, M., Hartman, D., Marwan, N., Paluš, M., Kurths, J.: Identifying causal gateways and mediators in complex spatio-temporal systems. Nat. Commun. 6, 8502 (2015)
Agarwal, A., Caesar, L., Marwan, N., Maheswaran, R., Merz, B., Kurths, J.: Network-based identification and characterization of teleconnections on different scales. Sci. Rep. 9(1), 8808 (2019)
Thompson, D.W.J., Wallace, J.M.: The Arctic oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 25(9), 1297 (1998)
Thompson, W.J., Wallace, David, J.M.: Annular modes in the extratropical circulation. Part I: month-to-month variability. J. Clim. 13(5), 1000 (2000)
Preisendorfer, R.: Principal Component Analysis in Meteorology and Oceanography. Developments in Atmospheric Science. Elsevier, New York (1988)
Haszpra, T., Topál, D., Herein, M.: On the time evolution of the Arctic Oscillation and related wintertime phenomena under different forcing scenarios in an ensemble approach. J. Clim. (under review) (2019)
Maher, N., Matei, D., Milinski, S., Marotzke, J.: Enso change in climate projections: forced response or internal variability? Geophys. Res. Lett. 45(20), 11 (2018)
Haszpra, T., Herein, M., Bódai, T.: On the time evolution of ENSO and its teleconnections in an ensemble view—a new perspective. Earth Syst. Dynam. Discuss. (under review) (2019). https://doi.org/10.5194/esd-2019-57
Fultz, D., Long, R.R., Owens, G.V., Bohan, W., Kaylor, R., Weil, J.: Studies of Thermal Convection in a Rotating Cylinder with Some Implications for Large-Scale Atmospheric Motions, pp. 1–104. American Meteorological Society, Boston, MA (1959)
Hide, R.: Some experiments on thermal convection in a rotating liquid. Q. J. R. Meteorol. Soc. 79(339), 161 (1953)
Read, P.L., Pérez, E.P., Moroz, I.M., Young, R.M.B.: Modeling Atmospheric and Oceanic Flows, Chap. 1, pp. 7–44. American Geophysical Union (AGU), Washington DC (2014)
Gyüre, B., Bartos, I., Jánosi, I.M.: Nonlinear statistics of daily temperature fluctuations reproduced in a laboratory experiment. Phys. Rev. E 76, 037301 (2007)
von Larcher, T., Viazzo, S., Harlander, U., Vincze, M., Randriamampianina, A.: Instabilities and small-scale waves within the Stewartson layers of a thermally driven rotating annulus. J. Fluid Mech. 841, 380 (2018)
Vincze, M., Borchert, S., Achatz, U., von Larcher, T., Baumann, M., Liersch, C., Remmler, S., Beck, T., Alexandrov, K.D., Egbers, C., Fröhlich, J., Heuveline, V., Hickel, S., Harlander, U.: Benchmarking in a rotating annulus: a comparative experimental and numerical study of baroclinic wave dynamics. Meteorol. Z. 23(6), 611 (2015)
Young, R.M.B., Read, P.L.: Predictability of the thermally driven laboratory rotating annulus. Q. J. R. Meteorol. Soc. 142(695), 911 (2016)
Vallis, G.K.: Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation, 2nd edn. Cambridge University Press, Cambridge (2017)
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D., Hof, B.: The onset of turbulence in pipe flow. Science 333(6039), 192 (2011)
Avila, M., Hof, B.: Nature of laminar-turbulence intermittency in shear flows. Phys. Rev. E 87, 063012 (2013)
Avila, M., Mellibovsky, F., Roland, N., Hof, B.: Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502 (2013)
Feudel, U., Pisarchik, A.N., Showalter, K.: Multistability and tipping: from mathematics and physics to climate and brain–Minireview and preface to the focus issue. Chaos 28(3), 033501 (2018)
Lenton, T.M., Held, H., Kriegler, E., Hall, J.W., Lucht, W., Rahmstorf, S., Schellnhuber, H.J.: Tipping elements in the Earth’s climate system. Proc. Nat. Acad. Sci. 105(6), 1786 (2008)
Crowley, T.J., Hyde, W.T., Peltier, W.R.: CO2 levels required for deglaciation of a “Near-Snowball” Earth. Geophys. Res. Lett. 28(2), 283 (2001)
Feulner, G., Kienert, H.: Climate simulations of Neoproterozoic snowball Earth events: similar critical carbon dioxide levels for the Sturtian and Marinoan glaciations. Earth Planet. Sci. Lett. 404, 200 (2014)
Brugger, J., Feulner, G., Petri, S.: Baby, it’s cold outside: climate model simulations of the effects of the asteroid impact at the end of the Cretaceous. Geophys. Res. Lett. 44(1), 419 (2017)
Ghil, M.: Climate stability for a Sellers-type model. J. Atmos. Sci. 33(1), 3 (1976)
Lucarini, V., Fraedrich, K., Lunkeit, F.: Thermodynamic analysis of snowball Earth hysteresis experiment: efficiency, entropy production and irreversibility. Q. J. R. Meteorol. Soc. 136(646), 2 (2010)
Bódai, T., Lucarini, V., Lunkeit, F., Boschi, R.: Global instability in the Ghil-Sellers model. Clim. Dyn. 44(11), 3361 (2015)
Lucarini, V., Bódai, T.: Edge states in the climate system: exploring global instabilities and critical transitions. Nonlinearity 30(7), R32 (2017)
Tantet, A., Lucarini, V., Lunkeit, F., Dijkstra, H.A.: Crisis of the chaotic attractor of a climate model: a transfer operator approach. Nonlinearity 31(5), 2221 (2018)
Lucarini, V., Bódai, T.: Transitions across melancholia states in a climate model: reconciling the deterministic and stochastic points of view. Phys. Rev. Lett. 122, 158701 (2019)
Ashwin, P., Perryman, C., Wieczorek, S.: Parameter shifts for nonautonomous systems in low dimension: bifurcation- and rate-induced tipping. Nonlinearity 30(6), 2185 (2017)
Alkhayuon, H.M., Ashwin, P.: Rate-induced tipping from periodic attractors: partial tipping and connecting orbits. Chaos 28(3), 033608 (2018)
Kaszás, B., Feudel, U., Tél, T.: Tipping phenomena in typical dynamical systems subjected to parameter drift. Sci. Rep. 9(1), 8654 (2019)
Gardiner, C.: Stochastic Methods: A Handbook for the Natural and Social Sciences. Springer, Berlin (2009)
Lucarini, V., Bodai, T.: Global stability properties of the climate: Melancholia states, invariant measures, and phase transitions (2019). arXiv:1903.08348
Kaszás, B., Haszpra, T., Herein, M.: The snowball Earth transition in a climate model with drifting parameters: splitting of the snapshot attractor. Chaos 29(11), 113102 (2019)
Haszpra, T., Tél, T.: Topological entropy: a Lagrangian measure of the state of the free atmosphere. J. Atmos. Sci. 70(12), 4030 (2013)
Haszpra, T.: Intensification of large-scale stretching of atmospheric pollutant clouds due to climate change. J. Atmos. Sci. 74(12), 4229 (2017)
Haszpra, T., Herein, M.: Ensemble-based analysis of the pollutant spreading intensity induced by climate change. Sci. Rep. 9(1), 3896 (2019)
Newhouse, S., Pignataro, T.: On the estimation of topological entropy. J. Stat. Phys. 72(5–6), 1331 (1993)
Reichl, L.E.: A Modern Course in Statistical Physics. Wiley, Weinheim (2016)
Lovejoy, S.: What is climate? Eos Trans. Am. Geophys. Union 94(1), 1 (2013)
Thomas, G.B., Weir, M.D., Hass, J.R.: Thomas’ Calculus, 13th edn. Pearson, Cambridge (2014)
Acknowledgements
Open access funding provided by Eötvös Loránd University (ELTE). This paper was supported by the Hungarian Research, Development and Innovation Office – NKFIH under grants K-125171, FK-124256, FK-125024, and PD-121305 (T.H.), PD-124272 (M.H.), by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences (T.H., M.V.), by the ÚNKP-18-2 (B.K.) and ÚNKP-18-4 (T.H., M.V.) grants of the New National Excellence Program of the Hungarian Ministry of Human Capacities, by the Institute for Basic Science (IBS), Republic of Korea, under IBS-R028-D1 (T.B.), and by the European Social Fund under CAIB grant PD/020/2018 Margalida Comas (G.D.).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Valerio Lucarini.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Snapshot/Pullback Attractors in Elementary Calculus
Appendix A: Snapshot/Pullback Attractors in Elementary Calculus
Here we show that the concept of snapshot/pullback attractor is implicitly part of elementary calculus. In the class of dissipative linear ordinary differential equations it is strongly related to the concept of particular solution. As an illustrative example, let us consider a second order inhomogeneous equation of constant coefficients (an example in a first order equation was given in [9]):
where \(a,b>0\) and f(t) represents a driving force (a driven, damped harmonic oscillator subjected to an arbitrary time-dependent driving).
As we know (see e.g. [145]), the general solution is
where \(x_{\mathrm {p}}(t)\) is any particular solution. The initial condition \(x_0,v_0\) prescribed at some time \(t_0\) is fulfilled by an appropriate choice of \(C_1\) and \(C_2\) requiring \(x(t_0)=x_0\) and \({\dot{x}}(t_0)=v_0\). Due to dissipation, the real part of both exponents is negative (we order them such that \(0> Re(\lambda _1) > Re(\lambda _2)\)), hence the exponential terms decay rapidly (faster than any power law).
Since \(x_{\mathrm {p}}(t)\) is independent of the initial condition \(x_0,v_0,t_0\) in (11), it also follows from the above that the difference between any two particular solutions \(x'_{\mathrm {p}}(t)\) and \(x''_{\mathrm {p}}(t)\) can be written as
As a consequence, any two particular solutions converge to each other: after a few multiples of the relaxation time \(\tau =-1/Re(\lambda _1)\), they coincide with exponential accuracy.
According to (12), the object to which any particular solution converges is also obtained in the limit when the initial conditions are prescribed in the remote past: \(t_0 \rightarrow - \infty \). By definition, this object is the pullback attractor \(x^*(t)\) of the system, and, in view of (12), it is obtained as one of the particular solutions, which we shall call the ‘bare particular solution’ \(x_\mathrm {bp}(t)\):
The other phase space component, the velocity, of the pullback attractor is of course \(v^*(t)={\dot{x}}^*(t)\).
At any finite time instant \(t'\) the slice of the pullback attractor, the snapshot attractor, is \(x^*(t')=x_{bp}(t')\), a single number. On the \((x,{\dot{x}})\) phase plane, the snapshot attractor \((x^*(t'),{\dot{x}}^*(t'))=(x_\mathrm {bp}(t'), {\dot{x}}_\mathrm {bp}(t'))\) is a point. The snapshot attractor of this system is thus fixed-point-like, but this “fixed point” is moving in time.
As a specific case, let us consider a linear driving force: \(f(t)= ct + d\). The bare particular solution is also of this type, \(x_\mathrm {bp}=At+B\): \(x_\mathrm {bp}\)is a particular solution, and any addition of exponential functions as in (12) vanishes for \(t_0 \rightarrow -\infty \). The values of A and B follow after substitution, and we finally obtain the pullback attractor as
The snapshot attractor at time \(t'\) is \((x^*(t'),{\dot{x}}^*(t))=({c t'}/{a} +{d}/{a} - {bc}/{a^2}, c/a)\), a “fixed point” moving with a uniform speed (c / a) parallel to the x axis.
As our last example, let us consider a combined case: a constant driving is present up to time zero, but from there on a linearly changing forcing applies:
In other words, at time zero, \(t=0\), a kind of climate change sets in.
In the negative time region, the pullback attractor is obviously \(x^*(t)=d/a\). For positive times one particular solution is \(x_{\mathrm {p}}(t) = \frac{c}{a} t +\frac{d}{a} - \frac{bc}{a^2}\) as in the previous example. This solution, however, does not fit to the pullback attractor characterizing the negative times since there is a jump at time zero. Meanwhile, the pullback attractor has to be continuous, since it is a solution of a differential equation of second order. Here we recall that \(A_1 e^{\lambda _1 t} + A_2 e^{\lambda _2 t} + x_{\mathrm {p}}(t)\) is also a particular solution for \(t>0\). The coefficients \(A_1,A_2\) can be chosen to make this new particular solution join the constant solution at time \(t=0\) continuously. Since this is how the constant solution continues for \(t>0\), this special particular solution is the pullback attractor for positive times.Footnote 17 The overall pullback attractor is thus given as
Left panel: The pullback attractor of the system defined by (10) and (15), given by (16), represented as the thick black curve. Several trajectories started from various initial conditions are shown with different colors. Right panel: Evolution of the snapshot attractor in the phase space (x, \({\dot{x}}\)). The points are time-colored (darker colors show later time instants, starting from \(t'=0\)). Parameters: \(a = 4\), \(b= 5\), \(c= -1\), \(d=0\), \(\lambda _1=-1\)\(\lambda _2=-4\), \(\tau =1\) (Color figure online)
The pullback attractor described by (16) is displayed schematically in the left panel of Fig. 9 (for the numerical choice of constants, see the caption). The pullback attractor starts turning in the direction of the linear trend at the onset of climate change. The linear trend is taken over with some delay, the length of which is on the order of the relaxation time \(\tau =-1/Re(\lambda _1)\).
The right panel exhibits the snapshot attractors on the \((x, v=\dot{x})\) phase space. Color dots mark the position of the attractor at subsequent time instants \(t'\), starting from \(t'=0\).
The individual trajectories marked with different colors all reach the pullback attractor after a convergence time \(t_c\) which is a multiple of the relaxation time \(\tau \): \(t_c \approx 3 \tau =3\). Here we see again that after a convergence time \(t_c\), i.e. for \(t > t_\mathrm {in} +t_c\) when initiation takes place at \(t_\mathrm {in}\), all trajectories properly represent the pullback attractor, irrespective of how the simulations stars. A comparison with Fig. 3 shows a qualitative similarity. It is remarkable to see that the convergence to the pullback attractor is of the same type both in a linear differential equation and in a climate model. The real difference shows up in the character of the attractor, which is chaotic-like/turbulent in the realistic case and exhibits unpredictability/internal variability.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tél, T., Bódai, T., Drótos, G. et al. The Theory of Parallel Climate Realizations. J Stat Phys 179, 1496–1530 (2020). https://doi.org/10.1007/s10955-019-02445-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-019-02445-7