Modeling Cell Size Dynamics in a Confined Nonuniform Dense Cell Culture

Abstract

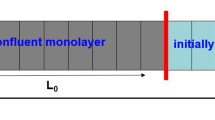
In this work, we analyze an ensemble of dividing and growing living cells that maintain contact with each other. The dynamics of the cell area distribution in a confined system is theoretically investigated in both uniform and nonuniform settings. The effective pressure is introduced to model the experimentally observed phenomenon in which the average cell size dramatically decreases over time. For a nonuniform system, the cell shift due to the gradient of the effective pressure is considered and its effect on the average cell area profiles is examined.

Appendix

Considering only the processes of cell division and cell growth after division for cells that are not in contact with each other, one needs to solve the equation for cell area distribution

$$\begin{aligned} \frac{\partial f}{\partial t} + \frac{\partial }{\partial a}\left( f \, \frac{da}{dt}\right) = - \alpha (a)\,f(a) + 4\,\alpha (2a)\,f(2a). \end{aligned}$$

(4)

accompanied by the equation for single cell growth

$$\begin{aligned} \frac{da}{dt} = \gamma (a), \end{aligned}$$

(5)

where $\alpha (a)$ is the rate of cell division and $\gamma (a)$ is the rate for cell growth. Inspired by numerical simulations, we consider the following ansatz, $f(a,t)=n(t)\,g(a)$, which is valid at large times. Substituting this ansatz and Eq. 5 into Eq. 4 and dividing by $n(t)\,g(a)$, we get:

$$\begin{aligned} \frac{1}{n(t)} \frac{dn}{dt} = - \frac{1}{g(a)} \frac{d [\gamma (a)\,g(a)]}{da} + \frac{4\alpha (2a)g(2a)}{g(a)} - \alpha (a). \end{aligned}$$

(6)

Since the total number of particles $N(t) = \int n(t)g(a)da$, one can change n(t) to N(t) in the left-hand side of the equation above. Notice also that the left-hand side of this equation depends only on time t, while the right-hand side depends only on cell area a. Therefore, both expressions are constant, let us denote this constant by k. This immediately means that the number of cells growth exponentially with time, $N(t)\sim \exp (kt)$. The constant k depends on the function g(a) and on cell division rate $\alpha (a)$. To derive this dependence, one can first show that $dN/dt = \int \alpha (a)f(a,t)da$; this is rather intuitive, since the the number of cells grows only due to proliferation. Therefore, the left-hand side of Eq. 6 becomes

$$\begin{aligned} k=\frac{1}{N}\frac{dN}{dt} = \frac{\int \alpha (a) g(a) da}{\int g(a) da}. \end{aligned}$$

The resulting equation includes both g(a) and g(2a), therefore it should be solved separately in intervals ($a_{max}/2$, $a_{max}$), ($a_{max}/4$, $a_{max}/2$) etc. With the profiles shown in Fig. 1 in mind, let us consider first the interval ($a_{max}/2$, $a_{max}$). In this case, $g(2a)=0$, and we have

$$\begin{aligned} \frac{d \gamma (a)\,g(a)}{da} + \alpha (a)g(a) + kg(a) =0. \end{aligned}$$

(7)

This results in

$$\begin{aligned} \ln [\gamma (a)g(a)] = -\int \frac{\alpha (a)+k}{\gamma (a)} da, \end{aligned}$$

(8)

where the constant k is given above.

One can look for an approximate solution of this equation, computing k by assuming that the major contributions to the integral $\int \alpha (a) g(a) da$ (and to the integral in the right-hand side of Eq. 8) comes from the region of maximal g. For example, if we consider the profile with maximum at $a_{max}$, $k \simeq \alpha (a_{max})$ and then $\gamma (a)g(a)\sim (a_{max}-a)^{\beta }$, so $g(a)\sim (a_{max}-a)^{\beta -1}$, where $\beta \simeq 2\alpha (a_{max})/c$ and we used the expression for $\gamma (a)$ from Eq. 2 for zero effective pressure: $\gamma (a) = c\,(a_{max} - a)$. For $\beta <1$, g is maximal at $a_{max}$, which agrees with the results shown in Fig. 1. Indeed, for curves that have maximum at $a_{max}$ correspond to $\beta = 2*(1/18)/(1/7)=0.78<1$ (while curves that tend to zero at $a_{max}$ correspond to $\beta = 2*(1/9)/(1/7)=1.56>1$). We have also checked that the solution $g(a)\sim (a_{max}-a)^{\beta -1}$ is in an excellent agreement with numerics at the interval ($a_{max}/2$, $a_{max}$), Fig. 8. In addition, the number of cells N(t) indeed increases exponentially with time. To get more precise theoretical values of $\beta$ and k, this solution can be substituted back to Eq. 8 and to the expression for k. After a few iterations, we get $\beta \simeq 0.69$ (the numerical value is 0.67) and $k\simeq 0.043$ (the numerical value is 0.047). This theoretical asymptotics for the total number of cells, $N = N_0 \exp (kt)$ is shown in the lower panel of Fig. 1, and a good agreement with the numerical simulations for stage I is observed. Once the solution for the interval ($a_{max}/2$, $a_{max}$) is known, one can find the solution for the interval ($a_{max}/4$, $a_{max}/2$) since now g(2a) has been already computed.

Fig. 8

Scaled cell area distribution g(a) at the end of stage I at times $t=48$ h (blue solid curve), $t=54$ h (red dash-dotted curve) and $t=60$ h (green dotted curve). With the scaling $g(a_{max}/2)=1$ the three lines collapse on a single curve. Black dashed line is the theoretical prediction (see text) for the interval ($a_{max}/2$, $a_{max}$). The maximal cell division rate of $\alpha _1 =1/18$ h$^{-1}$, the cell growth rate $c=1/7$ h$^{-1}$, $a_{max} = 1000\,{\upmu \mathrm{m}}^2$, and the bin size $\delta _a = 100\,{\upmu \mathrm{m}}^2$ (Color figure online)