Abstract
The theory of quasifree quantum stochastic calculus for infinite-dimensional noise is developed within the framework of Hudson–Parthasarathy quantum stochastic calculus. The question of uniqueness for the covariance amplitude with respect to which a given unitary quantum stochastic cocycle is quasifree is addressed, and related to the minimality of the corresponding stochastic dilation. The theory is applied to the identification of a wide class of quantum random walks whose limit processes are driven by quasifree noises.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum stochastic calculus for gauge-invariant quasifree representations of the canonical commutation (and anticommutation) relations was originally developed in the 1980s; see [8, 22, 23, 27]. The possibilities afforded for semigroup dilation using such a calculus were further developed in [1] and [30], with the latter treatment using a theory of integral-sum kernel operators. One-dimensional squeezed noise is analysed in [20], where additive and multiplicative cocycles over a finite-dimensional quantum probability space are studied and an Itô table is generated. Recently, quasifree stochastic calculus has been extended to the cases of squeezed states and infinite-dimensional noise [31, 32]. A key ingredient of the latter theory is a partial transpose defined on a class of unbounded operators affiliated to the noise algebra, which defies the failure of complete boundedness for the transpose.
Use of quasifree stochastic calculus may be preferred to the standard theory founded by Hudson and Parthasarathy [24, 35] for both physical and mathematical reasons [23]. On the one hand, it describes systems which are more physically realistic, at non-zero temperatures for example. On the other hand, the quasifree theory boasts a fully satisfactory martingale representation theorem [22, 31], in contrast to the standard theory, whose representation theorem is restricted by regularity assumptions which seem hard to overcome [36, 37].
The purpose of this article is twofold. The first is to develop quasifree stochastic calculus in a simplified form within the standard theory, restricting to quasifree states with bounded covariance amplitudes and unitary quantum stochastic cocycles with norm-continuous vacuum-expectation semigroups (Sects. 4 and 5). The second is to give a deeper explanation of the continuous limit of the Hamiltonian description of a repeated-interactions model at non-zero temperature. Various limits in a similar setting were investigated by Attal and Joye in [5, 6]. In particular, the paper [6] describes how the quantum Langevin equation, obtained as limit of a repeated-interactions model with particles in a thermal state, is driven by noises satisfying quasifree Itô product relations (Sect. 6). Those parts relating to the first objective are written so as to facilitate the second. Our main results are Theorems 6.4 and 6.8, which may be summarised as follows. From a faithful, normal state \(\rho \) on \(B(\mathfrak {p})\), with the latter viewed as the particle observable algebra, and a total Hamiltonian \(H_{\textsf {T}}(\tau )\) of repeated-interaction form, acting on the tensor product \(\mathfrak {p}\otimes \mathfrak {h}\) for a system space \(\mathfrak {h}\), we derive a gauge-invariant covariance amplitude \(\Sigma (\rho )\) and a quantum stochastic cocycle Y with the following properties: Y satisfies a quantum Langevin equation of a particular form, with respect to \(\Sigma (\rho )\)-quasifree noise, and the scaled quantum random walks generated by \(H_{\textsf {T}}(\tau )\) converge to Y as the time-step parameter \(\tau \) converges to 0.
The quasifree CCR representations that we employ are of Araki–Woods type, determined by two maps: the doubling map
where \((\overline{\textsf {k}}, k)\) is the Hilbert space conjugate to the quasifree noise-dimension space \(\textsf {k}\), and an operator
for which the real-linear map \(\Sigma \circ \iota \) is symplectic. The corresponding Weyl operators \(W_\Sigma (f)\) act on the double Boson Fock space
in the following manner:
where W(g) denotes the Fock–Weyl operator with test function g, and the operators \(\iota \) and \(\Sigma \) are extended to act on functions pointwise; for example, \(( \Sigma ^0_1 f )(t) := \Sigma ^0_1 f(t)\) for all \(t\in {\mathbb {R}_+}\). The symplectic hypothesis ensures that \(W_\Sigma \) defines a CCR representation. This class of representations is sufficiently general to include a range of interesting examples, while being concrete enough to render the resulting stochastic calculus straightforward to employ with a minimum of technicalities. Details of this representation theory are given in Sect. 2.
Section 3 collects the relevant results from standard quantum stochastic analysis, chosen in light of the requirements for the passage to quasifree stochastic calculus in Sect. 4. We motivate the definition of quasifree stochastic integrals by combining the Itô-type quantum stochastic integration of simple processes with the realisation of quasifree creation and annihilation operators in terms of creation and annihilation operators for the Fock representation, for the case of finite degrees of freedom. It is notable that quasifree stochastic integrability is unaffected by squeezing the state; indeed, the resulting transformation of quasifree integrands may be viewed as a change-of-variables formula for quasifree stochastic calculus (Theorem 4.4). Our approach demonstrates the central rôle in the theory played by a partial conjugation, which constrains the class of admissible integrands when the noise is infinite dimensional. This corresponds to the partial-transpose operation at the heart of the general quasifree stochastic analysis in [31, 32]. Viewing quasifree integrals as particular cases of standard quantum stochastic integrals allows us to employ the existing modern quantum stochastic theory [28] and to avoid any application of Tomita–Takesaki theory. While maintaining strict mathematical rigour, the simplicity of our approach makes it very suitable for applications.
Some uniqueness questions are addressed in Sect. 5. We first show that the change-of-variables effect of squeezing on quasifree integrals means that, for present purposes, we may restrict to gauge-invariant quasifree states. Then the stochastic generators of quasifree Hudson–Parthasarathy cocycles on an initial Hilbert space \(\mathfrak {h}\) are parameterised by triples of operators (A, H, Q), where \(A \in B(\textsf {k})\) is non-negative, \(H \in B(\mathfrak {h})\) is self-adjoint, and \(Q \in B(\mathfrak {h}; \textsf {k}\otimes \mathfrak {h})\) is \(\textsf {k}\)-conjugatable; see Definition 4.2. The set of triples that generate the same cocycle is parameterised by a class of self-adjoint operators in \(B(\textsf {k})\). Uniqueness for quasifree Hudson–Parthasarathy cocycles inducing a given inner Evans–Hudson flow j (Definition 3.17) is related to the minimality of j, as a stochastic dilation of its vacuum-expectation semigroup, in the sense of [13].
The final section, Sect. 6, concerns quantum random walks and the repeated-interactions model [7]. After a brief summary of the relevant results from the standard theory of quantum random walks [9, 12], we extend the example of Attal and Joye in two directions: to allow infinite-dimensional noise, and to incorporate an enlarged class of interaction Hamiltonians. We show that their example is part of the following more general phenomenon. If the particles in the repeated-interactions model are in a faithful normal state with density matrix \(\varrho \) then the quantum Langevin equation which governs the limit cocycle U is driven by a gauge-invariant quasifree noise with covariance amplitude determined by the state. This is proved under the assumptions that \(\varrho \) enjoys exponential decay of its eigenvalues, and the interaction Hamiltonian is conjugatable (with respect to the Hilbert space \(\mathfrak {p}\) on which \(\varrho \) acts) and has no diagonal part with respect to the eigenspaces of \(\varrho \) (Theorem 6.8). The result also includes sufficient further conditions, on the matrix components of the interaction Hamiltonian, for the quasifree noise to be the unique one within the class for which U is quasifree. The GNS space given by the particle state splits naturally into mutually conjugate upper-triangular and lower-triangular parts; this splitting may be viewed as being the origin of the double Fock space arising in the relevant CCR representation.
We expect our results to be of interest to researchers in quantum optics and related fields; the importance of quantum stochastic calculus to quantum control engineering, for example, is clearly demonstrated in many of the papers contained in the collection [19]. In future work, we intend to explore quantum control theory within this quasifree framework. For initial results on quasifree filtering, which show the potential benefit of using squeezed fields for state restoration, see [14].
Notation and conventions
Throughout, the symbol \(\textsf {h}\), sometimes adorned with primes or subscripts, stands for a generic Hilbert space; with this understanding, we usually refrain from saying “let \(\textsf {h}\) and \(\textsf {h}'\) be Hilbert spaces”, et cetera. All Hilbert spaces considered are complex and separable, with inner products linear in their second argument. The space of bounded operators from \(\textsf {h}\) to \(\textsf {h}'\) is denoted \(B(\textsf {h}; \textsf {h}')\), and \(B ( \textsf {h})_{{\text {sa} }}\), \(B(\textsf {h})_+\), \(U( \textsf {h})\) and \(B(\textsf {h})^\times \) denote respectively the sets of self-adjoint and non-negative operators in \(B( \textsf {h}) := B(\textsf {h}; \textsf {h})\), and the groups of unitary operators on \(\textsf {h}\) and operators in \(B(\textsf {h})\) with bounded inverse.
A conjugate Hilbert space of \(\textsf {h}\) is a pair \(({\overline{\textsf {h}}}, k)\) consisting of an anti-unitary operator k from \(\textsf {h}\) to a Hilbert space \({\overline{\textsf {h}}}\); this is unique up to isomorphism in the natural sense. For any \(x \in \textsf {h}\) and \(A \in B(\textsf {h})\), the vector \(k x \in {\overline{\textsf {h}}}\) and the operator \(k A k^{-1}\in B( {\overline{\textsf {h}}})\) are abbreviated to \(\overline{x}\) and \(\overline{A}\) respectively. The closed linear span of a subset S of a Hilbert space is denoted \({{\,\mathrm{\overline{{{\,\mathrm{Lin}\,}}}}\,}}S\); the range of a bounded operator T and its closure are denoted \({{\,\mathrm{Ran}\,}}T\) and \({{\,\mathrm{\overline{{{\,\mathrm{Ran}\,}}}}\,}}T\) respectively. The domain of an unbounded operator T is denoted \({{\,\mathrm{Dom}\,}}T\). We employ the Dirac-inspired bra and ket notation
for any vector \(x \in \textsf {h}\).
Algebraic, Hilbert-space and ultraweak tensor products are denoted \(\, \, \underline{\otimes }\, \,\), \(\otimes \) and \(\overline{\otimes }\,\), respectively. The indicator function of a set S is denoted \(1_{S}\). The group of complex numbers with unit modulus is denoted \(\mathbb {T}\). The integer part of a real number r is denoted \(\lfloor r \rfloor \).
2 CCR Representations
In this section, we collect some key facts on CCR representations and quasifree states. In particular, we introduce the squeezing matrices and AW amplitudes that determine the class of quasifree states that are relevant to us.
Recall that every real-linear operator \(T: \textsf {h}\rightarrow \textsf {h}'\) is uniquely decomposable as \(L + A\), where L is complex linear and A is conjugate linear; L and A are referred to as the linear and conjugate-linear parts of T. Explicitly,
Definition 2.1
A real-linear operator \(Z: \textsf {h}\rightarrow \textsf {h}'\) is symplectic if it satisfies
We denote the space of symplectic operators from \(\textsf {h}\) to \(\textsf {h}'\) by \(S(\textsf {h}; \textsf {h}')\), or \(S(\textsf {h})\) when \(\textsf {h}' = \textsf {h}\), and the group of symplectic automorphisms of \(\textsf {h}\) by \(S(\textsf {h})^\times \).
For a complex linear map T from \(\textsf {h}\) to \(\textsf {h}'\), it is easily verified that T is isometric if and only if it is symplectic. In particular, \(U(\textsf {h})\) is the subgroup of \(S(\textsf {h})^\times \) consisting of its complex-linear elements.
It is shown in the appendix that symplectic automorphisms of \(\textsf {h}\) are automatically bounded. Thus \(S ( \textsf {h})^\times \) is a subgroup of the group of bounded invertible real-linear operators on \(\textsf {h}\).
A parameterisation \(B = B_{V,C,P}\) for the elements of \(S(\textsf {h})^\times \) is also given in the appendix.
For the rest of this section, we fix a Hilbert space \(\textsf {H}\) and let \(({\overline{\textsf {H}}}, K)\) be its conjugate Hilbert space.
2.1 Fock Space
As emphasised by Segal [41], the Boson Fock space over \(\textsf {H}\) has two interpretations, particle and wave:
Here \(\textsf {H}^{\vee n}\) denotes the nth symmetric tensor power of \(\textsf {H}\), with \(\textsf {H}^{\vee 0} := \mathbb {C}\), and \(\varepsilon (x)\) is the exponential vector corresponding to the test vector x:
The normalised exponential vector \(\exp ( - \tfrac{1}{2}||x ||^2 ) \varepsilon (x)\) is denoted \(\varpi (x)\), and the distinguished vector \(\varepsilon (0) = \varpi (0)\) is denoted \(\Omega _\textsf {H}\) and called the Fock vacuum vector. For all \(x,y \in \textsf {H}\),
and the map \(\lambda \mapsto \varepsilon (x + \lambda y )\) is holomorphic from \(\mathbb {C}\) to \(\Gamma ( \textsf {H})\). As well as being total in \(\Gamma (\textsf {H})\), the exponential vectors are linearly independent.
For any orthogonal decomposition \( \textsf {H}= \textsf {H}_1 \oplus \textsf {H}_2\), the Boson Fock space \(\Gamma ( \textsf {H})\) is identified with the tensor product \(\Gamma ( \textsf {H}_1 ) \otimes \Gamma ( \textsf {H}_2 )\) via the natural isometric isomorphism which sends the exponential vector \(\varepsilon (x_1, x_2)\) to \(\varepsilon (x_1) \otimes \varepsilon ( x_2)\) for all \(x_1 \in \textsf {H}_1\) and \(x_2 \in \textsf {H}_2\).
For any \(x \in \textsf {H}\), the Fock–Weyl operator\(W_\textsf {H}(x)\) is the unique unitary operator on \(\Gamma (\textsf {H})\) such that
For all \(x,y \in \textsf {H}\),
2.2 CCR Representations
We let \(CCR(\textsf {H})\) denote the universal \(C^*\)-algebra generated by unitary elements \(\{ w_x : x \in \textsf {H}\}\) satisfying the canonical commutation relations in Weyl form:
Its existence, uniqueness and simplicity were established in [43]. By universality, each operator \(B \in S(\textsf {H})^\times \), determines a unique automorphism \(\alpha _B\) of \(CCR(\textsf {H})\) such that
see [15, 39]. The gauge transformations of \(CCR(\textsf {H})\) are the automorphisms induced by the unitary operators on \(\textsf {H}\) of the form \(x \mapsto \lambda x\), where \(\lambda \in \mathbb {T}\).
If W is a map from \(\textsf {H}\) to \(U(\textsf {h})\) satisfying the Weyl form of the canonical commutation relations, then \(W = \pi \circ w\) for a unique representation \(\pi \) of \(CCR(\textsf {H})\) on \(\textsf {h}\). We therefore often refer to W itself as the representation. A representation W of \(CCR(\textsf {H})\) is regular if, for all \(x \in \textsf {H}\), the unitary group \(( W(tx) )_{t \in \mathbb {R}}\) is strongly continuous; in this case, the Stone generator R(x) of the group is called the field operator corresponding to the test vector x for the regular representation W.
2.3 Fock Representation
It follows from the definition (2.2) and properties (2.3a) and (2.3b) that the map \(x \mapsto W_\textsf {H}(x)\) defines a regular representation of \(CCR(\textsf {H})\) with cyclic vector \(\Omega _\textsf {H}\); this is called the Fock representation. If \(\{ R_\textsf {H}(y) : y \in \textsf {H}\}\) is the corresponding set of field operators then, for any \(x \in \textsf {H}\), the creation operator\(a^{+}_\textsf {H}(x)\) and annihilation operator\(a^{-}_\textsf {H}(x)\) are defined by setting
They are closed and mutually adjoint operators with common domain \({{\,\mathrm{Dom}\,}}R_\textsf {H}(ix) \cap {{\,\mathrm{Dom}\,}}R_\textsf {H}(x)\), on which the following canonical commutation relations hold [15]:
For any dense subspace \(\mathcal {D}\) of \(\textsf {H}\), the subspace \({{\,\mathrm{Lin}\,}}\{ \varepsilon (z): z \in \mathcal {D}\}\) is a common core for all Fock creation and annihilation operators, on which their actions are as follows:
2.4 Quasifree States and Representations
Let \(\mathfrak {a}\) be a non-negative real quadratic form on \(\textsf {H}\), and suppose
Then there is a unique state \(\varphi \) on \(CCR(\textsf {H})\) such that
see [15, 39]. Being non-negative, the form \(\mathfrak {a}\) polarises to a symmetric bilinear form [25]; in other words, the following map is real linear in each argument:
In particular, the following regularity property holds: for all \(x, y \in \textsf {H}\), the map \(t \mapsto \mathfrak {a}[ x + t y ]\) is continuous on \(\mathbb {R}\). If \(\dim \textsf {H}< \infty \) then \(\mathfrak {a}\) is bounded and therefore there exists a bounded non-negative real-linear operator T on \(\textsf {H}\) such that \(\mathfrak {a}[x] = {{\,\mathrm{Re}\,}}\langle x , Tx \rangle \) for all \(x \in \textsf {H}\).
Definition 2.2
A state \(\varphi \) on \(CCR(\textsf {H})\) is said to be (mean zero) quasifree if it satisfies (2.5) for some non-negative real quadratic form \(\mathfrak {a}\) satisfying (2.4); then \(\mathfrak {a}\) is called the covariance of\(\varphi \), and any real-linear operator \(Z: \textsf {H}\rightarrow \textsf {h}\) such that \(|| Z x ||^2 = \mathfrak {a}[x]\) for all \(x \in \textsf {H}\) is called a covariance amplitude for \(\varphi \).
A state \(\varphi \) on \(CCR(\textsf {H})\) is gauge invariant if it is invariant under each gauge transformation, so that \(\varphi ( w_{\lambda x } ) = \varphi ( w_{ x } )\) for all \(\lambda \in \mathbb {T}\) and \(x \in \textsf {H}\).
Remark
Covariances of gauge-invariant quasifree states on \(CCR(\textsf {H})\) are precisely the complex quadratic forms \(\mathfrak {a}\) on \(\textsf {H}\) such that
Example 2.3
The Fock vacuum state\(\varphi _\textsf {H}\) on \(CCR(\textsf {H})\), given by the identity
is the basic example of a gauge-invariant quasifree state, in view of (2.6) and the identity (2.3c).
Lemma 2.4
Let \(Z \in S{({\textsf {H}}; {\textsf {h}})}\). Then Z is a covariance amplitude for a quasifree state \(\varphi \) on CCR (H) . Moreover, if Z is complex linear then \(\varphi \) is gauge invariant.
Proof
The first part follows since
The second part is immediate. \(\square \)
Remark
Proposition 2.6 below shows that a covariance amplitude of a quasifree state need not be complex linear for the state to be gauge invariant.
Definition 2.5
The doubling map for\(\textsf {H}\) is the following bounded real-linear operator defined in terms of its conjugate Hilbert space \((\overline{\textsf {H}}, K)\):
Note that the range of the doubling map is total, since
Now set
and note that \(AW_0(\textsf {H}) = \big \{ \Sigma _A: A \in B( \textsf {H})_+ \big \}\), where
Proposition 2.6
Let \(\Sigma \in AW_0{({\textsf {H}})}\). The bounded real-linear operator \(\Sigma \circ \iota \) is symplectic, and the quasifree state on CCR(H) with covariance amplitude \(\Sigma \circ \iota \) is gauge invariant.
Conversely, let \(\varphi \) be a gauge-invariant quasifree state on CCR(H), the covariance of which is a bounded complex quadratic form on H. Then \(\varphi \) has a covariance amplitude of the form \(\Sigma \circ \iota \) for a unique operator \(\Sigma \in AW_0{({\textsf {H}})}\).
Proof
Let \(\Sigma = \left[ {\begin{matrix} C &{} 0 \\ 0 &{} \overline{S} \end{matrix}}\right] \in AW_0(\textsf {H})\), and set \(A := \sinh ^{-1} S \in B(\textsf {H})_+\), so that \(\Sigma = \Sigma _A\). Then, for all x, \(y \in \textsf {H}\),
It follows that \(\Sigma \circ \iota \) is symplectic, and is therefore a covariance amplitude of a quasifree state \(\varphi \) on \(CCR(\textsf {H})\). The resulting covariance \(\mathfrak {a}_\Sigma : x \mapsto || \Sigma \iota (x) ||^2\) satisfies
and is thereby manifestly gauge invariant.
Conversely, let \(\mathfrak {a}\) be the covariance of a gauge-invariant quasifree state on \(CCR(\textsf {H})\) and suppose that \(\mathfrak {a}\) is bounded. Since \(\mathfrak {a}\) is bounded and such that \(\mathfrak {a}[x] \geqslant || x ||^2\) for all \(x \in \textsf {H}\), there is a unique operator \(R \in B(\textsf {H})\) such that \(\langle x , Rx \rangle = \mathfrak {a}[x]\) for all \(x \in \textsf {H}\), and \(R \geqslant I_\textsf {H}\). The map \(A \mapsto \cosh 2A\) is a bijection from \(B(\textsf {H})_+\) onto \(\{ R \in B(\textsf {H})_+ : \, R \geqslant I_\textsf {H}\}\), and therefore, by the identity (2.8), it follows that \(\mathfrak {a}= \mathfrak {a}_\Sigma \) for a unique operator \(\Sigma = \Sigma _A\in AW_0(\textsf {H})\). \(\square \)
We now introduce the notion of squeezing, important in quantum optics. For any \(B \in S(\textsf {H})^\times \), set
where L and A are the linear and conjugate-linear parts of B. Thus \(M_B \in B( \textsf {H}\oplus \overline{\textsf {H}} )\).
Proposition 2.7
-
(a)
If \(B\in S{({\textsf {H}})}^\times \) then \(M_B\) is the unique operator \(M \in B({\textsf {H}}\oplus {\overline{{\textsf {H}}})}\) such that \(M \circ \iota = \iota \circ B\).
-
(b)
The map \(B \mapsto M_B\) is a faithful representation of the group \(S{({\textsf {H}})}^\times \) on \({\textsf {H}}\oplus {\overline{{\textsf {H}}}}\).
-
(c)
The map \(( A, B ) \mapsto \Sigma _A M_B\) from \(B({\textsf {H}})_+ \times S({\textsf {H}})^\times \) to \(B({\textsf {H}}\oplus {\overline{{\textsf {H}}})}\) is injective.
Proof
(a) First note that
The uniqueness part follows from the totality of \({{\,\mathrm{Ran}\,}}\iota \).
(b) By definition, the operator \(M_{I_\textsf {H}}\) equals \(I_{ \textsf {H}\oplus {\overline{\textsf {H}}}}\). It follows from (a) that, for all \(B, B' \in S(\textsf {H})^\times \),
and so \(M_B M_{B'} = M_{B B'}\). Thus, for each \(B \in S(\textsf {H})^\times \), the operator \(M_B\) is invertible and \(( M_B )^{-1} = M_{B^{-1}}\). Furthermore, if B, \(B' \in S(\textsf {H})^\times \) are such that \(M_B = M_{B'}\), then \(\iota \circ B = \iota \circ B'\), so \(B = B'\) by the injectivity of \(\iota \). Hence (b) holds.
(c) Suppose \(( A_1, B_1 )\), \(( A_2, B_2 ) \in B( \textsf {H})_+ \times S( \textsf {H})^\times \) are such that \(\Sigma _{A_1} M_{B_1} = \Sigma _{A_2} M_{B_2}\). It follows from part (b) that \(\Sigma _{A_1} = \Sigma _{A_2} M_B\), where \(B = B_2 B_1^{-1}\). Set \(C_i = \cosh A_i\) and \(S_i = \sinh A_i\), for \(i = 1\), 2, and let L and A be the linear and conjugate-linear parts of B. Then
As \(C_2\) and K are invertible, this implies that \(A = 0\), so B is complex linear and thus unitary, and \(C_1 = C_2 B\). This implies that \(C_1^2 = C_2 B B^* C_2 = C_2^2\), so \(C_1 = C_2\) and \(C_1 = C_1 B\). As \(C_1\) is invertible, it follows that \(B = I_\textsf {H}\) and (c) holds. \(\square \)
Definition 2.8
Set
We refer to the elements of \(M(\textsf {H})\), \(AW(\textsf {H})\) and \(AW_0(\textsf {H})\) respectively as squeezing matrices, AW amplitudes and gauge-invariant AW amplitudes for \(\textsf {H}\).
Remarks
-
(i)
The AW abbreviation is in acknowledgement of Araki and Woods [2].
-
(ii)
Each AW amplitude for \(\textsf {H}\) is of the form \(\Sigma _{A,B}\) for a unique pair \(( A, B ) \in B(\textsf {H})_+ \times S(\textsf {H})^\times \), by Proposition 2.7.
-
(iii)
Let \(\Sigma = \Sigma _{A,B}\in AW(\textsf {H})\). Then \(\Sigma \circ \iota \) is symplectic, since it is the composition of symplectic maps \(( \Sigma _A\circ \iota ) \circ B\), and so is a covariance amplitude of a quasifree state on \(CCR(\textsf {H})\), by Lemma 2.4.
-
(iv)
In terms of the parameterisation \(B = B_{V,C,P}:= V( \cosh P - C \sinh P )\) of \(B \in S(\textsf {H})^\times \) as in Theorem A.2, the squeezing matrices take the following form:
$$\begin{aligned} M_B&= M^{V,C,P}:= \begin{bmatrix} V \cosh P&V C \sinh P \cdot K^{-1} \\ K V C \sinh P&\overline{V \cosh P} \end{bmatrix}, \nonumber \\ ( M_B )^{-1}&= M_{B^{-1}}= M^{V^*, -VCV^*, VPV^*} \end{aligned}$$(2.9)and
$$\begin{aligned} \Sigma _{A,B}&= \Sigma ^{A,V,C,P}:= \begin{bmatrix} \cosh A \cdot V \cosh P&\cosh A \cdot V C \sinh P \cdot K^{-1} \\ K \sinh A \cdot V C \sinh P&\overline{ \sinh A \cdot V \cosh P} \end{bmatrix}. \end{aligned}$$(2.10)
2.5 Araki–Woods Representations
We are interested in the class of representations \(W_\Sigma \) of \(CCR(\textsf {H})\) of Araki–Woods type, and the corresponding quasifree states \(\varphi _\Sigma \), determined by AW amplitudes \(\Sigma = \Sigma _{A,B}\) as follows:
Remark
Let \(\Sigma = \Sigma _{A,B}\in AW(\textsf {H})\). On one hand, if A is injective then \({{\,\mathrm{Ran}\,}}\Sigma \circ \iota \) is total in \(\textsf {H}\oplus \overline{\textsf {H}}\) from which it follows that \(\Omega _{\textsf {H}\oplus {\overline{\textsf {H}}}}\) is a cyclic vector for the representation \(W_\Sigma \) [42] (see [28, Proposition 2.1]). On the other hand, if \(A = 0\) then \(W_\Sigma (x) = W_\textsf {H}( Bx) \otimes I_{\Gamma ({\overline{\textsf {H}}})}\) for all \(x \in \textsf {H}\), so \({{\,\mathrm{\overline{{{\,\mathrm{Lin}\,}}}}\,}}\{ W_\Sigma (x) \Omega _{\textsf {H}\oplus {\overline{\textsf {H}}}}: x \in \textsf {H}\} = \Gamma (\textsf {H}) \otimes \Omega _{\overline{\textsf {H}}}\).
These AW representations \(W_\Sigma \) inherit regularity from the Fock representation \(W_{\textsf {H}\oplus {\overline{\textsf {H}}}}\). As in the Fock case, given any \(x \in \textsf {H}\), setting
defines creation and annihilation operators via the quasifree field operators \(\{ R_\Sigma (z): z \in \textsf {H}\}\), which are the Stone generators of the corresponding unitary groups \(( W_\Sigma (t z) )_{t \in \mathbb {R}}\). We now relate these to Fock creation and annihilation operators.
Let the AW amplitude \(\Sigma \in B(\textsf {H}\oplus {\overline{\textsf {H}}})\) have the block-matrix form \(\left[ {\begin{matrix} \Sigma ^0_0 &{} \Sigma ^0_1 \\ \Sigma ^1_0 &{} \Sigma ^1_1 \end{matrix}}\right] \). The identification \(\Gamma ( \textsf {H}\oplus {\overline{\textsf {H}}}) = \Gamma ( \textsf {H}) \otimes \Gamma ( {\overline{\textsf {H}}})\) gives that
It follows that \(R_\Sigma (x)\) is the closure of the operator
by [40, Theorem VIII.33], which implies that
Thus, in terms of a parameterisation \(\Sigma = \Sigma ^{A,V,C,P}\), as in (2.10),
In particular, for a gauge-invariant AW amplitude \(\Sigma = \Sigma _A\),
Remark
The absence of minus signs in these relations is due to our choice of signs in the definition of the doubling map \(\iota \), and the choice of parameterisation of the symplectic automorphism B.
3 Quantum Stochastic Calculus
In this section we summarise the relevant elements of standard quantum stochastic calculus [17, 28, 34, 35] in a way which is adapted to the requirements of the quasifree stochastic calculus developed in Sect. 4. This section ends with discussions of the non-uniqueness of implementing quantum stochastic cocycles for an Evans–Hudson flow, and Bhat’s minimality criterion for quantum stochastic dilations.
For the rest of this article, we fix a Hilbert space \(\mathfrak {h}\), which is referred to as the initial space or system space. For this section, we also fix a Hilbert space \(\textsf {K}\) as the multiplicity space or noise dimension space. In later sections, this will vary or have further structure.
Notation
We use the abbreviations \(\Omega \), \(W\), \(a^{+}\), \(a^{-}\) and \(\mathcal {F}\) for \(\Omega _\textsf {H}\), \(W_\textsf {H}\), \(a^{+}_\textsf {H}\), \(a^{-}_\textsf {H}\) and \(\Gamma (\textsf {H})\), respectively, where the Hilbert space \(\textsf {H}\) equals \(L^2( {\mathbb {R}_+}; \textsf {K})\). As is customary, we abbreviate the simple tensor \(u \otimes \varepsilon (f)\) to \(u \varepsilon (f)\) whenever \(u \in \mathfrak {h}\) and \(f \in L^2( {\mathbb {R}_+}; \textsf {K})\).
For each \(t \in {\mathbb {R}_+}\) we have the decomposition \(\mathcal {F}= \mathcal {F}_{t)} \otimes \mathcal {F}_{[t}\), where \(\mathcal {F}_{t)} := \Gamma \bigl ( L^2( [ 0, t ); \textsf {K}) \bigr )\) and \(\mathcal {F}_{[t} := \Gamma \bigl ( L^2( [ t, \infty ); \textsf {K}) \bigr )\).
The space of compactly supported step functions from \({\mathbb {R}_+}\) to \(\textsf {K}\) is denoted \(\mathbb {S}\). Although we view \(\mathbb {S}\) as a subspace of \(L^2( {\mathbb {R}_+}; \textsf {K})\), we always take the right-continuous version of each step function, thus allowing us to evaluate these functions at any point in \({\mathbb {R}_+}\).
Note that \(\mathbb {S}\) enjoys the following useful properties:
-
(i)
If \(f \in \mathbb {S}\) and \(t\in {\mathbb {R}_+}\) then \(1_{[0,t)} f \in \mathbb {S}\);
-
(ii)
the exponential subspace\(\mathcal {E}:= {{\,\mathrm{Lin}\,}}\{ \varepsilon (f): f \in \mathbb {S}\}\) is dense in \(\mathcal {F}\);
-
(iii)
the subspace \({{\,\mathrm{Lin}\,}}\{ f( t ) : t \in {\mathbb {R}_+}\}\) is finite dimensional, for all \(f \in \mathbb {S}\).
In what follows we restrict our attention, as much as possible, to processes composed of bounded operators.
Definition 3.1
An \(\textsf {h}\)-\(\textsf {h}'\) process, or \(\textsf {h}\) process if \(\textsf {h}= \textsf {h}'\), is a function
which is adapted, so that
where \(I_{[t}\) is the identity operator on \(\mathcal {F}_{[t}\), and measurable, so that the function
is weakly measurable for all \(\xi \in \textsf {h}\otimes \mathcal {F}\). By separability, weak measurability may be replaced with strong measurability here.
An \(\textsf {h}\)-\(\textsf {h}'\) process X is
-
(i)
simple if it is piecewise constant and right continuous, so that there exists a strictly increasing sequence \((t_n)_{n \ge 1} \subseteq {\mathbb {R}_+}\) such that \(t_1 = 0\) and \(t_n \rightarrow \infty \) as \(n \rightarrow \infty \), with X constant on each interval \([t_n, t_{n+1})\);
-
(ii)
continuous if \(t \mapsto X_t \xi \) is continuous for all \(\xi \in \textsf {h}\otimes \mathcal {F}\);
-
(iii)
unitary if \(X_t\) is a unitary operator for all \(t \in {\mathbb {R}_+}\).
Every \(\textsf {h}\)-\(\textsf {h}'\) process X has an adjoint process, namely the \(\textsf {h}'\)-\(\textsf {h}\) process \(X^*: t \mapsto X_t^*\). Clearly \(X^*\) is simple if X is.
Notation
It is convenient to augment the multiplicity space, by setting
Thus \({\widehat{\textsf {K}}}\otimes \textsf {h}= \textsf {h}\oplus ( \textsf {K}\otimes \textsf {h})\) and any operator \(T \in B( {\widehat{\textsf {K}}}\otimes \textsf {h}; {\widehat{\textsf {K}}}\otimes \textsf {h}' )\) has a block-matrix form
Remark
One may also begin with a non-trivial Hilbert space \({\widehat{\textsf {K}}}\) and, by choosing a distinguished unit vector \(\omega \in {\widehat{\textsf {K}}}\), obtain \(\textsf {K}\) by setting \(\textsf {K}:= {\widehat{\textsf {K}}}\ominus \mathbb {C}\omega \). This observation will be useful in Sect. 6.
Definition 3.2
A \(\textsf {K}\)-integrand process on\(\mathfrak {h}\), or simply an integrand process, is a \({\widehat{\textsf {K}}}\otimes \mathfrak {h}\) process F such that, in terms of its block-matrix form \(\left[ {\begin{matrix} K &{} M \\ L &{} N \end{matrix}}\right] \),
for all \(v \in \mathfrak {h}\) and \(g \in \mathbb {S}\).
Remark
Suppose F is a \({\widehat{\textsf {K}}}\otimes \mathfrak {h}\) process such that, for all x, \(y \in \textsf {K}\), the function
is locally integrable. Then F is an integrand process.
Theorem 3.3
For any integrand process F, there exists a unique family \(\Lambda (F) := ( \Lambda (F)_t )_{t \geqslant 0}\) of linear operators, with common domain \(\mathfrak {h}\, \, \underline{\otimes }\, \,\mathcal {E}\) and codomain \(\mathfrak {h}\otimes \mathcal {F}\), such that
for all u, \(v \in \mathfrak {h}\), f, \(g \in \mathbb {S}\) and \(t \in {\mathbb {R}_+}\). Furthermore, if r, \(t \in {\mathbb {R}_+}\) are such that \(r \leqslant t\) then
for all u, \(v \in \mathfrak {h}\) and f, \(g \in \mathbb {S}\), where \(C(g) := ||g || + ( 1 + ||g ||^2 )^{1/2}\).
Proof
See [28, Theorem 3.13]. \(\square \)
Remark
The identity (3.1) is known as the first fundamental formula of quantum stochastic calculus.
Corollary 3.4
If \(F = \left[ {\begin{matrix} K &{} M \\ L &{} N \end{matrix}}\right] \) is an integrand process and its adjoint process \(F^* = \left[ {\begin{matrix} K^* &{} L^* \\ M^* &{} N^* \end{matrix}}\right] \) is also an integrand process then \(\Lambda (F^*)_t \subseteq \Lambda (F)^*_t\) for all \(t \in {\mathbb {R}_+}\).
Remark
If the integrand process F is such that the operator \(\Lambda (F)_t\) is bounded, for all \(t \in {\mathbb {R}_+}\), then taking the closure of each operator defines a continuous \(\mathfrak {h}\) process which, by a slight abuse of notation, we also denote by \(\Lambda (F)\).
Notation
Let \(F = \left[ {\begin{matrix} K &{} M \\ L &{} N \end{matrix}}\right] \) be an integrand process. Then
are the time, creation, annihilation and preservation integrals, respectively.
The following proposition, which is readily verified, connects the definition of quantum stochastic integrals of Theorem 3.3 with the classical Itô integration of simple processes.
Proposition 3.5
Suppose the noise dimension space \({\textsf {K}}\) is finite dimensional, with orthonormal basis \((e_i)_{i \in \mathbb {I}}\). Let \(F = \left[ {\begin{matrix} K &{} M \\ L &{} N \end{matrix}}\right] \) be a simple integrand process, let \(t > 0\), and suppose the partition \(\{ 0 = t_0< t_1< \cdots < t_n = t \}\) contains the points of discontinuities of F on [0, t). Then
and
where \(L^i(s) := ( \langle e_i \vert \otimes I_{\mathfrak {h}\otimes \mathcal {F}} ) L(s)\) and \(M_i(s) := M(s) ( \vert e_i \rangle \otimes I_{\mathfrak {h}\otimes \mathcal {F}} )\).
Remark
The preservation integral \(A^\times (N)\) has a similar expression (see [35]) and the time integral is given by the straightforward prescription
The following result is the quantum Itô product formula, or second fundamental formula. To state it, we define the quantum Itô projection
which is ampliated to \(\left[ {\begin{matrix} 0 &{} 0 \\ 0 &{} I_{\textsf {K}\otimes \textsf {h}} \end{matrix}}\right] \) for appropriate choices of \(\textsf {h}\) without change of notation.
Theorem 3.6
Let F and G be integrand processes, let \(X_0, Y_0 \in B(\mathfrak {h}) \otimes I_\mathcal {F}\), and, for all \(t \in {\mathbb {R}_+}\), set \(X_t = X_0 + \Lambda (F)_t\) and \(Y_t = Y_0 + \Lambda (G)_t\). Then
for all u, \(v \in \mathfrak {h}\), f, \(g \in \mathbb {S}\) and \(t \in {\mathbb {R}_+}\).
Proof
See [28, Theorem 3.15]. \(\square \)
Definition 3.7
The map
is called the vacuum expectation. For all \(t \in {\mathbb {R}_+}\), let \(\sigma ^\textsf {K}_t\) be the normal \(*\)-endomorphism of \(B(\mathcal {F})\) such that
The family \(\sigma ^\textsf {K}:= ( \sigma ^\textsf {K}_t)_{t\geqslant 0}\) is called the CCR flow of index\(\textsf {K}\). We set
Remark
The vacuum expectation is normal, unital and completely positive, and the family \(\sigma = (\sigma _t)_{t \geqslant 0}\), is an \(E_0\) semigroup [3] such that:
Definition 3.8
An \(\mathfrak {h}\) process Y is a quantum stochastic cocycle on \(\mathfrak {h}\) if
and an elementary QS cocycle if its vacuum expectation semigroup \(( \mathbb {E}_\Omega [ Y_t ] )_{t \geqslant 0}\) is norm continuous. A Hudson–Parthasarathy cocycle, or HP cocycle in short, is a unitary elementary QS cocycle.
Remark
The fact that \( ( \mathbb {E}_\Omega [ Y_t ] )_{t \geqslant 0}\) is a one-parameter semigroup follows from the adaptedness relations
and the identity (3.2): note that
Notation
Let
Theorem 3.9
-
(a)
Let \(F \in B( \widehat{{\textsf {K}}} \otimes \mathfrak {h})\). The following are equivalent.
-
(i)
\(F = \left[ {\begin{matrix} K &{} -L^* W \\ L &{} W - I_{{\tiny {\textsf {K}}} \otimes \mathfrak {h}} \end{matrix}}\right] \) where \(K = \mathrm {i}H - \tfrac{1}{2}L^*L\), for a self-adjoint operator H and unitary operator W.
-
(ii)
\(F^* + F + F^* \Delta F = 0 = F + F^* + F \Delta F^*\).
-
(iii)
There is a unitary \(\mathfrak {h}\) process U such that
$$\begin{aligned} U_t = I_{\mathfrak {h}\otimes \mathcal {F}} + \Lambda ( F \cdot U )_t \qquad \text {for all } t \in {\mathbb {R}_+}, \end{aligned}$$(3.3)where \((F \cdot U)_s := ( F \otimes I_\mathcal {F})( I_{\hat{{\textsf {K}}}} \otimes U_s )\) for all \(s \in {\mathbb {R}_+}\).
In this case, U is the unique unitary \(\mathfrak {h}\) process satisfying (3.3).
-
(i)
-
(b)
Let U be a unitary \(\mathfrak {h}\) process. The following are equivalent.
-
(i)
U satisfies (3.3) for some operator \(F \in B(\widehat{{\textsf {K}}} \otimes \mathfrak {h})\).
-
(ii)
U is an HP cocycle.
In this case,
$$\begin{aligned} \langle {\widehat{x}}\otimes u , ( F + \Delta ) {\widehat{y}}\otimes v \rangle = \lim _{t \rightarrow 0+} t^{-1} \bigl \langle u \varepsilon ( x 1_{[0,t)} ), ( U_t - I_{\mathfrak {h}\otimes \mathcal {F}} ) v \varepsilon ( y 1_{[0,t)} ) \bigr \rangle \end{aligned}$$(3.4)for all u, \(v \in \mathfrak {h}\) and x, \(y \in {\textsf {K}}\). In particular, the vacuum expectation semigroup of U has generator K, where K is the top left entry of the block matrix operator F.
-
(i)
-
(c)
If \(F \in B(\widehat{{\textsf {K}}} \otimes \mathfrak {h})_0\) then (i) and (ii) of (a) have the respective equivalents.
-
(i)
\(F = \left[ {\begin{matrix} K &{} -L^* \\ L &{} 0 \end{matrix}}\right] \), where \(K + \tfrac{1}{2}L^* L\) is skew-adjoint.
-
(ii)
\(F^* + F + F^* \Delta F = 0\).
-
(i)
Proof
Part (a) is covered by Theorems 7.1 and 7.5 of [33]. For (b), see [28]. The identity (3.4) is a straightforward consequence of (3.3), the first fundamental formula (3.1) and the strong continuity of U. \(\square \)
Remark
The quantum stochastic equation (3.3) is referred to as the quantum Langevin equation in the physics literature [18, 45].
Definition 3.10
Given an HP cocycle U, the unique operator F, or triple (H, L, W), associated with U via (3.4) is called its stochastic generator. Conversely, for an operator \(F \in B({\widehat{\textsf {K}}}\otimes \mathfrak {h})\) having the block-matrix form given in Theorem 3.9(a)(i), the unique HP cocycle satisfying (3.3) is denoted \(Y^F\) or \(U^{(H,L,W)}\).
Remark
If F is the stochastic generator of an HP cocycle then Theorem 3.9 implies that \(F^*\) is also such a generator, since
where \(\widetilde{W} = W^*\), \(\widetilde{L} = -W^*L\) and \(\widetilde{H} = -H\). However, it is usually not the case that \(Y^{F^*}\) and \(( Y^F)^*\) are equal. An exception is when \(\mathfrak {h}= \mathbb {C}\), described in Example 3.13.
In this article, we are mainly concerned with the following subclass of HP cocycles discussed in [29].
Definition 3.11
An HP cocycle is Gaussian if its stochastic generator lies in \(B({\widehat{\textsf {K}}}\otimes \textsf {h})_0\). Equivalently, its parameterisation has the form \((H, L, I_{\textsf {K}\otimes \mathfrak {h}} )\).
Corollary 3.12
The prescription \((H,L,W) \mapsto U^{(H,L,W)}\) defines a bijection
and the restriction \((H,L) \mapsto U^{(H,L,I)}\) defines a bijection
Example 3.13
(Pure-noise cocycles) For any \(z \in \textsf {K}\), setting \(W^z := ( W( z 1_{[0,t)} ) )_{t \geqslant 0}\) defines an HP cocycle on \(\mathbb {C}\). An operator \(F \in B( {\widehat{\textsf {K}}})\) is the generator of an HP cocycle on \(\mathbb {C}\) if and only if
The Gaussian pure-noise cocycles are precisely those of the form \(( e^{ \mathrm {i}\alpha t} W^z_t )_{t\geqslant 0}\) for some \(\alpha \in \mathbb {R}\) and \(z \in \textsf {K}\).
As \(B( \mathcal {F}_{r)} ) \otimes I_{[r}\) and \(\sigma ^\textsf {K}_r\bigl ( B( \mathcal {F}) \bigr ) = I_{r)} \otimes B( \mathcal {F}_{[r} )\) commute for all \(r \in {\mathbb {R}_+}\), the adjoint process \((Y^F)^*\) is equal to the HP cocycle \(Y^{F^*}\) in this case.
Lemma 3.14
Let U be an HP cocycle on \(\mathfrak {h}\) and let u be a pure-noise HP cocycle with the same noise dimension space. Then
is an HP cocycle on \(\mathfrak {h}\). Moreover, the stochastic generators \(\widetilde{F}\sim ( \widetilde{H}, \widetilde{L}, \widetilde{W})\) of \(\widetilde{U}\), \(F \sim (H, L, W)\) of U and \(f \sim (\alpha , \vert z \rangle , w)\) of u are related as follows:
or, equivalently,
Proof
That the unitary process \(\widetilde{U}\) is a QS cocycle follows from the fact that \(\sigma _r(U_t)\) and \(I_\mathfrak {h}\otimes u_r\) commute for all r, \(t \in {\mathbb {R}_+}\). The quantum Itô product formula, Theorem 3.6, implies that \(\widetilde{U}_t = I_{\mathfrak {h}\otimes \mathcal {F}} + \Lambda ( \widetilde{F}\cdot \widetilde{U})_t\) for all \(t \in {\mathbb {R}_+}\), where \(\widetilde{F}= ( f \otimes I_\mathfrak {h}) + F + ( f \otimes I_\mathfrak {h}) \Delta F\). It now follows from the uniqueness part of Theorem 3.9 that \(\widetilde{U}\) equals the HP cocycle \(Y^{\widetilde{F}}\), so that \(\widetilde{U}= U^{( \widetilde{H}, \widetilde{L}, \widetilde{W})}\) where \(( \widetilde{H}, \widetilde{L}, \widetilde{W})\) is given by (3.5). \(\square \)
Remark
More general conditions under which the product of two elementary QS cocycles is a QS cocycle are given in [44].
Definition 3.15
A quantum dynamical semigroup\(\mathcal {P} = ( \mathcal {P}_t )_{t \geqslant 0}\) is a semigroup of completely positive contractive normal maps on \(B(\mathfrak {h})\) which is pointwise weak operator continuous. If \(\mathcal {P}_t\) is unital for all \(t \in {\mathbb {R}_+}\) then \(\mathcal {P}\) is called conservative.
Remark
The generator \(\mathcal {L}\) of a norm-continuous conservative quantum dynamical semigroup is expressible in Lindblad form [26]: there exists a separable Hilbert space \(\textsf {K}\), a self-adjoint operator \(H \in B(\mathfrak {h})\) and an operator \(L \in B( \mathfrak {h}; \textsf {K}\otimes \mathfrak {h})\) such that
where \([\ ,\ ]\) and \(\{\ ,\ \}\) denote the commutator and anti-commutator, respectively.
Theorem 3.16
Let U be an HP cocycle with stochastic generator (H, L, W). For all \(t \in {\mathbb {R}_+}\), let
and let
-
(a)
If \(j^{{\textsf {K}}} := ( {{\,\mathrm{id}\,}}_{B({\hat{{\textsf {K}}}})} \overline{\otimes }\,j_t)_{t \geqslant 0}\), so that
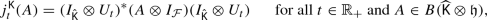
then \(\bigl ( ( j^{{\textsf {K}}}_t \circ \theta )(a) \bigr )_{t \geqslant 0}\) is an integrand process for all \(a \in B( \mathfrak {h})\) and
$$\begin{aligned} j_t(a) = a \otimes I_\mathcal {F}+ \Lambda \bigl ( ( j^{{\textsf {K}}} \circ \theta )(a) \bigr )_t \qquad \text {for all } a \in B(\mathfrak {h}) \text { and } t \in {\mathbb {R}_+}. \end{aligned}$$(3.8)Furthermore, the family \(j = ( j_t )_{t \geqslant 0}\) is the unique mapping process consisting of normal \(*\)-homomorphisms that satisfies (3.8).
-
(b)
The mapping process j obeys the cocycle relation
$$\begin{aligned} j_{r+t} = \widehat{\jmath }_r \circ \sigma _r \circ j_t \qquad \text {for all } r,t \in {\mathbb {R}_+}, \end{aligned}$$where \(\widehat{\jmath }_r\) is the normal *-homomorphism from \({{\,\mathrm{Ran}\,}}\sigma _r\) to \(B(\mathfrak {h}\otimes \mathcal {F})\) such that
$$\begin{aligned} \widehat{\jmath }_r(a \otimes b) = j_r(a) ( I_\mathfrak {h}\otimes b ) \qquad \text {for all } a \in B(\mathfrak {h}) \text { and } b \in {{\,\mathrm{Ran}\,}}\sigma ^{{\textsf {K}}}_r \subseteq B(\mathcal {F}). \end{aligned}$$Moreover, setting \(\mathcal {P} := ( \mathbb {E}_\Omega \circ j_t )_{t \geqslant 0}\) defines a norm-continuous conservative quantum dynamical semigroup on \(B(\mathfrak {h})\), the vacuum expectation semigroup of j.
-
(c)
For all \(a \in B(\mathfrak {h})\), u, \(v \in \mathfrak {h}\) and x, \(y\in {\textsf {K}}\),
$$\begin{aligned} \bigl \langle {\widehat{x}}\otimes u, ( \theta (a) + \Delta \otimes a ){\widehat{y}}\otimes v \bigr \rangle = \lim _{t \rightarrow 0+} t^{-1} \bigl \langle u \varepsilon ( x 1_{[0,t)} ), ( j_t(a) - a \otimes I_{\mathcal {F}} ) v \varepsilon ( y 1_{[0,t)} ) \bigr \rangle . \end{aligned}$$In particular, the vacuum expectation semigroup of j has generator \(\mathcal {L}\), given by (3.6).
Proof
That j satisfies (3.8) follows from the quantum Itô product formula. In turn, part (c) follows from (3.8), the first fundamental formula, Theorem 3.3, and the strong continuity of U. For (b) and the uniqueness part of (a), see [28] and [33]. \(\square \)
Definition 3.17
An inner Evans–Hudson flow on \(B(\mathfrak {h})\), or inner EH flow in short, is a mapping process j induced by an HP cocycle on \(\mathfrak {h}\), as above [16]. The map \(\theta \) is called the stochastic generator of j.
Remark
Let j be an inner EH flow on \(B(\mathfrak {h})\). Using the ampliations introduced in Theorem 3.16, the prescription \(J := ( \widehat{\jmath }_t \circ \sigma _t )_{t\geqslant 0}\) produces an \(E_0\) semigroup on \(B(\mathfrak {h}\otimes \mathcal {F})\) such that
where U is any HP cocycle inducing j. In turn, we can recover j from J, since \(j_t = J_t \circ \iota _\mathcal {F}\) for all \(t \in {\mathbb {R}_+}\), where the ampliation
Given an HP cocycle U, Lemma 3.14 provides sufficient conditions for an HP cocycle \(U'\) to induce the same EH flow as U. In the next result we show that these conditions are also necessary.
Proposition 3.18
Suppose j and \(j'\) are inner EH flows on \(B(\mathfrak {h})\) with noise dimension space \({\textsf {K}}\), induced by HP cocycles U and \(U'\) and having stochastic generators (H, L, W) and \((H',L',W')\), respectively. The following are equivalent.
-
(i)
The flows j and \(j'\) are equal.
-
(ii)
The process \(( U'_t U^*_t)_{t \geqslant 0}\) is the ampliation to \(\mathfrak {h}\) of a pure-noise HP cocycle.
-
(iii)
There is a scalar \(\alpha \in \mathbb {R}\), a vector \(z \in {\textsf {K}}\) and an operator \(w \in U({\textsf {K}})\) such that
$$\begin{aligned} w \otimes I_\mathfrak {h}&= W'W^*, \\ \vert z \rangle \otimes I_\mathfrak {h}&= L' - ( w \otimes I_\mathfrak {h}) L \\ \text {and} \qquad \alpha I_\mathfrak {h}&= H' - H - \tfrac{\mathrm {i}}{2} \bigl ( ( \langle w^* z \vert \otimes I_\mathfrak {h}) L - L^* ( \vert w^* z \rangle \otimes I_\mathfrak {h}) \bigr ). \end{aligned}$$
Proof
If (ii) holds then Lemma 3.14 implies that (iii) holds.
If (iii) holds then it is easily verified that \(\theta '\), defined from \((H',L',W')\) rather than (H, L, W), coincides with \(\theta \). Thus (i) holds by the uniqueness part of Theorem 3.16(a).
Finally, suppose that (i) holds, and let X denote the unitary process \(( U'_t U^*_t )_{t \geqslant 0}\). For all \(t \in {\mathbb {R}_+}\), the operator \(X_t\) commutes with all operators in \(B( \mathfrak {h}) \otimes I_\mathcal {F}\), so \(X_t = I_\mathfrak {h}\otimes u_t\) for some unitary operator \(u_t \in B(\mathcal {F})\). This implies that \(X_r\) commutes with \(\sigma _r( U_t^* )\) for all r, \(t \in {\mathbb {R}_+}\), and so
Hence \(u = (u_t)_{t \geqslant 0}\) is a unitary QS cocycle on \(\mathbb {C}\). Since \(( U')^*\) and \(U^*\) are both strongly continuous and unitary, u is strongly continuous and therefore its vacuum expectation semigroup P is too. As P is a semigroup on \(\mathbb {C}\), this implies that P is norm continuous. Thus u is an HP cocycle and therefore (ii) holds.\(\square \)
Remarks
Given a norm-continuous conservative quantum dynamical semigroup \(\mathcal {P}\) on \(B(\mathfrak {h})\), its generator \(\mathcal {L}\) is expressible in Lindblad form (3.6) for some separable Hilbert space \(\textsf {K}\) and operators \(H=H^* \in B(\mathfrak {h})\) and \(L \in B(\mathfrak {h}; \textsf {K}\otimes \mathfrak {h})\). In turn, Theorem 3.16 implies that the inner EH flow j induced by the HP cocycle with generator \((H,L,I_{\textsf {K}\otimes \mathfrak {h}})\) has vacuum expectation semigroup \(\mathcal {P}\). In this sense, the flow j is a stochastic dilation of\(\mathcal {P}\).
The non-uniqueness of triples \((\textsf {K},H,L)\) determining the generator \(\mathcal {L}\) of a norm-continuous quantum dynamical semigroup on \(B(\mathfrak {h})\) is analysed in [38]; this may be compared to the non-uniqueness of triples (H, L, W) determining the stochastic generator \(\theta \) of a given inner EH flow j characterised in Proposition 3.18.
The construction of stochastic dilations was a major motivation for the original development of quantum stochastic calculus [24, 35].
We end this summary of standard quantum stochastic calculus by connecting it to Bhat’s analysis of dilations of the above form, in particular the question of minimality.
Theorem 3.19
([13, Theorem 9.1]) Let j be an inner EH flow. The following are equivalent.
-
(i)
As a stochastic dilation of its vacuum expectation semigroup, the flow j is minimal:
$$\begin{aligned} {{\,\mathrm{\overline{{{\,\mathrm{Lin}\,}}}}\,}}\big \{ j_{t_1} ( a_1 ) \cdots j_{t_n} ( a_n ) u \Omega : u \in \mathfrak {h}, n \geqslant 1, a_i, \ldots , a_n \in B(\mathfrak {h}), t_1, \ldots , t_n \in {\mathbb {R}_+}\big \} = \mathfrak {h}\otimes \mathcal {F}. \end{aligned}$$ -
(ii)
The stochastic generator (H, L, W) of any HP cocycle which induces j satisfies
$$\begin{aligned} ( \langle z \vert \otimes I_\mathfrak {h}) L \notin \mathbb {C}I_\mathfrak {h}\ \text { for all } z \in {\textsf {K}}\setminus \{ 0 \}. \end{aligned}$$
Remarks
To see directly that (ii) is independent of the choice of HP cocycle which induces j, note that for two such HP cocycles with stochastic generators \((H_1,L_1,W_1)\) and \((H_2,L_2,W_2)\), it holds that
by Proposition 3.18. This also gives the following further equivalent condition.
-
(iii)
The stochastic generator (H, L, W) of any HP cocycle which induces j is such that the degeneracy space \(\textsf {K}^L\) equals \(\{ 0 \}\); for the definition of \(\textsf {K}^L\), see (5.1).
Bhat actually deals with the associated \(E_0\) semigroup \(J := ( \widehat{\jmath }_t \circ \sigma _t )_{t\geqslant 0}\) on \(B(\mathfrak {h}\otimes \mathcal {F})\) which, in view of the remark following Definition 3.17, is equivalent.
4 Quasifree Stochastic Calculus
In this section we produce a simplified form of the coordinate-free multidimensional quasifree stochastic calculus [31, 32] with respect to a fixed AW amplitude \(\Sigma = \Sigma _{A,B}\) for a Hilbert space \(\textsf {k}\), the quasifree noise dimension space, whose conjugate Hilbert space we denote by \(( \overline{\textsf {k}}, k)\).
In contrast to the approach of [31, 32], here we focus on that part of the quasifree stochastic calculus that may be obtained inside the standard theory summarised in Sect. 3. Thus, whilst being restricted to HP cocycles so that stochastic generators are all bounded, the results developed here do not require faithfulness of the quasifree states employed.
The conjugate Hilbert space of \(L^2({\mathbb {R}_+}; \textsf {k})\) is identified with \(L^2( {\mathbb {R}_+}; \overline{\textsf {k}})\) (conjugation being defined pointwise: \(\overline{f}(t) := \overline{f(t)}\)), and the orthogonal sum \(L^2({\mathbb {R}_+}; \textsf {k}) \oplus L^2( {\mathbb {R}_+}; \overline{\textsf {k}})\) is identified with \(L^2( {\mathbb {R}_+}; \textsf {k}\oplus \overline{\textsf {k}})\). Note that we are here working with the Boson Fock space \(\mathcal {F}\) over \(L^2( {\mathbb {R}_+}; \textsf {k}\oplus \overline{\textsf {k}})\).
Motivation
Let \(\left[ {\begin{matrix} \Sigma _0&\Sigma _1 \end{matrix}}\right] = \left[ {\begin{matrix} \Sigma ^0_0 &{} \Sigma ^0_1 \\ \Sigma ^1_0 &{} \Sigma ^1_1 \end{matrix}}\right] \) be the block-matrix form of the AW amplitude \(\Sigma \), with \(\Sigma _0 = \left[ {\begin{matrix} \Sigma ^0_0 \\ \Sigma ^1_0 \end{matrix}}\right] \in B(\textsf {k}; \textsf {k}\oplus \overline{\textsf {k}})\) and \(\Sigma _1 = \left[ {\begin{matrix} \Sigma ^0_1 \\ \Sigma ^1_1 \end{matrix}}\right] \in B(\overline{\textsf {k}}; \textsf {k}\oplus \overline{\textsf {k}})\). Following Proposition 3.5 and the relations (2.11a–b) expressing quasifree creation and annihilation operators \(a^{+}_\Sigma \) and \(a^{-}_\Sigma \) in terms of Fock creation and annihilation operators, the following requirements for quasifree stochastic integration become apparent.
Suppose the quasifree noise dimension space \(\textsf {k}\) is finite dimensional, with orthonormal basis \((e_i)_{i\in \mathbb {I}}\), let R be a simple (\(\textsf {k}\otimes \mathfrak {h}\))-\(\mathfrak {h}\) process, let \(t > 0\) and suppose the partition \(\{ 0 = t_0< \cdots < t_n = t\}\) contains the points of discontinuity of R on [0, t). (We are using the symbol R here for convenience; there is no suggestion of any connection with field operators, for which the symbol was used earlier.) Set
where
with \(\textsf {H}\) denoting \(L^2( {\mathbb {R}_+}; \textsf {k})\). Note that, for any \(u \in \mathfrak {h}\), f, \(g \in \mathbb {S}_\textsf {k}\) and x, \(y \in \textsf {k}\),
Thus
and therefore
Applying this reasoning to \(I_2(t)^*\), and exploiting adaptedness to commute the terms \(R_i(t_j)^*\) and \(I_\mathfrak {h}\otimes a^{-}_{\textsf {H}\oplus {\overline{\textsf {H}}}}( \Sigma ^0_1 \overline{e_i} 1_{[t_j, t_{j +1})}, \Sigma ^1_1 \overline{e_i} 1_{[t_j, t_{j +1})} )\), where \(i \in \mathbb {I}\) and \(j = 0, \ldots , n - 1\), yields the relation
where \(R^\textsf {T}\) is the \(\mathfrak {h}\)-\((\overline{\textsf {k}}\otimes \mathfrak {h})\) process such that
\(R^\textsf {T}\) is said to be partially transpose to R. It follows that
and therefore
Moreover, this also shows, for a suitable \(\mathfrak {h}\)-\((\textsf {k}\otimes \mathfrak {h})\) process Q, that
where \(Q^\textsf {T}\) is the \((\overline{\textsf {k}}\otimes \mathfrak {h})\)-\(\mathfrak {h}\) process partially transpose to Q, given by \(( Q^{* \textsf {T}*}_t )_{t\geqslant 0}\).
Hence
The preceding discussion shows clearly the need for a partial transpose operation for infinite-dimensional \(\textsf {k}\). A comprehensive theory is developed in [31, 32]. Here we specialise to our context of AW amplitudes, and it is convenient to concentrate on the composition of the partial transpose and adjoint operations.
First note that, for any \(Y \in B(\textsf {h}_1; \textsf {h}\otimes \textsf {h}_2)\), the quantity
is independent of the choice of orthonormal basis \((e_i)_{i \in \mathbb {I}}\) for \(\textsf {h}\). When it is finite,
where \(|| \cdot ||_2\) denotes the Hilbert–Schmidt norm. Let \(HS( \textsf {h}; \textsf {h}' )\) denote the space of Hilbert–Schmidt operators from \(\textsf {h}\) to \(\textsf {h}'\).
Theorem 4.1
Let \(Y \in B({\textsf {h}}_{1}; {\textsf {h}}\otimes {\textsf {h}}_{2})\).
-
(a)
The following are equivalent.
-
(i)
There is an operator \(Y^\textsf {c}\in B( {\textsf {h}}_{2}; \overline{{\textsf {h}}} \otimes {\textsf {h}}_{1})\) such that
$$\begin{aligned} ( \langle \overline{y} \vert \otimes I_{ {{\textsf {h}}}_1} ) Y^\textsf {c}= Y^* ( \vert y \rangle \otimes I_{{{\textsf {h}}}_2} ) \qquad \text {for all } y \in {\textsf {h}}. \end{aligned}$$(4.1) -
(ii)
The quantity \(c(Y)\) is finite.
In this case, the operator \(Y^\textsf {c}\) is unique and \(c(Y) = || Y^\textsf {c} ||\); furthermore, \(c( Y^\textsf {c}) = ||Y ||\) and \(Y^{\textsf {c}\textsf {c}} = Y\).
-
(i)
-
(b)
Suppose that \(c(Y) < \infty \), and let
$$\begin{aligned} X \in B({\textsf {h}}'; {\textsf {h}}''), \quad X_1 \in B({\textsf {h}}_{1}'; {\textsf {h}}_{1}), \quad Z_2 \in B({\textsf {h}}_{2}; {\textsf {h}}_{2}') \quad \text {and} \quad Z \in B({\textsf {h}}). \end{aligned}$$The following statements hold.
-
(i)
\(c(Y \otimes X) < \infty \) and \(( Y \otimes X )^\textsf {c}= Y^\textsf {c}\otimes X^*\), so \(c(Y \otimes X) = c(Y) || X ||\);
-
(ii)
\(c(Y X_1) < \infty \) and \((Y X_1)^\textsf {c}= ( I_{{\bar{{\textsf {h}}}}} \otimes X_1^* ) Y^\textsf {c}\);
-
(iii)
\(c( ( I_{{{\textsf {h}}}} \otimes Z_2 ) Y ) < \infty \) and \(\bigl ( ( I_{{{\textsf {h}}}} \otimes Z_2 ) Y \bigr )^\textsf {c}= Y^\textsf {c}Z_2^*\);
-
(iv)
\(c( ( Z \otimes I_{{{\textsf {h}}}_2} ) Y ) < \infty \) and \(\bigl ( ( Z \otimes I_{{{\textsf {h}}}_2} ) Y \bigr )^\textsf {c}= ( \overline{Z} \otimes I_{{{\textsf {h}}}_2} ) Y^\textsf {c}\).
-
(i)
-
(c)
Suppose that \(c(Y \otimes I_{{{\textsf {h}}}'} ) < \infty \) for some non-zero Hilbert space \({\textsf {h}}'\). Then \(c(Y) < \infty \) and \(Y^\textsf {c}\otimes I_{{{\textsf {h}}}'} = ( Y \otimes I_{{{\textsf {h}}}'})^\textsf {c}\).
-
(d)
Let \(T \in HS({\textsf {h}}_0; {\textsf {h}})\) and \(A \in B({\textsf {h}}_1; {\textsf {h}}_2)\). Then \(c( T \otimes A ) = ||T ||_2 \, ||A || < \infty \).
Proof
Let \((e_i)_{i \in \mathbb {I}}\) be an orthonormal basis for \(\textsf {h}\) and note the trivial identity
For (a), note first that if \(c(Y)<\infty \) then the prescription \(u \mapsto \sum _{i \in \mathbb {I}} \overline{ e_i } \otimes Y^* ( e_i \otimes u )\) defines an operator \(Y^\textsf {c}\) from \(\textsf {h}_2\) to \({\overline{\textsf {h}}}\otimes \textsf {h}_1\) which is bounded with norm \(c(Y)\) and such that
so that (4.1) holds. Conversely, suppose that an operator \(Y^\textsf {c}\in B( \textsf {h}_2; {\overline{\textsf {h}}}\otimes \textsf {h}_1)\) satisfies (4.1). Then (4.2) implies that
so (ii) holds. Uniqueness of the operator \(Y^\textsf {c}\) is immediate. The fact that \(Y^{\textsf {c}\textsf {c}} = Y\) follows from taking the adjoint of identity (4.1); therefore \(||Y || = ||Y^{\textsf {c}\textsf {c}} || = c( Y^\textsf {c}) \).
Parts (b) and (d) are readily verified, and part (c) follows from the identity
which is valid for all \(u \in \textsf {h}\) and any unit vector \(u'\in \textsf {h}'\). \(\square \)
Definition 4.2
We let
and note that it is a subspace of \(B(\textsf {h}_1; \textsf {h}\otimes \textsf {h}_2)\) on which \(c\) defines a norm. The elements of this space are \(\textsf {h}\)-conjugatable or partially conjugatable operators, and partial conjugation is the conjugate-linear isomorphism
An \(\textsf {h}\)-\((\textsf {k}\otimes \textsf {h}')\) process Q is conjugatable if, for all \(t \in {\mathbb {R}_+}\), the operator \(Q_t\) is \(\textsf {k}\)-conjugatable; in this case \(Q^\textsf {c}:= ( Q^\textsf {c}_t )_{t \geqslant 0}\) is an \(\textsf {h}'\)-\((\overline{\textsf {k}}\otimes \textsf {h})\) process.
Remark
Given any \(T \in B( \textsf {h}_1; \textsf {h}_2)\) and \(x \in \textsf {h}\), the operator \(\vert x \rangle \otimes T\) is \(\textsf {h}\)-conjugatable, with the result \(( \vert x \rangle \otimes T )^\textsf {c}= \vert \overline{x} \rangle \otimes T^*\). In particular, if \(\dim \textsf {h}< \infty \) then every operator Y in \(B( \textsf {h}_1; \textsf {h}\otimes \textsf {h}_2)\) is \(\textsf {h}\)-conjugatable and \(|| Y^\textsf {c} || \le ( \dim \textsf {h}) ||Y ||\).
Definition 4.3
A \({\widehat{\textsf {k}}}\otimes \mathfrak {h}\) process G with noise dimension space \(\textsf {k}\) and block matrix form \(\left[ {\begin{matrix} K &{} R \\ Q &{} 0 \end{matrix}}\right] \) is a \(\Sigma \)-integrand process on\(\mathfrak {h}\) if, setting \(\textsf {K}= \textsf {k}\oplus \overline{\textsf {k}}\),
-
(a)
the processes Q and \(R^*\) are conjugatable, and
-
(b)
the \({\widehat{\textsf {K}}}\otimes \mathfrak {h}\) process \(G^\Sigma := \left[ {\begin{matrix} K &{} M \\ L &{} 0 \end{matrix}}\right] \) is a \(\textsf {K}\)-integrand process, in the sense of Definition 3.2, where
$$\begin{aligned} L_t := ( \Sigma \otimes I_{\mathfrak {h}\otimes \mathcal {F}} ) \begin{bmatrix} Q_t \\ R^{ * \textsf {c}}_t \end{bmatrix} \quad \text {and} \quad M_t := \begin{bmatrix} R_t&Q^{ \textsf {c}* }_t \end{bmatrix} ( \Sigma ^* \otimes I_{\mathfrak {h}\otimes \mathcal {F}} ) \quad \text {for all } t \in {\mathbb {R}_+}. \end{aligned}$$
In this case, the quasifree stochastic integral of G is the process \(\Lambda ^\Sigma ( G ) := \Lambda ( G^\Sigma )\).
Remarks
If G is a \(\Sigma \)-integrand process on \(\mathfrak {h}\), with block-matrix form \(\left[ {\begin{matrix} K &{} R \\ Q &{} 0 \end{matrix}}\right] \), then
A sufficient condition for a \({\widehat{\textsf {k}}}\otimes \mathfrak {h}\) process \(\left[ {\begin{matrix} K &{} R \\ Q &{} 0 \end{matrix}}\right] \) to be a \(\Sigma \)-integrand process is that the function
is locally integrable on \({\mathbb {R}_+}\). If \(\dim \textsf {k}< \infty \) then this reduces to the local integrability of the function \(t \mapsto || K_t || + || Q_t ||^2 + || R_t ||^2\).
We will now show that \(\Sigma \)-integrability is unaffected by squeezing. The transformation of integrands resulting from squeezing the AW amplitude may be viewed as a change-of-variables formula.
Theorem 4.4
Let \(\widetilde{\Sigma }= \Sigma \, M\), where M is a squeezing matrix for \({\textsf {k}}\), and let G be a \(\Sigma \)-integrand process. Then there is a \(\widetilde{\Sigma }\)-integrand process \(\widetilde{G}\) such that \(\Lambda ^{\widetilde{\Sigma }} ( \widetilde{G}) = \Lambda ^\Sigma ( G )\).
Proof
Let G have block-matrix form \(\left[ {\begin{matrix} K &{} R \\ Q &{} 0 \end{matrix}}\right] \), let \(M = M^{V,C,P}\) as in (2.9), and let
for all \(t \geqslant 0\), where \(c := \cosh P\), \(s:= \sinh P\) and \(I:= I_{\mathfrak {h}\otimes \mathcal {F}}\). To show that \(\widetilde{G}:= \left[ {\begin{matrix} K &{} \widetilde{R} \\ \widetilde{Q} &{} 0 \end{matrix}}\right] \) is as desired, it now suffices to verify the following.
-
(a)
The processes \(\widetilde{Q}\) and \(\widetilde{R}\) are conjugatable.
-
(b)
For all \(t \in {\mathbb {R}_+}\), it holds that
$$\begin{aligned} ( \widetilde{\Sigma }\otimes I ) \begin{bmatrix} \widetilde{Q}_t \\ \widetilde{R}^{ * \textsf {c}}_t \end{bmatrix} = ( \Sigma \otimes I ) \begin{bmatrix} Q_t \\ R^{ * \textsf {c}}_t \end{bmatrix} \quad \text {and} \quad \begin{bmatrix} R_t&Q^{ \textsf {c}* }_t \end{bmatrix} ( \Sigma \otimes I )^* = \begin{bmatrix} \widetilde{R}_t&\widetilde{Q}^{ \textsf {c}* }_t \end{bmatrix} ( \widetilde{\Sigma }\otimes I )^*; \end{aligned}$$equivalently,
$$\begin{aligned} ( \widetilde{\Sigma }\otimes I ) \begin{bmatrix} \widetilde{Q}_t&\widetilde{R}^*_t \\ \widetilde{R}^{ * \textsf {c}}_t&\widetilde{Q}^\textsf {c}_t \end{bmatrix} = ( \Sigma \otimes I ) \begin{bmatrix} Q_t&R^*_t \\ R^{ * \textsf {c}}_t&Q^\textsf {c}_t \end{bmatrix} \qquad \text {for all } t \in {\mathbb {R}_+}. \end{aligned}$$
Now, Theorem 4.1 gives (a), and the following identities:
for all \(t \in {\mathbb {R}_+}\). Together these imply that
and so (b) holds, as required. \(\square \)
The following identity is the first fundamental formula for quasifree stochastic integrals. In view of Theorem 3.3, it holds by definition.
Proposition 4.5
Let G be a \(\Sigma \)-integrand process on \(\mathfrak {h}\). With the notation given in (4.3),
for all u, \(v \in \mathfrak {h}\), f, \(g\in \mathbb {S}_{{\textsf {K}}}\) and \(t \in {\mathbb {R}_+}\).
The following is readily verified from the definitions. Let \(\mathcal {F}^\textsf {H}= \Gamma \bigl ( L^2( {\mathbb {R}_+}; \textsf {H}) \bigr )\) for any choice of \(\textsf {H}\).
Corollary 4.6
Suppose that the AW amplitude \(\Sigma \) is gauge invariant, so has the form \(\Sigma _A\), and let \({\textsf {k}}_0 := {{\,\mathrm{Ker}\,}}A\). Then any \(\Sigma \)-integrand process G on \(\mathfrak {h}\) compresses to a \({\textsf {k}}_0\)-integrand process \(G^0\) on \(\mathfrak {h}\) and \(\Lambda (G^0)_t\) is the compression of \(\Lambda ^\Sigma ( G )_t\) to \(\mathfrak {h}\otimes \mathcal {F}^{{{\textsf {k}}}_0}\), for all \(t \in {\mathbb {R}_+}\).
Remark
Here \(\textsf {k}_0\) is being viewed as a subspace of \(\textsf {K}:= \textsf {k}\oplus \overline{\textsf {k}}\) as well as of \(\textsf {k}\), and \(\mathcal {F}^{\textsf {k}_0}\) is being identified with the subspace \(\mathcal {F}^{\textsf {k}_0} \otimes \Omega _{\textsf {K}\ominus \textsf {k}_0}\) of \(\mathcal {F}^{\textsf {K}}\).
This observation shows the quasifree stochastic calculus constructed here incorporates standard quantum stochastic integrals as well as purely quasifree stochastic integrals (i.e. QS integrals with respect to integrators which are quasifree for a faithful state), making them useful for the investigation of repeated interaction systems with particles in a non-faithful state; see Sect. 6 and [11].
The following result is the second fundamental formula for quasifree stochastic integrals, and should be compared with Theorem 3.6. The final term on the right-hand side is the quasifree Itô correction term.
Theorem 4.7
Let \(X := ( X_0 + \Lambda ^\Sigma ( G )_t )_{t\geqslant 0}\) and \(Y := ( Y_0 + \Lambda ^\Sigma ( H )_t )_{t\geqslant 0}\), where \(G = \left[ {\begin{matrix} K &{} R \\ Q &{} 0 \end{matrix}}\right] \) and \(H = \left[ {\begin{matrix} J &{} T \\ S &{} 0 \end{matrix}}\right] \) are \(\Sigma \)-integrand processes and \(X_0\), \(Y_0 \in B(\mathfrak {h}) \otimes I_\mathcal {F}\). In the notation of (4.3),
for all u, \(v \in \mathfrak {h}\), f, \(g\in \mathbb {S}_{{\textsf {K}}}\) and \(t \in {\mathbb {R}_+}\).
Proof
This follows immediately from Theorem 3.6, Definition 4.3 and the identity
which holds for all x, \(y \in \textsf {K}\), u, \(v \in \mathfrak {h}\), f, \(g\in \mathbb {S}_\textsf {K}\) and \(s \in {\mathbb {R}_+}\). \(\square \)
Theorem 4.8
Let \(G \in B( \widehat{{\textsf {k}}} \otimes \mathfrak {h})_0\). The following are equivalent.
-
(i)
The operator G has block-matrix form \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \), where Q is conjugatable and
$$\begin{aligned} K + K^* + L^* L = 0 \qquad \text {for the operator } L := ( \Sigma \otimes I_\mathfrak {h}) \begin{bmatrix} Q \\ -Q^{ \textsf {c}} \end{bmatrix}. \end{aligned}$$ -
(ii)
There is a unitary \(\mathfrak {h}\) process U with noise dimension space \({\textsf {K}}= {\textsf {k}}\oplus \overline{{\textsf {k}}}\) such that
-
(a)
\(G \cdot U := ( ( G \otimes I_\mathcal {F}) ( I_{\widehat{\small {{\textsf {k}}}}} \otimes U_t ) )_{t \geqslant 0}\) is a \(\Sigma \)-integrand process, and
-
(b)
\(U_t = I_{\mathfrak {h}\otimes \mathcal {F}} + \Lambda ^\Sigma ( G \cdot U )_t\) for all \(t \in {\mathbb {R}_+}\).
-
(a)
If either condition holds then U is the unique \(\mathfrak {h}\) process satisfying (a) and (b) of (ii).
Proof
Suppose that (i) holds and set
Then \(F \in B( {\widehat{\textsf {K}}}\otimes \mathfrak {h})_0\) and \(F^* + F + F^* \Delta F = 0\). Appealing to Theorem 3.9 and Definition 3.10, there exists a unitary process \(U := Y^F\). Since \(( G \cdot U )^\Sigma = F \cdot U\), so \(G \cdot U\) is a \(\Sigma \)-integrand process and \(\Lambda ^\Sigma ( G \cdot U )_t = \Lambda ( F \cdot U )_t = U_t - I_{\mathfrak {h}\otimes \mathcal {F}}\) for all \(t \in {\mathbb {R}_+}\), hence (ii) holds.
Conversely, suppose that (ii) holds for a unitary \(\mathfrak {h}\) process U, and let \(\left[ {\begin{matrix} K &{} R \\ Q &{} 0 \end{matrix}}\right] \) be the block-matrix form of G. Theorem 4.1 implies that the operators Q and \(R^*\) are conjugatable, and
Assumption (b) gives that \(U_t = I_{\mathfrak {h}\otimes \mathcal {F}} + \Lambda ( F \cdot U )_t\) for all \(t \in {\mathbb {R}_+}\), and so, by Theorem 3.9, it holds that \(F^* + F + F^* \Delta F = 0\) and \(U = Y^F\). In particular, the uniqueness claim is established. The condition \(F^* + F + F^* \Delta F = 0\) is equivalent to
-
(a)
\(\begin{bmatrix} R&Q^{ \textsf {c}* } \end{bmatrix} ( \Sigma ^* \otimes I_{\mathfrak {h}} ) = -\Bigl ( ( \Sigma \otimes I_{\mathfrak {h}} ) \left[ {\begin{matrix} Q \\ R^{ * \textsf {c}} \end{matrix}}\right] \Bigr )^*\) and
-
(b)
\(0 = K^* + K + L^* L\), where \(L = ( \Sigma \otimes I_{\mathfrak {h}} ) \left[ {\begin{matrix} Q \\ R^{ * \textsf {c}} \end{matrix}}\right] \),
so it remains to prove that \(X := Q + R^* = 0\). Note that (a) is equivalent to \(( \Sigma \otimes I_{\mathfrak {h}} ) \left[ {\begin{matrix} X \\ X^{ \textsf {c}} \end{matrix}}\right] = 0\) and, in terms of the parameterisation \(\Sigma ^{A,V,C,P}\) of the AW amplitude \(\Sigma \) given in (2.10) and the notation k for the conjugation map from \(\textsf {k}\) to \(\overline{\textsf {k}}\), this is equivalent to
It follows from (4.5) that \(X = - ( \tanh P \cdot C k^{-1} \otimes I_\mathfrak {h}) X^{ \textsf {c}}\), and so, by Theorem 4.1 and the fact that C commutes with P and \(C^2 = I_\textsf {k}\),
thus \(0 = \bigl ( ( I_\textsf {k}- \tanh ^2 P ) \otimes I_\mathfrak {h}\big ) X = ( \cosh ^2 P \otimes I_\mathfrak {h})^{-1} X\) and so \(X=0\). \(\square \)
Remark
From the preceding proof, we see that the unique unitary \(\mathfrak {h}\) process U determined by an operator \(G \in B({\widehat{\textsf {k}}}\otimes \mathfrak {h})_0\) satisfying Theorem 4.8(i) equals \(Y^F\), where \(F = G^\Sigma \) as defined in (4.4). In particular, U is an HP cocycle. Cocycle aspects of quasifree processes are further investigated in [32].
Definition 4.9
An HP cocycle U on \(\mathfrak {h}\) with noise dimension space \(\textsf {k}\oplus \overline{\textsf {k}}\) is \(\Sigma \)-quasifree and has \(\Sigma \)-generatorG if \(U = Y^F\) for \(F = G^\Sigma \), in which \(G \in B( {\widehat{\textsf {k}}}\otimes \mathfrak {h})_0\) has the block-matrix form \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \), where Q is \(\textsf {k}\)-conjugatable and
Remark
Thus \(\Sigma \)-quasifree HP cocycles form a subclass of the collection of Gaussian HP cocycles with noise dimension space \(\textsf {K}\) having a decomposition \(\textsf {k}\oplus \overline{\textsf {k}}\).
Example 4.10
(Pure-noise cocycles) For a gauge-invariant AW amplitude \(\Sigma = \Sigma _A\), the quasifree pure-noise cocycles are of the form \(\big ( e^{\mathrm {i}\alpha t} W_\Sigma ( x 1_{[0,t)} ) \big )_{t \geqslant 0}\) for some \(x \in \textsf {k}\) and \(\alpha \in \mathbb {R}\), with corresponding \(\Sigma \)-generator \(\left[ \begin{array}{ccc} \mathrm {i}\alpha - \tfrac{1}{2}|| \sqrt{ \cosh 2A }\, x ||^2 &{} &{} -\langle x \vert \\ \vert x \rangle &{} &{} 0 \end{array}\right] \).
Corollary 4.11
Let U be a Gaussian HP cocycle on \(\mathfrak {h}\) with noise dimension space \({\textsf {k}}\oplus \overline{{\textsf {k}}}\) and stochastic generator \(\left[ {\begin{matrix} K &{} -L^* \\ L &{} 0 \end{matrix}}\right] \), let \(\left[ {\begin{matrix} L_1 \\ L_2 \end{matrix}}\right] \) be the block matrix form of L, and suppose that the AW-amplitude is gauge-invariant, say \(\Sigma = \Sigma _A\). Then the following are equivalent.
-
(i)
The cocycle U is a \(\Sigma \)-quasifree HP cocycle.
-
(ii)
The operator L equals \(( \Sigma \otimes I_\mathfrak {h}) \left[ {\begin{matrix} Q \\ -Q^\textsf {c} \end{matrix}}\right] \) for a \({\textsf {k}}\)-conjugatable operator \(Q \in B(\mathfrak {h}; {\textsf {k}}\otimes \mathfrak {h})\).
-
(iii)
The operator \(L_1\) is \({\textsf {k}}\)-conjugatable and \(L_2 = - ( \overline{ \tanh A } \otimes I_\mathfrak {h}) L_1^\textsf {c}\).
-
(iv)
The operator \(L_2\) is \(\overline{{\textsf {k}}}\)-conjugatable and \(L_2^\textsf {c}= - ( \tanh A \otimes I_\mathfrak {h}) L_1\).
When these hold, the cocycle U has \(\Sigma \)-generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \) and
Proof
By Theorem 4.8 and Definition 4.9, (i) is equivalent to (ii), and these imply that U has \(\Sigma \)-generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \). Properties of the partial conjugation, Theorem 4.1, now imply that (ii) is equivalent to (iii); they also imply that (iii) is equivalent to (iv). When these conditions hold, since
the identity (4.7) follows from the fact that \(\cosh ^2 A - \sinh ^2 A = I_\textsf {k}\). \(\square \)
Theorem 4.12
Let U be a \(\Sigma \)-quasifree HP cocycle with \(\Sigma \)-generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \in B( \widehat{{\textsf {k}}} \otimes \mathfrak {h})_0\), and let j be the corresponding inner EH flow. Set \(L:= ( \Sigma \otimes I_{\mathfrak {h}} ) \left[ {\begin{matrix} Q \\ -Q^\textsf {c} \end{matrix}}\right] \) and \(H := \tfrac{1}{2 \mathrm {i}} ( K - K^*)\), and define the map
Then \(\bigl ( (j^{{\textsf {k}}}_t \circ \psi )(a) \bigr )_{t\geqslant 0}\) is a \(\Sigma \)-integrand process for all \(a \in B( \mathfrak {h})\), where \(j_t^{\small {{\textsf {k}}}} := {{\,\mathrm{id}\,}}_{B(\widehat{\small {{\textsf {k}}}})} \overline{\otimes }\,j_t\), and
Proof
It is straightforward to verify that
where \(j^\textsf {K}_s := {{\,\mathrm{id}\,}}_{B({\widehat{\textsf {K}}})} \overline{\otimes }\,j_s\) for \(\textsf {K}= \textsf {k}\oplus \overline{\textsf {k}}\), and \(\theta \) is the map from \(B(\mathfrak {h})\) to \(B( {\widehat{\textsf {K}}}\otimes \mathfrak {h})\) defined in (3.7). It therefore follows from Theorem 3.16 that
as claimed. \(\square \)
5 Uniqueness Questions
In this section, issues of uniqueness are considered. We begin with the question of uniqueness of AW amplitudes for quasifree HP cocycles. Given an HP cocycle U with noise dimension space \(\textsf {K}\) and stochastic generator \(F = \left[ {\begin{matrix} K &{} -L^*W \\ L &{} W - I_{\textsf {K}\otimes \mathfrak {h}} \end{matrix}}\right] \), we examine the class of pairs \(( \Sigma , Q )\) such that
so that \(G := \left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \) is a \(\Sigma \)-quasifree generator and \(F = G^\Sigma \). Immediate necessary conditions for this class to be non-empty are that the HP cocycle U is Gaussian, thus \(F \in B( {\widehat{\textsf {K}}}\otimes \mathfrak {h})_0\), so \(W = I_{\textsf {K}\otimes \mathfrak {h}}\), and \(\textsf {K}\) has a decomposition \(\textsf {k}\oplus \overline{\textsf {k}}\), so \(\textsf {K}\) must not have finite odd dimension.
We also consider the uniqueness of quasifree HP cocycles implementing a given EH flow j and relate this to the minimality of j as a stochastic dilation of its expectation semigroup.
For the remainder of this section, we fix a quasifree noise dimension space \(\textsf {k}\), and set \(\textsf {K}= \textsf {k}\oplus \overline{\textsf {k}}\). Theorem 4.4 has the following consequence.
Corollary 5.1
Let \(\widetilde{\Sigma }= \Sigma \, M\), where \(\Sigma \) and M are an AW amplitude and squeezing matrix for \({\textsf {k}}\), respectively. Then every \(\Sigma \)-quasifree HP cocycle is also \(\widetilde{\Sigma }\)-quasifree.
In light of the above corollary, we restrict to gauge-invariant AW amplitudes for the rest of this section. For an operator \(X \in B(\mathfrak {h}; \textsf {k}\otimes \mathfrak {h})\), let the \(\textsf {k}\)-degeneracy space of X be
Proposition 5.2
Let \(\Sigma =\Sigma _A\) be a gauge-invariant AW amplitude for \({\textsf {k}}\), and suppose U is a \(\Sigma \)-quasifree HP cocycle with stochastic generator \(\left[ {\begin{matrix} K &{} -L^* \\ L &{} 0 \end{matrix}}\right] \) and \(\Sigma \)-generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \), where L has block-matrix form \(\left[ {\begin{matrix} L_1 \\ L_2 \end{matrix}}\right] \). Then
Furthermore, if \(\widetilde{\Sigma }= \Sigma _{\widetilde{A}}\) is another gauge-invariant AW amplitude for \({\textsf {k}}\), then the following are equivalent.
-
(i)
The cocycle U is also \(\widetilde{\Sigma }\)-quasifree.
-
(ii)
\(\big ( ( \tanh \widetilde{A}- \tanh A ) \otimes I_\mathfrak {h}\big ) L_1 = 0\).
Proof
Corollary 4.11 implies that \(L_2\) is \(\overline{\textsf {k}}\)-conjugatable and Q is \(\textsf {k}\)-conjugatable, with
Thus (5.2) follows from the invertibility of \(\cosh A\). Corollary 4.11 also implies that (i) holds if and only if \(L_2^\textsf {c}= - ( \tanh \widetilde{A}\otimes I_\mathfrak {h}) L_1\). Therefore (i) and (ii) are equivalent, by (5.3). \(\square \)
For an HP cocycle U with noise dimension space \(\textsf {k}\oplus \overline{\textsf {k}}\), let
be the set of gauge-invariant AW amplitudes for \(\textsf {k}\) for which U is \(\Sigma \)-quasifree.
Corollary 5.3
Let U be an HP cocycle with stochastic generator \(\left[ {\begin{matrix} K &{} -L^* \\ L &{} 0 \end{matrix}}\right] \). If U is quasifree with respect to a gauge-invariant AW amplitude \(\Sigma _A\) then
In particular, if \({\textsf {k}}^{L_1} = \{ 0 \}\) then U is quasifree with respect to at most one gauge-invariant AW amplitude.
We now turn to the question of implementability of inner EH flows by quasifree HP cocycles.
Proposition 5.4
Let U and \(\widetilde{U}\) be quasifree HP cocycles on \(\mathfrak {h}\) with respect to a gauge-invariant AW amplitude \(\Sigma \) for \({\textsf {k}}\), and let \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \),  be their respective \(\Sigma \)-generators and \(H := \tfrac{1}{2 \mathrm {i}} ( K - K^*)\) and \(\widetilde{H}:= \tfrac{1}{2 \mathrm {i}} ( \widetilde{K}- \widetilde{K}^*)\). The following are equivalent.
be their respective \(\Sigma \)-generators and \(H := \tfrac{1}{2 \mathrm {i}} ( K - K^*)\) and \(\widetilde{H}:= \tfrac{1}{2 \mathrm {i}} ( \widetilde{K}- \widetilde{K}^*)\). The following are equivalent.
-
(i)
The cocycles U and \(\widetilde{U}\) induce the same inner EH flow.
-
(ii)
There exist \(x \in {\textsf {k}}\) and \(\alpha \in \mathbb {R}\) such that
$$\begin{aligned} \widetilde{Q}- Q = \vert x \rangle \otimes I_\mathfrak {h}\quad \text {and} \quad \widetilde{H}- H - \tfrac{\mathrm {i}}{2} \bigl ( ( \langle x \vert \otimes I_\mathfrak {h}) Q - Q^* ( \vert x \rangle \otimes I_\mathfrak {h}) \bigr ) = \alpha I_\mathfrak {h}. \end{aligned}$$
Proof
Let C and T denote \(\cosh A\) and \(\tanh A\), respectively, where \(\Sigma = \Sigma _A\), and let
By Proposition 3.18, (i) is equivalent the existence of \(z = (z_1, \overline{z_2} ) \in \textsf {k}\oplus \overline{\textsf {k}}\) and \(\alpha \in \mathbb {R}\) such that
If \(z = ( z_1, \overline{z_2} ) \in \textsf {k}\oplus \overline{\textsf {k}}\) and \(\alpha \in \mathbb {R}\) are such that (5.4) holds then
so \(z_2 = - T z_1\), and therefore \(z = \Sigma \iota (x)\), where \(x = C^{-1} z_1\). It follows from (4.7) that (ii) holds.
Conversely, suppose that (ii) holds, with \(x \in \textsf {k}\) and \(\alpha \in \mathbb {R}\), and set \(z := \Sigma \iota ( x )\). Then
so \(\widetilde{Q}- Q = \vert C^{-1} z_1 \rangle \otimes I_\mathfrak {h}= \vert x \rangle \otimes I_\mathfrak {h}\) and, by (4.7), condition (5.4) is satisfied. \(\square \)
Theorem 5.5
Let j be an inner EH flow which is a minimal dilation of its vacuum expectation semigroup. Then there is at most one gauge-invariant AW amplitude \(\Sigma \) such that j is induced by a \(\Sigma \)-quasifree HP cocycle.
Proof
Suppose that j is induced by a \(\Sigma \)-quasifree HP cocycle U and a \(\widetilde{\Sigma }\)-quasifree HP cocycle \(\widetilde{U}\), where \(\Sigma =\Sigma _A\) and \(\widetilde{\Sigma }= \Sigma _{\widetilde{A}}\) are gauge-invariant AW amplitudes for \(\textsf {k}\). Then U and \(\widetilde{U}\) are Gaussian and so have stochastic generators of the form \(\left[ {\begin{matrix} K &{} -L^* \\ L &{} 0 \end{matrix}}\right] \) and \(\left[ {\begin{matrix} K &{} -\widetilde{L}^* \\ \widetilde{L} &{} 0 \end{matrix}}\right] \) respectively. Letting \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \) and  be their respective quasifree generators, it follows that
be their respective quasifree generators, it follows that
and Proposition 3.18 implies that \(\widetilde{L}= L + \vert z \rangle \otimes I_\mathfrak {h}\) for some \(z = (z_1, \overline{z_2})\) in \(\textsf {k}\oplus \overline{\textsf {k}}\). If \(T := \tanh A\) and \(\widetilde{T}:= \tanh \widetilde{A}\) then
so if \(y \in {{\,\mathrm{Ran}\,}}( T - \widetilde{T})^*\) then
Therefore, by Theorem 3.19, the minimality of j implies that \({{\,\mathrm{Ran}\,}}( T - \widetilde{T})^* = \{ 0 \}\), so \(\widetilde{T}= T\), \(\widetilde{A}= A\) and \(\widetilde{\Sigma }= \Sigma \). \(\square \)
6 Quantum Random Walks
In this section we first review the basic theory of unitary quantum random walks for particles in a vector state and their convergence to quantum stochastic cocycles [9]; for an elementary treatment via the semigroup decomposition of quantum stochastic cocycles, see [12]. Stronger theorems for more general walks may be found in [10], for particles in a faithful normal state, and in [11], for particles in a general normal state. We then construct quantum random walks in the repeated-interactions model for particles in a faithful normal state \(\rho \). Thus let \(\rho \) be such a state on \(B(\mathfrak {p})\), for a Hilbert space \(\mathfrak {p}\). Under the assumption that the interaction Hamiltonian  has no diagonal component with respect to the eigenspaces of the density matrix of \(\rho \), we demonstrate convergence to HP cocycles of the form \(U \otimes I\) where I is the identity operator of the Fock space over \(L^2({\mathbb {R}_+}; \textsf {K}_0)\) for a subspace \(\textsf {K}_0\) of the GNS space of \(\rho \). The construction yields a quasifree noise dimension space \(\textsf {k}\) together with natural conjugate space \(\overline{\textsf {k}}\) and, under the assumption of exponential decay of the eigenvalues of the density matrix corresponding to \(\rho \), a gauge-invariant AW amplitude \(\Sigma (\rho )\) for \(\textsf {k}\). We then show that U is \(\Sigma (\rho )\)-quasifree, assuming only that
has no diagonal component with respect to the eigenspaces of the density matrix of \(\rho \), we demonstrate convergence to HP cocycles of the form \(U \otimes I\) where I is the identity operator of the Fock space over \(L^2({\mathbb {R}_+}; \textsf {K}_0)\) for a subspace \(\textsf {K}_0\) of the GNS space of \(\rho \). The construction yields a quasifree noise dimension space \(\textsf {k}\) together with natural conjugate space \(\overline{\textsf {k}}\) and, under the assumption of exponential decay of the eigenvalues of the density matrix corresponding to \(\rho \), a gauge-invariant AW amplitude \(\Sigma (\rho )\) for \(\textsf {k}\). We then show that U is \(\Sigma (\rho )\)-quasifree, assuming only that  is \(\mathfrak {p}\)-conjugatable. We also show that if the lower-triangular matrix components of \(H_{\textsf {I}}\) are strongly linearly independent then \(\Sigma (\rho )\) is the unique gauge-invariant AW amplitude with respect to which U is quasifree.
is \(\mathfrak {p}\)-conjugatable. We also show that if the lower-triangular matrix components of \(H_{\textsf {I}}\) are strongly linearly independent then \(\Sigma (\rho )\) is the unique gauge-invariant AW amplitude with respect to which U is quasifree.
6.1 Particles in a Vector State
For this subsection, we fix a noise dimension space \(\textsf {K}\).
Definition 6.1
The toy Fock space\(\Upsilon \) over \(\textsf {K}\) is the tensor product of a sequence of copies of \({\widehat{\textsf {K}}}:= \mathbb {C}\oplus \textsf {K}\) with respect to the constant stabilising sequence given by \(\omega := \left( {\begin{matrix} 1 \\ 0 \end{matrix}}\right) \):
We also set
and denote the identity operator on \(\Upsilon _{[m}\) by \(I_{[m}\).
As is readily verified [9, 12], toy Fock space over \(\textsf {K}\) approximates Boson Fock space over \(\textsf {K}\) in the following sense. Let \(\mathcal {F}_J = \Gamma \bigl ( L^2( J; \textsf {K}) \bigr )\) for any subinterval \(J \subseteq {\mathbb {R}_+}\), with \(\Omega _J\) its vacuum vector, and, for all \(\tau > 0\), let
be the isometric linear operator such that
for any finitely-supported sequence \(( x_n )\) in \(\textsf {K}\). Then \(D_\tau D_\tau ^* \rightarrow I_\mathcal {F}\) in the strong operator topology as \(\tau \rightarrow 0+\).
Definition 6.2
For any \(G \in U( {\widehat{\textsf {K}}}\otimes \mathfrak {h})\), the quantum random walk generated byG is the sequence \(( U_n )_{n\geqslant 0}\) in \(B( \mathfrak {h}\otimes \Upsilon )\) defined recursively as follows:
where the normal \(*\)-monomorphism
and \(\sigma _n := {{\,\mathrm{id}\,}}_{B(\mathfrak {h})} \overline{\otimes }\,\sigma _n^\Upsilon \) is the ampliation of the right shift \(*\)-endomorphism of \(B(\Upsilon )\) with range \(I_{{\widehat{\textsf {K}}}^{\otimes n}} \otimes B(\Upsilon _{[n})\).
Scaling maps on \(B( {\widehat{\textsf {K}}}\otimes \mathfrak {h})\) are defined by setting
Remarks
If the generator is an elementary tensor \(A \otimes X\) then the quantum random walk takes the simple form
For us here, generators are of the form \(\exp {\mathrm {i}H}\) for operators \(H \in B( {\widehat{\textsf {K}}}\otimes \mathfrak {h})_{{\text {sa} }}\).
In [12] we worked with left QRW’s and generators in \(B( \mathfrak {h}\otimes {\widehat{\textsf {K}}})\) instead; the two are, of course, equivalent.
Henceforth we focus on the repeated-interactions model of [7]. Recall that in this model one has a family of discrete-time evolutions of an open quantum system consisting of a system \(\textsf {S}\) coupled to a heat reservoir modeled by an infinite chain of identical particles in some (thermal) state \(\rho \), repeatedly interacting with the system over a short time period of length \(\tau \). The corresponding discrete-time evolution has unitary generator
where the total Hamiltonian decomposes as

for a system Hamiltonian , a particle Hamiltonian
, a particle Hamiltonian and an interaction Hamiltonian\(H_{\textsf {I}}\in B({\widehat{\textsf {K}}}\otimes \mathfrak {h})_{{\text {sa} }}\). The continuous limit of this model (embedded into Boson Fock space) at zero temperature is captured by the following theorem in which, for each \(\tau > 0\), \(( U(\tau )_n )_{n \geqslant 0}\) denotes the quantum random walk with unitary generator \(\exp {\mathrm {i}\tau H_{\textsf {T}}( \tau )}\).
and an interaction Hamiltonian\(H_{\textsf {I}}\in B({\widehat{\textsf {K}}}\otimes \mathfrak {h})_{{\text {sa} }}\). The continuous limit of this model (embedded into Boson Fock space) at zero temperature is captured by the following theorem in which, for each \(\tau > 0\), \(( U(\tau )_n )_{n \geqslant 0}\) denotes the quantum random walk with unitary generator \(\exp {\mathrm {i}\tau H_{\textsf {T}}( \tau )}\).
Theorem 6.3
Suppose that  , so that
, so that  has block-matrix form \(\left[ {\begin{matrix} 0 \\ L \end{matrix}}\right] \) for some \(L \in B( \mathfrak {h}; {\textsf {K}}\otimes \mathfrak {h})\). For all \(\tau > 0\), set
has block-matrix form \(\left[ {\begin{matrix} 0 \\ L \end{matrix}}\right] \) for some \(L \in B( \mathfrak {h}; {\textsf {K}}\otimes \mathfrak {h})\). For all \(\tau > 0\), set
and

Then \(F^* + F + F^* \Delta F = 0\) and, as \(\tau \rightarrow 0+\),
where \(Y^F\) is a Gaussian HP cocycle with stochastic generator F, as in Definition 3.10.
Proof
That F satisfies the structure relation is readily verified. The final claim holds by [9, Theorem 7.6 and Remarks 4.8 and 5.10] (see also [12, Theorem 4.3]), since
\(\square \)
6.2 Particles in a Faithful State
We now fix a non-zero Hilbert space \(\mathfrak {p}\), referred to as the particle space, and a faithful normal state \(\rho \) on \(B(\mathfrak {p})\). Let \((\gamma _\alpha )_{\alpha \geqslant 0}\) be the eigenvalues of its density matrix \(\varrho \), ordered to be strictly decreasing, the index set being either \(\mathbb {Z}_+\) or \(\{ 0, 1, \ldots , N \}\) for some non-negative integer N. For any index \(\alpha \), let \(P_\alpha \in B(\mathfrak {p})\) be the orthogonal projection with range \(\textsf {k}_\alpha \), the eigenspace of \(\varrho \) corresponding to the eigenvalue \(\gamma _\alpha \). Thus \(\varrho = \sum _{\alpha \geqslant 0} \gamma _\alpha P_\alpha \) and \(\sum _{\alpha \geqslant 0} \gamma _\alpha d_\alpha = 1\), where \(d_\alpha := \dim \textsf {k}_\alpha = {{\,\mathrm{tr}\,}}( P_\alpha )\).
Let \(( {\widehat{\textsf {K}}}, \pi , \eta )\) denote the GNS representation of \(\rho \). Thus \(( \pi , {\widehat{\textsf {K}}})\) is a normal unital \(*\)-representation of \(B(\mathfrak {p})\), \(\eta \) is an operator from \(B(\mathfrak {p})\) to \({\widehat{\textsf {K}}}\) with dense range,
In particular, \(\rho (X) = \langle \omega , \pi (X) \omega \rangle \) and \(\eta (X) = \pi (X) \omega \) for all \(X \in B(\mathfrak {p})\), where \(\omega := \eta (I_\mathfrak {p})\). As is well known, the GNS representation is unique up to isomorphism; here, we take the triple defined as follows:
where \(HS( \mathfrak {p})\) denotes the Hilbert–Schmidt class of operators on \(\mathfrak {p}\) and \(L_X\) denotes the operator of left multiplication by X. In particular, \(\omega = \varrho ^{1/2}\). Now let
so that \(( \widetilde{\pi }, {\widehat{\textsf {K}}}\otimes \mathfrak {h})\) is a normal unital \(*\)-representation of \(B( \mathfrak {p}\otimes \mathfrak {h})\) and \(\widetilde{\rho }\) is a normal unital completely positive map from \(B( \mathfrak {p}\otimes \mathfrak {h})\) to \(B( \mathfrak {h})\). For all \(\alpha , \beta \geqslant 0\), let
and let
Let k be the anti-unitary operator from \(\textsf {k}\) to \(\overline{\textsf {k}}\) obtained by restricting the adjoint operation on \({\widehat{\textsf {K}}}= HS( \mathfrak {p})\). Then
and \(( \overline{\textsf {k}}, k )\) is a realisation of the conjugate Hilbert space of \(\textsf {k}\). Note also that
We now identify the one-dimensional subspace \(\mathbb {C}\omega \) of \({\widehat{\textsf {K}}}\) with \(\mathbb {C}\), so that
Theorem 6.4
Let the operators  ,
,  and
and  be self-adjoint, and assume that
be self-adjoint, and assume that  for all \(\alpha \geqslant 0\). Then we have the following.
for all \(\alpha \geqslant 0\). Then we have the following.
-
(a)
The operator
 has the block-matrix form
has the block-matrix form  for some
for some  .
. -
(b)
For all
 , let \(\widetilde{U}^\tau := \bigl ( ( I_\mathfrak {h}\otimes D_\tau ) \widetilde{U}(\tau )_{\lfloor t/\tau \rfloor } ( I_\mathfrak {h}\otimes D_\tau )^* \bigr )_{t \geqslant 0}\), where \(( \widetilde{U}( \tau )_n )_{n \geqslant 0}\) is the quantum random walk generated by
, let \(\widetilde{U}^\tau := \bigl ( ( I_\mathfrak {h}\otimes D_\tau ) \widetilde{U}(\tau )_{\lfloor t/\tau \rfloor } ( I_\mathfrak {h}\otimes D_\tau )^* \bigr )_{t \geqslant 0}\), where \(( \widetilde{U}( \tau )_n )_{n \geqslant 0}\) is the quantum random walk generated by  and
and 
and let \(\widetilde{F}:= F \oplus 0_{\small {{\textsf {K}}}_0 \otimes \mathfrak {h}}\), where

Then \(\widetilde{F}^* + \widetilde{F}+ \widetilde{F}^* \Delta \widetilde{F}= 0\) and, as \(\tau \rightarrow 0+\),
$$\begin{aligned} \sup _{t \in [0,T]} \bigl \Vert ( \widetilde{U}^\tau _t - Y^{\widetilde{F}}_t ) \xi \bigr \Vert \rightarrow 0 \qquad \text {for all } \xi \in \mathfrak {h}\otimes \mathcal {F}\text { and } T \in {\mathbb {R}_+}. \end{aligned}$$
Proof
(a) It must be shown that
If u, \(v \in \mathfrak {h}\) and \(T \in \textsf {k}_{\alpha \alpha }\) for some index \(\alpha \), and \(H^u_v:= ( I_\mathfrak {p}\otimes \langle u \vert ) H_{\textsf {I}}( I_\mathfrak {p}\otimes \vert v \rangle )\), then
and so (6.2) follows from (6.1).
(b) Note that \(\widetilde{\pi }\bigl ( \exp \mathrm {i}\tau H_{\textsf {T}}( \tau ) \bigr ) = \exp \mathrm {i}\tau \widetilde{H_{\textsf {T}}}( \tau ) \in B( {\widehat{\textsf {K}}}\otimes \mathfrak {h})\) for all \(\tau > 0\), where

Furthermore  and it is straightforward to verify that
and it is straightforward to verify that
which implies that F is as claimed. The conclusion now follows from Theorem 6.3, since \(\omega \) is identified with \(\left( {\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}}\right) \in \widehat{ \textsf {K}_1 } \otimes \textsf {K}_0\) and \(\mathbb {C}\omega \) with \(\mathbb {C}\). \(\square \)
Remarks
Under the identification \(\mathfrak {h}\otimes \mathcal {F}^{\textsf {K}} = \mathfrak {h}\otimes \mathcal {F}^{\textsf {K}_1} \otimes \mathcal {F}^{\textsf {K}_0}\), where \(\mathcal {F}^\textsf {H}:= \Gamma \bigl ( L^2( {\mathbb {R}_+}; \textsf {H}) \bigr )\), the limit process decomposes as
The condition on \(H_{\textsf {I}}\) has the following physical interpretation: there is no contribution from the interaction Hamiltonian unless the particle undergoes a transition.
Assumption 6.5
We impose an exponential-decay condition on the eigenvalues of the density matrix \(\varrho \), by insisting that
This ensures that the following lemma yields an AW amplitude for \(\textsf {k}\). To avoid it would require more of the general theory developed in [31, 32].
For all indices \(\alpha \) and \(\beta \), let \(P_{\alpha \beta }\) denote the orthogonal projection with range \(\textsf {k}_{\alpha \beta }\).
Lemma 6.6
Suppose the state \(\rho \) satisfies Assumption 6.5. Define an operator
where the series converges in the strong sense, and, let \(C(\rho ) := \sqrt{ I_{{\textsf {k}}}+ S(\rho )^2 }\), then
Proof
If \(\alpha , \beta \geqslant 0\) with \(\alpha > \beta \), and \(\zeta \in \textsf {k}_{\alpha '}\) and \(\eta \in \textsf {k}_{\beta '}\) with \(\alpha '\), \(\beta ' \in I\), then
where \(\delta \) is the Kronecker delta. From (6.5a) it follows that (6.3) defines a non-negative bounded operator \(S(\rho )\) on \(\textsf {k}\), and from (6.5c) it follows that \(\overline{ P_{\alpha \beta }} = P_{\beta \alpha }\) for all \(\alpha > \beta \geqslant 0\), so the identities (6.4) follow from (6.5b) and (6.5c). \(\square \)
Thus, under Assumption 6.5, with \(S(\rho )\) and \(C(\rho )\) as in the preceding lemma,
defines a gauge-invariant AW amplitude for \(\textsf {k}\).
Our goal now is to prove that the HP cocycle generated by F in Theorem 6.4 is \(\Sigma (\rho )\)-quasifree, provided that the interaction Hamiltonian \(H_{\textsf {I}}\) is \(\mathfrak {p}\)-conjugatable. To this end, note first that, for all \(T \in B( \mathfrak {p})\) and all indices \(\alpha , \beta , \alpha '\) and \(\beta '\), \(P_\alpha T P_\beta \) and \(P_{\alpha '} T P_{\beta '}\) are orthogonal vectors in \(HS( \mathfrak {p})\) unless \(\alpha ' = \alpha \) and \(\beta ' = \beta \), and therefore
and
so the following prescriptions define bounded operators:
For the next proposition we adopt the notation
Recall that Theorem 4.1 gives the inclusion \(HS( \mathfrak {p}) \, \, \underline{\otimes }\, \,B( \mathfrak {h}) \subseteq B_c( \mathfrak {p}\otimes \mathfrak {h})\). We will show that the maps \(\phi _\rho |_{HS( \mathfrak {p})} \, \, \underline{\otimes }\, \,{{\,\mathrm{id}\,}}_{ B( \mathfrak {h}) }\) and \(\overline{\phi }_\rho |_{HS( \mathfrak {p})} \, \, \underline{\otimes }\, \,{{\,\mathrm{id}\,}}_{ B( \mathfrak {h}) }\) extend to operators from \(B_c( \mathfrak {p}\otimes \mathfrak {h})^*\) to \(B(\mathfrak {h}; \textsf {k}\otimes \mathfrak {h})\) and from \(B_c( \mathfrak {p}\otimes \mathfrak {h})^*\) to \(B(\mathfrak {h}; \overline{\textsf {k}}\otimes \mathfrak {h})\), respectively, and that the resulting maps are related via partial conjugation.
Proposition 6.7
There are unique operators
such that
for all \(A \in B_c( \mathfrak {p}\otimes \mathfrak {h})^*\), u, \(v \in \mathfrak {h}\) and \(\zeta \in {\textsf {k}}_\alpha \), \(\eta \in {\textsf {k}}_\beta \) with \(\alpha > \beta \). Furthermore, we have that
and the following properties hold.
-
(a)
If \(A \in B_c( \mathfrak {p}\otimes \mathfrak {h})^* \cap B_c( \mathfrak {p}\otimes \mathfrak {h})\) then \(\phi ^\mathfrak {h}_\rho ( A )\) is \({\textsf {k}}\)-conjugatable, \(\overline{\phi }^\mathfrak {h}_\rho ( A^* )\) is \(\overline{{\textsf {k}}}\)-conjugatable and \(\phi ^\mathfrak {h}_\rho ( A )^{\textsf {c}} = \overline{\phi }^\mathfrak {h}_\rho ( A^* )\). Thus
$$\begin{aligned} c\bigl ( \phi ^\mathfrak {h}_\rho ( A ) \bigr ) = || \overline{\phi }^\mathfrak {h}_\rho ( A^* ) || \leqslant c( A ) \qquad \text { and } \qquad c\bigl ( \overline{\phi }^\mathfrak {h}_\rho ( A^* ) \bigr ) = || \phi ^\mathfrak {h}_\rho ( A ) || \leqslant c( A^* ). \end{aligned}$$ -
(b)
The maps \(\phi ^\mathfrak {h}_\rho \) and \(\overline{\phi }^\mathfrak {h}_\rho \) are extensions of \(\phi _\rho |_{HS( \mathfrak {p})} \, \, \underline{\otimes }\, \,{{\,\mathrm{id}\,}}_{ B( \mathfrak {h}) }\) and \(\overline{\phi }_\rho |_{HS( \mathfrak {p})} \, \, \underline{\otimes }\, \,{{\,\mathrm{id}\,}}_{ B( \mathfrak {h}) }\), respectively.
Proof
Uniqueness is clear. For existence, let \(A \in B_c( \mathfrak {p}\otimes \mathfrak {h})^*\). For each \(\alpha \geqslant 0\), choose an orthonormal basis \(\big ( e^i_\alpha \big )_{i=1}^{d_\alpha }\) for \(\textsf {k}_\alpha \), and note that if \(u \in \mathfrak {h}\) then
Hence
defines an operator \(\phi ^\mathfrak {h}_\rho (A)\) from \(\mathfrak {h}\) to \(\textsf {k}\otimes \mathfrak {h}\) such that \(|| \phi ^\mathfrak {h}_\rho ( A ) || \leqslant c( A^* ) \); it also satisfies (6.8a) since, for all u, \(v \in \mathfrak {h}\), \(\zeta \in \textsf {k}_\alpha \) and \(\eta \in \textsf {k}_\beta \), where \(\alpha > \beta \),
In particular, the operator \(\phi ^\mathfrak {h}_\rho ( A )\) does not depend on the choice of orthonormal bases made above. Similarly, there is an operator \(\overline{\phi }^\mathfrak {h}_\rho (A)\) from \(\mathfrak {h}\) to \(\overline{\textsf {k}}\otimes \mathfrak {h}\) such that \(|| \overline{\phi }^\mathfrak {h}_\rho ( A ) || \leqslant c( A^* )\), the identity (6.8b) holds and, for any choice of orthonormal bases \(\bigl ( e^i_\alpha \bigr )_{i=1}^{d_\alpha }\) for \(\textsf {k}_\alpha \),
(a) If \(A \in B_c( \mathfrak {p}\otimes \mathfrak {h})^* \cap B_c( \mathfrak {p}\otimes \mathfrak {h})\), u, \(v \in \mathfrak {h}\) and \(\zeta \in \textsf {k}_\alpha \), \(\eta \in \textsf {k}_\beta \) with \(\alpha > \beta \), then
Therefore, by linearity,
so \(\phi ^\mathfrak {h}_\rho ( A )\) is \(\textsf {k}\)-conjugatable and \(\phi ^\mathfrak {h}_\rho ( A )^\textsf {c}= \overline{\phi }^\mathfrak {h}_\rho ( A^* )\).
(b) Let \(T \in HS( \mathfrak {p})\) and \(X \in B( \mathfrak {h})\). Then \(T \otimes X \in B_c( \mathfrak {p}\otimes \mathfrak {h})^* \cap B_c( \mathfrak {p}\otimes \mathfrak {h})\), by Theorem 4.1. Comparing matrix elements, the identities
are readily verified, so (b) follows. \(\square \)
Recall that a countable family of bounded operators \(\mathcal {C}\) is said to be strongly linearly independent if there is no non-zero function \(\alpha : \mathcal {C} \rightarrow \mathbb {C}\) such that \(\sum _{T \in \mathcal {C} } \alpha ( T ) T\) converges to zero in the strong sense.
Theorem 6.8
Let  ,
,  and
and  , where
, where  for all indices \(\alpha \) and, as in Theorem 6.4, set \(F = \left[ {\begin{matrix} K &{} - L^* \\ L &{} 0 \end{matrix}}\right] \in B\big ( \widehat{{\textsf {K}}_1 } \otimes \mathfrak {h}\big )_0\) where
for all indices \(\alpha \) and, as in Theorem 6.4, set \(F = \left[ {\begin{matrix} K &{} - L^* \\ L &{} 0 \end{matrix}}\right] \in B\big ( \widehat{{\textsf {K}}_1 } \otimes \mathfrak {h}\big )_0\) where

J being the natural isometry from \({\textsf {k}}\oplus \overline{{\textsf {k}}}\) to \(\mathbb {C}\oplus ({\textsf {k}}\oplus \overline{{\textsf {k}}} ) \oplus {\textsf {K}}_0\).
Suppose that the state \(\rho \) satisfies Assumption 6.5, and the operator  is \(\mathfrak {p}\)-conjugatable. Then the HP cocycle \(U := Y^F\) is \(\Sigma (\rho )\)-quasifree with \(\Sigma (\rho )\)-generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \), where
is \(\mathfrak {p}\)-conjugatable. Then the HP cocycle \(U := Y^F\) is \(\Sigma (\rho )\)-quasifree with \(\Sigma (\rho )\)-generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \), where  .
.
Suppose further that, with respect to some orthonormal bases \(\big ( e^i_\alpha \big )_{i=1}^{d_\alpha }\) for each \({\textsf {k}}_\alpha \), the family  is strongly linearly independent. Then \(\Sigma (\rho )\) is the unique gauge-invariant AW amplitude with respect to which the HP cocycle U is quasifree.
is strongly linearly independent. Then \(\Sigma (\rho )\) is the unique gauge-invariant AW amplitude with respect to which the HP cocycle U is quasifree.
Proof
Since U is a Gaussian HP cocycle with stochastic generator \(\left[ {\begin{matrix} K &{} - L^* \\ L &{} 0 \end{matrix}}\right] \), Corollary 4.11 implies that, for the first part, it suffices to verify the identity
Since \(H_{\textsf {I}}\) is a self-adjoint \(\mathfrak {p}\)-conjugatable operator, by assumption, Proposition 6.7 ensures that the operators Q and \(R := \mathrm {i}\overline{\phi }^\mathfrak {h}_\rho ( H_{\textsf {I}})\) are well defined and conjugatable, with \(Q^\textsf {c}= -\mathrm {i}\phi ^\mathfrak {h}_\rho ( H_{\textsf {I}})^\textsf {c}= -R\). Thus, for all \(\zeta \in \textsf {k}_\alpha \) and \(\eta \in \textsf {k}_\beta \) with \(\alpha > \beta \), and all u, \(v \in \mathfrak {h}\),
where \(H^u_v:= ( I_\mathfrak {p}\otimes \langle u \vert ) H_{\textsf {I}}( I_\mathfrak {p}\otimes \vert v \rangle )\). Hence, by Lemma 6.6,
On the other hand, by definition, the operator L is such that
Thus, in terms of the block-matrix decomposition \(L = \left[ {\begin{matrix} L_1 \\ L_2 \end{matrix}}\right] \in B( \mathfrak {h}; ( \textsf {k}\oplus \overline{\textsf {k}}) \otimes \mathfrak {h})\),
as required.
Finally, for each index \(\alpha \), let \(( e^i_\alpha )_{i=1}^{d_\alpha }\) be an orthonormal basis for \(\textsf {k}_\alpha \) and, for indices \(\alpha \) and \(\beta \), set \(e^{ij}_{\alpha \beta }:= \vert e^i_\alpha \rangle \langle e^j_\beta \vert \) for all \(i = 1\), ..., \(d_\alpha \) and \(j = 1\), ..., \(d_\beta \). Then, for all \(x \in \textsf {k}\setminus \{ 0 \}\), the family \(\bigl \{ \langle x , e^{ij}_{\alpha \beta } \rangle : \alpha > \beta \geqslant 0, \ i = 1, \ldots , d_\alpha , \ j = 1, \ldots , d_\beta \bigr \}\) is not identically zero and so, under the strong linear independence assumption,
In other words \(\textsf {k}^{L_1} = \{ 0 \}\) and therefore, by Corollary 5.3, there is no other gauge-invariant AW amplitude \(\Sigma \) with respect to which the HP cocycle U is \(\Sigma \)-quasifree. \(\square \)
Remark
Theorems 6.4 and 6.8 comprise a significant generalisation of the main result of [6, Theorem 7]. The restriction to finite-dimensional noise or particle space, is removed, and the interaction Hamiltonian is of a more general form. In [6], the operator \(H_{\textsf {I}}\) is taken to have the form \(\left[ {\begin{matrix} 0 &{} V^* \\ V &{} 0 \end{matrix}}\right] \) so that \(\mathrm {i}H_{\textsf {I}}\) is of the above form with \(L = \mathrm {i}V\). This assumption corresponds to the \(\Sigma (\rho )\)-quasifree generator \(\left[ {\begin{matrix} K &{} -Q^* \\ Q &{} 0 \end{matrix}}\right] \) satisfying
In conclusion, a large class of unitary quantum random walks, with particles in a faithful normal state, converge to HP cocycles governed by a quasifree quantum Langevin equation.
The results in this section could be applied to bipartite systems, as studied in [4], in non-zero temperature. In this model, two non-interacting quantum systems are both coupled to an environment comprising an infinite chain of identical and independent particles, with each particle now in the same non-zero temperature state. For the zero temperature case see [4, Theorem 3.1] and [12, Theorem 8.2]; the methods developed in [12] adapt nicely to the quasifree context.
References
Applebaum, D.: Quasi-free stochastic evolutions. In: Accardi, L., von Waldenfels, W. (eds) Quantum Probability and Applications II. Lecture Notes in Math, vol. 1136, pp. 46–56. Springer, Berlin (1985)
Araki, H., Woods, E.J.: Representations of the canonical commutation relations describing a nonrelativistic infinite free Bose gas. J. Math. Phys. 4, 637–662 (1963)
Arveson, W.: Noncommutative Dynamics and \(E\)-Semigroups. Springer Monographs in Mathematics. Springer, New York (2003)
Attal, S., Deschamps, J., Pellegrini, C.: Entanglement of bipartite quantum systems driven by repeated interactions. J. Stat. Phys. 154(3), 819–837 (2014)
Attal, S., Joye, A.: Weak coupling and continuous limits for repeated quantum interactions. J. Stat. Phys. 126(6), 1241–1283 (2007)
Attal, S., Joye, A.: The Langevin equation for a quantum heat bath. J. Funct. Anal. 247(2), 253–288 (2007)
Attal, S., Pautrat, Y.: From repeated to continuous quantum interactions. Ann. Henri Poincaré 7(1), 59–104 (2006)
Barnett, C., Streater, R.F., Wilde, I.F.: Quasi-free quantum stochastic integrals for the CAR and CCR. J. Funct. Anal. 52(1), 19–47 (1983)
Belton, A.C.R.: Random-walk approximation to vacuum cocycles. J. Lond. Math. Soc. 81(2), 412–434 (2010)
Belton, A.C.R.: Quantum random walks and thermalisation. Commun. Math. Phys. 300(2), 317–329 (2010)
Belton, A.C.R.: Quantum random walks with general particle states. Commun. Math. Phys. 328(2), 573–596 (2014)
Belton, A.C.R., Gnacik, M., Lindsay, J.M.: Strong convergence of quantum random walks via semigroup decomposition. Ann. Henri Poincaré 19(6), 1711–1746 (2018)
Bhat, B.V.R.: Cocycles of CCR flows. Mem. Am. Math. Soc. 149, 709 (2001)
Bouten, L.: Squeezing enhanced control. Report No. 0407, Department of Mathematics, University of Nijmegen (2004)
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum Statistical Mechanics II: Equilibrium States. Models in Quantum Statistical Mechanics. Texts and Monographs in Physics, 2nd edn. Springer, Berlin (1997)
Evans, M.P.: Existence of quantum diffusions. Probab. Theory Relat. Fields 81(4), 473–483 (1989)
Fagnola, F.: Quantum Markov semigroups and quantum flows. Proyecciones 18(3), 144 (1999)
Gardiner, C.W., Collett, M.J.: Input and output in damped quantum systems: quantum stochastic differential equations and the master equation. Phys. Rev. A 31(6), 3761 (1985)
Gough, J.: Principles and applications of quantum control engineering. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 370(1979), 5237–5451 (2012)
Hellmich, J., Honegger, R., Köstler, C., Kümmerer, B., Rieckers, A.: Couplings to classical and non-classical squeezed white noise as stationary Markov processes. Publ. Res. Inst. Math. Sci. 38(1), 1–31 (2002)
Honegger, R., Rieckers, A.: Squeezing Bogoliubov transformations on the infinite mode CCR-algebra. J. Math. Phys. 37(9), 4292–4309 (1996)
Hudson, R.L., Lindsay, J.M.: A noncommutative martingale representation theorem for non-Fock quantum Brownian motion. J. Funct. Anal. 61(2), 202–221 (1985)
Hudson, R.L., Lindsay, J.M.: Uses of non-Fock quantum Brownian motion and a quantum martingale representation theorem. In: Accardi, L., von Waldenfels, W. (eds.) Quantum Probability and Applications II. Lecture Notes in Math, vol. 1136, pp. 276–305. Springer, Berlin (1985)
Hudson, R.L., Parthasarathy, K.R.: Quantum Itô’s formula and stochastic evolutions. Commun. Math. Phys. 93(3), 301–323 (1984)
Kurepa, S.: The Cauchy functional equation and scalar product in vector spaces. Glasnik Mat.-Fiz. Astronom. Ser. II Društvo Mat. Fiz. Hrvatske 19, 23–36 (1964)
Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48(2), 119–130 (1976)
Lindsay, J.M.: Fermion martingales. Probab. Theory Relat. Fields 71(2), 307–320 (1986)
Lindsay, J.M.: Quantum stochastic analysis—an introduction, In: Schürmann, M., Franz, U. (eds.) Quantum Independent Increment Processes I. Lecture Notes in Math, vol. 1865. Springer, Heidelberg (2005)
Lindsay, J.M.: Quantum stochastic Lie–Trotter product formula II. Int. Math. Res. Not. IMRN rnx306. https://doi.org/10.1093/imrn/rnx306
Lindsay, J.M., Maassen, H.: Stochastic calculus for quantum Brownian motion of nonminimal variance—an approach using integral-sum kernel operators. In: Mark Kac Seminar on Probability and Physics, CWI Syllabi, vol. 32, pp. 97–167. Math. Centrum, Centrum Wisk. Inform., Amsterdam (1992)
Lindsay, J.M., Margetts, O.: Quasifree martingales. arXiv:1203.6693 [math.OA]
Lindsay, J.M., Margetts, O.: Quasifree stochastic analysis.
Lindsay, J.M., Wills, S.J.: Existence, positivity, and contractivity for quantum stochastic flows with infinite dimensional noise. Probab. Theory Relat. Fields 116(4), 505–543 (2000)
Meyer, P.-A.: Quantum Probability for Probabilists. Lecture Notes in Math, vol. 1538, 2nd edn. Springer, Berlin (1993)
Parthasarathy, K.R.: Introduction to Quantum Stochastic Calculus. Monographs in Mathematics, vol. 85. Birkhäuser, Basel (1992)
Parthasarathy, K.R., Sinha, K.B.: Stochastic integral representation of bounded quantum martingales in Fock space. J. Funct. Anal. 67(1), 126–151 (1986)
Parthasarathy, K.R., Sinha, K.B.: Unifications of quantum noise processes in Fock space. In: Accardi, L., von Waldenfels, W. (eds.) Quantum Probability and Related Topics VI, pp. 371–384. World Scientific, Singapore (1991)
Parthasarathy, K.R., Sinha, K.B.: Quantum Markov processes with a Christensen-Evans generator in a von Neumann algebra. Bull. Lond. Math. Soc. 31(5), 616–626 (1999)
Petz, D.: An Invitation to the Algebra of Canonical Commutation Relations. Leuven Notes in Mathematical and Theoretical Physics. Series A: Mathematical Physics, vol.2, Leuven University Press, Leuven (1990)
Reed, M., Simon, B.: Methods of Modern Mathematical Physics I: Functional Analysis. Academic Press, New York (1972)
Segal, I.E.: Mathematical Problems of Relativistic Physics. Lectures in Applied Mathematics, vol. II. American Mathematical Society, Providence, RI (1963)
Skeide, M.: Indicator functions of intervals are totalising in the symmetric Fock space \(\Gamma ( L^2({\mathbb{R}_+}) )\). In: Accardi, L., Kuo, H.-H., Obata, N., Saito, K., Si, Si, Streit, L. (eds.) Trends in Contemporary Infinite Dimensional Analysis and Quantum Probability. Volume in Honour of Takeyuki Hida. Istituto Italiano di Cultura, Kyoto (2000)
Slawny, J.: On factor representations and the \(C^*\)-algebra of canonical commutation relations. Commun. Math. Phys. 24, 151–170 (1972)
Wills, S.J.: On the generators of operator Markovian cocycles. Markov Process Relat. Fields 13(1), 191–211 (2007)
Zoller, P., Gardiner, C.W.: Quantum noise in quantum optics: the stochastic Schrödinger equation. In: Les Houches, S. Reynaud, E. Giacobino & J. Zinn-Justin (eds.) Fluctuations Quantiques, vol. 1997, pp. 79–136. North-Holland, Amsterdam (1995)
Acknowledgements
This work was supported by the Leverhulme Trust Research Project Grant RPG-2014-196 Quantum random walks and quasi-free quantum stochastic calculus.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In this appendix, we prove that symplectic automorphisms of a Hilbert space \(\textsf {h}\) are necessarily bounded, and give a parameterisation for the elements of the group \(S(\textsf {h})^\times \). For the convenience of the reader, this is a streamlined version of the proof given in [21], which also covers the case of unbounded symplectic automorphisms of separable pre-Hilbert spaces.
Proposition A.1
Let \(B \in S({\textsf {h}})^\times \). Then B is bounded.
Proof
Let L and A be the linear and conjugate-linear parts of B, as in (2.1). For all z, \(x \in \textsf {h}\),
Thus L has everywhere-defined adjoint \(x \mapsto \tfrac{1}{2}\bigl ( B^{-1} x - \mathrm {i}B^{-1} ( \mathrm {i}x ) \bigr )\), and so is closed, and therefore bounded, by the closed graph theorem. Similarly, the conjugate-linear operator A has everywhere-defined adjoint \(x \mapsto -\tfrac{1}{2}\bigl ( B^{-1} x + \mathrm {i}B^{-1} ( \mathrm {i}x ) \bigr )\), and so is also bounded. Thus B is bounded. \(\square \)
For a triple (V, C, P) consisting of a unitary operator V on \(\textsf {h}\), a bounded non-negative operator P on \(\textsf {h}\) and a conjugation (a self-adjoint anti-unitary operator) C on \(\textsf {h}\), such that P and C commute, we define the following bounded real-linear operator on \(\textsf {h}\):
Remark
Since, with (V, C, P) as above, the map \(-C\) is also a conjugation on \(\textsf {h}\) that commutes with P, a deliberate choice is being made here. The reason for this particular choice is that it eliminates minus signs elsewhere.
Theorem A.2
-
(a)
Let (V, C, P) be a triple as above.
-
(i)
The operator \(B_{V,C,P}\) is a symplectic automorphism, with bounded inverse
$$\begin{aligned} ( \cosh P + C \sinh P ) V^* = B_{V^*,-VCV^*,VPV^*}. \end{aligned}$$ -
(ii)
Suppose that \(B_{V,C,P}= B_{V',C',P'}\) for another such triple \((V',C',P')\). Then
$$\begin{aligned} V' = V, \quad P' = P \quad \text {and }C'\text { agrees with }C\text { on }{{\,\mathrm{Ran}\,}}P. \end{aligned}$$
-
(i)
-
(b)
Conversely, let \(B \in S( {\textsf {h}})^\times \). Then there is a triple (V, C, P) as above, such that \(B = B_{V,C,P}\).
Proof
(a) (i) This is readily verified.
(ii) Set \(B = B_{V,C,P}\), and let L and A be its linear and conjugate-linear parts. Then
Since the bounded operators \(\cosh P\) and \(\cosh P'\) are non-negative and invertible, and V and \(V'\) are unitary, the uniqueness of polar decompositions implies that \(V' = V\) and \(\cosh P' = \cosh P\). The non-negativity of \(P'\) and P therefore implies that \(P' = P\), and thus also \(C' \sinh P' = C \sinh P\). It follows that \(C' f( P' ) = C f( P )\) for all continuous functions \(f: {\mathbb {R}_+}\rightarrow \mathbb {C}\) satisfying \(f(0) = 0\); in particular \(C' P = C P\), so \(C'\) and C agree on \({{\,\mathrm{Ran}\,}}P\).
(b) Let L and A denote the linear and conjugate-linear parts of B. It follows from the proof of Proposition A.1 that \(L^*\) and \(- A^*\) are respectively the linear and conjugate-linear parts of \(B^{-1}\), so
Therefore, taking linear and conjugate-linear parts,
Applying the first of these identities to the symplectic automorphism \(B^{-1}\), we see that
Let V|L| and W|A| be the polar decompositions of L and A, respectively, and set \(\textsf {K}:= {{\,\mathrm{Ker}\,}}| A |\) and \(\textsf {K}^* := {{\,\mathrm{Ker}\,}}| A^* |\). The conjugate-linear partial isometry W has initial space \(\textsf {K}^\perp \) and final space \(\textsf {K}^{* \perp }\), and the identities (A.2) and (A.3) imply that L is invertible, so V is unitary, and \(| L | \geqslant I_\textsf {h}\). Thus there exists a unique non-negative operator \(P \in B(\textsf {h})\) such that \(| L | = \cosh P\) and \(| A | = ( | L |^2 - I_\textsf {h})^{1/2} = \sinh P\). Now \(| L^* | = V | L | V^*\) and \(| L | = V^* | L^* | V\) so, for all \(x \in \textsf {K}\) and \(z \in \textsf {K}^*\),
which implies that \(V \textsf {K}\subseteq \textsf {K}^*\) and \(V^* \textsf {K}^* \subseteq \textsf {K}\). Hence \(V \textsf {K}= \textsf {K}^*\), and therefore also \(V \textsf {K}^\perp = \textsf {K}^{* \perp }\). It follows that, on \(\textsf {h}= \textsf {K}\oplus \textsf {K}^\perp \), \(V^*W\) has the form \(\{ 0 \} \oplus D_1\) for an anti-unitary operator \(D_1\) on \(\textsf {K}^\perp \). Therefore, setting \(D := D_0 \oplus D_1\) for an arbitrary conjugation \(D_0\) on \(\textsf {K}\),
\(|A| D = |A| V^*W\) and \(V^*W |A| = D |A|\). Thus, using the identities (A.2) and (A.3) once more,
Therefore D commutes with \(| A | = \sinh P\) and so commutes with all continuous functions of \(\sinh P\) such as P itself and |L|. The second identity in (A.2) now implies that
so D and \(D^*\) agree on \({{\,\mathrm{\overline{{{\,\mathrm{Ran}\,}}}}\,}}|A| = \textsf {K}^\perp \), and thus \(D^*_1 = D_1\). But \(D^*_0 = D_0\), since \(D_0\) is a conjugation on \(\textsf {K}\), therefore \(D^* = D\) and so the anti-unitary operator D is a conjugation on \(\textsf {h}\). The proof is now completed by letting C be the conjugation \(-D\). \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Belton, A.C.R., Gnacik, M., Lindsay, J.M. et al. Quasifree Stochastic Cocycles and Quantum Random Walks. J Stat Phys 176, 1–39 (2019). https://doi.org/10.1007/s10955-019-02273-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-019-02273-9
Keywords
- Quantum stochastic calculus
- Quasifree representation
- Heat bath
- Repeated quantum interactions
- Noncommutative Markov chain
- Quantum Langevin equation



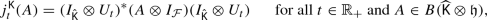
 has the block-matrix form
has the block-matrix form  for some
for some  .
. , let
, let  and
and 
