Abstract
A particle with internal degrees of freedom is in contact with a bath of photons (necessitating a relativistic treatment). The occurrence of decoherence is established and the density matrix is found to be diagonal in momentum space. In the case of non-trivial internal degrees of freedom and selection rules there is a first order phase transition separating those degrees of freedom. Finally, because probability amplitudes become probabilities, Einstein’s proposal that more than one detector could respond to a signal is answered.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In a recent publication [1] we showed that—subject to technical assumptions—a particle that is bombarded by others tends to a diagonal state in momentum space. Moreover, that diagonal state is just the thermal state \(\propto \exp (-\beta m{\varvec{p}}^2/2)\) with \(\beta \) the inverse temperature (and the Boltzmann constant taken to be unity). In other words it decoheres, but is left with a not-quite-diagonal density matrix in coordinate space, namely there are off-diagonal terms on the scale of the thermal wavelength, \(\lambda _\mathrm {thermal} \sim \hbar \sqrt{\beta /m}\). This result contradicted certain results in the literature [2]. Moreover, it established the spatial limits of decoherence, limits that were not probed when scattering was treated with a no-recoil assumption [3]. In [1], as well as in [4] and [5], the no-recoil assumption was dropped.
In the present paper the bombardment comes from a bath of photons. The conditions suggest a relativistic treatment and it turns out that this is much simpler to implement. Here too we make certain technical assumptions, but again find that the limiting density matrix for a particle in a thermal bath of photons is itself a thermal state, diagonal in momentum space.
We also make the usual physical assumptions. Namely we live with contradictory views of the scattering process. On the one hand, the \(S\)-matrix is used to describe a single scattering; on the other—even though the \(S\)-matrix nominally goes from time \(=-\infty \) to time \(=+\infty \)—we imagine that many scatterings take place. The use of \(S\)-matrix theory is nevertheless justified if the collisions are reasonably separated from one another (obviating the use of this method to draw conclusions about liquids or solids) and if the collisions are exponentially distributed as they are expected to be.
In a concluding section we examine some of the consequences of our calculation, including the possibility of phase transitions, a topic not discussed in [1], since internal degrees of freedom were not considered. We also address an old question of Einstein.
2 Defining the States
The microscopic state of the particle is \((p,\tau )\), with \(\tau =1,\dots ,n\) labeling the internal degrees of freedom and \(p=(p^\mu )=(p^0,{\varvec{p}})\) is the 4-momentum. When the particle has internal state \(\tau \) its energy is
with \(M_\tau \) the internal mass and \(c=1\).
The photons are considered to form a bath and are characterized by occupation numbers \(\{N_k\}\), with k the 4-momentum (so that \(k^2=0\)).
The density matrix of the particle is
For the photon bath the density matrix is
For a thermal bath of photons at temperature \(\beta ^{-1}\), \({\rho _{_B}}\) is diagonal and
3 Evolution of the Particle Density Matrix
The initial density matrix for the particle and bath is \({\rho _{_S}}\otimes {\rho _{_B}}\). The evolution is given by the \(S\)-matrix
followed by a trace over the bath occupation numbers. The dynamics is defined by the \(S\)-matrix. Its asymptotic states are \((p,\tau )\) and \(\{N_{0,k}\}\) and S is defined by the underlying Hamiltonian dynamics. S satisfies conservation of 4-momentum
where \(p_i^0(\tau _i)\) is given by Eq. (1). The evolution induces a “superoperator” R on the density matrix of the particle, given by
The sum in Eq. (7) is over the various collections of occupation numbers; the integral is over the momenta together with a summation on the internal states of the particle. The integrals over energy are left in the formulas despite the presence of \(\delta \)-functions in S so as not to clutter our expressions with square roots of the energy. Conservation of momentum gives
We examine the special case where the photon bath density matrix is diagonal. Then \(N_{0,k}=N_{0,k}'\) for any k. Subtracting Eq. (8) from Eq. (9) gives
which implies that
In particular, the diagonal element of \(R{\rho _{_S}}\), namely \((R{\rho _{_S}})(p_1,\tau _1|p_1',\tau _1')\), depends only on the diagonal elements of \({\rho _{_S}}\), i.e., \({\rho _{_S}}(p_0\tau _0|p_0\tau _0)\). In other words, R induces a stochastic matrix, \(R(p_1,\tau _1|p_0,\tau _0)\) so that
In general \((R{\rho _{_S}})(p_1,\tau _1|p_1',\tau _1')\) depends only on the elements \({\rho _{_S}}(p_0,\tau _0|p_0',\tau _0')\) satisfying Eq. (10) (or equivalently Eqs. (11)–(12)).
Again we consider the case where the photon bath is thermal (Eq. (4)). Then the thermal state of the particle
is preserved under the dynamics. In other words, if the system is in a thermal state, it stays there.
Proof
Insert Eqs. (4) and (14) into \(R{\rho _{_S}}\) given by Eq. (7). It has already been shown that \(R\rho \) is diagonal. Moreover, by conservation of energy
(here \(\tau _0=\tau _0'\), \(\tau _1=\tau _1'\)), so that
In the last term of Eq. (16) we sum first over \((p_0\tau _0)\) and \(\{N_{0,k}\}\) and by unitarity
Finally, by normalization
Therefore in Eq. (16)
\(\square \)
4 Decoherence and Convergence to the Thermal State
4.1 Proof that the Non-diagonal Elements of \(R^N{\rho _{_S}}\) in a Momentum Basis Tend to Zero as \(N\rightarrow \infty \) for a Diagonal Photon Bath
We know that \((R{\rho _{_S}})(p_1,\tau _1|p_1',\tau _1')\) depends only on the elements \({\rho _{_S}}(p_0,\tau _0|p_0',\tau _0')\) with
Define
One can write
with
Here the sum is over occupation numbers as well as on \(\tau _1\). If \(q=0\), then by unitarity
If \(q\ne 0\), then by the Cauchy–Schwarz inequality
with strict inequality in Eq. (23) if
for at least one state \((p_1,\{N_{1,k}\})\) or \(\{N_{0,k}\}\).
Moreover, in the second term in Eq. (23) each factor in the product is 1, by the unitarity of S. Therefore
It follows that for \(q\ne 0\)
4.2 Convergence to Thermal Equilibrium
The diagonal elements of \(R\rho \) are given by Eq. (13). We assume that the stochastic matrix \(R(p_1,\tau _1|p_0,\tau _0)\) in the second term of Eq. (13) is irreducible. In that case the diagonal elements of \(R^N\rho \) converge to the thermal state as \(N\rightarrow \infty \) because the thermal state is a stationary state for the stochastic matrix R and is unique if R is irreducible. Therefore \(R^N\rho \) converges to the thermal state when \(N\rightarrow \infty \).
4.3 Detailed Balance
Finally, the stochastic matrix R of Eq. (13) which describes the evolution of the diagonal elements of \(\rho \) satisfies detailed balance
This implies that R has real eigenvalues.
4.4 Phase Transitions
We order the internal parameters, \(\tau \) so that
Thus
The summation is over the two collections of occupation numbers.
To obtain a phase transition it is necessary and sufficient that the first m eigenvalues after 1 be almost degenerate with 1 and that smaller eigenvalues be much smaller [6,7,8,9]. Thus, if the eigenvalues are ordered by magnitude, \(1\equiv \lambda _0\gtrsim \lambda _1 \gtrsim \dots \gtrsim \lambda _m \gg |\lambda _{m+1}|\). For the situation at hand we assume that transitions in the internal parameter are relatively rare so that in this case \(n=m+1\). R can then be decomposed in diagonal blocks with small matrix elements connecting different blocks, representing the transitions between internal quantum numbers. Each diagonal block represents a phase, while inside a block the dynamics is given by rapid equilibration, leading to smaller (more rapid) eigenvalues.
Suppose, for example, that the transitions between \(\tau _0=1\) and a nearby value, say \(\tau _1=2\), is strongly forbidden (this could be due to conservation of angular momentum at some level of perturbation theory). Then the \(S\)-matrix values connecting \((p_0,\tau _0=1)\) and \((p_1,\tau _1=2)\) are very small, so that
for some small \(\epsilon \) (for \((p_0,\tau _0=1)\) and \((p_1,\tau _1=2)\)). In this case R is almost degenerate and we have a phase transition, which each phase having a different value of \(\tau \).
Remark
If \(M_1\ll M_2 \le M_3\le \dots \), a transition from \((p_0,\tau _0=1)\) to \((p_1,\tau _1=2)\) requires at least the absorption of a photon of momentum k with \(k^0\ge M_2-M_1\) and thus by Eq. (25)
which is very small at low temperatures. But \(R(p_0,\tau _0|p_1,\tau _1)\) can still be large, so that condition Eq. (28) alone does not imply a phase transition.
5 Conclusions
We have shown that the eventual state of a bombarded particle leaves it in a thermal state, and in particular one that is not diagonal in coordinate space, but rather in momentum space. The scale of the coordinate space off-diagonal elements is \(\lambda _\mathrm {thermal} \sim \hbar \sqrt{\beta /m}\). The present calculation is performed for bombardment by photons, and although a relativistic treatment is called for and might have been considered troublesome, it actually turns out to be easier than the non-relativistic calculation.
We have also found that one can allow the internal state of the particle to change. Moreover, if there is an approximate conservation law that causes there to be selection rules, the matrix of transition probabilities turns out to exhibit the features of a phase transition—eigenvalues near unity with a subsequent dropoff. (All eigenvalues are real, because of detailed balance, which was also demonstrated.) These different internal states correspond to “channels” in scattering theory.
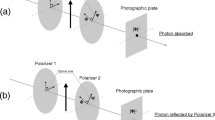
There is another old question partially answered by this calculation. Back in 1927 Einstein asked [10]Footnote 1 (paraphrasing), “Why don’t we get two detector clicks from the same electron?” “Why when a particle is surrounded by a collection of detectors does it excite only one of them?” In fact, this was eventually tested experimentally [11] and indeed there was but one click per particle. Einstein’s question was asked at the fifth Solvay conference and in our opinion was not satisfactorily answered by those advocating the Copenhagen interpretation. In the present calculation we have shown that a photon bath will convert probability amplitudes to probabilities, that is, on the scale of the thermal wavelength the density matrix is diagonal. The thermal wavelength due to cosmic background radiation is already quite small (\(\lambda _\mathrm {thermal} \sim 10^{-34} \sqrt{1/2.7\times 1.4\times 10^{-23} \times 10^{-30}} \sim 15\,\hbox {nm}\) for an electron in MKS units), answering Einstein’s question, at least for electrons and typical detectors.
Notes
Apropos of seeing “two clicks,” one could also imagine seeing two channels excited in a single scattering event—something never observed. Einstein saw a way out of his rejection of various interpretations through ideas advocated by de Broglie, specifically he said
In my opinion, one can only lift this objection the following way: the process is not only described by the Schrodinger wave, but at the same time one localizes the particle during its propagation. I think M. de Broglie is right to search in this direction. If one uses only Schrödinger waves, then approach II to \(|\psi |^2\) implies, in my opinion, a contradiction to the postulate of relativity.
The ideas of de Broglie have been developed in [12,13,14,15]. Interestingly, in Bohm’s article [12] Einstein is thanked.
References
Gaveau, B., Schulman, L.S.: Decoherence, the density matrix, the thermal state and the classical world. J. Stat. Phys. 169, 889–901 (2017)
Tegmark, M.: Apparent wave function collapse caused by scattering. Found. Phys. Lett. 6, 571–590 (1993)
Joos, E., Zeh, H.D.: The emergence of classical properties through interaction with the environment. Z. Phys. B 59, 223–243 (1985)
Diósi, L.: Quantum master equation of a particle in a gas environment. EPL 30, 63–68 (1995)
Hornberger, K., Sipe, J.E.: Collisional decoherence reexamined. Phys. Rev. A 68, 012105 (2003)
Gaveau, B., Schulman, L.S.: Theory of non-equilibrium first order phase transitions for stochastic dynamics. J. Math. Phys. 39, 1517–1533 (1998)
Gaveau, B., Schulman, L.S.: Multiple phases in stochastic dynamics: geometry and probabilities. Phys. Rev. E 73, 036124 (2006)
Biroli, G., Kurchan, J.: Metastable states in glassy systems. Phys. Rev. E 64, 016101 (2001)
Macieszczak, K., Gut̨ă, M., Lesanovsky, I., Garrahan, J.P.: Towards a theory of metastability in open quantum dynamics. Phys. Rev. Lett. 116, 240404 (2016)
Einstein, A.: In the \(5^{{\rm th}}\) Solvay conference, in October 1927. Reprinted in A. Einstein, Oevres Choisies, Tome 1, pp. 210–211, eds. F. Balibar, O. Darrigol, and B. Jech, Ed. du Seuil, Ed. du CNRS, Paris (1989)
Hegerfeldt, G.C.: private communication
Bohm, D.: A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 85, 166–179 (1952)
Nelson, E.: Dynamical Theories of Brownian Motion. Princeton University Press, Princeton (1st edn., 1967; 2nd edn., 2001)
Riccia, G.D., Wiener, N.: Wave mechanics in classical phase space, brownian motion, and quantum theory. J. Math. Phys. 7, 1372–1383 (1966)
Dürr, D., Goldstein, S., Zanghi, N.: Quantum equilibrium and the origin of absolute uncertainty. J. Stat. Phys. 67, 843–907 (1992)
Acknowledgements
Open access funding provided by the Max Planck Society.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gaveau, B., Schulman, L.S. Decoherence and Phase Transitions in Quantum Dynamics. J Stat Phys 174, 800–807 (2019). https://doi.org/10.1007/s10955-018-2214-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-018-2214-7