Minority Population in the One-Dimensional Schelling Model of Segregation

Abstract

Schelling models of segregation attempt to explain how a population of agents or particles of two types may organise itself into large homogeneous clusters. They can be seen as variants of the Ising model. While such models have been extensively studied, unperturbed (or noiseless) versions have largely resisted rigorous analysis, with most results in the literature pertaining models in which noise is introduced, so as to make them amenable to standard techniques from statistical mechanics or stochastic evolutionary game theory. We rigorously analyse the one-dimensional version of the model in which one of the two types is in the minority, and establish various forms of threshold behaviour. Our results are in sharp contrast with the case when the distribution of the two types is uniform (i.e. each agent has equal chance of being of each type in the initial configuration), which was studied in Brandt et al. (in: STOC ’12: proceedings of the 44th symposium on theory of computing, pp. 789–804, 2012) and Barmpalias et al. (in: 55th Annual IEEE symposium on foundations of computer science, Oct 18–21, Philadelphia, FOCS’14, 2014).

1 Introduction

The economist Thomas Schelling introduced his model of segregation in [30] (developed later in [28, 29]), with the explicit intention of explaining the phenomenon of racial segregation in large cities. Perhaps the earliest agent-based model studied by economists, since then it has become an archetype of agent-based modelling, prominently featuring in libraries of modelling software tools such as NetLogo [35] and often being the subject of experimental analysis and simulations in the modeling and AI communities [11, 12, 15, 16, 18, 19, 21, 32, 36]. Many versions of the model have been analysed theoretically, from a number of different viewpoints and disciplines: statistical mechanics [8, 14] and [4, Sect. 3.1], evolutionary game theory [37,38,39,40] the social sciences [9, 10, 27], and more recently computer science and AI [1, 5, 7, 13]. It was observed in [7], however, that despite the vast amount of work that has been done on the Schelling model in the last 40 years, rigorous mathematical analyses in the previous literature generally concern altered versions of the model, in which noise is introduced in the dynamics, i.e. where one allows that agents may make non-rational decisions that are detrimental to their welfare with small probability. The introduction of such ‘perturbations’ may be justifiable from a ‘bounded rationality’ standpoint.

The model (which will be formally defined shortly) concerns a population of agents arranged geographically, each being of one of two types. Each agent has a certain neighbourhood around them that they are concerned with, and also an intolerance parameter $\tau \in [0,1]$ which we shall assume here to be the same for all agents. An agent’s behaviour is dictated by the proportion of the agents in their neighbourhood which are of its own type. So long as this proportion is $\ge \tau$ the agent may be considered ‘happy’ and will not move. Starting with a random configuration, one then considers a discrete time dynamical process. At each stage unhappy agents may be given the opportunity to move, swapping positions with another agent, so as to increase the proportion of their own type within their neighbourhood. Now one might justify a perturbed version of these dynamics, in which agents will occasionally move in such a way as to decrease their utility (i.e. the proportion of their own type within their neighbourhood) by arguing, for example, that it is reasonable to suppose that only incomplete information about the make-up of each neighbourhood is available to the agents. It is a fact, however, that

• (a) the methods used for the analysis of the perturbed models do not apply to the unperturbed model;

• (b) the segregation occurring in the perturbed models is very different than in the unperturbed model.

In the unperturbed models the underlying Markov chain does not have the regularities that are found in the perturbed case (e.g. the Markov process is irreversible). The presence of a large variety of absorbing states means that entirely different and more combinatorial methods are now required. Beyond the basic aim of a rigorous analysis for these unperturbed models, which have been so extensively studied via simulations, further motivation is provided by the fact that the Schelling model is part of a large family of models, arising in a broad variety of contexts—spin glass models, Hopfield nets, cascading phenomena as studied by those in the networks community—all of which aim at understanding the discrete time dynamics of competing populations on underlying network structures of one kind or another, and for many of which the unperturbed dynamics are of significant interest. The hope is that techniques developed in analysing unperturbed Schelling segregation may pave the way for similar analyses in these variants of the model.

The first rigorous analysis of an unperturbed Schelling model was described by Brandt et al. in [7]. In this work it was also demonstrated that the eventual state of the process differs significantly from the stochastically stable states of the perturbed models. This study focused on the one-dimensional Schelling model and provided an asymptotic analysis, in the sense that the results hold with arbitrarily high probability for all sufficiently large neighbourhoods and population. More significantly, however, it dealt only with the symmetric case where intolerance parameter $\tau =0.5$ (i.e. an agent is happy when at least 50% of the agents in its neighbourhood are of its own type). In [1] a much more general analysis of the unperturbed one-dimensional Schelling model for $\tau \in [0,1]$ was provided. In fact it was shown there that various forms of surprising threshold behaviour exist. A significant symmetry assumption underlying the results in [1, 7] is that the populations of the two types of agents are assumed to be uniform (i.e. each agent has equal chance of being of each type in the initial configuration). Indeed, there is no rigorous study of the unperturbed spacial proximity model with swapping agents for the rather realistic case where the distribution of the two types of agents is skewed. In fact, the question as to what type of segregation occurs with a skewed population distribution was raised by Brandt et al. in [7, Sect. 4] as well as in popular expositions of the Schelling model like [20].

The purpose of the present work is to give an answer to this question. We show that complete segregation is the likely outcome if and only if the intolerance parameter is larger than 0.5. Moreover in the case that the minority type is at most 25%, there is a dichotomy between complete segregation and almost complete absence of segregation.

Table 1 Parameters of the Schelling model

1.1 Definition of the Model

Schelling’s model of residential segregation belongs to a large family of agent-based models, where a system of competitive agents perform actions in order to increase their personal welfare, while possibly decreasing the welfare of other individuals. This phenomenon roughly corresponds to the so-called spontaneous order approach¹ in economics literature, which studies the emergence of norms from the endogenous agreements among rational individuals.

The Schelling model that we study is a direct generalisation of that in [7] and also that studied by the authors in [1]. The one-dimensional model with parameters $n, w, \tau , \rho$ (as listed in Table 1) is defined as follows. We consider n individuals which occupy an equal number of sites $0,\dots , n-1$ (ordered clockwise) on a circle. Each of the individuals belongs to one of the two types $\alpha$ and $\beta$. The type assignment of individuals is independent and identically distributed (i.i.d.), with each individual having probability $\rho$ of being type $\beta$. Without loss of generality we always assume that $\rho \le 0.5$, i.e. that the individuals of type $\beta$ are the expected minority (so long as $\rho \ne 0.5$). This random type assignment takes place at stage 0 of the process, and defines the initial state. At the end of stage 0, we let $\rho _{*}$ be the actual proportion of the individuals that are of type $\beta$ (i.e. $\rho _{*}$ is the random proportion, as opposed to the expected proportion $\rho$).

Unless stated otherwise, addition and subtraction on indices for sites are performed modulo n. Given two sites u, v in any configuration of the individuals on the circle, the interval [u, v] consists of the individuals that occupy sites between u and v (inclusive). For example, if $0\le v<u<n$ then we let [u, v] denote the set of nodes $[u,n-1] \cup [0,v]$ (while [v, u] is, of course, understood in the standard way). When we talk about a particular configuration, we identify each individual with the site it occupies, referring to both entities as a node. The neighbourhood of node u consists of the interval $[(u-w),\ \ (u+w)]$ where w is a parameter of the model that we call the (neighbourhood) radius. The tolerance threshold $\tau \in (0,1)$ is another parameter of the model that reflects how tolerant a node is to nodes of different a type in its neighbourhood. We say that a node is happy if the proportion of the nodes in its neighbourhood which are of its own type is at least $\tau$.

Given the initial type assignment (colouring) of the nodes, the Schelling process then evolves dynamically in stages as follows. At each stage $s>0$ we pick uniformly at random a pair of unhappy nodes of different type, and we swap them provided that in both cases the number of nodes of the same type in the new neighbourhood is at least that in the original neighbourhood. If at some stage there are no further legal swaps the process terminates. If at some stage all nodes of the same type are grouped into a single block (i.e. a contiguous interval), we say that at that stage we have complete segregation.

This completes the definition of the Schelling process with parameters $n,w,\tau$ and $\rho$, which we denote by the tuple $(n, w, \tau , \rho )$. The process can be seen as a Markov chain with $2^n$ states corresponding to the configurations that we get by varying the type of each node between $\alpha$ and $\beta$. A state is called dormant if either all $\alpha$-nodes are happy, or all $\beta$-nodes are happy. We shall be interested in the case that w is large, and that n is large compared to w. In this context it will turn out that the absorbing states of the Schelling process are exactly the dormant states and, in fact, the only recurrence classes of the Schelling process are the dormant states and complete segregation. Complete segregation is, strictly speaking, a recurrence class of the process, consisting of the rotations of the two blocks, one consisting of all the $\alpha$-nodes and the other consisting of all the $\beta$-nodes. Hence, modulo symmetries, we may regard complete segregation as an absorbing state. Dormant states are a different kind of absorbing state, as the process actually stops when it hits a dormant state. Note that a static process cannot come to complete segregation, since it does not allow a sufficient number of swaps for the complete separation of the node types on the ring to be formed, starting from a random state. Note that the number of nodes of type $\alpha$ and of type $\beta$ does not change between transitions, once the initial state has been chosen.

1.2 Our Results

Given the Schelling process $(n, w, \tau , \rho )$ we wish to determine with high probability the type of equilibrium that will eventually occur in the system. Given a constant $c\ge 0$, we write ‘for $c\ll w\ll n$’, to mean ‘for all w sufficiently large compared to c, and all n sufficiently large compared to w’; formally, we say that a result with parameters w, n holds for $c\ll w\ll n$, if there exist functions $c\mapsto W_c$, $w\mapsto N_w$ such that the result holds for each $w>W_c$ and $n\ge N_w$. We are interested in asymptotic results, i.e. statements that hold with arbitrarily high probability for $0\ll w\ll n$. The following definition encapsulates the type of asymptotic statements about the Schelling process $(n,w,\tau , \rho )$ that we are interested in establishing.

Definition 1

(Properties with high probability and static processes) Suppose that R is a property which may or may not be satisfied by any given run of the Schelling process $(n, w, \tau , \rho )$, and T is a property of $\tau , \rho$. The sentence “if $T(\tau , \rho )$, then with high probability $R(n, w, \tau , \rho )$” means that, provided that $\tau , \rho$ satisfy T, for all $\epsilon >0$ and $1/\epsilon \ll w\ll n$, the process $(n, w, \tau , \rho )$ satisfies R with probability at least $1-\epsilon$. We say that the process $(n,w,\tau ,\rho )$ is static if, given $\epsilon >0$, with high probability the number of nodes that ever change their type in the entire duration of the process is $\le \epsilon \cdot n$.²

By [1, 7], the asymptotic behaviour of the process $(n,w,\tau ,\rho )$ is known for $\rho =0.5$ (except on the threshold $\tau =\kappa _0\approx 0.353$). The present work is dedicated to the case where one type of node is the minority, i.e. when $\rho <0.5$. We show that with probability 1 the process will either reach complete segregation or reach a dormant state. Moreover we show that when $\tau >0.5$ the highly probable outcome is complete segregation. Moreover, in many cases when $\tau \le 0.5$ the outcome is negligible segregation (i.e. the process is static). Let $\kappa _0\approx 0.353$ and $\lambda _0\approx 0.4115$ be the unique solutions of $\left( 0.5-x \right) ^{0.5-x} = \left( 1-x \right) ^{1-x}$ and $2\tau \cdot \left( 0.5-\tau \right) ^{1-2\tau }= (1-\tau )^{2(1-\tau )}$ respectively in [0, 0.5].³

Theorem 1

(Main result) If $\tau >0.5$, $\rho <0.5$ and $\tau +\rho \ne 1$, then with high probability the Schelling process $(n,w,\tau ,\rho )$ reaches complete segregation. The process is static (with high probability) if

$$ \begin{aligned}{}[\tau \le \lambda _0\, \& \,\rho \le \lambda _0] \quad \mathrm{or}\quad [\tau \le \kappa _0\, \& \,\rho <0.5]\quad \mathrm{or}\quad [\tau \le 0.5\, \& \,\rho \le 0.25] \end{aligned}$$

or, more generally, if $2\rho \cdot (1-2\kappa _0)+\tau +\kappa _0<1$.⁴

The values of $(\tau ,\rho )$ for which we show that the process is static, correspond to the triangular area of the first diagram (or, equivalently, the collapsed part of the surface of the third diagram) of Fig. 1. The case when $\rho \le 0.25$ presents a remarkable contrast as $\tau$ crosses the boundary of 0.5. In this case, when $\tau$ exceeds the threshold 0.5, the process changes from static to the other extreme of complete segregation.

Corollary 1

(Phase transition on 0.5) If $\rho \le 0.25$, then with high probability the process $(n, w, \tau , \rho )$

• converges to complete segregation if $\tau >0.5$;

• is static, if $\tau \le 0.5$.

Moreover with high probability it reaches its final state in time ${\mathbf{o}}\,\big ({n}\big )$, if $\tau \le 0.5$ and time $\varOmega (n)$, if $\tau > 0.5$.

Fig. 1

Threshold behaviour when $\tau ,\rho$ are in [0, 0.5]. The two-dimensional axes refer to $\tau$ and $\rho$. In the first figure, the process is static except for the $(\tau ,\rho )$ in the small area at the top right corner. The second figure is a plot of $\mathbb {P}_{\text {stab}}$ and $\mathbb {P}_{\text {unhap}}$ (for w = 100) as functions of $(\tau ,\rho )$. The third figure is a plot of $g(\tau ,\rho )$ for w = 100

Table 2 The main result

We display these results in Table 2. In Sects. 2–4 we present the argument that proves these results. This argument uses a number of smaller results which are stated without proof, and are the building blocks of the proof of Theorem 1. It is our intention that the reader gets a fairly good understanding of our analysis in this part of the paper, without the burden of having to verify some of the more technical parts of the proof. Sect. 5 contains the detailed proofs of all the facts that were used in Sects. 2–4, and completes the proofs of Theorem 1 and Corollary 1.

Table 3 Two cases for the process $(n, w, \tau , \rho )$ and the corresponding expectations of the number of initially happy nodes

Our proof of Theorem 1 is nonuniform, and the analysis is roughly divided in the two cases displayed in Table 3: balanced happiness (when $\tau +\rho >1$, $\tau >0.5$) and unbalanced happiness (when $\tau +\rho <1$, $\tau >0.5$). Here happiness refers to the numbers of initially happy nodes of the two types, and determines the dynamics that drives the process to an equilibrium. Of the two cases, unbalanced happiness is the most challenging to deal with, and the dynamics is driven by a small number of unhappy $\alpha$-nodes against the large number of unhappy $\beta$-nodes, which in fact is preserved throughout a significant part of the process.

1.3 Schelling Models and Relation to Spin-1 Physical Models

The definition of the Schelling model in Sect. 1.1 is rather standard, close to the spacial proximity model from [28, 30] and identical to the model studied in [1, 7]. Most significantly, it is an unperturbed Schelling model, where agents cannot make moves that are detrimental to their welfare. We have already remarked in the introduction that various rigorously analysed perturbed versions of the model in the literature (such as [38]) actually force ‘regularity’ on the process, which makes it fit an already existing methodology (such as Markov chains with a unique stationary distribution, or with properties that guarantee stochastically stable states). Even if we commit to the absence of perturbations in the model, it is possible to add complications to the simple dynamics defined in Sect. 1.1. For example, the agents may take into account the distance they need to travel before they move, and such considerations separate models with ‘short-range’ interactions from models with ‘long-range’ interactions, such as the Schelling model. Although similar models but with ‘short-range’ interactions have been studied in the past, e.g. [17], rigorous results for the corresponding models with “long-range” interactions are currently under study.

Numerous authors, for example [14, 23, 25, 26, 34], have noted the close relationship between Schelling models and variants of the Ising Model, widely studied by statistical physicists to understand phase transitions. In this situation, perturbed or noisy versions of the model correspond to a temperature $T>0$, which can productively be analysed using the Boltzmann distribution. Typically the limit $T \rightarrow 0$ is then studied. Thus the current work can be viewed as a study of a family of 1-dimensional kinetic Ising models with range of interaction w, as non-equilibrium systems under rapid cooling, that is at $T=0$ (where radically different behaviour can be observed than in the limit $T \rightarrow 0$). In this situation, the Boltzmann distribution is no longer a viable tool, and the use of the threshold $\tau$ can be seen as a simple alternative in determining whether or not a spin will update if selected.

In the current work, the model evolves by swapping pairs of agents of opposite types, corresponding to “closed” spin-1 systems under Kawasaki dynamics in which magnetization is conserved (and which are used to model alloy systems), whereas versions such as [2] in which individual agents switch type correspond to “open” spin-1 systems under Glauber dynamics in which magnetization is not conserved. To make the connection explicit, (temporarily) write $S_i(t) = +1 (\text {respectively} -1)$ if site i is occupied by a node of type $\alpha$ (respectively $\beta$) at time t. Then the spin at site i is unhappy (and thus willing to swap) if and only if

$$\begin{aligned} \displaystyle \left| \sum _{j: |j - i| \le w} S_i S_j - (2 \tau - 1) (2w+1) \right| < 0. \end{aligned}$$

In our view, it is the simplicity of the original Schelling model, contrasted by the complexity of the analysis required to specify its behaviour, as demonstrated in [1, 7] and the present work, that make this topic fundamental and interesting. Under the above requirement for simplicity and proximity to the original model, there remain a number of ways that the model can be altered or generalised. For example, note that in the case that $\tau >0.5$ in the model of Sect. 1.1, two nodes may swap although the number of same-type nodes in their neighbourhoods remain the same after the swap. One may alternatively require that for such a swap, the corresponding numbers of same-type nodes in the neighbourhoods increase (note that such a modification would not make a difference if $\tau \le 0.5$). Our choice on this issue follows Brandt et al. in [7, §2]. One generalisation, considered in [2], is to allow different tolerance thresholds for the two types of individuals. Another generalization, already present in [30], is to introduce a number of vacancies, i.e. to allow the total number of individuals to be smaller than the number of sites.

We can also alter the dynamics. Instead of switching two chosen individuals at each stage, we could choose one individual and change his type. Such an action may be interpreted as the departure of the individual to some external location and the arrival of an individual of the opposite type at the site that has just become available. Models with this dynamics are often said to have switching agents (see [2], where such a model was analysed) as opposed to the swapping agents of the current model. Finally one can consider versions of this model in higher dimensions, where the most relevant recent works are [3, 22] and concern switching agents.

1.4 Objectives of the Analysis of the Unperturbed Model and Related Work

We use the notation of Sect. 1.1, so that the symbol n always means the population variable of the process, and w always is the parameter of the process which determines the length of the neighbourhood of nodes. Similarly, $\tau , \rho$ always refer to the parameters of the Schelling process.

In Sect. 2.2.3 we show that, with probability one, the process $(n, w, \tau , \rho )$ either reaches complete segregation or it reaches a dormant state. In the second case, we wish to determine the extent of segregation in the dormant state. In view of the large number of states that the process may have (most of them ‘random’) a question arrises as to how to classify or even talk precisely about different states that may be the outcome of the process. Brandt et al. noticed in [7] that, at least in the case $\tau =\rho =0.5$ that they considered, the extent of the segregation that occurs in the final state depends crucially on w. In fact, they showed that the dependence on w is at most ‘polynomial’. We may say that a state is regarded as polynomial segregation if, with high probability a randomly chosen node belongs to a contiguous block⁵ of size that is proportional to the value of a polynomial on w. A similar definition applies to exponential segregation. These two notions turn out to provide a very useful language for explaining the eventual outcome of the Schelling process. A full characterization (extending the work of Brandt, Immorlica, Kamath, and Kleinberg [7]) of the asymptotic behaviour of the process $(n,w, \tau , \rho )$ for $\rho =0.5$ and $\tau \in [0,1]$ was provided by the authors in [1] in terms of polynomial and exponential segregation, as well as static processes. Intuitively, a random state is non-segregated, while polynomial and exponential segregation correspond to highly non-random states.

Table 4 Segregation regions in the case $\rho =0.5$

Fig. 2

500K population with $w=3000, \rho =0.5$ and $\tau =0.485, 0.49, 0.495, 0.5$. All made about 130K swaps

The characterization from [1] is summarized in Table 4. It is rather striking that when intolerance is increased from, say, 0.4–0.5 the segregation is decreased. This phenomenon is akin to the many paradoxes that stem from the missing link between local motives of agents and global behaviour of a system (e.g. see Schelling’s classic monograph [31], and in particular Chapter 4 which relates to his segregation models). Even more strikingly, the authors showed in [1] that the paradox occurs for all $\tau \in (\kappa _0, 0.5)$, i.e. as $\tau$ approaches 0.5 the segregation (in the final state) decreases.

This paradoxical phenomenon is also clear in many simulations of the model. Figure 2 shows typical runs of the processes $(5\times 10^5, 3\times 10^3, \tau , 0.5)$ for $\tau \in \{0.485, 0.49,0.495, 0.5\}$. The final state is depicted in the circle, where the nodes of one type are black and the nodes of the other type are grey. We use the space between the centre of the ring and the ring in order to record the actual process, as it evolves in time. In particular, if a grey node switches its place with a black node, we put a black node (the colour of the more recent node) between the location of the node and the centre of the ring, at a distance from the centre which is proportional to the stage where the swap occurred. Hence we may observe “cascades’ of swaps of nodes of the same type, which are less severe as $\tau$ approaches 0.5. Such cascades are crucial in the rigorous analysis of the model, both in [7] and in [1]. Figure 2 shows that as $\tau$ approaches 0.5, the segregation is decreased. This behaviour can be traced to the probability that a node is unhappy in the initial configuration, and in fact, the threshold constant $\kappa _0$ is derived by comparing related probabilities in [1].

In the case $\rho =0.5$ the two constants $\kappa _0$ and 0.5 mark phase transitions in the limit state of the process $(n, w, \tau , \rho )$, as $\tau$ takes values in [0, 1]. This brings us to another important objective of the analysis of the Schelling process, which is the discovery of phase transitions with respect to the parameters $\tau , \rho$. Incidentally, we note that the discovery of phase transitions has been one of the original motivations for the study of the one and two dimensional Ising model, when one varies the temperature (see the end of Sect. 1.3 for a brief discussion of the analogy between the Ising and the Schelling models). Finally we are also interested in the expected time that the process takes to converge.

1.5 Overview of Our Analysis

We use different methods for the cases $\tau \le 0.5$ (Sect.4) and $\tau >0.5$ (Sects. 2 and 3). If $\tau \le 0.5$, in order to derive conditions under which the process is static, we analyse and compare the probabilities of initially unhappy nodes and stable intervals.⁶ If $\tau >0.5$ we consider the two cases $\tau +\rho <1$ (Sect. 3) and $\tau +\rho >1$ (Sect. 2) and argue (using distinct arguments) that in each of them complete segregation is the high probability outcome.

Fig. 3

The logic of the proof that if $\tau >0.5$, with high probability the process reaches complete segregation

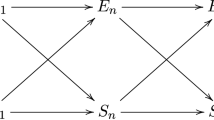
Case ${\varvec{\tau }}>\mathbf{{0.5}}$ This case is divided to the cases $\tau +\rho >1$ and $\tau +\rho <1$, and the structure of the analysis is depicted as a flowchart in Fig. 3 (along with the sections where the various implications are analysed), and in more detail in Fig. 4. First, we show that asymptotically (on w, n), from any state there is a series of transitions that leads to either a dormant state, or complete segregation. Hence, since there are only finitely many states, with probability one the process will reach either a dormant state or complete segregation. So in order to establish complete segregation as the eventual outcome, it suffices to show that the process maintains unhappy nodes of each colour during all stages.

Fig. 4

The logic of the proof that if $\tau >0.5$, with high probability the process reaches complete segregation. Here ‘$\beta$-block’ refers to the persistent $\beta$-block of Sect. 3.1

First, assume that $\tau +\rho >1$, a case which is dealt with in Sect. 2. In this case we can show in Sect. 2.2.3 that, assuming that the actual proportion of $\beta$-nodes is sufficiently close to $\rho$ (which is very likely according to the law of large numbers), every reachable state is not dormant. More precisely, we show that given such numbers of $\alpha$ and $\beta$-nodes, every permutation of them on the ring corresponds to a state which has both unhappy $\alpha$ and unhappy $\beta$-nodes. Since the numbers of nodes of each type do not change during each transition, this argument suffices for this case. States with the property that no series of transitions from them leads to dormant states are called safe. So, in the case $\tau +\rho >1$ we argue that (with high probability) the initial state is safe.

Second, we assume that $\tau +\rho <1$, which is a considerably harder case that we deal with in Sect. 3. Under this hypothesis, in the initial configuration we have ${\mathbf{o}}\,\big ({n}\big )$ many unhappy $\alpha$-nodes and $\varOmega (n)$ many unhappy $\beta$-nodes. As before, it suffices to show that (with high probability) the process never reaches a dormant state. It is not hard to see that (with high probability) the initial state is not dormant. However it is no longer clear if the initial state is safe. In Sect. 2 we show that given the expected numbers of nodes of the two types in the initial state (or numbers sufficiently close to their expectations) any permutation of the nodes on a ring corresponds to a state with at least one unhappy $\beta$-node. Hence, with high probability, the process will never run-out of unhappy $\beta$-nodes and we only need to argue about the preservation of unhappy $\alpha$-nodes. Already it should be clear that this is an asymmetric case where the $\alpha$-nodes (the majority) and the $\beta$-nodes (the minority) play different roles. When $\tau +\rho <1$ there are many permutations of the nodes (which correspond to states where all $\alpha$-nodes are happy, i.e. dormant states. So the argument that was used in the case $\tau +\rho >1$ is no longer relevant for arguing for the preservation of unhappy $\alpha$-nodes in the process. The argument we use instead (technically overviewed in Sect. 3.2 and executed in Sects. 3.3, 3.4) is based on the asymmetry between the number of unhappy $\beta$-nodes and the unhappy $\alpha$-nodes, which creates a dynamic that favours the preservation of unhappy $\alpha$-nodes. More precisely, it favours the preservation of $\beta$-blocks of length $>w$, which is a condition implying the existence of unhappy $\alpha$-nodes (indeed, the $\alpha$-nodes neighbouring a $\beta$-block of length at least w are unhappy). Hence if we show that the expected number of unhappy $\alpha$-nodes remains small during the stages of the process, then we can expect the existence of unhappy $\alpha$-nodes (and unhappy $\beta$-nodes) up to the point where the total number of unhappy nodes is small.

In addition we show that if the total number of unhappy nodes in a state is sufficiently small, then this state is safe, i.e. there is no series of transitions from it to a dormant state. The argument is concluded in Sect. 3.5 by showing that it is very likely that by stage n the process will arrive at a state with appropriately low number of unhappy nodes, before it reaches a dormant stage. Figure 5 is a plot of the numbers of unhappy $\alpha$-nodes and the unhappy $\beta$-node during the stages, taken from two typical simulations (one with large and one with small population), when $\tau +\rho <1$.⁷ The process we described is clearly visible: the number of unhappy $\alpha$-nodes remains small, until the number of unhappy $\beta$-nodes becomes small. Up to the later point, as we explained, the dynamics favours the preservation of unhappy $\alpha$-nodes.

Fig. 5

The first plot is from the process (200, 000, 50, 0.6, 0.3) and the second one from the process (1000, 20, 0.6, 0.3). These simulations illustrate that the number $\alpha$-nodes in the infected area remains bounded, until the number of $\beta$-nodes outside the infected area becomes small. The second figure also illustrates the fact that the number of unhappy nodes fluctuates locally

Case ${\varvec{\tau }}\le \mathbf{{0.5}}$ In this case, dealt with in Sect. 4, we have $\tau +\rho <1$, and this means that in the initial configuration the $\alpha$-population is happy with a few exceptions, while the $\beta$-population is unhappy, with a few exceptions. Recall that in this case we wish to show that the process is static. By the definition of the dynamics of the model $\alpha$-to-$\beta$ swaps can only occur in areas where there are unhappy $\alpha$-nodes. Hence in this case the $\alpha$-to-$\beta$ swaps will be concentrated in a very few selected areas in the ring, at least in the first stages of the process. This concentration of $\alpha$-to-$\beta$ swaps creates cascades of $\alpha$-node evictions which can be clearly seen in simulations such as the one displayed in Fig. 6.⁸ If we could argue that such cascades are restricted to small areas around the initially unhappy $\alpha$-nodes, then it is not hard to argue that the process reaches a dormant state rather quickly, having affected only a very small number of nodes. The way we do this is through stable intervals, a device that was also used in [1]. Roughly speaking, these are intervals that do not allow the spread of unhappy $\alpha$-nodes through them.

Fig. 6

The evolution of the infected area when $\tau +\rho <1$. The current state in the outer circle, the initial state is in the inner circle, and each move of an $\alpha$-node is represented by a dot at the coordinates of the new position, but at a distance from the center which is proportional to the stage where the swap occurred. This representation of the process in time illustrates the cascades of swaps that occur and start from the initial unhappy $\alpha$-nodes

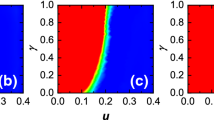
If $\rho$ is very small, or if $\tau$ is very small, then stable intervals occur with high probability. On the other hand, if $\rho ,\tau$ get sufficiently large, the probability of a stable interval tends to 0 as $w\rightarrow \infty$. This contrasts with prevalence of unhappy $\alpha$-nodes. When $\tau , \rho$ are small, the probability of (the occurrence of) an unhappy $\alpha$-node is small, while it gets large when $\tau , \rho$ increase. Figure 7 shows the actual probabilities (as calculated in Sect. 4) as functions of $\tau ,\rho$ for the specific value of $w=100$ (the shape of the plots does not change significantly for different values of w). The interesting case is the range for $\tau ,\rho$ where both probabilities tend to 0 as $w\rightarrow \infty$, i.e. both events become rare. Somewhere on the horizontal $\tau$-$\rho$ plane there is a line marking the intersection of the two surfaces. This is where the probability of a stable interval becomes less than the probability of an unhappy $\alpha$-node. Moreover, as $w\rightarrow \infty$ the ratio of the two probabilities tends to infinity or zero, depending whether $\tau ,\rho$ sit on one side of the plain (with respect to the intersection line) or the other. The crux of the argument in Sect. 4 is that for many values of $\tau ,\rho$ stable intervals are much more common than unhappy $\alpha$-nodes in the initial configuration. This allows us to argue that, in this case, the process has to reach a dormant state after ${\mathbf{o}}\,\big ({n}\big )$ many swaps, which implies that the process is static.

Fig. 7

The probabilities of a stable interval and an unhappy $\alpha$-node, as functions of $\tau ,\rho \le 0.5$ when $w=100$

1.6 Probability Terminology and Asymptotic Notation

In Sect. 5.1 we summarize some facts from probability theory that are used in our analysis. In Sect. 5.2 we state and prove some basic probabilistic facts about the Schelling model, which are also needed in our analysis. Asymptotic notation will be useful in expressing various statements in our analysis. We already defined the notation $0\ll w\ll n$ in Sect. 1.2. Given two functions f, g on the positive integers, (as is standard) we say that f is ${\mathbf{O}}\,\big ({g}\big )$ if there exists a positive constant c such that $f(t)\le c\cdot g(t)$ for all t. We say that g is $\varOmega (f)$ if f is ${\mathbf{O}}\,\big ({g}\big )$, and that g is $\varTheta (f)$ if both f is ${\mathbf{O}}\,\big ({g}\big )$ and f is $\varOmega (g)$. We also use this notation, however, in a more general sense: we say that f is $g({\mathbf{O}}\,\big ({t}\big ))$ if there exists some $c>0$ such that $f\le g(ct)$ for all t. For example, when we say that a function f is $ne^{-{\mathbf{O}}\,\big ({t}\big )}$, this means that there is $c>0$ such that $f(t)\le ne^{-ct}$ for all t. Or, if we say that f is $n(1-e^{-{\mathbf{O}}\,\big ({t}\big )})$, this means that there is $c>0$ such that $f(t)\le n(1-e^{-ct})$ for all t. Similarly, we use $\varTheta$ in a more general sense. We say that f is $g(\varTheta (t))$ to mean that there exist constants $c_0$ and $c_1$ such that $g(c_0\cdot t) \le f(t) \le g(c_1 \cdot t)$ for all t. We say that $f={\mathbf{o}}\,\big ({g}\big )$ if $\lim _t f(t)/g(t)=0$. The (often hidden) variable underlying the asymptotic notation in the various expressions will be w. In other words, for fixed values of $\rho$ and $\tau$, the choice of constants required in the asymptotic notation, will always depend only on w. We also combine the ‘high probability’ terminology with the asymptotic notation in a manner which is worth clarifying. When we say, for example, that ‘with high probability the number of initially unhappy $\alpha$-nodes in the process $(n,w,\tau ,\rho )$ is $n\cdot (1-\rho )\cdot e^{-\varTheta (w)}$’, this means that there exist constants $c_0$ and $c_1$ such that, with high probability, the number of initially unhappy $\alpha$-nodes in the process $(n,w,\tau ,\rho )$ lies between $n\cdot (1-\rho )\cdot e^{-c_0 \cdot w}$ and $n\cdot (1-\rho )\cdot e^{-c_1 \cdot w}$.

2 Metrics and Reaching Complete Segregation ($\tau>0.5, \tau +\rho >1$)

One of the most challenging problems in the analysis of the segregation process is the large number of absorbing states. In order to understand which transitions are possible, we use certain metrics that describe the current state.

2.1 Welfare, Mixing, and Expectations

We define global metrics that reflect the welfare of the entire population.⁹ These metrics and their properties are essential in all of the proofs that will follow. An obvious choice is the number of happy nodes at a given state. It is not hard to devise transitions of the process which reduce the total number of happy nodes (see the second plot of Fig. 5). However it is possible to show that if $\tau >0.5$ the total number of happy nodes is approximately non-decreasing (in the sense that it is $\varTheta (g)$ for some nondecreasing function g on the stages, where the underlying constant depends only on w).¹⁰ Let the utility of a node (at a certain state) be the number of nodes of the same type in its neighborhood. A better behaved global metric of welfare of a state (compared to the number of happy nodes) is the sum of the utilities of the nodes in the state. We call this parameter the social welfare of the state and denote it by $\mathtt {V}$. A consequence of the transition rule and the definition of utility is that the social welfare does not decrease along the stages of the process. Furthermore, if $\tau \le 0.5$, every transition of the process strictly increases the social welfare. Let the mixing index of a node be the number of nodes in its neighbourhood that are of different type. The mixing index $\textsc {mix}$ of a state is the sum of the mixing indices of the $\alpha$-nodes in that state. The mixing index of a state is also equal to the sum of the mixing indices of the $\beta$-nodes in that state. The relationship between the two metrics is

$$\begin{aligned} \mathtt {V}= (2w+1)\cdot n - 2\cdot \textsc {mix}. \end{aligned}$$

Hence the mixing index is non-increasing along the transitions. Note that a single swap cannot decrease the mixing index by more than 4w. On the other hand, by linearity of expectation we can calculate that

$$\begin{aligned} \text {the expectation of the mixing index in the initial state of } (n,w,\tau ,\rho )\text { is } 2nw\rho (1-\rho ). \end{aligned}$$

The mixing index of complete segregation (in nontrivial cases) is $w(w+1)$. Since $\rho \le 1/2$, this means that (with high probability) the process can reach complete segregation only after $(n\rho -(w+1))/4 >n\rho /5$ stages, i.e. $\varOmega (n)$ stages. On the other hand, a case analysis shows that if $\tau \le 0.5$, each step in the process decreases the mixing index by at least 4. This happens because each time a swap occurs, the mixing index decreases by at least 4 (so its not possible that a constant number of nodes swap more than ${\mathbf{o}}\,\big ({n}\big )$ times). We have shown that the second clause of Corollary 1 (concerning the time to the final state) follows from the first clause.

As another measure of mixing, we may consider the number $\mathtt {k}_{\beta }$ of maximal $\beta$-blocks in the state. These are the contiguous $\beta$-blocks that are maximal, in the sense that they cannot be extended to a larger contiguous $\beta$-block. Let $\mathtt {U}$ be the number of unhappy nodes in a state. It is not hard to show that if $\tau >0.5$ then $\textsc {mix}=\varTheta (\mathtt {U})=\varTheta (\mathtt {k}_{\beta })$ and in particular

$$\begin{aligned} \textsc {mix}\le w\cdot (w+1) \cdot \mathtt {k}_{\beta } \le w\cdot (w+1) \cdot \mathtt {U}< \textsc {mix}\cdot 2w/(1-\tau ). \end{aligned}$$

(1)

This means that the number of unhappy nodes at a certain state reflects the progress of the process towards segregation. More precisely, the metrics $\textsc {mix}$, $\mathtt {k}_{\beta }$, $\mathtt {U}$ are mutually proportional when $\tau >0.5$, where the analogy coefficient depends on w (see Fig. 5). In Table 5 we display these global metrics of welfare, along with their dynamics. A function (on the stages of the process) has positive dynamics if it is non-decreasing and approximately positive dynamics if it is $\varTheta (g)$ for some nondecreasing function g, where the multiplicative constant does not depend on n. Similar definitions apply for ‘negative’. The first clause of Theorem 1 (the case when $\tau >0.5$) is the hardest to prove. It turns out that in this case we can deduce a non-trivial lower bound on the mixing index of dormant states.

Lemma 1

(Mixing in dormant states) Consider the process $(n, w, \tau , \rho )$ with $\tau >0.5$. The mixing index in a dormant state is more than $n(w+1)\tau \rho _{*}$, as long as $w>1/(2\tau -1)$.

Table 5 Metrics of welfare

The case $\tau >0.5$ is further divided in two cases, which reflect the proportions of happy nodes in the initial state. We display these in Table 3, along with the corresponding expectations for the numbers of happy nodes of each type. Lemma 1 is crucial for the proof of the first clause of Theorem 1 (in particular the case $\tau +\rho <1$).

2.2 Accessibility of Dormant States and Complete Segregation

Here we prove Theorem 1 for the case $\tau >0.5$ and $\tau +\rho >1$. However Lemma 3 is more general and will also be used in Sect. 3 which deals with the harder part of the proof of Theorem 1.

2.2.1 Overview of the Proof of Theorem 1 for $\tau >0.5$ and $\tau +\rho >1$

This argument consists of two parts. First, we show that in this case with high probability the initial state is such that every state with the same number of $\alpha$-nodes has unhappy nodes of both types (i.e. it is not dormant). Hence under these conditions, no accessible state is dormant. The second part consists of showing that from every state there is a sequence of transitions to either a dormant state or complete segregation. Moreover the latter fact holds in general, for any values of $\tau ,\rho$, so it can be reused for the case when $\tau +\rho <1$, in Sect. 3. This latter case is more challenging, as it can be seen that there are permutations of the initial state which are dormant.

Lemma 2

(Existence of unhappy nodes) Suppose that $\tau >0.5$ and $\rho _{*}<\tau$ Then for $0\ll w\ll n$, every state of the process $(n, w, \tau , \rho )$ has unhappy $\beta$-nodes. If in addition $\tau +\rho _{*}>1$, every state also has unhappy $\alpha$-nodes.

Given $\rho$, by the law of large numbers with high probability (tending to 1, as n tends to infinity) $\rho _{*}$ will be arbitrarily close to $\rho$. Hence we may deduce the absence of dormant states (with high probability) in the case that $\tau +\rho >1$.

Corollary 2

(Absence of dormant states when $\tau >0.5$ and $\tau +\rho >1$) If $\rho \le 0.5<\tau$ and $\tau +\rho >1$ then with high probability none of the accessible states of the process $(n, w, \tau , \rho )$ is dormant.

It remains to show the accessibility of either a dormant state or complete segregation, from any state of the process. An inductive argument can be used in order to prove this fact, which along with Corollary 2 shows Theorem 1 for $\tau >0.5$ and $\tau +\rho >1$.

Lemma 3

(Complete segregation or dormant state) Given $0\ll w\ll n$, from any state of the process $(n, w, \tau , \rho )$ there exists a series of transitions to complete segregation or to a dormant state.

Here is a sketch of the proof. If $\tau \le 0.5$ the mixing index is strictly decreasing through the transitions, so it is immediate that the process will reach a dormant state (indeed, 0 is a lower bound for the mixing index). For the case where $\tau >0.5$ (which we assume for the duration of this discussion) we can argue inductively, in four steps. First we show that from a stage with few unhappy nodes of one type (here $5w^4$ is a convenient upper bound of what we mean by ‘few’, which is by no means optimal) there is a series of transitions which lead to either a state with a contiguous block of length 2w or a dormant state. Second, from a state with a contiguous block of length $\ge 2w$ there is a series of transitions to complete segregation or to a dormant state. Third, from any state which has at least $w^4$ unhappy nodes of each type, there is a series of transitions to a state with a contiguous block of length at least w. Finally from a state that has a contiguous block of length $\ge w$ and at least 4w unhappy nodes of opposite type from the block, there is a series of transitions to a state with a contiguous block of length $\ge 2w$. The combination of these four statements constitutes a strategy for arriving to a dormant state or a state of complete segregation, from any given state. We illustrate this strategy in Fig. 8, where two arrows leaving a node indicate that at least one of these routes are possible.

Fig. 8

The path to a dormant state or complete segregation when $\tau >0.5$, proved in Sect. 2.2.3

2.2.2 Proof of Lemma 2 and Corollary 2

It is crucial to understand the dormant states and assess their accessibility from an initial state. We demonstrate that this issue ultimately depends on the given parameters $\tau , \rho$. We show that if $\tau +\rho >1$ then with high probability we may assert that no dormant state is accessible from the initial state.¹¹ The following lemma implies Lemma 2.

Lemma 4

(Existence of unhappy nodes) Suppose $\gamma \in \{\alpha , \beta \}$ and let $\theta _{*}$ be the proportion of $\gamma$-nodes in a state of the process $(n, w, \tau , \rho )$. If $\tau >0.5$ and $\theta _{*}<\tau$, then for $0\ll w \ll n$ there exist unhappy $\gamma$-nodes in the state.

Proof

Given the parameters $\theta _{*}, \tau$, w which is large, and any state of the process $(n, w, \tau , \rho )$ with no unhappy $\gamma$-nodes, it suffices to produce an upper bound on n (which does not depend on the particular state but only on $\theta _{*},\tau , w$ and the fact that no $\gamma$-nodes are unhappy). Let $\delta \in \{\alpha , \beta \} -\{\gamma \}$. Since $\tau >0.5$ and all $\gamma$-nodes are happy, there are no $\delta$-blocks of length $\ge w$. We may assume that $n> 3w+1$. Define the bias $\mathtt {B}(I)$ of an interval I of nodes to be the difference between the number of $\gamma$-nodes in the interval and the number of $\delta$-nodes in the interval. Without loss of generality suppose that the node occupying site w is a $\gamma$-node (otherwise consider a rotation). We define a sequence $(u_i)$ of $\gamma$-nodes in the state, starting with $u_0=w$. Let $N_i$ denote the neighbourhood of $u_i$. Given $u_i$, define $u_{i+1}$ to be the rightmost $\gamma$-node in $N_i$. Since there are no $\delta$-blocks of length $\ge w$, the sequence $(u_i)$ is well defined and it never happens that $u_i=u_{i+1}$. Let m be the largest number such that none of the neighbourhoods $N_i$ for $0<i\le m$ contain the node at site 0. Since $n> 3w+1$ we have $m>0$. Let $I_m= \cup _{i=0}^m N_i$ and $V_m=\sum _{i=0}^m \mathtt {B}(N_i)$. Note that $I_m$ contains all of the nodes except at most w. Moreover since $u_{i+1}-u_i\le w$ we have

$$\begin{aligned} |I_m|\le 2w+1+mw. \end{aligned}$$

(2)

Let $L_i$, and $R_i$ be the leftmost and rightmost w-many nodes in $N_i$ respectively. Since $N_i$ contains at least $\tau (2w+1)$ nodes of type $\gamma$:

$$\begin{aligned} \mathtt {B}(N_i)\ge (2w+1) (2\tau -1)\quad \text {and} \quad V_m\ge (m+1)(2w+1) (2\tau -1). \end{aligned}$$

(3)

Note, however, that some nodes have been counted multiple times in the sum that defines $V_m$, since the intervals $N_i$ are not disjoint. For each $k\in \mathbb {N}$ let $J^m_k$ consist of the nodes in $I_m$ which belong to exactly k distinct intervals $N_i$.

By the definition of $(u_i)$, the node $u_{i+2}$ is always outside $N_i$ (since it is a $\gamma$-node, and if it was in $N_i$ then $u_{i+1}$ would not be the rightmost $\gamma$-node in $N_i$). Similarly, $u_{i+4}$ is always outside $N_{i+2}$. This means that it is not possible for the neighbourhoods of 5 consecutive terms of $(u_i)$ to have a nonempty intersection.¹² This, in turn, implies that $J^m_k=\emptyset$ for each $k>4$. A similar consideration shows that $J^m_4$ consists entirely of $\delta$-nodes (hence $\mathtt {B}(J^m_4)\le 0$). Next, note that $J_1^m\subseteq L_0\cup R_m$, so $|J_1^m|\le 2w$. Hence by counting the multiplicities of the nodes in the sum which defines $V_m$, we have

$$\begin{aligned} V_m = 2\mathtt {B}(I_m)-\mathtt {B}(J^m_1)+\mathtt {B}(J^m_3) +2\mathtt {B}(J^m_4)\quad \text {and}\quad V_m \le 2\mathtt {B}(I_m)+2w+\mathtt {B}(J^m_3). \end{aligned}$$

(4)

Let $N_i'=N_{i-1}\cap N_{i+1}$ and note that $N_i'=R_{i-1}\cap L_{i+1}$. Moreover let $L_i'=N_i'\cap L_i$ and $R_i'=N_i'\cap R_i$. By the definition of $(u_i)$ it follows that if $R_i'$ is nonempty, then it consists entirely of $\delta$-nodes. Since $u_i\in J^m_3$ for each $i\in [1, m-1]$, $N_i'=L_{i}'\cup R_i'\cup \{u_i\}$ and $J^m_3\subseteq \bigcup _{i\in [1, m-1]} N_i'$, we have:

$$\begin{aligned} \mathtt {B}(J^m_3)< m + \sum _{i=1}^{m-1} (|L_i'|-|R_i'|). \end{aligned}$$

(5)

Let $d_i=u_i-u_{i-1}$. Then $|R_i'|=w-d_i$ and $|L_k'|=w-d_{i+1}$. Hence $|L_i'|=|R_{i+1}'|$ and

$$\begin{aligned} \sum _{i=1}^{m-1} (|L_i'|-|R_i'|)\le |L_{m-1}'|-|R_{1}'|\le w. \end{aligned}$$

Then from (5) we get $\mathtt {B}(J_3^m)< m+w$. From the second clause of (3) and (4) we have

$$\begin{aligned} 2\mathtt {B}(I_m) > (m+1)(2w+1)(2\tau -1)-3w-m. \end{aligned}$$

(6)

If $x_m,y_m$ are the numbers of $\gamma$ and $\delta$ nodes in $I_m$ respectively, then $x_m+y_m=|I_m|$ and $x_m-y_m=\mathtt {B}(I_m)$. Hence $2x_m=|I_m|+\mathtt {B}(I_m)$. By hypothesis we have $x_m\le n\theta _{*}$. Moreover, since $n\le |I_m| +w$ we have $x_m\le (|I_m| +w)\theta _{*}$. Hence $\mathtt {B}(I_m)\le (2\theta _{*}-1)|I_m| + 2w\theta _{*}$, so by (2),

$$\begin{aligned} \mathtt {B}(I_m)\le mw(2\theta _{*}-1) + 2w(3\theta _{*}-1) +2\theta _{*}-1. \end{aligned}$$

By (6) we may deduce that

$$\begin{aligned} 2m\cdot [2w(\tau -\theta _{*})-(1-\tau )]< w(12\theta _{*}-4\tau +1) +4\theta _{*}-2\tau -1. \end{aligned}$$

(7)

We may assume that w is larger than $(1-\tau )/[2(\tau -\theta _{*})]$. By this condition and the fact that $\tau -\theta _{*}> 0$, the left side of (7) is positive. Also, $n\le |I_m|+w$, so by (2) we have $n\le 3w+1+mw$. If we combine the latter inequality with (7) we get

$$\begin{aligned} n< 3w+1 + w\cdot \frac{w(12\theta _{*}-4\tau +1) +4\theta _{*}-2\tau -1}{4w(\tau -\theta _{*})-2(1-\tau )} \end{aligned}$$

which is the required bound on n. $\square$

Note that in the above result, the lower bound that is required on w depends only on $\tau , \rho _{*}$, while the lower bound that is required on n depends on $\tau , \rho _{*}$ and w. We may now apply Lemma  4 in order to establish the conditional existence of unhappy nodes of both types.

Corollary 3

(Existence of unhappy nodes) Suppose that $\tau >0.5$ and $\rho _{*}<\tau$. Then if $0\ll w\ll n$, every state of the process $(n, w, \tau , \rho )$ has unhappy $\beta$-nodes, and if $\tau +\rho _{*}>1$ then every state also has unhappy $\alpha$-nodes.

Given $\rho$, by the law of large numbers with high probability (tending to 1, as n tends to infinity) $\rho _{*}$ will be arbitrarily close to $\rho$. Hence we may deduce the absence of dormant states (with high probability) in the case that $\tau +\rho >1$.

Corollary 4

(Absence of dormant states) If $\rho \le 0.5<\tau$ and $\tau +\rho >1$ then with high probability none of the accessible states of the process $(n, w, \tau , \rho )$ is dormant.

This corollary along with the remark made in Footnote 11 establishes the main dichotomy in the analysis of the process.

2.2.3 Proof of Lemma 3 (Accessibility of Complete Segregation or Dormant State)

A central part of our analysis is the fact that from any state there is a transition to either a dormant state or complete segregation. This is what we prove in this section. This also means that the only absorbing states of the process are the dormant states.

If $\tau \le 0.5$ then it is clear that the only absorbing states of the process are the dormant states, since unhappy pairs of nodes of different type can always swap. Consider the mixing index which is non-negative and strictly decreasing in stages for $\tau \le 0.5$. This means that there can only be finitely many swaps in the process, and so a dormant state must eventually be reached.

For the case where $\tau >0.5$ more effort is required. We argue in four steps. The numbers in what follows are fairly arbitrary. First we show that from a state with at most a small number of unhappy nodes of one type (here $5w^4$ is a convenient upper bound of what we mean by ‘small’, which is by no means optimal) there is a series of transitions which lead to either a state with a contiguous block of length 2w or a dormant state. Second, from a state with a contiguous block of length $\ge 2w$ there is a series of transitions to complete segregation or to a dormant state. Third, any state which has at least $2w^4$ unhappy nodes of each type, there is a series of transitions to a state with a contiguous block of length at least w, and at least $w^4$ unhappy nodes of each type. Finally from a state that has a contiguous block of length $\ge w$ and at least 4w unhappy nodes of opposite type from the block, there is a series of transitions to a state with a contiguous block of length $\ge 2w$. The combination of these four statements constitutes a strategy for arriving at a dormant state or a state of complete segregation, from any given state.

In the following arguments we will often make use of the following two rather simple facts that hold when $\tau >0.5$. One is that (if $w>(1-\tau )/(2\tau -1)$), any $\beta$-node that is adjacent to a happy $\alpha$-node is unhappy. The second concerns the situation where next to a happy $\alpha$-node there is a $\beta$-node, and we swap the $\beta$-node for another $\alpha$-node. Then, provided that before the swap the the second $\alpha$ node is outside the neighbourhood of the $\beta$-node, both $\alpha$-nodes will be happy after the swap.

Lemma 5

(Shortage of unhappy nodes) Suppose that $\tau >0.5$ and $0\ll w \ll n$. From a state with less than $5w^4$ unhappy nodes of one of the types, there is a series of transitions to either a dormant state or to a state containing a contiguous block of length at least 2w.

Proof

Without loss of generality suppose that the state has less than $5w^4$ unhappy $\alpha$-nodes. Since $\rho _{*}\in (0,1)$, and $0\ll w \ll n$, if there does not already exist a contiguous block of length 2w then there exists an interval [u, v] of 2w nodes which contains at least one $\alpha$-node and such that any unhappy $\alpha$-node is at distance at least $2w^2$ from any node in [u, v].¹³ Any unhappy $\alpha$ node which cannot see any node in [u, v] can move to any position in [u, v] that is adjacent to an $\alpha$-node (because by doing so, it becomes happy and because if a swap is legal for one member of a potential swapping pair then it is legal for both). Hence we can start successively replacing the $\beta$-nodes in [u, v] which are adjacent to $\alpha$-nodes, with unhappy $\alpha$-nodes, each time choosing unhappy $\alpha$-nodes that have maximal distance from u, v. Note that this recursive procedure is valid because all $\alpha$-nodes in [u, v] are happy after each swap. Ultimately we either run out of unhappy $\alpha$-nodes, or else [u, v] becomes an $\alpha$-block. $\square$

Lemma 6

(Toward a block of length w) Suppose $\tau >0.5$. If $0\ll w \ll n$ then from any state which has at least $2w^4$ unhappy nodes of each type, there is a series of transitions to a state with an $\alpha$-block or $\beta$-block of length at least w, and at least $w^4$ many unhappy nodes of each type.

Proof

Suppose that we are given a certain state of the process. Define a sequence $u_i,$ $i\le w^2$ of $\alpha$-nodes with neighbourhoods $N_{u_i}$ respectively, by induction as follows. Let $u_0$ be the least $\alpha$-node whose neighbourhood contains the minimum number of $\alpha$-nodes amongst all neighbourhoods of $\alpha$-nodes. If $u_i$ is defined and $i<w^2$, define $u_{i+1}$ to be the least $\alpha$-node whose neighbourhood is disjoint from $\cup _{j\le i} N_{u_i}$ and whose neighbourhood contains the minimum number of $\alpha$-nodes amongst all $\alpha$-nodes with the same property (i.e. with neighbourhoods that are disjoint from $\cup _{j\le i} N_{u_i}$). This completes the definition of $(u_i)$, which is sound provided that n is sufficiently large. We define a sequence $v_i,$ $i\le w^2$ of $\beta$-nodes with neighbourhoods $N_{v_i}$ respectively, in a way entirely analogous to the above definition, ensuring also that all neighbourhoods $N_{u_i}$ and $N_{v_j}$ are disjoint.

The sequences $(u_i)$ and $(v_i)$ provide a pool of nodes which will be used for legitimate swaps in a series of transitions which will lead to the desired state of the process. We start by considering an interval J of nodes of length 3w which is disjoint from $\cup _{j\le w^2} N_{u_i}$ and disjoint from $\cup _{j\le w^2} N_{v_i}$. Such an interval exists, provided that n is sufficiently large. Let I consist of the w-many nodes in J that are at distance at least $w+1$ from any node outside the interval. Clearly any swap that occurs between a node in I and one of the nodes $u_i$, does not affect the composition of the neighbourhoods $N_{u_j}$ for $j\ne i$, or $N_{v_j}$ for $j\le w^2$ (and similarly for a swap between a node in I and one of the $v_i$).

Let $t_i,$ $i<w$ be the nodes of I enumerated from left to right. We shall describe a swapping process, involving less than $w^2$ swaps. At the end of this process of legal swaps, all nodes in I will be of the same type, (but which type that is will not be determined until the end of the process). This process has w-many steps, with each step s involving up to s swaps. Let $\gamma _s$ be the type of $t_s$ at the end of stage s. Also, let $V_{s}$ contain the nodes $u_i, v_i, i\le w^2$ which are of type $\gamma _{s}$ and have not been involved in a swap by the end of stage s. The construction is designed so that $\gamma _s$ is the type of all $t_i, i\le s$ st the end of stage s. This feature guarantees that at the end of the process, all nodes in I have the same type. Stage 0 is null (i.e. we carry out no instructions at stage 0).

At stage $s+1$ we check if $t_{s+1}$ has type $\gamma _s$. If so, then we go to the next stage. If not, then suppose first that $t_{s+1}$ is unhappy. In the case that $t_s$ is happy, any unhappy $\gamma _s$-node outside J can swap with $t_{s+1}$ (because an unhappy $\gamma _s$-node moving next to a happy $\gamma _s$-node cannot decrease its utility). In the case that $t_s$ is unhappy, we claim that any node x from $V_s$ can legitimately swap with $t_{s+1}$. In order to see this, note that the number of $\gamma _s$-nodes in the neighbourhood of $t_s$ is at least as large as this number at the beginning of the process. By the definition of $V_s$, this number is at least as large as the number of $\gamma _s$ nodes in the neighbourhood of x. This means that if x moves to the place that $t_{s+1}$ occupies, its utility will not decrease.

The last case in the procedure is if $t_{s+1}$ is happy and of type different than $\gamma _s$. In this case we define $\gamma _{s+1}\in \{\alpha ,\beta \}-\{\gamma _s\}$ and swap all $t_i, i\le s$ with distinct nodes in $V_{s+1}$, starting with $t_s$ and moving to the left. These are legitimate swaps, as nodes of type $\gamma _{s+1}$ move next to happy nodes of the same type (so their utility is not decreased after the swap). This concludes the description of the process.

By the end of stage $w-1$, all nodes in I are of the same type. Since we perform less than $w^2$ many swaps, there are less than $2(2w+1)w^2$ many nodes whose neighbourhoods are affected by these swaps. Since w is large, there are therefore at least $w^4$ many unhappy nodes remaining of each type remaining. $\square$

Lemma 7

(Toward a contiguous block of length 2w) Suppose that $\tau > 0.5$ and $0 \ll w \ll n$. From a state that has an $\alpha$-block of length $\ge w$ and at least $w^4$ unhappy nodes of each type, there is a series of transitions to a state with an $\alpha$-block of length $\ge 2w$. The same holds for $\beta$-blocks.

Proof

Consider the given state and assume that there is no $\alpha$-block of length $\ge 2w$ (otherwise 0 transitions suffice). Let [x, y] be the longest $\alpha$-block in the given state, and let J consist of all the nodes that are at distance at least w from the interval $[y-2w,y]$. Note that $x-1$ is a $\beta$-node and since $\tau >0.5$ it is unhappy. Let z be the rightmost $\alpha$-node to the left of x. If z is unhappy, then we may swap it with $x-1$ since its utility will not decrease. Otherwise, if z is happy, then it is at a distance at most w from x and we may successively swap the $\beta$-nodes in (z, x), starting from $z+1$ and moving to the right, for an equal number of unhappy $\alpha$-nodes in J. This is possible because each time that we move an $\alpha$ node next to a happy $\alpha$-node, the new $\alpha$ node becomes happy. We repeat this process until an $\alpha$-block of length 2w has been formed. Each step of the process increases the length of the $\alpha$-block that is adjacent and to the left of y the process will terminate. We also perform at most w many swaps, meaning that we shall not run out of unhappy nodes to perform the swaps with. $\square$

Lemma 8

(Complete segregation or dormant state from long block) Suppose $\tau >0.5$ and that $0\ll w \ll n$. From a state with a contiguous block of length $\ge 2w$ there is a series of transitions to complete segregation or to a dormant state.

Proof

Consider any state which is not completely segregated, but which has a contiguous block of length at least 2w. Without loss of generality, suppose that this is a block of $\alpha$ nodes occupying the interval [u, v], where this interval is chosen to be of maximum possible length. Our aim is to show that from this state, one may legally reach another with a contiguous block of greater length (or else a dormant state). Now if the nodes u and v are both happy then the length of the interval ensures that all nodes in the block are happy.¹⁴ In this case, if there exists an unhappy $\alpha$ node $u'$, then let $t\in \{ u,v \}$ be distance at least $w+1$ from $u'$. Then $u'$ and the $\beta$ neighbour of t may legally be swapped, increasing the length of the run by at least 1.

So suppose instead that at least one of the nodes u and v is not happy, and without loss of generality suppose that u has bias less than or equal to v, where the bias of a node is the number of $\alpha$-nodes minus the number of $\beta$-nodes in its neighbourhood. Then u and $v+1$ may legally be swapped. Performing this swap causes position $v+1$ to have at least the same bias as v did before the swap, and causes $u+1$ to have at most the same bias as u did before the swap. Thus, the swap has the effect of shifting the run one position to the right and may be repeated until the length of the run is increased by at least 1, i.e. for successive $i\ge 0$ we can swap the nodes $u+i$ and $v+i+1$, so long as the latter is of type $\beta$. The first stage at which the latter is of type $\alpha$ the length of the contiguous block has been increased. Putting these observations together, we conclude that from any state which has a contiguous block of length at least 2w it is possible to reach full segregation. $\square$

Finally, we piece together the above processes in order to show the following comprehensive statement.

Corollary 5

(Complete segregation or dormant state) From any state of the process $(n, w, \tau , \rho )$ with $0\ll w\ll n$, there exists a series of transitions to complete segregation or to a dormant state.

Proof

The case $\tau \le 0.5$, we considered earlier. Suppose that $\tau >0.5$. We may assume that $\rho _{*}\in (0,1)$, because otherwise every state is a dormant state. If there exist at most $5w^4$ unhappy nodes of each type in the state, Lemma 5 shows how to reach a dormant state or a state with a contiguous block of length $\ge 2w$. In the latter case, Lemma 8 shows that there is a series of transitions to complete segregation or to a dormant state. So we may assume that the given state has more than $5w^4$ unhappy nodes of each type. Then Lemma 6 shows how to reach a state with a contiguous block of length $\ge w$ and at least $w^4$ many unhappy nodes of each type. Furthermore, from such a state Lemma 7 shows how to reach a dormant state or a state with a contiguous block of length $\ge 2w$. In the latter case, Lemma 8 shows that there is a series of transitions to complete segregation or to a dormant state. This is an exhaustive analysis that establishes a path to a dormant state or complete segregation, from every state. $\square$

This completes our proof of Theorem 1 for the case that $\tau +\rho >1$.

3 Reaching Complete Segregation when $\tau >0.5$, $\tau +\rho <1$

This case of Theorem 1 is challenging because we need to show that the process avoids accessible dormant states, until it reaches a safe state i.e. a state from which no dormant state is accessible. The reason for this avoidance is (in contrast with the case $\tau +\rho >1$ of Sect. 2.2) the dynamics of the process with the given parameters. The methodology we use is based on a martingale argument, which involves a great deal of the analytical tools (e.g. the metrics of social welfare) and their properties that were developed in the previous sections. Having shown that dormant states are avoided until the process reaches a safe state, Lemma 3 gives Theorem 1 (for the case where $\tau >0.5$ and $\tau +\rho <1$). An overview of this argument is given in Fig. 3.

3.1 The Persistence of Large Contiguous $\beta$-Blocks

According to our plan, we wish to establish the existence of unhappy nodes of both types until a safe state is reached.¹⁵ By Lemma 2, we do not have to worry about the existence of unhappy $\beta$-nodes. One device that guaranties the existence of unhappy $\alpha$-nodes is a contiguous block of $\beta$-nodes, of length at least w. Such a block exists in the initial random state (with high probability). One way to argue for its preservation in subsequent stages is to consider the ratio of the unhappy nodes of the two types. Even more relevant is the ratio between the number of unhappy $\alpha$-nodes, and the number of $\beta$-nodes which are not just unhappy, but actually sufficiently unhappy that they can swap with any unhappy $\alpha$-node.

Definition 2

(Very unhappy $\beta$-nodes) Given a stage of the process, a node of type $\beta$ is very unhappy if there are at least $(2w+1)\tau$ nodes of type $\alpha$ in its neighbourhood. The number of very unhappy $\beta$-nodes is denoted by $\mathtt {U}_{\beta }^{*}$.

In the case that we study ($\tau >0.5$ and $\tau +\rho <1$) initially, the number of very unhappy $\beta$-nodes is $\varOmega (n)$ while the number of unhappy $\alpha$-nodes is ${\mathbf{o}}\,\big ({n}\big )$. The following lemma says that as long as this imbalance (large number of very unhappy $\beta$-nodes versus small number of unhappy $\alpha$-nodes) is preserved, it is very likely that a sufficiently long contiguous block of $\beta$-nodes is preserved.

Lemma 9

(Persistent $\beta$-block) Consider the process $(n,w,\tau ,\rho )$ with $\tau >0.5$ and let $s_{*}$ be the least stage where the ratio between the very unhappy $\beta$-nodes and the unhappy $\alpha$-nodes becomes less than $4w^2$ (putting $s_{*}=\infty$ if no such stage exists). Then with high probability there is a $\beta$-block of length $\ge 2w$ at all stages $<s_{*}$ of the process.

Since a $\beta$-block of length at least w is a guarantee for unhappy $\alpha$-nodes, we get the following corollary.

Corollary 6

(Conditional existence of unhappy $\alpha$-nodes) Under the hypotheses of Lemma 9, with high probability there are unhappy $\alpha$-nodes at all stages $<s_{*}$ of the process.

It remains to construct an elaborate martingale argument in order to show that the imbalance between $\mathtt {U}_{\alpha }$ and $\mathtt {U}^{*}_{\beta }$ persists for a sufficiently long time (until the process reaches a safe state).

3.2 Overview of the Infected Area of the Schelling Process

In the case of unbalanced happiness (i.e. when $\tau >0.5$, $\tau +\rho <1$, see Table 3) the unhappy $\alpha$-nodes are initially very rare, so the interesting activity (namely $\alpha$-to-$\beta$ swaps) occurs in small intervals of the entire population (at least in the early stages). These intervals contain the unhappy $\alpha$-nodes, and gradually expand, while outside these intervals all $\beta$-nodes are very unhappy. Figure 9 shows the development of this process, where the height of the nodes (perpendicular lines) is proportional to the number of $\alpha$-nodes in their neighborhood and the horizontal black line denotes the threshold where an $\alpha$-node becomes unhappy. Hence nodes with high proportion of $\alpha$-nodes in their neighbourhood will be higher than the nodes with low proportion of $\alpha$-nodes in their neighbourhood. The three horizontal bars are snapshots of the process, and show cascades forming, originating from the initially unhappy $\alpha$-nodes. Figure 6 shows the same process, with the current state in the outer circle, and with swaps represented by a dot at a distance from the center which is proportional to the stage where the swap occurred. These cascades that spread the unhappy $\alpha$-nodes are due to the following domino effect. An unhappy $\alpha$-node moves out of a neighbourhood, thus reducing the number of $\alpha$-nodes in that interval. This in turn often makes another $\alpha$-node in the interval unhappy, which can move out at a latter stage, thus causing another $\alpha$-node nearby to be unhappy, and so on. The expanding intervals are the infected segments which start their life as incubators.¹⁶ Roughly speaking, incubators are a small intervals that surround the unhappy $\alpha$-nodes in the initial state. Moreover they are defined in such a way that, every $\beta$-node that is outside the incubators is very unhappy in the initial state. During the process, as we discussed above, these expand into larger infected segments, so that at each stage every unhappy $\alpha$-node is inside an infected segment. The union of all infected segments is called the infected area which, roughly speaking, consists of the areas containing unhappy $\alpha$-nodes (formal definition is given in the next section). At any stage, every $\beta$-node outside the infected area is very unhappy and every $\alpha$-node outside the infected area is happy. It is not hard to show that if $\tau +\rho <1$, the probability that a node belongs to an incubator is $e^{-\varTheta (w)}$. Hence with high probability the number of incubators as well as the number of nodes belonging to incubators of the process $(n,w,\tau ,\rho )$ is $n e^{-\varTheta (w)}$.

Fig. 9

Formation and dynamics of the infected area when $\tau +\rho <1$. Here instead of a circle, we lay the nodes horizontally, representing them as perpendicular lines of a fixed length, which appear lower or higher according to the proportion of $\alpha$-nodes in their neighborhood. The horizontal line represents the level below which an $\alpha$-node becomes unhappy

It turns out that the number of unhappy $\beta$-nodes in an interval of nodes, is conveniently bounded in terms of the number of $\alpha$-nodes in the interval. This means that if the number of $\alpha$-nodes in the infected area remains ${\mathbf{o}}\,\big ({n}\big )$, then the number of unhappy $\beta$-nodes in the infected area also remains ${\mathbf{o}}\,\big ({n}\big )$. In order to give a clear sketch of the argument depicted in Fig. 3 (for the current case when $\tau >0.5$ and $\tau +\rho <1$) let us define the global variables in Table 6.¹⁷ Let $\mathbf {Z}_s$ be the number of the $\alpha$-nodes in the infected area and $\mathbf {Y}_s$ be the number of unhappy $\beta$-nodes in the infected area at stage s. Also let $\mathbf {G}_s$ be the number of $\beta$-nodes outside the infected area and let $\mathbf {C}$ be the number of nodes inside the incubators (in the initial state). Let $\mathtt {U}_s$ be the number of unhappy nodes at stage s (this metric was discussed in Sect. 2.1 in the context of a fixed state).

Note that $\mathtt {U}_s\le \mathbf {G}_s + \mathbf {Y}_s + \mathbf {Z}_s$. A combinatorial argument can be used in order to show that $\mathbf {Y}_s\le \mathbf {Z}_s/(1-\tau )+2w\mathbf {C}$ (see Sect. 5.5 for the proof). Hence

$$\begin{aligned} \mathtt {U}_s\le w\mathbf {C}+ \mathbf {G}_s + 2\mathbf {Z}_s /(1-\tau ). \end{aligned}$$

(8)

By (1) we know that a stage where the number of unhappy nodes is less than $n\tau \rho _{*}/w$ is a safe stage. Hence we wish to show that (with high probability) the process will arrive at a stage where each of the three summands in (8) are at most $n\tau \rho _{*}/(3w)$. We know that $\mathbf {C}$ can be bounded appropriately. Our main argument will show how to obtain a similar bound for $\mathbf {Z}_s$. Note that $\mathbf {G}_s$ plays a different role, since it is initially large and shrinks monotonically (as the infected area expands monotonically). In order to find a stage where $\mathbf {G}_s$ becomes sufficiently small, it is instructive to consider what is a typical swap in the process. At the start of the process the infected area is a very small proportion of the entire ring. The vast majority of unhappy $\beta$-nodes occur outside the infected area, while all unhappy $\alpha$-nodes are inside the infected area. It follows that with high probability a swap will involve an $\alpha$-node in the infected area and a $\beta$-node outside the infected area. A bogus swap is a swap is one that is not of this kind.

Definition 3

(Bogus swaps) A swap which involves a $\beta$-node currently inside the infected area is called bogus. Given an infected segment I, a bogus swap in I is a swap that moves an $\alpha$-node into I.

Table 6 Random variables indicating the number of certain nodes in infected area at stage s of the process

Note that any swap which is not bogus, reduces $\mathbf {G}_s$ by at least 1. Hence if we show that the bogus swaps have small probability throughout a significant part of the process, we can ensure that $\mathbf {G}_s$ becomes sufficiently small. In order to be more precise, recall the stopping time $s_{*}$ from Lemma 9. We introduce a few more stopping times, all of which will turn out to be earlier than $s_{*}$ (with high probability). These basically concern the satisfaction of conditions which will ensure that the mixing index is sufficiently low as to guarantee a safe state. By (1) we have $\textsc {mix}\le \mathtt {U}\cdot w(w+1)$ and in order to ensure a safe state (by Lemma 1) we want $\textsc {mix}<n(w+1)\tau \rho _{*}$. So we want $\mathtt {U}<n\tau \rho _{*}/w$ at some stage of the process. Let $T_{\text {mix}}$ be the first stage which satisfies this condition. Similarly, consider the stopping times $T_g, T_{\text {stop}}$ of Table 7 (for simplicity, we will not consider $T_y$ in the present discussion). Here $T_g$ is the first stage where $\mathbf {G}_s\le \tau \rho \cdot n/(4w)$ and $T_{\text {stop}}$ is the first stage at which there are no more unhappy $\alpha$-nodes.

We use an elaborate martingale argument in order to show the following.

Table 7 Critical stages in the unbalanced happiness process, as stopping times for certain conditions

Lemma 10

(Bounding the $\alpha$-nodes in the infected area) If $\tau >0.5$ and $\tau +\rho <1$, with high probability we have $\mathbf {Z}_s={\mathbf{o}}\,\big ({n}\big )$ and $\mathbf {p}_s={\mathbf{o}}\,\big ({1}\big )$ for all $s<T_g$.

This lemma in combination with Lemma 9 implies that $T_g\le s_{*}\le T_{\text {stop}}$. Hence every stage up to $T_g$ involves a swap. Then it follows from the second clause of Lemma 10 that $T_g<n$ (since $\mathbf {G}_s$ is reduced by at least 1 at every non-bogus swap). Hence by (8) we have established (with high probability) the existence of a stage $T_g<n$ such that

$$\begin{aligned} \mathtt {U}_{T_g}\le w\mathbf {C}+ \mathbf {G}_{T_g} + \frac{2\mathbf {Z}_{T_g}}{1-\tau } \le {\mathbf{o}}\,\big ({n}\big ) + \frac{n\tau \rho _{*}}{4w}+ {\mathbf{o}}\,\big ({n}\big ) <\frac{n\tau \rho _{*}}{w}. \end{aligned}$$

Hence by (1) we have $T_{\text {mix}}\le T_g$, which means that by stage $T_g$ a safe state has been reached. Then by Corollary 3 the process will reach complete segregation, with probability $1-{\mathbf{o}}\,\big ({1}\big )$.

Corollary 7

(Safe state arrival) Suppose that $\tau +\rho <1$. Then with high probability the process $(n,w,\tau ,\rho )$ reaches a safe state by stage n, and eventually complete segregation.

This argument (with the full details given in the following sections) concludes the proof of Theorem 1 for the case $\tau >0.5$. The case $\tau \le 0.5$ is dealt with in Sect. 4.

3.3 Infected Area and Random Variables (Formal Definitions)

In this case of unbalanced happiness (i.e. when $\tau >0.5$ and $\tau +\rho <1$, see Table 3) the unhappy $\alpha$-nodes are initially very rare, so the interesting activity (namely $\alpha$-to-$\beta$ swaps) occurs in small intervals of the entire population (at least in the early stages). These intervals contain the unhappy $\alpha$-nodes, and gradually expand, while outside these intervals all $\beta$-nodes are very unhappy. Figure 9 (produced from a simulation) shows the development of this process, where the height of the nodes (perpendicular lines) is proportional to the number of $\alpha$-nodes in their neighborhood and the horizontal black line denotes the threshold where an $\alpha$-node becomes unhappy. These cascades that spread the unhappy $\alpha$-nodes are due to the following domino effect. An unhappy $\alpha$-node moves out of a neighbourhood, thus reducing the number of $\alpha$-nodes in that interval. This in turn often makes another $\alpha$-node in the interval unhappy, which can move out at a latter stage, thus causing another $\alpha$-node nearby to be unhappy, and so on. The expanding intervals are the infected segments which start their life as incubators.

Definition 4

(Incubators) Consider the set I of nodes in the initial state which belong to an interval of nodes of length w with less than $\epsilon _{*}=w(1-\rho +\tau )/2$ many $\alpha$-nodes. Let $I^{*}$ be the set of nodes whose neighborhood contains a node in I. An incubator is a maximal interval of nodes that is entirely contained in $I^{*}$.

Each incubator in the initial state may initiate a cascade of $\alpha$-to-$\beta$ swaps, which generates additional unhappy $\alpha$-nodes nearby, and which sustains itself by motivating additional $\alpha$-to-$\beta$ swaps, thus creating a cycle of $\alpha$-to-$\beta$ swaps and unhappy nearby $\alpha$-nodes. The infected segment around an incubator I is, informally speaking, the minimum interval containing I which is affected by this process, i.e. by the appearance of additional nearby unhappy $\alpha$-nodes. The infected area is the union of all of these infected segments, and it is always expanding during the process. We give a precise inductive definition of this notion in order to eliminate any ambiguity that may confuse the reader. An interval of nodes is called active at a certain state if it contains an unhappy $\alpha$-node.

Definition 5

(Infected segments) For each incubator I, let the infected segment $I_0$ corresponding to I at stage 0 be I itself. At the end of stage $s+1$, suppose that the infected segment $I_s$ is defined for each incubator I, and define $I_{s+1}$ for each incubator I as follows. Starting at position 0 and moving clockwise, consider each $I_s$ which is currently active and was also active at the end of stage s, and define $I_{s+1}=I_{s}\cup J$, where J consists of the nodes which do not already belong to another active infected segment (by the time we consider $I_s$) and whose neighborhood contains an unhappy $\alpha$-node in $I_{s}$ at stage $s+1$. Finally we define $I_{s+1}$ for those incubators I which are no longer active by letting $I_{s+1}=I_s-Q$, where Q consists of the nodes in $I_s$ which now belong to an active infected segment.

The infected area is the union of the infected segments. The fresh infected segment corresponding to infected segment I is $I-I_0$, i.e. consists of the nodes I except the nodes in its incubator. Hence a fresh infected segment consists of two growing intervals of nodes. The fresh infected area is the infected area except the nodes in the incubators. The interior of a set of nodes J consists of those nodes whose neighbourhood is entirely contained in J. The boundary of J consists of the nodes in J which are not in the interior. It is not hard to show that if $\tau +\rho <1$, the probability that a node belongs to an incubator is $e^{-\varTheta (w)}$. Hence with high probability the number of incubators as well as the number of nodes belonging to incubators of the process $(n,w,\tau ,\rho )$ is $n e^{-\varTheta (w)}$.

Our goal is now to show that the number of unhappy $\alpha$-nodes remains suitably bounded throughout a significant part of the process. Formally, the main idea is to bound this number with a martingale. Intuitively though, why should the number of unhappy $\alpha$-nodes remain fairly small? At the start of the process the infected area is a very small proportion of the entire ring. The vast majority of unhappy $\beta$-nodes occur outside the infected area, while all unhappy $\alpha$-nodes are inside the infected area. It follows that with high probability a swap will involve an $\alpha$-node in the infected area and a $\beta$-node outside the infected area.

In the absence of bogus swaps, it is not hard to show that the $\alpha$-nodes in the infected area (except those in the incubators) are unhappy. This in turn can be used in order to show that the $\alpha$-nodes in the infected area (and so, the unhappy $\alpha$-nodes too) are likely to remain ${\mathbf{o}}\,\big ({n}\big )$. However there will be bogus swaps, and these can make certain $\alpha$-nodes in the infected area happy.

Definition 6

(Anomalous nodes) A node is called actively anomalous at some stage of the process if it is a happy $\alpha$-node in the interior of the fresh infected area; it is called anomalous if it has been actively anomalous in this or a previous stage. Finally a node is called generally anomalous at some stage, if it is in the current infected area and has been or will be actively anomalous at some later stage of the process.

Clearly actively anomalous implies anomalous, which in turn implies generally anomalous (but not the other way around). Let $\mathbf {D}_s$ denote the number of anomalous nodes at stage s, and let $\bar{\mathbf {D}}_s$ denote the number of generally anomalous nodes at stage s. A martingale argument will be used in order to show that as long as $\mathbf {D}_s={\mathbf{o}}\,\big ({n}\big )$, the $\alpha$-nodes in the infected area are likely to remain ${\mathbf{o}}\,\big ({n}\big )$. The definition of anomalous nodes and $\bar{\mathbf {D}}_s$ may seem strange at this point, not least because $\bar{\mathbf {D}}_s$ is not predictable at stage s. The reason that we introduce $\bar{\mathbf {D}}_s$ is that $\mathbf {D}_s$ is very hard to analyze, and very hard to bound directly via a martingale (adapted to the stages of the process). However it is possible to bound $\bar{\mathbf {D}}_s$ via a martingale argument of a more general type (i.e. which is not adapted to the stages of the process). Since $\mathbf {D}_s\le \bar{\mathbf {D}}_s$, this suffices for our purposes.

Define the global variables Table 6 (also recall Table 5). By the definitions we have $\mathbf {D}_s\le \mathbf {D}_{s+1}$,

$$\begin{aligned} (\mathrm{{a}})\;\;\mathtt {U}_{\alpha }(s)\le \mathbf {Z}_s \quad (\mathrm{{b}})\;\;\mathtt {U}_{\beta }(s)\le \mathbf {G}_s+\mathbf {Y}_s \quad (\mathrm{{c}})\;\;\mathbf {G}_s\le \mathtt {U}_{\beta }^{*}(s) \quad (\mathrm{{d}})\;\;\mathbb {E}\left[ {\mathbf {C}}\right] = n e^{-\varTheta (w)} \end{aligned}$$

Here (d) holds because of the likely total size of the incubators and (c) holds because $\beta$-nodes outside the infected area are very unhappy.

3.4 Probabilities in the Infected Area and Anomalous Nodes

Our current goal is to show that the number of unhappy $\alpha$-nodes remains suitably bounded for a significant part of the process.¹⁸ The basic idea is that if the number of unhappy $\alpha$-nodes increases sufficiently, then the infected area must become quite large, and it becomes very likely that the next swap will involve an unhappy $\alpha$-node in the interior of the infected area. We shall be able to argue that there are good chances that the swap is not bogus. This means that this $\alpha$-node will move outside the infected area and will become happy. The anomalous nodes, however, present a difficulty with this line of argument. The eviction of the $\alpha$-node from the infected area (and its replacement by a $\beta$-node) may produce more unhappy $\alpha$-nodes in its neighbourhood. So it is not absolutely true that the total number of unhappy $\alpha$-nodes will decrease. In fact, as the simulations of Fig. 5 suggest, at the early stages of the process this number is likely to increase slightly.

If we assume the absence of bogus swaps, then it is not hard to show that the nodes in the interior of the infected area and outside the incubators have neighborhoods with proportion of $\alpha$-nodes well below $(2w+1)\tau$. In this case it is straightforward to employ a martingale argument which shows that the number of $\alpha$-nodes in the infected area (hence also the total number of unhappy $\alpha$-nodes) remains bounded with high probability throughout the process. Indeed, in this case there will be no happy $\alpha$-nodes in the interior of the fresh infected area, so (according to the argument we outlined above) the likely swap absolutely reduces the total number of unhappy $\alpha$-nodes.

In the presence of bogus swaps, we will use a more sophisticated martingale argument to bound the anomalous nodes. This bound can be used by another simpler martingale argument, in order to bound the number of unhappy $\alpha$-nodes, at least up to some stopping time of the process and with high probability. This plan requires the calculation of certain probabilities.

Lemma 11

(Probability of a bogus swap) At each stage $s+1$, the probability that the current swap will be bogus is bounded above by $\mathbf {Y}_s/\mathbf {G}_s$.

Proof

The number of pairs which can cause a bogus swap is bounded by $\mathtt {U}_{\alpha }(s)\cdot \mathbf {Y}_s$. On the other hand, any unhappy $\alpha$-node can swap with a $\beta$-node outside the infected area. Indeed, this is because the number of $\alpha$-nodes in the neighbourhood of any $\beta$-node outside the infected area is at least $(2w+1)\tau$. Hence there are at least $\mathtt {U}_{\alpha }(s)\cdot \mathbf {G}_s$ pairs of nodes that can swap at stage $s+1$. We can conclude that the probability of a bogus swap is bounded by $\mathtt {U}_{\alpha }(s)\mathbf {Y}_s/\mathtt {U}_{\alpha }(s)\mathbf {G}_s=\mathbf {Y}_s/\mathbf {G}_s$. $\square$

The calculation of the following probabilities is a first step towards our martingale argument.

Lemma 12

(Probabilities for $Z_s$ ) The numbers

$$\begin{aligned} \frac{\mathbf {G}_s}{\mathtt {U}_{\alpha }(s)}\cdot \frac{\mathbf {Z}_s-\mathbf {D}_s-2w\cdot \mathbf {C}}{\mathbf {G}_s+\mathbf {Y}_s}\quad \quad and\quad 2w\cdot \mathbf {C}\cdot \frac{\mathbf {G}_s+\mathbf {Y}_s}{\mathbf {G}_s\cdot \mathtt {U}_{\alpha }(s)} \end{aligned}$$

(9)

are a lower bound for the probability that $\mathbf {Z}_{s+1}<\mathbf {Z}_s$ and an upper bound for the probability that $\mathbf {Z}_{s+1}>\mathbf {Z}_s$, respectively.

Proof

The probability that $\mathbf {Z}_{s+1}<\mathbf {Z}_s$ is at least as much as the probability that the swap is not bogus and it involves a node in the interior of the infected area at stage $s+1$. Indeed, in this case the swap moves an $\alpha$-node from the interior of the infected area to outside the infected area, so $\mathbf {Z}_{s+1}=\mathbf {Z}_s-1$, because the length of the infected area remains the same.¹⁹ The unhappy $\alpha$-nodes of the infected area that cannot be part of such a swap are the ones that belong to the boundary of the infected area, so they are at most $2w\mathbf {C}$ many. This means that there are at least $\mathbf {Z}_s-\mathbf {D}_s-2w\mathbf {C}$ nodes of type $\alpha$ which can be picked as part of a swapping pair at stage $s+1$ such that $\mathbf {Z}_{s+1}-\mathbf {Z}_s$ is negative. Note that each of these $\alpha$-nodes forms a swapping pair with any $\beta$-node outside the infected area, since all such $\beta$-nodes are very unhappy. Therefore there are at least $(\mathbf {Z}_s-\mathbf {D}_s-2w\mathbf {C})\cdot \mathbf {G}_s$ many swapping pairs which make $\mathbf {Z}_{s+1}-\mathbf {Z}_s$ negative. On the other hand, the total number of swapping pairs are at most $(\mathbf {G}_s+\mathbf {Y}_s)\cdot \mathtt {U}_{\alpha }(s)$ many. Hence the first expression of (9) is a lower bound for the probability that $\mathbf {Z}_{s+1}<\mathbf {Z}_s$.

For the second clause, note that $\mathbf {Z}_{s+1}>\mathbf {Z}_s$ can only happen in the case that the infected area expands at stage $s+1$. This can only occur if the swapping pair involves an $\alpha$-node that belongs to the boundary of the infected area of stage s. There are at most $2w\mathbf {C}$ such nodes so there are at most $2w\mathbf {C}\cdot (\mathbf {G}_s+\mathbf {Y}_s)$ swapping pairs that can cause $\mathbf {Z}_{s+1}<\mathbf {Z}_s$. Moreover there are at least $\mathbf {G}_s\cdot \mathtt {U}_{\alpha }(s)$ possible swapping pairs for stage $s+1$. Hence the second expression of (9) is an upper bound for the probability that $\mathbf {Z}_{s+1}>\mathbf {Z}_s$. $\square$

We may now identify our first supermartingale. Note that the following fact is the reason why we defined the anomalous nodes the way we did. The fact that $\mathbf {D}_s$ is nondecreasing is a necessary part of the following proof.

Lemma 13

(Non-anomalous nodes in an infected segment) The following process is a supermartingale, for all $s<T_y$: $\mathbf {Z}^{*}_s:=\max \{\mathbf {Z}_s-\mathbf {D}_s, 11w^2\cdot \mathbf {C}\}$

Proof

At the end of stage s (and given all information as to how the process has unfolded so far) denote the probability that $\mathbf {Z}_{s+1}<\mathbf {Z}_s$ by q and the probability that $\mathbf {Z}_{s+1}>\mathbf {Z}_s$ by p. Let E be the expected value of $\mathbf {Z}_{s+1}$. Now at stage $s+1$ the infected area can expand by at most w nodes. Moreover, it is not possible that at stage $s+1$, an $\alpha$-node which is not in the infected area of stage s is moved to a position in the infected area of stage $s+1$. This is because all $\alpha$-nodes outside the infected area of stage s are happy at stage s. It follows that $\mathbf {Z}_{s+1}-\mathbf {Z}_s\le w$ at each stage s. Therefore

$$\begin{aligned} E\le p\cdot (\mathbf {Z}_s+w) + q\cdot (\mathbf {Z}_s-1) + (1-p-q)\cdot \mathbf {Z}_s = \mathbf {Z}_s + wp-q. \end{aligned}$$

(10)

By Lemma 12, in order to ensure that $wp-q\le 0$, it suffices that

$$\begin{aligned} 2w^2\cdot \mathbf {C}\cdot \frac{\mathbf {G}_s+\mathbf {Y}_s}{\mathbf {G}_s\cdot \mathtt {U}_{\alpha }(s)} \le \frac{\mathbf {G}_s}{\mathtt {U}_{\alpha }(s)}\cdot \frac{\mathbf {Z}_s-\mathbf {D}_s-2w^2\cdot \mathbf {C}}{\mathbf {G}_s+\mathbf {Y}_s} \quad \\ \text {so} \quad \mathbf {Z}_s\ge \mathbf {D}_s + 2w^2\cdot \mathbf {C}\cdot \left[ 1+ \left( 1+\frac{\mathbf {Y}_s}{\mathbf {G}_s}\right) ^2\right] . \end{aligned}$$

Since $s<T_y$ the expression inside the parentheses in the latter inequality is bounded above by 2. Hence for the condition $wp-q\le 0$ it is sufficient that $\mathbf {Z}_s\ge \mathbf {D}_s +10w^2\cdot \mathbf {C}$ for all $s<T_y$. So now we divide into two cases. If $\mathbf {Z}_s< \mathbf {D}_s +10w^2\cdot \mathbf {C}$ then $\mathbf {Z}_{s+1}^{*}=\mathbf {Z}_{s}^{*}= 11w^2\cdot \mathbf {C}$. Otherwise, $E\le \mathbf {Z}_s$ and the result follows from the fact that $\mathbf {D}_s$ is non-decreasing. $\square$

Now to get from $\mathbf {Z}_s^{*}$ to $\mathbf {Z}_s$, we need to bound $\mathbf {D}_s$. Intuitively, we expect the proportion of the $\alpha$-nodes in neighborhoods of nodes in the interior of the infected area to be rather low, e.g. considerably lower than the threshold $(2w+1)\tau$. The following lemma gives a justification for such an expectation and is also the reason why we chose $\epsilon _{*}=(1-\tau -\rho )/2$ in the definition of incubators, Definition 4. Here is an intuitive explanation of this fact. Let us say that a node in the infected area which is not in the interior of the infected area is in the boundary of the infected area. A node in the boundary of the infected area can see a node outside the infected area. The nodes in the complement of the infected area have never seen unhappy $\alpha$-nodes, hence the proportion of $\alpha$-nodes in their semi-neighbourhoods can only increase. This means that one of the semi-neighbourhoods of each node in the boundary of the infected area has not been affected by $\alpha$-to-$\beta$ swaps. The following lemma says that such a node can only be included in the interior of the infected area if the semi-neighbourhood of it which has been affected by $\alpha$-to-$\beta$ swaps, is affected by at least $\epsilon _{*}w$ such swaps. In other words, the expansion of the infected area requires a considerable number of stages. The particular statement refers to the case where the infection travels from right to left. By symmetry, an analogous statement holds for the case where the infection travels the opposite direction.

Lemma 14

(Concentration of $\alpha$-to-$\beta$ swaps) Let [a, d] be an interval of nodes in the initial state of the process, and $\delta >0$ such that for each $u\in [a,d]$ the proportion of $\alpha$-nodes in each semi-neighbourhood of u is at least $\tau +\delta$. Consider a stage of the process up to which there have been no $\alpha$-to-$\beta$ swaps in $[a-w, a)$. For each $u\in [a,d]$ and any stage in this interval, if there is an unhappy $\alpha$-node in [a, u] then there have been at least $2w\delta$ many $\alpha$-to-$\beta$ swaps in the right semi-neighbourhood of u by that stage.

Proof

Let s be a stage of the process and suppose that there have been no $\alpha$-to-$\beta$ swaps in $[a-w, a)$ by stage s. Suppose that there is an unhappy $\alpha$-node in $[a-w, u]$ at stage s. Then there must have been an unhappy $\alpha$-node in $[u-w, u]$ at some stage $\le s$. Consider the first such stage $t_0$ and let $v_0$ be the rightmost $\alpha$-node in $(u-w, u]$ which became unhappy at stage $t_0$. By our hypothesis, up to stage $t_0$ there has been no $\alpha$-to-$\beta$ swaps in $(v_0,u]$. Hence all of the $\alpha$-to-$\beta$ swaps that occurred in the right semi-neighbourhood of $v_0$ are also in the right semi-neighbourhood of u. The proportion of the $\alpha$-nodes in the left semi-neighbourhood of $v_0$ is more than $\tau +\delta$. Since $v_0$ is unhappy at $t_0$, the proportion of the $\alpha$-nodes in its neighbourhood is less than $\tau$. Hence the proportion of the $\alpha$-nodes in its right semi-neighbourhood is at most $\tau -\delta$ at stage t. Hence by hypothesis, by stage t at least $2w\delta$ many $\alpha$-to-$\beta$ swaps have occurred in the right semi-neighbourhood of v. By the above discussion, these swaps have also occurred in the right semi-neighbourhood of u. $\square$

According to the definition of incubators, this fact is relevant for $\delta =(1-\tau -\rho )/2$ and shows that the infected area expands reasonably slowly in the stages of the process $(n,w,\tau ,\rho )$. Indeed, the proportion of $\alpha$-nodes in the neighbourhood of any node outside the infected area at any particular stage is at least $\tau +(1-\tau -\rho )/2$. This also shows that, in the absence of bogus swaps, all $\alpha$-nodes in the interior of the fresh infected area are always unhappy (i.e. there are no anomalous nodes). In the presence of bogus swaps this is no longer true, and this is why we have to work in order to bound the spread of anomalous nodes.

3.5 Bounding the Anomalous Nodes

Recall that $\mathbf {D}_s$ denotes the number of anomalous nodes at stage s. In this section we construct a martingale process which shows that $\mathbf {D}_s$ is likely to be bounded appropriately, throughout a significant part of the Schelling process. This argument requires us to consider the random variables localized into the individual infected segments. Recall the stopping times defined in Table 7. We use $\tau \rho n/(4w)$ rather than $\tau \rho n/(3w)$ in the definition of $T_g$ so as to allow for the slight discrepancy which one might expect between $\rho$ and $\rho _{*}$.

Definition 7

(Stopping times) Let $T_g$ be the least stage such that $\mathbf {G}_{T_g}\le \tau \rho n/(4w)$. Define $T_y$ to be the first stage which is either $T_g$ or else such that $\mathbf {Y}_s>\mathbf {G}_s$. Finally let $T_{mix }$ be the first stage for which $\textsc {mix}<n(w+1)\tau \rho _{*}$. In all cases, if the stage described does not exist then we define the corresponding stopping time to be $\infty$.

Given an infected segment I, let $\bar{D}_s=\bar{D}_s(I)$ be the number of nodes in $I_s$ that will ever become anomalous, up to stage $T_g$. This is a version of the generally anomalous nodes $\bar{\mathbf {D}}_s$. A stage is called an I-stage if a swap occurs involving a node from I.

$$\begin{aligned} \text {If }(\nu (s))\text { is an enumeration of the }I\text {-stages, let } \bar{D}_{s}^{*}=\bar{D}_{\nu (sw^5)}\text { and }I^{*}_s=I_{\nu (sw^5)}. \end{aligned}$$

We use $*$ as a superscript in other variables in the following, in order to indicate that they are ‘jump processes’ in the sense that they are not updated at every stage or even every I-stage of the Schelling process. For example, $D_{s}^{*}$ is only updated every $w^5$ many I-stages of the Schelling process.

We may view the underlying probability space $\varOmega$ as a tree, where the nodes are states and branchings correspond to state transitions. Let $\varOmega \wedge T_g$ denote the subspace restricted to the stages up to time $T_g$ (which may be infinite). Normally we would say that an event $\mathcal {A}\subseteq \varOmega \wedge T_g$ is I-independent if it did not impose any branching restrictions regarding the I-stages that occur in the reals in it. We give a sightly more general definition which is more appropriate for the argument to follow. An event $\mathcal {A}\subseteq \varOmega \wedge T_g$ is called I-independent if for each $\beta \in \mathcal {A}$ and any s such that the transition from $\beta \upharpoonright _{s}$ to $\beta \upharpoonright _{s+1}$ occurs at an I-stage, $\beta \upharpoonright _{s}*S\in \mathcal {A}$ for every state that is obtained from $\beta \upharpoonright _s$ through a non-bogus swap. A filtration $\mathcal {A}_s\subseteq \mathcal {A}_{s+1} \subseteq \varOmega \wedge T_g$ is called I-independent if for each s the event $\mathcal {A}_s$ is I-independent. Analogously, a process $(\mathbf {J}_s)$ on $\varOmega$ is called I-independent if the natural filtration of it is I-independent. Intuitively, a process $(\mathbf {J}_s)$ on the underlying probability space $\varOmega$ is I-independent, if for each s, fixing the value of $\mathbf {J}_s$ does not impose any restriction on (i.e. is compatible with all) the transitions of the Schelling process from stage s to stage $s+1$ that involve a non-bogus swap and a node from I. Here we use boldface font for $\mathbf {J}_s$ because this process will typically be global, in the sense that it involves information about the process that is not restricted to the infected segment I. In the following lemma we use $(\mathbf {J}^{*}_s)$ for the underlying I-independent global process in order to indicate that it refers to the subsequence of stages $sw^5$ of the process, much like $\bar{D}_{s}^{*}$.

Lemma 15

(I-supermartingale) Given an infected interval I, the process $\bar{D}_{s}^{*}-10ws$ is a supermartingale relative to any I-independent process $\mathbf {J}^{*}_s$ to which $\bar{D}_{s}^{*}$ is adapted.

Proof

Given an I-independent process $\mathbf {J}^{*}_s$ such that $\bar{D}_{s}^{*}$ is adapted to $\mathbf {J}^{*}_s$ (i.e. $\bar{D}_{s}^{*}$ is a function of $\mathbf {J}^{*}_s$) it suffices to show that $\mathbb {E}\left[ {\bar{D}_{s}^{*}}\ \big |\ {J_{s-1}} \right] \le \bar{D}_{s-1}^{*} +10w$ for all s. Let $\bar{D}_{s}^{*0}$ be the number of nodes in the fresh part of $I_s$, to the left of its incubator, that will ever become anomalous, up to stage $T_g$. Similarly let $\bar{D}_{s}^{*1}$ be the number of nodes in the fresh part of $I_s$, to the right of its incubator, that will ever become anomalous, up to stage $T_g$. Clearly $\bar{D}_{s}^{*}=\bar{D}_{s}^{*0}+\bar{D}_{s}^{*1}$. So it suffices to show that

$$\begin{aligned} \mathbb {E}\left[ {\bar{D}_{s}^{*i}}\ \big |\ {\mathbf {J}^{*}_{s-1}} \right] \le D_{s}^{*i} +5w \text { for each }i=0,1. \end{aligned}$$

Similarly, let $I^{*0}_s$ be the left interval of the fresh part of $I_s^{*}$ and let $I^{*1}_s$ be the right interval of the fresh part of $I_s^{*}$. Fix $i=0,1$ and set $H^{*i}_{s}=I^{*i}_{s}-I^{*i}_{s-1}$. In order to bound the expectation of $D^{*i}_s$, we consider the following cases (where each case applies only if the one above it fails):

• (a) $|H^{*i}_{s}|< 4w$;

• (b) There are bogus swaps in the I-stages $(s-1)w^5$ to $sw^5$;

• (c) A happy $\alpha$-node appears in the interior of $J^{i}_{s}$ before the interior becomes all $\beta$-nodes;

• (d) The above $\beta$-firewall forms, but it shrinks by 4w at some later I-stage $tw^5$.

• (e) Otherwise.

We will show that all of these events yield small expectation (conditional on $J_s$) on the number of happy $\alpha$-nodes that will ever appear in the interval $H^{*i}_{s}$ after I-stage $sw^5$ of the original process (in particular, the probabilities of (b)-(d) are very small). We decide to accept 4w happy $\alpha$ nodes in $H^{i}_{s}$ as a desirable (i.e. not too high) count. So, irrespective of likelihood, event (a) is desirable. Note that by Lemma 14,

$$\begin{aligned} \text {in }w^5\text { many }I\text {-stages }I\text { cannot grow by more than } 2w^5/(1-\tau -\rho ). \end{aligned}$$

(11)

Note that Lemma 11 also holds locally, by the same proof. In other words, given an interval of nodes of length $\ell$, then the probability that at stage $s+1$ a bogus swap will occur involving a $\beta$-node from the given interval is bounded above by $\ell /\mathbf {G}_s$. Since all stages are bounded by $T_g$, it follows that the probability (conditional on $\mathbf {J}^{*}_{s-1}$) of a bogus swap in an area of length $\ell$ is less than $4w\ell /n\tau \rho$. Hence by (11), event (b) has probability (conditional on $\mathbf {J}^{*}_{s-1}$) upper bounded by $w^{2\cdot 5+2}/n$. In this case we can bound the expectation trivially by $w^{3\cdot 5+2}/n=w^{17}/n$.

Now suppose that (a), (b) do not occur so that, by Lemma  14, each subinterval of length w in the interior of $H^{*i}_{s}$ has $\alpha$-proportion at most $\tau -\epsilon _{*}$ at I-stage $sw^5$, where recall that $(\epsilon _{*}=1-\tau -\rho )/2$. In particular, all $\alpha$ nodes in the interior of $H^{*i}_{s}$ are unhappy, and remain so unless $w\delta$ bogus swaps happen in $H^{i}_{s}$. We wish to show that in this case

$$\begin{aligned} \text {event (c) has probability (conditional on }\mathbf {J}^{*}_{s-1}) \text { upper bounded by }(w^{3\cdot 5}/n)^{w\delta }. \end{aligned}$$

Indeed couple this process (conditional on $\mathbf {J}^{*}_{s-1}$, where each stage is either a non-bogus swap in $H^{*i}_{s}$, or something else) with a gambler’s ruin process, where the gambler has $w^5/\delta$ chips and the house has $w\delta$ chips, and the ratio of the winning probabilities is less than $q=4w^{5+2}/n$ in favor of the house. Then we can estimate an upper bound the probability that $w\delta$ bogus swaps occur in $J^{i}_{s}$ before all the interior turns into a $\beta$-firewall. According to the standard gambler’s ruin result, this is

$$\begin{aligned} \frac{1-q^{w^5/\delta }}{q^{-w\delta }-q^{w^5/\delta }}< \frac{1}{q^{-w\delta }}<(w^{3\cdot 5}/n)^{w\delta } \end{aligned}$$

which is also a bound on the (conditional) probability of event (c). Now assume that (a)-(c) do not occur, and lets estimate an upper bound for the probability of (d). Again, couple this process (conditionally on $\mathbf {J}^{*}_{s-1}$) with a biased random walk where a negative move corresponds to a bogus swap moving something from the w border (one or the other) of the firewall, and a positive move is swapping the $\alpha$-node at the edge with a $\beta$-node (other events are ignored). The ratio of the probabilities is bounded above by $2w/(n\tau \rho /4w)$ which is bounded by $w^3/n$. Also note that a negative move chips (at most) w away from the firewall, while a positive move only contributes (at least) one node to the firewall. Then the probability that it will eat up tw at any future time is bounded by $w\cdot (w^3/n)^{t-1}$. For $t=4$ we get

$$\begin{aligned} \text {event (d) has probability (conditional on }\mathbf {J}^{*}_{s-1})\text { upper bounded by }w^{10}/n^3. \end{aligned}$$

Then the expectation of the number of anomalous nodes that will ever appear in $H^{*i}_s$ is bounded by

$$\begin{aligned} 4w+ 2\frac{w^{2\cdot 5+2}}{n}\cdot w^5\le 4w+\frac{w^{3\cdot 5+3}}{n}<5w. \end{aligned}$$

Finally under case (e) it is clear that the conditional expectation of $D_{s}^{*i}$ is also bounded by $\bar{D}_{s-1}^{*i} +5w$. Considering all the different cases, by the law of alternatives for conditional expectation we have that $\mathbb {E}\left[ {\bar{D}_{s}^{*i}}\ \big |\ {\mathbf {J}^{*}_{s-1}} \right] \le \bar{D}_{s-1}^{*i} +5w$, which concludes the proof. $\square$

Let $I_j, j<t$ be the infected segments (and $I_j[s]$ their state at stage s). Recall that $\bar{\mathbf {D}}_s$ is the sum of all $\bar{D}_{s}(I_j)$, $j<t$. In order to bound $\bar{\mathbf {D}}_s$ we need to prove a global version of Lemma 15. An immediate obstacle is the asynchrony of the I-stages with respect to the various infected segments I. We need to find a process $\mathbf {L}_s$ relative to which $\bar{\mathbf {D}}_s$ (or some ‘asynchronous’ version $\hat{\mathbf {D}}_s$ of it) is a supermartingale.

For each $j<t$ let $\tau _s(j)$ be the stage where exactly $s\cdot w^5$ many $I_j$-stages have occurred. Also let $(\tau _i)$ be a monotone enumeration of the times $\{\tau _s(j)\ |\ j<t, s\in \mathbb {N}\}$. Let $\lambda _s(j)$ be $\tau _m(j)$ for the maximum m such that $\tau _m(j)\le s$. Let $\hat{\mathbf {D}}_s$ be the sum of all $\bar{D}_{\lambda _s(j)}(I_j)$, $j<t$. The point of this definition is that $\hat{\mathbf {D}}_s$ considers values of $\bar{D}(I_j), j<t$ at the last stage $\le s$ where they completed a cycle (which happens at every $w^5$ many $I_j$-stages) and outputs their sum. Define $\mathbf {L}_s$ to be the vector containing the tuples $(\bar{D}_{\lambda _s(j)}, \lambda _s(j))$ for each $j<t$. In this way, the process $(\hat{\mathbf {D}}_s)$ is adapted to $(\mathbf {L}_s)$ (in other words, for each s, the value of $\hat{\mathbf {D}}_s$ is a function of $\mathbf {L}_s$). Note that $\hat{\mathbf {D}}_s$ remains constant in the intervals $[\tau _s, \tau _{s+1})$, just as $\bar{D}_{\lambda _j(s)}$ remains constant in the interval $[\tau _s(j), \tau _{s+1}(j))$.

Lemma 16

The process $\hat{\mathbf {D}}_{\tau _{s}}-20ws$ is a supermartingale relative to the process $\mathbf {L}_{\tau _{s}}$.

Proof

Using the law of alternatives for conditional expectation, it suffices to show that for each s there is a (finite) partition $\mathcal {A}$ of events relative to $\mathbf {L}_{\tau _{s}}$ such that for each $A\in \mathcal {A}$ we have

$$\begin{aligned} \mathbb {E}_{A}\left[ {\hat{\mathbf {D}}_{\tau _{s+1}}} \ \big |\ {\mathbf {L}_{\tau _{s}}} \right] \le \hat{\mathbf {D}}_{\tau _{s}} +20w\ \ \ \ \text {for all }s. \end{aligned}$$

(12)

Each event $A\in \mathcal {A}$ describes which pair of infected intervals $I_j$ completes a cycle at stage $\tau _{s+1}$, and the sequence of $I_j$-stages (for each of the two j) from $\lambda _j(\tau _s)$ to $\tau _{s+1}$. Formally, event A is a tuple one tuple $(m_0,m_1)$ where $m_i<t$, and for each $i=0,1$ an increasing sequence of stages starting from $\lambda _{m_i}(\tau _s)$ and ending on the same number a. If $m_0=m_1$ then the two sequences should be the same. The meaning of A is that $\tau _{s+1}=a$ and infected intervals with indices $m_i$ are hit at stage a, with the sequence of stages representing the exact stages from $\lambda _{m_i}(\tau _s)$ to a where a swap occurs in $I_{m_i}$. By the definition of A, this event is $I_{m_i}$-independent for $i=0,1$. At stage $\tau _{s+1}$ of the process there must be exactly one tuple $(m_0,m_1)$ where $i<t$, such that the swap occurred in $I_{m_0}$ and $I_{m_1}$. For each such event A on $\mathbf {L}_{\tau _s}$ we have

$$\begin{aligned} \mathbb {E}_{A}\left[ {\hat{\mathbf {D}}_{\tau _{s+1}}} \ \big |\ {\mathbf {L}_{\tau _{s}}} \right] = \sum _{j<t} \mathbb {E}_{A}\left[ {\hat{D}_{\tau _{s+1}}(I_j)} \ \big |\ {\mathbf {L}_{\tau _{s}}} \right] \end{aligned}$$

But for $j\ne m_0, m_1$ we have $\mathbb {E}_{A}\left[ {\bar{D}_{\tau _{s+1}}(I_j)} \ \big |\ {\mathbf {L}_{\tau _{s}}} \right] =\bar{D}_{\tau _{s}}(I_j)$ and by Lemma 15 we have

$$\begin{aligned} \mathbb {E}_{A}\left[ {\bar{D}_{\tau _{s+1}}(I_{m_i})} \ \big |\ {\mathbf {L}_{\tau _{s}}} \right] \le \bar{D}_{\tau _{s}}(I_{m_i})+10w\hbox { for }i=0,1 \end{aligned}$$

since A is $I_{m_i}$-independent for $i=0,1$. Therefore (12) holds for each of the events A. By the law of alternatives, and since there can be at most two infected segments that complete a cycle at stage $\tau _{s+1}$, we get

$$\begin{aligned} \mathbb {E}\left[ {\hat{\mathbf {D}}_{\tau _{s+1}}}\ \big |\ {\mathbf {L}_{\tau _{s}}} \right] \le \hat{\mathbf {D}}_{\tau _{s}} +20w\ \ \ \ \text {for all }s. \end{aligned}$$

Therefore $\hat{\mathbf {D}}_{\tau _s}-10ws$ is a supermartingale adapted to $\mathbf {L}_{\tau _{s}}$. $\square$

Corollary 8

Let $a\in \mathbb {N}$. With probability $>1-1/a$, for all $s<T_g$ we have $\mathbf {D}_{s}< a+ \frac{20s}{w^{k-1}} +n e^{-O(w)}$.

Proof

By Lemma 16 and the maximal inequality for supermartingales, given any $a>1$, with probability at least $1-1/a$ we have $\hat{\mathbf {D}}_{\tau _s}< a+ 20ws$ for all $s<T_g$. Since each stage can be an $I_j$-stage for at most two distinct $j<t$, we have $|\{i\ |\ \tau _i\le s\}|\le 2s/w^5$. Hence for each $a>1$ we have

$$\begin{aligned} \text {with probability }>1-1/a,\ \ \ \ \hat{\mathbf {D}}_{s}< a+ \frac{20s}{w^{4}} \ \ \ \text {for all }s<T_g. \end{aligned}$$

(13)

Also, note that at each stage s we have $\bar{D}_s(I_j)\le \bar{D}_{\lambda _j(s)} (I_j)+w^5$ for each $j<t$. Hence $\bar{\mathbf {D}}_s\le \hat{\mathbf {D}}_s +nw^5 e^{-O(w)}$. Since we also have $\mathbf {D}_s\le \bar{\mathbf {D}}_s$ for all s, the corollary follows from (13). $\square$

3.6 Bounding the Arrival Time to a Safe State

By Lemma 13 and Corollary 8 we have the desired bound on $\mathbf {Z}_s$.

Corollary 9

Let $a\in \mathbb {N}$. With probability $>1-1/a$, for all $s<T_y$ we have $\mathbf {Z}_{s}< a+ \frac{20s}{w^{4}} +n e^{-O(w)}$.

By Lemma 11 and Corollaries 12 and 9 we have the following

Corollary 10

Let $a\in \mathbb {N}$. With probability $>1-1/a$, for all $s<\min \{T_y,n\}$ we have $w^3 \cdot \mathbf {Z}_{s}={\mathbf{o}}\,\big ({n}\big )$ and $\mathbf {p}_s={\mathbf{o}}\,\big ({1}\big )$.

The following result is the technical basis for the result that with high probability a safe state will be reached (at some finite stage). It says that, with high probability the stopping times $T_y, T_g$ are equal and are bounded by n.

Lemma 17

(Stopping times) With probability $1-{\mathbf{o}}\,\big ({1}\big )$ we have $T_y=T_g<n$.

Proof

Let $\epsilon >0$ such that $1-\epsilon > \rho +1/8$. By Hoeffding’s inequality for Bernoulli trials we may consider n large enough such that the probability that $\mathbf {G}_0>(\rho +1/8) n$ is less than $\epsilon /4$. Recall that $\mathbf {p}_s$ is the probability of a bogus swap at stage $s+1$. Suppose that w is large enough such that with probability at least $1-\epsilon /4$

• (a) $w^2\mathbf {C}<n\tau \rho /32$;

• (b) $w\mathbf {Z}_{s}< n\tau \rho \cdot (1-\tau )/32$ for each $s\le \min \{T_y, n\}$;

• (c) $\mathbf {p}_s<\epsilon ^3/16$ for each $s\le \min \{T_y, n\}$.

Clause (a) can be ensured by Lemma 33. Clause (b) can be ensured by Corollary 9. Clause (c) can be ensured by Corollary 10. First, for a contradiction, assume that $T_y<T_g$. Then $\mathbf {G}_{T_y}< \mathbf {Y}_{T_y}$. By Corollary 10 and since (by definition) $T_y\le T_g$ we have

$$\begin{aligned} n\cdot \tau \rho /4< w\cdot \mathbf {G}_{T_y}< w\cdot \frac{\mathbf {Z}_{T_y}}{1-\tau }+w^2\cdot \mathbf {C}< \frac{n\tau \rho (1-\tau )}{32} + \frac{n\tau \rho }{32}< \frac{n\tau \rho }{16} \end{aligned}$$

which is the required contradiction. Hence with probability $>1-\epsilon /4$ we have $T_y=T_g$. Second, we show that with probability at least $1-\epsilon /2$ we have $T_y< n$. By clause (c) above,

$$\begin{aligned} \text {with probability at least }1-\epsilon /4\text {, at all stages } s<\min \{T_y,n\}\text { we have }\mathbf {p}_s <\epsilon ^2/4. \end{aligned}$$

(14)

By (14), with probability at least $1-\epsilon /4$, the expectation of the number of bogus swaps that have occurred by stage $T_y$ is $<\epsilon ^2\cdot T_y/4$. Hence, conditionally on the event that $\mathbf {p}_s <\epsilon ^2/4$ for all stages $s\le \min \{T_y, n\}$, the probability that by stage $\min \{T_y, n\}$ more than $\epsilon n$ bogus swaps have occurred is less than $\epsilon /4$. Hence the unconditional probability that by stage $\min \{T_y, n\}$ at most $\epsilon T_y$ bogus swaps have occurred is at least $(1-\epsilon /4)^2>1-\epsilon /2$.

We conclude the argument. We have established that the probability of the event $T_y<T_g$ or $\mathbf {G}_0>n(\rho +1/8)$ is bounded by $\epsilon /2$. It remains to show that outside this rare event, $T_y<n$. Since every non-bogus swap reduces $\mathbf {G}_s$ by (at least) 1, and $\mathbf {G}_0\le n(\rho +1/8)$, $\rho <0.5$, with probability at least $1-\epsilon /2$ we have

$$\begin{aligned} \mathbf {G}_{T_y}\le \mathbf {G}_0-(1-\epsilon ) T_y \Rightarrow T_y\le (\mathbf {G}_0-\mathbf {G}_{T_y})/(1-\epsilon )\le n(\rho +1/8)/(1-\epsilon )<n \end{aligned}$$

which shows that $T_z=T_g<n$ with probability at least $1-\epsilon$. $\square$

Corollary 11

(Safe state arrival) Suppose that $\tau +\rho <1$, $\tau >0.5$. Then with high probability the process $(n,w,\tau ,\rho )$ reaches a safe state, and then complete segregation.

Proof

Let $\epsilon >0$. By the law of large numbers, with probability at least $1-\epsilon /4$ and sufficiently large n we have $3\rho <4\rho _{*}$. Pick w, n large enough such that

• (a) $T_g=T_y<n$ with probability $>1-\epsilon /4$;

• (b) $2w\mathbf {Z}_{T_g}/(1-\tau )<n\tau \rho /4$ with probability $>1-\epsilon /4$;

• (c) $\mathbf {C}(w+1)<n\tau \rho /(4w)$ with probability $>1-\epsilon /4$.

Clause (a) can be ensured by Lemma 17 and clause (b) can be ensured by Corollary 9. Clause (c) can be ensured by Lemma 33. By the definition of $T_g$, $\mathbf {G}_{T_g}\le \tau \rho n/(4w)$. Hence by Corollary 10 we have

$$\begin{aligned} \mathtt {U}_{T_g}\le \mathbf {G}_{T_g} + \mathbf {Y}_{T_g} + \mathbf {Z}_{T_g}\le \mathbf {C}(w+1) + \mathbf {G}_{T_g} + 2\mathbf {Z}_{T_g} /(1-\tau )\le \frac{3\rho }{4}\cdot \frac{n\tau }{w}< \frac{n\tau \rho _{*}}{w} \end{aligned}$$

with probability $>1-\epsilon$. But $\textsc {mix}\le \mathtt {U}\cdot w(w+1)$ so the mixing index at stage $T_g$ is less than $n\tau \rho _{*}\cdot (w+1)$. In other words, $T_{\text {mix}}\le T_g$, so by Proposition 1 the process at stage $T_g$ is in a safe state, with probability more than $1-\epsilon$. Hence by Corollary 5, the process will arrive to complete segregation with probability at least $1-\epsilon$. $\square$

4 The Case When Intolerance is at Most 50% ($\tau \le 0.5$)

In this case the behaviour of the process $(n,w,\tau ,\rho )$ is very different, since the mixing index is strictly decreasing.²⁰ This means that the process is bound to arrive to a dormant state, with absolute certainty. Note that if $\tau \le 0.5$ then complete segregation is a dormant state, but it can be shown that the final state is never complete segregation. We show that in most typical cases for $\rho$, the outcome is static when $\tau \le 0.5$.

4.1 Overview of the Argument When $\tau \le 0.5$

We assume that $\rho <0.5$ because the case $\rho =0.5$ has already been analysed in [1, 7] and the case $\rho >0.5$ is symmetric. Hence on the hypothesis $\tau \le 0.5$ we have $\rho + \tau <1$ and by Table 3 the unhappy $\alpha$-nodes are an arbitrarily small proportion of the $\alpha$-nodes as $w\rightarrow \infty$. In any case, since $\rho<0.5<1-\rho$ we have $\tau -\rho < 1-\tau -\rho$, so the probability that an $\alpha$-node is unhappy is much smaller than the probability that a $\beta$-node is unhappy. However what matters in the analysis for $\tau \le 0.5$ is the relationship between the likelihood of stable intervals and unhappy $\alpha$-nodes. This analysis is a reminiscent of the work in [1], but has some new features.

Definition 8

(Stable intervals) A stable interval is an interval of nodes of length w which contains at least $(2w+1)\tau$ nodes of one or the other type. An interval is $\alpha$-stable if it contains at least $(2w+1)\tau$ nodes of type $\alpha$.

The $\beta$-stable intervals are defined analogously. Note that no $\alpha$-node which is inside an $\alpha$-stable interval can swap during the process. The reason is that such $\alpha$-nodes are happy just because of the presence of the other $\alpha$-nodes in the same interval. Then a simple induction shows that they will continue to be happy throughout the process, thereby remaining immune to swaps and fixed in their initial positions. A similar observation applies to $\beta$-stable intervals. The existence of stable intervals is characteristic to the case $\tau \le 0.5$.

The events we are interested in are the occurrences of $\alpha$-stable intervals and unhappy $\alpha$-nodes. The probabilities $\mathbb {P}_{\text {stab}}, \mathbb {P}_{\text {unhap}}$ of these two rare events can be viewed as tails of certain binomial distributions. Consider the variables, probabilities and distributions of Table 8. It is not hard to see that

$$\begin{aligned} \mathbb {P}_{\text {stab}}=\mathbb {P}[{Z_{\text {stab}}\ge (2w+1)\tau }] \quad \text {and} \quad \mathbb {P}_{\text {unhap}}\ge \mathbb {P}[{Z_{\text {unhap}}\ge 2w(1-\tau )}]. \end{aligned}$$

We are interested in the event where the ratio $\mathbb {P}_{\text {unhap}}/\mathbb {P}_{\text {stab}}$ becomes small, because of the following fact.

Lemma 18

(Static processes) Suppose that $\tau , \rho$ are such that $\mathbb {P}_{\text {unhap}}= {\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big )$ for some $c >1$. Then with high probability the process $(n,w,\tau , \rho )$ is static, and in fact there exists some $c_{*}>1$ such that with high probability the process stops after at most $n\cdot c_{*}^{-w}$ many steps.

Table 8 Likelihood of various properties in the initial configuration under certain conditions, when $\rho \le 0.5$ and $\tau \le 0.5$

The intuition here is that, if the unhappy $\alpha$-nodes are much more rare than the $\alpha$-stable intervals (i.e. if $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$) then it is very likely that unhappy $\alpha$-nodes are enclosed in small intervals which are guarded by $\alpha$-stable intervals. This means that the familiar cascades that can be caused by the eviction of an unhappy $\alpha$-node are bound to be contained in small areas of nodes. The very definition of stable intervals ensures that such cascades cannot pass through them. Hence the condition $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$ guarantees that any $\alpha$-to-$\beta$ swaps are contained in small areas of nodes of total size ${\mathbf{o}}\,\big ({n}\big )$. Due to the monotonicity of the mixing index, this means that there can only be at most ${\mathbf{o}}\,\big ({n}\big )$ swaps in this case.

The second item in Fig. 1 shows the probabilities $\mathbb {P}_{\text {stab}}, \mathbb {P}_{\text {unhap}}$ (for $w=100$) with respect to $\tau ,\rho$. We see that for points away from (0.5, 0.5), the surface $\mathbb {P}_{\text {unhap}}$ is above $\mathbb {P}_{\text {stab}}$, and there is a threshold curve beyond which the opposite relationship is established. Using basic results about the tail of the binomial distribution, and Stirling’s approximation we can derive the following sufficient condition for $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$:

$$\begin{aligned} g(\tau ,\rho )>0,\quad \text {where} \quad g(\tau ,\rho )=\frac{1}{2}\cdot \left( \frac{(1-\tau )^{1-\tau }}{(0.5-\tau )^{0.5-\tau }} \right) ^{2}-\rho . \end{aligned}$$

(15)

The third item of Fig. 1 is a representation of $g(\tau ,\rho )$ in the space, up to where it becomes negative, at which point we project it on the plane. The values of $\tau ,\rho$ that we are interested correspond to points on the plane, outside the collapsed area. This boundary (a curve) is more clear in the first item of Fig. 1 which is the projection of the surface to the plane, with different colours indicating the points which make g positive or negative. This boundary can be simplified (with slight loss of generality) if we consider the line that passes from the two points where the boundary curve intersects the lines $\tau =0.5$ and $\rho =0.5$. Hence if $2\rho \cdot (1-2\kappa _0)+\tau +\kappa _0<1$, we are in the stable region, which shows a clause of Theorem 1. Note that both of the partial derivatives of g are negative when $\tau ,\rho \in [0,0.5)$. If we fix $\rho =0.5$ then the largest value of $\tau$ that keeps $g(\tau ,\rho )\ge 0$ is the solution ($\kappa _0\approx 0.353092313$) of the first equation of Table 9. Hence we may conclude that if $\tau <\kappa _0$ and $\rho \in (0, 0.5]$ then $\mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big )$ for some $c>1$. We can also look for the largest square that is contained in the large area of the first item of Fig. 1 (where the process is static). The edge of this square is given in Table 9. Hence if $\rho , \tau \in (0, \lambda _0)$ then $\mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big )$ for some $c>1$.

We have one last observation to make about the function g. If we let do not restrict the values of $\tau \in (0,0.5)$ then we wish to find the values of $\rho$ such that $g(\tau , \rho )$. According to the properties of g (in particular its negative derivative on $\rho$), these are all the positive numbers which are less than the limit (which is also an infimum)

$$\begin{aligned} \lim _{\tau \rightarrow 0.5} \frac{1}{2} \cdot \left( \frac{(1-\tau )^{1-\tau }}{(0.5-\tau )^{0.5-\tau }} \right) ^{2} = 0.25 \end{aligned}$$

Hence we may conclude that if $\rho \le 0.25$ and $\tau \in (0, 0.5)$ then $\mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big )$ for some $c>1$. This concludes the proof of the second clause of Theorem 1.

Table 9 Threshold constants of interest and their derivation equations

4.2 Proofs for the Case $\tau \le 0.5$ (Stable Intervals)

Let $\mathbb {P}_{\text {stab}}$ be the probability that an interval of length w in the initial configuration is $\alpha$-stable. In order to express $\mathbb {P}_{\text {stab}}$ as a tail of the binomial distribution with w trials and probability of success $1-\rho$ let $Z_{\text {stab}}\sim B(w, 1-\rho )$. Then a w-block is $\alpha$-stable if and only if there are at least $(2w+1)\tau$ successes. Similarly, let $Z_{\text {unhap}}$ be the probability that a node u in the initial configuration is $\alpha$ and unhappy. Note that if u is an $\alpha$-node then it is unhappy if and only if there are more than $(2w+1)(1-\tau )=2w(1-\tau )+1-\tau$ nodes of type $\beta$ in $\mathcal {N}(u)-\{u\}$. If w is sufficiently large, this is equivalent to having more than $2w(1-\tau )$ nodes of type $\beta$ in $\mathcal {N}(u)-\{u\}$. These are 2w Bernoulli trials with probability of success $\rho$, and any unhappy $\alpha$-node has at least $2w(1-\tau )$ successes. In order to express $\mathbb {P}_{\text {unhap}}$ as a tail of the binomial distribution with 2w trials and probability of success $\rho$ let $Z_{\text {unhap}}\sim B(2w, \rho )$. Then

$$\begin{aligned} \mathbb {P}_{\text {stab}}=\mathbb {P}[{Z_{\text {stab}}\ge (2w+1)\tau }] \quad \text {and} \quad \mathbb {P}_{\text {unhap}}\ge \mathbb {P}[{Z_{\text {unhap}}\ge 2w(1-\tau )}]. \end{aligned}$$

We are interested in the event where the ratio $\mathbb {P}_{\text {unhap}}/\mathbb {P}_{\text {stab}}$ becomes small. Note that $\mathbb {P}_{\text {unhap}}, \mathbb {P}_{\text {stab}}$ are functions of w. Hence, using the asymptotic notation, we may say that we are interested in finding conditions on $\tau ,\rho$ such that $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$, which means that $\mathbb {P}_{\text {unhap}}/\mathbb {P}_{\text {stab}}\rightarrow 0$ as $w\rightarrow \infty$. By Hoeffding’s inequality for Bernoulli trials, if $2\tau +\rho <1$ stable intervals are common. Hence

$$\begin{aligned} \text {if } 2\tau +\rho <1 \text { then } \mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big ). \end{aligned}$$

(16)

Note that if $\tau <1/4$ we have $2\tau +\rho <1$, so we have what we want (independently of $\rho$). In other words, if $\tau \le 1/4$ and $\rho < 1/2$ then $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$. Similarly, if $\rho <1/3$ and $\tau <1/3$ then $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$. When $2\tau +\rho >1$, we have $\mathbb {P}_{\text {stab}}\rightarrow 0$ and $\mathbb {P}_{\text {unhap}}\rightarrow 0$ so the previous argument does not apply. The analysis in this case requires some work, and gives better results than the ones we just discussed.

We wish to derive conditions on $\tau , \rho$ under which we have $\mathbb {P}_{\text {unhap}}={\mathbf{o}}\,\big ({\mathbb {P}_{\text {stab}}}\big )$. Our argument only requires that $\tau , \rho < 0.5$ and $\tau +\rho <1$. However it is particularly essential for the case where (in addition) $2\tau +\rho >1$, which is not covered by our previous discussion. We start by calculating suitable bounds for $\mathbb {P}_{\text {unhap}}, \mathbb {P}_{\text {stab}}$.

$$\begin{aligned} \mathbb {P}_{\text {stab}}\ge \mathbb {P}[{Z_{\text {stab}}= {\lceil (2w+1)\tau \rceil }}] =\left( {\begin{array}{c}w\\ {\lceil (2w+1)\tau \rceil }\end{array}}\right) \cdot (1-\rho )^{{\lceil (2w+1)\tau \rceil }}\cdot \rho ^{w-{\lceil (2w+1)\tau \rceil }} \end{aligned}$$

Hence by Lemma 24 there exists a quadratic polynomial $w\mapsto p(w)$ such that, $\mathbb {P}_{\text {stab}}$ is bounded below by

$$\begin{aligned}&\frac{p(w)^{-1} \cdot w^w\cdot (1-\rho )^{2w\tau }\cdot \rho ^{w(1-2\tau )}}{((2w+1)\tau )^{2w\tau }\cdot (w(1-2\tau ))^{w(1-2\tau )}} = p(w)^{-1} \\&\quad \cdot \left( \rho ^{1-2\tau }(1-\rho )^{2\tau }\cdot (1-2\tau )^{2\tau -1} \cdot (2\tau )^{-2\tau }\cdot (1+\frac{1}{2w})^{-2\tau } \right) ^{w} \end{aligned}$$

Since $(1+1/(2w))^{2w}\ge e^{-1}$ we get

$$\begin{aligned} \mathbb {P}_{\text {stab}}\ge p(w)^{-1} \cdot e^{\tau }\cdot \left( \rho ^{1-2\tau }(1-\rho )^{2\tau }\cdot (1-2\tau )^{2\tau -1} \cdot (2\tau )^{-2\tau } \right) ^{w} \end{aligned}$$

(17)

The next step is to establish a suitable upper bound for $\mathbb {P}_{\text {unhap}}$. For this reason, and since $\rho <1-\tau$, we may use Lemma 25 with $h(2w)={\lfloor 2w(1-\tau )\rfloor }$ and parameter $k\in (\tau \rho /(1-\rho )(1-\tau ), 1)$ in order to get

$$\begin{aligned} \mathbb {P}_{\text {unhap}}\le \frac{1}{1-k}\cdot \left( {\begin{array}{c}2w\\ {\lfloor 2w(1-\tau )\rfloor }\end{array}}\right) \cdot \rho ^{{\lfloor 2w(1-\tau )\rfloor }}\cdot (1-\rho )^{2w-{\lfloor 2w(1-\tau )\rfloor }}. \end{aligned}$$

Then by Lemma 24 there exists a quadratic polynomial $w\mapsto q(w)$ such that

$$\begin{aligned} \mathbb {P}_{\text {unhap}}\le q(w)\cdot \frac{(2w)^{2w}\cdot \rho ^{2w(1-\tau )} \cdot (1-\rho )^{2w\tau }}{(2w(1-\tau ))^{2w(1-\tau )} \cdot (2w\tau )^{2w\tau }}= \left[ (1-\rho )^{2\tau }\cdot \rho ^{2-2\tau } \cdot (1-\tau )^{2\tau -2} \cdot \tau ^{-2\tau }\right] ^{w} \end{aligned}$$

Hence, combining this inequality with (17), there exists a quadratic polynomial $w\mapsto r(w)$ such that

$$\begin{aligned} \frac{\mathbb {P}_{\text {unhap}}}{\mathbb {P}_{\text {stab}}} < p(w)\cdot \left[ \rho \cdot \left( \frac{2-2\tau }{1-2\tau } \right) ^{2\tau }\cdot \frac{1-2\tau }{(1-\tau )^2} \right] ^w \end{aligned}$$

(18)

We are interested in conditions on $\tau , \rho$ which guarantee that $\mathbb {P}_{\text {unhap}}/\mathbb {P}_{\text {stab}}\rightarrow 0$ as $w\rightarrow \infty$. The latter condition is equivalent to the condition that the expression inside the square brackets in (18) is less than 1. So for $\mathbb {P}_{\text {unhap}}/\mathbb {P}_{\text {stab}}\rightarrow 0$ it suffices that

$$\begin{aligned} \rho <\left( \frac{1-2\tau }{2-2\tau } \right) ^{2\tau }\cdot \frac{(1-\tau )^2}{1-2\tau } = 2^{-2\tau }\cdot \frac{(1-\tau )^{2(1-\tau )}}{(1-2\tau )^{1-2\tau }}= \frac{1}{2}\cdot \left( \frac{(1-\tau )^{1-\tau }}{(0.5-\tau )^{0.5-\tau }} \right) ^{2} \end{aligned}$$

i.e. that the function (15) is positive. The first illustration of Fig. 1 is a representation of $g(\tau ,\rho )$ in the space, up to where it becomes negative, at which point we project it on the plane. The values of $\tau ,\rho$ that we are interested correspond to points on the plane, outside the collapsed area. This boundary is more clear in the second illustration of Fig. 1 which is the projection of the surface to the plain, with different colours indicating the points which make g positive or negative (along with three areas which we are going to discuss in the following). Note that both of the partial derivatives of g are negative when $\tau ,\rho \in [0,0.5)$. If we fix $\rho =0.5$ then the largest value of $\tau$ that keeps $g(\tau ,\rho )\ge 0$ is the solution of the equation

$$\begin{aligned} (1-\tau )^{1-\tau }=\left( 0.5-\tau \right) ^{0.5-\tau } \end{aligned}$$

(19)

This equation was previously considered in [1]. It has a unique solution in [0, 0.5] which is $\kappa _0\approx 0.353092313$. Hence (as indicated in the second illustration of Fig. 1) we may conclude that

$$\begin{aligned} \hbox {if } \tau <\kappa _0\; \;\hbox { and } \;\rho \in (0, 0.5]\;\hbox { then }\; \mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big )\; \hbox { for some }\; c>1. \end{aligned}$$

(20)

Let us find the largest number $\lambda _0$ such that for all $\tau ,\rho \le \lambda _0$ we have $g(\tau , \rho )\ge 0$. In other words, we are asking for the edge of the largest square that is contained in the large area of the second illustration of Fig. 1. According to the dynamics of g, this is the solution of the equation $g(x,x)=0$ in [0, 0.5], i.e. the solution to $2\tau \cdot \left( 0.5-\tau \right) ^{1-2\tau } = (1-\tau )^{2(1-\tau )}$, which is $\lambda _0 \approx 0.411493631109785$, so we may conclude that

$$\begin{aligned} \hbox { if }\;\rho , \tau \in (0, \lambda _0) \; \hbox { then }\; \mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big ) \hbox { for } \; \hbox { some }\; c>1. \end{aligned}$$

(21)

We have one last observation to make about the function g. If we let do not restrict the values of $\tau \in (0,0.5)$ then we wish to find the values of $\rho$ such that $g(\tau , \rho )$. According to the properties of g (in particular its negative derivative on $\rho$), these are all the positive numbers which are less than the limit

$$\begin{aligned} \lim _{\tau \rightarrow 0.5} \frac{1}{2} \cdot \left( \frac{(1-\tau )^{1-\tau }}{(0.5-\tau )^{0.5-\tau }} \right) ^{2} = 0.25 \end{aligned}$$

Hence we may conclude that

$$\begin{aligned} \hbox { if } \rho \le 0.25 \hbox { and } \tau \in (0, 0.5) \hbox { then } \mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big ) \hbox { for }\;\hbox { some }\; c>1. \end{aligned}$$

(22)

This area of $(\tau , \rho )$ is indicated in the second illustration of Fig. 1.

We wish to show that, for some $c>1$, the condition $\mathbb {P}_{\text {unhap}}={\mathbf{O}}\,\big ({c^{-w}\cdot \mathbb {P}_{\text {stab}}}\big )$ implies that the process is static. Recall that the definition of static processes (see Definition 1) is given in terms of the number of swaps that occur throughout the process. Before we lay out the main argument, we note that this definition can be alternatively and equivalently given in terms of the number of nodes that swap throughout the process, or even in terms of the growth of the infected area throughout the process. In particular, we show that a process is static if and only if one of the following conditions hold:

• an arbitrarily small proportion of nodes are ever involved in swaps

• the final length of the infected area is an arbitrarily small proportion of the population.

The number of swaps $S_T$ that have occurred before we arrived at a certain state T tells us how late into the process we are by the time we hit that state. If $M_T$ is the number of nodes that changed colour by the time we arrived in $S_T$ then

$$\begin{aligned} 4S_T/(2w+1)^2 \le M_T\le 2S_T \end{aligned}$$

which means that the variables $S_T, M_T$ provide similar information about the history of the process before state T was reached (recall that a state can be reached at most once through the process). The second inequality is clear, while the first one requires justification. If the same bunch of, say, k nodes keep getting swapped with each other, then the welfare progress is concentrated in their neighbourhoods, which consist of at most $(2w+1)k$ nodes. Since each swap increases the social welfare by at least 4, and the total social welfare of the $(2w+1)k$ nodes cannot exceed $(2w+1)^2$, it follows that that a collection of k nodes can sustain at most $(2w+1)^2k/4$ swaps. Hence $S_T$ swaps have to produce at least $4S_T/(2w+1)^2$ many moved nodes. So $M_T\ge 4S_T/(2w+1)^2$.

Another metric that provides similar information, is the length of the infected area at that state. It can be shown that the two metrics agree, in the sense that knowing one can provide a bound for the other. We only need one direction of this ‘equivalence’, which we encapsulate in the following lemma.

Lemma 19

(Length of infected area and number of swaps) Suppose that the infected area at stage t of the process has length $\ell$. Then the number of swaps that have occurred up to stage t is bounded above by $(w+1)\ell$.

Proof

In general, when a swap occurs (and $\tau \le 0.5$) the $\beta$-welfare increases by at least 2 (one for the one which moved and one from the difference of the other $\beta$-nodes in the two neighbourhoods). Note that each swap (whether it is bogus or not) moves a $\beta$-node into a position inside the interior of the infected area. This is because at the end of each stage, only the interior of the infected area contains unhappy $\alpha$-nodes. Moreover the infected area does not shrink. We wish to count the increase of the $\beta$-welfare inside the infected area at each swap. If a swap is bogus, then an $\alpha$-node inside the interior of the infected area moves to a position which is on the boundary of the infected area. In this case we count only part of the decrease of the $\beta$-welfare in the new position of $\alpha$. But since the total decrease is less than the increase (which occurs inside the new neighbourhood of the $\alpha$-node, entirely included in the infected area) there is still a positive increase of at least 2 overall, of the total $\beta$-welfare inside the infected area. Hence we may conclude that each bogus swap strictly increases the $\beta$-welfare of the nodes in the infected area. On the other hand each non-bogus swap involves the swap between an $\alpha$-node inside the interior of the infected area and a $\beta$-node outside the infected area. Again the difference in the $\beta$-welfare in the two neighbourhoods is at least 2, and we only have to count the over all increase of the $\beta$-welfare in the interior of the infected area (which is even larger than the overall increase of the $\beta$-welfare in the total population). It follows that every swap increases the $\beta$-welfare of the infected area by at least 2. Now consider the process $(n,w,\tau ,\rho )$ up to some stage t. The $\beta$-welfare of the nodes in the infected area at stage t can be at most $(2w+1)\ell$, so there can be at most $(2w+1)\ell /2$ i.e. swaps up to stage t. $\square$

Recall that the probabilities $\mathbb {P}_{\text {unhap}}, \mathbb {P}_{\text {stab}}$ (as functions of w) are completely determined by the parameters $\tau , \rho$. By the definition of $\alpha$-stable intervals, the infected area cannot pass through them. Indeed, only the creation of unhappy $\alpha$-nodes can spread the infected area, but no such event can happen through an $\alpha$-stable interval. Based on this observation, we show Lemma 18, i.e. that the cases that we exhibited earlier in this section lead to static processes.

Proof of Lemma 18

By our previous discussion it suffices to show that, under the hypothesis of the lemma, there exists some $d_{*}>1$ such that for every $\epsilon >0$ and $0\ll w\ll n$, with probability at least $1-\epsilon$ the process $(n,w,\tau , \rho )$ stops after at most $nd_{*}^{-w}$ many steps. Given a node u in a non-dormant state, let $x_u$ be the first node v to the left of u which has one of the following properties:

• (a) it belongs to an $\alpha$-stable interval;

• (b) there is an unhappy $\alpha$-node in its neighbourhood.

Moreover let $y_u$ be the first node to the right of u which satisfies (a) or (b). Note that $x_u, y_u$ are well defined and for each u it is not possible that $x_u$ or $y_u$ satisfy both (a), (b) (because an $\alpha$-stable interval does not contain unhappy $\alpha$-nodes). Given a state of the process, we say that a node u is exposed if at least one of $x_u, y_u$ satisfies clause (b). Moreover, let us use the term exposed area for the collection of the exposed nodes.

Let us bound the probability that a node is exposed (in the initial configuration). By our hypothesis there exists constants $c_1>0$ and $c_2>1$ such that $\mathbb {P}_{\text {stab}}>c_1 \cdot c_2^{\delta w}\cdot \mathbb {P}_{\text {unhap}}$ for all w. Then by Lemma 27, if n is sufficiently large, the probability that $x_u$ belongs to a stable interval is at least

$$\begin{aligned} \mathbb {P}_{\text {stab}}/(\mathbb {P}_{\text {stab}}+(2w+1)\mathbb {P}_{\text {unhap}})\ge c_1/(c_1+(2w+1)c_2^{-w}) \ge 1-d_1^{-w} \end{aligned}$$

for some $d>1$ and all w. Moreover the same bound applies to the probability that $y_u$ belongs to a stable interval, so the probability that u is not exposed is at least $(1-d_1^{-w})^2\ge 1-d_2^{-w}$, where $d_2>1$ is a suitable number (e.g. $d_2=d_1/2$ is sufficient, provided that w is sufficiently large). Hence the probability that a random node is exposed is at most $d_2^{- w}$. So the expectation for the length of the exposed area is at most $n\cdot d_2^{-w}$. By the definition of the $\alpha$-stable intervals, it follows that the interior of the infected area remains a subset of the exposed area for the entire process. Moreover the expectation of the number of blocks of the infected area is bounded by $nd_3^{-w}$ for some $d_3>1$ which does not depend on w, n. Hence by Lemma 19 and the linearity of expectation, the expected total number of swaps that occur throughout the process is bounded by $(w+1)\cdot (n\cdot d_2^{-w} + n \cdot 2w \cdot d_3^{-w} ) \le n \cdot d_4^{-w}$ for $\delta _4>1$ that does not depend on w, n. In order to conclude the argument, pick $\epsilon >0$ and set $d_{*}=d_4/2$. It suffices to show that, for $0\ll w\ll n$, the probability that the process takes more than $nd_{*}^{-w}$ steps is bounded by $\epsilon$. Note that if w is sufficiently large, $nd_{4}^{-w}< \epsilon nd_{*}^{-w}$. Hence, under such conditions, if the of the total number of swaps exceeds $\epsilon \cdot nd_{*}^{-w}$, it exceeds $nd_{4}^{-w}$ by a multiple of at least $1/\epsilon$. On the other hand, we showed that $d_{4}^{-w}$ is a bound on the expectation of of the total number of swaps. So (for $0\ll w\ll n$) if the total number of swaps exceeds $\epsilon \cdot nd_{*}^{-w}$, it is at least $1/\epsilon$ times its mean. By Markov’s inequality, the probability of such an event is bounded by $\epsilon$. $\square$

5 Deferred Background and Proofs

5.1 Background on Probability

Recall Hoeffding’s inequality for independent Bernoulli trials.²¹

Lemma 20

(Tight Hoeffding for Bernoulli variables) Let $Z_i$ be independent Bernoulli trials with expected value p, and let $S_k=\sum _{i<k} Z_i$. Then $\mathbb {P}[{S_k\le k(p-\epsilon )}]\le e^{-2\epsilon ^2 k}$ and $\mathbb {P}[{S_k\ge k(p+\epsilon )}]\le e^{-2\epsilon ^2 k}$ for each $\epsilon >0$. If $p\le 1/2$ then $\mathbb {P}[{S_k\ge k(p+\epsilon )}]\ge 1/4\cdot e^{-2\epsilon ^2 k/p}$ for each $\epsilon >0$ such that $\epsilon \le 1-2p$.

Since there are complex dependences amongst the random variables of the Schelling process, we often need to ‘approximate’ certain processes with canonical processes like simple random walks. Here a random walk with respect to the integer-valued random variables $(Z_i)$ is the stochastic process $R_k= r+\sum _{i<k} Z_k$, for some $r\in \mathbb {N}$. We say that $(R_i)$ is ruined at step k if k is the least number such that $R_k\le 0$. The following two facts are folklore.

Lemma 21

(Random walk simulation) Let $t_0,t_1\in \mathbb {N}$, $X_i\in \{-t_0,0,t_1\}$ be (possibly dependent) random variables, let $\hat{X}_i\in \{-t_0,0,t_1\}$ be independent Bernoulli trials and let $Y_k= \sum _{i<k} X_k$, $\hat{Y}_k=\sum _{i<k} \hat{X}_k$ be the associated random walks. Provided that, no matter what occurs at stages prior to i, at stage i we have $\mathbb {P}[{X_i=-t_0}]\le \mathbb {P}[\hat{X}_i=-t_0]$ and $\mathbb {P}[{X_i=t_1}]\ge \mathbb {P}[\hat{X}_i=t_1]$, then for all $k,x\in \mathbb {N}$ the probability that $(Y_i+x)$ is ruined by step k is bounded above by the probability that $(\hat{Y}_i+x)$ is ruined by step k.

Lemma 22

(Biased random walks) Let $t_0,t_1,r \in \mathbb {N}$, and let $X_i\in \{-t_0,0,t_1\}$ be (possibly dependent) random variables such that at stage i, no matter what has occurred at previous stages, we have $\mathbb {P}[{X_i=t_1} \, |\, {X_i\ne 0}]>t_0/(t_0+t_1)+\delta$ for some $\delta >0$. Let $Y_j= r+\sum _{i<j} X_i$, be the associated random walk. Then the probability that $(Y_j)$ is ever ruined is bounded above by $e^{-2r\delta ^2/t_0}/(1-e^{-2\delta ^2})$.

Our analysis depends on various exponential bounds that we can obtained on the expectations of certain parameters (e.g. the number of unhappy $\alpha$-nodes). The following fact will be routinely used in order to express such bounds in a canonical form. In the following statement the variables $Z_s$ concern stage s of the Schelling process $(n, w, \tau , \rho )$ and the constants $q,q',p$ are independent of n, w.

Lemma 23

(Expectation bounds) Let f be a polynomial, $p<1$ and $Z_s$ a random variables such that $\mathbb {E}(Z_s)<np$ for all s. If $\mathbb {E}(Z_s)\le n \cdot f(w)\cdot e^{-wq}$ for some $q>0$ and all all s and all sufficiently large w then there exists $q'>0$ such that $\mathbb {E}(Z_s)\le n\cdot e^{-wq'}$ for all w, s.

The binomial distribution with t trials and success probability p is denoted by B(t, p), and $Z\sim B(t,p)$ means that random variable Z follows this distribution. Stirling’s formula asserts that $n! \approx n^{n + \frac{1}{2}} e^{-n}$, i.e. that the limit of the ratio of the two expressions tends to 1 as n tends to infinity.

Lemma 24

(Stirling’s approximation) There exists a polynomial $y\mapsto p(y)$ such that for all $k\in \mathbb {N}$ and all $x\in \mathbb {R}\cap (0, k)$

$$\begin{aligned} \text {there exists }\; q\in \left( \frac{1}{p(k)}, p(k)\right) \; \text { such that }\; \left( {\begin{array}{c}k\\ {\lceil x \rceil }\end{array}}\right) =q\cdot \left( {\begin{array}{c}k\\ {\lfloor x\rfloor }\end{array}}\right) . \end{aligned}$$

In our analysis of the Schelling process for the case when $\tau \le 0.5$ we will need to compare the tails of different binomial distributions. For this purpose we use the following fact from [6, Theorem 1.1].

Lemma 25

(Tails of the binomial distribution) Suppose that $X_N \sim B(N,p)$, $p,k \in (0,1)$ and for all sufficiently large N, $( 1+ k(1-p)/p )\cdot h(N)> N \ge h(N)> p\cdot N > 0$, where $h: \mathbb {N}\rightarrow \mathbb {N}$. Then

$$\begin{aligned} \mathbb {P}[{X_N = h(N)}] \ \ \le \ \ \mathbb {P}[{X_N \ge h(N)}] \ \ \le \ \ \mathbb {P}[{X_N = h(N)}]/(1-k) \end{aligned}$$

for all sufficiently large N. In asymptotic notation we have $\mathbb {P}[{X_N \ge h(N)}]= \varTheta \left( \mathbb {P}[{X_N = h(N)}] \right)$.

The combination of this result with Lemma 24 gives the required information about the asymptotic behaviour of the ratio of the two binomial probabilities of interest (unhappy nodes and stable intervals).

5.2 Probability in Schelling Segregation

We lay out a general way for arguing about the probability of the various properties $P_u$ that a node u can have in the initial configuration. For example, $P_u$ could be the property ‘at least half of the nodes in the neighborhood of u are of the same type as u’.

Definition 9

(Rare and common events in the initial configuration) A property of a node in the initial configuration is called rare (or a rare event) if it holds with probability at most $n\cdot e^{-\delta w}$, for some positive constant $\delta$ which may depend on $\tau ,\rho$ but not on w, n. A property whose negation is rare is called common.

Definition 10

(Local properties) Given $f:\mathbb {N}\rightarrow \mathbb {N}$, a property $P=P_u$ of a node u in the initial configuration is f-local if it only depends on the nodes that are at most f(w)-near from u. In other words, P is f-local if, for any two nodes u, v such that for all $i \in [-f(w),f(w)]$, $u+i$ is of the same type as $v+i$, we have that $P_u$ holds if and only if $P_v$ holds.

Note that the two probabilities mentioned in Lemma 26 are on different spaces. The first one refers to the product space where a point is an infinite series of initial states. The second one refers to the space of points on a random initial state.

Lemma 26

(Strong law of large numbers for the Schelling process) Given a local property $P_u$ of nodes in the initial state of the process $(n,w,\tau ,\rho )$, with probability one, as $n\rightarrow \infty$ the proportion of nodes u that satisfy $P_u$ tends to the probability of $P_u$.

Proof

Let p be the probability of $P_u$ and let f be the function indicating the area around u on which $P_u$ depends (as in Definition 10). We wish to use the strong law of large numbers, so we need to manufacture a series of independent trials of properties with given expectation. Let $m\in \mathbb {N}$ be a parameter that depends on n (to be specified shortly). We consider the ring as a union of intervals of length $mf(w)+2f(w)$ (which we think of an interval of length mf(w) with padding f(w) nodes on each side). We always assume that $mf(w)+2f(w)<n$. Starting from node 0, denote the ith such interval by $V_i$ so that $|V_i|=mf(w)+2f(w)$. Also, denote the subinterval of $V_i$ that results from deleting the f(w)-node prefix and the f(w)-node suffix of $V_i$ by $I_i$. Hence $|I_i|=mf(w)$. Let $M_n\in \mathbb {N}$ be the largest integer such that $M_n(mf(w)+2f(w))\le n$, so that $M_n\rightarrow \infty$ as $n\rightarrow \infty$ and $n-M_n(mf(w)+2f(w))<mf(w)+2f(w)$. Hence for each $i<M_n$, the intervals $V_i$ are defined and are disjoint. The same is true for $I_i$, $i<M_n$. Moreover, if S is the set of all nodes,

$$\begin{aligned} 2f(w)M_n \le |S-\cup _{i<M_n} I_i| < 2f(w)M_n+mf(w)+2f(w). \end{aligned}$$

(23)

For each $i<M_n$ let $Y_i$ be the number of nodes $u\in I_i$ such that $P_u$ holds, and note that these random variables are independent. Moreover, by linearity of expectation, $\mathbb {E}(Y_i)=pmf(w)$. Recall that $M_n\rightarrow \infty$ as $n\rightarrow \infty$. According to the strong law of large numbers,

$$\begin{aligned} \frac{\sum _{i<M_n} Y_i}{M_n}\rightarrow pmf(w) \; \text { as } n\rightarrow \infty ,\text { with probability 1.} \end{aligned}$$

(24)

By (23), the required proportion is

$$\begin{aligned} \frac{\sum _{i<M_n} Y_i +\zeta f(w)\cdot (2M_n+m+2)}{(M_n +\delta ) f(w)(m+2)}= \frac{\frac{\sum _{i<M_n} Y_i}{M_n} + \zeta f(w)\cdot (2+\frac{m+2}{M_n})}{(1 +\frac{\delta }{M_n}) f(w)(m+2)} \end{aligned}$$

where $\delta ,\zeta$ range in [0, 1) (depending on how close n is to being a multiple of $f(m)(m+2)$). If we take $0\ll m\ll n$, the ratio $m/M_n$ tends to 0, so by (24) the required proportion tends to

$$\begin{aligned} \big (pm f(w)+2f(w)\zeta \big )/\big (f(w)(m+2)\big )= \big (pm +2\zeta \big )/(m+2)= \big (p +2\zeta /m\big )/\big (1+2/m\big ). \end{aligned}$$

Since $0\ll m$, the required proportion tends to p. More formally, we may let $m=\log n$. In this case, as $n\rightarrow \infty$ we have $m/M_n\rightarrow 0$ because $(\log n)^2/n$ tends to 0. Moreover $M_n\rightarrow \infty$ and $m\rightarrow \infty$ when $n\rightarrow \infty$ so the previous argument applies as indicated. $\square$

The following fact concerns pairs of properties P and Q that a node can have, which may both be rare but one (say P) occurs with much higher probability than the other. It asserts that in this case, a random node u is much more likely to be nearer to a node v satisfying P than a node t satisfying Q (although it may be far from any node satisfying P or Q). In the statement and proof of this result we use $P_u$ as a Boolean random variable which asserts that ‘u satisfies P’ (and similar with $Q_u$).

Lemma 27

(Rare properties in the Schelling ring) Let $P_u$, $Q_u$ be $\ell$-local properties of nodes in the initial state (where $\ell =\ell _w$ is a function of w) and for each node u let $x_u$ be the first node v to the right of u such that either $P_v$ or $Q_v$ holds. If $\rho ,\lambda$ are the probabilities of $P_u, Q_u$ respectively, the probability that $P_{x_u}$ and there is no node v with $Q_v$ to the left of and at distance at most $\ell$ from $x_u$ tends to a number $\ge \rho /(\rho +\lambda (2\ell +1))$ as $n\rightarrow \infty$. An analogous result holds when ‘right’ is replaced by ‘left’.

Proof

Consider a partition of the ring into disjoint neighbourhoods, starting from a node $u_0$ as follows. Given $u=u_0$, suppose inductively that $u_t$ has been defined. Then define $u_{t+1}=x_{u_t}+2\ell +1$. This iteration continues as long as $u_{t+1}< n$. Let $k_n$ be the number of iterations in this recursive definition (i.e. the number of terms of the sequence $(u_t)$). Consider the property

$$\begin{aligned} T_u:\ \ \ \ P_{x_u}\text { holds and no node }v\text { to the left of } x_u\text { and at distance at most }\ell \text { satisfies }Q_v. \end{aligned}$$

The sequence $(u_i)$ can be seen as independent trials for this property. Let $\pi _n$ be the proportion of the terms of $(u_i)$ that satisfy of $T_{u_i}$ in a random initial state. Note that $k_n\rightarrow \infty$ as $n\rightarrow \infty$ with probability 1. If $\pi$ is the probability of $T_u$, by the strong law of large numbers we have that $\pi _n\rightarrow \pi$ as $n\rightarrow \infty$ with probability 1. Let $\rho _n$ be the proportion of nodes that satisfy $P_u$ and let $\lambda _n$ be the proportion of nodes that satisfy $Q_u$. Note that we view $\pi _n, \rho _n, \lambda _n$ as random variables that depend on the initial state. Then

$$\begin{aligned} \frac{\rho _n}{\lambda _n}\le \frac{(2\ell +1) \pi _n k_n}{(1-\pi _n)k_n}= \frac{(2\ell +1) \pi _n}{1-\pi _n}\Rightarrow \pi _n\ge \frac{\rho _n}{\rho _n+\lambda _n (2\ell +1)} \end{aligned}$$

By Lemma 26 we have $\rho _n\rightarrow \rho$ and $\lambda _n\rightarrow \lambda$ as $n\rightarrow \infty$, which gives the required asymptotic bound. $\square$

5.3 Deferred Proofs from Sect. 2.1: Welfare, Mixing, and Expectations

The social welfare $\texttt {V}$ of the state can easily be seen to be non-decreasing along the transitions of the process. Let us establish the relationship with the mixing index. Given a certain state of the process and a node u, we let $u^{\alpha }$ denote the number of $\alpha$ nodes that are located in the neighbourhood of u at this state. Similarly, we let $u^{\beta }$ denote the number of $\beta$-nodes that are located in the neighbourhood of u. Given a state, let $n_{\alpha }, n_{\beta }$ be the number of $\alpha$ and $\beta$-nodes respectively, and let $\alpha _i, i<n_{\alpha }$ and $\beta _j, j<n_{\beta }$ be the finite sequences of $\alpha$ and $\beta$ nodes respectively in the state. Hence $\alpha _j^{\beta }$ denotes the number of $\beta$-nodes that are located in the neighbourhood of $\alpha _j$ while $\beta _j^{\alpha }$ denotes the number of $\alpha$-nodes that are located in the neighbourhood of $\beta _j$. Then

$$\begin{aligned} \sum _{j<n_{\beta }} \beta _j^{\alpha } = \sum _{i<n_{\alpha }} \alpha _i^{\beta }. \end{aligned}$$

(25)

In order to prove this equality, consider the configuration of $\alpha$ and $\beta$ types in the state and start by removing all $\beta$ from their positions. Then, adding the $\beta$ types one-by-one back to their original positions we can see each placement incurs the same increase to the two sums. Hence by induction, the two sums are equal.

We call the number in (25) the mixing index of the state, because it can be used as a metric of how mixed (i.e. not segregated) the population of $\alpha$ and $\beta$ types is at the given state. Indeed, suppose that the state has at least $2w+1$ nodes of each type. In the state of complete segregation the sums in (25) take the value $2\cdot (1+\cdots +w)$, which is $w(w+1)$. This can be shown to be the minimum mixing index (in a state which has at least $2w+1$ nodes of each type). At the other extreme, if the two types are uniformly mixed (in the sense that every interval I has approximately $\rho _{*} \cdot |I|$ green nodes) then the sums in (25) take approximately the value $n\cdot 2w\cdot \rho _{*}(1-\rho _{*})$, which can be shown to be the maximum possible mixing index. We also have

$$\begin{aligned} \sum _{i<n_{\alpha }} \alpha _i^{\alpha } + \sum _{i<n_{\alpha }} \alpha _i^{\beta } = (2w+1)\cdot n_{\alpha } \quad \text { and }\quad \sum _{j<n_{\beta }} \beta _j^{\beta } + \sum _{j<n_{\beta }} \beta _j^{\alpha } = (2w+1)\cdot n_{\beta }. \end{aligned}$$

(26)

From (25) and (26) we get $\mathtt {V}= (2w+1)\cdot n - 2\cdot \textsc {mix}$.

Lemma 28

If $\tau \le 0.5$, each step in the process decreases the mixing index by at least 4.

Proof

Suppose that we swap an unhappy $\alpha$-node u with an unhappy $\beta$-node v. Let $N_u, N_v$ be the neighbourhoods of u, v respectively and let $I=N_u\cap N_v$. Here we view the nodes as stationary, so that a swap of nodes means a swap of their types. The mixing index of the nodes in I will not change after the swap. Since $\tau \le 0.5$ the number x of $\alpha$-nodes in $N_u-I-\{u\}$ is smaller the number y of $\alpha$-nodes in $N_v-I-\{u\}$. After the swap the mixing index of each of the $\alpha$-nodes in $N_u-I-\{u\}$ will increase by one while the mixing index of each of the $\beta$-nodes in the same set will decrease by one. If $t=2w+1$ is the length of the neighbourhood and i is the number of $\alpha$-nodes in I then the mixing index of u before and after the swap is $t-x-i$ (the size of the neighbourhood minus the $\alpha$-nodes in the neighbourhood) and $x+i$ (the number of $\alpha$-nodes in $N_u-I$ plus the number of $\alpha$-nodes in $I\subseteq N_u$) respectively. Hence the difference in the sum of the mixing indices of the nodes in $N_u-I$ before and after the swap is the addition of (a) the difference in the mixing index of u, and (b) the difference in the sum of the mixing indices of the nodes in $N_u-I-\{u\}$, where the differences refer to the stages before and after the swap. For (a) we have $(x+i)-(t-x-i)$. For (b) there is an increase (by 1) of the mixing indices of each $\alpha$-node in $N_u-I-\{u\}$ since u becomes a $\beta$-node. Moreover there is a decrease (by 1) of the mixing index of the $\beta$-nodes (as u ceased to be an $\alpha$-node). Hence for (b) we have $x-(t-x-i)$. Overall, the difference in the sum of the mixing indices of the nodes in $N_u-I$ before and after the swap is $x-(t-x-i)-(t-x-i)+(x+i)=4x-2t+3i$. A similar argument shows that the difference in the sum of the mixing indices of nodes in $N_v-I$ is $2t-3i-4y$. Hence overall (and since the nodes outside $N_u\cup N_v$ maintain the same mixing index before and after the swap) the difference in the (total) mixing index is $4(x-y)$. Since $x<y$ this means that a decrease by at least 4 occurs due to the swap. $\square$

In our analysis, one of the basic facts used is that dormant states have at least a reasonably high mixing index. If we can show that with high probability the process reaches a point where the mixing index is too low for dormant states to be accessible, then by Corollary 5 we will have shown that with high probability complete segregation is the eventual outcome. Proposition 1 below provides an appropriate bound for the mixing index of dormant states. First we prove a technical lemma, which will then be used in the proof of Proposition 1. Given $c\in \mathbb {N}$, we say that a node $\gamma$ is c-near to a node $\delta$ if either there are at most $c-1$ nodes between $\gamma$ and $\delta$ or there are at most $c-1$ nodes between $\delta$ and $\gamma$.

Lemma 29

Suppose that $\tau >0.5$, $\rho _{*}<\tau$, $0\ll w \ll n$. In a dormant state of the process $(n, w, \tau , \rho )$ every $\beta$-block has length at most $2{\lceil (1-\tau )w \rceil }$ and every $\beta$-node is ${\lceil (1-\tau )w \rceil }$-near to an $\alpha$-node.

Proof

Since the second claim implies the first, it suffices to prove the second claim. By Lemma 3 we can assume that there are unhappy $\beta$-nodes in the given state. For a contradiction, suppose that some $\beta$-node is not ${\lceil (1-\tau )w \rceil }$-near to any $\alpha$-node. Consider the $\alpha$-node which is adjacent to the block and to the right of it. For large w, $2{\lceil (1-\tau )w \rceil }+1 < w$, meaning that this $\alpha$-node has at least $2{\lceil (1-\tau )w \rceil }+1$ nodes of type $\beta$ in its neighbourhood. Hence the $\alpha$-node has at most $2w-2{\lfloor (1-\tau )w\rfloor }$ nodes of type $\alpha$ in its neighbourhood, which is less than $(2w+1)\tau$. The fact that this $\alpha$ node is unhappy means that the state is not dormant. $\square$

Proposition 1

(Mixing in dormant states) Suppose that $\tau >0.5$, $\rho _{*}<\tau$, and $0\ll w \ll n$. The mixing index in a dormant state of the process $(n, w, \tau , \rho )$ is more than $n(w+1)\tau \rho _{*}$.

Proof

Suppose that in a dormant state the mixing index is at most $n(w+1)\tau \rho _{*}$. Since there are $n\rho _{*}$ nodes of type $\beta$, there exists such a node u with mixing index at most $(w+1)\tau$. By Lemma 29 there exists an $\alpha$-node v within ${\lceil (1-\tau )w \rceil }$ nodes to the left or to the right of u. The number of $\alpha$-nodes in the neighbourhood of $\nu$ is therefore at most $(w+1)\tau +{\lceil (1-\tau )w \rceil }$ (because given $c\in \mathbb {N}$, the mixing index can change by at most c when we shift inside an interval of $\beta$-nodes of length c). However this same number must be at least $(2w+1)\tau$ since v is happy in a dormant state. This holding for arbitrarily large w would imply that $(1-\tau )\ge \tau$ which gives the required contradiction. $\square$

As another measure of mixing, we may consider the number $\mathtt {k}_{\beta }$ of maximal contiguous $\beta$-blocks in the state. Let $\beta _i$ be the ith node of type $\beta$ and let $\beta _i^{\alpha }$ denote the number of $\alpha$-nodes in the neighbourhood around $\beta _i$. Let [x, y] be a finite interval of integers such that $\{\beta _i : i\in [x,y] \}$ constitutes a block (i.e. there is no $\alpha$-node between $\beta _x$ and $\beta _y$). If $x-y\ge w$ then $\beta ^{\alpha }_x+\cdots +\beta ^{\alpha }_y$ is bounded above by $2\cdot (1+\cdots +w)=w(w+1)$. If $x-y< w$ the number $w(w+1)$ continues to be a bound for $\beta ^{\alpha }_x+\cdots +\beta ^{\alpha }_y$. Therefore

$$\begin{aligned} \sum _{i<n_\beta } \beta _i^{\alpha } \le w(w+1) \cdot \mathtt {k}_{\beta },\quad \text {where }\mathtt {k}_{\beta } \hbox { is the number of maximal } \beta \text {-blocks.} \end{aligned}$$

(27)

This inequality is a formal expression of the rather obvious fact that the fewer maximal $\beta$-blocks there are, the less mixed the two types are. By the definition of happy nodes, if $\tau >0.5$ and $w>(1-\tau )/(2\tau -1)$ then no two adjacent nodes of different types can both be happy. This means that, as we move around the circle of nodes, every time we cross the border between a maximal $\beta$-block and a maximal $\alpha$-block we may count an additional unhappy node. So, provided that $\tau >0.5$ and w is sufficiently large, the number of maximal $\beta$-blocks is bounded above by the number of unhappy nodes in the state. Then by (27) we get $\textsc {mix}\le w\cdot (w+1) \cdot \mathtt {k}_{\beta } \le w\cdot (w+1) \cdot \mathtt {U}$. Intuitively this inequality says that the only way to have a small number of unhappy nodes is a small mixing index, i.e. a large degree of segregation. On the other hand we may bound the number of unhappy nodes in terms of the mixing index. By (25) and the definition of unhappy nodes,²² $\mathtt {U}_{\alpha }\cdot (1-\tau )(2w+1)\le \textsc {mix}$ and $\mathtt {U}_{\beta }\cdot (1-\tau )(2w+1)\le \textsc {mix}$, where $\mathtt {U}_{\alpha }, \mathtt {U}_{\beta }$ are the numbers of unhappy nodes of type $\alpha$ and $\beta$ respectively. So

$$\begin{aligned} \textsc {mix}\le w\cdot (w+1) \cdot \mathtt {k}_{\beta } \le w\cdot (w+1) \cdot \mathtt {U}\le \textsc {mix}\cdot \frac{2w(1+1/w)}{(1-\tau )(2+1/w)}< \textsc {mix}\cdot \frac{2w}{1-\tau } \end{aligned}$$

and $\frac{1}{w}\cdot \frac{\textsc {mix}}{w+1} \le \mathtt {k}_{\beta } \le \mathtt {U}< \frac{2}{1-\tau }\cdot \frac{\textsc {mix}}{w+1}$ which means that if $\tau >0.5$ then $\mathtt {U}=\varTheta (\texttt {k}_{\beta })=\varTheta (\textsc {mix})$.

5.4 Deferred Proofs About Initial Expectations (Sects. 2.1 and 3.4)

An important part of our analysis relies on the values of the welfare metrics at the initial state. By measure concentration inequalities, with high probability, these will be near to their expected values, which we may compute. We start with the mixing index.

Lemma 30

The expectation of the mixing index in the initial state of $(n,w,\tau ,\rho )$ is $2nw\rho (1-\rho )$.

Proof

Consider the random variables $\beta _i^{\alpha }$ and note that $\mathbb {E}\left[ {\beta _i^{\alpha }}\right] =2w(1-\rho )$ for each i. If $n_{\beta }$ is the number of $\beta$-nodes, the expectation of the mixing index in the initial state is $n_{\beta }\cdot 2w(1-\rho )$ by the linearity of expectation. If we see $n_{\beta }$ as a random variable, its expected value is $n\rho$. By the rule of iterated expectation, the expected value of the mixing index is $2nw\rho (1-\rho )$. $\square$

Note that the expected value of the mixing index in the initial state is only slightly smaller than the maximum possible mixing index $n\cdot (2w+1)\cdot \rho _{*}(1-\rho _{*})$. This is hardly surprising, as a random state will be almost perfectly mixed, with the occasional non-uniformities that are implied by randomness (e.g. the existence of contiguous blocks of certain sizes).

Next, we are interested in the expected number of unhappy nodes of each type. It is not hard to see that this depends on whether $\tau +\rho <1$ or $\tau +\rho >1$ (we will not consider the special case where $\tau +\rho =1$).

Lemma 31

(Unhappy $\alpha$-nodes) Given $\rho , \tau$ such that $\rho +\tau <1$, with high probability the number of initially unhappy $\alpha$-nodes in the process $(n,w,\tau ,\rho )$ is $n\cdot e^{-\varTheta (w)}$.

Proof

Let $X_j$ be 1 if the jth node $u_j$ in the initial state is of type $\alpha$ and unhappy, and 0 otherwise. By Lemma 26, it suffices to show that $\mathbb {E}\left[ {X_j}\right]$ is $e^{-\varTheta (w)}$. Recall that the nodes are labelled independently, following a Bernoulli distribution, with the probability of a $\beta$-label being $\rho$. Let $\epsilon =1-\rho -\tau$ which is positive, according to our hypothesis. If $u_j$ is an unhappy $\alpha$-node, then the proportion of $\beta$-nodes in its neighbourhood $N(u_j)$ is larger than $1-\tau$. Hence the proportion of $\beta$-nodes in $N(u_i(j))-\{u_i(j)\}$ is larger than $1-\tau$, so it is at least $\rho +\epsilon$.

Let A be the event that $u_j$ is an $\alpha$-node and B the event that $u_j$ is unhappy, so that $\mathbb {P}[{A}]=1-\rho$ and $\mathbb {P}[{A\cap B}]= \mathbb {P}[{B} \, |\, {A}]\cdot \mathbb {P}[{A}]$. If we see the labels of the nodes in $N(u_j)-\{u_j\}$ as a series of 2w independent Bernoulli trials, by Hoeffding’s inequality for Bernoulli trials the probability that the proportion of $\beta$-nodes is at least $\rho +\epsilon$ is bounded by $e^{-4w\epsilon ^2}$. Hence by the above discussion, $\mathbb {P}[{B} \, |\, {A}]<e^{-4w\epsilon ^2}$. We may conclude that $\mathbb {P}[{X_j=1}]< (1-\rho )\cdot e^{-4w\epsilon ^2}$. Hence $\mathbb {E}\left[ {X_j}\right] \le (1-\rho )\cdot e^{-4w(1-\tau -\rho )^2}$. Similarly, by Lemma 20 we have $\mathbb {E}\left[ {X_j}\right] \ge (1-\rho )\cdot e^{-4w(1-\tau -\rho )^2/\rho }/4$. Hence $\mathbb {E}\left[ {X_j}\right]$ is $n\cdot e^{-\varTheta (w)}$, which concludes the proof. $\square$

Similar arguments give information about the number of the unhappy $\beta$-nodes and the incubators.

Lemma 32

(Unhappy $\beta$-nodes) Given $\tau ,\rho$ such that $\rho <\tau$, with high probability the number of initially happy $\beta$-nodes in the process $(n,w,\tau ,\rho )$ is $n\cdot e^{-{\mathbf{O}}\,\big ({w}\big )}$. If in addition $\tau +\rho <1$, with high probability this number is $n\cdot e^{-\varTheta (w)}$.

Proof

Let $Y_j$ be 1 if $u_j$ is of type $\beta$ and happy, and 0 otherwise. Then provided that $\rho <\tau$, by Hoeffding’s inequality for Bernoulli variables we have that $\mathbb {E}\left[ {X_j}\right] \le \rho \cdot e^{-4w(\tau -\rho )^2}$. Then Lemma 26 gives the first clause of the claim. Now lets assume that we also have $\tau +\rho <1$. Then by the second clause of Lemma 20 we get $\mathbb {E}\left[ {X_j}\right] \ge \rho \cdot e^{-4w(\tau -\rho )^2/\rho }$. This application is possible with $p=\rho$ and $\epsilon =\tau -\rho$ because $\rho <0.5$ and $\tau +\rho <1$, which means that $\epsilon <1-2p$. Then by Lemma 26 we get the second clause of the claim. $\square$

Lemma 33

(Number of incubators) If $\tau +\rho <1$, the probability that a node belongs to an incubator is $e^{-\varTheta (w)}$. Hence with high probability the number of incubators as well as the number of nodes belonging to incubators of the process $(n,w,\tau ,\rho )$ is $n e^{-\varTheta (w)}$.

Proof

Let $\epsilon _{*}=(1-\tau -\rho )/2$, and let $X_j$ be the index variable of the event that the left semi-neighbourhood of the jth node has less than $(\tau +\epsilon _{*})w$ many $\alpha$-nodes. Given that $\tau +\rho <1$, by Hoeffding’s inequality for Bernoulli variables (Lemma 20) and the tightness of it (Lemma 20), the probability that $X_j=1$ is $e^{-\varTheta (w)}$. Let $Y_j$ be the index variable of the event that the jth node belongs to an incubator, so that the probability that $Y_j=1$ is $e^{-\varTheta (w)}$ (since $(2w+1)e^{-\varTheta (w)}$ is $e^{-\varTheta (w)}$). Hence $\mathbb {E}(Y_j)$ is $e^{-\varTheta (w)}$. Then by Lemma 26 with high probability the number of nodes belonging to incubators of the process $(n,w,\tau ,\rho )$ is $n e^{-\varTheta (w)}$. $\square$

5.5 Deferred Proofs from Sect. 3.1: Persistent Blocks and Unhappy Nodes

Now we focus on the case where $\tau >0.5$ and $\tau +\rho <1$. Having established that a low number of unhappy nodes suffices to ensure dormant states are inaccessible, we now wish to show that such state is reached, before any dormant state is reached. Since in this case there are always unhappy $\beta$-nodes, we are only concerned about the existence of unhappy $\alpha$-nodes. One way to ensure this is to establish the existence of blocks of $\beta$-nodes of length $>w$.

Lemma 34

(Persistent $\beta$-block) Consider the process $(n,w,\tau ,\rho )$ with $\tau >0.5$ and let $s_{*}$ be the least stage where the ratio between the very unhappy $\beta$-nodes and the unhappy $\alpha$-nodes becomes less than $4w^2$ (putting $s_{*}=\infty$ if no such stage exists). Then with high probability there is a $\beta$-block of length $\ge 2w$ at all stages $<s_{*}$ of the process.

Proof

Let $\epsilon >0$, let $\delta = 2w/(2w+1)-w/(w+1)$, and let y be a sufficiently large integer so that

$$\begin{aligned} e^{-2(y-2w)\delta ^2/w}/(1-e^{-2\delta ^2})<\epsilon /2. \end{aligned}$$

(28)

Since the initial state is random, as $n\rightarrow \infty$ the probability that there is a $\beta$-block of length at least y in the initial state tends to 1. Hence (for sufficiently large n) we may assume that there is a $\beta$-block of length $\ge y$ in the initial state, with probability at least $1-\epsilon /2$. Fix such a block and note that during the stages it may expand or retract. It suffices to show that, conditionally on the existence of such a block in the initial state, the probability that it shrinks to a block of length less than 2w before stage $s_{*}$ is bounded by $\epsilon /2$. Let $\ell _s$ be the length of the block at stage s, so that $\ell _0= y$. Also let $X_0=0$ and for each $s>0$ let $X_s=\ell _s-\ell _{s-1}$. Then $X_s\ge -w$ for all s, and $\ell _s=\ell _0+\sum _{t\le s} X_s$. Let $Z_s$ be $-w$ if $X_s<0$, and let $Z_s$ be 1 if $X_s>0$ (and $Z_s=0$ if $X_s=0$). Also let $Y_s=\sum _{t\le s} Z_s +\ell _0-2w$, so if at stage s the length of the $\beta$-block becomes less than 2w, the random walk $(Y_i)$ is ruined (by stage $s_{*}$). Let $(\hat{Y}_i)$ be identical to $(Y_i)$, except for stages after $s_{*}$, at which it remains identical to $Y_{s_{*}-1}$. Hence it suffices to show that the probability that $(\hat{Y}_i)$ is ruined is bounded above by $\epsilon /2$. Let $p_s=\mathbb {P}[{X_s>0} \, |\, {X_s\ne 0}]$ and let $q_s=\mathbb {P}[{X_s<0} \, |\, {X_s\ne 0}]$, so that $p_s+q_s=1$.

Since $\tau >1/2$, as long as the length of the block is at least w, the nearest $\alpha$-node on each side is unhappy. Moreover these $\alpha$-nodes can swap with any very unhappy $\beta$-node. Any such swap at stage s would make $Z_s= 1$. On the other hand, the only way that $Z_s=-w$ (i.e. the length of the block is reduced) is that a $\beta$-node from one of the 2w outer nodes in the block (w on each side) is part of a swap at stage s (with an unhappy $\alpha$-node). Hence according to our hypothesis we have $p_s/q_s>2w$ for all $s<s_{*}$. So $\mathbb {P}[{X_s>0} \, |\, {X_s\ne 0}]>2w/(2w+1)> w/(w+1)+\delta$ which means that the walk $(\hat{Y}_i)$ meets the requirements of Lemma 22. Hence the probability that $(\hat{Y}_i)$ is ruined is bounded by the expression on the left-hand-side of (28). We sum up our argument. Given $\epsilon >0$, we start with a block of $\beta$-nodes of length y, with probability at least $1-\epsilon /2$. Conditionally on this starting assumption, our argument says that with probability at least $1-\epsilon /2$ this block will continue to have length more than 2w at all stages up to stage $s_{*}$. Hence the probability that there is no $\beta$-block of length $\ge 2w$ at some stage $<s_{*}$ is less than $\epsilon$. $\square$

Another tool that was used in our analysis is a bound on the number of unhappy $\beta$-nodes in the infected area, in terms of the number of $\alpha$-nodes in the infected area. This is based on the fact that, when the number of $\alpha$-nodes in an interval is limited, then the number of unhappy $\beta$-nodes in the same interval is also limited.

Lemma 35

(Proportions in a block of nodes) Consider a block of adjacent nodes which contains exactly x nodes of type $\alpha$. Then for each $y\in (0,1)$ there are at most $x/y+2w$ many $\beta$-nodes in the block for which the proportion of $\alpha$-nodes in their neighbourhood is at least y.

Proof

We are given a block of adjacent nodes A. Let us call a node weak if it is a $\beta$-node for which the proportion of $\alpha$-nodes in its neighbourhood is less than y. It suffices to show that the number of $\beta$-nodes in A which are not weak is at most $x/y +2w$. If we remove all of the weak nodes from A, thus obtaining a possibly different (and shorter) block B, then in the resulting configuration there are no weak nodes. It then suffices to show that the number of $\beta$-nodes in B is at most $x/y+2w$. Note that the number of $\alpha$-nodes in B remains x, since we did not remove any $\alpha$-nodes. Let $b_0<b_1$ be the endpoints of block B and define a finite sequence $(\beta _i)$ of $\beta$-nodes as illustrated in Fig. 10 and formally defined as follows. Let $\beta _0$ be the leftmost $\beta$-node in B such that the left endpoint of its neighbourhood is $\ge b_0$ and such that the neighbourhood of $\beta _0$ is entirely contained in B (if there exists such). Assuming that $\beta _i$ is defined and there are $\beta$-nodes between the right endpoint of $\beta _i$ and $b_1$, define $\beta _{i+1}$ to be the leftmost $\beta$-node in B which is to the right of $\beta _i$, whose neighbourhood is disjoint from that of $\beta _i$ and entirely contained in B. Let $\beta _i, i<k$ be the sequence defined in this way. Then $\beta _i, i<k$ have disjoint neighbourhoods, each of them containing at least $y(2w+1)$ nodes of type $\alpha$. Hence $ky(2w+1)\le x$ so $k(2w+1)\le x/y$ which means that the number of nodes that are contained in the union of these neighbourhoods is bounded by x / y. Since these are neighbourhoods of $\beta$-nodes that are not weak, the number of $\beta$-nodes that are contained in the union of these neighbourhoods is at most $x/y(1-y)=x/y-x$.

Fig. 10

Partition of patched block B in the proof of Lemma 35

Let $x_i$ be the distance between the right endpoint of the neighbourhood of $\beta _i$ and the left endpoint of the neighbourhood of $\beta _{i+1}$. Note that for each $i<k$ there is a block of at least $x_i$ nodes of type $\alpha$ in the left semi-neighbourhood of $\beta _{i+1}$. Indeed, according to the definition of $(\beta _i)$, the only reason why there is some distance d between the two endpoints is that a block of $\alpha$-nodes of length d immediately to the left of $\beta _{i+1}$. We may conclude that there are at least $\sum _i x_i$ nodes of type $\alpha$. By the hypothesis the $\alpha$-nodes are exactly x, so $\sum _i x_i\le x$. Hence the number of $\beta$-nodes in B that do not belong to the neighbourhood of some $\beta _i, i<k$ is at most $x+2w$ (where 2w is an upper bound for the number of $\beta$-nodes in the final segment of B to the right of the neighbourhood of $\beta _{k-1}$, or the whole of B if $k=0$). Hence, overall, there are at most $(x/y-x)+ (x+2w)=x/y+2w$ nodes of type $\beta$ in B, which concludes the proof. $\square$

A $\beta$-node is unhappy if and only if the proportion of $\alpha$-nodes in its neighbourhood is more than $1-\tau$. Hence we may apply L emma 35 with y equal to a value that is slightly larger than $1-\tau$ (taking the limit $y\rightarrow 1-\tau$ from above and taking into account that the number of nodes are integers) gives the following bound on the number of unhappy $\beta$-nodes in a block.

Corollary 12

(Unhappy $\beta$-nodes versus $\alpha$-nodes) Consider a block of adjacent nodes of type $\alpha$ or $\beta$ such that exactly x of these nodes are of type $\alpha$. Then there are at most $x/(1-\tau )+2w$ unhappy $\beta$-nodes in this block.

By applying this fact to each of the infected segments of the process, and adding up the numbers unhappy nodes in each of the segments we see that $\mathbf {Y}_s\le \mathbf {Z}_s/(1-\tau )+2w\mathbf {C}$, which is the fact used in the main part of our analysis.