Skip to main content
SpringerLink
Log in

Polychromatic Arm Exponents for the Critical Planar FK-Ising Model

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

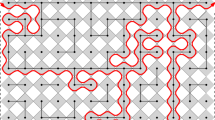
Schramm–Loewner evolution (SLE) is a one-parameter family of random planar curves introduced by Schramm in 1999 as the candidates for the scaling limits of the interfaces in the planar critical lattice models. This is the only possible process with conformal invariance and a certain “domain Markov property”. In 2010, Chelkak and Smirnov proved the conformal invariance of the scaling limits of the critial planar FK-Ising model which gave the convergence of the interface to \(\text {SLE}_{16/3}\). We derive the arm exponents of \(\text {SLE}_{\kappa }\) for \(\kappa \in (4,8)\). Combining with the convergence of the interface, we derive the arm exponents of the critical FK-Ising model. We obtain six different patterns of boundary arm exponents and three different patterns of interior arm exponents of the critical planar FK-Ising model on the square lattice.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. The pattern \(\sigma =(0110\cdots 10)\) with length \(2j+2\) starts with 01 and then it is followed by j pairs of 10.

References

  1. Alberts, T., Kozdron, M.J.: Intersection probabilities for a chordal SLE path and a semicircle. Electron. Commun. Prob. 13, 448–460 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  2. Beffara, V.: The dimension of the SLE curves. Ann. Probab. 36(4), 1421–1452 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  3. Beffara, V., Nolin, P.: On monochromatic arm exponents for 2D critical percolation. Ann. Probab. 39, 1286–1304 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chelkak, D., Smirnov, S.: Universality in the 2D Ising model and conformal invariance of fermionic observables. Invent. Math. 189(3), 515–580 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. Chelkak, D., Duminil-Copin, H., Hongler, C., Kemppainen, A., Smirnov, S.: Convergence of Ising interfaces to Schramm s SLE curves. C. R. Math. 352(2), 157–161 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chelkak, D., Duminil-Copin, H., Hongler, C.: Crossing probabilities in topological rectangles for the critical planar FK-Ising model. Electron. J. Probab. 21(5), 28 (2016)

    MathSciNet  MATH  Google Scholar 

  7. Dubédat, J.: Duality of Schramm-Loewner evolutions. Ann. Sci. Éc. Norm. Supér. (4), 42(5):697–724 (2009)

  8. Duminil-Copin, H.: Parafermionic observables and their applications to planar statistical physics models. Ens. Mat. 25, 1–371 (2013)

    MathSciNet  MATH  Google Scholar 

  9. Duminil-Copin, H., Sidoravicius, V., Tassion, V.: Continuity of the phase transition for planar random-cluster and Potts models with $1 \le q \le 4$. Commun. Math. Phys. 349(1), 47–107 (2017)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Duplantier, B.: Conformal fractal geometry and boundary quantum gravity. arXiv:mathph/0303034 (2003)

  11. Garban, C., Wu, H.: Dust analysis in FK-Ising percolation and convergence to chordal SLE$(16/3, 16/3-6)$ (in preparation)

  12. Kesten, H.: Scaling relations for 2d-percolation. Commun. Math. Phys. 109(1), 109–156 (1987)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Lawler, G.F.: Conformally Invariant Processes in the Plane. Mathematical Surveys and Monographs, vol. 114. American Mathematical Society, Providence, RI (2005)

  14. Lawler, G.F., Schramm, O., Werner, W.: Values of Brownian intersection exponents. I. Half-plane exponents. Acta Math. 187(2), 237–273 (2001)

    Article  MATH  Google Scholar 

  15. Lawler, G.F., Schramm, O., Werner, W.: One-arm exponent for critical 2D percolation. Electron. J. Probab. 7(2), 13 (2002)

    MathSciNet  MATH  Google Scholar 

  16. McCoy, B.M., Wu, T.T.: Theory of Toeplitz determinants and the spin correlations of the two-dimensionalising model. II. Phys. Rev. 155, 438–452 (1967)

    Article  ADS  Google Scholar 

  17. Miller, J., Sheffield, S.: Imaginary geometry I. Probab. Theory Relat. Fields 164(3–4), 553–705 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  18. Miller, J., Sheffield, S.: Imaginary geometry IV. Probab. Theory Relat. Fields 169(3–4), 729–869 (2017)

    Article  MATH  Google Scholar 

  19. Miller, J., Hao, W.: Intersections of SLE paths: the double and cut point dimension of SLE. Probab. Theory Relat. Fields 167(1–2), 45–105 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  20. Pommerenke, Ch.: Boundary Behaviour of Conformal Maps. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 299. Springer, Berlin (1992)

  21. Rohde, S., Schramm, O.: Basic properties of SLE. Ann. Math. (2), 161(2), 883–924 (2005)

  22. Schramm, O.: Scaling limits of loop-erased random walks and uniform spanning trees. Israel J. Math. 118, 221–288 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  23. Schramm, O., Sheffield, S., Wilson, D.B.: Conformal radii for conformal loop ensembles. Commun. Math. Phys. 288(1), 43–53 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Schramm, O., Wilson, D.B.: SLE Coordinate Changes. N. Y. J. Math. 11, 659–669 (2005)

    MathSciNet  MATH  Google Scholar 

  25. Smirnov, S.: Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C. R. Acad. Sci. Paris I 333(3), 239–244 (2001)

  26. Smirnov, S., Werner, W.: Critical exponents for two-dimensional percolation. Math. Res. Lett. 8(5–6), 729–744 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wu, H., Zhan, D.: Boundary arm exponents for SLE. Electron. J. Probab. 22(89), 1–26 (2017)

    MathSciNet  MATH  Google Scholar 

  28. Wu, H.: Alternating arm exponents for the critical planar Ising model. Ann. Probab. (to appear). arXiv:1605.00985

Download references

Acknowledgements

H.W.’s work is supported by NCCR/SwissMAP, ERC AG COMPASP, the Swiss NSF as well as the startup Funding No. 042-53331001017 of Tsinghua University. The author acknowledges Hugo Duminil-Copin, Aran Raoufi, Stanislav Smirnov, and Vincent Tassion for helpful discussion on the critical lattice models. The author thanks Gregory Lawler, David Wilson and Dapeng Zhan for helpful discussions on SLE estimates. The author also acknowledges two anonymous referees for the helpful comments on the earlier version of the article.

Author information

Authors and Affiliations

  1. Yau Mathematical Sciences Center, Tsinghua University, Jingzhai 311, Tsinghua University, Beijing, 100084, China

    Hao Wu

Authors
  1. Hao Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hao Wu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, H. Polychromatic Arm Exponents for the Critical Planar FK-Ising Model. J Stat Phys 170, 1177–1196 (2018). https://doi.org/10.1007/s10955-018-1983-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-018-1983-3

Keywords

Search

Navigation