Abstract
We present a version of the Hubbard model with a gapless nearly-flat lowest band which exhibits ferromagnetism in two or more dimensions. The model is defined on a lattice obtained by placing a site on each edge of the hypercubic lattice, and electron hopping is assumed to be only between nearest and next nearest neighbor sites. The lattice, where all the sites are identical, is simple, and the corresponding single-electron band structure, where two cosine-type bands touch without an energy gap, is also simple. We prove that the ground state of the model is unique and ferromagnetic at half-filling of the lower band, if the lower band is nearly flat and the strength of on-site repulsion is larger than a certain value which is independent of the lattice size. This is the first example of ferromagnetism in three dimensional non-singular models with a gapless band structure.




Similar content being viewed by others
Notes
The reason why we choose L to be an odd integer is only technical. We can treat the case of even L with a slight modification.
This condition is also imposed to simplify the argument. It is easy to apply the present method to the model with open boundary conditions.
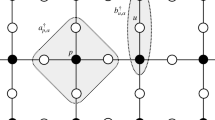
For \(\alpha \) in \(\mathcal {V}\) or x in \(\varLambda \) defined by (3), \(|\alpha |\) or |x| denotes the usual Euclidean distance. For a set X, we use the same symbol |X| to denote the number of elements in X.
One finds that our model with \(s=0\) is unitary equivalent to Mielke’s flat-band model by performing a gauge transformation \(c_{x,\sigma }\rightarrow -c_{x,\sigma }\) at all sites in one of the two sublattices, say, \(\{x=m(\alpha ,\,\alpha +\delta _1)|\alpha \in \mathcal {V}\}.\)
In Ref. [15], a similar lemma is proved relying on numerical calculations.
The regular square p is in the plane including the l-axis and the \(l^\prime \)-axis.
Note that \(|\mathcal {I}|=|\mathcal {P}_0|+|\mathcal {D}|+|\mathcal {J}|=|\mathcal {P}_0|+|\mathcal {C}_0|\) which equals the dimension of \(\mathcal {H}_b^\perp .\)
We think of \(-\pi \) as \(\pi \) when \(\nu \) is even (\(\pi \) is in \(\mathcal {J}\)).
We could easily find the condition for this equality in the case of the kagome lattice [14], but we have to consider this carefully in the present model. The condition for the equality depends on the form of the finite energy condition (74). This point should be kept in mind in applying the present method to other models.
Note that \(|I_\uparrow \cap I_\downarrow \cap \mathcal {D}|=n\) implies \(|I_\uparrow \cap {\bar{I}_\downarrow }\cap (\mathcal {J}\backslash \{0\})|=\nu -n\) when \(N(I_\uparrow ;\,I_\downarrow )=\nu .\) Then, considering in a similar way below (83), we obtain \(R_n.\)
Put \(I_\uparrow ^\prime =\{k\}\cup I_\uparrow \) and \(I_\downarrow ^\prime =\{-k\}\cup I_\downarrow .\) If \(k\in I_\uparrow \) or \(-k\in I_\downarrow ,\) we have \(\tilde{g}(k,\,I_\uparrow ;\,-k,\,I_\downarrow )=0\) by the definition; otherwise, since \(N(I_\uparrow ^\prime ;\,I_\downarrow ^\prime )=\nu \) and \(|I_\uparrow ^\prime \cap I_\downarrow ^\prime \cap \mathcal {D}|\ne \nu ,\) we have \(g(I_\uparrow ^\prime ;\,I_\downarrow ^\prime )=0,\) which implies \(\tilde{g}(k,\,I_\uparrow ;\,-k,\,I_\downarrow )=0.\)
Put \(I_\uparrow ^\prime =\{l\}\cup I_\uparrow \) and \(I_\downarrow ^\prime =\{l\}\cup I_\downarrow .\) If \(I_\uparrow ^\prime \cap I_\downarrow ^\prime \cap \mathcal {D}\ne \mathcal {D},\) we have \(\tilde{g}(l,\,I_\uparrow ;\,l,\,I_\downarrow )=0\) (see also footnote 12). If \(I_\uparrow ^\prime \cap I_\downarrow ^\prime \cap \mathcal {D}=\mathcal {D},\, |I_\uparrow \cap I_\downarrow \cap \mathcal {D}|=\nu -1\) and there is only one element l in \(\mathcal {D}\) for which \({\tilde{g}\left( l,\,I_\uparrow ;\,l,\,I_\downarrow \right) }\) can be non-zero.
References
Lieb, E.H.: The Hubbard model: some rigorous results and open problems. In: Baeriswyl, D., Campbell, D.K., Carmelo, J.M.P., Guinea, F., Louis, E. (eds.) The Hubbard Model, pp. 1–19. Springer, New York (1995)
Tasaki, H.: From Nagaoka’s ferromagnetism to flat-band ferromagnetism and beyond: an introduction to ferromagnetism in the Hubbard model. Prog. Theor. Phys. 99, 489–548 (1998)
Tasaki, H.: The Hubbard model: an introduction and selected rigorous results. J. Phys. Condens. Matter 10, 4353 (1998)
Lieb, E.H.: Two theorems on the Hubbard model. Phys. Rev. Lett. 62, 1201 (1989)
Nagaoka, Y.: Ferromagnetism in a narrow, almost half-filled s band. Phys. Rev. 147, 392 (1966)
Mielke, A.: Ferromagnetic ground states for the Hubbard model on line graphs. J. Phys. A 24, L73 (1991)
Mielke, A.: Ferromagnetism in the Hubbard model on line graphs and further considerations. J. Phys. A 24, 3311 (1991)
Mielke, A.: Exact ground states for the Hubbard model on the Kagome lattice. J. Phys. A 25, 4335 (1992)
Tasaki, H.: Ferromagnetism in the Hubbard models with degenerate single-electron ground states. Phys. Rev. Lett. 69, 1608 (1992)
Mielke, A.: Ferromagnetism in the Hubbard model and Hund’s rule. Phys. Lett. A 174, 443–448 (1993)
Mielke, A., Tasaki, H.: Ferromagnetism in the Hubbard model: examples from models with degenerate single-electron ground states. Commun. Math. Phys. 158, 341–371 (1993)
Tasaki, H.: Ferromagnetism in Hubbard models. Phys. Rev. Lett. 75, 4678 (1995)
Tasaki, H.: Ferromagnetism in the Hubbard model: a constructive approach. Commun. Math. Phys. 242, 445–472 (2003)
Tanaka, A., Ueda, H.: Stability of ferromagnetism in the Hubbard model on the kagome lattice. Phys. Rev. Lett. 90, 067204 (2003)
Lu, L.: The stability of ferromagnetism in the Hubbard model on two-dimensional line graphs. J. Phys. A 42, 265002 (2009)
Tanaka, A., Tasaki, H.: Metallic ferromagnetism in the Hubbard model: a rigorous example. Phys. Rev. Lett. 98, 116402 (2007)
Tanaka, A., Tasaki, H.: Metallic ferromagnetism supported by a single band in a multi-band Hubbard model. J. Stat. Phys. 163, 1049 (2016)
Acknowledgements
I would like to thank Hal Tasaki for valuable discussions. The present work was supported by JSPS Grants-in-Aid for Scientific Research No. 25400407.
Author information
Authors and Affiliations
Corresponding author
Appendix: Proof of Theorem 1 for \(s=0;\) Flat-Band Ferromagnetism
Appendix: Proof of Theorem 1 for \(s=0;\) Flat-Band Ferromagnetism
Throughout this section, we assume that \(s=0\) and the other parameters t and U take arbitrary positive values.
As we have seen in Sect. 3, the single-electron ground state energy is zero and \(|\mathcal {V}|\)-fold degenerate for \(s=0,\) and the single-electron ground states are given by \(a_{\alpha ,\sigma }^\dagger \varPhi _0\) with \(\alpha \in \mathcal {V}.\) Since both \(H_\mathrm {hop}\) with \(s=0\) and \(H_\mathrm {int}\) are positive semidefinite, we find that the energy eigenvalue of H is bounded from below by zero. Taking a state \(\varPhi _\mathrm {ferro}\) in (90) as a variational state, we conclude that the ground state energy of H for \(N_\mathrm {e}=|\mathcal {V}|\) is exactly zero.
To show the uniqueness of the ground state, we will use the following property which was pointed out by Mielke [10]. Consider Hubbard models with M-fold degenerate single-electron ground state energy. Then, we can construct a set of M single-electron ground states which satisfy the following condition. Let \(\varPhi _{1,\sigma }^{(i)}\) with \(i=1,\,2,\ldots ,M\) be linearly independent single-electron ground states with spin \(\sigma .\) For each i, there exists site \(x_i\) such that \(c_{x_i,\sigma }\varPhi _{1,\sigma }^{(i)} \ne 0 \) and \(c_{x_i,\sigma }\varPhi _{1,\sigma }^{(j)}=0\) for \(j\ne i.\)
In our model, we can construct single-electron ground states which possess the above property in the following manner. For each \(\alpha \in {\mathcal {V}},\) let us define a new fermion operator by
(recall that \(\mathcal {V}\) is periodic). Since \(\bar{a}_{\alpha ,\sigma }\) is a linear combination of \(a_{\beta ,\sigma }\) with \(\beta \in \mathcal {V},\) the single-electron states \(\bar{a}_{\alpha ,\sigma }^\dagger \varPhi _0\) apparently have energy 0. Furthermore, we have

These anticommutation relations imply that the single-electron states \(\bar{a}_{\alpha ,\sigma }^\dagger \varPhi _0\) with \(\alpha \in \mathcal {V}\) have the desired property. We note that (99) also implies the linear independence of these single-electron states.
Let us prove the uniqueness of the ground state by using \(\{\bar{a}_{\alpha ,\sigma }^\dagger \}_{\alpha \in {\mathcal {V}}}\) introduced as above. Let \(\varPhi _\mathrm {G}\) be a ground state, which must be a zero energy state for both \(H_\mathrm {hop}\) and \(H_\mathrm {int}.\) Since \(\varPhi _\mathrm {G}\) is a zero energy state for \(H_\mathrm {hop},\) we expand it as
with complex coefficients \(\varphi ^\prime (V_\uparrow ;\,V_\downarrow ).\) To be a zero energy state of the on-site interaction, \(\varPhi _\mathrm {G}\) in the form of (100) must further satisfy the condition \(c_{x,\downarrow }c_{x,\uparrow }\varPhi _\mathrm {G}=0\) for all x in \(\varLambda .\) We examine this condition for sites \(x=m(\alpha ,\,\alpha +\delta _\nu )\) with \(\alpha \in \mathcal {V}.\) Then, taking account of (99), we find that \(\varphi ^\prime (V_\uparrow ;\,V_\downarrow )\) is vanishing if \(V_\uparrow \cap V_\downarrow \ne \emptyset .\) A ground state \(\varPhi _\mathrm {G}\) is thus rewritten as
with new coefficients \(\varphi ^\prime (\{\sigma \}).\) Now we have expressed \(\varPhi _\mathrm {G}\) in the same fashion as in (94). Examining repeatedly the condition \(c_{x,\downarrow }c_{x,\uparrow }\varPhi _\mathrm {G}=0\) for sites \(x=m(\beta ,\,\beta +\delta _l)\) with \(l\ne \nu ,\) we obtain the same relation for \(\varphi ^\prime (\{\sigma \})\) as that in (96). Therefore, we conclude that the ground state is unique apart from the degeneracy due to the spin rotation symmetry. This completes the proof of Theorem 1 for \(s=0.\)
Rights and permissions
About this article
Cite this article
Tanaka, A. Ferromagnetism in the Hubbard Model with a Gapless Nearly-Flat Band. J Stat Phys 170, 399–420 (2018). https://doi.org/10.1007/s10955-017-1932-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-017-1932-6