Open Quantum Random Walks on the Half-Line: The Karlin–McGregor Formula, Path Counting and Foster’s Theorem

Abstract

In this work we consider open quantum random walks on the non-negative integers. By considering orthogonal matrix polynomials we are able to describe transition probability expressions for classes of walks via a matrix version of the Karlin–McGregor formula. We focus on absorbing boundary conditions and, for simpler classes of examples, we consider path counting and the corresponding combinatorial tools. A non-commutative version of the gambler’s ruin is studied by obtaining the probability of reaching a certain fortune and the mean time to reach a fortune or ruin in terms of generating functions. In the case of the Hadamard coin, a counting technique for boundary restricted paths in a lattice is also presented. We discuss an open quantum version of Foster’s Theorem for the expected return time together with applications.

Appendices

Appendix A: An Alternative Proof of Theorem 1.6

Before we present the proof we examine a class of examples which contains the splitting of the Hadamard coin studied later.

1.1 Appendix A.1: Class of Examples: L, R Row Matrices such that $L+R$ is Unitary

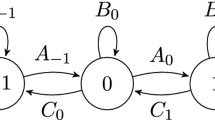
We briefly discuss some matrix computations, as this may be of independent interest, and a particular case will be needed for the analysis of Theorem 1.6 presented shortly. Let

$$\begin{aligned} R=\begin{bmatrix} a&b \\ 0&0 \end{bmatrix},\;\;\;L=\begin{bmatrix} 0&0 \\ c&d \end{bmatrix},\;\;\;\rho =\begin{bmatrix} \rho _{11}&\rho _{12} \\ \overline{\rho _{12}}&\rho _{22}\end{bmatrix}. \end{aligned}$$

(8.1)

If we let

$$\begin{aligned} f_L(\rho ) = c(\rho _{11}\overline{c}{+}\rho _{12}\overline{d}){+}d(\overline{\rho _{12}}\overline{c}+\rho _{22}\overline{d}),\;\;\;g_R(\rho )=a(\rho _{11}\overline{a}+\rho _{12}\overline{b})+b(\overline{\rho _{12}}\overline{a}+\rho _{22}\overline{b}),\nonumber \\ \end{aligned}$$

(8.2)

then routine calculations show that

$$\begin{aligned} L^n\rho L^{n*}=\begin{bmatrix} 0&0 \\ 0&|d|^{2n-2}f_L(\rho )\end{bmatrix},\;\;\;\;\;\; R^n\rho R^{n*}=\begin{bmatrix} |a|^{2n-2}g_R(\rho )&0 \\ 0&0\end{bmatrix},\;\;\;n=1,2,3,\dots \nonumber \\ \end{aligned}$$

(8.3)

Also,

$$\begin{aligned} LR\rho R^*L^*= & {} \begin{bmatrix} 0&0 \\ 0&|c|^{2}g_R(\rho )\end{bmatrix},\;\;\;RL\rho L^*R^*=\begin{bmatrix} |b|^{2}f_L(\rho )&0 \\ 0&0 \end{bmatrix}, \end{aligned}$$

(8.4)

$$\begin{aligned} L^nR\rho R^*L^{n*}= & {} \begin{bmatrix} 0&0 \\ 0&|d|^{2n-2}|c|^{2}g_R(\rho )\end{bmatrix},\;\;\;R^nL\rho L^*R^{n*}=\begin{bmatrix} |a|^{2n-2}|b|^{2}f_L(\rho )&0 \\ 0&0 \end{bmatrix}\qquad \end{aligned}$$

(8.5)

and

$$\begin{aligned} L^2R^2\rho R^{*2}L^{*2}=\begin{bmatrix} 0&0 \\ 0&|d|^{2}|c|^{2}|a|^2g_R(\rho ) \end{bmatrix},\;\;\;R^2L^2\rho L^{*2}R^{*2}=\begin{bmatrix} |a|^{2}|b|^{2}|d|^2f_L(\rho )&0 \\ 0&0 \end{bmatrix}\nonumber \\ \end{aligned}$$

(8.6)

Let $M=L^{l_k}R^{r_k}\cdots L^{l_{1}}R^{r_1}\rho R^{r_1*}L^{l_1*}\cdots R^{r_k*}L^{l_k*}$, $l_i,r_i=0,1,2,\dots$. Note that M is a composition of the maps $M_L(X)=LXL^*$ and $M_R(X)=RXR^*$. Then, by an induction argument we can show that the following occurs:

• (1) M is a multiple of $E_{11}$ whenever $l_k=0$ and $r_k>0$, that is, whenever $M=R\cdots \rho \cdots R^*$ and M is a multiple of $E_{22}$ whenever $l_k>0$, that is, whenever $M=L\cdots \rho \cdots L^*$. In words, the nonzero position is determined by the last conjugation performed on $\rho$.

• (2) In the nonzero entry of M, we have a term $f_L(\rho )$ whenever $r_1=0$ and $l_1>0$, that is, whenever $M=\cdots L\rho L^*\cdots$ and we have a term $g_R(\rho )$ whenever $r_1>0$, that is, whenever $M=\cdots R\rho R^*\cdots$. In words, a term $f_L$ or $g_R$ appears if the first conjugation performed on $\rho$ is $M_L$ or $M_R$, respectively.

• (3) In the nonzero entry of M, a $|c|^2$ contribution appears whenever a L-conjugation follows after a R-conjugation. A $|d|^2$ contribution appears after one such conjugation change (or in the case a R-conjugation never occurs). Similarly, a $|b|^2$ contribution appears whenever a R-conjugation follows after a L-conjugation; an $|a|^2$ contribution appears after one such conjugation change (or in the case a L-conjugation never occurs).

Example 8.1

Let $M=K\rho K^*$, where $K=K_{13}\cdots K_{1}=RRRRLLLRRLRLR$. Then $K_1=R$ implies a contribution $g_R(\rho )$ and the remaining entries $K_{13}\cdots K_{2}$ give the contributions

$$\begin{aligned} K_{13}\cdots K_2= & {} RRRRLLLRRLRL\;\Longrightarrow \; |aaabddcabcbc|^2 \end{aligned}$$

(8.7)

$$\begin{aligned} \Longrightarrow \; M= & {} \begin{bmatrix} |aaabddcabcbc|^2g_R(\rho )&0 \\ 0&0 \end{bmatrix}=\begin{bmatrix} |a^4|^2|b^3|^2|c^3|^2|d^2|^2g_R(\rho )&0 \\ 0&0 \end{bmatrix}.\qquad \end{aligned}$$

(8.8)

$\square$

Example 8.2

This particular example will be the one appearing in Theorem 1.6. For the Hadamard matrix, $|a|^2=|b|^2=|c|^2=|d|^2=1/2$, and

$$\begin{aligned} g_R(\rho )=\frac{1}{2}(1+2Re(\rho _{12})),\;\;\;f_L(\rho )=\frac{1}{2}(1-2Re(\rho _{12})). \end{aligned}$$

(8.9)

Also one can show that if $C=C_n\cdots C_1$, where each $C_i\in \{L,R\}$ then

$$\begin{aligned} \mathrm {Tr}(C\rho C^*)=\left\{ \begin{array}{rl} \frac{1}{2^n}(1+2Re(\rho _{12})), &{} \text { if } C_1=R,\\ \frac{1}{2^n}(1-2Re(\rho _{12})), &{} \text { if } C_1=L. \end{array} \right. \end{aligned}$$

(8.10)

$\square$

1.2 Counting Boundary Restricted Lattice Paths

In this section we follow Kobayashi et al. [24]. Define the Fibonacci polynomial by

$$\begin{aligned} f(z,t)=\sum _{i=0}^{\lfloor \frac{t}{2} \rfloor } (-1)^i\left( {\begin{array}{c}t-i\\ i\end{array}}\right) z^{2i}. \end{aligned}$$

(8.11)

It holds that $f(\sqrt{-1},t)$, $t=0,1,2,\dots$ is the Fibonacci sequence and it has been shown that, for $t\ge 1$,

$$\begin{aligned} f(z,t)=\prod _{k=1}^t\Big [1-2z\cos \Big (\frac{k\pi }{t+1}\Big )\Big ]. \end{aligned}$$

(8.12)

By [24], the generator B(z, s, t) that gives the number of paths restricted between the upper boundary s and the lower boundary $-t$ starting from the origin 0 and ending at the upper boundary s, $s,t\ge 0$ (see the figure below) is given by

$$\begin{aligned} B(z,s,t)=z^s\frac{f(z,t)}{f(z,t+s+1)}, \end{aligned}$$

(8.13)

see [24]. This counts the number of paths in a boundary restricted Pascal triangle. This can be used to count the desired paths, and also to distinguish between paths that have as first step a move up or down. As an example, consider all lattice paths beginning at 0, restricted to heights $-3$ and 1. We have

$$\begin{aligned} B(z,1,3)= & {} z+2z^3+5z^5+14z^7+41z^9+122z^{11}+365z^{13}+1094z^{15}\nonumber \\&+3281z^{17}+9842z^{19}+O(z^{21}), \end{aligned}$$

(8.14)

so the number of paths of length k with such restrictions is given by $[z^k]B(z,1,3)$, the coefficient of $z^k$ in the series expansion of B(z, 1, 3). Due to the parity of the boundaries in this case, all paths are of odd length, as it is clear from the above series. In the next section we will make use of this generating function in order to count the ways a gambler will first reach a goal or ruin, noting that paths such as the ones above of length k will be associated to reaching a goal/ruin in $k+1$ steps (Fig. 4).

Fig. 4

We illustrate 2 of the 5 lattice paths of length 5, bounded below by $-t=-3$, above by $s=1$, beginning at height 0 and finishing at the upper bound 1. The number of such paths is counted by the coefficient of $z^5$ of the generating function B(z, 1, 3). It is also drawn one of the 14 lattice paths of length 7, bounded below by $-t=-3$, above by $s=1$, beginning at height 0 and finishing at the upper bound 1

Remark 8.3

We recall that the number of paths from i to j of length n in any given graph equals the entry (i, j) of the n-th power of the associated adjacency matrix (the matrix of 0’s and 1’s such that an entry equals 1 if, and only if, there is an edge connecting the vertices) so, in principle, this can also be used to study our problem.

1.3 Gambler’s Ruin: Hadamard OQW Version

We remark that this discussion is different from the one made in [28], where the authors studied only the probability that the gambler would go bankrupt, and this being only in the case of OQW where transition matrices admit simultaneous diagonalization. In this section we consider a splitting of the Hadamard matrix. We recall that, by Example 8.2, if

$$\begin{aligned} R=\frac{1}{\sqrt{2}}\begin{bmatrix} 1&1 \\ 0&0\end{bmatrix},\;\;\;L=\frac{1}{\sqrt{2}}\begin{bmatrix} 0&0 \\ 1&-1\end{bmatrix}, \end{aligned}$$

(8.15)

then the value of $\mathrm {Tr}(C\rho C^*)$, C being a product of L’s and R’s, is essentially determined by the first matrix (from right to left) in such product.

Let $p=p_{k\rightarrow M}$ be the probability that the gambler reaches the fortune of M before ruin, given that he starts with k dollars, $0<k<M$. Let $\pi _{j}([1,M-1];k)$ denote the set of matrix products associated to all paths between 1 and $M-1$ (inclusive) of length j, beginning at height k and reaching height $M-1$ at the last step. In symbols,

$$\begin{aligned} \pi _j([1,M-1];k) = \left\{ B^{\epsilon _1} \cdots B^{\epsilon _j} \; \left| \begin{array}{l} \epsilon _1,\ldots ,\epsilon _j \in \{-1,+1\}, \\ \epsilon _1 + \cdots + \epsilon _j = M+1-k, \\ -k< \epsilon _1 + \cdots + \epsilon _i < M+1-k \text{ for } i=1,\ldots ,j-1 \end{array} \right. \right\} ,\nonumber \\ \end{aligned}$$

(8.16)

with $B^{-1} :=L$ and $B^{+1} := R.$ Let $\pi _{j;d}([1,M-1];k)$ and $\pi _{j;u}([1,M-1];k)$ denote the set of matrix products in $\pi _{j}([1,M-1];k)$ associated to a path for which the first move is down (a player loses a bet) and up (the player wins a bet), respectively. Then

$$\begin{aligned} p(\rho )= & {} p_{k\rightarrow M}(\rho )=\sum _{j=1}^\infty \sum _{C\in \pi _{j}([1,M-1];k)} \mathrm {Tr}\left( B_{M-1}^MC\rho C^*B_{M-1}^{M*}\right) \nonumber \\= & {} \sum _{j=1}^\infty \Big [\sum _{C\in \pi _{j;d}([1,M-1];k)} \mathrm {Tr}\left( B_{M-1}^MC\rho C^*B_{M-1}^{M*}\right) \nonumber \\&+\sum _{C\in \pi _{j;u}([1,M-1];k)} \mathrm {Tr}\left( B_{M-1}^MC\rho C^*B_{M-1}^{M*}\right) \Big ]\nonumber \\= & {} \sum _{j=1}^\infty \Big [d(j)\frac{1}{2^{j+1}}(1-2Re(\rho _{12}))+u(j)\frac{1}{2^{j+1}}(1+2Re(\rho _{12}))\Big ], \end{aligned}$$

(8.17)

where $d(j)=d(j;k;M)$ and $u(j)=u(j;k;M)$ denote the number of elements in $\pi _{j;d}([1,M-1];k)$ and $\pi _{j;u}([1,M-1];k)$, respectively.

We move from the gambler’s ruin notation to Kobayashi’s notation in the following way. We consider walks between $s=M-1-k$ and $-t=1-k$. For instance, if $M=6$ and $k=3$ we are considering paths between 1 and 5 which, after the translation $k\rightarrow 0$ gives us $s=2$ and $-t=1-3=-2$.

If ${\mathcal {C}}_{0,(s,t)}^n$ denotes the paths of length n between $-t$ and s, beginning at 0, ending at s, then we can calculate ${\mathcal {C}}_{0,(s,t);u}^n$ and ${\mathcal {C}}_{0,(s,t);d}^n$, the paths in ${\mathcal {C}}_{0,(s,t)}^n$ such that the first move is up (resp. down), and these are given by

$$\begin{aligned} {\mathcal {C}}_{0,(s,t);u}^n={\mathcal {C}}_{1,(s,t)}^{n-1},\;\;\;{\mathcal {C}}_{0,(s,t);d}^n={\mathcal {C}}_{-1,(s,t)}^{n-1}. \end{aligned}$$

(8.18)

By this fact, we have that

$$\begin{aligned} u(j)= & {} {\mathcal {C}}_{0,(s,t);u}^j={\mathcal {C}}_{0,(s-1,t+1)}^{j-1}=[z^{j-1}]B(z,s-1,t+1). \end{aligned}$$

(8.19)

$$\begin{aligned} d(j)= & {} {\mathcal {C}}_{0,(M-k,-(1-k));d}^j={\mathcal {C}}_{0,(s+1,t-1)}^{j-1}=[z^{j-1}]B(z,s+1,t-1). \end{aligned}$$

(8.20)

Combining (8.17) with (8.19) and (8.20) gives us the probability expression

$$\begin{aligned} p_{k\rightarrow M}(\rho )= & {} \sum _{j=1}^\infty \frac{1}{2^{j+1}}\Big [[z^{j-1}]B(z,s+1,t-1)(1-2Re(\rho _{12}))\nonumber \\&+[z^{j-1}]B(z,s-1,t+1)(1+2Re(\rho _{12}))\Big ]. \end{aligned}$$

(8.21)

Assuming the Hadamard pieces described above and an initial density $\rho$, suppose we wish to calculate the probability of ever reaching a fortune of $M=6$, assuming that the gambler begins with an initial fortune of 1, 2, 3, with the remaining cases being done in an analogous way.

Case $k=1$ : if $M=6$ and $k=1$ we consider paths between 1 and 5 which, after the translation $k\rightarrow 0$ gives us $s=M-1-k=4$ and $-t=1-k=1-1=0$, that is, paths between 0 and 4. Then

$$\begin{aligned} u(j)=[z^{j-1}]B(z,s-1,t+1)=[z^{j-1}]B(z,3,1), \end{aligned}$$

(8.22)

and note that $d(j)=0$ since, in this situation, if the player loses its first play then he goes bankrupt. Then, for instance,

$$\begin{aligned} u(4)=[z^3]B(z,3,1)=1,\;\;\;u(6)=[z^5]B(z,3,1)=4, \end{aligned}$$

(8.23)

and also as a simple path counting confirms. Now to every path counted by u(2j) we have a probability of $1/2^{2j+1}(1+2Re(\rho _{12}))$, noting that we need 2j steps to reach 5 and one more to reach 6 in the final step. Therefore,

$$\begin{aligned} p_{1\rightarrow 6}= & {} \sum _{j=1}^\infty \frac{u(2j)}{2^{2j+1}}(1+2Re(\rho _{12}))=\sum _{j=1}^\infty \frac{[z^{2j-1}]B(z,3,1)}{2^{2j+1}}(1+2Re(\rho _{12}))\nonumber \\= & {} \frac{1}{6}+\frac{1}{3}Re(\rho _{12}). \end{aligned}$$

(8.24)

This should be compared with the classical calculation: $p_{1\rightarrow 6}=k/M=1/6$.

Now we turn to the problem of calculating $E_1(\tau )$ (i.e., we begin at $X_0=1$). In this example $\tau$ is the time required to be absorbed at one of 0 or 6. We need to calculate $p_{1\rightarrow 6}$ and $p_{1\rightarrow 0}$ in $2k+1$ steps. From the above we see that

$$\begin{aligned} p_{1\rightarrow 6}(\rho ;2j+1)=\frac{[z^{2j-1}]B(z,3,1)}{2^{2j+1}}(1+2Re(\rho _{12})). \end{aligned}$$

(8.25)

As for $p_{1\rightarrow 0}$, we note that if we reflect the plane with respect to the x-axis, then the paths starting at 0 and ending at $-t$, bounded below by $-t$ and above by s become the paths starting at 0, bounded below by $-s$ and above by t, and this computation can be made by Kobayashi’s generating function. Therefore $p_{1\rightarrow 0}$ can be calculated as the calculation of all the ways of reaching t, with lower bound equal to $-s$ and upper bound equal to t, except that the probabilities of going up or down have to be exchanged to account for the reflection on the x-axis. For the case $M=6$, $k=1$ this calculation gives $-t=-4$, $s=0$ so $p_{1\rightarrow 0}(\rho ;1)=\frac{1}{2}(1-2Re(\rho _{12}))$ and

$$\begin{aligned} p_{1\rightarrow 0}(\rho ;2j+1)=\frac{[z^{2j}]B(z,0,4)}{2^{2j+1}}(1+2Re(\rho _{12})),\;\;\;j=1,2,\dots \end{aligned}$$

(8.26)

Therefore,

$$\begin{aligned} E_1(\tau )= & {} p_1(\tau =1)+\sum _{j=1}^\infty (2j+1)p_1(\tau =2j+1)\nonumber \\= & {} \frac{1}{2}(1-2Re(\rho _{12}))+\sum _{j=1}^\infty (2j+1)[p_{1\rightarrow 0}(\rho ;2j+1)+p_{1\rightarrow 6}(\rho ;2j+1)]\nonumber \\= & {} \frac{1}{2}(1-2Re(\rho _{12}))+\sum _{j=1}^\infty \frac{(2j+1)}{2^{2j+1}}\Big [[z^{2j}]B(z,0,4)(1+2Re(\rho _{12}))\nonumber \\&+\,[z^{2j-1}]B(z,3,1)(1+2Re(\rho _{12})) \Big ]=5+8Re(\rho _{12}). \end{aligned}$$

(8.27)

This should be compared with the classical calculation, where $E_1(\tau )=k(M-k)=1(6-1)=5$.

Case $k=2$ : if $M=6$ and $k=2$ we consider paths between 1 and 5 which, after the translation $k\rightarrow 0$ gives us $s=M-1-k=3$ and $-t=1-k=1-2=-1$, that is, paths between $-1$ and 3. Then

$$\begin{aligned} u(j)= & {} [z^{j-1}]B(z,s-1,t+1)=[z^{j-1}]B(z,2,2). \end{aligned}$$

(8.28)

$$\begin{aligned} d(j)= & {} [z^{j-1}]B(z,s+1,t-1)=[z^{j-1}]B(z,4,0). \end{aligned}$$

(8.29)

Now to every path counted by $u(2j-1)$ we have a probability of $1/2^{2j}(1+2Re(\rho _{12}))$, noting that we need $2j-1$ steps to reach 5 and one more to reach 6 in the final step. The reasoning for $d(2j-1)$ is the same except that the probability equals $1/2^{2j+1}(1-2Re(\rho _{12}))$. Then

$$\begin{aligned} p_{2\rightarrow 6}= & {} \sum _{j=1}^\infty \Big [\frac{u(2j-1)}{2^{2j}}(1+2Re(\rho _{12}))+\frac{d(2j-1)}{2^{2j}}(1-2Re(\rho _{12}))\Big ]\nonumber \\= & {} \sum _{j=1}^\infty \frac{1}{2^{2j}}\Big [[z^{2j-2}]B(z,2,2)(1+2Re(\rho _{12}))+[z^{2j-2}]B(z,4,0)(1-2Re(\rho _{12}))\Big ]\nonumber \\= & {} \frac{1}{3}+\frac{1}{3}Re(\rho _{12}). \end{aligned}$$

(8.30)

This should be compared with the classical calculation: $p_{2\rightarrow 6}=k/M=1/3$.

Now we calculate $E_2(\tau )$ (i.e., we begin at $X_0=2$). Recall $\tau$ is the time required to be absorbed at one of 0 or 6. We need to calculate $p_{2\rightarrow 6}$ and $p_{2\rightarrow 0}$ in 2k steps. The former has been calculated already. Since $M=6$, $k=2$ this calculation becomes

$$\begin{aligned} p_{2\rightarrow 6}(\rho ;2j){=}\frac{1}{2^{2j}}\Big [[z^{2j-2}]B(z,2,2)(1{+}2Re(\rho _{12}))+[z^{2j-2}]B(z,4,0)(1-2Re(\rho _{12}))\Big ].\nonumber \\ \end{aligned}$$

(8.31)

For $p_{2\rightarrow 0}(\rho ;2j)$, we borrow the expressions for $p_{4\rightarrow 6}$ but with probabilities of going up and down interchanged, as remarked above. That is: if $M=6$ and $k=4$ we consider paths between 1 and 5 which, after the translation $k\rightarrow 0$ gives us $s=M-1-k=1$ and $-t=1-k=1-4=-3$, that is, paths between $-3$ and 1. Then

$$\begin{aligned} u(j)= & {} [z^{j-1}]B(z,s-1,t+1)=[z^{j-1}]B(z,0,4). \end{aligned}$$

(8.32)

$$\begin{aligned} d(j)= & {} [z^{j-1}]B(z,s+1,t-1)=[z^{j-1}]B(z,2,2). \end{aligned}$$

(8.33)

Hence,

$$\begin{aligned} p_{2\rightarrow 0}(\rho ;2j)= & {} \frac{u(2j-1)}{2^{2j}}(1-2Re(\rho _{12}))+\frac{d(2j-1)}{2^{2j}}(1+2Re(\rho _{12}))\nonumber \\= & {} \frac{1}{2^{2j}}\Big [[z^{2j-2}]B(z,0,4)(1{-}2Re(\rho _{12}))+[z^{2j-2}]B(z,2,2)(1{+}2Re(\rho _{12}))\Big ].\nonumber \\ \end{aligned}$$

(8.34)

Therefore $p_2(\tau =2)=\frac{1}{4}(1-2Re(\rho _{12}))$ and

$$\begin{aligned} p_2(\tau =2j)= & {} p_{2\rightarrow 6}(\rho ;2j)+p_{2\rightarrow 0}(\rho ;2j)\nonumber \\= & {} \frac{1}{2^{2j}}\Big [[z^{2j-2}]B(z,2,2)(1+2Re(\rho _{12}))+[z^{2j-2}]B(z,4,0)(1-2Re(\rho _{12}))\Big ]\nonumber \\&+\,\frac{1}{2^{2j}}\Big [[z^{2j-2}]B(z,0,4)(1{-}2Re(\rho _{12})){+}[z^{2j-2}]B(z,2,2)(1{+}2Re(\rho _{12}))\Big ].\nonumber \\ \end{aligned}$$

(8.35)

Hence

$$\begin{aligned} E_2(\tau )= & {} \sum _{j=1}^\infty \frac{2j}{2^{2j}}\Big [2[z^{2j-2}]B(z,2,2)(1+2Re(\rho _{12}))+[z^{2j-2}]B(z,4,0)(1-2Re(\rho _{12}))\nonumber \\&+\,[z^{2j-2}]B(z,0,4)(1{-}2Re(\rho _{12}))\Big ]=8{+}4Re(\rho _{12}). \end{aligned}$$

(8.36)

This should be compared with the classical calculation, where $E_2(\tau )=k(M-k)=2(6-2)=8$.

Case $k=3$ : if $M=6$ and $k=3$ we consider paths between 1 and 5 which, after the translation $k\rightarrow 0$ gives us $s=M-1-k=2$, $-t=1-k=1-3=-2$, and

$$\begin{aligned} u(j)=[z^{j-1}]B(z,1,3),\;\;\;d(j)=[z^{j-1}]B(z,3,1). \end{aligned}$$

(8.37)

Now we can calculate $p_{3\rightarrow 6}$. Note that since $6-3=3$ is odd, we only need to examine odd coefficients of B(z, 1, 3) and B(z, 3, 1) and for this we calculate d(2j) and u(2j), $j=1,2,\dots$. We have

$$\begin{aligned} p_{3\rightarrow 6}(\rho )=\sum _{j=1}^\infty \Big [d(2j)\frac{1}{2^{2j+1}}(1-2Re(\rho _{12}))+u(2j)\frac{1}{2^{2k+1}}(1+2Re(\rho _{12}))\Big ]\quad \end{aligned}$$

(8.38)

(recall that $d(j)=d(j;k;M)$ and $u(j)=u(j;k;M)$). Therefore,

$$\begin{aligned} p_{3\rightarrow 6}(\rho )= & {} \sum _{j=1}^\infty \Big [[z^{2j-1}]B(z,3,1)\frac{1}{2^{2j+1}}(1-2Re(\rho _{12}))\nonumber \\&+\,[z^{2j-1}]B(z,1,3)\frac{1}{2^{2k+1}}(1+2Re(\rho _{12}))\Big ]=\frac{1}{2}+\frac{1}{3}Re(\rho _{12}). \end{aligned}$$

(8.39)

This should be compared with the classical calculation: $p_{3\rightarrow 6}=k/M=1/2$. Now we calculate $E_3(\tau )$ (i.e., we begin at $X_0=3$). We need to calculate $p_{3\rightarrow 6}$ and $p_{3\rightarrow 0}$ in $2k+1$ steps. The former has been calculated already. For the case $M=6$, $k=3$ this calculation becomes

$$\begin{aligned} p_{3\rightarrow 6}(\rho ;2j+1)= & {} [z^{2j-1}]B(z,3,1)\frac{1}{2^{2j+1}}(1-2Re(\rho _{12}))\nonumber \\&+\,[z^{2j-1}]B(z,1,3)\frac{1}{2^{2j+1}}(1+2Re(\rho _{12})). \end{aligned}$$

(8.40)

$$\begin{aligned} p_{3\rightarrow 0}(\rho ;2j+1)= & {} [z^{2j-1}]B(z,3,1)\frac{1}{2^{2j+1}}(1+2Re(\rho _{12}))\nonumber \\&+\,[z^{2j-1}]B(z,1,3)\frac{1}{2^{2j+1}}(1-2Re(\rho _{12})). \end{aligned}$$

(8.41)

Therefore, $p_3(\tau =1)=0$ and

$$\begin{aligned} p_3(\tau =2j+1)= & {} p_{3\rightarrow 6}(\rho ;2j+1)+p_{3\rightarrow 0}(\rho ;2j+1)=[z^{2j-1}]B(z,3,1)\frac{1}{2^{2j}}\nonumber \\&+\,[z^{2j-1}]B(z,1,3)\frac{1}{2^{2j}}\nonumber \\= & {} [z^{2j}]B(z,2,2)\frac{1}{2^{2j}},\;\;\;j=1,2,\dots \end{aligned}$$

(8.42)

$$\begin{aligned} \Longrightarrow \; E_3(\tau )= & {} \sum _j j p_3(\tau =j)=\sum _{k=1}^\infty (2j+1)[z^{2j}]B(z,2,2)\frac{1}{2^{2j}}=9. \end{aligned}$$

(8.43)

This equals the classical calculation: $E_3(\tau )=k(M-k)=3(6-3)=9$.

1.4 Tables

We show particular examples of the expressions

$$\begin{aligned} p_{k\rightarrow M}(\rho )=\frac{k}{M}+\frac{2}{M}Re(\rho _{12}),\;\;\;\;\;\; E_k(\tau )=k(M-k)+(2M-4k)Re(\rho _{12}), \end{aligned}$$

(8.44)

for $M=3,4,5,6,7$. The case $M=6$ is the one shown above, and we omit the calculations for the remaining ones, as these are analogous. We remark that these expressions can also be obtained by the first visit functions described by Theorem 1.7 (Tables 1, 2, 3, 4, 5).

Table 1 Statistics for $M=3$, which corresponds to a gambler with an initial fortune k equal to 1 or 2

Table 2 Statistics for $M=4$, which corresponds to a gambler with an initial fortune k between 1 and 3

Table 3 $M=5$, k between 1 and 4

Table 4 $M=6$, k between 1 and 5

Table 5 $M=7$, k between 1 and 6

Appendix B: Combinatorial Proofs

Proof of Eq. (4.3)

First of all, we will see that if $n+i+j$ is odd, the expression vanishes. The direct walk between vertices i and j have $j-i$ steps. Notice that the number of steps of all walks between the same vertices must have the same parity. Then, n and $j-i$ have the same parity, and therefore their difference is even, i.e. $n+i-j$ must be even. As 2j is even too, we have that $n+i-j$ is even iff $n+i+j$ is even. Then, if $n+i+j$ is odd, the numbers n and $j-i$ does not have the same parity, and then N(i, j, n) vanishes.

Now, let $n+i-j$ be even. Let ${\mathcal {N}}(i,j,n)$ the set of all $n-$step walks starting at vertex $|i\rangle$ and finishing at vertex $|j\rangle$ on the half-line. Then, $N(i,j,n)=|{\mathcal {N}}(i,j,n)|.$ Let $\mathcal {{\tilde{N}}}(i,j,n)$ the set of all $n-$step walks starting at vertex $|i\rangle$ and finishing at vertex $|j\rangle$ on the entire line. We have:

$$\begin{aligned} |\mathcal {{\tilde{N}}}(i,j,n)| = \left( \begin{array}{c} n\\ \frac{n-(j-i)}{2}\\ \end{array}\right) = \left( \begin{array}{c} n\\ \frac{n+i-j}{2}\\ \end{array}\right) . \end{aligned}$$

(9.1)

By the reflection principle we have that the set difference $\mathcal {{\tilde{N}}}(i,j,n) \backslash {\mathcal {N}}(i,j,n)$ corresponds to set of all $n-$step walks starting at vertex $(-i-2)$ (because we are reflecting with respect to $-1$ the initial part of the walk until the first passage to the vertex $-1$) and finishing at vertex j on the entire line. Then, we have that

$$\begin{aligned} |\mathcal {{\tilde{N}}}(i,j,n) \backslash {\mathcal {N}}(i,j,n)| = \left( \begin{array}{c} n\\ \frac{n-(j-(-i-2))}{2}\\ \end{array}\right) = \left( \begin{array}{c} n\\ \frac{n+i+j}{2}+1\\ \end{array}\right) . \end{aligned}$$

(9.2)

Combining the two previous equations, we have:

$$\begin{aligned} N(i,j,n) = \left( \begin{array}{c} n\\ \frac{n+i-j}{2}\\ \end{array}\right) - \left( \begin{array}{c} n\\ \frac{n+i+j}{2}+1\\ \end{array}\right) . \end{aligned}$$

(9.3)

$\square$

Proof of Eqs. (4.14), (4.15) and (4.16)

We prove Eq. (4.14) by induction on k. For $k = 1,$ we have:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{1}{\pi }\int _{-\pi }^{0}\cos ^{2}\theta \,d\theta =\frac{1}{\pi }\frac{\pi }{2} = \frac{1}{2}, \\ \frac{(2k)!}{2^{2k}k!k!} = \frac{1}{2}. \end{array}\right. } \end{aligned}$$

(9.4)

Let $k>1.$ Suppose Eq. (4.14) is true for k. We have:

$$\begin{aligned} \int _{-\pi }^{0}\cos ^{2k}\theta \,d\theta= & {} \int _{-\pi }^{0}\cos ^{2k-1}\theta \cos \theta \,d\theta = \left[ \cos ^{2k-1}\theta \cos \theta \right] _{-\pi }^{0}\nonumber \\&-\int _{-\pi }^{0}(2k-1)\cos ^{2k-2}\theta (-\sin \theta )\sin \theta \,d\theta \nonumber \\= & {} (2k-1)\int _{-\pi }^{0}\cos ^{2k-2}\theta (1-\cos ^2\theta ) \,d\theta \nonumber \\= & {} (2k-1)\int _{-\pi }^{0}\cos ^{2(k-1)}\theta \,d\theta - (2k-1)\int _{-\pi }^{0}\cos ^{2k}\theta \,d\theta . \end{aligned}$$

(9.5)

From

$$\begin{aligned} \int _{-\pi }^{0}\cos ^{2k}\theta \,d\theta = (2k-1)\int _{-\pi }^{0}\cos ^{2(k-1)}\theta \,d\theta - (2k-1)\int _{-\pi }^{0}\cos ^{2k}\theta \,d\theta , \end{aligned}$$

(9.6)

we have:

$$\begin{aligned} \frac{1}{\pi }\int _{-\pi }^{0}\cos ^{2k}\theta \,d\theta = \frac{2k-1}{2k}\cdot \frac{1}{\pi }\int _{-\pi }^{0}\cos ^{2(k-1)}\theta \,d\theta . \end{aligned}$$

(9.7)

By induction hypothesis,

$$\begin{aligned} \frac{1}{\pi }\int _{-\pi }^{0}\cos ^{2k}\theta \,d\theta = \frac{2k-1}{2k}\frac{(2(k-1))!}{2^{2(k-1)}(k-1)!(k-1)!} = \frac{(2k-1)!}{2^{2k-1}k!(k-1)!} = \frac{(2k)!}{2^{2k}k!k!}.\qquad \end{aligned}$$

(9.8)

For the first part of Eq. (4.15), we have:

$$\begin{aligned} \frac{1}{\pi } \int _{-\pi }^{0} \cos ^{2k}\theta \sin ^2\theta \,d\theta= & {} \frac{1}{\pi } \int _{-\pi }^{0} \cos ^{2k}\theta \,d\theta - \frac{1}{\pi } \int _{-\pi }^{0} \cos ^{2(k+1)}\theta \,d\theta , \qquad \end{aligned}$$

(9.9)

$$\begin{aligned} \frac{(2k)!}{2^{2k}k!k!}- \frac{(2k+2)!}{2^{2k+2}(k+1)!(k+1)!}= & {} \frac{(2k)!2^2(k+1)^2-(2k+2)!}{2^{2k+2}(k+1)!(k+1)!}\nonumber \\= & {} \frac{(2k)!(2k+2)}{2\cdot 2^{2k+1}(k+1)!(k+1)!}\nonumber \\= & {} \frac{(2k)!(k+1)}{2^{2k+1}(k+1)!(k+1)!} \nonumber \\= & {} \frac{1}{2^{2k+1}} \frac{(2k)!}{k!(k+1)!} = \frac{1}{2^{2k+1}} |{\mathcal {C}}_k|. \end{aligned}$$

(9.10)

For the second part, with $\alpha = \theta + \pi /2$ we have:

$$\begin{aligned} \int _{-\pi }^{0} \cos ^{2k+1}\theta \sin ^2\theta \,d\theta= & {} \int _{-\pi /2}^{\pi /2} \cos ^{2k+1}(\alpha -\pi /2) \sin ^2(\alpha -\pi /2) \,d\alpha \nonumber \\= & {} \int _{-\pi /2}^{\pi /2} \sin ^{2k+1}\alpha (-\cos \alpha )^2 \,d\alpha =\int _{-\pi /2}^{\pi /2} \sin ^{2k+1}\alpha \cos ^2\alpha \,d\alpha .\nonumber \\ \end{aligned}$$

(9.11)

Let $\phi (\alpha ) :=\sin ^{2k+1}\alpha \cos ^2\alpha$. We have

$$\begin{aligned} \phi (-\alpha ) =(\sin (-\alpha )) ^{2k+1}(\cos (-\alpha ))^2 = (-\sin \alpha ) ^{2k+1}(\cos \alpha )^2 = -\sin ^{2k+1}\alpha \cos ^2\alpha ,\nonumber \\ \end{aligned}$$

(9.12)

i.e., $\phi$ is an odd function. Therefore,

$$\begin{aligned} \int _{-\pi /2}^{\pi /2} \sin ^{2k+1}\alpha \cos ^2\alpha \,d\alpha =\int _{-\pi /2}^{\pi /2} \phi (\alpha ) \,d\alpha =0. \end{aligned}$$

(9.13)

Now, we calculate $\frac{1}{2\pi }A^{-k-1}E_i\int _{-2d_i}^{2d_i}x^k\sqrt{4 - (xd_i^{-1})^2}dx$. Let $x = 2d_i \cos \theta$, then:

$$\begin{aligned}&\frac{1}{2\pi }A^{-k-1}E_i\int _{-2d_i}^{2d_i}x^k\sqrt{4 - (xd_i^{-1})^2}dx \nonumber \\&\quad = \frac{1}{2\pi }d_i^{-k-1}E_i\int _{-\pi }^{0}(2d_i\cos \theta )^k\sqrt{4 - 4\cos ^2\theta }(-2d_i\sin \theta )d\theta \nonumber \\&\quad =\frac{1}{2\pi }2^{k+1}E_i\int _{-\pi }^{0}(\cos \theta )^k2\sqrt{1 - \cos ^2\theta }(-\sin \theta )d\theta \nonumber \\&\quad =\frac{1}{\pi }2^{k+1}E_i\int _{-\pi }^{0}(\cos \theta )^k\left| \sin \theta \right| (-\sin \theta )d\theta \nonumber \\&\quad =\frac{1}{\pi }2^{k+1}E_i\int _{-\pi }^{0}(\cos \theta )^k\sin ^2\theta d\theta . \end{aligned}$$

(9.14)

By Eq. (4.15), we have

$$\begin{aligned} \frac{1}{\pi }2^{k+1}E_i\int _{-\pi }^{0}(\cos \theta )^k\sin ^2\theta d\theta = {\left\{ \begin{array}{ll}E_i|{\mathcal {C}}_{k/2}|, \text{ if } {} \textit{k} \text{ is } \text{ even, }\\ \quad 0 \qquad \text{ otherwise. } \\ \end{array}\right. } \end{aligned}$$

(9.15)

Then,

$$\begin{aligned} \frac{1}{2\pi } A^{-k-1} \int _{{\mathbb {R}}} x^{k}(D^+(x))^{1/2}dx= & {} \frac{1}{2\pi } A^{-k-1}E_1\int _{-2d_1}^{2d_2}x^k\sqrt{4 - \left( xd_1^{-1}\right) ^2}dx \nonumber \\&+ \frac{1}{2\pi } A^{-k-1}E_2\int _{-2d_2}^{2d_2}x^k\sqrt{4 - \left( xd_2^{-1}\right) ^2}dx\nonumber \\= & {} E_1|{\mathcal {C}}_{k/2}|+E_2|{\mathcal {C}}_{k/2}| = I|{\mathcal {C}}_{k/2}|, \end{aligned}$$

(9.16)

if k is even, otherwise it vanishes. This proves Eq. (4.16). $\square$

Proof of Proposition 4.2:

Let $P_n$ be a sequence such as required. Isolating $P_{n+1},$ we have an equation equivalent to (4.10):

$$\begin{aligned} {\left\{ \begin{array}{ll} P_{0}(x) = I, \; P_{1}(x) = xA^{-1}-A^{-1}B, \\ P_{n+1}(x) = P_1(x)P_{n}(x) - P_{n-1}(x), \qquad n \ge 1. \end{array}\right. } \end{aligned}$$

(9.17)

We will prove Eq. (4.11), that is,

$$\begin{aligned} P_n = \sum _{j=0}^{\lfloor \frac{n}{2} \rfloor } (-1)^j \left( \begin{array}{c} n-j\\ j\\ \end{array}\right) P_1^{n-2j}, \quad n\ge 0, \end{aligned}$$

by induction on n. The case $n=0$ follows by $\left( \begin{array}{c} 0\\ 0\\ \end{array}\right) = 1,$ and $\left( \begin{array}{c} n\\ k\\ \end{array}\right) = 0$ for all $k<0.$ The case $n=1$ follows, since $\left( \begin{array}{c} 1\\ 0\\ \end{array}\right) = 1.$ Now let $n\ge 1$ and suppose that (4.11) is true for $k\in \{0, \ldots , n\}$. We prove that (4.11) is also true for $n+1$. By (9.17), we have: $P_{n+1} = P_1P_{n} - P_{n-1}.$ By the induction hypothesis, we have:

$$\begin{aligned} P_1P_{n} = \sum _{j=0}^{\lfloor \frac{n}{2} \rfloor } (-1)^j \left( \begin{array}{c} n-j\\ j\\ \end{array}\right) P_1^{n+1-2j}= \sum _{j=0}^{\lfloor \frac{n+1}{2} \rfloor } (-1)^j \left( \begin{array}{c} n-j\\ j\\ \end{array}\right) P_1^{n+1-2j}, \end{aligned}$$

(9.18)

as the sum will not change if we let j be a little bit higher. In fact, if n is even, we have $\lfloor \frac{n+1}{2} \rfloor = \lfloor \frac{n}{2} \rfloor .$ The same is not true if n is odd but then, the term vanishes: we have

$$\begin{aligned} j =\lfloor \frac{n+1}{2} \rfloor \Rightarrow j = \frac{n+1}{2} \Rightarrow \left( \begin{array}{c} n-j\\ j\\ \end{array}\right) = \left( \begin{array}{c} \frac{n-1}{2}\\ \frac{n+1}{2}\\ \end{array}\right) =0. \end{aligned}$$

(9.19)

Also by the induction hypothesis, we have:

$$\begin{aligned} -P_{n-1}= & {} - \sum _{k=0}^{\lfloor \frac{n-1}{2} \rfloor } (-1)^k \left( \begin{array}{c} n-k-1\\ k\\ \end{array}\right) P_1^{n-2k-1}\nonumber \\= & {} (-1)\sum _{j=1}^{\lfloor \frac{n+1}{2} \rfloor }(-1)^{j-1} \left( \begin{array}{c} n-j\\ j-1\\ \end{array}\right) P_1^{n-2j+2-1}\nonumber \\= & {} \sum _{j=1}^{\lfloor \frac{n+1}{2} \rfloor }(-1)^{j} \left( \begin{array}{c} n-j\\ j-1\\ \end{array}\right) P_1^{n+1-2j}, \end{aligned}$$

(9.20)

where $j = k+1$. As $\left( \begin{array}{c} n\\ -1\\ \end{array}\right) = 0,$ the sum is not changed if we include the term corresponding to $j=0.$ Then, we have

$$\begin{aligned} -P_{n-1}= \sum _{j=0}^{\lfloor \frac{n+1}{2} \rfloor }(-1)^{j} \left( \begin{array}{c} n-j\\ j-1\\ \end{array}\right) P_1^{n+1-2j}, \end{aligned}$$

(9.21)

so

$$\begin{aligned} P_{n+1} = P_1P_{n} - P_{n-1}= & {} \sum _{j=0}^{\lfloor \frac{n+1}{2} \rfloor } (-1)^j \left( \begin{array}{c} n-j\\ j\\ \end{array}\right) P_1^{n+1-2j} + \sum _{j=0}^{\lfloor \frac{n+1}{2} \rfloor } (-1)^j \left( \begin{array}{c} n-j\\ j-1\\ \end{array}\right) P_1^{n+1-2j}\nonumber \\= & {} \sum _{j=0}^{\lfloor \frac{n+1}{2} \rfloor } (-1)^j \left[ \left( \begin{array}{c} n-j\\ j\\ \end{array}\right) + \left( \begin{array}{c} n-j\\ j-1\\ \end{array}\right) \right] P_1^{n+1-2j} \nonumber \\= & {} \sum _{j=0}^{\lfloor \frac{n+1}{2} \rfloor } (-1)^j \left( \begin{array}{c} n+1-j\\ j\\ \end{array}\right) P_1^{n+1-2j}, \end{aligned}$$

(9.22)

i.e., (4.11) is also true for $n+1$. $\square$