Phase Transition and Uniqueness of Levelset Percolation

Abstract

The main purpose of this paper is to introduce and establish basic results of a natural extension of the classical Boolean percolation model (also known as the Gilbert disc model). We replace the balls of that model by a positive non-increasing attenuation function $l:(0,\infty ) \rightarrow [0,\infty )$ to create the random field $\Psi (y)=\sum _{x\in \eta }l(|x-y|),$ where $\eta$ is a homogeneous Poisson process in ${\mathbb {R}}^d.$ The field $\Psi$ is then a random potential field with infinite range dependencies whenever the support of the function l is unbounded. In particular, we study the level sets $\Psi _{\ge h}(y)$ containing the points $y\in {\mathbb {R}}^d$ such that $\Psi (y)\ge h.$ In the case where l has unbounded support, we give, for any $d\ge 2,$ a necessary and sufficient condition on l for $\Psi _{\ge h}(y)$ to have a percolative phase transition as a function of h. We also prove that when l is continuous then so is $\Psi$ almost surely. Moreover, in this case and for $d=2,$ we prove uniqueness of the infinite component of $\Psi _{\ge h}$ when such exists, and we also show that the so-called percolation function is continuous below the critical value $h_c$.

1 Introduction

In the classical Boolean continuum percolation model (see [14] for an overview), one considers a homogeneous Poisson process $\eta$ of rate $\lambda >0$ in ${\mathbb {R}}^d$, and around each point $x\in \eta$ one places a ball B(x, r) of radius r. The main object of study is then

$$\begin{aligned} {\mathcal {C}}:=\bigcup _{x\in \eta }B(x,r), \end{aligned}$$

(1.1)

which is referred to as the occupied set. It is well known (see [14, Chap. 3]) that there exists an $r_c=r_c(d)\in (0,\infty )$ such that

$$\begin{aligned} r_c:=\inf \{r:{\mathbb {P}}({\mathcal {C}}(r) \text { contains an unbounded component})>0\}. \end{aligned}$$

It is also well known that ${\mathbb {P}}({\mathcal {C}}(r) \text { contains an unbounded component})\in \{0,1\}.$ An immediate scaling argument shows that varying $\lambda$ is equivalent to varying r,  and so one can fix $\lambda =1.$ This model was introduce by Gilbert in [8] and further studied in [2, 3, 15, 17] (to name a few), while a dynamical version of this model was studied in [1].

We consider a natural extension of this model. Let $\eta$ be a Poisson process with rate $\lambda$ in ${\mathbb {R}}^d,$ and let $x\in \eta$ denote a point in this process (here we use the standard abuse of notation by writing $x\in \eta$ instead of $x\in \mathrm{supp}(\eta )$). Furthermore, let $l:(0,\infty ) \rightarrow [0,\infty )$ be a non-increasing function that we will call the attenuation function. We then define the random field $\Psi =\Psi (l,\eta )$ at any point $y\in {\mathbb {R}}^d$ by

$$\begin{aligned} \Psi (y):=\sum _{x\in \eta }l(|x-y|). \end{aligned}$$

(1.2)

In order for this to be well defined at every point, we let $l(0):=\lim _{r \rightarrow 0}l(r)$ (which can possibly be infinite). One can think of $\Psi$ as a random potential field where the contribution from a single point $x\in \eta$ is determined by the function l.

For any $0<h<\infty ,$ we define

$$\begin{aligned} \Psi _{\ge h}:=\{y\in {\mathbb {R}}^d: \Psi (y)\ge h\}, \end{aligned}$$

which is simply the part of the random field $\Psi$ which is at or above the level h. Sometimes we also need

$$\begin{aligned} \Psi _{> h}:=\{y\in {\mathbb {R}}^d: \Psi (y)> h\}. \end{aligned}$$

We note that if we consider our general model with $l(|x|)=I(|x|\le r)$ (where I is an indicator function), we have that ${\mathcal {C}}$ and $\Psi _{\ge 1}$ have the same distribution, so the Boolean percolation model can be regarded as a special case of our more general model.

When l has unbounded support, adding or removing a single point of $\eta$ will affect the field $\Psi$ at every point of ${\mathbb {R}}^d.$ Thus, our model does not have a so-called finite energy condition which is the key to many standard proofs in percolation theory. This is what makes studying $\Psi$ challenging (and in our opinion interesting). However, if we assume that l has bounded support, a version of finite energy is recovered (see also the remark in Sect. 4 after the proof of our uniqueness result, Theorem 1.4).

It is easy to see that varying h and varying $\lambda$ is not equivalent. However, we will nevertheless restrict our attention to the case $\lambda =1$. In fact, there are many different sub-cases and generalizations that can be studied. For instance: We can let $\lambda \in {\mathbb {R}},$ we can study l having bounded or unbounded support, we can let l be a bounded or unbounded function, let l be continuous or discontinuous and we can study $\Psi _{\ge h}$ or $\Psi _{> h}$, to name a few possibilities. While some results (Theorems 2.3 and 2.1) include all or most of the cases listed, others (Proposition 3.1 and Theorems 1.4 and 1.5) require more specialized proofs. The purpose of this paper is not to handle all different cases. If l has bounded support, then our model is very similar to the classical Boolean percolation model, and therefore we will (unless otherwise stated) throughout make the following assumption.

Assumption 1.1

The attenuation function l is non-increasing and has unbounded support.

The assumption of l being non-increasing is certainly not necessary for most of our results. However, this assumption is very convenient and removes the need for overly technical statements. Se the last remark after the statement of Theorem 1.3. In addition to Assumption 1.1, we will also always assume that $d\ge 2.$

We will now proceed to state our main results, but first we have the following natural definition.

Definition 1.2

If $\Psi _{\ge h}$ ($\Psi _{> h}$) contains an unbounded connected component, we say that $\Psi$ percolates at (above) level h,  or simply that $\Psi _{\ge h}$ ($\Psi _{> h}$) percolates.

One would of course expect that percolation occurs either with probability 0 or with probability 1, and indeed this can be proven through classical ergodicity arguments. Therefore, it is natural to define

$$\begin{aligned} h_c:=\sup \{h:\Psi _{\ge h} \text { percolates with probability 1}\}. \end{aligned}$$

If we define $\tilde{h}_c$ as above, but with $\Psi _{\ge h}$ replaced by $\Psi _{>h},$ then $h_c=\tilde{h}_c.$ Indeed, $\tilde{h}_c \le h_c$ is clear. Conversely, if $h<h_c$ then for $h< h^{\prime } < h_c$ we have that $\Psi _{\ge h^{\prime }}$ percolates. Hence $\Psi _{> h}$ percolates and $h \le \tilde{h}_c$.

One of the main efforts of this paper is to establish conditions under which $h_c$ is nontrivial.

Theorem 1.3

With l as in Assumption 1.1, $0<h_c<\infty$ if and only if $\int _{1}^\infty r^{d-1}l(r)dr<\infty .$

Remark

• The choice of the lower integral boundary 1 in $\int _{1}^\infty r^{d-1}l(r)dr$ is somewhat arbitrary, as replacing it with $\int _{c}^\infty r^{d-1}l(r)dr$ for any $0<c<\infty ,$ would give the same result.

• As we shall see in the proof of Theorem 1.3, if $\int _{1}^\infty r^{d-1}l(r)dr=\infty ,$ then almost surely $\Psi (y)=\infty$ for every $y\in {\mathbb {R}}^d$.

• Mere a.s. finiteness of the field $\Psi$ does not guarantee that there is a nontrivial phase transition. Indeed, one can construct an example (following the examples of [14, Chap. 7.7]) of a stationary process together with a suitable attenuation function so that the ensuing field is finite a.s., while $h_c=\infty .$

• The result is qualitatively different when l has bounded support, see Theorem 2.3.

• Consider briefly the non-monotone attenuation function $l(r)=|r-1|^{-d}.$ Obviously, we then have that $\int _{1}^\infty r^{d-1}l(r)dr=\infty .$ However, the tail behaviour of l is such that a suitably modified version of Theorem 1.3 would still hold for this case. This is the main reason for including non-increasingness in Assumption 1.1.

We have the following uniqueness result.

Theorem 1.4

Let l be continuous and satisfy Assumption 1.1. If h is such that $\Psi _{\ge h}$ ($\Psi _{>h}$) contains an unbounded component with probability one, then for $d=2$, there is with probability one a unique such unbounded component.

Remark

• We will prove this theorem first for $\Psi _{>h}$ and then infer it for $\Psi _{\ge h}$, see also the discussion before the proof of the theorem.

• There are of course a number of possible generalizations of this statement, and perhaps the most interesting/natural would be to investigate it for $d\ge 3.$ We discuss this in some detail after the proof of Theorem 1.4.

• The statement is trivially true if $\int _1^\infty r^{d-1}l(r)dr=\infty$ because of the second remark after the statement of Theorem 1.3.

Let ${\mathcal {C}}_{o,\ge }(h)$ (${\mathcal {C}}_{o,>}(h)$) be the connected component of $\Psi _{\ge h}$ ($\Psi _{> h}$) that contains the origin o. Define the percolation function

$$\begin{aligned} \theta _{\ge }(h):={\mathbb {P}}({\mathcal {C}}_{o,\ge }(h) \text { is unbounded}), \end{aligned}$$

and similarly define $\theta _>(h)$. Our last result of the introduction is the following.

Theorem 1.5

If l is continuous and satisfies Assumption 1.1, the functions $\theta _{\ge }(h)$ and $\theta _{>}(h)$ are equal and continuous for $h<h_c$.

The rest of the paper is organized as follows. In Sect. 2 we prove Theorem 1.3 along with some related secondary results. In Sect. 3 we prove the continuity of the field $\Psi$ whenever l is continuous, and this results is then used in Sect. 4 in order to prove Theorem 1.4. In turn, Theorem 1.4 allows us to prove Theorem 1.5 which is also done in Sect. 4.

2 Proof of Theorem 1.3.

The proof of Theorem 1.3 is naturally divided into two parts ($h_c>0$ and $h_c<\infty$ respectively). For completeness, we will briefly consider attenuation functions of (possibly) bounded support. Thus, let $r_l:=\sup \{r:l(r)>0\}$ and recall the definition of $r_c.$

Theorem 2.1

For $d\ge 3,$ $h_c>0$ if $r_l> r_c$ while $h_c=0$ if $r_l< r_c.$ Furthermore, for $d=2,$ then $h_c>0$ iff $r_l> r_c.$

Remark

As is clear from the proof, the gap when $r_l=r_c$ for $d\ge 3,$ is simply due to the fact that for $d \ge 3$ it is unknown whether ${\mathbb {P}}({\mathcal {C}}(r_c) \text { contains an unbounded component})$ is 0 (as when $d=2)$ or 1.

Proof of Theorem 2.1

Recall the constructions (1.1) and (1.2). Observe that by using the same realization of $\eta ,$ we can couple $\Psi$ and ${\mathcal {C}}$ on the same probability space in the canonical way. By using this coupling, we see that for any $h>0,$ $\Psi _{\ge h}\subset {\mathcal {C}}(r_l).$ In the case $d=2,$ it is known (see [14, Theorem 4.5]) that ${\mathcal {C}}(r_c)$ does not percolate, showing that $h_c=0$ when $d=2$ and $r_l\le r_c.$ For $d\ge 3,$ the statement follows by observing that ${\mathcal {C}}(r)$ does not percolate for $r<r_c$ by definition of $r_c.$

Assume instead that $r_l> r_c.$ Let $r_c<r<r_l,$ and $h=h(r)$ be any h such that

$$\begin{aligned} B(0,r) \subset \{y:l(|y|)\ge h\}. \end{aligned}$$

With this choice of h,  we see that any point y within radius r from some $x\in \eta$ will also belong to $\Psi _{\ge h}$ so that

$$\begin{aligned} {\mathcal {C}}(r)\subset \Psi _{\ge h}. \end{aligned}$$

Since $r>r_c,$ ${\mathcal {C}}(r)$ a.s. contains an unbounded component and hence so does $\Psi _{\ge h}.$ $\square$

We will make frequent use of the following theorem, both of whose statements are sometimes called “Campbell’s formula”.

Theorem 2.2

Let $\eta$ be a (possibly non-homogeneous) Poisson process on ${\mathbb {R}}^d$ with intensity measure $\mu .$ Then we have that for any $g(x):{\mathbb {R}}^d \rightarrow [0,\infty )$ such that $\sum _{x\in \eta } g(x)$ converges a.s.,

$$\begin{aligned} {\mathbb {E}}\left[ \sum _{x\in \eta }g(x)\right] =\int _{{\mathbb {R}}^d}g(x)\mu (dx). \end{aligned}$$

(2.1)

Furthermore, we have that

$$\begin{aligned} {\mathbb {E}}\left[ \exp \left( s\sum _{x\in \eta }g(x)\right) \right] =\exp \left( \int _{{\mathbb {R}}^d}e^{sg(x)}-1\mu (dx)\right) . \end{aligned}$$

(2.2)

For a proof of Theorem 2.2 we refer the reader to [11] page 28 or [5, Chaps. 5.5, 9.4 and 9.5].

We now return to Theorem 1.3, which will be proved once we have established the following result.

Theorem 2.3

If the attenuation function l satisfies $\int _{1}^\infty r^{d-1}l(r)dr<\infty$ and Assumption 1.1, then $h_c<\infty .$ If instead $\int _{1}^\infty r^{d-1}l(r)dr=\infty ,$ then almost surely $\Psi (y)=\infty$ for every $y\in {\mathbb {R}}^d$, and so $h_c=\infty .$

Remark

Note also that if l has bounded support, we must have that $\int _{1}^\infty r^{d-1}l(r)dr<\infty .$ As will be clear, the proof in fact also covers this case.

The proof of Theorem 2.3 is much more involved than the proof of Theorem 2.1, and will require a number of preliminary lemmas to be established first. In order to see what the purpose of these will be, we will start by giving an outline of the strategy of our proof along with introducing some of the relevant notation. Let $\alpha {\mathbb {Z}}^d$ denote the lattice with spacing $\alpha >0.$ For any $z\in \alpha {\mathbb {Z}}^d,$ let $B(z,\alpha )$ denote the closed box of side length $\alpha$ centered at z,  and define ${\mathcal {B}}_\alpha :=\{B(z,\alpha ):z\in \alpha {\mathbb {Z}}^d\}.$ For convenience, we assume from now on that $\alpha <1.$

Claim

There exists an $\epsilon >0$ such that if for fixed $0<\alpha <1$ and $0<h<\infty$ we have that

$$\begin{aligned} {\mathbb {P}}(\sup _{y\in B_1}\Psi (y)\ge h, \ldots , \sup _{y\in B_k}\Psi (y)\ge h) \le \epsilon ^k, \end{aligned}$$

(2.3)

for every k and every collection $B_1,\ldots ,B_k\in {\mathcal {B}}_\alpha$, then $\Psi _{\ge h}$ does a.s. not contain an unbounded component.

Of course, whether the condition (2.3) of the claim actually holds, will depend on the specific choice of $\alpha$ and h.

This claim can be proved using standard percolation arguments as follows. Let $B^o\in {\mathcal {B}}_\alpha$ be the cube containing the origin o and let ${\mathcal {O}}$ denote the event that $B^o$ intersects an unbounded component of $\Psi _{\ge h}$. If ${\mathcal {O}}$ occurs, then for any k,  there must exist a sequence $B_1,B_2,\ldots B_k\in {\mathcal {B}}_\alpha$ such that $B_1=B^o,$ $B_i \ne B_j$ for every $i\ne j,$ $B_i\cap B_{i+1}\ne \emptyset$ for every $i=1,\ldots ,k-1$ and with the property that $\sup _{y\in B_i}\Psi (y)\ge h$ for every $i=1,\ldots ,k.$ We note that the number of such paths must be bounded by $3^{dk}$, as any box has fewer than $3^d$ ’neighbors’. Thus, from (2.3) we get that ${\mathbb {P}}({\mathcal {O}})\le 3^{dk}\epsilon ^k,$ and since this holds for arbitrary k this proves the claim by taking $\epsilon <3^{-d}$.

One issue when proving (2.3) is that we want to consider the supremum of the field within the boxes $B_1,\ldots ,B_k.$ However, this is fairly easily dealt with by introducing an auxiliary field $\tilde{\Psi }$ with the property that for any $B\in {\mathcal {B}}_\alpha$ $\tilde{\Psi }(y_c(B))\ge \sup _{y\in B} \Psi (y)$ where $y_c(B)$ denotes the center of B (see further (2.9)). This allows us to consider k fixed points of the new field $\tilde{\Psi }$ rather than the supremums involved in (2.3).

One of the main problems in proving (2.3) is the long range dependencies involved whenever l has unbounded support (as discussed in the introduction). The strategy to resolve this issue is based on the simple observation that

$$\begin{aligned} \left\{ \sup _{y\in B_1}\Psi (y)\ge h, \ldots , \sup _{y\in B_k}\Psi (y)\ge h\right\} \subset \left\{ \sum _{l=1}^k \tilde{\Psi }(y_c(B_l))\ge kh \right\} . \end{aligned}$$

(2.4)

The event on the right hand side of (2.4) can be analyzed through the use of (2.2). An obvious problem with this is that if l is unbounded and if a single point of $\eta$ falls in $\bigcup _{l=1}^k B_l$, then the sum in (2.4) is infinite. However, by letting $\alpha$ above be very small, we can make sure that with very high probability, “most” of the boxes $B_1,\ldots ,B_k$ will not contain any points of $\eta$ (and in fact there will not even be a point in a certain neighborhood of the box). We then use a more sophisticated version of (2.4) (i.e. (2.10)) where we condition on which of the boxes $B_1,\ldots ,B_k$ have a point of $\eta$ in their neighborhood, and then sum only over the boxes whose neighborhoods are vacant of points. This in turn introduces another problem, namely that we now have to deal with a Poisson process conditioned on the presence and absence of points of $\eta$ in the neighborhoods of the boxes $B_1,\ldots ,B_k.$ In particular, we have to control the damage from knowing the presence of such points. This is the purpose of Lemmas 2.4 and 2.5, which will tell us that our knowledge is not worse than having no information at all plus adding a few extra points to the process. Later, Lemma 2.6 will enable us to control the effect of this addition of extra points.

We now start presenting the rigorous proofs. Our first lemma is elementary, and the result is presumably folklore. However, we give a proof for sake of completeness.

Lemma 2.4

Let X be a Poisson distributed random variable with parameter $\lambda .$ We have that for any $k\ge 0,$

$$\begin{aligned} {\mathbb {P}}(X\ge k | X\ge 1)\le {\mathbb {P}}(X\ge k-1). \end{aligned}$$

(2.5)

Proof

We claim that for any $X^n\sim$ Bin(n, p) where $np=\lambda ,$ and any $0\le k \le n,$ we have that

$$\begin{aligned} {\mathbb {P}}(X^n\ge k| X^n \ge 1)\le {\mathbb {P}}(X^n\ge k-1). \end{aligned}$$

(2.6)

We observe that from (2.6) we get that

$$\begin{aligned} {\mathbb {P}}(X\ge k | X\ge 1) =\lim _{n \rightarrow \infty }{\mathbb {P}}(X^n\ge k| X^n \ge 1) \le \lim _{n \rightarrow \infty }{\mathbb {P}}(X^n\ge k-1)= {\mathbb {P}}(X \ge k-1). \end{aligned}$$

This establishes (2.5), and so we need to prove (2.6).

We will prove (2.6) through induction, and we start by observing that it trivially holds for $n=1$ and $k=0,1.$ Assume therefore that (2.6) holds for n and any $k=0,\ldots ,n.$ We will write $X^n=X_1+\cdots +X_{n}$ where $\left( X_i\right) _{i\ge 1}$ is an i.i.d. sequence with ${\mathbb {P}}(X_i=1)=1-{\mathbb {P}}(X_i=0)=p.$ Of course, (2.6) trivially holds for $n+1$ and $k=0.$ Furthermore, we have that for any $k=1,\ldots ,n,$

$$\begin{aligned}&{{\mathbb {P}}(X^{n+1} \ge k | X^{n+1}\ge 1)}\\&\quad ={\mathbb {P}}(X^{n+1} \ge k | X^{n+1}\ge 1, X_{n+1}=1){\mathbb {P}}(X_{n+1}=1 |X^{n+1}\ge 1)\\&\qquad +\,{\mathbb {P}}(X^{n+1} \ge k | X^{n+1}\ge 1, X_{n+1}=0){\mathbb {P}}(X_{n+1}=0 |X^{n+1}\ge 1)\\&\quad ={\mathbb {P}}(X^{n} \ge k-1){\mathbb {P}}(X_{n+1}=1 |X^{n+1}\ge 1) +{\mathbb {P}}(X^{n} \ge k | X^{n}\ge 1){\mathbb {P}}(X_{n+1}=0 |X^{n+1}\ge 1)\\&\quad \le {\mathbb {P}}(X^{n} \ge k-1), \end{aligned}$$

where we use the induction hypothesis that ${\mathbb {P}}(X^{n} \ge k | X^{n}\ge 1) \le {\mathbb {P}}(X^{n} \ge k-1)$ in the last inequality. Finally,

$$\begin{aligned} {\mathbb {P}}(X^{n+1} =n+1 | X^{n+1}\ge 1) ={\mathbb {P}}(X^{n} = n){\mathbb {P}}(X_{n+1}=1 |X^{n+1}\ge 1) \le {\mathbb {P}}(X^{n} = n), \end{aligned}$$

and this establishes (2.6) for $n+1$ and any $k=0,\ldots ,n+1.$ $\square$

In what follows, we shall deal with a number of different point processes $\eta ,\xi ,\ldots$ on ${\mathbb {R}}^d$, both Poisson and other. We will primarily view these as (random) counting measures on ${\mathbb {R}}^d$ so that for instance $\eta (A)$ is the number of points of $\eta$ in the set $A\subset {\mathbb {R}}^d.$ However, we will sometimes use a standard abuse of notation by identifying $\eta$ with its support. For instance, $\eta \subset \xi$ simply means that the support of $\eta$ is a subset of the support of $\xi ,$ or (somewhat more informally) a point in $\eta$ is also a point in $\xi .$

Let $A_1,A_2,\ldots ,A_n$ be subsets of ${\mathbb {R}}^d,$ and let $C_1,\ldots ,C_m$ be a partition of $\cup _{i=1}^n A_i$ such that for any i, 

$$\begin{aligned} A_i=\cup _{k=1}^l C_{i_k}, \end{aligned}$$

(2.7)

for some collection $C_{i_1},\ldots ,C_{i_l}.$ Let $\eta _A$ be a homogeneous Poisson process of rate $\lambda >0$ on $\cup _{i=1}^n A_i$ conditioned on the event $\cap _{i=1}^n\{\eta (A_i)\ge 1\},$ and let $\eta ^{\prime }_A$ be a homogeneous (unconditioned) Poisson process of rate $\lambda >0$ on $\cup _{i=1}^n A_i.$ Furthermore, let $\xi _A$ be a point process on $\cup _{i=1}^n A_i$ consisting of exactly one point in each of the sets $C_1,\ldots ,C_m$ such that the position of the point in $C_i$ is uniformly distributed within the set, and so that this position is independent between sets.

Our next step is to use Lemma 2.4 to prove a result relating the conditioned Poisson process $\eta _A$ to the sum $\eta ^{\prime }_A+\xi _A,$ where $\eta ^{\prime }_A$ and $\xi _A$ are independent. For two point processes $\eta _1,\eta _2$ in ${\mathbb {R}}^d$, we write $\eta _1\preceq \eta _2$ if there exists a coupling of $\eta _1,\eta _2$ so that ${\mathbb {P}}(\eta _1\subset \eta _2)=1.$

Lemma 2.5

Let $\eta _A,\eta ^{\prime }_A$ and $\xi _A$ be as above, and let $\eta ^{\prime }_A$ and $\xi _A$ be independent. We have that

$$\begin{aligned} \eta _A \preceq \eta ^{\prime }_A+\xi _A. \end{aligned}$$

Remark

Informally, Lemma 2.5 tells us that if we consider a homogeneous Poisson process conditioned on the presence of points in $A_1,\ldots ,A_k$, it is not worse than taking an unconditioned process and adding single points to all the sets $C_1,\ldots ,C_m$ (which are used as the building blocks for the sets $A_1,\ldots ,A_k$).

Proof of Lemma 2.5

We shall prove the lemma by giving an explicit coupling. We do this by simultaneously constructing two point-processes $\bar{\eta }_1$ and $\bar{\eta }_2$ in such a way that $\bar{\eta }_1 \subset \bar{\eta }_2$. We will then proceed to prove that $\bar{\eta }_1$ has the same distribution as $\eta _A$ while $\bar{\eta }_2$ has the same distribution as $\eta ^{\prime }_A+\xi _A.$ Furthermore, we will assume that $\bar{\eta }_1$ and $\bar{\eta }_2$ are point processes on $\bigcup _{i=1}^n A_i,$ since outside this set the processes $\eta _A,\eta _A^{\prime }$ are simply homogeneous Poisson processes and so we can take them to be equal there. Of course, $\xi _A$ has no points outside of $\bigcup _{i=1}^n A_i.$

In what follows, we will let $J=(j_1,\ldots ,j_m)\in \{0,1\}^m,$ and for any point process $\xi ,$ we let $L(\xi )\in \{0,1\}^m$ be such that $L_j(\xi )=1$ iff $\xi (C_j)\ge 1.$ Thus, $L(\xi )$ tells us which of the sets $C_1,\ldots ,C_m$ that are empty. As usual, $\eta$ denotes a homogeneous Poisson process in ${\mathbb {R}}^d.$

For the coupling construction we will use the auxiliary random variables $(U_l)_{l=1}^m$ which are independent and U([0, 1]) distributed. We will also use the sequences $(V_{l,k})_{k=1}^\infty$ where $l=1,\ldots ,m$. These random variables are taken to be mutually independent and also independent of $(U_l)_{l=1}^m$. The random variables $(V_{l,k})_{k=1}^\infty$ are uniformly distributed on the set $C_l.$

We start by constructing $\bar{\eta }_1$:

• Step 1: Let $X\in \{0,1\}^m$ be such that $X=J$ with probability ${\mathbb {P}}(L(\eta )=J | \cap _{i=1}^n\{\eta (A_i)\ge 1\})$.

• Step 2: Given that the result of Step 1 was that $X=J$, we let $Y_l=0$ if $j_l=0.$ If instead $j_l=1,$ then we let $Y_l=k_l$ if

  $$\begin{aligned} {\mathbb {P}}(\eta (C_l)\ge k_l+1| \eta (C_l)\ge 1)\le U_l < {\mathbb {P}}(\eta (C_l)\ge k_l | \eta (C_l)\ge 1), \end{aligned}$$

  where $k_l=1,2,\ldots$

• Step 3: Given the numbers $Y_1,\ldots ,Y_m$ from step 2, we let the restriction of $\bar{\eta }_1$ to $C_l$ be $\sum _{k=1}^{Y_l} \delta _{V_{l,k}}$ where $\delta _x$ denotes a point mass at x.

We proceed by constructing $\bar{\eta }_2$:

• Step ${1}^{\prime }$: We let $Z_l=k_l$ if

  $$\begin{aligned} {\mathbb {P}}(\eta (C_l)\ge k_l)\le U_l < {\mathbb {P}}(\eta (C_l)\ge k_l-1 ), \end{aligned}$$

  where again $k_l=1,2,\ldots$

• Step ${2}^{\prime }$: Given the numbers $Z_1,\ldots ,Z_m$ from step 2, we let the restriction of $\bar{\eta }_2$ to $C_l$ be $\sum _{k=1}^{Z_l} \delta _{V_{l,k}}.$

Clearly, if $Y_l=0$ we have that $Y_l \le Z_l.$ Furthermore, according to Lemma 2.4 we have that

$$\begin{aligned} {\mathbb {P}}(\eta (C_l)\ge k_l| \eta (C_l)\ge 1) \le {\mathbb {P}}(\eta (C_l)\ge k_l-1 ). \end{aligned}$$

Therefore, if $U_l<{\mathbb {P}}(\eta (C_l)\ge k_l| \eta (C_l)\ge 1)$ (so that $Y_l \ge k_l$) then $U_l<{\mathbb {P}}(\eta (C_l)\ge k_l-1)$ (so that $Z_l \ge k_l$), and therefore we have that $Z_l \ge Y_l.$ We conclude that for every l,  $Y_l \le Z_l.$ Finally, since we are using the same random variables $(V_{l,k})_{k=1}^\infty$ in Step 3 and Step $2^{\prime }$ we conclude that indeed $\bar{\eta }_1 \subset \bar{\eta }_2.$

What remains is to verify the distributions of $\bar{\eta }_1,\bar{\eta }_2$ and we start with $\bar{\eta }_1.$ We say that $J\in \{0,1\}^m$ is admissible if

$$\begin{aligned} \{L(\eta )=J\}=\bigcap _{l:j_l=1}\{\eta (C_l)\ge 1\} \bigcap _{l:j_l=0}\{\eta (C_l)=0\} \subset \cap _{i=1}^n\{\eta (A_i)\ge 1\}. \end{aligned}$$

Then, we have that for any sequence $k_1,\ldots ,k_m$

$$\begin{aligned}&{{\mathbb {P}}(\eta _A(C_1)=k_1,\ldots ,\eta _A(C_m)=k_m)}\\&\quad ={\mathbb {P}}(\eta (C_1)=k_1,\ldots ,\eta (C_m)=k_m |\cap _{i=1}^n\{\eta (A_i)\ge 1\} )\\&\quad =\sum _{J \text { admissible}} {\mathbb {P}}(\eta (C_1)=k_1,\ldots ,\eta (C_m)=k_m |L(\eta )=J) {\mathbb {P}}(L(\eta )=J|\cap _{i=1}^n\{\eta (A_i)\ge 1\} )\\&\quad =\sum _{J \text { admissible}} \prod _{l: j_l=1}{\mathbb {P}}(\eta (C_l)=k_l| \eta (C_l)\ge 1) \prod _{l: j_l=0}{\mathbb {P}}(\eta (C_l)=k_l| \eta (C_l)=0) \\&\qquad \times \,{\mathbb {P}}(L(\eta )=J|\cap _{i=1}^n\{\eta (A_i)\ge 1\} ). \end{aligned}$$

The last equality follows since the conditioning $L(\eta )=J$, involves conditioning on events concerning the disjoint sets $C_1,\ldots ,C_m.$

Turning to $\bar{\eta }_1$, we let $\beta _{l,k_l}:={\mathbb {P}}(\eta (C_l)\ge k_l| \eta (C_l)\ge 1)$ and note that

$$\begin{aligned} {\mathbb {P}}(\beta _{l,k_l+1}\le U_l <\beta _{l,k_l}) ={\mathbb {P}}(\eta (C_l)=k_l| \eta (C_l)\ge 1). \end{aligned}$$

(2.8)

Furthermore, we observe that for J not admissible,

$$\begin{aligned} {\mathbb {P}}(X=J)={\mathbb {P}}(L(\eta )=J | \cap _{i=1}^n\{\eta (A_i)\ge 1\})=0. \end{aligned}$$

Therefore, we have that

$$\begin{aligned}&{{\mathbb {P}}(\bar{\eta }_1(C_1)=k_1,\ldots ,\bar{\eta }_1(C_m)=k_m)}\\&\quad =\sum _{J\text { admissible}}{\mathbb {P}}(\bar{\eta }_1(C_1)=k_1, \ldots ,\bar{\eta }_1(C_m)=k_m |X=J){\mathbb {P}}(X=J) \\&\quad =\sum _{J\text { admissible}} {\mathbb {P}}(\beta _{l,k_l+1}\le U_l<\beta _{l,k_l}\text { for }l:j_l=1 | \eta (C_l)\ge 1) \prod _{l: j_l=0}I(k_l=0){\mathbb {P}}(X=J) \\&\quad =\sum _{J\text { admissible}} \prod _{l: j_l=1}{\mathbb {P}}(\beta _{l,k_l+1}\le U_l <\beta _{l,k_l} | \eta (C_l)\ge 1) \prod _{l: j_l=0}I(k_l=0){\mathbb {P}}(X=J) \\&\quad =\sum _{J\text { admissible}} \prod _{l: j_l=1}{\mathbb {P}}(\eta (C_l)=k_l| \eta (C_l)\ge 1) \prod _{l: j_l=0}{\mathbb {P}}(\eta (C_l)=k_l| \eta (C_l)=0) \\&\qquad \times \,{\mathbb {P}}(L(\eta )=J|\cap _{i=1}^n\{\eta (A_i)\ge 1\} ), \end{aligned}$$

where we use Step 1, Step 2, the independence of the $U_l$ and finally (2.8) in the four equalities. We conclude that for every $k_1,\ldots ,k_m$ we have that

$$\begin{aligned} {\mathbb {P}}(\eta _A(C_1)=k_1,\ldots ,\eta _A(C_m)=k_m) ={\mathbb {P}}(\bar{\eta }_1(C_1)=k_1,\ldots ,\bar{\eta }_1(C_m)=k_m). \end{aligned}$$

The fact that $\eta _A$ and $\bar{\eta }_1$ are equal in distribution follows since conditioned on the event $\{\eta _A(C_1)=k_1,\ldots ,\eta _A(C_m)=k_m\},$ the distribution of the points of $\eta _A$ in the disjoint sets $C_1,\ldots ,C_m$ are independent and uniform within their corresponding set $C_l$. To see this, let $\xi _{|C_l}$ denote the restriction of a point process $\xi$ to the set $C_l,$ and let ${\mathcal {A}}_l$ denote an event measurable with respect to $\xi _{|C_l}.$ We then have that for $k_1,\ldots ,k_m$ such that ${\mathbb {P}}(\eta _A(C_1)=k_1,\ldots ,\eta _A(C_m)=k_m)>0$ (so that $\{\eta _A(C_1)=k_1,\ldots ,\eta _A(C_m)=k_m\} \subset \cap _{i=1}^n\{\eta (A_i)\ge 1\}$),

$$\begin{aligned}&{{\mathbb {P}}(\eta _{A|C_1}\in {\mathcal {A}}_1,\ldots ,\eta _{A|C_m}\in {\mathcal {A}}_m |\eta _A(C_1)=k_1,\ldots ,\eta _A(C_m)=k_m)}\\&\quad ={\mathbb {P}}(\eta _{|C_1}\in {\mathcal {A}}_1,\ldots ,\eta _{|C_m}\in {\mathcal {A}}_m |\eta (C_1)=k_1,\ldots ,\eta (C_m)=k_m)\\&\quad =\frac{{\mathbb {P}}(\eta _{|C_1}\in {\mathcal {A}}_1\cap \eta (C_1)=k_1,\ldots , \eta _{|C_m}\in {\mathcal {A}}_m,\eta (C_m)=k_m)}{{\mathbb {P}}(\eta (C_1)=k_1,\ldots ,\eta (C_m)=k_m)}\\&\quad =\frac{\prod _{l=1}^m{\mathbb {P}}(\eta _{|C_l}\in {\mathcal {A}}_l\cap \eta (C_l)=k_l)}{\prod _{l=1}^m{\mathbb {P}}(\eta (C_l)=k_l)} =\prod _{l=1}^m {\mathbb {P}}( \eta _{|C_l}\in {\mathcal {A}}_l|\eta (C_l)=k_l) \end{aligned}$$

where we use the independence property of Poisson processes on disjoint sets.

For $\bar{\eta }_2,$ a straightforward calculation shows that

$$\begin{aligned} {\mathbb {P}}(\bar{\eta }_2(C_1)=k_1,\ldots ,\bar{\eta }_2(C_m)=k_m) ={\mathbb {P}}((\eta ^{\prime }_A+\xi _A)(C_1)=k_1,\ldots ,(\eta ^{\prime }_A+\xi _A)(C_m)=k_m) \end{aligned}$$

for every $k_1,\ldots ,k_m$, from which the statement easily follows. $\square$

We now turn to the issue of taking the supremum of the field over a box. Therefore, let $0<\alpha <1,$ and define the auxiliary attenuation function $\tilde{l}_\alpha$ by

$$\begin{aligned} \tilde{l}_\alpha (r)= \left\{ \begin{array}{ll} l(0) &{}\quad \text {if } r\le \alpha \sqrt{d}/2 \\ l(r-\alpha \sqrt{d}/2) &{}\quad \text {if } r\ge \alpha \sqrt{d}/2, \end{array} \right. \end{aligned}$$

for every $r\ge 0.$ If $y_{c}(B)$ denotes the center of the box $B\in {\mathcal {B}}_\alpha ,$ we note that for any $y\in B$ and $x\in {\mathbb {R}}^d,$

$$\begin{aligned} \tilde{l}_\alpha (|x-y_c(B)|) \ge \tilde{l}_\alpha (|x-y|+|y-y_c(B)|) \ge \tilde{l}_\alpha (|x-y|+\alpha \sqrt{d}/2) = l(|x-y|). \end{aligned}$$

Therefore, if we let $\tilde{\Psi }$ be the field we get by using $\tilde{l}$ in place of l in (1.2), we get that

$$\begin{aligned} \tilde{\Psi }(y_c(B))=\sum _{x\in \eta }\tilde{l}_\alpha (|x-y_c(B)|) \ge \sup _{y\in B}\sum _{x\in \eta } l(|x-y|)=\sup _{y\in B} \Psi (y). \end{aligned}$$

(2.9)

Our next lemma will be a central ingredient of the proof of Theorem 2.3. It will deal with the effect to the field $\tilde{\Psi }$ of adding extra points to $\eta$. To that end, let $A_o$ be the box of side length $\alpha (4\lceil \sqrt{d}\rceil +1)$ centered around the origin o. For any box $B\in {\mathcal {B}}_\alpha$ with $B\cap A_o=\emptyset ,$ place a point $x_B$ in B at the closest distance to the origin, and let $\xi$ denote the corresponding (deterministic) point set. Let

$$\begin{aligned} \tilde{\Psi }_{A_o}(y):=\sum _{x \in \xi }\tilde{l}_\alpha (|x-y|), \end{aligned}$$

be the corresponding deterministic field.

Lemma 2.6

Let l satisfy Assumption 1.1 and $\int _1^\infty r^{d-1}l(r)dr<\infty .$ Then, there exists a constant $C<\infty$ depending on d but not on $\alpha$ and such that for every $0<\alpha <1,$

$$\begin{aligned} \tilde{\Psi }_{A_o}(o)\le \frac{C}{\alpha ^d} I_\alpha , \end{aligned}$$

where

$$\begin{aligned} I_\alpha =\int _{\alpha /2}^\infty r^{d-1} l(r)dr<\infty . \end{aligned}$$

Proof

Consider some $B\in {\mathcal {B}}_\alpha$ such that $B\cap A_o=\emptyset .$ We have that

$$\begin{aligned} \tilde{l}_\alpha (|x_B|)\le \frac{1}{Vol(B)}\int _{B}\tilde{l}_\alpha (|x|-\mathrm{diam}(B))dx =\frac{1}{\alpha ^d}\int _{B}\tilde{l}_\alpha (|x|-\alpha \sqrt{d})dx. \end{aligned}$$

Therefore,

$$\begin{aligned} \tilde{\Psi }_{A_o}(o)\le & {} \frac{1}{\alpha ^d}\int _{{\mathbb {R}}^d{\setminus } A_o}\tilde{l}_\alpha (|x|-\alpha \sqrt{d})dx\\\le & {} \frac{C}{\alpha ^d}\int _{\alpha (2\lceil \sqrt{d}\rceil +1/2)}^\infty r^{d-1}l(r-2\alpha \sqrt{d})dr \\\le & {} \frac{C}{\alpha ^d}\int _{\alpha /2}^\infty (r+\alpha (2\lceil \sqrt{d}\rceil ))^{d-1} l(r) dr \nonumber \\\le & {} \frac{C}{\alpha ^d}\int _{\alpha /2}^\infty (r+r(4\sqrt{d}+2))^{d-1} l(r) dr \nonumber \\= & {} \frac{C}{\alpha ^d}\int _{\alpha /2}^\infty r^{d-1} l(r)dr \end{aligned}$$

where the constant $C=C(d)<\infty$ is allowed to vary in the steps of the calculations. Finally, the fact that $I_\alpha <\infty ,$ follows easily from the fact that $\int _{1}^\infty r^{d-1} l(r)dr<\infty .$ $\square$

We have now established all necessary tools in order to prove Theorem 2.3. However, since the proofs of the two statements of Theorem 2.3 are very different, we start by proving the first one as a separate result.

Theorem 2.7

If l satisfies Assumption 1.1 and $\int _1^\infty r^{d-1}l(r)<\infty ,$ then $h_c<\infty .$

Proof

We shall prove that for any $\epsilon >0,$ (2.3) holds for $\alpha$ small enough and h large enough. This will prove our result as explained just below (2.3).

For any $B\in {\mathcal {B}}_\alpha ,$ let A be the box concentric to B and with side length $\alpha (4\lceil \sqrt{d}\rceil +1)$. We will say that a box B is good if $\eta (A)=0,$ and observe that ${\mathbb {P}}(\eta (A)=0) \rightarrow 1$ as $\alpha \rightarrow 0.$ Goodness of the boxes $B\in {\mathcal {B}}_\alpha$ naturally induces a percolation model on ${\mathbb {Z}}^d$ with a finite range dependency. Since the marginal probability ${\mathbb {P}}(\eta (A)=0)$ of being good can be made to be arbitrarily close to 1 by taking $\alpha$ small enough, we can use the results in [12] (see also Theorem B26 of [13]) to let the induced ”goodness-process” dominate an i.i.d. product measure with density $p=p(\alpha )$ on the boxes $B\in {\mathcal {B}}_\alpha .$ That is, Furthermore, by the same theorem, we can take $p(\alpha )\rightarrow 1$ as $\alpha \rightarrow 0.$

Fix k, a collection of distinct cubes $B_1,B_2,\ldots , B_k \in {\mathcal {B}}_\alpha$, and let $A_i=A(B_i)$. Let $K(\eta )\in \{0,1\}^k$ be such that $K_j(\eta )=1$ iff $B_j$ is good, and identify $K(\eta )$ with the corresponding subset of $\{1,\ldots ,k\}.$ Thus we write $j\in K(\eta )$ iff $B_j$ is good. We then have that

$$\begin{aligned}&{\mathbb {P}}\left( \sup _{y\in B_1}\Psi (y)\ge h, \ldots , \sup _{y\in B_k}\Psi (y)\ge h\right) \nonumber \\&\quad \le \sum _{J\in \{0,1\}^k} {\mathbb {P}}(\tilde{\Psi }(y_c(B_1))\ge h,\ldots ,\tilde{\Psi }(y_c(B_k))\ge h|K(\eta )=J){\mathbb {P}}(K(\eta )=J) \nonumber \\&\quad \le \sum _{|J|\ge k/2} {\mathbb {P}}(\tilde{\Psi }(y_c(B_1))\ge h,\ldots ,\tilde{\Psi }(y_c(B_k))\ge h|K(\eta )=J) {\mathbb {P}}(K(\eta )=J) \nonumber \\&\qquad +\,{\mathbb {P}}(|K(\eta )|<k/2) \end{aligned}$$

(2.10)

by using (2.9) in the first inequality. $\square$

Fig. 1

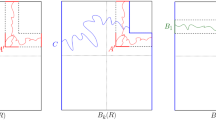
A picture with $k=5.$ The blue boxes are $B_1,B_2,B_3,B_4$ and $B_5,$ while the red boxes are $A_1,A_2,A_3,A_4$ and $A_5$. The two black dots are points in the Poisson process $\eta .$ The solid red area is $D_3=A_3{\setminus } \left( A_4 \cup A_5\right) .$ In this picture, $K(\eta )=(0,0,0,1,1)$ which is identified with $K(\eta )=\{4,5\}.$ Obviously, the goodness of $B_1$ depends on the goodness of $B_2,$ but it is independent on the goodness of $B_3,B_4$ and $B_5$ (Color figure online)

If we take $\Gamma =|\{ (B_i)_{i=1}^k: B_i \text { is good}\}|,$ then by the above domination of a product measure of density p,  we see that $\Gamma$ is stochastically larger than $\Gamma ^{\prime }\sim$Bin(p, k). Therefore, we have that

$$\begin{aligned}&{{\mathbb {P}}(|K(\eta )|<k/2) \le {\mathbb {P}}\left( \Gamma ^{\prime }\le k/2\right) }\nonumber \\&\quad ={\mathbb {P}}\left( e^{\Gamma ^{\prime } \log (1-p)}\ge e^{(k\log (1-p))/2}\right) \le e^{-(k\log (1-p))/2}{\mathbb {E}}\left[ e^{\Gamma ^{\prime }\log (1-p)}\right] \\&\quad =e^{-(k\log (1-p))/2}\left( pe^{\log (1-p)}+1-p\right) ^k \le 2^k e^{k\log (1-p))/2}=e^{-d(\alpha )k}, \nonumber \end{aligned}$$

(2.11)

where we can take $d(\alpha )\rightarrow \infty$ as $\alpha \rightarrow 0,$ by taking $p(\alpha )\rightarrow 1.$

For any $J\in \{0,1\}^k,$ we let $\eta _J$ be a Poisson process on ${\mathbb {R}}^d$ of rate 1, conditioned on the event $K(\eta )=J.$ Furthermore, for $j\in J^c,$ let

$$\begin{aligned} D_j:=A_j {\setminus } \bigcup _{i\in J} A_i. \end{aligned}$$

We see that $\eta _J$ can be expressed as the sum of $\tilde{\eta }$ and $\eta _D$ where $\tilde{\eta }$ is a Poisson process on ${\mathbb {R}}^d {\setminus } \bigcup _{n=1}^k A_n$ of unit rate, while $\eta _D$ is a Poisson process on $\bigcup _{j\in J^c} D_j$ conditioned on the event $\bigcap _{j\in J^c} \{\eta (D_j)\ge 1\}.$ We let $C_1,\ldots ,C_m\in {\mathcal {B}}_\alpha$ be a partition (up to sets of measure zero) of $\bigcup _{j\in J^c} D_j$, and use Lemma 2.5 to see that $\eta _D\preceq \eta _D^{\prime }+\xi _D$. Here of course, $\eta ^{\prime }_D$ is Poisson process on $\bigcup _{j\in J^c} D_j$ while $\xi _D$ is a point process consisting of one point added uniformly and independently to every box $C_i$ for $i=1,\ldots ,m.$ As in Lemma 2.5 $\eta ^{\prime }_D$ and $\xi _D$ are independent (Fig. 1).

We conclude that $\eta _J=\eta _D+\tilde{\eta } \preceq \eta ^{\prime }_D+\xi _D+\tilde{\eta }$, and observe that $\eta ^{\prime }_D+\tilde{\eta }$ is just a homogeneous Poisson process on ${\mathbb {R}}^d{\setminus } A_J$ where $A_J:=\bigcup _{j\in J} A_j.$ Writing $\eta _{A_J^c}$ for this sum, we have that $\eta _J\preceq \xi _D+\eta _{A_J^c}$ and by first using this, and then Markov’s inequality, we get that

$$\begin{aligned}&{{\mathbb {P}}\big (\tilde{\Psi }(y_c(B_1)\big )\ge h,\ldots ,\tilde{\Psi }(y_c(B_k))\ge h |K(\eta )=J)}\nonumber \\&\quad \le {\mathbb {P}}_{\xi _D+\eta _{A_J^c}} (\tilde{\Psi }(y_c(B_1))\ge h,\ldots ,\tilde{\Psi }(y_c(B_k))\ge h) \\&\quad \le {\mathbb {P}}_{\xi _D+\eta _{A_J^c}} \left( s\sum _{j\in J}\tilde{\Psi }(y_c(B_j))\ge h|J|s\right) \le e^{-h|J|s}{\mathbb {E}}_{\xi _D+\eta _{A_J^c}} \left[ e^{s\sum _{j\in J}\tilde{\Psi }(y_c(B_j))}\right] , \nonumber \end{aligned}$$

(2.12)

where ${\mathbb {P}}_{\xi _D+\eta _{A_J^c}}$ is the probability measure corresponding to $\xi _D+\eta _{A_J^c},$ and where ${\mathbb {E}}_{\xi _D+\eta _{A_J^c}}$ denotes expectation with respect to this probability measure. We have

$$\begin{aligned} \tilde{\Psi }(y_c(B_j))= & {} \sum _{x\in \xi _D+\eta _{A_J^c}} \tilde{l}_\alpha (|y_{c}(B_j)-x|)\\= & {} \sum _{x\in \eta _{A_J^c}}\tilde{l}_\alpha (|y_{c}(B_j)-x|) +\sum _{x\in \xi _D}\tilde{l}_\alpha (|y_{c}(B_j)-x|) \\= & {} \tilde{\Psi }_{\eta _{A_J^c}}(y_c(B_j)) +\tilde{\Psi }_{\xi _D}(y_c(B_j)), \end{aligned}$$

using obvious notation. Thus, using independence, we have that

$$\begin{aligned} {\mathbb {E}}_{\xi _D+\eta _{A_J^c}} \left[ e^{s\sum _{j\in J}\tilde{\Psi }(y_c(B_j))}\right] ={\mathbb {E}}_{\eta _{A_J^c}} \left[ e^{s\sum _{j\in J}\tilde{\Psi }_{\eta _{A_J^c}}(y_c(B_j))}\right] {\mathbb {E}}_{\xi _D}\left[ e^{s\sum _{j\in J}\tilde{\Psi }_{\xi _D}(y_c(B_j))}\right] .\nonumber \\ \end{aligned}$$

(2.13)

Consider the function $g_J(y):=\sum _{j\in J} \tilde{l}_\alpha (|y_{c}(B_j)-y|),$ so that

$$\begin{aligned}&\sum _{x\in \eta _{A_J^c}} g_J(x) =\sum _{x\in \eta _{A_J^c}}\sum _{j\in J} \tilde{l}_\alpha (|y_{c}(B_j)-x|)\\&\quad =\sum _{j\in J}\sum _{x\in \eta _{A_J^c}}\tilde{l}_\alpha (|y_{c}(B_j)-x|) =\sum _{j\in J}\tilde{\Psi }_{\eta _{A_J^c}}(y_{c}(B_j)), \end{aligned}$$

and similarly

$$\begin{aligned} \sum _{x\in \xi _D} g_J(x)=\sum _{j\in J}\tilde{\Psi }_{\xi _D}(y_{c}(B_j)). \end{aligned}$$

By (2.2) we get that

$$\begin{aligned} {\mathbb {E}}_{\eta _{A_J^c}} \left[ e^{s\sum _{j\in J} \tilde{\Psi }_{\eta ^{\prime }_D+\tilde{\eta }}(y_{c}(B_j))}\right] =\exp \left( {\int _{{\mathbb {R}}^d{\setminus } A_J}e^{sg_J(x)}-1 dx}\right) , \end{aligned}$$

(2.14)

since the intensity measure for $\eta _{A_J^c}$ is simply 0 on $A_J$ and Lebesgue measure outside of $A_J.$ We proceed by bounding the right hand side of this expression and start by noting that for $x\in {\mathbb {R}}^d{\setminus } A_J,$

$$\begin{aligned} g_J(x)\le \tilde{\Psi }_{A_o}(o)\le C I_\alpha \alpha ^{-d} \end{aligned}$$

so that by Lemma 2.6, $g_J(x)$ is uniformly bounded by $CI_\alpha /\alpha ^d$ where $CI_\alpha <\infty$ is as in that lemma. We can therefore use that $e^x-1\le 2x$ for $x\le 1,$ to see that for $0<s\le \alpha ^d/(CI_\alpha ),$ we have $e^{sg_J(x)}-1\le 2sg_J(x).$ Hence,

$$\begin{aligned} \int _{{\mathbb {R}}^d{\setminus } A_J}e^{sg_J(x)}-1 dx\le & {} \int _{{\mathbb {R}}^d{\setminus } A_J}2sg_J(x) dx\nonumber \\= & {} 2s\int _{{\mathbb {R}}^d{\setminus } A_J}\sum _{j\in J} \tilde{l}_\alpha (|y_{c}(B_j)-x|) dx \\\le & {} 2s\sum _{j\in J}\int _{{\mathbb {R}}^d{\setminus } A(B_j)} \tilde{l}_\alpha (|y_{c}(B_j)-x|) dx =2sD|J|, \nonumber \end{aligned}$$

(2.15)

where by using that the side length of $A(B_j)$ is $\alpha (4\lceil \sqrt{d}\rceil +1)$, we have that

$$\begin{aligned} D= & {} \int _{{\mathbb {R}}^d{\setminus } A(B_j)}\tilde{l}_\alpha (|y_{c}(B_j)-x|) dx\\= & {} \int _{{\mathbb {R}}^d{\setminus } A_o}\tilde{l}_\alpha (|x|)dx \le \int _{{\mathbb {R}}^d{\setminus } A_o}\tilde{l}_\alpha (|x|-\alpha \sqrt{d})dx \le CI_\alpha \end{aligned}$$

as in the proof of Lemma 2.6. Using (2.15) in (2.14), we get that

$$\begin{aligned} {\mathbb {E}}_{\eta _{A_J^c}}\left[ e^{s\sum _{j\in J} \tilde{\Psi }_{\eta _{A_J^c}}(y_{c}(B_j))}\right] \le e^{2sCI_\alpha |J|}. \end{aligned}$$

(2.16)

We now turn to the second factor on the right hand side of (2.13). Observe that for any k,  $J\in \{0,1\}^k$ and $j\in J$ we have that

$$\begin{aligned} \tilde{\Psi }_{\xi _D}(y_{c}(B_j))\le \tilde{\Psi }_{A_o}(o). \end{aligned}$$

Using Lemma 2.6, it follows that

$$\begin{aligned} {\mathbb {E}}_{\xi _D}\left[ e^{s\sum _{j\in J} \tilde{\Psi }_{\xi _D}(y_{c}(B_j))}\right] \le e^{2sCI_\alpha |J|/\alpha ^d}. \end{aligned}$$

(2.17)

Using (2.16) and (2.17), with (2.13) we see from (2.12) that

$$\begin{aligned} {\mathbb {P}}\big (\tilde{\Psi }(y_c(B_1)\big )\ge h,\ldots ,\tilde{\Psi }(y_c(B_k))\ge h|L(\eta )=J) \le e^{-h|J|s}e^{2sCI_\alpha |J|}e^{2s|J|CI_\alpha /\alpha ^d}. \end{aligned}$$

Inserting this into (2.10), and using (2.11), we get

$$\begin{aligned}&{\mathbb {P}}\left( \sup _{y\in B_1}\Psi (y)\ge h, \ldots , \sup _{y\in B_k}\Psi (y)\ge h\right) \\&\quad \le \sum _{|J|\ge k/2} e^{-h|J|s}e^{2sCI_\alpha |J|}e^{2s|J|CI_\alpha /\alpha ^d} {\mathbb {P}}(K(\eta )=J)+e^{-d(\alpha )k} \nonumber \\&\quad \le k e^{-shk/2}e^{2skCI_\alpha (1+\alpha ^{-d})} +e^{-d(\alpha )k}. \nonumber \end{aligned}$$

Then, by setting $s=\alpha ^d/(CI_\alpha )$ (i.e. the largest possible s in order to use (2.15)) we get that

$$\begin{aligned}&{\mathbb {P}}\left( \sup _{y\in B_1}\Psi (y)\ge h, \ldots , \sup _{y\in B_k}\Psi (y)\ge h\right) \\&\quad \le k e^{-\alpha ^d h/(2CI_\alpha )}e^{2k(\alpha ^d+1)} +e^{-d(\alpha )k}. \end{aligned}$$

Finally, by first letting $\alpha$ be so small that $e^{-d(\alpha )}\le \epsilon /2,$ and then taking h large enough, (2.3) follows. $\square$

We will now prove Theorem 2.3 in its entirety.

Proof of Theorem 2.3

The first statement is simply Theorem 2.7 and so we turn to the second statement.

Consider the auxiliary attenuation function $l^{\prime }(r):=l(r+1)$, and let $\Psi ^{\prime }$ denote the corresponding random field. We observe that for any $y\in B(o,1)$ and $x\in {\mathbb {R}}^d,$ $l^{\prime }(|x|)=l(|x|+1)\le l(|x-y|-|y|+1)\le l(|x-y|),$ so that

$$\begin{aligned} \Psi ^{\prime }(o)=\sum _{x\in \eta }l^{\prime }(|x|) \le \inf _{y\in B(o,1)}\sum _{x\in \eta }l(|x-y|) =\inf _{y\in B(o,1)}\Psi (y). \end{aligned}$$

We proceed to show that ${\mathbb {P}}(\Psi ^{\prime }(o)=\infty )=1,$ since then it follows that ${\mathbb {P}}\left( \inf _{y\in {\mathbb {R}}^d}\Psi (y)=\infty \right) =1$ by a standard countability argument. Therefore, let $A_0:=B(o,1),$ and $A_k:=B(o,k+1){\setminus } B(o,k)$ and note that $Vol(A_k)=\kappa _d((k+1)^d-k^d)\ge d\kappa _d k^{d-1},$ where $\kappa _d$ denotes the volume of the unit ball in dimension d. Furthermore, let ${\mathcal {A}}_k$ denote the event that $\eta (A_k)\ge \kappa _d k^{d-1}.$ For any $X\sim Poi(\lambda ),$ a standard Chernoff type bound yields

$$\begin{aligned} {\mathbb {P}}(X\le \lambda /2)\le \frac{e^{-\lambda }\left( e\lambda \right) ^{\lambda /2}}{\left( \lambda /2\right) ^{\lambda /2}} =\left( \frac{e}{2}\right) ^{-\lambda /2}=e^{-c\lambda }, \end{aligned}$$

for some $c>0.$ Therefore, ${\mathbb {P}}({\mathcal {A}}_k^c)\le e^{-cd\kappa _d k^{d-1}}$ so that ${\mathbb {P}}({\mathcal {A}}_k^c \text { i.o.})=0$ by the Borell-Cantelli lemma. Thus, for a.e. $\eta ,$ there exists a $K=K(\eta )<\infty ,$ so that ${\mathcal {A}}_k$ occurs for every $k\ge K.$ Furthermore, we have that if ${\mathcal {A}}_k$ occurs, then for any $k\ge 3$,

$$\begin{aligned}&\sum _{x\in \eta (A_k)}l^{\prime }(|x|)\ge \kappa _d k^{d-1}l^{\prime }(k+1)\\&\quad =\kappa _d k^{d-1}l(k+2) \ge \kappa _d \frac{k^{d-1}}{(k+3)^{d-1}}\int _{k+2}^{k+3}r^{d-1}l(r)dr \ge \frac{\kappa _d}{2}\int _{k+2}^{k+3}r^{d-1}l(r)dr. \end{aligned}$$

Therefore we get that by letting $K\ge 3,$

$$\begin{aligned} \Psi ^{\prime }(o)=\sum _{x\in \eta }l^{\prime }(|x|) \ge \sum _{k=K}^\infty \frac{\kappa _d}{2}\int _{k+2}^{k+3}r^{d-1}l(r)dr =\frac{\kappa _d}{2}\int _{K+2}^{\infty }r^{d-1}l(r)dr=\infty . \end{aligned}$$

$\square$

3 Continuity of the Field $\Psi$

In this section, we turn to the everywhere continuity of the field $\Psi$. This result will then be of use when proving Theorem 1.4.

Of course, if l is not continuous, everywhere continuity of $\Psi$ cannot hold. However, if l is continuous then everywhere continuity of the field $\Psi$ would be expected. We note that in the case of l being unbounded (i.e. $\lim _{r \rightarrow 0}l(r)=\infty$), we simply define $\Psi (y)=\infty$ for every $y\in \eta .$

Proposition 3.1

If l satisfies Assumption 1.1, $\int _1^\infty r^{d-1}l(r)dr<\infty$ and is continuous, then the random field $\Psi$ is a.s. everywhere continuous.

Proof of Proposition 3.1

We start by proving the statement in the case when l is bounded. Fix $\alpha ,\epsilon >0$, let $g_{y,z}(x)=|l(|x-y|)-l(|x-z|)|,$ and let $\{D_n\}_{n\ge 1}$ be a sequence of bounded subsets of ${\mathbb {R}}^d$ such that $D_n \uparrow {\mathbb {R}}^d.$ Observe that for any $\delta >0,$

$$\begin{aligned} \begin{aligned}&{\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } |\Psi (y)-\Psi (z)|\ge \epsilon \right) \\&\quad \le {\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } \sum _{x\in \eta } g_{y,z}(x)\ge \epsilon \right) \\&\quad \le {\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } \sum _{x\in \eta (D_n)} g_{y,z}(x)\ge \epsilon /2\right) \\&\qquad +{\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } \sum _{x\in \eta (D_n^c)} g_{y,z}(x)\ge \epsilon /2\right) . \end{aligned} \end{aligned}$$

(3.1)

We will proceed by bounding the two terms on the right hand side of (3.1). Consider therefore the second term

$$\begin{aligned}&{\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } \sum _{x\in \eta (D_n^c)} g_{y,z}(x)\ge \epsilon /2\right) \nonumber \\&\quad \le {\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } \sum _{x\in \eta (D_n^c)} l(|x-y|)+l(|x-z|)\ge \epsilon /2\right) \nonumber \\&\quad \le {\mathbb {P}}\left( \sup _{y\in B(o,1)} \sum _{x\in \eta (D_n^c)} l(|x-y|)+ \sup _{z\in B(o,1)} \sum _{x\in \eta (D_n^c)}l(|x-z|)\ge \epsilon /2\right) \nonumber \\&\quad ={\mathbb {P}}\left( \sup _{y\in B(o,1)} \sum _{x\in \eta (D_n^c)} l(|x-y|)\ge \epsilon /4\right) . \end{aligned}$$

(3.2)

Furthermore, we have that for any $\epsilon >0,$

$$\begin{aligned}&{\mathbb {P}}\left( \sup _{y\in B(o,1)} \sum _{x\in \eta (D_n^c)}l(|x-y|)\ge \epsilon \right) \le \frac{1}{\epsilon }{\mathbb {E}}\left[ \sup _{y\in B(o,1)} \sum _{x\in \eta (D_n^c)}l(|x-y|)\right] \nonumber \\&\quad \le \frac{1}{\epsilon }{\mathbb {E}}\left[ \sum _{x\in \eta (D_n^c)}\sup _{y\in B(o,1)}l(|x-y|)\right] =\frac{1}{\epsilon } \int _{{\mathbb {R}}^d{\setminus } D_n} \sup _{y\in B(o,1)}l(|x-y|) dx \\&\quad \le \frac{1}{\epsilon } \int _{{\mathbb {R}}^d{\setminus } D_n} l\left( \max (|x|-2,0)\right) dx \rightarrow 0 \text { as } n\rightarrow \infty , \nonumber \end{aligned}$$

(3.3)

where we use (2.2) in the equality and the fact that the intensity measure of $\eta (D_n^c)$ is Lebesgue measure outside of $D_n.$ We also use the integrability assumption $\int _0^\infty r^{d-1}l(r)dr<\infty$ (which follows from $\int _1^\infty r^{d-1}l(r)dr<\infty$ and l being bounded) when taking the limit. By combining (3.2) and (3.3), we see that by taking n large enough, the second term of (3.1) is smaller than $\alpha .$

For the first term, we get that

$$\begin{aligned}&{\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } \sum _{x\in \eta (D_n)} g_{y,z}(x) \ge \epsilon /2\right) \nonumber \\&\quad \le \frac{1}{\epsilon } {\mathbb {E}}\left[ \sum _{x\in \eta (D_n)}\sup _{y,z\in B(o,1):|y-z|<\delta } |l(|x-y|)-l(|x-z|)|\right] \\&\quad =\frac{1}{\epsilon } \int _{D_n}\sup _{y,z\in B(o,1):|y-z|<\delta } |l(|x-y|)-l(|x-z|)| dx. \nonumber \end{aligned}$$

(3.4)

Since $D_n$ is bounded, we have that for any $x\in D_n,$

$$\begin{aligned} \sup _{y,z\in B(o,1):|y-z|<\delta } |l(|x-y|)-l(|x-z|)| \le \sup _{(r_1,r_2)\in E_n}(l(r_1)-l(r_2)) \end{aligned}$$

where $E_n=\{(r_1,r_2)\in {\mathbb {R}}^2:0\le r_1<r_2\le 2\,\mathrm{diam}(D_n),|r_1-r_2|<\delta \}$. Since l(r) is continuous, it is uniformly continuous on $[0,2~\mathrm{diam}(D_n)]$. Therefore, for any fixed n,  the right hand side of (3.4) is smaller than $\alpha$ for $\delta$ small enough.

We conclude that for any $\epsilon ,\alpha >0,$ there exists $\delta >0,$ small enough so that

$$\begin{aligned} {\mathbb {P}}\left( \sup _{y,z\in B(o,1):|y-z|<\delta } |\Psi (y)-\Psi (z)|\ge \epsilon \right) \le 2 \alpha . \end{aligned}$$

(3.5)

To conclude the proof, assume that $\Psi (y)$ is not a.s. continuous everywhere. Then, with positive probability, there exists $\epsilon >0$ and a point $w\in B(o,1/2)$ such that for any $\delta >0$

$$\begin{aligned} \sup _{y:|y-w|<\delta } |\Psi (y)-\Psi (w)|\ge \epsilon , \end{aligned}$$

contradicting (3.5).

We now turn to the case where l is unbounded. Then, for any $M<\infty ,$ we let $l_M(r)=\min (l(r),M),$ and define $\Psi _M(y)$ to be the random field obtained by using $l_M$ instead of l. If we let

$$\begin{aligned} B_M(x)=\{y\in {\mathbb {R}}^d:l(|x-y|)\ge M\}, \end{aligned}$$

we see that $\Psi _M(y)=\Psi (y)$ for every $y\in {\mathbb {R}}^d{\setminus }\cup _{x\in \eta }B_M(x).$ By the first case, $\Psi _M(y)$ is continuous everywhere, and so $\Psi (y)$ is continuous for any $y\in {\mathbb {R}}^d{\setminus }\cup _{x\in \eta }B_M(x).$ Since $M<\infty$ was arbitrary, the statement follows after observing that $\lim _{y \rightarrow x}\Psi (y)=\infty$ whenever $x\in \eta .$ $\square$

4 Uniqueness

In this section we restrict ourselves to $d=2$. We will first consider the case of $\Psi _{> h}$, and then explain how the second case of Theorem 1.4 quickly follows from it. For convenience we formulate the following separate statement.

Theorem 4.1

Let h be such that $\Psi _{> h}$ contains an unbounded component. If l is continuous and with unbounded support, then for $d=2$, there is a unique such unbounded component.

Our strategy will be to adapt the argument in [7] which proves uniqueness for a class of models on ${\mathbb {Z}}^d$. In order to perform this adaptation it is much easier to work with arcwise connectedness rather than connectedness. The reason for this is that we can easily form new arcs from intersecting arcs, while the corresponding result for connectedness is rather challenging topologically.

However, in our continuous context, we have defined percolation in terms of connectedness, as is usually done. But, since $\Psi$ is a.s. continuous by Proposition 3.1, the set $\Psi _{>h}$ is a.s. an open set. For open sets, connected and arcwise connected are the same thing, as is well known. Hence, if x and y are in the same connected component of $\Psi _{>h}$, then there is a continuous curve from x to y in $\Psi _{>h}$. This observation makes $\Psi _{>h}$ easier to study than $\Psi _{\ge h}$ directly, and is the reason for proving Theorem 4.1 separately.

In the sequel we try to balance between the fact that we do not want or need to repeat the whole argument of [7] on the one hand, and the need to explain in detail what changes are to be made and what these changes constitute on the other hand.

In [7], uniqueness of the infinite cluster in two-dimensional discrete site percolation is proved under four conditions. Consider a probability measure $\mu$ on $\{0,1\}^{\mathbb {Z}^2}$ and let $\omega \in \{0,1\}^{\mathbb {Z}^2}$ be a configuration. If $\omega (x)=1$ we call $x\in {\mathbb {Z}}^2$ open and if $\omega (x)=0$ we call it closed. The four conditions which together imply uniqueness of the infinite open component are:

• 1. $\mu$ is invariant under horizontal and vertical translations and under axis reflections.

• 2. $\mu$ is ergodic (separately) under horizontal and vertical translations.

• 3. $\mu (E \cap F) \ge \mu (E)\mu (F)$ for events E and F which are both increasing or both decreasing (The FKG inequality).

• 4. The probability that the origin is in an infinite cluster is non-trivial, that is, strictly between 0 and 1.

In our context, conditions analogous to Conditions 1 and 2 clearly hold. Some care is needed for Condition 3 though. We will say that an event E is increasing if a configuration in E remains in E if we add additional points to the point process $\eta$ (and adapt the field accordingly). Furthermore, E is decreasing if $E^c$ is increasing. With these definitions, one can prove the analogue of the FKG inequality as in the proof of Theorem 2.2 in [14].

Condition 4 is natural in the discrete context. Indeed, if the probability that the origin is in an infinite cluster is 0, then by translation invariance, no infinite cluster can exist a.s. The case in which the probability that the origin is in an infinite cluster is 1 was excluded only for convenience, and this assumption is not used in the proof in [7]. In our continuous context, we need to be slightly more careful. Suppose that $\Psi _{>h}$ contains an unbounded component with positive probability. Since $\Psi _{>h}$ is an open set by continuity of the field, any such unbounded component must be open as well. Hence there must be an $\epsilon >0$ and an $x \in {\mathbb {R}}^2$ so that $B(x,\epsilon )$ is contained in an infinite component with positive probability, since a countable collection of such balls covers the plane. By translation invariance, the same must then be true for any $x\in {\mathbb {R}}^2$. Hence, any point $x \in {\mathbb {R}}^2$ is contained in an infinite component with positive probability, and Condition 4 holds.

Gandolfi, Keane and Russo prove uniqueness by showing that there exists a $\delta >0$ such that any box $B_n=[-n,n]^2$ is surrounded by an open path with probability at least $\delta$. Hence the probability that all such boxes are surrounded by an open path is at least $\delta$, and since the latter event is translation invariant it must have probability one. This ensures uniqueness, as is well known since 1960, see [10]. For the proof of Theorem 4.1, we can in principle follow the structure of their argument, with a number of modifications, as follows.

Proof of Theorem 4.1

For any set $A\subset {\mathbb {R}}^d,$ we will let $\Gamma _A:=\sup _{x\in A} \Psi (x).$

The first step is to show that it is impossible to have percolation in a horizontal strip $Q_M$ of the form

$$\begin{aligned} Q_M: =\{(x,y) \in {\mathbb {R}}^2; -M \le y \le M\}, \end{aligned}$$

and similarly for vertical strips. In their case this claim simply follows from the fact that closed sites exist (by virtue of Condition 4) and then it follows from Condition 3 that there is a positive probability that a strip is blocked completely by closed sites. Finally, ergodicity (or rather stationarity) shows that a strip is blocked infinitely many times in either direction.

Since we work in a continuous setting, this argument does not go through immediately. However, we can adapt it to our context. To this end, consider the set $C= C(N,M):=[N,N+1] \times [-M, M]$, that is, a vertical “strip” in $Q_M$. Since the field is a.s. finite, by deleting points one by one from $\eta$, say in increasing order with respect to distance to C, we have that upon deleting these points, $\Gamma _C \downarrow 0$. Hence, after deleting sufficiently many points it must be the case that $\Gamma _C <h$, for any given $h >0$. If we let ${\mathcal {D}}^o(L)$ denote the event that the contribution of points outside the box $B_{L}$ to $\Gamma _C$ is at most h, we conclude that for some (random) number L, ${\mathcal {D}}^o(L)$ occurs. It then follows that for some deterministic $L_0,$ ${\mathbb {P}}({\mathcal {D}}^o(L_0))>0.$ Note also that ${\mathcal {D}}^o(L_0)$ only depends on the points of $\eta$ outside $B_{L_0}$.

Let ${\mathcal {D}}^i(L_0)$ denote the event that there are no points of $\eta$ in $B_{L_0}$ itself. Then ${\mathbb {P}}({\mathcal {D}}^i(L_0))>0$ and by independence of ${\mathcal {D}}^i(L_0)$ and ${\mathcal {D}}^o(L_0)$, it also follows that ${\mathbb {P}}({\mathcal {D}}^i(L_0) \cap {\mathcal {D}}^o(L_0))>0$. Furthermore, on the event ${\mathcal {D}}^i(L_0) \cap {\mathcal {D}}^o(L_0),$ we have that $\Gamma _C <h$, and we conclude that for any $h>0$ there is positive probability that the field $\Psi$ does not exceed h on C. So any vertical strip in $C(N,M) \subset Q_M$ has positive probability to satisfy $\Gamma _C <h$ and by stationarity there must be infinitely many of such strips in both directions. So there can not be percolation in $Q_M$.

Having established this, we now turn to the second step of the argument. As mentioned above, in [7], they construct open paths whose union, by virtue of their specific construction, surround a given box. They show that for any given box, such a construction can be carried out with a uniform positive probability. It is at this point of the argument that two-dimensionality is crucial as the two-dimensional topology forces certain paths to intersect.

The remainder of the proof of uniqueness proceeds in two steps. First we prove uniqueness under the assumption that the half-plane $H^+:=\{(x,y); y \ge 0\}$ percolates. After that, we prove uniqueness under the assumption that $H^+$ does not percolate.

For $x \in {\mathbb {R}}^2, A, B \subset {\mathbb {R}}^2$, we write E(x, A, B) for the event that there is a continuous path in $\Psi _{>h}$ from x to A which is contained in B, and $E(x, \infty , B)$ if there is an unbounded continuous path from x in B. We write $L_N:=\{(x,y); y=N\}$, $L_N^+:=\{(x,y); y=N, x \ge 0\}$ and $L_N^-:=\{(x,y); y=N, x \le 0\}$. Finally we write $H_N^+:=\{(x,y); y \ge N\}$, so that $H_0^+ = H^+$.

Let $E :=E(0,\infty , H^+)$, let D be a box centered at the origin, and let $D_N := D + (0,N)$. Finally, let $\tilde{E}_N := E(0, \infty , H^+ \backslash D_N)$ and observe that while $\tilde{E}_N$ is clearly increasing in $\eta ,$ the event $\Gamma _{D_N}\le h$ is decreasing in $\eta .$ Therefore, by the FKG inequality we have that

$$\begin{aligned} {\mathbb {P}}(E){\mathbb {P}}(\Gamma _{D}\le h) \ge {\mathbb {P}}(\tilde{E}_N){\mathbb {P}}(\Gamma _{D_N}\le h) \ge {\mathbb {P}}\big (\tilde{E}_N \cap \left\{ \Gamma _{D_N}\le h\right\} \big ) = {\mathbb {P}}\big (E \cap \left\{ \Gamma _{D_N}\le h\right\} \big ). \end{aligned}$$

Since our system is mixing (see e.g. [14, p. 26] plus the fact that the field is a deterministic function of the Poisson process), we have that $\lim _{N \rightarrow \infty } {\mathbb {P}}(E \cap \left\{ \Gamma _{D_N}\le h\right\} ) ={\mathbb {P}}(E){\mathbb {P}}(\Gamma _{D}\le h)$. It follows that when $N \rightarrow \infty$, ${\mathbb {P}}(\tilde{E}_N) \rightarrow {\mathbb {P}}(E)$. In words, if percolation occurs from the origin in $H^+$ with positive probability, then the conditional probability that there is an unbounded path avoiding $D_N$ tends to 1 as $N \rightarrow \infty$.

Hence, if the probability that $y_{-N}:=(0,-N)$ percolates in $H^+_{-N}$ is $\delta >0$, then for N large enough,

$$\begin{aligned} {\mathbb {P}}(E(y_{-N}, \infty , H_{-N}^+\backslash D))\ge \delta /2. \end{aligned}$$

Since the strip $Q_N$ does not percolate, if $y_{-N}$ percolates in $H^+_{-N}\backslash D$, we conclude that the event $E(y_{-N}, L_N, Q_N\backslash D)$ must occur, so that ${\mathbb {P}}(E(y_{-N}, L_N, Q_N\backslash D)) \ge \delta /2$.

The endpoint of the curve in the event $E(y_{-N}, L_N, Q_N\backslash D)$ is either in $L_N^+$ or in $L_N^-$, and by reflection symmetry, both options have the same probability. Hence,

$$\begin{aligned} {\mathbb {P}}(E(y_{-N}, L_N^+, Q_N\backslash D))\ge \delta /4. \end{aligned}$$

By reflection symmetry, it then follows that also

$$\begin{aligned} {\mathbb {P}}(E(y_{N}, L_{-N}^+, Q_N\backslash D))\ge \delta /4, \end{aligned}$$

and by combining the curves in the last two displayed formulas and the FKG inequality, we find that

$$\begin{aligned} {\mathbb {P}}(E(y_{N}, y_{-N}, Q_N\backslash D))\ge \delta ^2/16. \end{aligned}$$

(4.1)

Any curve in the event $E(y_{N}, y_{-N}, Q_N\backslash D)$ either has D on the left or on the right (depending whether it has positive or negative winding number) and again by reflection symmetry, both possibilities must have probability at least $\delta ^2/32$. Let $J^+$ ($J^-$) be the sub-event of $E(y_{N}, y_{-N}, Q_N\backslash D)$ where there exists a curve with positive (negative) winding number. By the FKG inequality, we have that ${\mathbb {P}}(J^+ \cap J^-) \ge \delta ^4/1024$. But on $J^+ \cap J^-$, the box D is surrounded by a continuous curve in $\Psi _{>h}$, and we are done.

Finally, we consider the case in which the half space does not percolate. We can modify the argument in [7] similarly and we do not spell out all details. In the first case we showed that if we have percolation from the origin in $H^+$, the conditional probability that there is an unbounded path avoiding $D_N$ tends to 1 as $N \rightarrow \infty$. In this second case it turns out that we need to show that this remains true if we in addition also want to avoid $D_{-N}$. For this, the usual mixing property that we used above, does not suffice, and a version of 3-mixing is necessary. As in [7], we use Theorem 4.11 in [6] for this, in which it is shown that ordinary weak mixing implies 3-mixing along a sequence of density 1. Since our system is weakly mixing, this application of Theorem 4.11 in [6] is somewhat simpler than in [7], but other than that our argument is the same, and we do not repeat it here. $\square$

Finally we show how Theorem 4.1 implies Theorem 1.4.

Proof of Theorem 1.4

We first claim that $\Psi _{>h}$ percolates with probability one if and only if $\Psi _{\ge h}$ percolates with probability one. The “only if” is clear, since $\Psi _{> h} \subset \Psi _{\ge h}$.

Next, suppose that $\Psi _{\ge h}$ percolates with probability one. By definition, this implies that $\Psi _{\ge h}$ a.s. contains an unbounded connected component. Let us denote this event by $C_h$. Let A be a bounded region with positive area. Since the probability of $C_h$ is 1, it must be the case that

$$\begin{aligned} {\mathbb {P}}(C_h| \eta (A)=0)=1, \end{aligned}$$

where $\eta (A)$ is (as usual) the number of points of the Poisson process in A. Since we can sample from the conditional distribution of the process given $\eta (A)=0$ by first sampling unconditionally and then simply remove all points in A, it follows that we cannot destroy the event of percolation by removing all points in A.

Hence if we take all points out from A, the resulting field $\Psi ^A$, say, will be such that $\Psi ^A_{\ge h}$ percolates a.s. But if $\eta (A) >0$, then it is the case that $\Psi ^A_{\ge h} \subseteq \Psi _{>h}$, and it is precisely here we assume that the attenuation function l has unbounded support. Hence, with positive probability we have that $\Psi _{>h}$ percolates, and by ergodicity this implies that $\Psi _{>h}$ contains an infinite component a.s.

We can now quickly finish the proof. Suppose that $\Psi _{\ge h}$ percolates. Then, as we just saw, also $\Psi _{>h}$ percolates. Hence we can apply the proof of Theorem 4.1, and conclude that $\Psi _{>h}$ does contain continuous curves around each box. Since $\Psi _{\ge h}$ is an even larger set, the same must be true for $\Psi _{\ge h}$ and uniqueness for this latter set follows as before. $\square$

In light of Theorem 1.4, it is of course natural to expect that uniqueness should hold also for $d\ge 3.$ The classical argument for uniqueness in various lattice models and continuum percolation consists of two parts. Below we examine these separately.

Let $N_h$ be the number of unbounded components in $\Psi _{\ge h}$. Following the arguments of [16] (which is for the lattice case but can easily be adapted to the setting of Boolean percolation, see [14] Proposition 3.3) one starts by observing that ${\mathbb {P}}(N_h=k)=1$ for some $k\in \{0,1,\ldots \}\cup \{\infty \}.$ Assume for instance that ${\mathbb {P}}(N_h=3)=1$, and proceed by taking a box $[-n,n]^d$ large enough so that at least two of these infinite components intersect the box with positive probability. Then, glue these two components together by the use of a finite energy argument. That is, turn all sites in the box to state 1 in the discrete case, or add balls to the box in the Boolean percolation case. In this way, we reduce $N_h$ by (at least) 1, showing that ${\mathbb {P}}(N_h=3)<1,$ a contradiction. If one attempts to repeat this procedure in our setting (with the support of l being unbounded), one finds that by adding points to the field, the gluing of two infinite components might at the same time result in the forming of a completely new infinite component somewhere outside the box. Therefore, one cannot conclude that ${\mathbb {P}}(N_h=3)<1$.

The second difficulty occurs when attempting to rule out the possibility that ${\mathbb {P}}(N_h=\infty )=1.$ For the Boolean percolation model one uses an argument by Burton and Keane in [4], adapted to the case of Boolean percolation (see [14] proof of Theorem 3.6). However this argument hinges on the trivial but crucial fact that for this model any unbounded component must contain infinitely many points of the Poisson process $\eta$. This is not the case in our setting. An unbounded component can in principle contain only a finite number of points of $\eta$, or indeed none at all.

We now turn to the last result of this paper, Theorem 1.5. In order to prove continuity, we will give separate arguments for left- and right-continuity. The strategy to prove right-continuity will be similar to the corresponding result (i.e. left-continuity) for discrete lattice percolation (see [9, Sect. 8.3]). However, while the other case is trivial for discrete percolation, this is where most of the effort in proving Theorem 1.5 lies. Before giving the full proof, we will need to establish two lemmas that will be used to prove left-continuity. See also the remark after the end of the proof of Theorem 1.5.

Let $X^0\sim$Poi$(\lambda )$, and let $X^1=X^0+1.$ The following lemma provides a useful coupling.

Lemma 4.2

There exist random variables $Y^0\mathop {=}\limits ^{d}X^0$ and $Y^1\mathop {=}\limits ^{d}X^1$ coupled so that

$$\begin{aligned} {\mathbb {P}}\big (Y^0\ne Y^1\big ) =\frac{\lambda ^{\lfloor \lambda \rfloor }+1}{(\lfloor \lambda \rfloor +1)!} e^{-\lambda }. \end{aligned}$$

Proof

In what follows, sums of the form $\sum _{l=M}^{M-1} a_l$ is understood to be 0, and in order not to introduce cumbersome notation, expressions such as $\lambda ^k/k!$ will be interpreted as 0 for $k<0.$ Note also that

$$\begin{aligned} \frac{{\mathbb {P}}(X^0=k)}{{\mathbb {P}}(X^1=k)} =\frac{\frac{\lambda ^k}{k!}e^{-\lambda }}{\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda }} =\frac{\lambda }{k}\ge 1 \quad \text {iff}\,\,\, k\le \lambda . \end{aligned}$$

(4.2)

We start by giving the coupling and then verify that it is well defined and has the correct properties. Let $U \sim U[0,1]$ and for $1\le k \le \lambda$ let $Y^0=Y^1=k$ if

$$\begin{aligned} \sum _{l=0}^{k-2}\frac{\lambda ^{l}}{l!}e^{-\lambda } <U\le \sum _{l=0}^{k-1}\frac{\lambda ^{l}}{l!}e^{-\lambda } \end{aligned}$$

(4.3)

while for $k>\lambda$ we let $Y^0=Y^1=k$ if

$$\begin{aligned} \sum _{l=0}^{\lfloor \lambda \rfloor }\frac{\lambda ^l}{l!}e^{-\lambda } +\sum _{l=\lfloor \lambda \rfloor +2}^{k-1}\frac{\lambda ^l}{l!}e^{-\lambda } <U\le \sum _{l=0}^{\lfloor \lambda \rfloor }\frac{\lambda ^l}{l!}e^{-\lambda } +\sum _{l=\lfloor \lambda \rfloor +2}^{k}\frac{\lambda ^l}{l!}e^{-\lambda } \end{aligned}$$

(4.4)

Furthermore, we let $Y^0=k$ if $k\le \lambda$ and

$$\begin{aligned} 1-\frac{\lambda ^k}{k!}e^{-\lambda } < U\le 1-\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda } \end{aligned}$$

(4.5)

while $Y^1=k$ if $k> \lambda$ and

$$\begin{aligned} 1-\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda }<U \le 1-\frac{\lambda ^{k}}{k!}e^{-\lambda }. \end{aligned}$$

(4.6)

Consider now (4.5). Since $k\le \lambda$ it follows from (4.2) that

$$\begin{aligned} 1-\frac{\lambda ^k}{k!}e^{-\lambda } \le 1-\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda }, \end{aligned}$$

with equality iff $k=\lambda .$ It follows that (4.5) is well defined, and similarly we can verify that (4.6) is also well defined.

We proceed to verify that (4.3)–(4.6) gives the correct distributions of $Y^0$ and $Y^1$. To this end, observe that from (4.3) and (4.5) we have that for $0\le k\le \lambda$

$$\begin{aligned} {\mathbb {P}}\big (Y^0=k\big )=\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda } +\frac{\lambda ^{k}}{k!}e^{-\lambda }-\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda } =\frac{\lambda ^{k}}{k!}e^{-\lambda }. \end{aligned}$$

Furthermore, from (4.3) we get that for $k>\lambda ,$

$$\begin{aligned} {\mathbb {P}}(Y^0=k)=\frac{\lambda ^{k}}{k!}e^{-\lambda } \end{aligned}$$

so that indeed $Y^0\sim$Poi$(\lambda ).$

Similarly, we see from (4.3) that for $1\le k \le \lambda$ we have that

$$\begin{aligned} {\mathbb {P}}\big (Y^1=k\big )=\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda }, \end{aligned}$$

while by summing the contributions from (4.4) and (4.6) we get that for $k>\lambda$

$$\begin{aligned} {\mathbb {P}}(Y^1=k) =\frac{\lambda ^k}{k!}e^{-\lambda }+\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda } -\frac{\lambda ^{k}}{k!}e^{-\lambda } =\frac{\lambda ^{k-1}}{(k-1)!}e^{-\lambda }, \end{aligned}$$

so that $Y^1$ has the desired distribution.

Finally, the lemma follows by observing that

$$\begin{aligned} {\mathbb {P}}(Y^0\ne Y^1)={\mathbb {P}}\left( U>\sum _{l=0}^{\lfloor \lambda \rfloor }\frac{\lambda ^l}{l!}e^{-\lambda } +\sum _{l=\lfloor \lambda \rfloor +2}^{\infty }\frac{\lambda ^l}{l!}e^{-\lambda }\right) =\frac{\lambda ^{\lfloor \lambda \rfloor }+1}{(\lfloor \lambda \rfloor +1)!} e^{-\lambda }. \end{aligned}$$

$\square$

Let $\eta ^0_n$ be a homogeneous Poisson process in ${\mathbb {R}}^2$ with rate 1, and let $\eta ^1_n$ be a point process such that $\eta ^1_n\mathop {=}\limits ^{d} \eta ^0_n+\delta _{V_n}$ where $V_n\sim$U$(B_n)$ and $B_n=[-n,n]^2$. Thus $\eta ^1_n$ is constructed by adding a point uniformly located within the box $B_n$ to a homogeneous Poisson process in ${\mathbb {R}}^2$. Let ${\mathbb {P}}_n^i$ be the distribution of $\eta ^i_n$ for $i=0,1$ and let

$$\begin{aligned} d_{TV}\big ({\mathbb {P}}_n^0,{\mathbb {P}}_n^1\big ):=\sup _{A}|{\mathbb {P}}_n^0(A)-{\mathbb {P}}_n^1(A)| \end{aligned}$$

be the total variation distance between ${\mathbb {P}}_n^0$ and ${\mathbb {P}}_n^1$, where the supremum is taken over all measurable events A.

Lemma 4.3

For any $n\ge 1$ we have that

$$\begin{aligned} d_{TV}\big ({\mathbb {P}}_n^0,{\mathbb {P}}_n^1\big )\le \frac{(4n^2)^{4n^2+1}}{(4n^2+1)!}e^{-4n^2} \le n^{-1}. \end{aligned}$$

Proof

Let $\lambda =4n^2$ and pick $Y^0,Y^1$ as in Lemma 4.2. Furthermore, let $\eta$ be a homogeneous Poisson process in ${\mathbb {R}}^2,$ independent of $Y^0$ and $Y^1,$ and let $(U_k)_{k\ge 1}$ be an i.i.d. sequence independent of $Y^0,Y^1$ and $\eta$ and such that $U_k\sim$U$(B_n)$. Then, define

$$\begin{aligned} \eta _n^0:=\eta \big (B_n^c\big )+\sum _{k=1}^{Y^0}\delta _{U_k}, \end{aligned}$$

and

$$\begin{aligned} \eta _n^1:=\eta \big (B_n^c\big )+\sum _{k=1}^{Y^1}\delta _{U_k}. \end{aligned}$$

It is easy to see that $\eta _n^i\sim {\mathbb {P}}_n^i$ and that

$$\begin{aligned} {\mathbb {P}}\Big (\eta _n^0\ne \eta _n^1\Big )={\mathbb {P}}(Y^0\ne Y^1). \end{aligned}$$

(4.7)

Thus, for any measurable event A, we have that

$$\begin{aligned}&|{\mathbb {P}}_n^0(A)-{\mathbb {P}}_n^1(A)|={\mathbb {P}}(\eta _n^0\in A, \eta _n^1 \not \in A) +{\mathbb {P}}(\eta _n^1\in A, \eta _n^0 \not \in A)\\&\quad \le {\mathbb {P}}(\eta _n^0\ne \eta _n^1) \le \frac{(4n^2)^{4n^2+1}}{(4n^2+1)!}e^{-4n^2}, \end{aligned}$$

by using (4.7) and Lemma 4.2.

Furthermore, by Stirling’s approximation, we see that

$$\begin{aligned} \frac{(4n^2)^{4n^2+1}}{(4n^2+1)!}e^{-4n^2} \le \frac{(4n^2)^{4n^2}}{4n^2!}e^{-4n^2} \le \frac{(4n^2)^{4n^2}}{\sqrt{2\pi }(4n^2)^{4n^2+1/2}e^{-4n^2}}e^{-4n^2} \le n^{-1}. \end{aligned}$$

$\square$

Remark

Although we choose to state and prove this only for $d=2,$ a version of this lemma obviously holds for all $d\ge 1.$

We are now ready to give the proof of our last result.

Proof of Theorem 1.4

We start by proving the left-continuity of $\theta _{>}(h).$ We claim that

$$\begin{aligned} \lim _{g \uparrow h} \theta _{>}(g)={\mathbb {P}}({\mathcal {C}}_{o,>}(g) \text { is unbounded for every } g<h)={\mathbb {P}}({\mathcal {C}}_{o,\ge }(h) \text { is unbounded}).\nonumber \\ \end{aligned}$$

(4.8)

To see this, observe first that trivially

$$\begin{aligned} \left\{ {\mathcal {C}}_{o,\ge }(h) \text { is unbounded}\} \subset \bigcap _{g<h} \{{\mathcal {C}}_{o,>}(g) \text { is unbounded}\right\} . \end{aligned}$$

Secondly, assume that ${\mathcal {C}}_{o,\ge }(h)$ is bounded. Since ${\mathcal {C}}_{o,\ge }(h)$ and $\Psi _{\ge h} {\setminus } {\mathcal {C}}_{o,\ge }(h)$ are disconnected, there exist open sets $G_1,G_2$ such that $G_1$ is connected, ${\mathcal {C}}_{o,\ge }(h) \subset G_1$, $\Psi _{\ge h} {\setminus } {\mathcal {C}}_{o,\ge }(h)\subset G_2$ and $G_1 \cap G_2=\emptyset .$ Therefore, the set $G_3=G_1{\setminus } {\mathcal {C}}_{o,\ge }(h)$ is an open connected set separating the origin o from $\infty .$ Since $G_3$ is then also arcwise connected, it follows that it must contain a circuit surrounding the origin. That is, there exists a continuous function $\gamma :[0,1] \rightarrow {\mathbb {R}}^2$ such that $\gamma (0)=\gamma (1)$ and $\gamma$ separates o from $\infty .$ Since $\gamma$ is continuous, the image of $\gamma$ (Im$(\gamma )$) is compact, and so $\sup _{t\in [0,1]}\Psi (\gamma (t))$ is obtained, since $\Psi$ is continuous by Proposition 3.1. By construction, $G_3 \subset {\mathbb {R}}^2{\setminus } \Psi _{\ge h}$ and so Im$(\gamma ) \subset {\mathbb {R}}^2 {\setminus } \Psi _{\ge h}.$ We conclude that $\sup _{t\in [0,1]}\Psi (\gamma (t))<h.$ Therefore, for any g such that $\sup _{t\in [0,1]}\Psi (\gamma (t))<g<h$ we must have that ${\mathcal {C}}_{o,>}(g)$ is bounded. This proves (4.8).

Let n be any integer and take

$$\begin{aligned} \eta \in \{{\mathcal {C}}_{o,\ge }(h) \text { is unbounded}\} {\setminus } \{{\mathcal {C}}_{o,>}(h) \text { is unbounded}\}. \end{aligned}$$

Let $\eta ^1_n=\eta +\delta _{V_n}$ where $V_n\sim$U$(B_n)$ and observe that since l has unbounded support,

$$\begin{aligned} \eta _n^1\in \{{\mathcal {C}}_{o,>}(h) \text { is unbounded}\}. \end{aligned}$$

Using Lemma 4.3 we get that

$$\begin{aligned}&{\mathbb {P}}({\mathcal {C}}_{o,\ge }(h) \text { is unbounded}) \\&\quad \le {\mathbb {P}}^1_n({\mathcal {C}}_{o,>}(h) \text { is unbounded}) \le {\mathbb {P}}^0_n({\mathcal {C}}_{o,>}(h) \text { is unbounded})+n^{-1} =\theta _{>}(h)+n^{-1}. \end{aligned}$$

This together with (4.8) yields

$$\begin{aligned} \lim _{g \uparrow h} \theta _{>}(g)\le \lim _{n \rightarrow \infty }\theta _{>}(h)+n^{-1} =\theta _{>}(h). \end{aligned}$$

It remains to prove that

$$\begin{aligned} \lim _{g \downarrow h} \theta _{>}(g)=\theta _{>}(h), \end{aligned}$$

(4.9)

for $h<h_c,$ and we will use a similar approach as above. We note that

$$\begin{aligned} \lim _{g \downarrow h} {\mathbb {P}}({\mathcal {C}}_{o,>}(g) \text { is unbounded}) ={\mathbb {P}}({\mathcal {C}}_{o,>}(g) \text { is unbounded for some } g>h). \end{aligned}$$

(4.10)

Assume that ${\mathcal {C}}_{o,>}(h)$ contains an unbounded component, and consider any $h<g<h_c.$ Since $\Psi _{>g}$ also must contain an unbounded component $I_g,$ and since by Theorem 1.4 we know that this is unique, we conclude that $I_g \subset {\mathcal {C}}_{o,>}(h).$ As above, ${\mathcal {C}}_{o,>}(h)$ is an open set, and therefore arcwise connected. Thus, for $z\in I_g,$ there exists a continuous function $\phi :[0,1]\rightarrow {\mathbb {R}}^2$ such that $\phi (0)=o$ and $\phi (1)=z.$ Since $\phi$ is continuous, Im$(\phi )$ is compact, and so $\inf _{t\in [0,1]}\Psi (\phi (t))$ is obtained, since $\Psi$ is continuous by Proposition 3.1. Furthermore, since Im$(\phi ) \subset {\mathcal {C}}_{o,>}(h),$ we conclude that $\inf _{t\in [0,1]}\Psi (\phi (t))>h.$ Therefore, for some $h<g^{\prime }<h_c$ we also have that $\inf _{t\in [0,1]}\Psi (\phi (t))>g^{\prime }$, and so ${\mathcal {C}}_{o,>}(g^{\prime })$ contains an unbounded component. We conclude that

$$\begin{aligned} {\mathbb {P}}({\mathcal {C}}_{o,>}(g) \text { is unbounded for some } g>h) ={\mathbb {P}}({\mathcal {C}}_{o,>}(h) \text { is unbounded}). \end{aligned}$$

(4.11)

Combining Eqs. (4.10) and (4.11) we conclude that (4.9) holds.

In order to complete the proof, we simply observe that for any $g<h$ we have that $\theta _>(h)\le \theta _{\ge }(h)\le \theta _>(g)$ so that

$$\begin{aligned} \theta _>(h)\le \theta _{\ge }(h) \le \liminf _{g \uparrow h} \theta _{>}(g)=\theta _>(h), \end{aligned}$$

so that indeed $\theta _>(h)=\theta _{\ge }(h)$ for every $h<h_c.$ $\square$

Remark

Consider the event $\{o\leftrightarrow \partial B_n\}$, that the origin is connected to the boundary of $B_n.$ In the discrete case, it is trivial that ${\mathbb {P}}_p(o \leftrightarrow \partial B_n)$ is continuous as a function of the percolation parameter p,  since it is an event that depends on the state of only finitely many edges. This then gives an easy proof of right-continuity (corresponding to left-continuity in our case). In our model, points of $\eta$ at any distance contribute to the field in $B_n.$ Therefore, we cannot claim immediate continuity of ${\mathbb {P}}(o \leftrightarrow \partial B_n)$, although our methods above can be used to prove it.