Leveraging Environmental Correlations: The Thermodynamics of Requisite Variety

Abstract

Key to biological success, the requisite variety that confronts an adaptive organism is the set of detectable, accessible, and controllable states in its environment. We analyze its role in the thermodynamic functioning of information ratchets—a form of autonomous Maxwellian Demon capable of exploiting fluctuations in an external information reservoir to harvest useful work from a thermal bath. This establishes a quantitative paradigm for understanding how adaptive agents leverage structured thermal environments for their own thermodynamic benefit. General ratchets behave as memoryful communication channels, interacting with their environment sequentially and storing results to an output. The bulk of thermal ratchets analyzed to date, however, assume memoryless environments that generate input signals without temporal correlations. Employing computational mechanics and a new information-processing Second Law of Thermodynamics (IPSL) we remove these restrictions, analyzing general finite-state ratchets interacting with structured environments that generate correlated input signals. On the one hand, we demonstrate that a ratchet need not have memory to exploit an uncorrelated environment. On the other, and more appropriate to biological adaptation, we show that a ratchet must have memory to most effectively leverage structure and correlation in its environment. The lesson is that to optimally harvest work a ratchet’s memory must reflect the input generator’s memory. Finally, we investigate achieving the IPSL bounds on the amount of work a ratchet can extract from its environment, discovering that finite-state, optimal ratchets are unable to reach these bounds. In contrast, we show that infinite-state ratchets can go well beyond these bounds by utilizing their own infinite “negentropy”. We conclude with an outline of the collective thermodynamics of information-ratchet swarms.

Appendices

Appendix 1: Optimally Leveraging Memoryless Inputs

It is intuitively appealing to think that memoryless inputs are best utilized by memoryless ratchets. In other words, the optimal ratchet for a memoryless input is a memoryless ratchet. We prove the validity of this intuition in the following. We start with the expression of work production per time step:

$$\begin{aligned} \beta \langle W \rangle&= \sum _{x,x',y,y'} \pi _{x \otimes y} M_{x \otimes y \rightarrow x' \otimes y'} \ln \frac{M_{x' \otimes y' \rightarrow x \otimes y}}{M_{x \otimes y \rightarrow x' \otimes y'}} \\&= \sum _{x,x',y,y'} \pi _{x \otimes y} M_{x \otimes y \rightarrow x' \otimes y'}\ln \frac{\pi _{x' \otimes y'}M_{x' \otimes y' \rightarrow x \otimes y}}{\pi _{x \otimes y}M_{x \otimes y \rightarrow x' \otimes y'}} \nonumber \\&\qquad -\sum _{x,x',y,y'} \pi _{x \otimes y} M_{x \otimes y \rightarrow x' \otimes y'}\ln \frac{\pi _{x' \otimes y'}}{\pi _{x \otimes y}}, \nonumber \end{aligned}$$

with $\beta =1/k_B T$. The benefit of the decomposition in the second line will be clear in the following. Let us introduce several quantities that will also be useful in the following:

$$\begin{aligned} p(x,y,x',y')&=\pi _{x \otimes y} M_{x \otimes y \rightarrow x' \otimes y'}, \\ p_R(x,y,x',y')&= \pi _{x' \otimes y'} M_{x' \otimes y' \rightarrow x \otimes y}, \\ \pi ^X_x&=\sum _y \pi _{x \otimes y}, \\ \pi ^Y_y&=\sum _x \pi _{x \otimes y}, \\ p^X(x,x')&=\sum _{y,y'}p(x,y,x',y'),~\text {and}\\ p^Y(y,y')&=\sum _{x,x'}p(x,y,x',y'). \end{aligned}$$

For a memoryless input process, sequential inputs are statistically independent. This implies $Y_N$ and $X_N$ are independent, so the stationary distribution $\pi _{x \otimes y}$ can be written as a product of marginals:

$$\begin{aligned} \pi _{x \otimes y} = \pi ^X_x \pi ^Y_y. \end{aligned}$$

(16)

In terms of the above quantities, we can rewrite work for a memoryless input process as:

$$\begin{aligned} \beta \langle W \rangle&= -D_{KL}(p \Vert p_R) \\&\quad \quad - \sum _{y,y'}p^Y(y,y')\ln \frac{\pi ^Y_{y'}}{\pi ^Y_y} -\sum _{x,x'}p^X(x,x')\ln \frac{\pi ^X_{x'}}{\pi ^X_x}, \end{aligned}$$

where $D_{KL}(p \Vert p_R)$ is the relative entropy of the distribution p with respect to $p_R$ [52]. Note that the last term in the expression vanishes, since the ratchet state distribution is the same before and after an interaction interval:

$$\begin{aligned} \sum _x p^X(x,x') =\sum _x p^X(x',x) =\pi ^X_{x'}, \end{aligned}$$

(17)

and so:

$$\begin{aligned} \sum _{x,x'} p^X(x,x') \ln \frac{\pi ^X_{x'}}{\pi ^X_x}&= \sum _{x,x'}p^X(x,x')\ln \pi ^X_{x'}-\sum _{x,x'}p^X(x,x')\ln \pi ^X_{x} \\&= \sum _{x'}\pi ^X_{x'}\ln \pi ^X_{x'}-\sum _{x}\pi ^X_{x}\ln \pi ^X_{x} \\&= 0. \end{aligned}$$

Thus, we find find the average work production to be:

$$\begin{aligned} \beta \langle W \rangle =-D_{KL}(p \Vert p_R)-\sum _{y,y'}p^Y(y,y') \ln \frac{\pi ^Y_{y'}}{\pi ^Y_y} ~. \end{aligned}$$

(18)

Let us now use the fact that the coarse graining of any two distributions, say p and q, yields a smaller relative entropy between the two [52, 61]. In the work formula, $p^Y$ is a coarse graining of p and $p^Y_R$ is a coarse graining of $p^R$, implying:

$$\begin{aligned} D_{KL}(p^Y \Vert p^Y_R) \le D_{KL}(p \Vert p_R) ~. \end{aligned}$$

(19)

Combining the above relations, we find the inequality:

$$\begin{aligned} \beta \langle W \rangle \le -D_{KL}(p^Y \Vert p^Y_R)-\sum _{y,y'}p^Y(y,y')\ln \frac{\pi ^Y_{y'}}{\pi ^Y_y}. \end{aligned}$$

Now, the marginal transition probability $p^Y(y,y')$ can be broken into the product of the stationary distribution over the input variable $\pi ^Y_{y}$ and a Markov transition matrix $M^Y_{y \rightarrow y'}$ over the input alphabet:

$$\begin{aligned} p^Y(y,y') = \pi ^Y_yM^Y_{y \rightarrow y'}, \end{aligned}$$

which for any ratchet M is:

$$\begin{aligned} M^Y_{y \rightarrow y'}&= \frac{1}{\pi _y^Y} p^Y(y, y') \\&= \frac{1}{\pi _y^Y} \sum _{x,x'} \pi _{x \otimes y} M_{x \otimes y \rightarrow x' \otimes y'} \\&= \frac{1}{\pi _y^Y} \sum _{x,x'} \pi _x^X \pi _y^Y M_{x \otimes y \rightarrow x' \otimes y'} \\&= \sum _{x,x'} \pi _x^X M_{x \otimes y \rightarrow x' \otimes y'}. \end{aligned}$$

We can treat the Markov matrix $M^Y$ as corresponding to a ratchet in the same way as M. Note that $M^Y$ is effectively a memoryless ratchet since we do not need to refer to the internal states of the corresponding ratchet. See Fig. 2. The resulting work production for this ratchet $\langle W^Y \rangle$ can be expressed as:

$$\begin{aligned} \beta \langle W^Y \rangle&=\sum _{y,y'} \pi ^{Y}_y M^Y_{y \rightarrow y'} \ln \frac{M^Y_{y' \rightarrow y}}{M^Y_{y \rightarrow y'}} \\&= -D_{KL}(p^Y \Vert p^Y_R)-\sum _{y,y'}p^Y(y,y')\ln \frac{\pi ^Y_{y'}}{\pi ^Y_y} \\&\ge \beta \langle W \rangle . \end{aligned}$$

Thus, for any memoryful ratchet driven by a memoryless input we can design a memoryless ratchet that extracts at least as much work as the memoryful ratchet.

There is, however, a small caveat. Strictly speaking, we must assume the case of binary input. This is due to the requirement that the matrix M be detailed balanced (see Sect. 2) so that the expression of work used here is appropriate. More technically, the problem is that we do not yet have a proof that if M is detailed balanced then so is $M^Y$, a critical requirement above. In fact, there are examples where $M^Y$ does not exhibit detailed balance. We do, however, know that $M^Y$ is guaranteed to be detailed balanced if $\mathcal {Y}$ is binary, since that means $M^Y$ only has two states and all flows must be balanced. Thus, for memoryless binary input processes, we established that there is little point in using finite memoryful ratchets to extract work: memoryless ratchets extract work optimally from memoryless binary inputs.

Appendix 2: An IPSL for Information Engines

Reference [27] proposed a generalization of the Second Law of Thermodynamics to information processing systems (IPSL, Eq. 1) under the premise that the Second Law can be applied even when the thermodynamic entropy of the information bearing degrees of freedom is taken to be their Shannon information entropy. This led to a consistent prediction of the thermodynamics of information engines. It was also validated through numerical calculations. This appendix proves this assertion for the class of information engines considered here. The key idea is to use the irreversibility of the Markov chain dynamics followed by the engine and by the information bearing degrees of freedom to derive the IPSL inequality.

Fig. 10

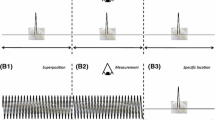
The demon $\text {D}$ interacts with one bit at a time for a fixed time interval; for example, with bit $\text {B}_N$ for the time interval $t = N$ to $t = N + 1$. During this, the demon changes the state of the bit from (input) $Y_N$ to (output) $Y'_N$. There is an accompanying change in $\text {D}$’s state as well, not shown. The joint dynamics of $\text {D}$ and $\text {B}_N$ is governed by the Markov chain $M_{\text {D}\otimes \text {B}_N}$

For the sake of presentation, we introduce new notation here. We refer to the engine as the demon $\text {D}$, following the original motivation for information engines. We refer to the information-bearing two-state systems as the bits $\text {B}$. According to our set up, $\text {D}$ interacts with an infinite sequence of bits, $\text {B}_0 \text {B}_1 \text {B}_2 \ldots$ as shown in Fig. 10. The figure also explains the connection of the current terminology to that in the main text. In particular, we show two snapshots of our setup, at times $t = N$ and $t = N + 1$. During that interval $\text {D}$ interacts with bit $\text {B}_\text {N}$ and changes it from (input) symbol $Y_N$ to (output) symbol $Y'_N$. The corresponding dynamics is governed by the Markov transition matrix $M_{\text {D}\otimes \text {B}_N}$ which acts only on the joint subspace of $\text {D}$ and $\text {B}_N$.

Under Markov dynamics the relative entropy of the current distribution with respect to the asymptotic steady-state distribution is a monotonically decreasing function of time. We now use this property for the transition matrix $M_{\text {D}\otimes \text {B}_N}$ to derive the IPSL. Denote the distribution of $\text {D}$’s states and the bits $\text {B}$ at time t by $P_{\text {D}\text {B}_{0:\infty }}(t)$. Here, $\text {B}_{0:\infty }$ stands for all the information-bearing degrees of freedom.¹ The steady-state distribution corresponding to the operation of $M_{\text {D}\otimes \text {B}_N}$ is determined via:

$$\begin{aligned} \lim _{n \rightarrow \infty } M_{\text {D}\otimes \text {B}_N}^n P_{\text {D}\text {B}_{0:\infty }} (N)&= \pi _{\text {D}\text {B}_N}^\text {eq} P_{\text {B}_{0:\infty /N}} (N) \end{aligned}$$

(20)

$$\begin{aligned}&\equiv \pi ^\text {s}(N), \end{aligned}$$

(21)

where $\pi _{\text {D}\text {B}_N}^\text {eq}$ denotes the steady-state distribution:

$$\begin{aligned} M_{\text {D}\otimes \text {B}_N} \pi _{\text {D}\text {B}_N}^\text {eq} = 0 \end{aligned}$$

and $P_{\text {B}_{0:\infty /N}} (N)$ the marginal distribution of all the bits other than the N-th bit at time $t = N$. We introduce $\pi ^\text {s}(N)$ in Eq. (21) for brevity.

The rationale behind the righthand side of Eq. (20) is that the matrix $M_{\text {D}\otimes \text {B}_N}$ acts only on $\text {D}$ and $\text {B}_N$, sending to their joint distribution to the stationary distribution $\pi _{\text {D}\text {B}_N}^\text {eq}$ (on repeated operation), while leaving intact the marginal distribution of the rest of $\text {B}$. The superscript $\text {eq}$ emphasizes the fact the distribution $\pi _{\text {D}\text {B}_N}^\text {eq}$ is an equilibrium distribution, as opposed to a nonequilibrium steady-state distribution, due to the assumed detailed-balance condition on $M_{\text {D}\otimes \text {B}_N}$. In other words, $\pi _{\text {D}\text {B}_N}^\text {eq}$ follows the Boltzmann distribution:

$$\begin{aligned} \pi _{\text {D}\text {B}_N}^\text {eq}(\text {D}= x, \text {B}_N = y) = e^{\beta [F_{\text {DB}_N} - E_{\text {DB}_N}(x, y)]} \end{aligned}$$

(22)

for inverse temperature $\beta$, free energy $F_{\text {DB}_N}$, and energy $E_{\text {DB}_N}(x,y)$. In the current notation we express the monotonicity of relative entropy as:

$$\begin{aligned} D(P_{\text {D}\text {B}_{0:\infty }} (N) \Vert \pi ^\text {s}(N)) \ge D(P_{\text {D}\text {B}_{0:\infty }} (N + 1) \Vert \pi ^\text {s}(N)) , \end{aligned}$$

(23)

where $D(p \Vert q)$ denotes the relative entropy of the distribution p with respect to q:

$$\begin{aligned} D(p \Vert q) = \sum _i p(i) \ln {\left[ \frac{p(i)}{q(i)}\right] } \end{aligned}$$

over $\text {D}$’s states i. The IPSL is obtained as a consequence of inequality Eq. (23), as we now show.²

First, we rewrite the lefthand side of Eq. (23) as:

$$\begin{aligned} D(P_{\text {D}\text {B}_{0:\infty }} (N) \Vert \pi ^\text {s} (N))&= - {\text {H}}_{\text {D}\text {B}_{0\infty }} (N) \ln {2} - \sum _{\text {D}\text {B}_{0:\infty }} P_{\text {D}\text {B}_{0:\infty }}(N) \ln {\pi ^\text {s}(N)} \nonumber \\&= - {\text {H}}_{\text {D}\text {B}_{0\infty }} (N) \ln {2} - \sum _{\text {D}\text {B}_{N}} P_{\text {D}\text {B}_{N}}(N) \ln \pi ^\text {eq}_{\text {DB}_N} \nonumber \\&\qquad - \sum _{\text {D}\text {B}_{0:\infty /N}} P_{\text {D}\text {B}_{0:\infty /N}}(N) \ln P_{\text {B}_{0:\infty /N}}(N) \nonumber \\&= - {\text {H}}_{\text {D}\text {B}_{0\infty }}(N) \ln {2} - \beta F_{\text {DB}_N} + \beta \langle E_{\text {D}\text {B}_N}\rangle (N) \nonumber \\&\quad + {\text {H}}_{\text {B}_{0:\infty /N}}(N) \ln {2} ~. \end{aligned}$$

(24)

The first line applies the definition of relative entropy. Here, ${\text {H}}_\text {X}$ denotes the Shannon entropy of random variable X in information units of bits (base 2). The second line employs the expression of $\pi ^\text {s}(N)$ given in Eq. (21). The final line uses the Boltzmann form of $\pi ^\text {eq}_{\text {DB}_N}$ given in Eq. (22). Here, $\langle E_{\text {D}\text {B}_N}\rangle (N)$ denotes the average energy of $\text {D}$ and the interacting bit $\text {B}_N$ at time $t = N$.

Second, in a similar way, we have the following expression for the righthand side of Eq. (23):

$$\begin{aligned} D(P_{\text {D}\text {B}_{0:\infty }} (N+1) \Vert \pi ^\text {s}_N)&= - {\text {H}}_{\text {D}\text {B}_{0:\infty }}(N + 1) \ln {2} + {\text {H}}_{\text {B}_{0:\infty /N}}(N) \ln {2} \nonumber \\&\quad + \beta \langle E_{\text {D}\text {B}_N}\rangle (N+1) - \beta F_{\text {DB}_N}. \end{aligned}$$

(25)

Note that the marginal distribution of the noninteracting bits $\text {B}_{0:\infty /N}$ does not change over the time interval $t = N$ to $t = N + 1$ since the matrix $M_{\text {D}\otimes \text {B}_N}$ acts only on $\text {D}$ and $\text {B}_N$, and the Shannon entropy of the noninteracting bits remains unchanged over the interval.

Third, combining Eqs. (23), (24), and (25), we get the inequality:

$$\begin{aligned} \ln {2} \Delta {\text {H}}_{\text {DB}_{0;\infty }} - \beta \Delta \langle E_{\text {DB}_N} \rangle \ge 0 , \end{aligned}$$

(26)

where $\Delta {\text {H}}_{\text {DB}_{0;\infty }}$ is the change in the Shannon entropy of $\text {D}$ and $\text {B}$ and $\Delta \langle E_{\text {DB}_N} \rangle$ is the change in the average energy of $\text {D}$ and $\text {B}$ over the interaction interval.

Fourth, according to the ratchet’s design, $\text {D}$ and $\text {B}$ are decoupled from the work reservoir during the interaction intervals. (The work reservoir is connected only at the end points of intervals, when one bit is replaced by another.) From the First Law of Thermodynamics, the increase in energy $\Delta \langle E_{\text {DB}_N} \rangle$ comes from the heat reservoir. In other words, we have the relation:

$$\begin{aligned} \Delta \langle E_{\text {DB}_N} \rangle = \langle \Delta Q \rangle , \end{aligned}$$

(27)

where $\Delta Q$ is the heat given to the system. (In fact, Eq. (27) is valid for each realization of the dynamics, not just on the average, since the conservation of energy holds in each realization.)

Finally, combining Eqs. (26) and (27), we get:

$$\begin{aligned} \ln {2} \Delta {\text {H}}_{\text {DB}_{0:\infty }} - \beta \langle \Delta Q\rangle \ge 0 , \end{aligned}$$

(28)

which is the basis of the IPSL as demonstrated in Ref. [27]; see, in particular, Eq. (A7) there.