1 Introduction

This paper studies a machine learning algorithm [3] that connects two different areas of interest: The graph cut problem and the diffuse interface model. We give a brief introduction of the two areas and their connections to statistical physics.

The graph cut problem originated in computer science for the purpose of partitioning nodes on a graph [6]. It is tightly related to statistical physics due to its connections with Markov random fields (MRF), and spin systems. In particular, the maximum a posteriori (MAP) estimation of the Ising model can be formulated in terms of a graph cut problem [17]. The results also generalizes to multiclass graph cut by extending to the generalized Potts model [5]. Therefore, efficient solutions to the graph cut problem provide a means of doing MAP estimations for these types of MRFs, and is computationally more efficient compared to techniques for generic MRFs such as belief propagation [32, 35]. Graph partitioning is also tightly related to the study of networks in statistical physics [21, 24, 36]. In [18], Hu et al. applied methods for solving graph cut problems to perform modularity optimization [16, 25, 36], a technique widely applied for community detection in networks.

On the other hand, diffuse interface models have been widely used in mathematical physics to model the free boundary of interfaces [9, 26]. Diffuse interface models are often built around the Ginzburg–Landau functional, defined as

$$\begin{aligned} GL(u)=\frac{\epsilon }{2}\int |\nabla u|^2+\frac{1}{\epsilon }\int W(u(x))dx. \end{aligned}$$
(1)

Evolution by the gradient flow of the Ginzburg–Landau functional has been used to model the dynamics of two phases in material science. The most common among them is the Allen–Cahn equation [9], the \(L^2\) gradient flow of the Ginzburg–Landau functional. Another commonly used model is the Cahn–Hilliard equation [2, 8]. The diffuse interface models can often be used as a proxy for total variation (TV) minimization since the \(\Gamma \)-limit of the Ginzburg–Landau functional is shown to be the TV semi-norm [20].

The key observation linking the two areas above is that the TV semi-norm, when suitably generalized to weighted graphs, coincides with the graph cut functional for discrete valued functions on graphs [29]. Hence techniques for TV minimization can also be applied to solve the graph cut problem. In [3], Bertozzi et al. generalized the Ginzburg–Landau functional to graphs, and developed an algorithm based on the Allen–Cahn equation to approximately solve the graph cut problem. This was made rigorous by the result that the graph Ginzburg–Landau functional \(\Gamma \)-converges to the graph TV functional [28]. Following this line of work, a series of new algorithms were developed for semi-supervised and unsupervised classification problems on weighted graphs [18, 23], applying techniques for TV minimization to the setting of weighted graphs.

The reason many PDE models defined on the Euclidean space \(\mathbb {R}^n\) can be generalized to discrete graphs is that the graph Laplacian matrix [30] shares many connections with the classical Laplacian operator. We recap the definition of the graph Laplacian and some of its basic properties below.

We consider a weighted graph G with vertices ordered \(\{1,2,\ldots ,n\}\). Each pair of vertices (i, j) is assigned a weight \(w_{ij}\ge 0\), with \(w_{ij} > 0\) representing an edge connecting i and j, and \(w_{ij} = 0\) otherwise. The weights \(w_{ij}\) form a weight matrix or adjacency matrix of the graph G. Given a weight matrix W, one can construct three different kinds of graph Laplacians:

$$\begin{aligned} L^u&=D-W\quad&\text {Unnormalized Laplacian,} \end{aligned}$$
(2)
$$\begin{aligned} L^{s}&=I-D^{-1/2}WD^{-1/2}\quad&\text {Symmetric Laplacian,}\end{aligned}$$
(3)
$$\begin{aligned} L^{rw}&=I-D^{-1}W\quad&\text {Random Walk Laplacian,} \end{aligned}$$
(4)

where D is the diagonal matrix \(d_{ii}=\sum _i w_{ij}\). Throughout this paper, we assume that each node i is connected to at least another node, so that \(d_{ii}>0, \forall i\) and Eqs. (3) and (4) are well-defined.

All three Laplacian matrices are commonly used in graph learning problems. In particular, the graph Dirichlet energy for the unnormalized graph Laplacian has the following property as shown in Eq. (5).

$$\begin{aligned} \frac{1}{2}\langle u,L^u u \rangle =\frac{1}{2}\sum _{ij} w_{ij}(u(i)-u(j))^2. \end{aligned}$$
(5)

Here u is a mapping from the set of nodes \(\{1, \ldots , N\}\) to \(\mathbb {R}\), identified with a vector in \(\mathbb {R}^N\). We use u(i) to denote the value of u on the node i. Similar to the classical Dirichlet energy, the graph Dirichlet energy penalizes similar nodes (i.e. pairs such that \(w_{ij}\) is large) from having different function values, bringing a notion of “smoothness” for functions defined on the graph. In this paper, we will mainly focus on the unnormalized Laplacian, and generalize to the other two cases whenever we can.

This paper studies the discrete graph Allen–Cahn scheme in [3] used for graph semi-supervised classification. We give a brief introduction of the semi-supervised learning problem and its relation to the graph Allen–Cahn scheme. Given a collection of objects indexed by \(Z = \{1, \ldots , N\}\) and a set of labels \(y(i)\in C\) for each object i, the task of semi-supervised learning is to infer the labels for all items given only the labels on a subset of objects \(Z' \subset Z\). We mainly focus on the case of binary classification, i.e., when \(|C| = 2\), since the original Ginzburg–Landau model in [3] was designed to handle the binary case. However, we also generalize modestly to incorporate multiclass classification in Sect. 5 as well. Following the convention in [3], the binary label set C is assumed to be \(C = \{-1, 1\}\). Next, we introduce the Ginzburg–Landau energy and the Allen–Cahn equation on graphs. Define the Ginzburg–Landau energy on graphs by replacing the spatial Laplacian with the graph LaplacianL.

$$\begin{aligned} GL(u)=\frac{\epsilon }{2}\langle u,Lu \rangle +\frac{1}{\epsilon }\sum _i W(u(i)), \end{aligned}$$
(6)

where W is the double-well potential \(W(x) = \frac{1}{4}(x^2 - 1)^2\). Let \(\varvec{W}(u) = \sum _i W(u(i))\). The Allen–Cahn equation on graphs is defined as the gradient flow of the graph Ginzburg–Landau functional.

$$\begin{aligned} u_t=-\nabla GL(u)=-\epsilon Lu-\frac{1}{\epsilon } \nabla \varvec{W}(u). \end{aligned}$$
(7)

The discrete graph Allen–Cahn scheme in [3] is a semi-implicit discretization of Eq. (7). The reason for being semi-implicit is to counter the ill-conditioning of the graph Laplacian

$$\begin{aligned} \frac{u^{k+1}-u^k}{dt}=-\epsilon Lu^{k+1}-\frac{1}{\epsilon }\nabla \varvec{W}(u^k). \end{aligned}$$
(8)

To do graph semi-supervised classification, we add a quadratic fidelity term \(\frac{1}{2}\sum _{i\in Z'} \eta (u(i) - y(i))^2\) to the graph Ginzburg–Landau energy, where y(i) are the known labels and \(\eta \) is a scalar parameter reflecting the strength of the fidelity. For our purpose, it is more convenient to adopt a matrix notation of the fidelity term, namely

$$\begin{aligned} F(u) = GL(u) + \frac{1}{2}\eta \Vert u-y\Vert ^2_\Lambda , \end{aligned}$$
(9)

where \(\Vert u-y\Vert ^2_\Lambda := \langle u - y, \Lambda (u - y) \rangle \), \(\Lambda \) is a diagonal matrix where \(\Lambda _{ii} = 1\) if \(i\in Z'\) and 0 otherwise. The value u(i) can be interpreted as a continuous label assignment, and thresholding \(u(i)>0\) and \(u(i) < 0\) gives a corresponding partition of the graph. Solving the gradient flow of F(u) via a semi-implicit discretization, we have:

$$\begin{aligned} \frac{u^{k+1}-u^k}{dt}=-\epsilon Lu^{k+1}-\frac{1}{\epsilon }\nabla \varvec{W}(u^k) - dt*\eta \Lambda (u^k-y). \end{aligned}$$
(10)

In later sections, we will study the scheme (8) first and then incorporate the fidelity term in the analysis.

Next, we introduce spectral truncation. Note in each iteration of (8) and (10), we need to solve a linear system of the form \((I + dtL)u = v\). In many applications, the number of nodes N on a graph is huge, and it is too costly to solve this equation directly. In [3, 23], a strategy proposed was to project u onto the m eigenvectors of the graph Laplacian with the smallest eigenvalues. In practice, spectral truncation gives accurate segmentation results but is computationally much cheaper. The reason spectral truncation works is because the first few eigenvectors of the graph Laplacian carry rich geometric information of the graph. In particular, the second eigenvector, named the Fiedler vector, approximates the solution to the normalized graph cut problem [30].

In practice, the selection of the stepsize dt is very important to the performance of the model, but is largely chosen empirically by trial and error in previous papers. In this paper, we intend to do a thorough and rigorous analysis on the range of stepsize for the scheme to be well-behaved. Our main contributions are below:

  • We prove that there exists a graph-independent upper bound c such that for all \(0\le dt \le c\), the schemes (8), (10) are monotone in the Ginzburg–Landau energy, and that under an a posteriori condition, the sequence \(\{u^k\}\) is convergent.

  • We show that the upper bound c depends linearly on \(\epsilon \), and is inversely proportional to the fidelity strength \(\eta \) in (10).

  • We generalize the results to incorporate spectral truncation and multiclass classification.

  • We conduct a variety of numerical experiments to compare practical performance with theory.

The paper is structured as follows: in Sect. 2, we prove that the scheme is bounded via a discrete version of the maximum principle. In Sect. 3, we use \(L^2\) estimates to prove monotonicity and convergence. In Sect. 4, we prove monotonicity and boundedness for spectral truncation under a graph-dependent stepsize bound \(dt = O(N^{-1})\), and provide an example for the dependency of dt on the graph size. In Sect. 5, we generalize the results to multiclass classification. In Sect. 6, a variety of numerical experiments are done to compare the theory with practical performance.

We present a list of notations and definitions used throughout the paper.

  • L placeholder variable for any choice of the three definitions of the graph Laplacian. The exact choice will be specified in the proposition or context it was referred to.

  • Z the set of nodes of the graph, with cardinality N; \(Z'\) the fidelity set, i.e., the set of nodes where the labels are known.

  • u \(Z \mapsto \mathbb {R}\), identified with a vector in \(\mathbb {R}^N\). u(j) denotes the evaluation of u on node j, and \(u^k\) denotes the kth iterate of some numerical scheme.

  • W double-well function, \(W(x) = \frac{1}{4}(x^2-1)^2\).

  • \(\varvec{W}(u) = \sum _iW(u(i))\) sum of the double-well function on all nodes.

  • \(\nabla \varvec{W}(u) = (W'(u(1)), \ldots , W'(u(N)))\) Gradient of \(\varvec{W}\) with respect to u.

  • \(y\in \mathbb {R}^{ N}\) Vector of known labels. \(y(i) \in \{-1, 1\}\) denotes the known label when \(i\in Z'\); \(y(i) = 0\) otherwise.

  • Diagonal Map: a (possibly non-linear) map \({\varvec{\mathcal {F}}}:\mathbb {R}^N \mapsto \mathbb {R}^N\) that satisfies \({\varvec{\mathcal {F}}}(u) = (\mathcal {F}^1(u(1)), \ldots , \mathcal {F}^N(u(N)))\) for \(u \in \mathbb {R}^N\). We call \(\mathcal {F}^i:\mathbb {R}\mapsto \mathbb {R}\) components of the diagonal map \({\varvec{\mathcal {F}}}\).

2 Maximum Principle-\(L^\infty \) Estimates

The main result for this section is the following:

Proposition 1

(A Priori Boundeness) Define \(u^k\) by the semi-implicit graph Allen–Cahn scheme

$$\begin{aligned} \frac{u^{k+1}-u^k}{dt}=-\epsilon Lu^{k+1}-\frac{1}{\epsilon }\nabla \varvec{W}(u^k), \end{aligned}$$
(11)

where L is the unnormalized graph Laplacian. If \(\Vert u^0\Vert _\infty \le 1\), and \(0\le dt\le 0.5\epsilon \), then \(\Vert u^k\Vert _\infty \le 1\), \(\forall k \ge 0\).

What is notable is that the stepsize restriction is independent of the graph size. We also note that the bound on dt depends linearly in \(\epsilon \), and we will generalize this dependency to include the fidelity term later in this section. To prove the proposition, we split the discretization (8) into two parts.

$$\begin{aligned} \left\{ \begin{aligned} v^k&=u^k-dt*\frac{1}{\epsilon }\nabla \varvec{W}(u^k),\\ u^{k+1}&=-dt*(\epsilon Lu^{k+1})+v^k.\\ \end{aligned}\right. \end{aligned}$$
(12)

We will prove that \(\Vert u^{k+1}\Vert _\infty \le \Vert v^k\Vert _\infty \) for all \(dt>0\) via the maximum principle, and show that the stepsize restriction essentially comes from the first line of (12). For future reference, we denote the first line of (12) as the forward step since it corresponds to a forward stepping scheme for the gradient flow and the second line a backward step correspondingly.

2.1 Maximum Principle

The classical maximum principle argument relies on the fact that \(\Delta u(x_0)\ge 0\) for \(x_0\) a local minimizer. This fact is also true for graphs and is an extension of the classical maximum principle for finite difference operators [10].

Proposition 2

(Second Order Condition on Graphs) Let u be a function defined on a graph, and L be either the unnormalized graph Laplacianor the random walkgraph Laplacian. Suppose u achieves a local minimum at a vertex i, where a local minimum at vertex i is defined as \(u(i)\le u(j), \forall w_{ij}> 0.\) Then we have \([L u](i)\le 0\).

Proof

For both the random walk and the unnormalized Laplacian, we have the following:

$$\begin{aligned} \left\{ \begin{aligned} L_{ii}&= -\sum _{j\ne i} L_{ij},\\ L_{ij}&\le 0.\\ \end{aligned}\right. \end{aligned}$$
(13)

Let i be a local minimizer. Then

$$\begin{aligned}{}[\textit{Lu}](i)&=L_{ii} u(i)+\sum _{j\ne i}L_{ij}u(j)\nonumber \\&=\sum _{j\ne i} L_{ij}(u(j)-u(i)) \le 0 \quad \square \end{aligned}$$
(14)

Next, we prove a maximum principle for discrete time. \(\square \)

Proposition 3

(Maximum Principle for Discrete Time) For any \(dt\ge 0\), let u be a solution to

$$\begin{aligned} u=-dt*(Lu)+v, \end{aligned}$$
(15)

where L is either the unnormalized or the random walk Laplacian, then \(\max _i u(i) \le max_i v(i)\), and \(\min _i u(i) \ge min_i v(i)\). Hence \(\Vert u\Vert _\infty \le \Vert v\Vert _\infty \).

Proof

Suppose \(i= {{\mathrm{arg\,min}}}_j u(j)\) is any node that attains the minimum for u. Then since \(u(i)=dt*(-Lu)(i)+v(i)\) and \((-Lu)(i)\ge 0\) by Proposition 2, we have \(\min _ju(j)=u(i)\ge v(i)\ge \min _jv(j)\). Arguing similarly with the maximum, we have that \(\Vert u\Vert _\infty \le \Vert v\Vert _\infty \). \(\square \)

2.2 Proof of Boundedness

We show that the stepsize bound for the sequence \(u^k\) to be bounded depends only on the forward step of the scheme.

Proposition 4

Let \(u^k\) be defined by

$$\begin{aligned} \left\{ \begin{aligned} v^k&=u^k-dt*\varvec{\Phi }(u^k),\\ u^{k+1}&=-\frac{dt}{\sigma }*Lu^{k+1}+v^k.\\ \end{aligned}\right. \end{aligned}$$
(16)

where \(\varvec{\Phi }\) is a diagonal map \(\varvec{\Phi }: (u(1),\ldots , u(N)) \mapsto (\Phi ^0(u(1)), \ldots , \Phi ^N(u(N)))\), L is the unnormalized graph Laplacian, and \(\sigma \) some constant greater than 0. Define the forward map \(\varvec{\mathcal {F}}_{dt}: u\mapsto u-dt*\varvec{\Phi }(u)\), and denote its components by \(\mathcal {F}^i_{dt}\). Suppose \(\exists M>0\) and some constant \(c(M, \varvec{\Phi })\) such that \(\forall 0 \le dt \le c\), and \(\forall i\), \(\mathcal {F}^i_{dt}([-M, M]) \subset [-M, M]\). Then if \(\Vert u^0\Vert _\infty \le M\), we have \(\Vert u^k\Vert _\infty \le M,\) \(\forall k \ge 0\).

Proof

Suppose \(\Vert u^k\Vert _\infty \le M\). By induction and our assumption on \(\mathcal {F}^i_{dt}\), \(\Vert v^k\Vert _\infty \le M\). By the maximum principle, \(\Vert u^{k+1}\Vert _\infty \le \Vert v^k\Vert _\infty \le M\). \(\square \)

We can now prove Proposition 1 by setting M and \(\varvec{\Phi }\) in Proposition 4 accordingly, and estimate the bound \(c(M, \Phi )\).

Proof

We set \(M=1\) and \(\varvec{\Phi } = (W', \ldots , W'), \) where W is the double-well function. Note that by replacing dt with \(dt/\epsilon \) and setting \(\sigma = \frac{1}{\epsilon ^2}\) in (16), we recover the original scheme (12). Therefore, we may assume \(\epsilon = 1\), and scale the bound obtained by \(\epsilon \). The component forward maps \(\mathcal {F}^i_{dt}\) are

$$\begin{aligned} \mathcal {F}^i_{dt}(x)=x-dt W'(x)=x - dtx(x^2-1):=\mathcal {F}_{dt}(x). \end{aligned}$$
(17)

The proposition is proved if we show \( \mathcal {F}_{dt}([-1,1])\subset [-1, 1]\) for \(0\le dt\le 0.5\), which is shown in Lemma (1). \(\square \)

Lemma 1

Define \(\mathcal {F}_{dt}\) as in (17). If \(0\le dt\le 0.5\), \( \mathcal {F}_{dt}([-1,1])\subset [-1, 1]\).

Proof

For a general M, we can estimate c by solving dt to satisfy (18)

$$\begin{aligned} \left\{ \begin{aligned} \max _{x\in [-M,M]} \mathcal {F}_{dt}(x)&\le M\\ \min _{x\in [-M,M]} \mathcal {F}_{dt}(x)&\ge -M \end{aligned}\right. \end{aligned}$$
(18)

Since \(\mathcal {F}_{dt}\) is cubic in x, (18) can be solved analytically via brute force calculation. Setting M = 1 and solving (18) for \(dt \ge 0\) gives \(0\le dt \le 0.5\). \(\square \)

The choice of the constant \(M=1\) is natural since the function value u(i) is ideally close to the binary class labels \(\{-1, 1\}\). However, if we merely want to prove boundedness without enforcing \(\Vert u^k\Vert _\infty \le 1\) we can get a larger stepsize bound by maximizing the bound obtained from (18) with respect to M, namely,

Lemma 2

For \(0\le dt\le 2.1\), \(\mathcal {F}_{dt}([-1.4,1.4]) \subset [-1.4,1.4]\).

The reason we are computing these constants explicitly is that we will compare them in Sect. 6 against results from real applications. For future reference, the \(dt \le 0.5\) bound will be called the “tight bound” where the \(dt \le 2.1\) bound will be called the “loose bound”.

2.3 Generalizations of the Scheme

In this section, we extend the previous result to the case where fidelity is added, and also to the case for the symmetric graph Laplacian \(L^s\).

We restate the graph Allen–Cahn scheme with fidelity:

$$\begin{aligned} \left\{ \begin{aligned} v^k&= u^k-dt*\left( \frac{1}{\epsilon }\nabla \varvec{W}(u^k)+\eta \Lambda (u^k-y)\right) ,\\ u^{k+1}&=-dt*(\epsilon Lu^{k+1})+v^k. \end{aligned} \right. \end{aligned}$$
(19)

\(\Lambda \) is a diagonal matrix where \(\Lambda _{ii} = 1\) if i is in the fidelity set \(Z'\) and 0 otherwise, and \(y(i)\in \{1,-1\}, i\in Z'\).

Proposition 5

(Graph Allen–Cahn with fidelity) Define \(u^k\) by (19) and suppose \(\Vert u^0\Vert _\infty \le 1\). If dt satisfies \(0\le dt\le \frac{1}{2+\eta }\epsilon \), we have \(\Vert u^k\Vert _\infty \le 1\) for all k.

Proof

Denote the forward map of (19) by \({\varvec{\mathcal {F}}}_{dt}\), i.e., \(\varvec{\mathcal {F}}_{dt}(u^k) = v^k\). Since \(\Lambda \) is a diagonal matrix, \(\varvec{\mathcal {F}}_{dt}\) is a diagonal map. Note \({\varvec{\mathcal {F}}}_{dt}\) has only three distinct component maps which we denote by \(F^i_{dt}, i = 1,\ldots ,3\). Namely, \(F^0_{dt}(u) = u-dt[\frac{1}{\epsilon }(u^2-1)u+\eta (u-1)]\), \(F^1_{dt}(u) = u-dt[\frac{1}{\epsilon }(u^2-1)u+\eta (u+1)]\), \(F^2_{dt}(u) = u-dt[\frac{1}{\epsilon }(u^2-1)u]\). By solving (18) with \(M=1\) for \(F^m_{dt}, m=0,\ldots ,2\) for non-negative dt, we get \(0 \le dt \le \frac{1}{2+\eta }\epsilon \). \(\square \)

The case for the symmetric graph Laplacianis a little different. Since \(L^s\) does not satisfy (13), we can no longer apply the arguments of maximum principle. However, we are still able to prove boundedness under the assumption that the graph satisfies a certain uniformity condition.

Proposition 6

(Symmetric graph Laplacian) Let \(d_i = \sum _j w_{ij}\) be the degree of node i. Suppose \(\rho \le 4\) where \(\rho \) is defined below

$$\begin{aligned} \rho =\frac{\max _i d_i}{\min _i d_i}. \end{aligned}$$
(20)

Define \(u^k\) by the semi-implicit scheme (11) where L is set to be the symmetric Laplacian \(L^s\). Suppose \(\Vert u^0\Vert _\infty \le 1\). If \(0 \le dt\le 0.25\epsilon \), we have \(\Vert u^k\Vert _\infty \le 2\), for all \( k \ge 1. \)

Proof

By definition of \(L^s\) and \(L^{rw}\), we have the relation

$$\begin{aligned} L^s=D^{1/2}L^{rw}D^{-1/2} \end{aligned}$$
(21)

Substituting (21) to line 2 of (12) with \(L = L^s\), we have

$$\begin{aligned} D^{-1/2}u^{k+1}=-dt*L^{rw}D^{-1/2}u^{k+1}+D^{-1/2}v^{k}. \end{aligned}$$
(22)

We will do a change of variables \(\tilde{u}^k= \alpha D^{-1/2}u^{k}\), and \(\tilde{v}^k= \alpha D^{-1/2}v^{k}\), where \(\alpha =(\min _i d_i)^{1/2}\), and write the scheme in terms of \(\tilde{u}^k\).

$$\begin{aligned} \left\{ \begin{aligned} \tilde{v}^k&=\tilde{u}^k-dt*\frac{1}{\epsilon }\alpha D^{-1/2}\nabla \varvec{W}\left( \frac{1}{\alpha }D^{1/2}\tilde{u}^k\right) ,\\ \tilde{u}^{k+1}&=-\epsilon dt*L^{rw}\tilde{u}^{k+1}+\tilde{v}^k.\\ \end{aligned}\right. \end{aligned}$$
(23)

By the definition of \(\alpha \), we have \(\Vert \tilde{u}^{0}\Vert _\infty \le 1\). We will use the same technique as before to show \(\Vert \tilde{u}^k\Vert \le 1, \forall k \). By the maximum principle, \(\Vert \tilde{u}^{k+1}\Vert _\infty \le \Vert \tilde{v}^k\Vert _\infty \). Define the forward map \({\varvec{\mathcal {F}}}_{dt}\) of (23), i.e., \({\varvec{\mathcal {F}}}_{dt}(\tilde{u}^k) = \tilde{v}^k\). Define \(G_{dt}(c, x) = x-\frac{dt}{c} W'(cx)=x - \frac{dt}{c}x(c^2x^2-1)\), the components of \({\varvec{\mathcal {F}}}_{dt}\) are:

$$\begin{aligned} \tilde{v}^k(i)=\mathcal {F}^i_{dt}(\tilde{u}^k(i))=G_{dt/\epsilon }(c_i, \tilde{u}^k(i)), \end{aligned}$$
(24)

where \(c_i=(\frac{d_i}{\min _j d_j})^{1/2} \in [1,2]\). We can prove the theorem if we show \(\mathcal {F}^i_{dt}\) maps \([-1,1]\) to itself for all \(i = 1, \ldots , N\). This is formalized in the next lemma, whose proof we omit since it involves only brute force calculations. \(\square \)

Lemma 3

For any \(0 \le dt\le 0.25\), and some fixed \(c\in [1, 2]\), \(G_{dt}(c,x) \) as a function of x maps \([-1,1]\) to itself.

Finally, since \(\Vert \tilde{u}^k\Vert \le 1\), we have \(\Vert u^k\Vert \le 2\) by definition of \(\tilde{u}^k\).

Remark 1

The condition \(\rho < M\) with \(M = 4\) is arbitrary and just chosen to simplify calculations for dt. The proposition here is weaker than Proposition 1 due to the loss of the maximum principle. We will see this again during the analysis of spectral truncation in Sect. 4.

3 Energy Method-\(L^2\) Estimates

In this section, we derive estimates in terms of the \(L^2\) norm. Our goal is to prove that the graph Allen–Cahn scheme is monotone in function value, and derive convergence results of the sequence \(\{u^k\}\). We will drop the subscript for 2 norms in this section. Our proof is loosely motivated by the analysis of convex-concave splitting in [11, 33]. In [11], Eyre proved the following monotonicity result:

Proposition 7

(Eyre) Let \(E_1\), \(E_2\) be real valued \(C^1\) functions \(\mathbb {R}^n \rightarrow \mathbb {R}\), where \(E_1\) is convex and \(E_2\) concave. Let \(E=E_1+E_2\). Then for any \(dt>0\), the semi-implicit scheme

$$\begin{aligned} u^{k+1}=u^k-dt \nabla E_1(u^{k+1})-dt\nabla E_2(u^k), \end{aligned}$$
(25)

is monotone in E, namely,

$$\begin{aligned} E(u^{k+1})\le E(u^k), \quad \forall k\ge 0. \end{aligned}$$

In our proof, we will set \(E=GL(u)\), \(E_1=\frac{\epsilon }{2}\langle u,Lu\rangle \) and \(E_2=\frac{1}{\epsilon } \varvec{W}(u)\). Since \(E_2\) is not concave, we will have to generalize Proposition 7 for general \(E_2\). But first, we digress a bit and establish the connection between the semi-implicit scheme (25) and the proximal gradient method, which simply assumes \(E_1\) to be sub-differentiable. The reason for this generalization is to have a unified framework for dealing with \(E_1\) taking extended real values, which is the case when we study spectral truncation in Sect. 4.

The proximal gradient iteration [4] is defined as

$$\begin{aligned} u^{k+1}=\textit{Prox}_{dtE_1}(u^k-dt \nabla E_2(u^k)), \end{aligned}$$
(26)

where the \(\textit{Prox}\) operator is defined as \(\textit{Prox}_{\gamma f}(x)={{\mathrm{arg\,min}}}_u \{f(u)+\frac{1}{2\gamma }\Vert u-x\Vert ^2\}\). This scheme is in fact equivalent to the semi-implicit scheme (25) when \(E_1\) is differentiable. This is clear from the implicit gradient interpretation of the proximal map. Namely, if \(y=\textit{Prox}_{\gamma f}(x)\),

$$\begin{aligned} y\in x-\gamma \partial f(y). \end{aligned}$$
(27)

\(\partial f\) is the subgradient of f, which coincides with the gradient if f is differentiable.

The Prox operator is well-defined if f is a proper closed convex functions taking extended real values, namely, if the domain of f is non-empty, f is convex, and the epigraph of f is closed. We prove an energy estimate for the proximal gradient methods when \(E_2\) is a general function.

Proposition 8

(Energy Estimate) Let \(E=E_1+E_2\). Suppose \(E_1\) is a proper closed and convex function, and \(E_2\in C^2\). Define \(x^{k+1}\) by the proximal gradient scheme \(x^{k+1}\in x^k-dt\partial E_1(x^{k+1})-dt \nabla E_2(x^{k})\). Suppose M satisfies

$$\begin{aligned} M \ge \max _{\xi \in S } \Vert \nabla ^2 E_2(\xi ) \Vert , \end{aligned}$$
(28)

where \(S = \{ \xi | \xi = t x^k + (1-t)x^{k+1}, t\in [0,1]\} \) is the line segment between \(x^k\) and \(x^{k+1}\), we have

$$\begin{aligned} E(x^{k})-E(x^{k+1})\ge \left( \frac{1}{dt}- \frac{M}{2}\right) \Vert x^{k+1}-x^{k}\Vert ^2. \end{aligned}$$
(29)

Proof

$$\begin{aligned} \begin{aligned} E(x^{k})-E(x^{k+1})&= E_1(x^k)-E_1(x^{k+1})+E_2(x^k)-E_2(x^{k+1})\\&\ge \langle \partial E_1(x^{k+1}),x^k-x^{k+1}\rangle +E_2(x^k)-E_2(x^{k+1})\\&= E_2(x^k)-E_2(x^{k+1}) - \langle \nabla E_2(x^k),x^k-x^{k+1}\rangle + \frac{1}{dt}\Vert x^{k+1}-x^k\Vert ^2 \\&\ge \frac{1}{dt}\Vert x^{k+1}-x^k\Vert ^2- \frac{M}{2}\Vert x^{k+1}-x^{k}\Vert ^2.\\ \end{aligned} \end{aligned}$$

The second line is by definition of subgradients, and \(\partial E_1(x^{k+1})\) could be any vector in the subgradient set. The third line is by substituting the particular subgradient \(\partial E_1(x^{k+1})\) in the definition of \(x^{k+1}\). The fourth line is obtained by one variable Taylor expansion of the function \(E_2\) along the line segment between \(x^k\) and \(x^{k+1}\). \(\square \)

Next, we apply estimate (8) and the boundedness results in Sect. 2 to prove that the graph Allen–Cahn scheme is monotone in the Ginzburg–Landau energy under a graph-independent stepsize.

Proposition 9

(Monotonicity of the Graph Allen–Cahn Scheme) Let \(u^k\) be the graph Allen–Cahn scheme with fidelity defined below:

$$\begin{aligned} u^{k+1} = u^k-dt*(\epsilon Lu^{k+1}+\frac{1}{\epsilon }\nabla \varvec{W}(u^k)+\eta \Lambda (u^k-y)), \end{aligned}$$
(30)

where L is the unnormalized graph Laplacian. If \(\Vert u^0\Vert _\infty \le 1\), then \(\forall 0\le dt\le \min (\frac{\epsilon }{2+\eta }, \frac{2\epsilon }{2+\eta \epsilon })\), the scheme is monotone under the Ginzburg–Landau energy with fidelity, namely, \(E(u^k) = GL(u^k) + \frac{\eta }{2}\Vert u^k - y\Vert ^2_\Lambda \ge E(u^{k+1}) = GL(u^{k+1}) + \frac{\eta }{2}\Vert u^{k+1} - y\Vert ^2_\Lambda \). The result holds for symmetric Laplacians if we add the uniformity condition (20) for the graph.

Proof

From Proposition 1, we have \(\Vert u^k\Vert _\infty \le 1, \forall k\) if \(0\le dt\le \frac{\epsilon }{2+\eta }\). We set \(E_2(u) = \frac{1}{\epsilon }\varvec{W}(u) + \frac{\eta }{2} \Vert u^k - y\Vert ^2_\Lambda \), and \(E_1(u) = \frac{\epsilon }{2}\langle u, Lu \rangle \). Since (30) is equivalent to the proximal gradient scheme with \(E_1\) and \(E_2\) defined above, we can apply Proposition 8. Since the \(L^\infty \) unit ball is convex, line segments from \(u^k\) to \(u^{k+1}\) lie in the set \(\{\Vert u\Vert _\infty \le 1\}\), and we can estimate M by the inequality below

$$\begin{aligned} \max _{\Vert u\Vert _\infty \le 1} \Vert \nabla ^2 E_2(u)\Vert _2 \le \max _{|x|\le 1} \Big |\frac{1}{\epsilon }W''(x)+\eta \Big |=\frac{2}{\epsilon }+\eta . \end{aligned}$$

Thus we can set \(M = \frac{2}{\epsilon }+\eta \). Let \(c = \min \Big (\frac{\epsilon }{2+\eta }, \frac{2}{M}\Big ) = \min \Big (\frac{\epsilon }{2+\eta }, \frac{2\epsilon }{2+\eta \epsilon }\Big )\). We have \(\forall 0 \le dt \le c\),

$$\begin{aligned} E(u^{k})-E(u^{k+1})\ge \left( \frac{1}{dt}-\frac{M}{2}\right) \Vert u^{k+1}-u^{k}\Vert ^2\ge 0. \end{aligned}$$
(31)

Hence \(u^k\) is monotone in E. The case for the symmetric Laplacian can be proved in a similar manner by computing an estimate of \(\max _{\Vert \xi \Vert _\infty \le 2} \Vert \nabla ^2 E_2\Vert \). \(\square \)

Next, we discuss the convergence of the iterates \(\{u^k\}\). First, we prove subsequence convergence of \(\{u^k\}\) to a stationary point of E(u). We first need a lemma on the sequence \(\{u^{k+1} - u^k\}\).

Lemma 4

Let \(u^k\), dt, be as in Proposition 9, then \(\sum _{k=0}^{\infty }\Vert u^{k+1}-u^{k}\Vert ^2 < \infty \). Hence \(\lim _{k \rightarrow \infty } \Vert u^{k+1} - u^k\Vert = 0\).

Proof

Summing Eq. (31), we have the following

$$\begin{aligned} E(u^{0})-E(u^{n})\ge \left( \frac{1}{dt}-\frac{M}{2}\right) \sum _{k=0}^{n-1}\Vert u^{k+1}-u^{k}\Vert ^2, \end{aligned}$$
(32)

holds for all n. Since \(E(u^n) \ge 0\) and \(dt\le \frac{2}{M}\), we prove the lemma. \(\square \)

Proposition 10

(Subsequence convergence to stationary point) Let \(u^k\), dt, be as in Proposition 9. Let S be the set of limit points of the set \(\{ u^k\}\). Then \(\forall u^* \in S\), \(u^*\) is a critical point of E, i.e., \(\nabla E(u^*)= 0\). Hence any convergent subsequence of \(u^k\) converges to a stationary point of E.

Proof

By definition, \(u^{k+1} = u^k - dt\nabla E_1(u^{k+1}) - dt\nabla E_2(u^k)\). Hence we have

$$\begin{aligned} \Vert \nabla E_1(u^k) + \nabla E_2(u^k)\Vert \le \left( \Vert \nabla E_1(u^{k+1}) - \nabla E_1(u^k)\Vert + \frac{1}{dt}\Vert u^{k+1} - u^k\Vert \right) . \end{aligned}$$
(33)

Since \(\{u^k\}\) is bounded and \(\nabla E_1\) is continuous, we have \(\lim _{k \rightarrow \infty } \Vert \nabla E(u^k)\Vert = 0\), where we use \(\lim _{k \rightarrow \infty } \Vert u^{k+1} - u^k\Vert = 0\). \(\square \)

In general, we can not prove that the full sequence \(\{u^k\}\) is convergent, since it is possible for the iterates \(\{u^k\}\) to oscillate between several minimum. However we show that when the set of limit points is finite, we do have convergence. This is stated in the Lemma 5, which is proved in the Appendix.

Lemma 5

Let \(u^k\) be a bounded sequence in \(\mathbb {R}^N\), and \(\lim _{k \rightarrow \infty } \Vert u^{k+1} - u^k\Vert = 0\). Let S be the set of limit points of the set \(\{u^k | k \ge 1\}\). If S has only finitely many points, then S contains only a single point \(u^*\), and hence \(\lim _{k\rightarrow \infty } u^k = u^*\).

Finally, we provide an easy to check a posteriori condition that guarantees convergence using the lemma above. The condition states that the iterates \(u^k\) must take values reasonably close to the double-well minimum \(-1\) and 1. Empirically, we have observed that the values of \(u^k\) are usually around \(-1\) and 1 near convergence, hence the condition is not that restrictive in practice.

Proposition 11

(Convergence with A Posteriori Condition) Let \(u^k\), dt, be as in Proposition 9. Let \(\delta > 0\) be any positive number. If for some K, we have \(|u^k(i)| \ge \frac{1}{\sqrt{3}} + \delta \), for all \( k \ge K\) and i, then we have \(\lim _{k\rightarrow \infty } u^k = u^*\), where \(u^*\) is some stationary point of the energy E.

Proof

We only need to show that the set of stationary points of E on the domain \(D = [\frac{1}{\sqrt{3}} + \delta , 1]^N\) is finite. Computing the Hessian of E, we have \(\nabla ^2 E(u) = \epsilon L + \frac{1}{\epsilon } (3u^2 - I) + \eta \Lambda \), where \(u^2\) is the diagonal matrix whose entries are \(u(i)^2\). Note that \(\nabla ^2 E(u)\) is positive definite on D since \(\eta \Lambda \) and L are semi-positive definite, and \(3u^2 - I\) is positive definite on D. Therefore, the stationary points of E are isolated on D. Since D is bounded, this implies the set of stationary points is finite. \(\square \)

4 Analysis on Spectral Truncation

In this section, we generalize the analysis of the previous sections to incorporate spectral truncation. We establish a bound \(dt = O(N^{-1})\) for monotonicity and boundedness when the initial condition \(u^0 \in V_m\) where \(V_m\) is defined below, and \(dt = O(N^{-\frac{3}{2}})\) for the general case. First of all, we formally define the spectral truncated graph Allen–Cahn scheme. All conclusions in this section hold for both the unnormalized Laplacian and the symmetric Laplacian, therefore we will not make the distinction and will denote both by L.

Let \(\{\phi ^1,\phi ^2,\ldots , \phi ^m\}\) be eigenvectors of the graph Laplacian L ordered by eigenvalues in ascending order, i.e., \(\lambda _1 \le \lambda _2 \dots \le \lambda _N\). Define the mth eigenspace as \(V_m=\textit{span}\{\phi ^1,\phi ^2,\ldots , \phi ^m\}\), and \(P_m\) as the orthogonal projection operator onto the space \(V_m\). Then the spectral truncated scheme is defined as

$$\begin{aligned} \left\{ \begin{aligned} v^k&=u^k-dt*\frac{1}{\epsilon }\nabla \varvec{W}(u^k),\\ u^{k+1}&=P_m[-dt*(\epsilon Lu^{k+1})+v^k].\\ \end{aligned}\right. \end{aligned}$$
(34)

Note that in practice, we do not directly solve the linear system on the second line of (34), but instead express \(u^{k+1}\) directly in terms of the eigenvectors as in (38). However, writing it in matrix form is notationally more convenient in the subsequent analysis. We want to apply the energy estimates in Sect. 3 for spectral truncation. To do this, we first show that spectral truncated scheme (34) can be expressed as a proximal gradient scheme for some \(E_1\) and \(E_2\).

Proposition 12

(Reformulation of Spectral Truncation) The spectral truncated scheme (34) is equivalent to the proximal gradient scheme (26) with \(E_1=\frac{\epsilon }{2}\langle u,Lu\rangle + I_{V_m}\), \(E_2=\frac{1}{\epsilon } \varvec{W}(u)\), where \(I_{V_m}\) is the indicator function of the mth eigenspace, i.e.

$$\begin{aligned} I_{V_m}(u) = \left\{ \begin{array}{ll} 0, &{} \quad u\in V_m\\ +\infty , &{} \quad \text {else}. \end{array}\right. \end{aligned}$$
(35)

Proof

Let v be any vector in \(\mathbb {R}^N\). Define \(u,u'\) by the spectral projection and the proximal step respectively, namely,

$$\begin{aligned} u= & {} P_m[-dt*(\epsilon Lu)+v].\end{aligned}$$
(36)
$$\begin{aligned} u'= & {} \mathop {\text {arg min}}\limits _y \frac{\epsilon }{2}\langle y,Ly\rangle +I_{V_m}(y)+\frac{1}{2dt}\Vert y-v\Vert ^2. \end{aligned}$$
(37)

We only have to show u = \(u'\). Decomposing (36) in terms of the eigenbasis \(\{\phi ^1,\phi ^2,\ldots , \phi ^m\}\), we have

$$\begin{aligned} u = \sum _{j\le m} \frac{\langle v, \phi ^j \rangle }{1+dt \epsilon \lambda _j} \phi ^j. \end{aligned}$$
(38)

Since \(I_{V_m}\) is \(+\infty \) outside \(V_m\), we have \(u' \in V_m\). Let \(u'=\sum _{i=1}^{m} c'_i \phi ^i\), and \(y = \sum _{i=1}^{m} c_i \phi ^i\) then the function in (37) becomes

$$\begin{aligned} \frac{\epsilon }{2}\langle y,Ly\rangle +\frac{1}{2dt}\Vert y-v\Vert ^2=\sum _{i=1}^m \left( \frac{\epsilon }{2}\lambda _i c_i^2+\frac{1}{2dt}(c_i-\langle v, \phi ^i \rangle )^2\right) + C. \end{aligned}$$
(39)

And therefore

$$\begin{aligned} c_i' = \mathop {\text {arg min}}\limits _c \frac{\epsilon }{2}\lambda _i c^2+\frac{1}{2dt}(c-\langle v, \phi ^i \rangle )^2 = \frac{\langle v, \phi ^i \rangle }{1+dt \epsilon \lambda _i}. \end{aligned}$$
(40)

Hence we have \(u = u'\). \(\square \)

Since the orthogonal projection \(P_m\) is expansive in the \(L^\infty \) norm, i.e., \(\Vert P_m u\Vert _\infty \le \Vert u\Vert _\infty \) does not always hold, we lose the maximum principle. However, we show that the energy estimate alone is enough to prove monotonicity and boundedness under a smaller stepsize.

Proposition 13

Let L be either the symmetric or unnormalized graph Laplacian and \(\rho _L = \max _i |\lambda _i|\). Set \(\epsilon = 1\) and define \(u^k\) by the spectral truncation scheme (34). Suppose \(\Vert u^0\Vert _\infty \le 1\), and \(u^0 \in V_m\). Then there exists \( \delta >0\) dependent only on \(\rho _L\) such that \(\forall 0\le dt \le \delta N^{-1}\), The sequence \(\{u^k\}\) is bounded and \(GL(u^{k+1})\le GL(u^{k}), \) for all k. Here N is the dimension of u, i.e., number of vertices in the graph.

The choice for \(\epsilon = 1\) is only to avoid complicated dependencies on \(\epsilon \) that obscures the proof. For the next two sections, we will assume \(\epsilon = 1\) throughout. To prove the theorem, we first establish the following lemmas.

Lemma 6

(Inverse Bound) Let M be any positive constant. Set \(\epsilon = 1\) in the GL functional. If \(GL(u)\le M\), then \(\Vert u\Vert _2^2\le N+2\sqrt{NM}\), where N is the dimension of u.

Proof

By definition, \(GL(u) = \frac{1}{4}\sum _i (u(i)^2-1)^2 + \frac{1}{2} \langle u,Lu\rangle \le M\). Since \(\frac{1}{2} \langle u,Lu\rangle \ge 0\), \(\frac{1}{4}\sum _i (u(i)^2-1)^2\le M\). Then from the Cauchy–Schwarz inequality, \(\sum _i (u(i)^2-1)\le 2\sqrt{NM}\), and hence \(\Vert u\Vert _2^2\le N+2\sqrt{NM}\). \(\square \)

Lemma 7

Let \(u^k\) and \(u^{k+1}\) be defined in (34). Then the following inequality holds:

$$\begin{aligned} \Vert u^{k+1}\Vert _2\le (1+dt)\Vert u^k\Vert _2+dt\Vert u^k\Vert _2^3. \end{aligned}$$
(41)

Proof

Since L is symmetric semi-positive definite and the orthogonal projection \(P_m\) is non-expansive in the \(L^2\) norm, we have \(\Vert u^{k+1}\Vert _2\le \Vert v^{k}\Vert _2\). Since \(v^k(i) = u^k(i)-dt*[u^k(i)(u^k(i)^2-1)]\), let \(g(i) = (u(i))^3\), then

$$\begin{aligned} \begin{aligned} \Vert v^k\Vert _2&\le (1+dt)\Vert u^k\Vert _2+dt\Vert g\Vert _2 = (1+dt)\Vert u^k\Vert _2+dt\Vert u^k\Vert _6^3 \\&\le (1+dt)\Vert u^k\Vert _2+dt\Vert u^k\Vert _2^3. \end{aligned} \end{aligned}$$
(42)

\(\square \)

Next, we prove the main proposition. The idea is to choose dt small enough such that monotonicity in GL is satisfied, and then apply Lemma 6 to have a bound on \(u^k\).

Proof

(Proposition 13.) Let \(E_1(u)=\frac{\epsilon }{2}\langle u,Lu\rangle + I_{V_m}\), \(E_2(u)=\frac{1}{\epsilon } \varvec{W}(u)\), and \(E=E_1 + E_2 = GL(u)+I_{V_m}\). By Proposition 12, (34) is equivalent to the proximal gradient scheme for the splitting \(E = E_1 + E_2\). We also have \(\forall k\ge 0\), \(E(u^k) = GL(u^k)\) since \(u^k \in V_m\). Therefore, we will denote \(E(u^k)\) and \(GL(u^k)\) interchangeably.

We claim that there exists constants \(\delta > 0\), independent of N such that \(\forall 0 \le dt\le \delta N^{-1}\), Eq. (43) holds for all k.

$$\begin{aligned} \begin{aligned} GL(u^k)&\le GL(u^0)\le C_0 N,\\ \Vert u^k\Vert _2&\le C_1 \sqrt{ N}, \end{aligned} \end{aligned}$$
(43)

where \(C_0 = (1+\rho _L)\), and \(C_1 = \sqrt{(1+2\sqrt{1+\rho _L}) N}\).

We argue by induction. For the case \(k = 0\), since \(\Vert u^0\Vert _\infty \le 1\), we have \(\Vert u^0\Vert _2\le \sqrt{N}<C_1 \sqrt{N} \). We also have \(GL(u^0)\le \rho _L\Vert u^0\Vert ^2_2+\sum _{i\le N}1\le C_0 N\), since \(\Vert u^0\Vert _2^2 \le N\).

Suppose (43) is satisfied for iteration k. We first prove the first line of (43) for \(k+1\). Since \(\Vert u^k\Vert _2\le C_1 \sqrt{N},\) we apply Lemma 7 and get \(\Vert u^{k+1} \Vert _2 \le \frac{A_1}{2} (1+dt)N^{1/2}+\frac{A_1}{2}dtN^{3/2}\) for some \(A_1\) independent of N. Therefore, we can choose \(\delta _1\) independent of N such that \(\forall 0 \le dt\le \delta _1 N^{-1}\), \(\Vert u^{k+1}\Vert _2\le A_1N^{1/2}\).

Next, we apply Proposition 8 and choose dt such that \(E(u^k) \ge E(u^{k+1})\). Since \(\Vert u^{k+1}\Vert _\infty \le \Vert u^{k+1}\Vert _2 \le A_1N^{1/2}\). We can set M in Proposition 8 by the estimate below:

$$\begin{aligned} \max _{\Vert \xi \Vert _\infty \le A_1\sqrt{N}}\Vert \nabla ^2 \varvec{(}W)(\xi )\Vert _2 \le \max _{|x|\le A_1\sqrt{N}}|W''(x)|= \max _{|x|\le A_1\sqrt{N}}|( 3x^2-1)| \le A_2 N, \end{aligned}$$

where \(A_2\) independent of N, and we can set \(M = A_2 N\). Let \(\delta _2 = \frac{2}{A_2}\), and \(\delta = \min (\delta _1, \delta _2)\), we have \(GL(u^{k+1})\le GL(u^k) \le C_0N\) for all \(0\le dt \le \delta N^{-1}\).

To prove the second line of (43), note that since \(GL(u^{k+1})\le C_0 N\), we can apply the inverse bound Lemma 6 and get \(\Vert u^{k+1}\Vert _2\le C_1 \sqrt{N} \). This completes the induction step. \(\square \)

In Proposition 13, we assumed the initial condition \(u^0\) to be in the subspace \(V_m\). This is not generally done in practice, as \(u^0\) is usually chosen to have binary values \(\{-1, 1\}\). The corollary below gives a monotonicity result for \(u^0\) not in \(V_m\).

Corollary 1

Let \(u^k\) be defined as in Proposition 13. Let \(u^0\) be any vector satisfying \(\Vert u^0\Vert _\infty \le 1\). Then exists \(\delta \) independent of N such that \(\forall dt < \delta N^{-3/2}\), \(\{u^k\}\) is bounded and \(GL(u^k) \le GL(u^{k+1})\) for \(k\ge 1\).

Proof

Since \(u^0\) is not in the feasible set \(V_m\), \(E(u^0) = +\infty \ne GL(u^0)\). However, since \(u^1\in V_m\), we can start the induction from \(k = 1\). Since \(\Vert u^1\Vert _2 \le \Vert v^0\Vert _2 \le \sqrt{N}\), we can estimate \(GL(u^1) \le \rho _L \Vert u^1\Vert _2^2 + \sum _{i=1}^N((u^1(i))^2 - 1)^2 \le C_0 N^2\) for some \(C_0\) independent of N. By Lemma 6, \(GL(u) = O(N^2)\) implies \(\Vert u\Vert _2 = O(N^{3/4})\), hence we can set the induction as below.

$$\begin{aligned} \left\{ \begin{aligned} GL(u^k)&\le C_0 N^2,\\ \Vert u^k\Vert _2&\le C_1 N^{\frac{3}{4}}, \end{aligned}\right. \end{aligned}$$
(44)

and \(k=1\) is already proved above. To prove (44) for general k, we apply Lemma 7 and choose \(0\le dt \le \delta _1 N^{-3/2}\) so that \(\Vert v^{k}\Vert _2 \le A_1 N^{3/4}\). We then apply Proposition 8 and estimate

$$\begin{aligned} \max _{|x|\le A_1\le N^{3/4}}|W''(x)| \le A_2 N^{3/2} := M, \end{aligned}$$

and set \(\delta _2 = \frac{2}{A2}\). By choosing \(\delta = \min (\delta _1, \delta _2)\), we prove monotonicity for \(0\le dt \le \delta N^{-3/2}\). \(\square \)

4.1 A Counter Example for Graph-Independent Stepsize Restriction

We proved that the spectral truncated scheme is monotone under stepsize range \(0\le dt \le \delta = O(N^{-1})\). One would hope to achieve a graph-free stepsize rule as in the case of the original scheme without spectral truncation (8). However, as we show in our example below, a constant stepsize to guarantee monotonicity over all graph Laplacians of all sizes is not possible.

Proposition 14

(Graph Size Dependent Stepsize Restriction) Define \(u^k\) as in (34), with \(\epsilon = 1\). For any \(\delta > 0\) and \(dt=\delta N^{-\alpha }, 0\le \alpha <1\), we can always find an unnormalized graph Laplacian \(L_{N\times N}\) and some initial condition \(\Vert u^0\Vert _\infty =1\) such that the scheme in (34) with truncation number \(m=2\) is not monotone in the Ginzburg–Landau energy.

Remark 2

\(\alpha = 0\) is the case for graph-independent stepsize. However, this result is stronger and claims that dt has to be at least \(O(N^{-1})\) for monotonicity to hold for all graphs.

To prove Proposition 14, we explicitly construct a collection of weighted graphs that require increasingly small stepsizes to guarantee monotonicity as the graph size N increases. The graph is defined in Definition 1, and illustrated in Fig. 1. To give the idea behind the construction, we note that the reason maximum principle fails for spectral truncation is because a general orthogonal projection P is expansive in the \(L^\infty \) norm. Namely, for some vector \(\Vert v\Vert _\infty \le 1\), we have in the worst case \(\Vert P(v)\Vert _\infty =O(\sqrt{N})\). Our strategy is to explicitly construct a graph such that projection operator \(P_m\) onto one of its eigenspaces \(V_m\) attains this worst case \(L^\infty \) norm expansion. This is made precise in Proposition 15.

Fig. 1
figure 1

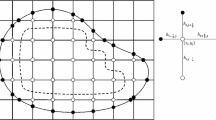
Illustration of counter example graph with \(N = 7\). We index the left most node by 1 and the right most node by 2, both marked by an “times” in the figure. Starting from the top left node marked by a circle, we rotate counter clock-wise and assign odd indices \(\{2k+1|k\ge 1\}\) to these nodes. We assign even indices \(\{2k|k\ge 2\}\) on the right similarly. We assume there are N nodes marked by circles on each side, and hence the graph has a total of \(2N+2\) nodes

Full size image

Definition 1

(Counter Example Graph)

  1. 1.

    Indexing We index the nodes as shown in Fig. 1. The graph has a total of \(2N+2\) nodes, where N is the number of nodes marked by a circle on each side.

  2. 2.

    Edge weights With reference to Fig. 1, we set the weights for the solid black edges to 10; the solid gray edges 1; and the dashed gray edges to \(\frac{\gamma }{N}\), where \(\gamma =\frac{2}{1 - N^{-1}}= 2 +o(1)\). Writing out the weight matrix, we have

    $$\begin{aligned} w_{ij} = \left\{ \begin{array}{ll} 10, &{} \quad i,j\;\text {of same parity and}\; \ne 1,2 \\ 1, &{} \quad (i,j) = (2k-1, 2k)\; \text {or}\;(2k-1, 2k), \;k\ge 2\\ \frac{\gamma }{N}, &{} \quad i = 1, j\ne 2\;\text {or}\;j = 1, i\ne 2 \end{array}\right. \end{aligned}$$
    (45)
  3. 3.

    Graph Laplacian We choose L to be the unnormalized graph Laplacian \(L = D - W\).

Proposition 15

Under the setup above, the second eigenvector of the graph Laplacianis

$$\begin{aligned} \phi ^2=\left( \frac{1}{2},-\frac{1}{2},\frac{1}{2\sqrt{N}},-\frac{1}{2\sqrt{N}},\ldots ,\frac{1}{2\sqrt{N}},-\frac{1}{2\sqrt{N}}\right) , \end{aligned}$$
(46)

and the second eigenvalue \(\lambda _2\) is O(1) with respect to N. Moreover, let \(u^0 = Sign(\phi ^2) = (1,-1,\ldots , 1,-1)\). Then the projection of \(u^0\) onto the subspace \(V_2 = \textit{span}\{\phi ^1, \phi ^2 \}\) satisfies \(P_2(u^0)=C\sqrt{N}\phi ^2\).

We refer to Appendix for the proof of this proposition. Next, we give a proof of Proposition 14. The idea is that after the first two iterations, \(|u^2(1)|\) is arbitrarily larger that that of \(|u^1(1)|\), and thus the scheme cannot be monotone in the Ginzburg–Landau energy.

Proof

(Proposition 14) Define \(u^k\) by the spectral truncated scheme (34) with \(u^0= Sgn(\phi ^2)\) and \(dt=\delta N^{-\alpha }\) for some \(\delta > 0\) and \(0<\alpha <1\).

Since \(|u^0(j)| = 1, \forall j\), \(v^0 = u^0\). Since \(v^0 \perp \phi ^1\), we have \(u^1 = \frac{\langle \phi ^2, v^0 \rangle }{1 + dt\lambda _2} \phi ^2\). By Proposition 15, \(u^1 = C_0 \sqrt{N} \phi ^2\), where \(C_0\) is O(1) with respect to N. Next, we compute \(v^1\). Note that \(|u^1(j)| = O(N^{1/2}), j = 1, 2\) and \(|u^1(j)| = O(1), j\ge 3\). By noting that \(W'(x) \sim cx^3\) asymptotically, we have \(v^1(j) = O(N^{3/2 - \alpha }), j = 1, 2\), and \(v^1(j) = O(1), j \ge 3\). Since \(v^1\perp \phi ^1\), we can write \(u^2 = \frac{\langle \phi ^2, v^1 \rangle }{1 + dt\lambda _2} \phi ^2\). By the estimates on \(v^1(j)\), \(\langle \phi ^2, v^1 \rangle = O(N^{3/2 - \alpha })\). Therefore, since \(\lambda _2 = O(1)\), we have \(u^2 = O(N^{3/2 - \alpha }) \phi ^2\). Since \(u^2(1)\) is asymptotically larger than \(u^1(1)\) with respect to N, we have \(GL(u^2) > GL(u^1)\) for N large, and the scheme is not monotone in GL for large N. \(\square \)

4.2 Heuristic Explanation for Good Typical Behavior

Despite the pathological behavior of the example given above, the stepsize for spectral truncation does not depend badly on N in practice. In this section, we attempt to give a heuristic explanation of this from two viewpoints.

The first view is to analyze the projection operator \(P_m\) in the \(L^\infty \) norm. The reason why the maximum principle fails is because \(P_m\) is expansive in the \(L^\infty \) norm. Namely, for some vector \(\Vert v\Vert _\infty \le 1\), we have \(\Vert P_m(v)\Vert _\infty =O(\sqrt{N})\) in the worst case. However, an easy analysis shows the probability of attaining such an \(O(\sqrt{N})\) bound decays exponentially as N grows large, as shown in a simplified analysis in Proposition 17 of Appendix. Thus in practice, it is very rare that adding \(P_m\) would violate the maximum principle “too much”.

The second view is to restrict our attention to data that come from a random sample. Namely, we assume that our data points \(x^i\) are sampled i.i.d. from a probability distribution p. In [31], it is proven under very general assumptions that the eigenfunctions, eigenvalues of the symmetric graph Laplacian converges to continuous limits almost surely. Moreover, the projection operators \(P_k\) converges in various senses (see [31] for details) to their continuous limits. More recently, results for continuous limits of graph-cut problems can be found in [27]. Under this set up, we can define the Allen–Cahn scheme on the continuous domain and discuss its properties on suitable function spaces. The spectral truncated scheme still would not satisfy the maximum principle, but at least the estimates involved would be independent of the size of the samples \(x^i\), which is also the size of the graph.

5 Results for Multiclass Classification

The analysis in previous sections can be carried over in a straight forward fashion to the multiclass case. Multiclass diffuse interface algorithm on graphs can be found in [15, 19, 23]. We state some basic notations. Let K be the number of classes, and N the number of nodes on the graph. We define u to be a real-valued \(N\times K\) matrix, and obtain the classification results with respect to the matrix u by taking the row-wise maximum. Specifically, the predicted label of node i will be \({{\mathrm{arg\,max}}}_j u_{ij}\). We think of the matrix u as a vector valued function on the graph, and denote its rows by u(i).

The multiclass Ginzburg–Landau functional is defined as

$$\begin{aligned} GL(u) = \frac{\epsilon }{2}tr(uLu) + \frac{1}{\epsilon }\sum ^N_{i=1} W(u(i)). \end{aligned}$$
(47)

where \(e^k = (0,0,\ldots , 1,\dots , 0)^t,\) and W is the \(L^2\) “multi-well”.

$$\begin{aligned} W(x) = \left( \prod ^K_{k=1}\Vert x-e^k\Vert ^2_2\right) , \end{aligned}$$
(48)

In [14], a different well function is defined using the \(L^1\) norm instead of \(L^2\). However, the algorithm in [14] uses a subgradient descent followed by a projection onto the Gibbs simplex. Since the Gibbs simplex itself is already bounded, this renders the boundedness result trivial, and therefore we will only prove the results for the \(L^2\) well. Define \(\varvec{W}(u) = \sum ^N_{i=1} W(u(i)).\) We minimize GL by the semi-implicit scheme below

$$\begin{aligned} \left\{ \begin{aligned} v^k&=u^k-dt*\frac{1}{\epsilon } \nabla \varvec{W}(u^k),\\ u^{k+1}&=-dt*(\epsilon Lu^{k+1})+v^k.\\ \end{aligned}\right. \end{aligned}$$
(49)

The main proposition we prove is this.

Proposition 16

Let L be the unnormalized graph Laplacian. Suppose \(u^0 \in [0,1]^{N\times K}\), and define \(u^k\) by Eq. (49). Then \(\exists c\) dependent only on K such that if \(0\le dt \le c\), we have \(u^k \in [0,1]^{N\times K}\) for all \(k\ge 0\).

Remark 3

The choice for \(u^k \in [0,1]^{N\times K}\) instead of an \(L^\infty \) bound is natural in the multiclass algorithm since we want the final results to have components close to \(\{0,1\}\) instead of \(\{-1, 1\}\).

Proof

Suppose \(u^k \in [0,1]^{N\times K}\). Since line 2 of (49) is decoupled in columns of \(u^{k+1}\), we can apply maximum principle to each column and have \(\max _{ij} u^{k+1}_{ij} \le \max _{ij} v^k_{ij}\), and \(\min _{ij} u^{k+1}_{ij} \ge \min _{ij} v^k_{ij}\). Hence we only have to show \(v^k \in [0,1]^{N\times K}\). Since the rows in line 1 of (49) are decoupled, we only have to show that the forward map maps each row of \(u^k\) to \([0,1]^{K}\) for \(0\le dt \le c\). This is proven in the lemma below.

Lemma 8

Define \({\varvec{\mathcal {F}}}_{dt} :\mathbb {R}^K \rightarrow \mathbb {R}^K\) as \({\varvec{\mathcal {F}}}_{dt}(x) = x - dt \nabla \varvec{W}(x)\). Then \(\exists \) c dependent only on K such that \(\forall 0 \le dt \le c\), \({\varvec{\mathcal {F}}}_{dt}([0,1]^K)\subset [0,1]^K\).

Proof

Given \(x \in [0,1]^{K}\), we denote components of x by \(x_i\). Let \(y = {\varvec{\mathcal {F}}}_{dt}(x)\). For each i, \(y_i = (1 - 2 dt\sum _j G_j(x)) x_i + 2dt G_i(x)\), where \(G_j(x) = \prod _{k\ne j} \Vert x-e^k\Vert ^2_2\). We set \(\frac{1}{2c} = \max _{x\in [0, 1]^K} \sum _j G_j(x) \). Then \(\forall 0\le dt \le c\), we have \(1\ge (1 - 2 dt\sum _j G_j(x))\ge 0\). We then prove \(y_i \in [0,1]\). For one direction, since \(x_i\ge 0\), \(y_i \ge 2dtG_j(x) \ge 0\). In the other direction, \(y_i \le 1 - 2 dt\sum _j G_j(x) + 2dt G_i(x) \le 1\). \(\square \)

Remark 4

Using the same argument as in previous sections, we can extend the result to incorporate fidelity and also prove monotonicity. We omit these discussions for the sake of brevity.

6 Numerical Results

In this section, we construct a variety of numerical experiments on several different types of datasets. This helps demonstrate our theory, and also have some implications on the real world performance of the schemes. In the following subsections, we specify the exact type of graph Laplacian used for each experiment. For all of the experiments, we initialize \(u^0\) randomly from the uniform distribution on \([-1, 1]^N\).

6.1 Two Moons

The two moons data set was used by Buhler et al. [7] in exploring spectral clustering with p-Laplacians. It is constructed by sampling from two half circles of radius one on \(\mathbb {R}^2\), centered at (0,0) and (1,0.5). Gaussian noise of standard deviation 0.02 in \(\mathbb {R}^{100}\) is then added to the data points. The weight matrix is constructed using Zelnik-Manor and Perona’s procedure [34]. Namely, we set \(w_{ij} = e^{-\Vert x_i - x_j\Vert ^2/\sqrt{\tau _i\tau _j}}\), where \(\tau _i\) is the Mth closest distance to i. We will consider all three Laplacians \(L^u\), \(L^{rw}\), and \(L^s\) in this section, and we refer to the figure captions for exactly which type of Laplacian is used.

In the experiments below, we compute the maximum stepsize dt such that the scheme satisfies an a posteriori criterion that reflects either the boundedness or the monotonicity of the scheme. Namely, we define the boundedness criterion as

$$\begin{aligned} \Vert u^k\Vert _\infty \le M,\quad \forall k \le \text {MaxIter}, \end{aligned}$$
(50)

and define the monotonicity criterion as

$$\begin{aligned} E(u^k)\le E(u^{k+1}),\quad \forall k \le \text {MaxIter}. \end{aligned}$$
(51)

We set \(\text {MaxIter} = 500\), and use bisection to determine the maximum stepsize that satisfies the criterion given.

Figure 2 plots the maximum stepsize such that the graph Allen–Cahn scheme satisfies the boundedness criterion for \(M = 1, 10\), where the graphs are generated from the two moons dataset with \(N = 20{:}20{:}2000\). No fidelity terms are added and we set \(\epsilon =1\). We perform the experiment for both the random walk Laplacian and the unnormalized Laplacian. We observe empirically that the stepsizes are independent of graph size N, and also match the tight and loose bound nicely.

Fig. 2
figure 2

Maximum stepsize dt that satisfies the boundedness criterion in Eq. (50) for the two moons dataset. Left \(M = 1\). Right \(M = 10\). We set \(\epsilon = 1\), and \(N=20{:}20{:}2000\). The “tight” and “loose” bound is defined in Lemma 1 and 2

Full size image

Figure 3 plots the maximum stepsize dt such that the graph Allen–Cahn scheme satisfies the monotonicity criterion. We plot the results for all three types of Laplacians. On the left, we fix \(\epsilon =1\), and N is varied from 20 : 20 : 2000. As we can see, the typical maximum stepsize for monotonicity is between the tight and loose bound. On the right, we fix \(N = 2000\) and vary \(\epsilon \) in the range \(\epsilon = 0{:}0.02{:}1\). We observe empirically the maximum stepsize dt for the unnormalized Laplacian has an almost linear relation with \(\epsilon \). For random walk and symmetric Laplacians, the relation is linear for small values of \(\epsilon \), but deviates as \(\epsilon \) is larger.

Fig. 3
figure 3

Maximum stepsize dt that satisfies the monotonicity criterion in Eq. (51) for the two moons dataset. Left \(\epsilon =1\) and \(N = 20{:}20{:}2000\). Right \(N=2000\) and \(\epsilon =0{:}0.02{:}1\)

Full size image
Fig. 4
figure 4

Maximum stepsize dt that satisfies the monotonicity criterion in Eq. (51) for the two moons dataset. We set \(L=L^u\), and \(\epsilon = 1\). Left Spectral truncation versus full scheme with \(\textit{Neig} = 50\), \(N = 20{:}20{:}2000\). Right Varying fidelity strength c for different percentages of randomly sampled fidelity points. We fix \(N = 2000\), and \(c = 0.1{:}0.02{:}3.1\)

Full size image
Fig. 5
figure 5

Images of different resolution segmented under \(dt = 2\), \(\epsilon = 4\). a \(256\times 256\), b \(51\times 51\), c segmentation for \(256\times 256\) and d segmentation for \(51\times 51\)

Full size image

Figure 4 (left) plots the maximum stepsize dt that satisfy the monotonicity criterion for the scheme under spectral truncation. The truncation level is set at \(\textit{Neig} = 50\). The results are compared with the original scheme without spectral truncation, and we see that the maximum stepsizes are roughly in the same range across all sizes of graphs tested in the experiment. We suspect that the effects of varying the truncation level \(\textit{Neig}\) may be hard to observe as suggested in Fig. 4 (left), and will most likely depend on the specific data set and the graph construction parameters. Due to the length of the paper, we omit discussions of varying the truncation level. Figure 4 (right) plots the effects of adding a quadratic fidelity term with strength parameter c while keeping \(\epsilon =1\) fixed for different percentages of randomly sampled fidelity points. We observe empirically that the stepsize dt decays as c increases to a large value, which matches the bound obtained in Proposition 5.

6.2 Two Cows

The purpose of this experiment is to study the effects of Nyström extension on the maximum stepsize for monotonicity. Nyström extension is a sampling technique used to approximate eigenvectors without explicitly computing the graph Laplacian [1, 12, 13]. The technique is very useful since it is often computationally prohibitive to work with the full graph Laplacian when the graph size N is large, which is often the case in image processing applications.

The images of the two cows (see Fig. 5) are from the Microsoft Database, and has been used in previous papers for the task of image segmentation [3, 23]. The dimensions of the original image is \(312\times 280\). We generate 10 images with increasingly smaller sizes \((312/k)\times (280/k)\), \(k= 1,\ldots , 10\) by resizing the original image to the target dimensions. We use a feature window of size \(7\times 7\), and construct a fully connected graph with \(w_{ij} = e^{-\frac{\Vert x_i - x_j\Vert ^2}{2\sigma ^2}}\), where \(\sigma = 1\). We use the symmetric graph Laplacian for this dataset. The eigenvectors are constructed using the Nyström extension, the details of which could be found in [3]. Figure 5 shows two images with \(k = 1, 5\) being segmented under the same stepsize \(dt = 2\), \(\epsilon = 4\). For fidelity, we select a rectangular area (see blue and red boxes in Fig. 5) of pixels as fidelity, and set the fidelity strength to \(\eta = 1\).

Figure 6 plots the maximum stepsize for monotonicity versus \(N^{-1/2}\), where N is the size of the graph which equals to the number of pixels in the image. To ensure segmentation quality, smaller epsilon had to be chosen for images of lower resolution. We choose \(\epsilon = 4\) for \(k\le 5\) and \(\epsilon = 2\) for \(k\ge 5\). We plot the ratio \(\frac{dt}{\epsilon }\) versus \(N^{-1/2}\) in Fig. 6.

Fig. 6
figure 6

Maximum Stepsize dt that satisfies the monotonicity criterion in Eq. (51) for the Two Cows dataset under different image sizes. N is the number of nodes in the graph, which equals \(A\times B\) with A, B the height and width of an image. We set \(\epsilon = 4\) for \(k\le 5\) and \(\epsilon = 2\) for \(k\ge 5\), where k is the scale of the resizing

Full size image
Table 1 Maximum stepsize and classification accuracy for MNIST digit triplets
Full size table

6.3 MNIST

The purpose of this experiment is to study the stepsize bound for the multiclass graph Allen–Cahn scheme. The MNIST database [22] contains approximately 70, 000 \(28\times 28\) images of handwritten digits from zero to nine. The graph is constructed by first projecting each image to the 50 principal components obtained through PCA of the entire MNIST dataset. The weights are computed using the Zelnik-Manor and Perona’s scaling [34] with 50 nearest neighbors.

We consider subsets of the MNSIT dataset by choosing a triplet of digits (e.g. {4, 5, 6}). For each such subset, there are approximately 25, 000 images, where each image is a representation of one of the digits in the triplet. We test the maximum stepsizes that satisfy the monotonicity criterion on several such subsets as shown in Table 1. We set \(\epsilon = 1\), \(\eta = 1\), and randomly select \(5\%\) of data points as the fidelity set. We also use spectral truncation with 100 eigenvectors to speed up computations. Table 1 shows the maximum stepsizes for various choices of digit triplets, and the classification accuracy for \(dt = 0.5\). We observe that the maximum dt does not change when the choice of the triplet varies, and can all achieve a good classification accuracy under a stepsize close to the maximum stepsize allowed for monotonicity.

7 Discussion

The graph Allen–Cahn scheme has been used to approximate solutions to the graph cut problem. This paper studies the range of stepsizes for the graph Allen–Cahn scheme to converge, in relation with the graph Laplacian and other parameters. In summary, we obtain graph independent bounds on dt for which the graph Allen–Cahn scheme is bounded and monotone. Moreover, under a mild a posteriori condition, we show the iterates converge to a stationary point of the total energy E. We then prove a similar monotonicity and boundedness result for stepsize \(0\le dt\le O(N^{-1})\) when spectral truncation is applied. We show via an explicit example that the dependency of the stepsize dt on the number of nodes N is unavoidable in the worst case. We also extend the results to multiclass Ginzburg–Landau functional using similar techniques as in the binary case.

There are still some very interesting problems left to be explored. One interesting theoretical problem is to generalize the results for other well potentials of different asymptotic growth rate. It may also be worthwhile to explore the dependency of dt on \(\epsilon \) for the spectral truncation analysis, which the paper, for the sake of simplicity, does not address. Another potential problem is the relationship between the stepsize and the accuracy of the classification result. So far this analysis does not attempt to characterize the quality of the extrema reached, but experiments have shown that the classification accuracy does differ under different choices of stepsize.