Analytical Solutions for an Escape Problem in a Disc with an Arbitrary Distribution of Exit Holes Along Its Boundary

Abstract

We analytically construct solutions for the mean first-passage time and splitting probabilities for the escape problem of a particle moving with continuous Brownian motion in a confining planar disc with an arbitrary distribution (i.e., of any number, size and spacing) of exit holes/absorbing sections along its boundary. The governing equations for these quantities are Poisson’s equation with a (non-zero) constant forcing term and Laplace’s equation, respectively, and both are subject to a mixture of homogeneous Neumann and Dirichlet boundary conditions. Our solutions are expressed as explicit closed formulae written in terms of a parameterising variable via a conformal map, using special transcendental functions that are defined in terms of an associated Schottky group. They are derived by exploiting recent results for a related problem of fluid mechanics that describes a unidirectional flow over “no-slip/no-shear” surfaces, as well as results from potential theory, all of which were themselves derived using the same theory of Schottky groups. They are exact up to the determination of a finite set of mapping parameters, which is performed numerically. Their evaluation also requires the numerical inversion of the parameterising conformal map. Computations for a series of illustrative examples are also presented.

Appendices

Appendix 1: Schottky Groups and Associated Functions

In this appendix we provide definitions and properties of the S–K prime function and the integrals of the first kind, in terms of which we construct the main results, Eqs. (3.19) and (3.23), presented in this paper. With the exception of the contents of the section “Symmetry in the Real Axis”, much of this material can be found in earlier papers by Crowdy and the present author, including Crowdy [15] and Crowdy and Marshall [20, 21, 24, 25]. However, we include it here for completeness, and also because some aspects of it (in particular, issues relating to branches of the integrals of the first kind) are not explained in full detail in those earlier works. Further details of some of the material in this section can also be found in Baker [34], Hejhal [35], Belokolos et al. [36] and Mumford et al. [37].

1.1 The Schottky Group $\Theta$

We begin by defining a special group associated with our $(N+1)$-connected circular domain D. To do so, for $k=0,1,\ldots ,N$, we first define the Möbius map $\phi _k(\zeta )$ by

$$\begin{aligned} \phi _k(\zeta )=\delta _k+\frac{q_k^2}{\zeta -\delta _k}. \end{aligned}$$

(6.1)

So, for example, $\phi _0(\zeta )$ is simply $1/\zeta$. It is straightforward to check that

$$\begin{aligned} \phi _k(\zeta )=\overline{\zeta },~~~\mathrm{for}~\zeta \in C_k. \end{aligned}$$

(6.2)

We thus define the reflection of a point $\zeta$ in $C_k$ by $\varphi _k(\zeta )$, where

$$\begin{aligned} \varphi _k(\zeta )=\overline{\phi _k(\zeta )}. \end{aligned}$$

(6.3)

For example, $\varphi _0(\zeta )=1/\overline{\zeta }$. Now, for $k=0,1,\ldots ,N$, we introduce the Möbius map $\theta _k(\zeta )$ consisting of the composition of reflection in the unit circle, $C_0$, followed by reflection in the circle $C_k$, i.e.,

$$\begin{aligned} \theta _k(\zeta )=\overline{\phi _k(\overline{\zeta }^{-1})}. \end{aligned}$$

(6.4)

Note that $\theta _0(\zeta )$ is simply the identity map. It follows from Eqs. (6.4) and (6.1) that

$$\begin{aligned} \theta _k(\zeta )=\delta _k+\frac{q_k^2 \zeta }{1-\delta _k\zeta }. \end{aligned}$$

(6.5)

We also introduce the inverse of $\theta _k(\zeta )$, which we denote by $\theta _{-k}(\zeta )$. This consists of the composition of reflection in $C_k$ followed by reflection in $C_0$. One can thus check that

$$\begin{aligned} \theta _{-k}(\zeta )=\frac{1}{\phi _k(\zeta )}. \end{aligned}$$

(6.6)

Next, for $k=1,\ldots ,N$, we denote the reflection of $C_k$ in $C_0$ by $C_{-k}$. Also, we denote the reflection of D in $C_0$ by $D_{-1}$. $D_{-1}$ is the $(N+1)$-connected domain bounded by $C_0$, $C_{-1},\ldots ,C_{-N}$. Note that $D_{-1}$ will extend to infinity (as for the case sketched in Fig. 9) unless the origin lies in the interior of one of $C_1,\ldots ,C_N$. One can check that $C_k$ is the image of $C_{-k}$ under $\theta _k(\zeta )$ [for example, by considering the latter as the composition of reflections stated just before Eq. (6.4)]. In fact, it can be shown that $\theta _k(\zeta )$ maps the exterior of $C_{-k}$ onto the interior of $C_k$ (and hence, the interior of the former onto the exterior of the latter). It follows that the set, $\Theta$, consisting of all compositions of the maps $\theta _k(\zeta )$, $k=-N,\ldots ,N$, is a Schottky group (see, for example, [37]). We refer to the maps $\theta _{k}$, $k=1,\ldots ,N$, as the generators of $\Theta$. The (2N)-connected region, F, defined by

$$\begin{aligned} F=\overline{D}\cup D_{-1}, \end{aligned}$$

(6.7)

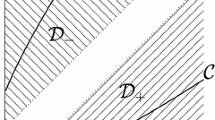
(where $\overline{D}$ denotes the closure of D) is called a fundamental region of the group $\Theta$. Its images under all elements of $\Theta$ are mutually disjoint and cover the whole of the $\zeta$-plane. Note that F consists of the exterior of the circles $C_1$,..., $C_N$, $C_{-1}$,..., $C_{-N}$, together with $C_1$,..., $C_N$. However, $C_{-1}$,..., $C_{-N}$ are not included in F. A schematic of an example of F for the case of $N=2$ is shown in Fig. 9 (for this example, D, and hence F, contains the origin and so F extends to infinity). Groups such as $\Theta$, whose fundamental regions are bounded by circles, are referred to as “classical” Schottky groups [36]. Furthermore, as the generators of $\Theta$ pair the circles $C_k$, $k=1,\ldots ,N$, with their reflections in another circle (namely $C_0$), this group is also said to be symmetric. The Schottky group $\Theta$ and its fundamental region F can be viewed as a model of a symmetric Riemann surface associated with D, known as its Schottky double. Furthermore, groups such as $\Theta$, for which one can define a fundamental region whose boundary circles are all centred along a common axis (in this case, the real axis) are sometimes referred to as Fuchsian Schottky groups [37].

Fig. 9

The shaded region is the fundamental region, F, arising from the circular domain, D, bounded by the circles $C_0$, $C_1$ and $C_2$. Note that $C_0$ is not part of the boundary of F. In this case, D contains the origin, and so F extends to infinity. We take branch cuts of the corresponding integrals of the first kind along the real intervals $I_1$ and $I_2$, and their reflections, $\varphi _0(I_1)$ and $\varphi _0(I_2)$, in $C_0$. In this case, $\varphi _0(I_1)$ passes through the point at infinity. The generators, $\theta _1$ and $\theta _2$, of the associated Schottky group, $\Theta$, and their actions, are also indicated

1.2 The Integrals of the First Kind

Associated with any Schottky group are what are known as its integrals of the first kind. We denote these by $\upsilon _j(\zeta )$, $j=1,\ldots ,N$. They are uniquely defined up to additive constants (i.e., terms independent of $\zeta$) as the functions analytic, but multi-valued, in F, with

(6.8)

where we integrate around $C_k$ and $C_{-k}$ in the anticlockwise direction (i.e., with the interior of F on the right), and $\delta _{jk}$ denotes the Kronecker delta function. Note that it is only their real part that is multi-valued; their imaginary part is single-valued. One can fix single-valued branches of them by introducing a set of branch cuts to divide F into a simply-connected region. We shall choose to do this with $2N-1$ cuts along the real axis along the intervals:

$$\begin{aligned} I_1,\ldots ,I_{N-1},I_N\cup \varphi _0(I_N),\varphi _0(I_1),\ldots ,\varphi _0(I_{N-1}), \end{aligned}$$

(6.9)

where we write $\varphi _0(I_j)$ to denote the reflection of $I_j$ in $C_0$. See, for example, Fig. 9. Note that we do not have a cut along $\varphi _0(I_0)\cup I_0$. Also, if one of $I_1,\ldots ,I_N$ contains the origin (as is the case for the example sketched in Fig. 9), then its image under reflection in $C_0$ will pass through the point at infinity. For the following, as will become evident, we need not specify which set of branches of the integrals of the first kind with this set of cuts we use. Committing a slight abuse of notation, we shall, henceforth in this appendix and all other sections of the paper, now use $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, to denote such a set of branches.

However, it is very important to note that, in practice, in order to actually compute the formulae given by Eqs. (3.19) and (3.23), one does not need to specify a set of branches with these cuts in one’s numerical coding. This is for the following reasons.

First, the imaginary parts of $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, appear in both Eqs. (3.19) and (3.23), but one can substitute these with the imaginary parts of any other set of branches, as the imaginary parts of the integrals of the first kind are single-valued. The only other terms in Eqs. (3.19) and (3.23) that depend on $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, are the constants $\lambda _j$ and $\Lambda _{jk}$, $j,k=1,\ldots ,N$, as we now explain. This dependence is via the matrix $\varvec{\tau }$ which appears in Eq. (3.11) and Eq. (3.17) and is defined as follows. For $j,k=1,\ldots ,N$, the entry, which we denote by $\tau _{jk}$, in the jth row and kth column of $\varvec{\tau }$ is defined by the following property of our branches, $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, of the integrals of the first kind:

$$\begin{aligned} \upsilon _j(\theta _k(\zeta ))-\upsilon _j(\zeta )\equiv \tau _{jk},~~~\forall \zeta \text{, } j,k=1,\ldots ,N. \end{aligned}$$

(6.10)

Equation (6.10) provides the continuation of $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, from F into the rest of the plane. Note that in performing this continuation, we must extend our cuts for $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, by supplementing the cuts already introduced in F [i.e., given by the intervals in Eq. (6.9)] with their images under all maps in $\Theta$. An analogous relation to that in Eq. (6.10) holds for any other set of branches of the integrals of the first kind. If such a set of branches has the same set of cuts, the corresponding $\tau _{jk}$’s will be the same. However, if such a set of branches has a different set of cuts, the corresponding $\tau _{jk}$’s will, in general, be different. However, it follows from the properties of the integrals of the first kind given by Eq. (6.8), that these differences will only be by the addition of integers. Furthermore, as we shall show [see Eq. (6.18)], our choice of branches, $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, lead to purely imaginary $\tau _{jk}$, $j,k=1,\ldots ,N$. Hence one can compute the corresponding constants for any choice of branches, and then take the imaginary parts of these to get $\tau _{jk}$ and hence $\lambda _j$ and $\Lambda _{jk}$, $j,k=1,\ldots ,N$, as are needed for Eqs. (3.19) and (3.23). For these reasons, one does not need to specify a set of branches of the integrals of the first kind with the cuts in Eq. (6.9) in order to compute the formulae given by Eqs. (3.19) and (3.23).

At this point, we should also mention that $\varvec{\tau }$ is known to be symmetric, i.e.,

$$\begin{aligned} \tau _{jk}=\tau _{kj},~~~\text{ for } j,k=1,\ldots ,N, \end{aligned}$$

(6.11)

and also invertible (see, for example, [35, p. 32]).

Furthermore, on the subject of the continuation of $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, from F into the rest of the plane, let us mention that it can be shown that these are analytic for all $\zeta$ except along their branch cuts and also at the so-called singular points of $\Theta$ (see, for example, [34]). The latter are points that can only be reached as the image of a point in F under infinitely many applications of the group generators, $\theta _k(\zeta )$, $k=1,\ldots ,N$, and their inverses.

Finally, we mention that for Fuchsian Schottky groups such as $\Theta$, there exists an explicit representation for the integrals of the first kind as an infinite product [34]. This is stated by Eq. (6.25). Together with Eq. (6.10), this can also be used to compute the constants $\tau _{jk}$, $j,k=1,\ldots ,N$, as discussed in “Explicit Representations” in this appendix.

1.3 The Schottky–Klein Prime Function

We may now define the Schottky–Klein (S–K) prime function associated with $\Theta$ as follows. It can be shown [35] that there exists a unique function, $X(\zeta ,\gamma )$, defined for all $\zeta$ by the following properties. For fixed $\gamma \in F$ (where we assume that $\gamma \ne \infty$ if the point at infinity is contained in F):

• (i) $X(\zeta ,\gamma )$ is analytic as a function of $\zeta$ for $\zeta \in F$, except for a double pole at $\zeta =\infty$ if the latter is contained in F;

• (ii) $X(\zeta ,\gamma )$ has a second-order zero at $\zeta =\gamma$ with

  $$\begin{aligned} \lim _{\zeta \rightarrow \gamma }X(\zeta ,\gamma )=(\zeta -\gamma )^2; \end{aligned}$$

  (6.12)

• (iii) For $\zeta \in F$ and $k=1,\ldots ,N$,

  $$\begin{aligned} X(\theta _k(\zeta ),\gamma ) =e^{-4\pi \mathrm{i}(\upsilon _k(\zeta )-\upsilon _k(\gamma )+\frac{1}{2}\tau _{kk})} \frac{\mathrm {d}\theta _k(\zeta )}{\mathrm {d}\zeta } X(\zeta ,\gamma ), \end{aligned}$$

  (6.13)

  where we re-iterate that $\upsilon _k(\zeta )$, $k=1,\ldots ,N$, denote our fixed branches of the integrals of the first kind, described above. However, one may check that the value of the right hand side of Eq. (6.13) is the same for any choice of branches of the integrals of the first kind, with any choice of cuts.

Then, the S–K prime function, which we denote by $\omega (\zeta ,\gamma )$, is uniquely defined by

$$\begin{aligned} \omega (\zeta ,\gamma )=(X(\zeta ,\gamma ))^{1/2}, \end{aligned}$$

(6.14)

where the branch of the square root is chosen so that, as $\zeta \rightarrow \gamma$,

$$\begin{aligned} \omega (\zeta ,\gamma )\sim (\zeta -\gamma ). \end{aligned}$$

(6.15)

It can be shown [35] that, considered as a function of $\zeta$ for fixed $\gamma \in F$ (where we assume that $\gamma \ne \infty$ if the latter is contained in F), $\omega (\zeta ,\gamma )$ is single-valued and analytic in $\zeta$ for all $\zeta$ and $\gamma$, except for a simple pole at infinity if the latter is contained in F, and singularities at the singular points of $\Theta$. Furthermore, $\omega (\zeta ,\gamma )$ also has a simple zero at $\zeta =\theta (\gamma )$, for all maps $\theta \in \Theta$. In view of these properties, the S–K prime function can, in some sense, be regarded as a natural generalisation of the monomial $(\zeta -\gamma )$, and indeed reduces to this in the case when D is simply-connected, as is discussed in “Simply-Connected Case (N=0)” in this appendix. In the case when D is doubly-connected the S–K prime function is closely related to the traditionally more commonly used elliptic functions, as is discussed in “Doubly-Connected Case (N=1)” in this appendix. However, the S–K prime function possesses the advantage over elliptic functions of being more easily extendible to all higher (finite) connectivities.

We also remark that, as for the integrals of the first kind, for Fuchsian Schottky groups such as $\Theta$, there exists an explicit representation for the S–K prime function as an infinite product. This is stated by Eq. (6.27).

1.4 Symmetry Properties

We now present some further important properties of our branches of the integrals of the first kind, $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, and the S–K prime function, $\omega (\zeta ,\gamma )$, that follow from the reflectional symmetries of D. Note that these do not hold for all Schottky groups in general.

1.4.1 Symmetry in $C_0$

First we report properties of these functions that follow from the reflectional symmetry of D in $C_0$.

Proposition 6.1

$$\begin{aligned} \upsilon _j(\zeta )=\overline{\upsilon _j(\overline{\zeta }^{-1})},~~~\forall \zeta \text{, } j=1,\ldots ,N. \end{aligned}$$

(6.16)

Proof

For $j=1,\ldots ,N$, one may check that $\overline{\upsilon _j(1/\overline{\zeta })}$ is analytic as a function of $\zeta$ for all $\zeta \in F$, except for the same branch cuts as $\upsilon _j(\zeta )$, i.e., as given by Eq. (6.9). (Note that it was in order to ensure this last fact that we chose our cuts of $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, in F to be reflectionally symmetric in $C_0$.) Next, for $k=1,\ldots ,N$, as $\zeta$ traverses $C_k$ in the anticlockwise direction, so $1/\overline{\zeta }$ traverses $C_{-k}$ in the clockwise direction. It then follows from Eq. (6.8) that the change in $\overline{\upsilon _j(1/\overline{\zeta })}$ after $\zeta$ has traversed $C_k$ in the anticlockwise direction is $\delta _{jk}$. Similarly, the change in $\overline{\upsilon _k(1/\overline{\zeta })}$ after $\zeta$ has traversed $C_{-k}$ in the anticlockwise direction is $-\delta _{jk}$. One may then deduce from the uniqueness of the integrals of the first kind up to additive constants, that we must have $\upsilon _j(\zeta )=\overline{\upsilon _j(1/\overline{\zeta })}+\kappa _j$, for some constant $\kappa _j$. Picking $\zeta \in C_0$, so that $1/\overline{\zeta }=\zeta$, it follows that $\kappa _j=2\mathrm {i}\mathrm {Im}\{\upsilon _j(\zeta )\}$. But since the integrals of the first kind are only defined up to additive constants, we have the freedom to pick

$$\begin{aligned} \mathrm {Im}\{\upsilon _j(\zeta )\}=0,~~~\text{ for } \zeta \in C_0. \end{aligned}$$

(6.17)

This then gives $\kappa _j=0$, and hence Eq. (6.16). $\square$

Proposition 6.2

$$\begin{aligned} \mathrm {Re}\{\tau _{jk}\}=0,~~~j,k=1,\ldots ,N. \end{aligned}$$

(6.18)

Proof

It follows from Eq. (6.10) that

$$\begin{aligned} \tau _{jk}=\upsilon _j(\zeta )-\upsilon _j(\overline{\zeta }^{-1})=2\mathrm {i}\mathrm {Im}\{\upsilon _j(\zeta )\}~~~\text{ for } \zeta \in C_k, \end{aligned}$$

(6.19)

where the first equality follows from the fact that $1/\overline{\zeta }=\theta _{-k}(\zeta )$ for $\zeta \in C_k$, and the second follows from Eq. (6.16). It then follows from Eq. (6.19) that $\tau _{jk}$ is purely imaginary. $\square$

Proposition 6.3

$$\begin{aligned} \omega (\zeta ,\gamma )=-\gamma \zeta \overline{\omega (\overline{\zeta }^{-1},\overline{\gamma }^{-1})},~~~\forall \zeta ,\gamma . \end{aligned}$$

(6.20)

A derivation of Eq. (6.20) using the explicit representation of the S–K prime function in Eq. (6.27) is given by Crowdy and Marshall [38]. A more general proof that relies only on the defining properties of the S–K prime function is given by Vasconcelos et al. [39].

1.4.2 Symmetry in the Real Axis

Next we state properties that follow from the reflectional symmetry of D in the real axis.

Proposition 6.4

$$\begin{aligned} \upsilon _j(\zeta )=-\overline{\upsilon _j(\overline{\zeta })}+\mu _j,~~~\forall \zeta \text{, } j=1,\ldots ,N, \end{aligned}$$

(6.21)

for some real constants $\mu _j$, $j=1,\ldots ,N$.

Proof

A simple proof of Eq. (6.21) follows using arguments similar to those used in the derivation of Eq. (6.16). For $j=1,\ldots ,N$, one may check that $\overline{\upsilon _j(\overline{\zeta })}$ is analytic as a function of $\zeta$ for all $\zeta \in F$, except for the same branch cuts as $\upsilon _j(\zeta )$, i.e., as given by Eq. (6.9). (Note that it was in order to ensure this last fact that we chose our cuts of $\upsilon _j(\zeta )$, $j=1,\ldots ,N$, in F to be reflectionally symmetric in the real axis.) Next, for $k=1,\ldots ,N$, as $\zeta$ traverses $C_k$ in the anticlockwise direction, so $\overline{\zeta }$ traverses $C_k$ in the clockwise direction. It then follows from Eq. (6.8) that the change in $\overline{\upsilon _j(\overline{\zeta })}$ after $\zeta$ has traversed $C_k$ in the anticlockwise direction is $-\delta _{jk}$. Similarly, the change in $\overline{\upsilon _k(\overline{\zeta })}$ after $\zeta$ has traversed $C_{-k}$ in the anticlockwise direction is $\delta _{jk}$. One may then deduce from the uniqueness of the integrals of the first kind up to additive constants, that Eq. (6.21) must hold for some additive constant $\mu _j$. To show that $\mu _j$ must be real, consider Eq. (6.21) for $\zeta \in I_0$ so that $\overline{\zeta }=\zeta$, and importantly, $\zeta$ does not lie on a branch cut of $\upsilon _j(\zeta )$. Then it follows that

$$\begin{aligned} \mu _j=2\mathrm {Re}\{\upsilon _j(\zeta )\}~~~\text{ for } \zeta \in I_0, \end{aligned}$$

(6.22)

and hence $\mu _j$ must be real. $\square$

Note that we cannot choose $\mu _j$ in Eq. (6.21), as we have already completely specified $\upsilon _j(\zeta )$ by fixing Eq. (6.17). Also, we point out that one should not conclude from Eq. (6.21) that $\mathrm {Re}\{\upsilon _j(\zeta )\}=\mu _j/2$ for all real $\zeta$. This is not the case. Letting $\zeta ^+$ and $\zeta ^-$ denote the limits as we approach a point $\zeta$ along the real axis, Eq. (6.21) really states that

$$\begin{aligned} \upsilon _j(\zeta ^+)+\overline{\upsilon _j(\zeta ^-)}=\mu _j,~~~j=1,\ldots ,N, \end{aligned}$$

(6.23)

and since $\upsilon _j(\zeta )$ has branch cuts along sections of the real axis, $\upsilon _j(\zeta ^+)$ and $\upsilon _j(\zeta ^-)$ are not necessarily equal. More specifically, whilst their imaginary parts will be the same, their real parts may not be (recall the imaginary part of $\upsilon _j(\zeta )$ is single-valued, but its real part is not). Nevertheless, letting $I_k^+$ denote the upper side of $I_k$ (i.e., the side facing into the upper half-plane) for $k=1,\ldots ,N$, one can show that $\mathrm {Re}\{\upsilon _j(\zeta )\}$ is still constant along $I_k^+$, just not necessarily equal to the same constant as it is along $I_0$. (Note that the same could be said for $\mathrm {Re}\{\upsilon _j(\zeta )\}$ at points along the lower side of $I_k$.) We omit further details here.

Proposition 6.5

$$\begin{aligned} \omega (\zeta ,\gamma )=\overline{\omega (\overline{\zeta },\overline{\gamma })},~~~\forall \zeta ,\gamma . \end{aligned}$$

(6.24)

Proof

A proof of Eq. (6.24) follows in a similar vein to that of Eq. (6.21). Consider the function $\overline{X(\overline{\zeta },\overline{\gamma })}$, $=\hat{X}(\zeta ,\gamma )$, say. One can check that $\hat{X}(\zeta ,\gamma )$ satisfies the defining properties of $X(\zeta ,\gamma )$, and hence by the uniqueness of the latter function, we must have $\hat{X}(\zeta ,\gamma )\equiv X(\zeta ,\gamma )$. Note that in order to check Eq. (6.13) of property (iii), one must make use of Eq. (6.21) and Eq. (6.18). Finally, $\omega (\zeta ,\gamma )$ is uniquely defined as the square root of $X(\zeta ,\gamma )$ such that Eq. (6.15) holds as $\zeta \rightarrow \gamma$. But in this limit, we have $\omega (\zeta ,\gamma )=\overline{\omega (\overline{\zeta },\overline{\gamma })}$, so we can conclude that the two must be identical. $\square$

1.5 Explicit Representations

In this section we report explicit representations for the above special functions.

For Fuchsian Schottky groups there exists an explicit representation for the integrals of the first kind as an infinite product which is known to converge [34, 36]. For $\Theta$, this is stated as:

$$\begin{aligned} \upsilon _j(\zeta ) =\frac{1}{2\pi \mathrm{i}} \log \Biggl ( \prod _{\theta \in \Theta _j} \frac{\zeta -\theta (B_j)}{\zeta -\theta (A_j)} \Biggr ) +d_j,~~~\text{ for } j=1,\ldots ,N, \end{aligned}$$

(6.25)

where $\Theta _j$ is the set consisting of all maps $\theta \in \Theta$ whose composition in terms of the group generators does not begin with $\theta _j$ or $\theta _{-j}$. For example, $\theta _1\theta _{2}$ is contained in $\Theta _1$ but $\theta _2\theta _1$ is not. Note also that the identity map is contained in $\Theta _j$. $A_j$ and $B_j$ are the fixed points of $\theta _j(\zeta )$, i.e., the solutions of $\theta _j(\zeta )=\zeta$. One can see from Eq. (6.5) that this is equivalent to a quadratic equation in $\zeta$. One can show that this quadratic has two solutions: one, which we denote $A_j$, in the interior of $C_{-j}$, and the other, $B_{j}$, in the interior of $C_j$ [34, 37]. Both of $A_j$ and $B_j$ are real. In fact, using elementary algebra, one can show that, provided $\delta _j\ne 0$,

$$\begin{aligned} A_j=\frac{(1+\delta _j^2-q_j^2)+\sqrt{(1+\delta _j^2-q_j^2)^2-4\delta _j^2}}{2\delta _j},~~~~~ B_j=\frac{1}{A_j}. \end{aligned}$$

(6.26)

If $\delta _j=0$, then $A_j=\infty$ and $B_j=0$. Note also that it can be shown that, for all $\theta \in \Theta _j$, $\theta (A_j)$ and $\theta (B_j)$ are real and lie outside F. In fact, they are singular points of $\Theta$, and so can only be reached as the image of a point in F under infinitely many applications of the group generators, $\theta _j(\zeta )$, $j=1,\ldots ,N$, and their inverses. Finally, $d_j$ is a constant (i.e., independent of $\zeta$). Since only the imaginary part of $\upsilon _j(\zeta )$ appears in Eqs. (3.19) and (3.23), we need only specify the imaginary part of $d_j$ here. This should be chosen so that Eq. (6.17) holds. We omit further details here.

An explicit, infinite product representation (which is independent of $\zeta$) for $\tau _{jk}$ can be derived from Eqs. (6.10) using (6.25) [34]. However, in doing so, one must account for the branch cuts and branches chosen for $\upsilon _j(\zeta )$, $j=1,\ldots ,N$. In practice, when performing computations such as those presented in Sect. 4, it is more straightforward to compute $\tau _{jk}$ by evaluating the left-hand side of Eqs. (6.10), using (6.25), for some particular, chosen $\zeta$. For example, a convenient choice is to pick $\zeta \in C_{-k}$, as then $\theta _{k}(\zeta )$ is simply $1/\overline{\zeta }$.

For such Fuchsian Schottky groups, there also exists an explicit, infinite product representation for the S–K prime function which is known to be convergent [34, 36]. For $\Theta$, this is stated as:

$$\begin{aligned} \begin{aligned} \omega (\zeta ,\gamma )= (\zeta -\gamma ) \prod _{\theta \in \Theta ''} \frac{(\zeta -\theta (\gamma ))(\gamma -\theta (\zeta ))}{(\zeta -\theta (\zeta ))(\gamma -\theta (\gamma ))}, \end{aligned} \end{aligned}$$

(6.27)

where $\Theta ''$ is the set containing precisely one of $\theta$ and $\theta ^{-1}$ (where we use the latter to denote the inverse of $\theta$), for all $\theta \in \Theta$. For example, if $\theta _1\theta _2$ is included in $\Theta ''$, then its inverse, $\theta _{-2}\theta _{-1}$, is not. Note that it can be shown that the value of the product given by Eq. (6.27) does not depend on which of $\theta$ and $\theta ^{-1}$ we choose to include in $\Theta ''$.

Finally we mention that, of course, for the infinite product representations given by Eqs. (6.25) and (6.27) (and also the special case, Eq. (6.32), of Eq. (6.27) reported in the section “Doubly-Connected Case (N = 1)” below) to be of practical use in numerical computations, one must be able to conveniently truncate them to a finite number of terms that are sufficient to ensure their convergence to within an acceptable degree of accuracy. As for the computations presented in Sect. 4, this may be done by taking truncations that consist of a product over finite subsets of $\Theta _j$ or $\Theta ''$ that contain all maps whose composition in terms of the group generators consists of no more than a specified number, say M, of “factors”. For example, for $N=2$, taking $M=4$ means that we include $\theta _1^3\theta _2$ in our subset of $\Theta _1$, but not $\theta _2\theta _1^3\theta _2$ (the former contains four factors, the latter contains five). In the terminology of Mumford et al. [37] (see also Crowdy and Marshall [24]), the number of such factors in such a composition of a map is referred to as the level of the map. Thus one may say that our truncated subsets consist of all maps of levels up to and including level M.

For general N, generally speaking, the infinite products given by Eq. (6.25) and Eq. (6.27) [and also Eq. (6.32)] converge faster (by which we mean, they converge after the product of all maps of up to lower levels) as the radii of the inner circles $C_j$, $j=1,\ldots ,N$, decrease. However convergence is generally slower if any of the circles $C_j$, $j=1,\ldots ,N$, are very close together. It is also generally slower if N is very large. In cases where these product representations are so slow to converge as to make their use inefficient, one may instead compute the integrals of the first kind and the S–K prime function using a numerical procedure recently developed by Crowdy et al. [26]. Codes for this are available from Crowdy [27] and Kropf [28].

1.6 Special Cases

The above theory simplifies greatly in the cases $N=0$ and $N=1$ (provided $\delta _1=0$ in the latter), as we now describe.

1.6.1 Simply-Connected Case (N=0)

In this case, D is simply the unit disc $\{\zeta :|\zeta |<1\}$. Then the associated Schottky group contains just the identity transformation, and so there are no integrals of the first kind and the S–K prime function reduces to

$$\begin{aligned} \omega (\zeta ,\alpha )=(\zeta -\alpha ). \end{aligned}$$

(6.28)

1.6.2 Doubly-Connected Case (N=1)

In this case, D has a single inner boundary, $C_1$. If we pick the centre of $C_1$ to be the origin, then D is the concentric annulus $\{\zeta :q_1<|\zeta |<1\}$, for some $0<q_1<1$. Then the associated Schottky group, $\Theta$, is generated by just a single map, which from Eq. (6.5) is given simply by $\theta _1(\zeta )=q^2\zeta$. It can be shown that in this case the single integral of the first kind is given by

$$\begin{aligned} \upsilon _1(\zeta )=\frac{1}{2\pi \mathrm{i}}\log \zeta , \end{aligned}$$

(6.29)

the matrix $\varvec{\tau }$ has just a single entry, $\tau _{11}$, which is given by

$$\begin{aligned} \tau _{11}=\frac{1}{\pi \mathrm {i}}\ln q, \end{aligned}$$

(6.30)

and the S–K prime function can be expressed as

$$\begin{aligned} \omega (\zeta ,\alpha )=-\frac{\alpha }{A^2}P(\zeta /\alpha ), \end{aligned}$$

(6.31)

where $P(\zeta )$ is defined by

$$\begin{aligned} P(\zeta )\equiv (1-\zeta )\prod _{m=1}^{\infty }(1-q^{2m}\zeta )(1-q^{2m}\zeta ^{-1}), \end{aligned}$$

(6.32)

and A is a constant given by $A=\prod _{m=1}^{\infty }(1-q^{2k})$. Note that it can be shown that the infinite product in Eq. (6.32) converges for all $\zeta$ and q with $0<q<|\zeta |<1$. $P(\zeta )$ is in fact related to the more commonly used elliptic functions. For example, by a straightforward change of variables, one can relate it to the first Jacobi theta function.

Two useful properties of $P(\zeta )$ which can be deduced directly from Eq. (6.32) are

$$\begin{aligned} P(q^2\zeta )=-\zeta ^{-1}P(\zeta ),~~~P(\zeta ^{-1})=-\zeta ^{-1}P(\zeta ). \end{aligned}$$

(6.33)

These are the reductions of Eqs. (6.13) and (6.20), respectively, in this case.

Appendix 2: An Extended Parameterisation

In this section we describe an extension of our parameterisation of $\Omega$ in terms of $\zeta$, described in Sect. 3, which we found to be helpful when performing computations, provided the absorbing sections of $\partial \Omega$ were not too large. This is obtained via the Möbius map:

$$\begin{aligned} \eta (\zeta )=\frac{\zeta -\alpha }{\zeta -\overline{\alpha }}. \end{aligned}$$

(7.1)

It is straightforward to check that $\eta (\zeta )$, as given by Eq. (7.1), maps the real intervals $I_j$, $j=0,1,\ldots ,N$, of $\partial D^+$ onto arcs of the unit circle (i.e., the circle centred on the origin and of radius 1) in the $\eta$-plane, with the semi-circles $C_j^+$, $j=0,1,\ldots ,N$, mapping onto circular arcs which protrude into the interior of this unit circle (and intersect it at right angles). For $j=0,1,\ldots ,N$, we label these images of $I_j$ and $C_j^+$ under the map in Eq. (7.1) by $\tilde{I}_j$ and $\tilde{C}_j^+$, respectively. Furthermore, the point $\alpha$ is mapped by this map to the origin. The image of $D^+$ under this map is thus the region interior to the union, $\bigcup _{j=0}^N\tilde{C}_j^+\cup \bigcup _{j=0}^N\tilde{I}_j$. We shall denote this image of $D^+$ by $\tilde{D}^+$, and its boundary by $\partial \tilde{D}^+$. Also, for $j=1,\ldots ,2(N+1)$, we label the image of $\zeta _j$ under the map in Eq. (7.1) by $\eta _j$. A schematic is shown in Fig. 10.

Fig. 10

An example of the domain, $\tilde{D}^+$, for the case of $N=2$. This is the image of $D^+$ under the Möbius map given by Eq. (7.1). For $j=0,1,2$, $\tilde{C}_j^+$ and $\tilde{I}_j$ are, respectively, the images of $C_j^+$ and $I_j$, while for $j=1,\ldots ,6$, $\eta _j$ is the image of $\zeta _j$. $\alpha$ maps to the origin

The one-to-one conformal map of $\tilde{D}^+$ onto $\Omega$, which we shall denote by $\tilde{z}(\eta )$, is then given by the composition of the inverse of the map in Eq. (7.1) followed by the map in Eq. (3.1), i.e.,

$$\begin{aligned} \tilde{z}(\eta )=z(\zeta (\eta )), \end{aligned}$$

(7.2)

where

$$\begin{aligned} \zeta (\eta )=\frac{\overline{\alpha }\eta -\alpha }{\eta -1} \end{aligned}$$

(7.3)

is the inverse of the map in Eq. (7.1). Furthermore the constraints on this parameterisation in terms of $\eta$ that are equivalent to those given by Eq. (3.2), are:

$$\begin{aligned} \tilde{z}(\eta _j)=z_j,~~~j=1,\ldots ,2(N+1). \end{aligned}$$

(7.4)

The computations that we carried out appear to suggest that, in the limit as the absorbing sections of $\partial \Omega$ become vanishingly small, so do their pre-images, $\tilde{C}_j^+$, $j=0,1,\ldots ,N$, in the $\eta$-plane, so that $\tilde{D}^+$ tends to the unit disc. In fact, it almost appears that, in this limit, in many cases $\eta _j$ roughly approximates $z_j/R$, suggesting that, up to a re-scaling by R, the map $\tilde{z}(\eta )$ is perhaps roughly tending to the identity. Data illustrating this for the examples presented in Sect. 4 is recorded in Table 3. We emphasise, however, that this is purely an empirical observation, and further investigation is required to support it. Nevertheless, as an apparent consequence, provided the absorbing sections of $\partial \Omega$ were not too large, use of this extended parameterisation of $\Omega$ in terms of $\eta$ appeared to assist us in performing computations in the following way. To solve for the unknown $2(N+1)$ real parameters, discussed in Sect. 3, we opted to use a multi-dimensional Newton iteration. However, rather than apply this the system of equations given by Eq. (3.2) we found it easier to apply it to the system given by Eq. (7.4) and solve for $\eta _j$, $j=1,\ldots ,2(N+1)$. This is possibly because, not only does our parameterisation in terms of $\eta$ appear to readily provide a reasonably accurate initial guess for $\eta _j$ ($j=1,\ldots ,2(N+1)$), namely $z_j/R$, but furthermore, perhaps because it is roughly tending towards a simple re-scaling, it appears to be less effected by crowding than our parameterisation in terms of $\zeta$ (the crowding exhibited by the latter is also mentioned in Sect. 4, where we in fact suggest how one might use it to one’s advantage), and as a result, the iteration appears to converge to a solution more easily.

Having computed $\eta _j$, $j=1,\ldots ,2(N+1)$, one may then retrieve the $2(N+1)$ real parameters for our parameterisation in terms of $\zeta$ as follows. Assuming that the one real degree of freedom has been used to fix c (it is straightforward to adapt the following if otherwise), one may first determine $\alpha$ from the relation

$$\begin{aligned} \alpha =\frac{\eta _2+\eta _1-2\eta _1\eta _2}{\eta _2-\eta _1} \end{aligned}$$

(7.5)

(which follows simply from Eq. (7.1) using the facts that $\zeta _1=1$ and $\zeta _2=-1$), and then $\delta _j$ and $q_j$, $j=1,\ldots ,N$, using Eq. (7.3). This is precisely the approach that we used to compute the examples presented in Sect. 4.

For the same reasons as those just stated, we also applied Newton iterations to our parameterisation in terms of $\eta$ to determine the pre-image in $\tilde{D}^+$ of a given point z in $\Omega$. We then determined the corresponding point in $D^+$ using Eq. (7.3). As discussed in Sect. 3, such pre-images in the $\zeta$-plane are needed in order to be able to evaluate our formulae given by Eqs. (3.19) and (3.23) for the MFPT and splitting probabilities at z.

Finally, we point out that the advantages, just stated, of this parameterisation in terms of $\eta$ still seem to be apparent when some of the absorbing sections are large, such as is the case for examples 4a and 4b, for which the approach just described still seemed to work. However, it does appear to begin to fail if the absorbing sections are too large, as we found to be the case for example 3. This is discussed in more detail in Sect. 4.

Table 3 A comparison of the points $z_j$ and our computed values of $\eta _j$, $j=1,\ldots ,6$, for the examples presented in Sect. 4. All values are listed in rounded decimal form

Appendix 3: Details for the Case of a Single Absorbing Section

In this section we report details of how Eq. (3.29) in Sect. 3.5 can be rewritten in terms of z and $\epsilon$, as in Eq. (3.30).

First, rearranging Eq. (3.27), one arrives at a quadratic equation for $\zeta$ in terms of z. Solving this gives

$$\begin{aligned} \zeta =-b+\sqrt{b^2-1}, \end{aligned}$$

(8.1)

where

$$\begin{aligned} b=\frac{(\alpha ^2+1)}{2\alpha }\biggl (\frac{z-R}{z+R}\biggr ), \end{aligned}$$

(8.2)

and where we pick the positive (rather than negative) square root in Eq. (8.1) so that, say, $z=0$ gives $\zeta =\alpha$. Using Eq. (8.1), one can then show, after some lengthy algebra, that

$$\begin{aligned} \frac{\alpha \zeta -1}{\zeta +\alpha } = \frac{R-z+\sqrt{(R-e^{\mathrm {i}\epsilon }z)(R-e^{-\mathrm {i}\epsilon }z)}}{-2\mathrm {i}R\sin (\epsilon /2)} \end{aligned}$$

(8.3)

In doing so, it is helpful to use the facts that

$$\begin{aligned} \biggl (\frac{1+\alpha }{1-\alpha }\biggr )^2=e^{\mathrm {i}\epsilon }, \end{aligned}$$

(8.4)

which follows from, say, $z(-1)=R e^{\mathrm {i}\epsilon }$, as well as,

$$\begin{aligned} \frac{\alpha ^2-1}{\alpha }=\frac{2\mathrm {i}}{\sin (\epsilon /2)}, \end{aligned}$$

(8.5)

which follows from Eq. (3.28).