Abstract
Metastability is a physical phenomenon ubiquitous in first order phase transitions. A fruitful mathematical way to approach this phenomenon is the study of rare transitions Markov chains. For Metropolis chains associated with statistical mechanics systems, this phenomenon has been described in an elegant way in terms of the energy landscape associated to the Hamiltonian of the system. In this paper, we provide a similar description in the general rare transitions setup. Beside their theoretical content, we believe that our results are a useful tool to approach metastability for non-Metropolis systems such as Probabilistic Cellular Automata.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we are interested in the phenomenon of metastability for systems evolving according to transformations satisfying the thermodynamic law for small changes of the thermodynamical parameters. Metastability is a physical phenomenon ubiquitous in first order phase transitions. It is typically observed when a system is set up in a state which is not the most thermodynamically favored one and suddenly switches to the stable phase as a result of abrupt perturbations.
Although metastable states have been deeply studied from the physical point of view, full rigorous mathematical theories based on a probabilistic approach have been developed only in the last three decades. We refer to [20] for a complete recent bibliography. Let us just stress that the three main points of interest in the study of metastability are the description of: (i) the first hitting time at which a Markov chain starting from the metastable state hits the stable one; (ii) the critical configurations that the system has to pass to reach the stable states; (iii) the tube of typical trajectories that the system typically follows on its transition to the stable state. These notions are central quantities of interest in many studies on metastability, which focus on proving convergence results in physically relevant limits, the most typical ones being the zero temperature limit and the infinite volume regime.
In this paper, we focus on the finite volume and zero temperature limit setup.
The first mathematically rigorous results were obtained via the pathwise approach, which has been first developed in the framework of special models and then fully understood in the context of the Metropolis dynamics [12, 34, 36]. In this framework, the properties of the first hitting time to the stable states are deduced via large deviation estimates on properly chosen tubes of trajectories. A different point of view, the potential theoretical approach, has been proposed in [5] and is based on capacity—like estimates. This last approach has recently been developed and generalized to the non reversible setting in [29]. We mention that a more recent approach has also been developed in [6, 7].
Here we adopt the pathwise point of view and generalize the theory to the general Freidlin–Wentzel Markov chains or Markov chains with rare transitions setup. For Metropolis chains associated to Statistical Mechanics systems and reversible with respect to the associated Gibbs measure, the metastability phenomenon can be described in an elegant and physically satisfactory way via the energy landscape associated with the Hamiltonian of the system [34, 36]. In particular the time needed by the system to hit the stable state can be expressed in terms of the height of one of the most convenient paths (that is a path with minimal energetic cost). Moreover, the state of the system at the top of such a path is a gate configuration in the sense that, in the low temperature regime, the system necessarily has to go through it before hitting the stable state. This description is very satisfactory from the physical point of view since both the typical time that the system spends in the metastable state before switching to the stable one and the mechanism that produces this escape can be quantified purely through the energy landscape. Let us mention that a simplified pathwise approach was proposed in [31], where the authors disentangled the study of the first hitting time from the study of the set of critical configurations and of the tube of the typical trajectories.
In this paper we show that a similar physically remarkable description can be given in the general rare transitions (Freidlin–Wentzel) framework, when the invariant measure of the system is a priori not Gibbsian. In this setup the pathwise study of metastability has been approached with a different scheme in [35], where the physical relevant quantities describing the metastable state are computed via a renormalization procedure. Here we show that the strategy developed in [31] can be extended at the cost of a higher complexity of techniques. A typical way of proceeding is to redefine the height of a path in terms of the exponential weight of the transition probabilities and of a function, the virtual energy, associated to the low temperature behavior of the invariant measure. In other words we reduce the pathwise study of metastability in the general rare transition case to the solution of a variational problem within the landscape induced by this notion of path height, using as a main tool the general cycle theory developed in [10, 11].
Summarizing, in [34, 36], in the framework of the pathwise approach, the problem of metastability has been addressed exclusively for Metropolis dynamics and the study of the exit time is striclty connected to that of the typical exit tube. In [31], with the same approach, the study has again been performed only for Metropolis dynamics but the results on the hitting time to the stable state have been disentagled from the detailed knowledge of the tube of typical trajectories followed during the transition from the metastable to the stable state. In [35], on the other hand, the authors consider the rare transition dynamics we address in this paper and develop a renormalization scheme to describe the exit from a general domain. The exit time estimate is, then, strictly related to the detailed study of the exit tube and all the results are given in terms of the intermediate renormalized chains. In [3–5] the problem of metastability has been studied via the potential theoretic approach only for reversible Markov chains. Finally, in [6, 8] the martingale approach to metastability has been developed. More recently, see [7, 29], in this framework the possibility to study non reversible chain has been considered. These results have been used to study the specific problem of the metastable behavior of the condensate of the one-dimensional totally asymmetric zero range model with periodic boundary conditions [30].
This paper addresses the problem of metastability in the very general case of rare transition dynamics possibly not reversible (specific examples are given in Sect. 2.2). Our aim is threefold: (i) generality of the results (in the sense specified above); (ii) developing a theory which reduces the computation of the exit time from the metastable state and the determination of the critical configuration to the solution of variational problems in a energy landscape defined in terms of the virtual energy and the cost function; (iii) developing a theory in which the results on the transition time from the metastable to the stable state is disentagled from the detailed knowledge of the critical configuration and of the tube of typical trajectories followed during the transition from the metastable to the stable state.
The technical difficulties that we had to overcome are rather evident: giving a satisfactory mathematical description of metastability in a context where no Hamiltonian is available is a priori rather challenging. We overcame this difficulty using two key ideas.
First idea In the seminal papers on the pathwise approach to metastability [34, 36] results were proved via detailed probability estimates on suitably chosen tube of trajectories. A simpler approach has been pointed out in [31], where, still in the framework of the Metropolis dynamics, the authors have shown that the main ingredient necessary to achieve the pathwise description of metastability is the classification of all the states of the systems in a sequence of decreasing (for the inclusion) subsets of the state space, whose elements have increasing stability, in the sense that starting from any one of them the height that has to be bypassed to reach a lower energy level becomes increasingly higher. Moreover, the authors use in a crucial way a recurrence property stating that starting from any state, the process reaches one of these stability level sets within a time controlled exponentially by the stability level of the set itself. We also use this idea in the present work.
Second idea One of the key tools in the pathwise study of metastability is the notion of cycle. In the context of general Markov chains, a cycle can be thought as a subset of the configuration states enjoying the following property: starting from anywhere within the cycle, with high probability the process visits all the states within the cycle before exiting the set itself. In the study of the metastable behavior of Metropolis chains a more physical definition of the notion of cycle was used: a cycle is a set of configurations such that starting from any of them any other can be reached by a path within the set with maximal energy height smaller than the minimal one necessary for the process to exit the set. In this paper, following [10], we use the fact that by defining the height of a path in terms of the virtual energy and of the exponential cost of transition, the two different approaches to cycles are equivalent.
The paper is organized as follows. In Sect. 2 we describe our setup and state the main results. Section 3 is devoted to the discussion of the theory of cycles. In Sect. 4 we prove our main results. In Appendix 1, we develop a condition under which the virtual energy is explicitly computable, and in Appendix 2, we make a quick recap about the virtual energy.
2 Model and Main Results
In this section we introduce our framework and state our main results on the metastable behavior of a system fitting to this framework. Then we give a fine description of this behavior in terms of the virtual energy.
2.1 The Freidlin–Wentzell Setup
In this paper we will deal with a finite state space Markov chain with rare transitions. We consider
-
an arbitrary finite state space \(\mathcal{X}\).
-
A rate function \(\Delta : \mathcal{X}\times \mathcal{X}\mapsto {\mathbb R}^{+}\cup \{ \infty \}\). We assume that \(\Delta \) is irreducible in the sense that for every \(x,y \in \mathcal{X}\), there exists a path \({\omega }=({\omega }_{1},\ldots , {\omega }_{n})\in \mathcal{X}^n\) with \({\omega }_{1} = x\), \({\omega }_{n} = y\) and for every \( 1 \le i \le n-1, \Delta (x_{i},x_{i+1}) < \infty \), where \(n\) is a positive integer.
Definition 2.1
A family of time homogeneous Markov chains \((X_{n})_{n \in {\mathbb N}}\) on \(\mathcal{X}\) with transition probabilities \(p_{\beta }\) indexed by a positive parameter \({\beta }\) is said to “satisfy the Freidlin–Wentzell condition with respect to the rate function \(\Delta \)” or “to have rare transitions with rate function \(\Delta \)” when
for any \(x,y\in \mathcal{X}\).
The particular case where \(\Delta (x,y)\) is infinite should be understood as the fact that, at low temperature, there is no transition possible between states \(x\) and \(y\). In many papers, instead of the \(\Delta = \infty \) condition, a connectivity matrix is introduced, that is a matrix whose non zero terms correspond to allowed transitions, see for instance [36] [Condition R, Chapter 6].
We also note that condition (2.1) is sometimes written more explicitly; namely, for any \(\gamma >0\), there exists \(\beta _0>0\) such that
for any \(\beta >\beta _0\) and any \(x,y\in \mathcal{X}\). See for instance [36] [Condition FW, Chap. 6] where the parameter \(\gamma \) is assumed to be a function of \(\beta \) vanishing for \(\beta \rightarrow \infty \), so that in particular the Freidlin-Wentzell setup covers this case.
From now on, we will always consider the general case of a family of homogeneous Markov chains satisfying the condition in Definition 2.1.
2.2 Examples
Since we are proving quite general results in an abstract, model-independent setup, it is worth pointing at some examples to which the techniques developed in this paper should apply. Note that some of the models we are mentioning are still quite poorly understood, and that our results may provide tools for further investigation regarding their metastable behavior.
Setups covered by the Freidlin Wentzell assumptions We first mention that the Freidlin Wentzell framework contains two setups which are themselves quite general and have been quite studied in the past.
-
1.
Metropolis algorithm with Hamiltonian \(U:\mathcal{X}\rightarrow {\mathbb R}\) (see, for instance, [36] [Condition M, Chap. 6] and [32]). It is the particular case where
$$\begin{aligned} \Delta (x,y):= \left\{ \begin{array}{ll} (U(y) - U(x))^{+} &{} \quad \text {if} \quad q(x,y)>0\\ \infty &{} \quad \text {otherwise} \\ \end{array} \right. , \end{aligned}$$(2.3)for any \((x,y) \in \mathcal{X}\times \mathcal{X}\) where \(q\) is an irreducible Markov matrix \(\mathcal{X}\times \mathcal{X}\rightarrow [0,1]\) which does not depend on \(\beta \). The Metropolis algorithm itself is a general framework which has as stationary measure the Gibbs measure.
-
2.
Weak reversible dynamics with respect to the potential \(U:\mathcal{X}\rightarrow {\mathbb R}\) or dynamics induced by the potential \(U:\mathcal{X}\rightarrow {\mathbb R}\).This is the case where the rate function \(\Delta \) is such that for any \((x,y) \in \mathcal{X}\times \mathcal{X}\)
$$\begin{aligned} U(x) + \Delta (x,y) = U(y) + \Delta (y,x) \end{aligned}$$(2.4)with the convention that \(+ \infty + r = + \infty \) for any \(r \in \mathbb {R}\). Even if the Metropolis dynamics is an example of a potential induced dynamics, these models form a broader class in which other important examples are reversible Probabilistic Cellular Automata; without going too much into details about these rather involved models, let us mention that in [14, 18, 28], the authors deal with models involving a potential \(G_{{\beta }}(x)\) depending on \({\beta }\) and satisfying the balance condition
$$\begin{aligned} p_{{\beta }}(x,y) e^{-G_{{\beta }}(x)} = p_{{\beta }}(y,x) e^{-G_{{\beta }}(y)} \end{aligned}$$for every positive \({\beta }\). To bypass the technical difficulties inherent to these models, which stem for a large part from the intricate dependence on \({\beta }\) of \(p_{{\beta }}(\cdot )\) and \(G_{{\beta }}(\cdot )\), the authors computed directly the expressions of the rate function \(\Delta (\cdot )\) in (2.1). In this way, they showed that the reversible PCA’s are in fact a weak reversible dynamics. Then, using solely the limit expressions obtained (that is the rates transitions \(\Delta (\cdot )\)), they described the metastable behavior for these models. We refer to Appendix 1 for a more general context in which these techniques still apply and we mention that our hope is that this generalization should cover some other relevant cases in which only the transitions rates are explicitly computable.
Next we mention two concrete models which do not fit in the above setups, and to which our techniques should apply. Note that as usual for models issued from statistical physics, the model dependent part of the analysis of each specific model should still be very heavy. See the papers [22–24] for recent examples in the Metropolis framework. In the following two examples, we denote by \(\mathcal{T}^{2}_{N}\) the \(2\) dimensional discrete torus with \(N^{2}\) sites.
An irreversible PCA model In the recent paper [25], the authors consider a non-reversible Probabilistic Cellular Automata, which informally should be understood as a massive parallel updating dynamics version of the classical Ising model. Note that the above examples of PCA’s were dealt with in the symmetric context, that is when the local updating rule is performed at each site on a box which is symmetric around this site. This is not the case in the model we describe now.
We denote by \(\mathcal{S}_{N} = \{-1,+1\}^{\mathcal{T}^{2}_{N}}\) the space of configurations. As is standard in the statistical physics literature, for a configuration \({\sigma }\in \mathcal{S}_{N}\) and \(x \in \mathcal{T}^{2}_{N}\), we denote by \({\sigma }^{x}\) the configuration coinciding with \({\sigma }\) at all sites except at site \(x\) (hence such that \({\sigma }^{x}(x) = - {\sigma }(x))\). For \(x = (i,j) \in \mathcal{T}^{2}_{N}\), we write
where the quantities have to be understood modulo \(N\). Given two configurations \({\sigma }, \tau \in \mathcal{S}_{N}\) and \(h > 0\), we then define the Hamiltonian
Finally, we consider the discrete time Markov chain on \(\mathcal{S}_{N}\) with transitions given by
It is clear that this Markov chain is irreducible and fits the setup of Definition 2.1. The behavior of this model for large enough (but fixed) \({\beta }\) and \(N \rightarrow \infty \) has been described in details in [25]. Up to the model dependent specificities ( which can be quite involved, as we already mentioned), our approach deals with the case of fixed volume in the low temperature asymptotics.
Irreversible Kawasaki type dynamics [21] We consider a conservative Kawasaki dynamics evolving on \(\Omega _{N} :=\{0,1\}^{\mathcal{T}^{2}_{N}}\). We let \(E_{N}\) be the set of oriented edges \((x,y)\) where \(x,y\) are nearest neighbors. For \(e = (x,y) \in E_{N}\), we write \(e^{-} = x, e^{+} =y\). We then define \(\mu \) as the probability measure on the configuration space \(\{0,1\}^{\mathcal{T}^{2}_{N}}\) by
where the Hamiltonian is given by
and \(\eta \) is a generic element of \(\Omega _{N}\). For \(\eta \in \Omega _{N}\), we write \(|\eta | = \sum _{x \in \mathcal{T}^{2}_{N}} \eta (x)\).
Now we define the notion of plaquette; it is a unit square of the form \((x,x+e^{(1)},x+e^{(1)}+e^{(2)}, x+e^{(2)} )\) or \((x,x+e^{(2)},x+e^{(1)}+e^{(2)}, x+e^{(1)} )\) where \((e^{(1)},e^{(2)})\) denotes the canonical basis of \({\mathbb Z}^{2}\). The first plaquette is counterclockwise oriented whereas the second one is clockwise oriented. Given an edge \(e \in E_{N}\), there are only two plaquettes to which \(e\) belongs. We denote by \(C^{+}(e)\) the one which is counterclockwise oriented and by \(C^{-}(e)\) the other one. Note that given a plaquette \(C\), there are exactly four edges \(e_{i}, i=1,\ldots ,4\) such that \(e_{i} \in C\).
For \(\Lambda \subset \mathcal{T}^{2}_{N}\), we define the energy restricted to \(\Lambda \) by:
In the above sum, we say that \(e \cap \Lambda \ne \emptyset \) as soon as \(\{e^{-},e^{+}\} \ne \emptyset \). Consider now \(w^{+} \ne w^{-}\) two positive real numbers. We define the transition rates by
Now we define the evolution with generator given by
where \(\eta ^{e}\) coincides with the configuration \(\eta \), except at sites \(e^{-}\) and \(e^{+}\), where the particle sitting at \(e^{-}\) in the configuration \(\eta \) has been moved to site \(e^{+}\). Note that this dynamics is conservative, namely, when started from a configuration \(\eta _{0} \in \Omega _{N}\), at any time \(t \ge 0\), it satisfies \(|\eta _{t}| = |\eta _{0}|\).
In [21], the authors show that the dynamics defined by (2.12) with rates defined in (2.11) satisfies the (continuous time analogous of) Freidlin Wentzell conditions. Its invariant measure is given by (2.8); furthermore, as soon as \(w^{+} \ne w^{-}\), this dynamics is not reversible. Solving the model dependent issues of this dynamics is currently work in progress.
2.3 Virtual Energy
A fundamental notion for the physical approach of the problem of metastability in the setup of rare transitions chains is the notion of virtual energy, whose definition is based on the following result.
Proposition 2.1
[10, Proposition 4.1] Consider a family of Markov chains satisfying the Freidlin–Wentzell condition in Definition 2.1. For \({\beta }\) large enough, each Markov chain is irreducible and its invariant probability distribution \(\mu _{{\beta }}\) is such that for any \(x \in \mathcal{X}\), the limit
exists and is a positive finite real number.
Definition 2.2
In view of Proposition 2.1, the limiting function
for \(x\in \mathcal{X}\), is called virtual energy.
The proof of Proposition 2.1 relies on some deep combinatorial results which are tailored to the Freidlin–Wentzell context. In general, the virtual energy has an exact expression in function of the transition rates \(\Delta \) (see, for instance, [10, Proposition 4.1], or the Appendix 2 at the end of the present work). Unfortunately, in the most general setup, this expression involving a certain family of graphs is intractable for all practical purposes when one is interested to study particular models.
Finally, we stress that in the particular cases of the setups in Sect. 2.2, the virtual energy, up to an additive constant, is precisely the potential which induces the dynamics.
Proposition 2.2
[10, Proposition 4.1] In the particular case of the dynamics induced by the potential \(U:\mathcal{X}\rightarrow {\mathbb R}\) (see Sect. 2.2) one can show the equality
for any \(x\in \mathcal{X}\).
2.4 General Definitions
In the present and in the following sections, we introduce some standard notions, which are natural generalizations of the analogous quantities in the reversible setup, see [31] or [36].
A real valued function \(f: {\mathbb R}^{+} \mapsto {\mathbb R}^{+}\) is super exponentially small (SES for short) if and only if
For \(x \in \mathcal{X}\), we let \(X^x_t\) be the chain started at \(x\). For a nonempty set \(A\subset \mathcal{X}\) and \(x \in \mathcal{X}\), we introduce the first hitting time \(\tau _{A}^{x}\) to the set \(A\) which is the random variable
A path is a sequence \({\omega }= ({\omega }_{1},\ldots , {\omega }_{n})\) such that \(\Delta ({\omega }_{i},{\omega }_{i+1}) < \infty \) for \(i=1,\ldots , n-1\). For a path \({\omega }= ({\omega }_{1},\ldots , {\omega }_{n})\), we define \(|{\omega }| = n\) its length. For \(x,y\in \mathcal{X}\) a path \({\omega }: x \rightarrow y\) joining \(x\) to \(y\) is a path \({\omega }= ({\omega }_{1},\ldots , {\omega }_{n})\) such that \({\omega }_{1} = x\) and \({\omega }_{n} = y\). For any \(x,y\in \mathcal{X}\) we write \(\Omega _{x,y}\) for the set of paths joining \(x\) to \(y\). For \(A,B\subset \mathcal{X}\) nonempty sets, we write \(\Omega _{A,B}\) for the set of paths joining a point in \(A\) to a point in \(B\).
A set \(A \subset \mathcal{X}\) with \(|A| > 1\) is connected if and only if for all \(x,y\in A\), there exists a path \({\omega }\in \Omega _{x,y}\) such that for any \(i \le |{\omega }|, {\omega }_{i} \in A\). By convention, we say that every singleton is connected.
For a nonempty set \(A\), we define its external boundary \(\partial A:=\{y\in \mathcal{X}{\setminus } A, \text {there exists } x \in A \text { such that } \Delta (x,y) < \infty \}\) and we write
The bottom \(\mathcal{F}(A)\) of \(A\) is the set of global minima of \(H\) on \(A\), that is
The set \(\mathcal{X}^\text {s}:=\mathcal{F}(\mathcal{X})\) is called the set of stable points or the set of ground states of the virtual energy.
2.5 Communication Height
A key notion in studying metastability is the one of the cost that the chain has to pay to follow a path. In the case of Metropolis dynamics this quantity is the highest energy level reached along a path. Such a notion has to be modified when general rare transitions dynamics are considered [14, 38]. We thus define the height or elevation \(\Phi (\omega )\) of a path \(\omega = (\omega _{1}, \ldots , \omega _{n})\) by setting
The communication height \(\Phi (x,y)\) between two states \(x,y \in \mathcal{X}\) is the quantity
Given two nonempty sets \(A,B\subset \mathcal{X}\), we define
the communication height between \(A\) and \(B\).
For \(A,B\) nonempty subsets of \(\mathcal{X}\), we define \(\Omega _{A,B}^\text {opt}\) as the set of optimal paths joining \(A\) to \(B\), that is the set of paths joining a point in \(A\) to a point in \(B\) and realizing the min–max \(\Phi (A,B)\) defined in (2.17).
For rare transitions dynamics induced by a potential (see Sect. 2.2) it is easy to see that the communication height between two states is symmetric. A non-trivial result due to A. Trouvé [38] states that this is the case even in the general setup adopted in this paper.
Proposition 2.3
[10, Proposition 4.14] The communication height between states is symmetric, that is, \(\Phi (x,y) = \Phi (y,x)\) for any \(x,y\in \mathcal{X}\).
Corollary 2.1
[10, Proposition 4.17] For any \(x,y\in \mathcal{X}\), the virtual energy satisfies
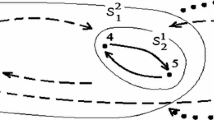
This corollary is quite interesting and its meaning is illustrated in Fig. 1. Indeed, in the case of a dynamics induced by a potential, the jump between two states can be thought of as in the left part of the figure: the chain can jump in both directions and the height reached in both cases is the same. This is not true anymore in general under the sole assumptions of Definition 2.1 (see the illustration on the right in the same figure). Provided the chain can perform the jump from \(x\) to \(y\), that is \(\Delta (x,y)<\infty \), it is not ensured that the reverse jump is allowed. Moreover, even in such a case, the heights which are attained during the two jumps in general are different. Nevertheless, the important Corollary 2.1 states that the virtual energies of the two states \(x\) and \(y\) are both smaller than the heights attained by performing any of the two jumps.
Illustration of the result in Corollary 2.1. The picture on the left refers to the weak reversible case, whereas the picture on the right refers to the general dynamics with rare transitions
2.6 Metastable States
The main purpose of this article is to define the notion of metastable states for a general rare transition dynamics and to prove estimates on the hitting time to the set of stable states for the dynamics started at a metastable state.
To perform this, we need to introduce the notion of stability level of a state \(x \in \mathcal{X}\). First define
which may be empty in general. Then we define the stability level of any state \(x\in \mathcal{X}\) by
and we set \(V_{x} = \infty \) in the case where \(\mathcal{I}_{x}\) is empty. Recalling the definition of the stable set \(\mathcal{X}^\text {s}:=\mathcal{F}(\mathcal{X})\), we also let
be the maximal stability level.
Metastable states should be thought of as the set of states where the dynamics is typically going to spend a lot of time before reaching in a drastic way the set of stable states \(\mathcal{X}^\text {s}\). Following [31] we define the set of metastable states \(\mathcal{X}^\text {m}\) as
and in the sequel, see Sect. 2.8, we will state some results explaining why \(\mathcal{X}^\text {m}\) meets the requirements that one would heuristically expect from the set of metastable states. For example, we prove that the maximal stability level \(V^\text {m}\) is precisely the quantity controlling the typical time that the system needs to escape from the metastable state.
More generally, for any \(a>0\), we define the metastable set of level \(a>0\) as follows
The structure of the sets \(\mathcal{X}_a\)’s is depicted in Fig. 2. It is immediate to realize that \(\mathcal{X}_a\subset \mathcal{X}_{a'}\) for \(a\ge a'\). Moreover, it is worth noting that \(\mathcal{X}_{V^\text {m}}=\mathcal{X}^\text {s}\).
Illustration of the structure of the sets \(\mathcal{X}_a\)’s (see Definition (2.22)) with \(0<a<V^\text {m}\)
2.7 Saddles, Gates, and Cycles
We stress that one of our main results (see Theorem 2.4 below) describes a family of sets which will be crossed with high probability by the dynamics during its escape from the metastable state.
To introduce these sets, we define as in [31] the notion of saddle points and of gates. These notions, which are standard in the Metropolis setup, can be generalized here at the cost of a higher complexity of definitions. To do so, we first introduce the set \( \hat{\mathcal{S}}(x,y) \subset \mathcal{X}\times \mathcal{X}\):

In words, the pair \((z,z')\) belongs to \(\hat{\mathcal{S}}(x,y)\) if the edge \((z,z')\) belongs to an optimal path joining \(x\) to \(y\), the cost of the one step transition from \(z\) to \(z'\) is equal to \(\Phi (z,z')\), which is itself equal to the overall cost \(\Phi (x,y)\).
We then define the projection of \(\hat{\mathcal{S}}(x,y) \) on its second component, that is the set
By analogy with the Metropolis setup (see [31, Definition (2.21)]), the set \(\mathcal{S}(x,y)\) is the set of saddles between \(x\) and \(y\). Other natural extensions borrowed from the Metropolis setup are then the following (see [31]). Given \(x,y \in \mathcal{X}\), we say that \(W \subset \mathcal{X}\) is a gate for the pair \((x,y)\) if \(W \subset \mathcal{S}(x,y)\) and every path in \(\Omega _{x,y}^\text {opt}\) intersects \(W\), that is
We also introduce \(\mathcal{W}(x,y)\) as being the collection of all the gates for the pair \((x,y)\).
A gate \(W\in \mathcal{W}(x,y)\) for \((x,y) \in \mathcal{X}\) is minimal if it is a minimal (for the inclusion relation) element of \(\mathcal{W}(x,y)\). Otherwise stated, for any \(W'\subsetneq W\), there exists \({\omega }'\in \Omega _{x,y}^\text {opt}\) such that \({\omega }'\cap W'=\emptyset \). In the metastability literature, the following set is also standard
namely, \(\mathcal{G}(x,y)\) is the set of saddles between \(x\) and \(y\) belonging to a minimal gate in \(\mathcal{W}(x,y)\).
Key notions in this work are the notions of cycle and of principal boundary of a set. In this section, we just give some basic facts on these, and we note that they will be discussed with more details in Sect. 3.
Definition 2.3
[10, Definition 4.2] A nonempty set \(C\subset \mathcal{X}\) is a cycle if it is either a singleton or for any \(x,y\in C\), such that \(x\ne y\),
In words, a nonempty set \(C\subset \mathcal{X}\) is a cycle if it is either a singleton or if for any \(x\in C\), the probability for the process starting from \(x\) to leave \(C\) without first visiting all the other elements of \(C\) is exponentially small. We will denote by \(\mathcal{C}(\mathcal{X})\) the set of cycles. The set \(\mathcal{C}(\mathcal{X})\) has a tree structure, that is:
Proposition 2.4
[10, Proposition 4.4] For any pair of cycles \(C,C'\) such that \(C \cap C' \ne \emptyset \), either \(C \subset C'\) or \(C' \subset C\).
Definition 2.4
Consider \(A \subset \mathcal{X}\) such that \(|A| \ge 2\) and \(x,y \in \mathcal{X}\). The tree structure of the set \(\mathcal{C}(\mathcal{X})\) has two fundamental consequences, which we will use repeatedly in the rest of this paper:
-
1.
there exists a minimal cycle \(\mathcal{C}_{A}\) (for the inclusion) containing the set \(A\). In the particular case where \(A = \{x,y\}\), we will always write \(C_{x,y}\) for the minimal cycle containing both \(x\) and \(y\);
-
2.
the decomposition into maximal strict subcycles of \(A\); i.e. a partition
$$\begin{aligned} A = \bigsqcup _{i \in I} C_{i} \end{aligned}$$(2.25)where \(|I| \ge 2\) and for every \(i\), \(C_{i}\) is a cycle. Furthermore, for any \(J \subsetneq I\), the set \(\bigcup _{j \in J} C_{j}\) is not a cycle. In the particular case where \(A = C_{x,y}\), we will write \(\mathcal{M}_{x,y} = (C_{i}, i \in I)\) for the partition of \(C_{x,y}\) into maximal strict subcycles. Finally, for \(u \in C_{x,y}\), in the rest of this paper we will use the notation \(C(u)\) to refer to the unique element of \(\mathcal{M}_{x,y}\) containing \(u\).
Next we introduce the important notion of principal boundary of an arbitrary subset of the state space \(\mathcal{X}\).
Proposition 2.5
[10, Proposition 4.2] For any \(D \subset \mathcal{X}\) and any \(x \in D\), the following limits exist and are finite:
and, for any \(y\in \mathcal{X}{\setminus } D\),
We stress that the limits appearing in the right hand side of (2.27) and (2.26) have explicit expressions which, as in Definition 2.2 for the virtual energy, seem to be intractable for practical purposes at least in the field of statistical mechanics (Fig. 3).
The meaning of the two functions introduced in the Proposition 2.5 is rather transparent: (2.26) provides an exponential control on the typical time needed to escape from a general domain \(D\) starting from a state \(x\) in its interior and \(\Gamma _D(x)\) is the mass of such an exponential. On the other hand, (2.27) provides an exponential bound to the probability to escape from \(D\), starting at \(x\), through the site \(y\in \mathcal{X}{\setminus } D\). Hence, we can think to \(\Delta _D(x,y)\) as a measure of the cost that has to be paid to exit from \(D\) through \(y\).
Now, we remark that, due to the fact that the state space \(\mathcal{X}\) is finite, for any domain \(D\subset \mathcal{X}\) and for any \(x\in D\) there exists at least a point \(y\in \mathcal{X}{\setminus } D\) such that \(\Delta _D(x,y)=0\). Thus, we can introduce the concept of principal boundary of a set \(D\subset \mathcal{X}\)
Illustration of the notion of gate between two configurations \(x\) and \(y\). The case depicted here is the following: \(\mathcal{S}(x,y)=\{w_1,\ldots ,w_6\}\). The optimal paths in \(\Omega ^\text {opt}_{x,y}\) are represented by the five black lines. The minimal gates are \(\{w_1,w_2,w_4,w_6\}\) and \(\{w_1,w_2,w_5,w_6\}\). Any other subset of \(\mathcal{S}(x,y)\) obtained by adding some of the missing saddles to one of the two minimal gates is a gate
We mention that the set of saddles is linked in a very intricate way to the principal boundaries of the elements of \(\mathcal{M}(x,y)\). More precisely, we prove the following equality in Sect. 4.
Proposition 2.6
For \(x,y \in \mathcal{X}\), it holds the equality
Note that this result implies the inclusion \(\mathcal{S}(x,y) \subset C_{x,y}\) (see Remark 3.5 for details).
This result is quite remarkable, in the sense that it links in a natural way two quantities which have been used in very different contexts. A priori, the set \(\mathcal{S}(x,y)\) has been defined purely in terms of a minmax principle, whereas the principal boundary of cycles have been defined in a rather abstract way.
2.8 Main Results
In this section we collect our results about the behavior of the system started at a metastable state. These results justify a posteriori why the abstract notion of metastable set \(\mathcal{X}^\text {m}\) fits with the heuristic idea of metastable behavior.
The first two results state that the escape time, that is the typical time needed by the dynamics started at a metastable state to reach the set of stable states, is exponentially large in the parameter \(\beta \). Moreover, they ensure that the mass of such an exponential is given by the maximal stability level; the first result is a convergence in probability, whereas the second ensures convergence in mean.
Theorem 2.1
For any \(x \in \mathcal{X}^{ \text {m}}\), for any \(\varepsilon >0\) there exists \(\beta _0<\infty \) and \(K>0\) such that, for all \({\beta }\ge {\beta }_{0}\),
and
Theorem 2.2
For any \(x \in \mathcal{X}^{ \text {m}}\), the following convergence holds
Theorem 2.3
Assume the existence of a state \(x_{0}\), satisfying the following conditions:
-
late escape from the state \(x_{0}\):
$$\begin{aligned} T_{{\beta }} := \inf \left\{ n \ge 0, {\mathbb P}_{\beta }\left[ \tau _{\mathcal{X}^{ \text {s}}}^{x_{0}}\le n\right] \ge 1 - e^{-1} \right\} \mathop {\longrightarrow }\limits ^{{\beta }\rightarrow \infty } \infty ; \end{aligned}$$(2.33) -
fast recurrence to \(x_{0}\): there exist two functions \(\delta _\beta ,T'_\beta :[0,+\infty ]\rightarrow {\mathbb R}\) such that
$$\begin{aligned} \lim _{{\beta }\rightarrow \infty } \frac{T_{{\beta }}'}{T_{{\beta }}} = 0 ,\;\;\; \lim _{{\beta }\rightarrow \infty } {\delta }_{{\beta }} = 0, \end{aligned}$$(2.34)and
$$\begin{aligned} {\mathbb P}_{\beta }\Big [\tau _{\{x_{0},\mathcal{X}^{ \text {s}}\}}^{x} > T_{{\beta }}' \Big ] \le {\delta }_{{\beta }} \end{aligned}$$(2.35)for any \(x\in \mathcal{X}\) and \(\beta \) large enough.
Then, the following holds
-
1.
the random variable \(\tau _{\mathcal{X}^{ \text {s}}}^{x_{0}}/T_{{\beta }}\) converges in law to an exponential variable with mean one;
-
2.
the mean hitting time and \(T_{{\beta }}\) are asymptotically equivalent, that is
$$\begin{aligned} \lim _{{\beta }\rightarrow \infty } \frac{1}{T_{{\beta }}}\, {\mathbb E}_{\beta }[\tau _{\mathcal{X}^{ \text {s}}}^{x_{0}}] = 1; \end{aligned}$$(2.36) -
3.
the random variable \(\tau _{\mathcal{X}^{ \text {s}}}^{x_{0}} /{\mathbb E}_{\beta }[\tau _{\mathcal{X}^{ \text {s}}}^{x_{0}}]\) converges in law to an exponential variable with mean one.
We stress that such exponential behaviors are not new in the literature; for the Metropolis case, we refer of course to [31, Theorem 4.15], and we refer to [1, 2] for the generic reversible case. In an irreversible setup, results appeared only much more recently; let us mention [8] and [33]. In the case where the cardinality of the state space \(\mathcal{X}\) diverges, more precise results than the one described in Theorem 2.3 were obtained in [27] and [26].
Our result is different from the ones we mention here, since we are able to give the explicit value of the expected value of the escape time in function of the transition rates of the family of Markov chains.
The above results are related to the properties of the escape time, the following one gives in particular some information about the trajectory that the dynamics started at a metastable state follows with high probability on its way towards the stable state.
Theorem 2.4
For any pair \(x,y\in \mathcal{X}\) we consider the set of gates \(\mathcal{W}(x,y)\) introduced in Sect. 2.7 and the corresponding set of minimal gates. For any minimal gate \(W\in \mathcal{W}(x,y)\), there exists \(c>0\) such that
for \({\beta }\) sufficiently large.
The typical example of application of this result is to consider \(x\in \mathcal{X}^\text {m}\), \(y\in \mathcal{X}^\text {s}\), and \(W\in \mathcal{W}(x,y)\); Theorem 2.4 ensures that, with high probability, on its escape from the metastable state \(x\), the dynamics has to visit the gate \(W\) before hitting the stable state \(y\). This is a strong information about the way in which the dynamics performs its escape from a metastable state. We remark that in the application to particular models, Theorem 2.4 allows to find the gates without describing in details the typical trajectories followed by the system during the transition.
We stress that our main tool to prove Theorem 2.4 is the construction of a set \(\mathcal{K}_{x,y}\) that contains the typical trajectories (see [36, Chap. 6]. In particular Sect. 6.7, Theorems 6.31 and 6.33 where an analogous description has been performed in the particular case of the Metropolis dynamics). The set \(\mathcal{K}_{x,y}\) is a subset of \(\Omega _{x,y}^\mathrm{{opt}}\) which can be described as follows:
-
1.
as soon as the dynamics enters an element \(C \in \mathcal{M}_{x,y}\), it exits \(C\) through its principal boundary \(\mathcal{B}(C)\). This implies in particular the fact that the dynamics stays within the cycle \(C_{x,y}\) during its transition from \(x\) to \(y\), as we will show later (see in particular Remark 3.5);
-
2.
as soon as the dynamics enters \(C(y)\) (recall that \(C(y)\) is the unique element of \(\mathcal{M}_{x,y}\) containing \(y\), Definition 2.4), it hits \(y\) before leaving \(C(y)\) for the first time.
We refer to equation (4.74) for a formal definition of \(\mathcal{K}_{x,y}\). We are ready to state the following proposition:
Proposition 2.7
For any \(x,y \in \mathcal{X}\), as \({\beta }\rightarrow \infty \), the set \(\mathcal{K}_{x,y}\) has probability exponentially close to \(1\), that is, for any \({\varepsilon }> 0\), there exists \({\beta }_{0}\) such that for any \({\beta }\ge {\beta }_{0}\):
We stress that in concrete models, such a detailed description of the exit tube relies on an exhaustive analysis of the energy landscape which is unlikely to be performed in general. Nevertheless, for the particular case of PCA’s, this analysis can be greatly simplified.
Remark 2.1
For reversible PCA’s, the analysis of the phenomenon of metastability was performed in [18] by studying the transition between the metastable state (the \(-\) phase) towards the stable state (the \(+\) phase in this specific model) using a particular case of Proposition 2.7. Indeed, the decomposition into maximal cycles \(C_{(-),(+)}\) was reduced to two cycles only, and the one containing the \((-)\) state was refered to as the subcritical phase. One of the main tasks was then to identify the set of saddles, which in this case was reduced to the principal boundary of the subcritical phase.
Our approach shows in which way this technique should be extended in the more general case of several maximal cycles involved in the maximal decomposition of the cycle \(C_{x,y}\). A practical way to perform this would be to use Propostion 2.6 to identify recursively the set of saddles.
2.9 Further Results on the Typical Behavior of Trajectories
In this section we collect some results on the set of typical trajectories in the large \({\beta }\) limit.
The first result of this section is a large deviation estimate on the hitting time to the metastable set \(\mathcal{X}_{a}\) at level \(a>0\). The structure of the sets \(\mathcal{X}_a\)’s is depicted in Fig. 2. Given \(a>0\), since states outside \(\mathcal{X}_a\) have stability level smaller that \(a\), it is rather natural to expect that, starting from such a set, the system will typically need a time smaller than \(\exp \{\beta a\}\) to reach \(\mathcal{X}_a\). This recurrence result is the content of the following lemma.
Proposition 2.8
For any \(a>0\) and any \({\varepsilon }>0\), the function
is SES.
Remark 2.2
Proposition 2.8 allows to disentangle the study of the first hitting time of the stable state from the results on the tube of typical trajectories performed in great details both in [35] and in [11]. This remarkable fact relies on Proposition 3.23, which guarantees the existence of downhill cycle paths to exit from any given set. In the Metropolis setup, this has been performed in [31] (see Theorem 3.1 and Lemma 2.28).
The following result is important in the theory of metastability and, in the context of Metropolis dynamics, is often referred to as the reversibility lemma. In that framework it is simply stated as the probability of reaching a configuration with energy larger than the one of the starting point in a time exponentially large in the energy difference between the final and the initial point. In our general it is of interest to state a more detailed result on the whole tube of trajectories overcoming this height level fixed a priori.
To make this result quantitative, given any \(x\in \mathcal{X}\) and \(h,\varepsilon >0\), for any integer \(n\ge 1\), we consider the tube of trajectories
which is the collection of trajectories started at \(x\) whose height at step \(n\) is at least equal to the value \(H(x)+h\).
Proposition 2.9
Let \(x\in \mathcal{X}\) and \(h>0\). For any \(\varepsilon \in (0,h)\), set
There exists \({\beta }_0>0\) such that
for any \({\beta }>{\beta }_0\).
In words, the set \( \mathcal{E}^{x,h}(\varepsilon )\) is the set of trajectories started at \(x\) and which reach the height \(H(x)+h\) at a time at most equal to \(\lfloor \exp \left( {\beta }(h-\varepsilon )\right) \rfloor \).
3 Cycle Theory in the Freidlin–Wentzell Setup
In this section we summarize some well known facts about the theory of cycles, which can be seen as a handy tool to study the phenomenon of metastability in the Freidlin–Wentzell setup. Indeed, in [34] the authors developed a peculiar approach to cycle theory in the framework of the Metropolis dynamics, see also [36]. This approach was generalized in [14] in order to discuss the problem of metastability in the case of reversible Probabilistic Cellular Automata. In the present setup however we need the more general theory of cycles developed in [10]. We showed in [20] that these two approaches actually coincide in the particular case of the Metropolis dynamics.
We recall in this section some results developed by [10], which will turn out to be the building bricks of our approach.
3.1 An Alternative Definition of Cycles
The definition of the notion of cycle given in Sect. 2.7 is based on a property of the chain started at a site within the cycle itself. The point of view developed in [34, Definition 3.1] for the Metropolis case and generalized in [14] in the framework of reversible Probabilistic Cellular Automata is a priori rather different. The authors introduced the notion of energy-cycle, which is defined through the height level reached by paths contained within the energy-cycle.
Definition 3.5
A nonempty set \(A\subset \mathcal{X}\) is an energy-cycle if and only if it is either a singleton or it verifies the relation
Even if the definitions 2.3 and 3.5 were introduced independently and in quite different contexts, it turns out that they actually coincide. More precisely, we will prove the following result (see the proof after Proposition 3.16):
Proposition 3.10
A nonempty set \(A\subset \mathcal{X}\) is a cycle if and only if it is an energy-cycle.
After proving Proposition 3.10, we will no longer distinguish the notions of cycle and of energy-cycle.
3.2 Depth of a Cycle
Here we introduce the key notion of depth of a cycle.
In the particular case where \(D\) is a cycle, a relevant property is the fact that, in the large \({\beta }\) limit, on an exponential scale, neither \(\tau _{D^{c}}^{x}\) nor \(X_{\tau _{D^{c}}}^{x}\) depend on the starting point \(x \in D\). More precisely, recalling the definitions of the quantities \(\Delta _C\) (see (2.26)) and \(\Gamma _C\) (see (2.27)), we can reformulate the following strenghthening of Proposition 2.5.
Proposition 3.11
[10, Proposition 4.6] For any cycle \(C\in \mathcal{C}(\mathcal{X})\), \(x,y\in C\), and \(z\in \mathcal{X}{\setminus } C\)
The quantity \(\Gamma (C)\) is the depth of the cycle \(C\).
Remark 3.1
For fixed \(x\), the quantity \(\Gamma _D(x)\) is monotone with respect to the inclusion, namely for \(D,D'\subset \mathcal{X}\), such that \(D'\subset D\), and \(x\in D'\), since \(\tau ^x_{\mathcal{X}{\setminus } D'}\le \tau ^x_{\mathcal{X}{\setminus } D}\), from (2.26) we deduce that \(\Gamma _{D'}(x)\le \Gamma _{D}(x)\). From Proposition 3.11 it follows that for any \(C,C'\in \mathcal{C}(\mathcal{X})\), \(C'\subset C\) implies \(\Gamma (C')\le \Gamma (C)\).
3.3 Cycle Properties in Terms of Path Heights
The natural extension of the notion of cycle which has been developped in the context of the Metropolis dynamics (see [34]) is Definition 3.5 (see also the generalization given in [14]). In this section we prove that this extension actually coincides with the Definition 2.3.
The following result links the minimal height of an exit path to the quantities we introduced previously.
Proposition 3.12
For any cycle \(C\in \mathcal{C}(\mathcal{X})\) and \(y\in \mathcal{X}{\setminus } C\)
where we recall the notation (2.14). Furthermore, given \(y \in \mathcal{X}{\setminus } C\), we have the equivalence \(y \in \mathcal{B}(C)\) if and only if there exists \(x \in C\) such that \( H(x) + \Delta (x,y) = H(C) + \Gamma (C)\).
Proof
Equality (3.42) is [10, Proposition 4.12].
On the other hand, the fact that \(y \in \mathcal{B}(C)\) implies that there exists \(x \in C\) such that \( H(x) + \Delta (x,y) = H(C) + \Gamma (C)\) is immediate.
Reciprocally, if there exists \(x \in C\) such that \( H(x) + \Delta (x,y) = H(C) + \Gamma (C)\), we get
and since we know that \(V_{C}(y) \ge 0\), we immediately deduce \(y \in \mathcal{B}(C)\). \(\square \)
The subsequent natural question is about the height that a path can reach within a cycle. We thus borrow from [10] the following result.
Proposition 3.13
[10, Proposition 4.13] For any cycle \(C\in \mathcal{C}(\mathcal{X})\), \(x\in C\), and \(y\in \mathcal{X}{\setminus } C\), there exists a path \(\omega =(\omega _{1},\ldots ,\omega _{n})\in \Omega _{x,y}\) such that \(\omega _{i} \in C\) for \(i=1,\ldots ,n-1\) and
For any \(x,y \in C\), there is a path \(\omega =(\omega _{1},\ldots ,\omega _{n})\in \Omega _{x,y}\) such that \(\omega _{i} \in C\) for \(i=1,\ldots ,n\) and
We stress that the right hand side term of (3.44) is infinite unless \(y\in \partial C\).
In an informal way, the first part of Proposition 3.13, together with Proposition 3.12, states that there exists a path \(\omega \) contained in \(C\) except for its endpoint and joining any given \(x \in C\) to any given point \(y \in \partial C\) whose cost is equal to the minimal cost one has to pay to exit at \(y\) starting from \(x\). Furthermore, the second part can be rephrased by saying that one can join two arbitrary points \(x\) and \(y\) within \(C\) by paying an amount which is strictly less than the minimal amount the process has to pay to exit from \(C\); indeed, using Remark 3.1, the right hand side of (3.45) can be bounded from above by \(H(C)+\Gamma (C)\).
We stress that this last property ensures the existence of at least one path contained in the cycle connecting the two states and of height smaller than the one that is necessary to exit from the cycle itself. But in general, there could exist other paths in the cycle, connecting the same states, with height larger than \(H(C)+\Gamma (C)\). This is a major difference with the Metropolis case, where every path contained in a cycle has height smaller than the one necessary to exit the cycle itself. From this point of view, the weak reversible case is closer to the general Freidlin–Wentzel setup than to the Metropolis one.
Another important property is the characterization of the depth of a cycle in terms of the maximal height that has to be reached by the trajectory to exit from a cycle.
Proposition 3.14
[10, Proposition 4.15] For any cycle \(C\in \mathcal{C}(\mathcal{X})\)
We state now a result in which we give a different interpretation of the depth of a cycle in terms of the minimal height necessary to exit the cycle.
Proposition 3.15
Let \(C\in \mathcal{C}(\mathcal{X})\) be a cycle. Then
Proof
Since any path connecting \(C\) to \(\mathcal{X}{\setminus } C\) has at least one direct jump from a state in \(C\) to a state outside of \(C\), we have that
Now, recalling that the principal boundary \(\mathcal{B}(C)\) is nonempty, by Proposition 3.12 we have
To get the opposite bound we pick \(\bar{x}\in C\) and \(\bar{y}\in \mathcal{X}{\setminus } C\) such that \(\bar{y}\in \mathcal{B}(C)\). Then, by the first part of Proposition 3.13 there exists a path \(\omega \in \Omega _{\bar{x},\bar{y}}\) such that \(\Phi (\omega )=H(C)+\Gamma (C)\). Hence, we have that \(\Phi (\bar{x},\bar{y})\le \Phi (\omega )=H(C)+\Gamma (C)\). Finally,
which completes the proof. \(\square \)
We are now ready to discuss the equivalence between the probabilistic [10] and energy [34] approaches to cycle theory. For any \({\lambda }\in {\mathbb R}\), consider the equivalence relation
Proposition 3.16
[10, Proposition 4.18] For any \(\lambda \in {\mathbb R}\) the equivalence classes in \(\mathcal{X}/\mathcal{R}_\lambda \) are either singletons \(\{x\}\) such that \(H(x)\ge \lambda \) or cycles \(C\subset \mathcal{C}(\mathcal{X})\) such that
Thus we have
The results we have listed above allow us to finally prove the equivalence between the probabilistic [10] and energy approaches [14, 34, 36] to cycle theory, that is Proposition 3.10.
Proof of Proposition 3.10
The case \(A\) is a singleton is trivial. We assume \(A\) is not a singleton and prove the two implications.
First assume \(A\) satisfies (3.40), then \(A\) is an equivalence class in \(\mathcal{X}/\mathcal{R}_{\Phi (A,\mathcal{X}{\setminus } A)}\). Thus, by Proposition 3.16, it follows that \(A\) is a cycle.
Reciprocally, assume that \(A\) is a cycle. By (3.48), there exists \(\lambda \) such that \(A\) is an equivalence class of \(\mathcal{X}/\mathcal{R}_\lambda \). Moreover, by (3.47) we have that
where in the last step we made use of Proposition 3.15. \(\square \)
We stress that the following properties are trivial in the Metropolis and in the weak reversible setups mentioned in Sect. 2.2, whereas in the general Freidlin–Wentzell setup, they are consequences of the non-trivial properties discussed previously in this section (see also [20]).
For example item 3.17 in the following proposition states that the principal boundary of a non-trivial cycle is the collection of the elements outside the cycle that can be reached from the interior via a single jump at height equal to the minimal height that has to be bypassed to exit from the cycle. This is precisely the notion of principal boundary adopted in [14, 18] in the context of reversible Probabilistic Cellular Automata. Note also that such a notion is an obvious generalization of the idea of set of minima of the Hamiltonian of the boundary of a cycle used in the context of Metropolis systems.
Proposition 3.17
Let \(C\in \mathcal{C}(\mathcal{X})\) be a cycle. Then
-
1.
\(\mathcal{B}(C)=\{y\in \mathcal{X}{\setminus } C,\, {\displaystyle \min _{x\in C}} [H(x)+\Delta (x,y)]=\Phi (C,\mathcal{X}{\setminus } C)\}\);
-
2.
\(V_x<\Gamma (C)\) for any \(x\in C{\setminus }\mathcal{F}(C)\);
-
3.
\(V_x\ge \Gamma (C)\) for any \(x\in \mathcal{F}(C)\).
Proof
Item [1.] This result is an immediate consequence of Propositions 3.15 and 3.12.
Item [2.] Pick \(x\in C{\setminus }\mathcal{F}(C)\) and \(y\in \mathcal{F}(C)\). By Proposition 3.10 we have that \(\Phi (x,y)<\Phi (C,\mathcal{X}{\setminus } C)\). Thus:
where we used \(H(C)<H(x)\).
Item[3.] Pick \(x\in \mathcal{F}(C)\). Since \(\mathcal{I}_x\subset \mathcal{X}{\setminus } C\), we have that \(\Phi (x,\mathcal{I}_x)\ge \Phi (C,\mathcal{X}{\setminus } C)\). Since \(H(x)=H(C)\), this entails
The item finally follows from Proposition 3.15 and definition (2.19). \(\square \)
3.4 Exit Times of Cycles
The main reason for which the notion of cycles has been introduced in the literature is that one has good control on their exit times in the large deviation regime. We summarize these properties in the following proposition.
Proposition 3.18
For any cycle \(C\in \mathcal{C}(\mathcal{X})\), \(x\in C\), and any \({\varepsilon }>0\), we have that
-
1.
the function
$$\begin{aligned} {\beta }\in {\mathbb R}^{+} \mapsto {\mathbb P}_\beta \big [\tau _{\partial C}^{x}>e^{{\beta }(\Gamma (C)+{\varepsilon })}\big ] \end{aligned}$$(3.49)is SES;
-
2.
the following inequality holds for any \(\delta > 0\):
$$\begin{aligned} \lim _{\beta \rightarrow \infty } -\frac{1}{{\beta }} \log {\mathbb P}_\beta \big [ \tau _{\partial C}^{x} < e^{{\beta }(\Gamma (C) - \delta )}\big ] \ge {\varepsilon }; \end{aligned}$$(3.50) -
3.
for any \(z \in C\)
$$\begin{aligned} \lim _{{\beta }\rightarrow \infty } -\frac{1}{{\beta }} \log {\mathbb P}_{{\beta }}\big [\tau ^{x}_{z} > \tau ^{x}_{\partial C}\big ] > 0; \end{aligned}$$(3.51) -
4.
for any \(y\in \partial C\)
$$\begin{aligned} \lim _{{\beta }\rightarrow \infty } -\frac{1}{{\beta }} \log {\mathbb P}_{{\beta }}\big [ X_{\tau ^x_{\partial C}} = y\big ] =\min _{x\in C}[H(x)+\Delta (x,y)] -[H(C) + \Gamma (C)]. \end{aligned}$$(3.52)
This result is the refinement of Proposition 2.5 in the sense that the control on the exit times and exit locations in (3.52) holds independently of the starting point of the process inside the cycle.
The results of Proposition 3.18 are proven in [10]. More precisely, item 3.18 is the content of the first part of [10, Proposition 4.19]. Item 3.18 is [10, Proposition 4.20]. Item 3.18 is nothing but the property defining the cycles, see Definition 2.3 above. Item 3.18 follows immediately by Propositions 2.5, 3.11, and 3.12.
By combining Proposition 3.12 and equations (3.49) and (3.52) we can deduce in a trivial wayFootnote 1 the following useful corollary.
Corollary 3.2
For any cycle \(C\in \mathcal{C}(\mathcal{X})\), \({\varepsilon }> 0\), \(x\in C\), and \(y \in \mathcal{B}(C)\), we have that
We discuss an interesting consequence of Proposition 2.9. For a given cycle \(C\), starting from the bottom of \(C\), the probability of reaching an energy level higher than the minimal cost necessary to exit \(C\) before exiting \(C\) is exponentially small in \({\beta }\). In an informal way, this means that at the level of the typical behavior of trajectories, at least for trajectories started from \(\mathcal{F}(C)\), the classical notion of cycle for the Metropolis dynamics (which is defined in terms of energies only, see for example [36, Chap. 6]) and the one of energy cycles are close even in the Freidlin–Wentzell setup. More precisely we state the following proposition.
Proposition 3.19
For any \(C \in \mathcal{C}(\mathcal{X})\), any \({\varepsilon }> 0\) and for \({\beta }\) large enough:
Let us remark that we expect Proposition 3.19 to hold as well starting from anywhere within \(C\), but the proof of this result should be more involved.
3.5 Downhill or via Typical Jumps Connected Systems of Cycles
Beside the estimate on the typical time needed to exit from a cycle, an important property is the one stated in (3.52) which implies that when the chain exits a cycle it will pass typically through the principal boundary. This leads us to introduce the collections of pairwise disjoint cycles such that it is possible to go from any of them to any other by always performing exits through the principal boundaries. To make this idea precise we introduce the following notion of oriented connection.
Definition 3.6
Given two disjoint cycles \(C,C'\in \mathcal{C}(\mathcal{X})\), we say that \(C\) is downhill connected or connected via typical jumps (vtj) to \(C'\) if and only if \(\mathcal{B}(C)\cap C'\ne \emptyset \).
The fact that we introduced two names for the same notion deserves a comment: in [31] downhill connection is introduced in the framework of the Metropolis dynamics. In our opinion its natural extension to the general rare transition setup is the typical jumps connection defined in [10, Proposition 4.10]. This is the reason for the double name, nevertheless, in the sequel, we will always use the second one, which appears to be more appropriate in our setup, and we will use the abbreviation vtj.
A vtj—connected path of cycles is a pairwise disjoint sequence of cycles \(C_1,\dots ,C_n\in \mathcal{C}(\mathcal{X})\) such that \(C_{i}\) is vtj—connected to \(C_{i+1}\) for all \(i=1,\ldots ,n-1\). A vtj—connected system of cycles is a pairwise disjoint collection of cycles \(\{C_1,\dots ,C_n\}\subset \mathcal{C}(\mathcal{X})\) such that for any \(1\le i<i'\le n\) there exists \(i_1,\dots , i_m\in \{1,\ldots ,n\}\) such that \(i_1=i\), \(i_m=i'\), and \(C_{i_1},\ldots ,C_{i_{m}}\) is a vtj—connected path of cycles.
We let an isolated vtj—connected system of cycles to be a vtj—connected system of cycles \(\{C_1,\dots ,C_n\}\subset \mathcal{C}(\mathcal{X})\) such that
for any \(1\le i\le n\).
Via typical jumps connected systems satisfy the following important property: the height that has to be reached to exit from any of the cycles within the system is the same. Moreover, if the system is isolated, then the union of the cycles in the system is a cycle. More precisely we state the following two propositions.
Proposition 3.20
Let \(\{C_1,\dots ,C_n\}\) be a vtj—connected system of cycles. Then, for any \(1\le i<i'\le n\), we have that \(\Phi (C_i,\mathcal{X}{\setminus } C_i)=\Phi (C_{i'},\mathcal{X}{\setminus } C_{i'})\).
Proof
Consider \(C_{i}\) and \(C_{j}\), \(1 \le i < j \le n\). By definition of a vtj—connected system, there exists a path of cycles consisting of vtj—connected elements joining \(C_{i}\) to \(C_{j}\), that is
where all the indexes \(k_{j},\) for \( j \le i_{m},\) belong to \([1,\ldots ,n]\).
Now, given \(k\in \{1,\ldots ,m-1\}\) consider \(x\in C_{i_k}\) and \(y\in \mathcal{B}(C_{i_k})\cap C_{i_{k+1}}\). By Proposition 3.10 and item 3.17 in Proposition 3.17 we have that \(\Phi (x,y)=\Phi (C_{i_k},\mathcal{X}{\setminus } C_{i_k})\). If \(\Phi (C_{i_{k+1}},\mathcal{X}{\setminus } C_{i_{k+1}})> \Phi (C_{i_{k}},\mathcal{X}{\setminus } C_{i_{k}})\), then we would have \(\Phi (y,x)>\Phi (x,y)\), which is absurd in view of Proposition 2.3. Thus
for any \(k=1,\ldots ,m-1\).
Iterating this inequality along the cycle path \(\left( C_{i_1},C_{i_2},\ldots ,C_{i_{m-1}},C_{i_m}\right) \), we get that \(\Phi (C_{i},\mathcal{X}{\setminus } C_{i}) \ge \Phi (C_{j},\mathcal{X}{\setminus } C_{j})\), and by symmetry we get
Since \(i\) and \(j\) were chosen arbitrarily in our vtj—connected system, we are done. \(\square \)
Proposition 3.21
Let \(\{C_1,\dots ,C_n\}\) be a vtj—connected system of cycles. Assume that the system is isolated (recall the definition given above). Then \(\bigcup _{j=1}^nC_j\) is a cycle.
Proof
Let \(C=\bigcup _{j=1}^nC_j\). From Proposition 3.20, there exists \(\lambda \in {\mathbb R}\) such that \(\lambda =\Phi (C_j,\mathcal{X}{\setminus } C_j)\) for any \(j=1,\ldots ,n\).
Consider \(x,x'\in C\) and let \(i,i'\in \{1,\ldots ,n\}\) such that \(x\in C_{i}\) and \(x'\in C_{i'}\). If \(i=i'\), then by Proposition 3.10 we have that \(\Phi (x,x')<\lambda \). If, on the other hand, \(i\ne i'\), by definition of vtj—connected system there exists \(i_1,\dots ,i_m\) such that \(C_{i_k}\) is vtj—connected to \(C_{i_{k+1}}\) for any \(k=1,\ldots ,m-1\). Thus, by using Proposition 3.10 and item 3.17 of Proposition 3.17, we can prove that \(\Phi (x,x')=\lambda \). In conclusion, we have proven that \(\Phi (x,x')\le \lambda \) for any \(x,x'\in C\).
Finally, since the system is isolated we have that \(\Phi (C_i,\mathcal{X}{\setminus } C)>\lambda \) for any \(i=1,\ldots ,n\) and hence, \(\Phi (C,\mathcal{X}{\setminus } C)>\Phi (x,x')\) for any \(x,x'\in C\). Thus, by Proposition 3.10, we have that \(C\) is a cycle. \(\square \)
3.6 Partitioning a Domain into Maximal Cycles
In the proof of our main results a fundamental tool will be the partitioning of a set into maximal subcycles. The existence of such a partition has been pointed out in Definition 2.4, and in Sect. 3.7 we describe a constructive way to get such a partition for any set \(D\).
Proposition 3.22
[10, Proposition 4.10] Consider a non trivial cycle \(C \in \mathcal{C}(\mathcal{X})\) (in particular \(|C| \ge 2\)), and its decomposition into maximal strict subcycles \(C = \bigsqcup _{j=1}^{n_{0}} C_{j}\) where \(C_{j}\) are disjoint elements of \(\mathcal{C}(\mathcal{X})\), \(n_{0} \ge 2\) (recall Definition 2.4).
The collection \(\{C_1,\dots ,C_{n_0}\}\) is an isolated vtj—connected system of cycles. Finally, from Propositions 3.20 and 3.15 it follows that
for any \(i,j \le n_{0}\).
Remark 3.4
We stress that the original Proposition 4.10 in [10] is actually much more exhaustive than the version presented here, and it allows in particular to construct the set of cycles \(\mathcal{C}(\mathcal{X})\) in a recursive way by computing at the same time the quantities \(\Gamma (C)\) and the \(\Delta _{C}(y)\) (for \(y \in \partial C\)) for any element \(C \in \mathcal{C}(\mathcal{X})\), but this version will be enough for our purposes. We refer to [10] for more details.
Remark 3.5
For \(x,y \in \mathcal{X}\), from Proposition 3.22 and from Proposition 2.6, one trivially gets the inclusion
A useful property of a partition of a domain into maximal cycles is contained in the following proposition.
Proposition 3.23
Consider a partition \(\{C_i, i\in I\}\) into maximal cycles of a nonempty set \(D\subset \mathcal{X}\). Let \(J\subset I\) such that \(\{C_j,\,j\in J\}\) is a vtj-connected system of cycles. Then this system is not isolated, namely, there exists \(j\in J\) such that
Proof
The proposition follows immediately by the maximality assumption on the partition of \(D\) and by Proposition 3.21. \(\square \)
As a consequence of the above property we show that any state in a nonempty domain can be connected to the exterior of the domain by means of a vtj—connected cycle path made of cycles belonging to the domain itself. This will be a crucial point in the proof of Proposition 2.8.
Proposition 3.24
Consider a nonempty domain \(D\subset \mathcal{X}\). For any state \(x\in D\) there exists a vtj—connected cycle path \(C_1,\ldots , C_n\subset D\) with \(n\ge 1\) such that \(x\in C_1\) and \(\mathcal{B}(C_n)\cap (\mathcal{X}{\setminus } D)\ne \emptyset \).
Proof
If \(D\) is a cycle the statement is trivial. Assume \(D\) is not a cycle and consider \(\{C_i,\,i\in I\}\) a partition of \(D\) into maximal cycles. Note that \(|I|\ge 2\).
Now, we partition \(\{C_i,\,i\in I\}\) into its maximal vtj—connected components \(\{C^{(j)}_k,\,k\in I^{(j)}\}\), for \(j\) belonging to some set of indexes \(J\). More precisely, we have the following:
-
1.
each collection \(\{C^{(j)}_k,\,k\in I^{(j)}\}\) is a vtj—connected system of cycles;
-
2.
\(\bigcup _{j\in J} \{C^{(j)}_k,\,k\in I^{(j)}\} = \{C_i,\,i\in I\}\);
-
3.
\(C^{(j)}_k\ne C^{(j')}_{k'}\) for any \(j,j'\in J\) such that \(j\ne j'\), any \(k\in I^{(j)}\), and \(k'\in I^{(j')}\).
-
4.
for any \(j\in J\) and \(C\in \bigcup _{j'\in J{\setminus }\{j\}}\{C^{(j')}_{k'},\,k'\in I^{(j')}\}\) we have that \(\{C^{(j)}_{k},\,k\in I^{(j)}\}\cup \{C\}\) is not a vtj—connected system of cycles.
By the property 3.6 above and by Proposition 3.23, if the union of the principal boundary of the cycles of one of those components does not intersect the exterior of \(D\), then it necessarily intersects one of the cycles of one of the other components. Otherwise stated, for any \(j\in J\)
Now, consider \(x\in D\) and \(j_0\in J\) such that \(x\in \cup _{k\in I^{(j_0)}} C^{(j_0)}_k\). We construct a sequence of indexes \(j_0,j_1,\dots \in J\) by using recursively the following rule
if \(\left( \bigcup _{k\in I^{(j_r)}} \mathcal{B}(C^{(j_r)}_{k})\right) \cap (\mathcal{X}{\setminus } D) =\emptyset \), choose \(j\in J\) such that there exists \(k'\in I^{(j)}\) satisfying \(\left( \bigcup _{k\in I^{(j_r)}} \mathcal{B}(C^{(j_r)}_{k}) \right) \cap C^{(j)}_{k'}\ne \emptyset \) and let \(j_{r+1}=j\)
until the if condition above is not fulfilled.
Note that all the indexes \(j_0,j_1,\dots \) are pairwise not equal, namely, the algorithm above does not construct loops of maximal vtj—connected components. Indeed, if there were \(r\) and \(r'\) such that \(j_r=j_{r'}\) then the union of the maximal vtj—connected components corresponding to the indexes \(j_{r},j_{r+1},\ldots ,j_{r'}\) would be a vtj—connected system of cycles and this is absurd by definition of maximal connected component (see property 4 above).
Thus, since the number of maximal vtj—connected components in which the set \(\{C_i,\,i\in I\}\) is partitioned is finite, the recursive application of the above rule produces a finite sequence of indexes \(j_0,j_1,\ldots ,j_{r_x}\) with \(r_x\ge 0\) such that \(\left( \bigcup _{k\in I^{(j_{r_x})}} \mathcal{B}(C^{(j_{r_x})}_{k})\right) \cap (\mathcal{X}{\setminus } D) \ne \emptyset \).
Finally, by applying the definition of vtj—connected system of cycles to each component \(\{C^{(j_r)}_k,\,k\in I^{(j_r)}\}\) for \(r=0,\ldots ,r_x\) we construct a vtj—connected cycle path \(C_1,\ldots ,C_n\subset D\) such that \(C_1\) is the cycle containing \(x\) and belonging to the component \(\{C^{(j_0)}_k,\,k\in I^{(j_0)}\}\) and \(C_n\) is one of the cycles in the component \(\{C^{(j_{r_x})}_k,\,k\in I^{(j_{r_x})}\}\) such that \(\mathcal{B}(C_n)\cap (\mathcal{X}{\setminus } D)\ne \emptyset \). \(\square \)
3.7 Example of Partition into Maximal Cycles
It is interesting to discuss a constructive way to exhibit a partition into maximal cycles of a given \(D \subset \mathcal{X}\). For this reason we now describe a method inherited from the Metropolis setup in [31]. For \(D \subset \mathcal{X}\) nonempty and \(x\in D\), we consider
namely, \(R_D(x)\) is the union of \(\{x\}\) and of the points in \(\mathcal{X}\) which can be reached by means of paths starting from \(x\) with height smaller that the height that it is necessary to reach to exit from \(D\) starting from \(x\).
Proposition 3.25
Given the nonempty set \(D\subset \mathcal{X}\) and \(x\in D\),
-
1.
the following inclusion holds: \(R_{D}(x) \subset D\);
-
2.
the set \(R_{D}(x)\) is a cycle;
-
3.
if \(x' \in R_{D}(x) \), then \(R_{D}(x) = R_{D}(x')\).
Proof
The first item is clear by the definition of communication heights. Indeed, by contradiction, assume that there exists \(y \in R_{D}(x) \cap (\mathcal{X}{\setminus } D)\), then \(\Phi (x,y)\) satisfies simultaneously
which is absurd.
Second item. We consider \(u,v \in R_{D}(x)\) and we show that \(\Phi (u,v) < \Phi (x,\mathcal{X}{\setminus } A)\). As a consequence, we will get that \(R_{D}(x)\) is a maximal connected subset of \(\mathcal{X}\) satisfying that the maximum internal communication cost is strictly smaller than the given threshold \(\Phi (x,\mathcal{X}{\setminus } D)\), and, by Proposition 3.16, these sets are cycles.
We use a concatenation argument. Namely, consider \({\omega }\in \Omega ^\text {opt}_{u,x}\) and \({\omega }'\in \Omega ^\text {opt}_{x,v}\) and let \({\omega }'' \in \Omega _{u,v}\) be the path obtained by concatenating \({\omega }\) and \({\omega }'\). We then have
and hence
By the symmetry property in Proposition 2.3, we get that \(\Phi (u,x) = \Phi (x,u)\). Since by construction \(\Phi (x,u) < \Phi (x,\mathcal{X}{\setminus } D)\) and \(\Phi (x,v) < \Phi (x,\mathcal{X}{\setminus } D)\), we get indeed \(\Phi (u,v) < \Phi (x,\mathcal{X}{\setminus } D)\).
Third item. We first claim that
To prove (3.59) pick \(x'\in R_D(x)\). First assume that \(\Phi (x',\mathcal{X}{\setminus } D) < \Phi (x,\mathcal{X}{\setminus } D)\). Then, we can consider a path \({\omega }\in \Omega _{x,x'}\) such that \(\Phi ({\omega }) < \Phi (x,\mathcal{X}{\setminus } D)\) and a path \({\omega }'\in \Omega ^\text {opt}_{x',\mathcal{X}{\setminus } D}\). Note that \(\Phi (\omega ')=\Phi (x',\mathcal{X}{\setminus } D)<\Phi (x,\mathcal{X}{\setminus } D)\). Now, by concatenation of the two preceding paths, we obtain a path \({\omega }''\in \Omega _{x,\mathcal{X}{\setminus } D}\) such that \(\Phi ({\omega }'') = \Phi ({\omega }) \vee \Phi ({\omega }') < \Phi (x,\mathcal{X}{\setminus } D)\), which is absurd. Hence, we have that \(\Phi (x',\mathcal{X}{\setminus } D) \ge \Phi (x,\mathcal{X}{\setminus } D)\).
To prove the opposite inequality, consider \({\omega }\in \Omega ^\text {opt}_{x',x}\). From the Proposition (2.3), we get that \(\Phi ({\omega })=\Phi (x',x)=\Phi (x,x')<\Phi (x,\mathcal{X}{\setminus } D)\). Similarly, consider a path \({\omega }' \in \Omega ^\text {opt}_{x,\mathcal{X}{\setminus } D}\) and note that \(\Phi ({\omega }')=\Phi (x,\mathcal{X}{\setminus } D)\). Then, the path \({\omega }''\in \Omega _{x',\mathcal{X}{\setminus } D}\) obtained by concatenating \({\omega }\) and \({\omega }'\) satisfies \(\Phi ({\omega }'')=\Phi (x,\mathcal{X}{\setminus } D)\), from which we deduce \(\Phi (x',\mathcal{X}{\setminus } D) \le \Phi (x,\mathcal{X}{\setminus } D)\). The proof (3.59) is thus completed.
Now we come back to the proof of the third item. We consider \(x'\in R_{D}(x)\) and proceed by double inclusion. We first show that \(R_{D}(x')\subset R_{D}(x)\). Pick up \(y \in R_{D}(x')\): from the definition of \(R_{D}(x')\) and (3.59), we get that \(\Phi (x',y) <\Phi (x',\mathcal{X}{\setminus } D)= \Phi (x,\mathcal{X}{\setminus } D)\). Now we consider \({\omega }\in \Omega ^\text {opt}_{x,x'}\), and by a concatenation argument similar to the one we already used twice, we get that
which implies \(R_{D}(x')\subset R_{D}(x)\).
On the other hand, the inclusion \(R_{D}(x)\subset R_{D}(x')\) proceeds in the same vein. Consider \(y\in R_{D}(x)\) so that \(\Phi (x,y) < \Phi (x,\mathcal{X}{\setminus } D)\). Pick up a path \({\omega }\in \Omega ^\text {opt}_{x',x}\). Using again the symmetry of \(\Phi \), we get that \(\Phi ({\omega })=\Phi (x',x)=\Phi (x,x')<\Phi (x,\mathcal{X}{\setminus } D)\). Moreover, a concatenation argument shows that
where we have also used that \(y\in R_{D}(x)\). Finally, from (3.59), we deduce \(\Phi (x',y) < \Phi (x',\mathcal{X}{\setminus } D)\), which implies \(y\in R_{D}(x')\). \(\square \)
The main motivation for introducing the sets (3.58) is the fact that they provide in a constructive way a partition of a given set into maximal subcycles. The existence of such a partition is ensured by the structure of the set of cycles, see Proposition 2.4, but we point out that this way of obtaining the maximal subcycles of a given set \(D\) seems to be new in the context of the irreversible dynamics. Before stating precisely this result, for \(D\subset \mathcal{X}\), we set
Proposition 3.26
Let \(D \subset \mathcal{X}\) nonempty, then \(\mathcal{R}_D\) is a partition into maximal cycles of \(D\).
Proof
In view of Definition (3.58) and Proposition 3.25, the only not obvious point of this result is the one concerning maximality. Note that the maximality condition on cycles can be stated equivalently as follows: any cycle \(C\in \mathcal{C}(\mathcal{X})\) such that there exists \(R\in \mathcal{R}_D\) verifying \(R\subset C\) and \(R\ne C\) satisfies \(C \cap (\mathcal{X}{\setminus } D)\ne \emptyset \).
Now, assume that \(C\in \mathcal{C}(\mathcal{X})\) is a cycle strictly containing \(R_{D}(x)\) for some \(x\in D\). We will show that necessarily \(C\cap (\mathcal{X}{\setminus } D)\ne \emptyset \).
By definition of \(R_{D}(x)\), \(C\) contains a point \(v \notin R_{D}(x)\), that is \(\Phi (x,v) \ge \Phi (x,\mathcal{X}{\setminus } D)\). As both \(x\) and \(v\) are elements of \(C\), recalling Proposition 3.10, we get that
On the other hand, we can choose \(y \in \mathcal{X}{\setminus } D\) such that there exists \({\omega }\in \Omega _{x,y}\) satisfying \(\Phi ({\omega }) = \Phi (x,\mathcal{X}{\setminus } D)\). Then the above bound implies that \(\Phi (C,\mathcal{X}{\setminus } C)>\Phi ({\omega })\) and in particular \(y\in \mathcal{X}{\setminus } D\). Hence the result. \(\square \)
4 Proof of Main Results
In this section we prove the results stated in Sects. 2.7, 2.8, and 2.9. The proofs of Theorems 2.2 and 2.3 are quite similar to the analogous ones in [31], nevertheless we chose to include them for the sake of completeness.
Proof of Proposition 2.6
Consider \(x,y \in \mathcal{X}\) and we recall the notations \(C_{x,y}, \mathcal{M}_{x,y}\) and \(C(u), u \in C_{x,y}\) from Definition 2.4.
We proceed by double inclusion.
-
\( \bigcup _{C \in \mathcal{M}_{x,y}} \mathcal{B}(C) \subset \mathcal{S}(x,y).\) Consider \(v \in \bigcup _{C \in \mathcal{M}_{x,y}} \mathcal{B}(C)\); there exists \(\hat{C} \in \mathcal{M}_{x,y}\) such that \(v \in \mathcal{B}(\hat{C})\), that is such that \(\Delta _{\hat{C}}(v) =0\). By Proposition 3.12, there exists \(u \in \hat{C}\) such that \(H(u) + \Delta (u,v) = H(\hat{C}) + \Gamma (\hat{C})\). We showed (see Proposition 3.22) that the quantity \( H(C) + \Gamma (C)\) does not depend on \(C \in \mathcal{M}_{x,y}\), and is equal to \(\Phi (x,y)\). Thus we have
$$\begin{aligned} H(u) + \Delta (u,v) = \Phi (x,y), \end{aligned}$$(4.61)and thus \(\Phi (u,v) \le \Phi (x,y)\).
Now, since \(u \in \hat{C}\) and \(v \notin \hat{C}\), we necessarily have \(\Phi (u,v) \ge \Phi (C,\mathcal{X}{\setminus } C) = \Phi (x,y)\). Hence \(\Phi (u,v) = \Phi (x,y) = H(u) + \Delta (u,v)\).
Now we show that \((u,v) \in \hat{\mathcal{S}}(x,y)\); first we construct \(\omega \in \Omega _{x,y}^\mathrm{{opt}}\) such that the edge \((u,v)\) belongs to \(\omega \). For this we use the fact that the system \(\bigcup _{C \in \mathcal{M}_{x,y}} C\) is a vtj-connected system of cycles. In particular there exists a path of v.t.j. connected cycles \((C_{1} = C_{x}, \ldots , C_{k} = \hat{C})\) (where \(k\) may be equal to \(1\)) joining \(C_{x}\) to \(\hat{C}\). There also exists a path of v.t.j. connected cycles \((\tilde{C}_{1},\ldots ,\tilde{C}_{k'})\) from \(C_{v}\) to \(C_{y}\).
Using the path \((C_{1}, \ldots , C_{k})\) and Proposition 3.13 recursively, by concatenation, it is easy to construct a path \(\omega _{1} \in \Omega _{x,u}\) such that \(\Phi (\omega _{1}) \le \Phi (x,y)\) (the inequality being strict when \(C(x) = C(u)\)). In the same way, one can construct a path \(\omega _{2} \in \Omega _{v,y}\) such that \(\Phi (\omega _{2}) \le \Phi (x,y)\). Then the path obtained by concatenation \(\omega = (\omega _{1},\omega _{2})\) belongs to \(\Omega _{x,y}^\mathrm{{opt}}\); indeed, \(\Phi (\omega ) = \max (\Phi (\omega _{1}), H(u) + \Delta (u,v),\Phi (\omega _{2})) = \Phi (x,y)\). Finally the edge \((u,v)\) belongs to \(\omega \) by construction.
-
\( \mathcal{S}(x,y) \subset \bigcup _{C \in \mathcal{M}_{x,y}} \mathcal{B}(C) .\) Let us consider \(v \in \mathcal{S}(x,y)\), and \(u \in \mathcal{X}\) such that \((u,v) \in \hat{\mathcal{S}}(x,y)\). We show that
$$\begin{aligned} v \in \mathcal{B}(C(u)). \end{aligned}$$(4.62)We first note that it follows from Proposition 3.13 that, since \( H(u) + \Delta (u,v) = \Phi (u,v) = \Phi (x,y)\), it necessarily holds \(C(u) \cap C(v) = \emptyset \). Indeed, we know that for any \(C \in \mathcal{M}_{x,y}\), \(\max _{s,t \in C} \Phi (s,t) < \Phi (C,\mathcal{X}{\setminus } C) = \Phi (x,y)\), and hence by contradiction \(u\) and \(v\) cannot belong to a common element of \(\mathcal{M}_{x,y}\). Hence \(v \in \mathcal{X}{\setminus } C(u)\).
We already noted that it follows from Proposition 3.22 that \(H(C(u)) + \Gamma (C(u)) = \Phi (x,y)\). Since, by hypothesis, \(H(u) + \Delta (u,v) = \Phi (x,y)\), we deduce the equality
$$\begin{aligned} H(u) + \Delta (u,v) = H(C(u)) + \Gamma (C(u)). \end{aligned}$$(4.63)Making use of the characterization of the principal boundary in Proposition 3.12, this last equality proves (4.62). This closes the proof. \(\square \)
Proof of Theorem 2.1
Proof of refcp01 Let \(C\) be the set of states \(y\in \mathcal{X}\) such that \(\Phi (x,y)<V^\text {m}+H(x)\). By Proposition 3.10 the set \(C\) is a cycle and, by construction, \(x\in \mathcal{F}(C)\) and \(\Phi (C,\mathcal{X}{\setminus } C)=V^\text {m}\). Hence, by Proposition 3.15 it follows that \(\Gamma (C)=V^\text {m}-H(x)\). Finally, since \(\mathcal{X}^\text {s}\cap C=\emptyset \) implies \(\tau ^x_{\mathcal{X}^\text {s}}\ge \tau ^x_{\partial C}\), we have that (2.30) follows by item 3.18 in Proposition 3.18.
Proof of (2.31) As we have already remarked at the end of Sect. 2.6, see also Fig. 2, \(\mathcal{X}_{V^\text {m}}=\mathcal{X}^\text {s}\). Hence, (2.31) is an immediate consequence of Proposition 2.8. \(\square \)
Before proving Theorem 2.2 we first state and prove the following preliminary integrability result.
Lemma 4.1
Given any real \({\delta }> 0\) and any state \(x \in \mathcal{X}\), the family of random variables \(Y_{{\beta }}^{x} = \tau _{\mathcal{X}^{ \text {s}}}^{x} e^{-{\beta }(V^{ \text {m}}+{\delta })}\) is uniformly integrable, more precisely, for any \(n\ge 1\)
for \(\beta \) large enough.
Proof
For any \(n \ge 1\), by making use of the Markov property, we directly get
Recalling that \(\mathcal{X}_{V^\text {m}} = \mathcal{X}^\text {s}\) (see the end of Sect. 2.6) and making use of Proposition 2.8, we get that the above quantity is bounded from above by \(2^{-n}\) as soon as \({\beta }\) large enough. \(\square \)
Proof of Theorem 2.2
Fix \(x \in \mathcal{X}^{\text {m}}\) and \({\delta }> 0\). Combining the convergence to zero in probability of the random variables \(Y_{{\beta }} = \tau _{\mathcal{X}^{\text {s}}}^{x} e^{-(V^{\text {m}}+{\delta }){\beta }}\), which has been shown in Theorem 2.1 and their uniform summability stated in Lemma 4.1, we get that the family of random variables \(Y_{{\beta }}\) converges to \(0\) in \(L^{1}\). Hence,
for \({\beta }\) large enough,
On the other hand, by making use of the Markov’s inequality we get the following bound:
Using once again Theorem 2.1, we obtain that there exists \(K > 0\) such that
as soon as \({\beta }\) is large enough.
The Theorem 2.2 finally follows from bounds (4.65) and (4.66). \(\square \)
Proof of Theorem 2.3
We first prove item 1. Let \(x_0\) be the recurrent state of Theorem 2.3 and recall (2.33)–(2.35). We consider \(s,t>0\) and let \(\tau ^{x_0}_{*}(t) = \inf \{ n \ge tT_{{\beta }},\, X_{n} \in \{x_{0},\mathcal{X}^{\text {s}} \}\}\) be the first hitting time to the set \(\{x_{0},\mathcal{X}^{\text {s}}\}\) after time \(t T_{{\beta }}\) for the chain \(X_n\) started at \(x_0\).
Then we decompose:
Using the Markov property and of the fact that \(\{ \tau _{\mathcal{X}^{\text {s}}}^{x_{0}} > \tau ^{x_0}_{*}(t) \} \subset \{X_{\tau ^{x_0}_{*}(t)} = x_{0} \}\), we directly get:
Combining monotonicity and the fast recurrence property (2.35), by the decomposition (4.67) we deduce
Here and later, we made use of the following obvious monotonicity property: for \(b,c \in {\mathbb R}\) such that \(b\ge c\),
where \(T\) is any random variable.
We bound the same quantity from above in a similar fashion. Namely, using (4.67) once again:
Consider \({\beta }\) large enough so that \(T_{{\beta }}' \le T_{{\beta }}\). For any given integer \(k \ge 1\), combining (4.69) and monotonicity, we get:
Given the definition of \(T_{{\beta }}\) (see (2.33)), there exists \(r \in (0,1)\) such that \({\delta }_{{\beta }} + {\mathbb P}_{\beta }[ \tau _{\mathcal{X}^{\text {s}}}^{x_{0}} > T_{{\beta }}] \le r\) as soon as \({\beta }\) is large enough. As a consequence, for \({\beta }\) large enough, the following inequality holds:
and this implies the tightness of the family \(\tau _{\mathcal{X}^{\text {s}}}^{x_{0}}/T_{{\beta }}\).
Combining the upper bound (4.69) and the lower bound (4.68), we deduce that the limit in law \(X\) of any subsequence \(\left( \tau _{\mathcal{X}^{\text {s}}}^{x_{0}}/T_{{\beta }}\right) _{{\beta }_{k}}\) satisfies the relation:
for any \(t,s \ge 0\) which are continuity points for the distribution of \(\tau _{\mathcal{X}^{\text {s}}}^{x_{0}}\). Since the set of such points is dense in \({\mathbb R}\) and a distribution function is always right continuous, (4.71) is valid for every \(s,t \ge 0\). This implies that \({\mathbb P}_{\beta }(X > t) = e^{-at}\) with \(a \in (0,\infty ]\). It is clear that the case \(a = \infty \) is excluded from the definition of \(T_{{\beta }}\), since it would imply that \(X\) is almost surely equal to zero, which is in contradiction with the fact that
By the Porte-Manteau theorem, we get that
and combining (4.72) and (4.73), we conclude that \(a = 1\).
As for item 2, combining the dominated convergence theorem and the uniform summability (4.70), we can write
which entails the convergence (2.36).
Item 3 directly follows from items 1 and 2 of the current theorem, which concludes the proof. \(\square \)
Now, given \(x,y\in \mathcal{X}\), we consider a minimal gate \(W \subset \mathcal{W}(x,y)\) as in Definition defgateFW and we go to the proofs of Theorem 2.4 and of Proposition 2.7.
To prove both these results, we first construct in a more formal way the set \(\mathcal{K}_{x,y}\) introduced in Sect. 2.8; we stress that this task is performed by making an extensive use of the notions developed in the previous sections. Then we show Proposition 2.7. Our task to prove Theorem 2.4 will then be reduced to show the inclusion \( \mathcal{K}_{x,y} \subset \{\tau ^x_W<\tau ^x_y\}\).
Recall the notations introduced in Sect. 2.7. Note that any path \(\Omega _{x,y}^\mathrm{{opt}}\) is contained in \(C_{x,y}\). Also, we already noted (and this is actually the major technical difference with the analogous result of [31]) that there might be paths contained in \(C_{x,y}\), joining \(x\) to \(y\) and which do not belong to \(\Omega _{x,y}^\mathrm{{opt}}\).
Let us discuss some geometrical properties of the decomposition \(\mathcal{M}_{x,y}\).
We first note that it is clear that \(x\) and \(y\) are not contained in the same element of \(\mathcal{M}_{x,y}\). Indeed, if they were contained in a common element \(\bar{C} \in \mathcal{M}_{x,y}\), we would have \(\Phi (x,y)<H(\bar{C})+\Gamma (\bar{C})\) and in particular, from the definition of \(C_{x,y}\), this would imply \(C_{x,y}\subset \bar{C}\), which is absurd from the non triviality of the decomposition \(\mathcal{M}_{x,y}\).
To define \(\mathcal{K}_{x,y}\), we shall start to restrict the set of trajectories to the set of trajectories \(\Omega _{x,y}\cap \{\tau ^{x}_{y}<\tau ^{x}_{\mathcal{X}{\setminus } C_{x,y}}\}\), for which the events we are going to introduce are well defined.
More precisely, for a given trajectory of the canonical process \( \omega \in \Omega _{x,y} \cap \{\tau ^{x}_{y} < \tau ^{x}_{\mathcal{X}{\setminus } C_{x,y}} \}\), we first define \(\theta ^{x}_{0} := 0, C^{x}_{0} = C(x) \) and for \(j \ge 1\):
and \(C^{x}_{j} = C(\omega _{\theta ^x_{j}})\) is the element of \(\mathcal{M}_{x,y}\) containing \(\omega _{\theta ^x_{j}}\). This construction goes on as long as \( j \le j_{x,y}\), where we consider
More generally, for any \(u \in C_{x,y}\), we introduce the similar quantities \((\theta ^{u}_{j})_{j}, (C^{u}_{j})_{j}\), with notations which are self explanatory.
Then we introduce the event
which is the event that the process hits \(y\) after entering \(C(y)\) before leaving \(C(y)\) for the first time.
For \( C \in \mathcal{M}_{x,y}\) and \(u \in C\), we introduce the event
where \((\omega ^{u}_{k})_{k\ge 0}\) denotes a trajectory of the canonical process starting from \(u\). Finally we can define the set \(\mathcal{K}_{x,y}\), the tube of trajectories of the dynamics on its transition between \(x\) and \(y\):
We refer to Sect. 2.8 for an informal definition of \(\mathcal{K}_{x.y}\).
Proof of Proposition 2.7
We prove that
as soon as \({\beta }\) is large enough.
Our proof first relies on the fact that, given \({\delta }> 0\), for \({\beta }\) large:
which follows from the finiteness of \(\mathcal{X}\) and Corollary 3.2. Then we will use the fact that for any \({\varepsilon }' > 0\), as soon as \({\beta }\) is large enough:
which we show at the end of the proof of Proposition 2.7.
Let us note that in [11], the authors showed a result related to ours, in the sense that they provide the precise cost on a large deviation scale of not following a path contained in \(\mathcal{K}_{x,y} \cap \Omega _{x,y}^\mathrm{{opt}}\) on the transition from \(x\) to \(y\). For our sake such a level of precision is not needed. On the other hand, we had to deal with the (easy) problem of giving an upper bound on the random variable \( j_{x,y}\), which was overcome in [11] by the notion of pruning tree.
We show how to deduce Proposition 2.7 from combining (4.75) and (4.76). For lightness of notations, we introduce the conditional probability
in the next sequence of inequalities. Of course, since \(y \in C_{x,y}\) and \(y \in C(y)\), applying the strong Markov property at time \(\tau ^{x}_{C(y)}\) and Definition 2.3 we immediately get that, for any \({\varepsilon }' > 0\), as soon as \({\beta }\) is large enough:
It follows from this inequality that similar inequalities to (4.75) and (4.76) also hold for the probability \(\widetilde{{\mathbb P}_{{\beta }}} \) instead of \({\mathbb P}_{{\beta }}\), and we will still refer to these slightly modified versions of (4.75) and (4.76) as (4.75) and (4.76) in the following.
Denoting by \({\varepsilon }'\) a (small) positive constant which may change from line to line, we then get:
where we used (4.77), (4.76) and the strong Markov property. Now from (4.75), we get
and considering \({\delta }> {\varepsilon }\), the statement of Proposition 2.7 follows.
Now we are left with the proof of (4.76).
Denote by \(n_{0}\) the cardinality of \(\mathcal{M}_{x,y}\). Since \(\mathcal{M}_{x,y}\) is an isolated vtj—connected system of cycles, we deduce that
as soon as \({\beta }\) is large enough.
Indeed, there exists a vtj connected path of cycles \((\tilde{C}^{u}_{1}, \ldots ,\tilde{C}^{u}_{m} )\) of length \(m\) (with \( m \le n_{0}\)) joining \(C(u)\) to \(C(y)\). For any \(u \in C_{x,y}\), applying the strong Markov property at the time of first entrance into \(\tilde{C}^{u}_{1}\) and proceeding iteratively, we get:
where in the third inequality we used Corollary 3.2 and the definition of vtj—connectedness. Since the last term does not depend on \(u\), we get (4.78).
Making use recursively of the strong Markov property at times \(\theta ^{x}_{ke^{{\varepsilon }{\beta }}/n_{0}}, k = 1,\ldots ,n_{0}\), of the trivial bound \(n_{0} \le |\mathcal{X}|\) and of (4.78), we get:
and (4.76) then follows by choosing \({\varepsilon }' \in (0,{\varepsilon }/|\mathcal{X}|^{2})\). This concludes the proof of Proposition 2.7. \(\square \)
Proof of Theorem 2.4
We first recall the following consequence of Proposition 3.22.
For any \(i=1,\dots , n_0\):
To get (4.81), we first note that, since \(y\in \mathcal{X}{\setminus } C(x)\), by Propositions 3.10 and 3.15, we have that \(\Phi (x,y) \ge H(C(x)) + \Gamma (C(x))\). On the other hand, assume by contradiction that \(\Phi (x,y) >H(C(x))+\Gamma (C(x))\). Recalling (3.56) in Proposition 3.22 and (3.44) in Proposition 3.13, it follows that there exists a path \(\omega \in \Omega _{x,y}^\mathrm{{opt}}\) such that \(\Phi (\omega )<\Phi (x,y)\), which is absurd.
Hence, we have proven that \(\Phi (x,y)=H(C(x))+\Gamma (C(x))\). By using again (3.56) in Proposition 3.22, we then deduce (4.81).
Then we note that considering Proposition 2.7, for Theorem 2.4 to hold, it is enough to show the inclusions
Indeed, this implies in particular the trivial bound
and Proposition 2.7 provides the requested lower bound on this last quantity.
We remark that the inclusions of (4.82) are strict in general.
The first inclusion follows immediately from the fact that an optimal path in \(\Omega ^\text {opt}_{x,y}\) exits from an element of \(\mathcal{M}_{x,y}\) through its principal boundary. Also, it is clear that some paths in the set \(\mathcal{K}_{x,y}\) might not be optimal, and hence that it might be strict in general.
The second inclusion of (4.82) is not straightforward and we stress that it relies crucially on Proposition 3.13. Let us detail it.
Consider first the case \(\omega \in \mathcal{K}_{x,y} \cap \Omega _{x,y}^\mathrm{{opt}}\). Since \(\omega \in \Omega _{x,y}^\mathrm{{opt}}\), by definition of a gate (see Sect. 2.7), it follows immediately that \(\omega \cap W \ne \emptyset \).
Consider now an element \(\omega \in \mathcal{K}_{x,y} {\setminus } \Omega _{x,y}^\mathrm{{opt}}\), that is \(\omega \) is an element of \(\mathcal{K}_{x,y}\) such that \(\Phi (\omega ) > \Phi (x,y)\).
To show the second inclusion of (4.82), the strategy is the following: we consider the sequence of points \((u_1,\ldots ,u_j)\) which are the successive points where \(\omega \) intersects \(\bigcup _{C \in \mathcal{M}_{x,y}} \mathcal{B}(C)\). The sequence \((u_1,\ldots ,u_j)\) is nonempty from the construction of \(\mathcal{K}_{x,y}\) and from the fact that \(C(x) \ne C(y)\). We are going to construct stepwise a path \(\widetilde{\omega } \in \mathcal{K}_{x,y} \cap \Omega _{x,y}^\mathrm{{opt}}\) such that
From the definition of a gate and from the fact that \(\widetilde{\omega }\) is optimal, we deduce that \(\widetilde{\omega } \cap W \ne \emptyset \). From this it follows that \(\widetilde{\omega } \cap W = \omega \cap W \ne \emptyset \), which indeed implies the second inclusion of (4.82).
To construct the path \(\widetilde{\omega }\), we proceed in a recursive way; more precisely, we construct a sequence of paths \((\omega ^{(k)})_{k \ge 0} \in \mathcal{K}_{x,y}\) which becomes stationary for \(k\) large enough. We initialize our recursion by setting \(\omega ^{(0)} := \omega \). Then, as long as the path \(\omega ^{(k)}\) is not optimal, we proceed in the following way: consider
and \(C_{k}\) the element of \(\mathcal{M}_{x,y}\) containing \(\omega ^{(k)}_{i_{k}}\). Then we distinguish two cases: \(\omega ^{(k)}_{i_{k}+1} \in \mathcal{B}(C_{k})\) and \(\omega ^{(k)}_{i_{k}+1} \in C_{k}\).
-
In the case where \(\omega ^{(k)}_{i_{k}+1} \in \mathcal{B}(C_{k})\), we make use of (3.44) in Proposition 3.13 and of (4.81) to get that there exists a path \(\omega ' \in \Omega _{\omega ^{(k)}_{i_{k}},\omega ^{(k)}_{i_{k}+1}}\) such that \(\Phi (\omega ') = \Gamma (C_{k}) + H(C_{k}) = \Phi (x,y)\) and for any \(j \le |\omega '|-1\), \(\omega _{j}' \in C_{k}\). We define the concatenated path
$$\begin{aligned} \omega ^{(k+1)} := \left( \left( \omega ^{(k)}_{j}\right) _{j \le i_{k}-1},\omega ',\left( \omega ^{(k)}_{j}\right) _{j \ge i_{k}+2}\right) . \end{aligned}$$(4.84)Note that \(\omega ^{(k+1)} \in \mathcal{K}_{x,y}\) and that \(u \in \omega ^{(k+1)}\). Then we continue the recursive construction.
-
In the case where \(\omega ^{(k)}_{i_{k}+1} \in C_{k}\), from (3.45) in Proposition 3.13, there exists \( \omega ' \in \Omega _{\omega ^{(k)}_{i_{k}},\omega ^{(k)}_{i_{k}+1}}\) such that \(\Phi (\omega ') < \Phi (C_{k}, \mathcal{X}{\setminus } C_{k}) = \Phi (x,y)\) and such that \(\omega '\) is entirely contained in \(C_{k}\). Then we define the path \(\omega ^{(k+1)}\) as in (4.84), and we note that in this case also \(\omega ^{(k+1)} \in \mathcal{K}_{x,y}\) and \(u \in \omega ^{(k+1)}\).
It is clear from the construction that the sequence of paths \((\omega ^{(k)})_{k \ge 0}\) is stationary after a number of steps at most \(|\omega |\), and that the final path \(\widetilde{\omega }\) obtained at the end of the recursion is an element of \(\mathcal{K}_{x,y} \cap \Omega _{x,y}^\mathrm{{opt}}\) satisfying (4.83). Hence the second inclusion in (4.82) follows, and thus Theorem 2.4 is proved. \(\square \)
Now we go to the proof of Proposition 2.8. We first note that, in the spirit of [31], we need a downhill cycle path (see the definition in Sect. 3.5) connecting any given point \(x\in \mathcal{X}{\setminus }\mathcal{X}_{a}\), for \(a>0\), to \(\mathcal{X}_{a}\). We recall that the notion of downhill cycle path given in [31] and [34], even if quite peculiar to the Metropolis dynamics setup, finds its natural extension to the general rare transition setup in [35] and in [11] through the notion of “via typical jumps” connection.
Proof of Proposition 2.8
Let \(a>0\), we assume that \(\mathcal{X}_{a}\) is a proper subset of \(\mathcal{X}\), otherwise there is nothing to prove. We consider \(x \in \mathcal{X}{\setminus }\mathcal{X}_{a}\) and note that, by Proposition 3.24, there exists a vtj—connected cycle path \(C_1,\ldots ,C_l\subset \mathcal{X}{\setminus }\mathcal{X}_a\) such that \(x\in C_1\) and \(\mathcal{B}(C_l)\cap \mathcal{X}_a\ne \emptyset \).
Since none of the cycles \(C_1,\ldots ,C_l\) can contain points of \(\mathcal{X}_a\), for any \(i=1,\ldots ,l\) and any \(z\in \mathcal{F}(C_i)\) the stability level \(V_z\) (recall definition (2.19)) of \(z\) satisfies \(V_{z} \le a\), and hence from item 3.17 in Proposition 3.17, we have \(\Gamma (C_i)\le a\) for any \(i=1,\ldots ,l\).
Then, from item 3.18 in Proposition 3.18, for any cycle \(C_i\) of the vtj—connected path, for any \(z\in C_i\), and for any \({\varepsilon }> 0\), the function
is SES.
We consider \(y\in \mathcal{B}(C_l)\cap \mathcal{X}_a\) and, for each \(2 \le i \le l\), we consider \(y_{i} \in \mathcal{B}(C_{i-1}) \cap C_{i}\). We define \(y_{1} = x\) and \(y_{l+1} = y\), and we consider the set of paths
consisting of the paths constructed by the concatenation of any \(l\)-uple of paths \({\omega }^{1},{\omega }^{2},\ldots ,{\omega }^{l}\) satisfying the following conditions:
-
1.
for any \(i=1.\ldots ,l\) the length of the path \({\omega }^{i}\) satisfies \(|{\omega }_{i}| \le e^{{\beta }(a+{\varepsilon }/4)}\);
-
2.
for any \(i=1,\ldots ,l\) the path \({\omega }^i\) joins \(y_{i}\) to \(y_{i+1}\), that is, \({\omega }^{i} \in \Omega _{y_{i},y_{i+1}}\) (recall the notation introduced in Sect. 2.4);
-
3.
\({\omega }^{i}_{j} \in C_{i}\) for any \(i=1,\ldots ,l\) and for any \(j=1,\ldots ,|{\omega }^{i}| -1\).
The existence of such a family of paths is ensured by Propositions 3.10, 3.15, 3.12, and 3.13. We stress that condition 4 restricts the set \(\mathcal{E}\) to paths which spend a time less than \(e^{{\beta }(a + {\varepsilon }/4)}\) in any cycle \(C_{i}, i \le l\).
For shortness, in the sequel, we shall use the notation \(\mathcal{E}\) for the set of trajectories defined in (4.85).
Note that the length of any \({\omega }\in \mathcal{E}\) satisfies the upper bound \(|{\omega }| \le |\mathcal{X}| e^{{\beta }(a+{\varepsilon }/4)}\). Moreover, since the state space \(\mathcal{X}\) is finite, we can assume that \({\beta }\) is large enough so that
Now, we write
where in the last step we have used the bound above on the length of the trajectories in \(\mathcal{E}\). Then we use Markov’s property to get that
Combining this inequality and (3.53) implies that, for any \({\varepsilon }'>0\),
as soon as \({\beta }\) is large enough.
Since the last term in the right hand side of the bound above does not depend on \(x \in \mathcal{X}_{a}\), we get that
Now we iterate this inequality by making use of the Markov’s property at the times \(ke^{{\beta }(a + {\varepsilon }/2)}\), \(k=1,\ldots , e^{{\beta }{\varepsilon }/2}\) to get that
for any \(x \in \mathcal{X}_{a}\).
Finally, picking up \({\varepsilon }' > 0\) small enough, we get that the function \({\beta }\mapsto e^{ - e^{ {\beta }({\varepsilon }/2-{\varepsilon }' |\mathcal{X}|) }}\) is SES, and thus Proposition 2.8 is proved. \(\square \)
Proof of Proposition 2.9
Set \(T:=\exp \left( \beta (h-\varepsilon ) \right) \); writing \(x_0=x\) and making use of the Markov property, we immediately get:
We multiply and divide by \(\mu _\beta (x)\) on the right hand side (recall that for \({\beta }\) large enough, the Markov chain is irreducible, and hence \(\mu _{{\beta }}\) is strictly positive over \(\mathcal{X}\)). Also, we estimate the first two terms with the sum over the first state, and we deduce
Now, making use of the stationarity of \(\mu _{{\beta }}\), we get
and hence
Recalling the convergences (2.1) and (2.3), we get that for any \({\varepsilon }' > 0\), as soon as \({\beta }\) is large enough:
where in the last step we used the definition of \(T\). Now, choosing \({\varepsilon }' \in (0,{\varepsilon }/4)\) concludes the proof of Proposition 2.9. \(\square \)
Proof of Proposition 3.19
Consider \( C \in \mathcal{C}(\mathcal{X})\), \(z \in \mathcal{F}(C)\) and \({\varepsilon }> 0\). By the finiteness of \(\mathcal{F}(C)\), it is enough to prove
for (3.54) to hold. We consider the following decomposition:
For the second term in the right hand side above, we deduce from item 3.18 in Proposition 3.18 that
as \({\beta }\rightarrow \infty \).
As for the first term, we first have the inequality:
Using the fact that \(z \in \mathcal{F}(C)\) (that is \(H(z) = H(C)\)), we have the equality of events:
where we have recalled (2.37) and (2.38). We deduce from Proposition 2.9 that the term in the right hand side of (4.89) is less than \(e^{-{\beta }{\varepsilon }/4}\) as \({\beta }\rightarrow \infty \). Combining this inequality with (4.87) and (4.88), we deduce (4.86), and, hence, Proposition 3.19. \(\square \)
Notes
To deduce the corollary we use the following elementary remark: given two events \(A,B\) such that \((1/{\beta }) \log {\mathbb P}_{\beta }(B) \rightarrow 0\) and \((1/{\beta }) \log {\mathbb P}_{\beta }(A) \rightarrow - \infty \) in the limit \({\beta }\rightarrow \infty \), we have that \((1/{\beta })\log {\mathbb P}_{\beta }(A^{c} \cap B) \rightarrow 0\), where \(A^{c}\) denotes the event complementary to \(A\). Indeed, since \({\mathbb P}_{\beta }(A^{c} \cap B) \ge {\mathbb P}_{\beta }(B) - {\mathbb P}_{\beta }(A)\), we get that \(\log {\mathbb P}_{\beta }(A^{c} \cap B) \ge \log {\mathbb P}_{\beta }(B) + \log (1-{\mathbb P}_{\beta }(A)/{\mathbb P}_{\beta }(B))\). Then \((1/{\beta })\log {\mathbb P}_{\beta }(B)\ge -{\varepsilon }\) as soon as \({\beta }\) is large enough, and on the other hand, since \(\log ({\mathbb P}_{\beta }(A)/{\mathbb P}_{\beta }(B))\rightarrow -\infty \) as \({\beta }\rightarrow \infty \), we get that \({\mathbb P}_{\beta }(A)/{\mathbb P}_{\beta }(B) \rightarrow 0\).
References
Aldous, D.J., Brown, M.: Inequalities for rare events in time-reversible Markov chains. I. In: Stochastic Inequalities (Seattle, WA, 1991). IMS Lecture Notes Monograph Series, vol. 22, pp. 1–16. Institute of Mathematical Statistics, Hayward, CA (1992)
Aldous, D.J., Brown, M.: Inequalities for rare events in time-reversible Markov chains. II. Stoch. Process. Appl. 44(1), 15–25 (1993)
Bovier, A., Eckhoff, M., Gayrard, V., Klein, M.: Metastability and small eigenvalues in Markov chains. J. Phys. A 33(46), L447–L451 (2000)
Bovier, A., Eckhoff, M., Gayrard, V., Klein, M.: Metastability in stochastic dynamics of disordered mean-field models. Probab. Theory Relat. Fields 119(1), 99–161 (2001)
Bovier, A., Eckhoff, M., Gayrard, V., Klein, M.: Metastability in reversible diffusion processes. I. Sharp asymptotics for capacities and exit times. J. Eur. Math. Soc. (JEMS) 6(4), 399–424 (2004)
Beltrán, J., Landim, C.: Metastability of reversible finite state Markov processes. Stoch. Process. Appl. 121(8), 1633–1677 (2011)
Beltrán, J., Landim, C.: Tunneling and metastability of continuous time Markov chains II, the nonreversible case. J. Stat. Phys. 149(4), 598–618 (2012)
Benois, O., Landim, C., Mourragui, M.: Hitting times of rare events in Markov chains. J. Stat. Phys. 153(6), 967–990 (2013)
Bovier, A.: Metastability: a potential theoretic approach. In: International Congress of Mathematicians, vol. III, pp. 499–518. European Mathematical Society, Zürich (2006)
Catoni, O.: Simulated annealing algorithms and Markov chains with rare transitions. In: Séminaire de Probabilités, XXXIII. Lecture Notes in Mathematics, vol. 1709, pp. 69–119. Springer, Berlin (1999)
Catoni, O., Cerf, R.: The exit path of a Markov chain with rare transitions. ESAIM Probab. Stat. 1, 95–144 (1995/97)
Cassandro, M., Galves, A., Olivieri, E., Vares, M.E.: Metastable behavior of stochastic dynamics: a pathwise approach. J. Stat. Phys. 35(5–6), 603–634 (1984)
Cirillo, E.N.M., Louis, P.-Y., Ruszel, W.M., Spitoni, C.: Effect of self-interaction on the phase diagram of a Gibbs-like measure derived by a reversible Probabilistic Cellular Automata. Chaos Solitons Fractals 64(SI), 36–47 (2014)
Cirillo, E.N.M., Nardi, F.R.: Metastability for a stochastic dynamics with a parallel heat bath updating rule. J. Stat. Phys. 110(1–2), 183–217 (2003)
Cirillo, E.N.M., Nardi, F.R.: Relaxation height in energy landscapes: an application to multiple metastable states. J. Stat. Phys. 150(6), 1080–1114 (2013)
Cirillo, E.N.M., Nardi, F.R., Polosa, A.D.: Magnetic order in the Ising model with parallel dynamics. Phys. Rev. E 64(5 pt 2), 057103 (2001)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Competitive nucleation in reversible probabilistic cellular automata. Phys. Rev. E (3) 78(4), 040601 (2008)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Metastability for reversible probabilistic cellular automata with self-interaction. J. Stat. Phys. 132(3), 431–471 (2008)
Cirillo, E.N.M. Nardi, F.R., Spitoni, C.: Competitive nucleation in metastable systems. In: Applied and Industrial Mathematics in Italy III. Series on Advances in Mathematics for Applied Sciences, vol. 82, pp. 208–219. World Science Publishing, Hackensack, NJ (2010)
Cirillo, E.N.M., Nardi, F.R., Sohier, J.: A comparison between different cycle decompositions for metropolis dynamics. Markov Process. Relat. Fields (2015)
de Carlo, Gabrielli, D.: A non reversible conservative kawasaki dynamics. Private communication, work in progress (2015)
den Hollander, F., Nardi, F.R., Troiani, A.: Kawasaki dynamics with two types of particles: stable/metastable configurations and communication heights. J. Stat. Phys. 145(6), 1423–1457 (2011)
den Hollander, F., Nardi, F.R., Troiani, A.: Kawasaki dynamics with two types of particles: critical droplets. J. Stat. Phys. 149(6), 1013–1057 (2012)
den Hollander, F., Nardi, F.R., Troiani, A.: Metastability for Kawasaki dynamics at low temperature with two types of particles. Electron. J. Probab. 17(2), 26 (2012)
Dai Pra, P., Scoppola, B., Scoppola, E.: Fast mixing for the low temperature 2D ising model through irreversible parallel dynamics. J. Stat. Phys. 159(1), 1–20 (2015)
Fernandez, R., Manzo, F., Nardi, F.R., Scoppola, E., Sohier. J.: Conditioned, quasi-stationary, restricted measures and metastability. Ann. Appl. Probab. (2015)
Fernandez, R., Manzo, F., Nardi, F.R., Scoppola, E.: Asymptotically exponential hitting times and metastability: a pathwise approach without reversibility. Electron. J. Probab. (2015)
Grinstein, G., Jayaprakash, C., He, Yu.: Statistical mechanics of probabilistic cellular automata. Phys. Rev. Lett. 55(23), 2527–2530 (1985)
Gaudillière, A., Landim, C.: A Dirichlet principle for non reversible Markov chains and some recurrence theorems. Probab. Theory Relat. Fields 158(1–2), 55–89 (2014)
Landim, C.: Metastability for a non-reversible dynamics: the evolution of the condensate in totally asymmetric zero range processes. Commun. Math. Phys. 330(1), 1–32 (2014)
Manzo, F., Nardi, F.R., Olivieri, E., Scoppola, E.: On the essential features of metastability: tunnelling time and critical configurations. J. Stat. Phys. 115(1–2), 591–642 (2004)
Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., Teller, E.: Equation of state calculations by fast computing machines. J. Chem. Phys. 21(6), 1087–1092 (1953)
Oliveira, R.I.: Mean field conditions for coalescing random walks. Ann. Probab. 41(5), 3420–3461 (2013)
Olivieri, E., Scoppola, E.: Markov chains with exponentially small transition probabilities: first exit problem from a general domain. I. The reversible case. J. Stat. Phys. 79(3–4), 613–647 (1995)
Olivieri, E., Scoppola, E.: Markov chains with exponentially small transition probabilities: first exit problem from a general domain. II. The general case. J. Stat. Phys. 84(5–6), 987–1041 (1996)
Olivieri, E., Vares, M.E.: Encyclopedia of Mathematics and Its Applications. Large deviations and metastability, vol. 100. Cambridge University Press, Cambridge (2005)
Trouvé, A.: Partially parallel simulated annealing: low and high temperature approach of the invariant measure. In: Applied Stochastic Analysis (New Brunswick, NJ, 1991). Lecture Notes in Control and Information Science, vol. 177, pp. 262–278. Springer, Berlin (1992)
Trouvé, A.: Cycle decompositions and simulated annealing. SIAM J. Control Optim. 34(3), 966–986 (1996)
Acknowledgments
JS acknowledges the support of NWO STAR grant: “Metastable and cut-off behavior of stochastic processes” and thanks University of Roma Tre for the kind hospitality. The authors thank A. Zocca for useful comments and discussions. ENMC thanks the Institute of Complex Molecular Systems (TU/e, Eindhoven) for the kind hospitality.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Computing Differences of Virtual Energy
In this appendix, we describe an abstract framework for which the virtual energy has a priori no explicit expression, but where we can construct it stepwise starting from a reference point acting as a point of null potential.
We consider a Freidlin Wentzell dynamics satisfying Definition 2.1 and such that for every \(x,y\in \mathcal{X}\)
Moreover, we assume that the dynamics satisfies the additional condition (where we recall that \(\mu _{{\beta }}\) is the invariant measure): for any \(\beta >0\), there exists a function \(\rho :{\mathbb R}_+\rightarrow {\mathbb R}_+\) such that \(\rho (\beta ) \rightarrow 0\) as \(\beta \rightarrow \infty \) and
for any \(x,y\in \mathcal{X}\).
Of course, the convergence (5.91) is nothing else than requesting the existence of a potential, which is equal to the virtual energy up to a constant (see (2.4) and Proposition 2.2).
Now we fix an arbitrary state \(\bar{x} \in \mathcal{X}\) and we define the Hamiltonian—like quantity
For any \(x \in \mathcal{X}, x \ne \bar{x}\), by irreducibility, there exists a path \({\omega }\in \Omega _{\bar{x}, x}\) such that \(|{\omega }| \le \mathcal{X}\). Given such a path, we define the quantity
and we set \(W_{{\omega }}(\bar{x}):= 0\).
Proposition 5.27
Given \(x\in \mathcal{X}\) and \(x\ne \bar{x}\), the quantity \(W_{{\omega }}(x)\) defined by (5.93) does not depend on the particular choice of the path \(\omega \in \Omega _{\bar{x},x}\), and hence it defines a function \(W: \mathcal{X}\rightarrow {\mathbb R}\). The function \(W(\cdot ) - \min _{\mathcal{X}} W\) coincides with the virtual energy \(H\).
In general, the virtual energy might have an expression too involved for practical purposes. Equation (5.93) provides a constructive way to compute explicitly \(H\) step by step just from the knowledge of the rates of the dynamics.
Proof
For any \(x,y\in \mathcal{X}\) and \(x\ne y\), we consider \({\omega },{\omega }' \in \Omega _{x,y}\) and show that
Indeed, using telescoping sums in the right hand side above, we can assume that all the \({\omega }'_{i}\)’s are distinct (and in particular \(|{\omega }'| \le |\mathcal{X}|\)).
By (5.91), we get the inequality
By triangular inequality, we then deduce that
Now we divide both sides by \({\beta }\) and we let \({\beta }\rightarrow \infty \) to deduce (5.94). \(\square \)
Appendix 2: Explicit Expression of the Virtual Energy
As noted in Sect. 2.3, the virtual energy \(H(x)\), for \(x\in \mathcal{X}\), has an explicit expression in terms of a specific graph construction. The same holds for the functions \(\Gamma _D(x)\) and \(\Delta _D(x,y)\), with \(D\subset \mathcal{X}\), \(x\in D\), and \(y\in \mathcal{X}{\setminus } D\), introduced in Proposition 2.5. These explicit expressions were not necessary for our purposes, but for the sake of completeness, we choose to summarize these formulas in this appendix.
We use the notations of [10], but since we do not want to develop the full theory here, we try to keep it as minimal as possible.
Definition 6.7
Given \(A\subset \mathcal{X}\) nonempty, let \(G(A)\) be the set of oriented graphs \(g\in \mathcal{X}\times \mathcal{X}\) verifying the following properties:
-
for any \(x\in \mathcal{X}{\setminus } A\), there exists a unique \(y\in \mathcal{X}\) such that \((x,y)\in g\) (namely for any point in \(\mathcal{X}{\setminus } A\), there exists a unique arrow of the graph \(g\) exiting from such a point);
-
for any edge \((x,y)\in g\), \(x\in \mathcal{X}{\setminus } A\) (no arrow of the graph \(g\) exits from \(A\));
-
for any \(x\in \mathcal{X}\), \(n\in {\mathbb N}\), \((x,x_1),(x_1,x_2),\dots ,(x_{n-1},x_n)\in g\) one has that \(x\ne x_i\) for \(i=1,\dots ,n\) (the graph \(g\) is without loops).
Since \(\mathcal{X}\) is finite, from this definition it follows that for \(x\in \mathcal{X}{\setminus } A\), there exists a sequence of arrows connecting \(x\) to \(A\). We borrow (and adapt to our notation) a beautiful description of the set \(G(A)\) from [35, below Definition 3.1]: \(G(A)\) is a forest of trees with roots in \(A\) and with branches given by arrows directed towards the root.
Definition 6.8
Given \(A\subset \mathcal{X}\) nonempty, \(x\in \mathcal{X}{\setminus } A\), and \(y\in A\), let \(G_{x,y}(A)\) be the collection of graphs \(g\in G(A)\) such that there exist \(n\in {\mathbb N}\) and \(x_1,\dots ,x_n\in \mathcal{X}\) such that \((x,x_1),(x_1,x_2)\dots ,(x_n,y)\in g\).
In words, \(G_{x,y}(A)\) is the set of graphs in \(G(A)\) connecting the point \(x\) to the point \(y\).
For any \(x\in \mathcal{X}\), the virtual energy \(H(x)\) is given by (see [10, Proposition 4.1])
Moreover (see [10, Proposition 4.2]), for any \(D\subset \mathcal{X}\) nonempty, \(x\in D\), and \(y\in \mathcal{X}{\setminus } D\), one has the following equality:
and similarly
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Cirillo, E.N.M., Nardi, F.R. & Sohier, J. Metastability for General Dynamics with Rare Transitions: Escape Time and Critical Configurations. J Stat Phys 161, 365–403 (2015). https://doi.org/10.1007/s10955-015-1334-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-015-1334-6