Abstract
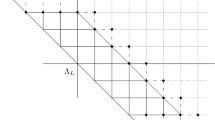
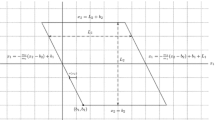
We introduce and analyze a class of quantum spin models defined on \(d\)-dimensional lattices \(\Lambda \subseteq {\mathbb Z}^d\), which we call Product Vacua with Boundary States (PVBS). We characterize their ground state spaces on arbitrary finite volumes and study the thermodynamic limit. Using the martingale method, we prove that the models have a gapped excitation spectrum on \({\mathbb Z}^d\) except for critical values of the parameters. For special values of the parameters we show that the excitation spectrum is gapless. We demonstrate the sensitivity of the spectrum to the existence and orientation of boundaries. This sensitivity can be explained by the presence or absence of edge excitations. In particular, we study a PVBS models on a slanted half-plane and show that it has gapless edge states but a gapped excitation spectrum in the bulk.

Similar content being viewed by others
References
Bachmann, S., Michalakis, S., Nachtergaele, B., Sims, R.: Automorphic equivalence within gapped phases of quantum lattice systems. Commun. Math. Phys. 309(3), 835–871 (2011)
Bachmann, S., Nachtergaele, B.: Product vacua with boundary states. Phys. Rev. B 86(3), 035149 (2012)
Bachmann, S., Nachtergaele, B.: On gapped phases with a continuous symmetry and boundary operators. J. Stat. Phys. 154, 91–112 (2014)
Borgs, C., Kotecký, R., Ueltschi, D.: Low temperature phase diagrams for quantum perturbations of classical spin systems. Commun. Math. Phys. 181(2), 409–446 (1996)
Bravyi, S., Hastings, M., Michalakis, S.: Topological quantum order: stability under local perturbations. J. Math. Phys. 51, 093512 (2010)
Bravyi, S., Hastings, M.B.: A short proof of stability of topological order under local perturbations. Commun. Math. Phys. 307, 609 (2011)
Chen, X., Gu, Z.-C., Liu, Z.-X., Wen, X.-G.: Symmetry protected topological orders and the group cohomology of their symmetry group. Phys. Rev. B 87, 155114 (2013)
Chen, X., Gu, Z.-C., Wen, X.-G.: Classification of gapped symmetric phases in one-dimensional spin systems. Phys. Rev. B 83(3), 035107 (2011)
Cirac, J.I., Michalakis, S., Perez-Garcia, D., Schuch, N.: Robustness in projected entangled pair states. Phys. Rev. B 88, 115108 (2013)
Datta, N., Fernández, R., Fröhlich, J.: Low-temperature phase diagrams of quantum lattice systems. i. stability for quantum perturbations of classical systems with finitely-many ground states. J. Stat. Phys. 84, 455 (1996)
Duivenvoorden, K., Quella, T.: Topological phases of spin chains. Phys. Rev. B 87, 125145 (2013)
Ginibre, J.: Existence of phase transitions for quantum lattice systems. Commun. Math. Phys. 14, 205–234 (1969)
Haegeman, J., Michalakis, S., Nachtergaele, B., Osborne, T.J., Schuch, N., Verstraete, F.: Elementary excitations in gapped quantum spin systems. Phys. Rev. Lett. 111, 080401 (2013)
Hastings, M.: Classifying quantum phases with the Kirby torus trick. Phys. Rev. B 88, 165114 (2013)
Kennedy, T., Tasaki, H.: Hidden symmetry breaking and the haldane phase in \(s=1\) quantum spin chains. Commun. Math. Phys. 147, 431–484 (1992)
Kirkwood, J.R., Thomas, L.E.: Expansions and phase transitions for the ground state of quantum ising lattice systems. Commun. Math. Phys. 88, 569–580 (1983)
Kitaev, A.: Periodic table for topological insulators and superconductors. In: Advances in theoretical physics : Landau Memorial Conference, Chernogolovka, Russia, 22–26 June 2008, AIP Conference Proceedings, vol. 1134. American Institute of Physics (2009)
Kitaev, A.Y.: Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2 (2003)
Matsui, T.: Uniqueness of the translationally invariant ground state in quantum spin systems. Commun. Math. Phys. 126, 453–467 (1990)
Michalakis, S., Pytel, J.: Stability of frustration-free hamiltonians. Commun. Math. Phys. 322, 277–302 (2013)
Nachtergaele, B.: The spectral gap for some quantum spin chains with discrete symmetry breaking. Commun. Math. Phys. 175, 565–606 (1996)
Nachtergaele, B., Ogata, Y., Sims, R.: Propagation of correlations in quantum lattice systems. J. Stat. Phys. 124, 1–13 (2006)
Perez-Garcia, D., Sanz, M., Gonzalez-Guillen, C.E., Wolf, M.M., Cirac, J.I.: Characterizing symmetries in a projected entangled pair state. New J. Phys. 12, 025010 (2010)
Schuch, N., Perez-Garcia, D., Cirac, I.: Classifying quantum phases using matrix product states and peps. Phys. Rev. B 84, 165139 (2011)
Schuch, N., Poilblanc, D., Cirac, J.I., Perez-Garcia, D.: Topological order in peps: transfer operator and boundary hamiltonians. Phys. Rev. Lett. 111, 090501 (2013)
Szehr, O., Wolf, M.M.: Perturbation theory for parent hamiltonians of matrix product states. arXiv:1402.4175, 2014, to appear in J. Stat. Phys
Yang, S., Lehman, L., Poilblanc, D., Van Acoleyen, K., Verstraete, F., Cirac, J.I., Schuch, N.: Edge theories in projected entangled pair state models. Phys. Rev. Lett. 112, 036402 (2014)
Yarotsky, D.A.: Ground states in relatively bounded quantum perturbations of classical lattice systems. Commun. Math. Phys. 261, 799–819 (2006)
Acknowledgments
This research was supported in part by the National Science Foundation: S.B. under Grant #DMS-0757581 and B.N. and A.Y. under Grant #DMS-1009502. A.Y. also acknowledges support from the National Science Foundation under Grant #DMS-0636297. A.Y. would also like to thank the Mathematisches Institut at Ludwig-Maximilians-Universität München and the Erwin Schrödinger International Institute for Mathematical Physics (ESI) in Vienna, Austria, where part of the work reported here was carried out. E. H gratefully acknowledges the support of a Fulbright scholarship spent at University of California, Davis.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Bachmann, S., Hamza, E., Nachtergaele, B. et al. Product Vacua and Boundary State Models in \(d\)-Dimensions. J Stat Phys 160, 636–658 (2015). https://doi.org/10.1007/s10955-015-1260-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-015-1260-7