Skip to main content
SpringerLink
Log in

A Method for Identifying Diffusive Trajectories with Stochastic Models

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

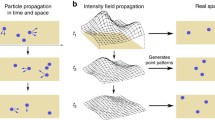
Single particle tracking is a tool that is being increasingly used to study diffusive or dispersive processes in many branches of natural science. Often the ability to collect these trajectories experimentally or produce them numerically outpaces the ability to understand them theoretically. On the other hand many stochastic models have been developed and continue to be developed capable of capturing complex diffusive behavior such as heavy tails, long-range correlations, nonstationarity, and combinations of these things. We describe a computational method for connecting particle trajectory data with stochastic models of diffusion. Several tests are performed to demonstrate the efficacy of the method, and the method is applied to polymer diffusion, RNA diffusion in E. coli, and RAFOS dispersion in the Gulf of Mexico.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Brown, R.: A brief account of microscopical observations made in the months of june, july and august 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. Philos. Mag. Ann. Chem. Math. Astron. Nat. Hist. Gen. Sci. 4(21), 161–173 (1828)

    Google Scholar 

  2. Einstein, A.: On the movement of small particles suspended in stationary liquids required by the molecular-kinetic theory of heat. Annalen der Physik 17(549–560), 16 (1905)

    Google Scholar 

  3. Ingenhousz, J.: Nouvelles Expériences et Observations sur Divers Oobjets de Physique. chez P. Théophile Barrois le jeune, Paris (1785)

    Google Scholar 

  4. Tsay, R.S.: Analysis of Financial Time Series. Wiley, Hoboken (2005)

    Book  MATH  Google Scholar 

  5. Taylor, S.J.: Modelling Financial Time Series. World Scientific Publishing, Singapore (2008)

    MATH  Google Scholar 

  6. Saxton, M.J., Jacobson, K.: Single-particle tracking: applications to membrane dynamics. Ann. Rev. Biophys. Biomol. Str. 26(1), 373–399 (1997)

    Article  Google Scholar 

  7. Golding, I., Cox, E.C.: Physical nature of bacterial cytoplasm. Phys. Rev. Lett. 96(9), 098102 (2006)

    Article  ADS  Google Scholar 

  8. Regner, B.M., Vučinić, D., Domnisoru, C., Bartol, T.M., Hetzer, M.W., Tartakovsky, D.M., Sejnowski, J.: Anomalous diffusion of single particles in cytoplasm. Biophys. J. 104(8), 1652–1660 (2013)

    Article  ADS  Google Scholar 

  9. Viswanathan, G.M., Afanasyev, V., Buldyrev, S.V., Prince, P.A., Stanley, H.E.: Levy flight search patterns in animal behavior. Nature 381, 413–415 (1996)

    Article  ADS  Google Scholar 

  10. Sims, D.W., Southall, E.J., Humphries, N.E., Hays, G.C., Bradshaw, C.J.A., Pitchford, J.W., James, A., Ahmed, M.Z., Brierley, A.S., Hindell, M.A., et al.: Scaling laws of marine predator search behaviour. Nature 451(7182), 1098–1102 (2008)

    Article  ADS  Google Scholar 

  11. Rossby, T., Dorson, D., Fontaine, J.: The rafos system. J. At. Ocean. Technol. 3(4), 672–679 (1986)

    Article  Google Scholar 

  12. Moroni, M., Cushman, J.H.: Three-dimensional particle tracking velocimetry studies of the transition from pore dispersion to fickian dispersion for homogeneous porous media. Water Resour. Res. 37(4), 873–884 (2001)

    Article  ADS  Google Scholar 

  13. Moroni, M., Cushman, J.H.: Statistical mechanics in 3d-ptv experiments in the study of anomalous dispersion: part ii experiment. Phys. Fluids 13(1), 81–91 (2001)

    Article  ADS  Google Scholar 

  14. Kantor, Y., Kardar, M.: Anomalous diffusion with absorbing boundary. Phys. Rev. E 76, 061121 (Dec 2007)

  15. Crandall, C.A., Kauffman, L.J., Katz, B.G., Metz, P.A., McBride, W.S., Berndt, M.P.: Simulations of ground-water flow and particle tracking analysis in the area contributing recharge to a public supply well near Tampa, FL. US Geol Surv Sci Invest Rep, 5231, (2008)

  16. Bijeljic, Branko, Mostaghimi, Peyman, Blunt, Martin J.: Signature of non-fickian solute transport in complex heterogeneous porous media. Phys. Rev. Lett. 107, 204502 (Nov 2011)

  17. Ono, J., Ohshima, K.I., Uchimoto, K., Ebuchi, N., Mitsudera, H., Yamaguchi, H.: Particle-tracking simulation for the drift/diffusion of spilled oils in the sea of okhotsk with a three-dimensional, high-resolution model. J. Oceanogr. 69(4), 413–428 (2013)

    Article  Google Scholar 

  18. O’Malley, D., Vesselinov, V.V.: Analytical solutions for three-dimensional reaction-advection-dispersion with anomalous dispersion. Adv. Water Resour. In Submission.

  19. Akaike, Hirotugu: A new look at the statistical model identification. Autom. Control IEEE Trans. 19(6), 716–723 (1974)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  20. Hurvich, C.M., Tsai, C.L.: Regression and time series model selection in small samples. Biometrika 76(2), 297–307 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  21. Burnham, K.P., Anderson, D.R.: Model Selection and Multi-Model Inference: A Practical Information-Theoretic Approach. Springer, Berlin (2002)

    Google Scholar 

  22. Ye, M., Meyer, P.D.: On model selection criteria in multimodel analysis. Water Resour. Res. 44(3), 07 (2008)

    Google Scholar 

  23. O’Malley, D., Cushman, J.H.: The ubiquity of, and geostatistics for, nonstationary increment random fields. Water Resour. Res. 49(7), 4525–4529 (2013)

    Article  ADS  Google Scholar 

  24. Falconer, K.: Fractal Geometry: Mathematical Foundations and Applications. Wiley, Hoboken (2007)

    Google Scholar 

  25. Gefen, Yuval, Aharony, Amnon, Alexander, Shlomo: Anomalous diffusion on percolating clusters. Phys. Rev. Lett. 50(1), 77 (1983)

    Article  ADS  Google Scholar 

  26. Bouchaud, Jean-Philippe, Georges, Antoine: Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195(4), 127–293 (1990)

    Article  ADS  MathSciNet  Google Scholar 

  27. Solomon, T.H., Weeks, E.R., Swinney, H.L.: Observation of anomalous diffusion and lévy flights in a two-dimensional rotating flow. Phys. Rev. Lett. 71(24), 3975 (1993)

    Article  ADS  Google Scholar 

  28. Tsallis, C., Bukman, D.J.: Anomalous diffusion in the presence of external forces: exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 54(3), R2197 (1996)

    Article  ADS  Google Scholar 

  29. Metzler, Ralf, Klafter, Joseph: The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Physics Rep. 339(1), 1–77 (2000)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  30. Sokolov, I.M.: Models of anomalous diffusion in crowded environments. Soft Matter 8(35), 9043–9052 (2012)

    Article  ADS  Google Scholar 

  31. Samorodnitsky, G., Taqqu, M.S.: Stable Non-Gaussian Processes. Chapman & Hall, New York (1994)

    MATH  Google Scholar 

  32. Benoit, B.: Fractional brownian motions, fractional noises and applications. SIAM Rev. 10(4), 422–437 (1986)

    Google Scholar 

  33. Kolmogorov, A.N.: Wienersche spiralen und einige andere interessante kurven im hilbertschen raum. C. R. (Doklady) Acad. Sci. URSS (N.S.) 26, 115–118 (1940)

    MathSciNet  Google Scholar 

  34. Taqqu, M.S.: Benoît mandelbrot and fractional brownian motion. Statist. Sci. 28(1), 1–5 (2013)

    Article  MathSciNet  Google Scholar 

  35. Lim, S.C., Muniandy, S.V.: Self-similar gaussian processes for modeling anomalous diffusion. Phys. Rev. E 66(2), 021114 (2002)

    Article  ADS  Google Scholar 

  36. Cushman, J.H., O’Malley, D.: Anomalous diffusion as modeled by a nonstationary extension of brownian motion. Phys. Rev. E 79(3), 032101 (2009)

    Article  ADS  Google Scholar 

  37. O’Malley, D., Cushman, J.H.: Fractional brownian motion run with a nonlinear clock. Phys. Rev. E 82(3), 032102 (2010)

    Article  ADS  Google Scholar 

  38. Nash, S.G.: Preconditioning of truncated-newton methods. SIAM J. Sci. Statist. Comput. 6(3), 599–616 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  39. Byrd, R., Lu, P., Nocedal, J., Zhu, C.: A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 16(5), 1190–1208 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  40. O’Malley, D., Cushman, J.H.: Scaling laws for fractional brownian motion with power-law clock. J. Statist. Mech.: Theory Exper. 01, L01001 (2011)

    Google Scholar 

  41. Rouse, P.E.: A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 21(7), 1272–1280 (1953)

    Article  ADS  Google Scholar 

  42. Panja, D.: Probabilistic phase space trajectory description for anomalous polymer dynamics. J. Phys. 23(10), 105103 (2011)

    Google Scholar 

  43. O’Malley, D., Cushman, J.H.: Random renormalization group operators applied to stochastic dynamics. J. Statist. Phys. 149(5), 943–950 (2012)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  44. Magdziarz, Marcin, Weron, Aleksander, Burnecki, Krzysztof, Klafter, Joseph: Fractional brownian motion versus the continuous-time random walk: a simple test for subdiffusive dynamics. Phys. Rev. lett. 103(18), 180602 (2009)

    Article  ADS  Google Scholar 

  45. O’Malley, D., Cushman, J.H., Johnson, G.: Random renormalization groups and bayesian scaling of dispersion/diffusion in lake michigan and the gulf of mexico. Geophys. Research Lett. 40(17), 4638–4642 (2013)

    Article  ADS  Google Scholar 

  46. Donohue, K., Hamilton, P., Leaman, K., Leben, R., Prater, M., Waddell, E., Watts, R.: Exploratory study of deepwater currents in the Gulf of Mexico. Technical Report MMS 2006–073, U.S. Department of the Interior, Minerals Management Service, Gulf of Mexico OCS, Region, 2006.

Download references

Acknowledgments

The authors wish to thank two anonymous reviewers for feedback that substantially improved the manuscript. DO and VVV wish to acknowledge the Environmental Programs Directorate of the Los Alamos National Laboratory; the Advanced Simulation Capability for Environmental Management (ASCEM) project, Department of Energy, Environmental Management; and the Integrated Multifaceted Approach to Mathematics at the Interfaces of Data, Models, and Decisions (DiaMonD) project, Department of Energy, Office of Science. JHC wishes to acknowledge NSF Grant \(\#\)EAR 1314828. The authors wish to thank Ido Golding and Edward C. Cox for the RNA data as well as BOEMRE for the Gulf of Mexico float data.

Author information

Authors and Affiliations

  1. Computational Earth Science, Los Alamos National Laboratory, Los Alamos, NM, USA

    D. O’Malley & V. V. Vesselinov

  2. Departments of Earth, Atmospheric and Planetary Sciences and Mathematics, Purdue University, West Lafayette, IN, USA

    J. H. Cushman

Authors
  1. D. O’Malley
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. V. Vesselinov
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. H. Cushman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. O’Malley.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

O’Malley, D., Vesselinov, V.V. & Cushman, J.H. A Method for Identifying Diffusive Trajectories with Stochastic Models. J Stat Phys 156, 896–907 (2014). https://doi.org/10.1007/s10955-014-1035-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-014-1035-6

Keywords

Search

Navigation