Skip to main content
SpringerLink
Log in

The Signed Loop Approach to the Ising Model: Foundations and Critical Point

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

The signed loop approach is a beautiful way to rigorously study the two-dimensional Ising model with no external field. In this paper, we explore the foundations of the method, including details that have so far been neglected or overlooked in the literature. We demonstrate how the method can be applied to the Ising model on the square lattice to derive explicit formal expressions for the free energy density and two-point functions in terms of sums over loops, valid all the way up to the self-dual point. As a corollary, it follows that the self-dual point is critical both for the behaviour of the free energy density, and for the decay of the two-point functions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

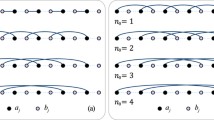
  1. A picture of the same configurations appears in [7] to point out the error in Vdovichenko’s paper; it is crucial here to take the multiplicities of the loops into account.

References

  1. Aizenman, M., Barsky, D.J., Fernández, R.: The phase transition in a general class of Ising-type models is sharp. J. Stat. Phys. 47(3–4), 343–374 (1987). MR894398 (89f:82013)

    Article  ADS  Google Scholar 

  2. Beffara, V., Duminil-Copin, H.: Smirnov’s fermionic observable away from criticality 40 (2012). arXiv:1010.0526 [math.PR]

  3. Burgoyne, P.N.: Remarks on the combinatorial approach to the Ising problem. J. Math. Phys. 4, 1320–1326 (1963). MR0155631 (27 #5565)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  4. Cimasoni, D.: A generalized Kac-Ward formula. J. Stat. Mech. Theory E (2010JUL), P07023 (2010). arXiv:1004.3158

  5. da Costa, G.A.T.F., Maciel, A.L.: Combinatorial formulation of Ising model revisited. Rev. Bras. Ensino Fis. 25(1), 49–59 (2003). arXiv:math-ph/0304033

    Article  Google Scholar 

  6. Dobrushin, R.L.: Existence of a phase transition in two-dimensional and three-dimensional Ising models. Teor. Veroâtn. Ee Primen. 10(2), 209–230 (1965). Translated as Theor. Probab. Appl. X(2), 193–213 (1965)

    MathSciNet  Google Scholar 

  7. Dolbilin, N.P., Shtan’ko, M.A., Shtogrin, M.I.: Combinatorial problems in the two-dimensional Ising model. Tr. Mat. Inst. Steklova 196, 51–65 (1991). Translated in Proc. Steklov Inst. Math. 1992 (4), 57–72. Discrete geometry and topology (Russian). MR1111292 (92i:05083)

    MathSciNet  MATH  Google Scholar 

  8. Dolbilin, N.P., Zinov’ev, Yu.M., Mishchenko, A.S., Shtan’ko, M.A., Shtogrin, M.I.: The two-dimensional Ising model and the Kac-Ward determinant. Izv. Ross. Akad. Nauk Ser. Mat. 63(4), 79–100 (1999). MR1717680 (2000j:82008)

    Article  MathSciNet  Google Scholar 

  9. Fisher, M.E.: Critical temperatures of anisotropic Ising lattices. II. General upper bounds. Phys. Rev. 162(2), 480–485 (1967)

    Article  ADS  Google Scholar 

  10. Glasser, M.L.: Exact partition function for the two-dimensional Ising model. Am. J. Phys. 38(8), 1033–1036 (1970)

    Article  MathSciNet  ADS  Google Scholar 

  11. Griffiths, R.B.: Peierls proof of spontaneous magnetization in a two-dimensional Ising ferromagnet. Phys. Rev. 136, A437–A439 (1964). MR0189681 (32 #7103)

    Article  ADS  Google Scholar 

  12. Griffiths, R.B.: Correlations in Ising ferromagnets. III. A mean-field bound for binary correlations. Commun. Math. Phys. 6(2), 121–127 (1967). MR1552524

    Article  ADS  Google Scholar 

  13. Helmuth, T.: Planar Ising model observables and non-backtracking walks (2012). arXiv:1209.3996

  14. Ising, E.: Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 31(1925FEB–APR), 253–258 (1925)

    ADS  Google Scholar 

  15. Kac, M., Ward, J.C.: A combinatorial solution of the two-dimensional Ising model. Phys. Rev. 88(6), 1332–1337 (1952)

    Article  ADS  MATH  Google Scholar 

  16. Kadanoff, L.P., Ceva, H.: Determination of an operator algebra for the two-dimensional Ising model. Phys. Rev. B 3(3), 3918–3939 (1971). MR0389111 (52 #9942)

    Article  MathSciNet  ADS  Google Scholar 

  17. Kaufman, B.: Crystal statistics. II. Partition function evaluated by spinor analysis. Phys. Rev. 76(8), 1232–1243 (1949)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  18. Kaufman, B., Onsager, L.: Crystal statistics. III. Short-range order in a binary Ising lattice. Phys. Rev. 76(8), 1244–1252 (1949)

    Article  ADS  MATH  Google Scholar 

  19. Landau, L.D., Lifshitz, E.M.: Statistical Physics, Part 1. Course of Theoretical Physics, vol. 5. Butterworth–Heinemann, Oxford (1980). Translated from the Russian by J.B. Sykes and M.J. Kearsley, 3rd edn., revised and enlarged

    Google Scholar 

  20. McCoy, B.M., Wu, T.T.: The Two-Dimensional Ising Model. Harvard University Press, Cambridge (1973)

    MATH  Google Scholar 

  21. Onsager, L.: Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. 65, 117–149 (1944). MR0010315 (5,280d)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  22. Palmer, J.: Planar Ising Correlations. Progress in Mathematical Physics, vol. 49. Birkhäuser, Boston (2007). MR2332010 (2008h:82001)

    MATH  Google Scholar 

  23. Peierls, R.: On Ising’s model of ferromagnetism. Proc. Camb. Philos. Soc. 32, 477–481 (1936)

    Article  ADS  MATH  Google Scholar 

  24. Sherman, S.: Combinatorial aspects of the Ising model for ferromagnetism. I. A conjecture of Feynman on paths and graphs. J. Math. Phys. 1, 202–217 (1960). MR0119512 (22 #10273)

    Article  MathSciNet  ADS  Google Scholar 

  25. Sherman, S.: Addendum: combinatorial aspects of the Ising model for ferromagnetism. I. A conjecture of Feynman on paths and graphs. J. Math. Phys. 4, 1213–1214 (1963). MR0156639 (27 #6560)

    Article  MathSciNet  ADS  Google Scholar 

  26. Simon, B.: The Statistical Mechanics of Lattice Gases, vol. I. Princeton Series in Physics. Princeton University Press, Princeton (1993). MR1239893 (95a:82001)

    MATH  Google Scholar 

  27. Smirnov, S.: Conformal invariance in random cluster models. I. Holomorphic fermions in the Ising model. Ann. Math. 172(2), 1435–1467 (2010). MR2680496 (2011m:60302)

    Article  MATH  Google Scholar 

  28. Vdovichenko, N.V.: A calculation of the partition function for a plane dipole lattice. Sov. Phys. JETP 20, 477–488 (1965). MR0181393 (31 #5622)

    MathSciNet  Google Scholar 

  29. Whitney, H.: On regular closed curves in the plane. Compos. Math. 4, 276–284 (1937). MR1556973

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, VU University, De Boelelaan 1081a, 1081 HV, Amsterdam, The Netherlands

    Wouter Kager, Marcin Lis & Ronald Meester

Authors
  1. Wouter Kager
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Marcin Lis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ronald Meester
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wouter Kager.

Additional information

The second author was financially supported by Vidi grant 639.032.916 of the Netherlands Organisation for Scientific Research (NWO).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kager, W., Lis, M. & Meester, R. The Signed Loop Approach to the Ising Model: Foundations and Critical Point. J Stat Phys 152, 353–387 (2013). https://doi.org/10.1007/s10955-013-0767-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-013-0767-z

Keywords

Search

Navigation