Abstract
The Ghirardi–Rimini–Weber (GRW) theory of spontaneous wave function collapse is known to provide a quantum theory without observers, in fact two different ones by using either the matter density ontology (GRWm) or the flash ontology (GRWf). Both theories are known to make predictions different from those of quantum mechanics, but the difference is so small that no decisive experiment can as yet be performed. While some testable deviations from quantum mechanics have long been known, we provide here something that has until now been missing: a formalism that succinctly summarizes the empirical predictions of GRWm and GRWf. We call it the GRW formalism. Its structure is similar to that of the quantum formalism but involves different operators. In other words, we establish the validity of a general algorithm for directly computing the testable predictions of GRWm and GRWf. We further show that some well-defined quantities cannot be measured in a GRWm or GRWf world.
Similar content being viewed by others
Notes
Here ℙ(Z∈B) denotes the probability of the event Z∈B; sets are always assumed to be measurable. The notion of “POVM” is defined in Sect. 3.1.
Some “observables” of the quantum formalism—the momentum, angular momentum, and energy operators—are the generators of symmetries of the theory, such as translation, rotation, and time translation invariance. By virtue of Noether’s theorem, then, they commute with the Hamiltonian. Since GRWm and GRWf, too, are translation, rotation, and time translation invariant (if the interaction potential is), the same self-adjoint operators occur here in the role of generators of symmetries (and commute with the Hamiltonian), even though a particular experiment that “measures,” in quantum mechanics, momentum, angular momentum, or energy may, in the GRW formalism, be associated with different operators.
But some connection with the Heisenberg picture exists indeed: keep in mind that the main theorem about POVMs concerns any experiment
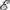 ; for example,
; for example, 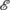 could consist of waiting for a while Δt and then “measuring position.” Then, the quantum operator associated with
could consist of waiting for a while Δt and then “measuring position.” Then, the quantum operator associated with 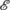 is the Heisenberg-evolved position operator,
is the Heisenberg-evolved position operator, 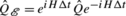 , and the reader might well expect that in GRWm or GRWf there is a different operator (in fact, a POVM) associated with
, and the reader might well expect that in GRWm or GRWf there is a different operator (in fact, a POVM) associated with 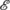 .
.However, there are reasons why every reasonable ontology suitable for the stochastic GRW wave function evolution law should lead to the same empirical predictions. Similarly, the empirical contents of CSLm, the Continuous Spontaneous Localization theory [35, 27, 5] with the matter density ontology, or with any other reasonable ontology, can presumably be summarized by a formalism very similar to the GRW formalism.
Pearle and Squires [36] have argued that λ should be chosen differently for every “particle,” with λ i proportional to the mass m i .
Note also that, in the unlikely event that many flashes occur in position 2 between t and t+Δt and thus create a discrepancy between the pointer position in GRWf and that in GRWm, the associated collapses would shrink the size of c 1 to a considerable extent; so much indeed, if the number of flashes in position 2 is sufficient, that |c 1(t+Δt)|2 is close to zero and |c 2(t+Δt)|2 close to 1; as a consequence, m(1,t+Δt)≪m(2,t+Δt). That is, even in the unlikely event of a discrepancy, the discrepancy persists only for a limited time—the time it takes the collapses centered at position 2 to make |c 1(t+Δt)|2 small.
Readers may worry that the factorization condition (42) never holds because of the symmetrization postulate: As soon as both the system and the apparatus contain electrons, the wave function has to be anti-symmetric in the electron variables q i , which conflicts with (42) if the latter is based on a splitting as in (16), grouping some variables q i together as “system variables” and others as “environment variables.” The answer is, (42) can hold nevertheless, as follows: For identical particles, the indices of the variables q 1,…,q N are mere mathematical labels, and the splitting into system and environment should not be based on these unphysical labels but instead on regions of space. Indeed, as mentioned already, if \(R_{\operatorname{sys}} \subseteq \mathbb{R}^{3}\) is a region of space such that both \(R_{\operatorname {sys}}\) and \(\mathbb{R}^{3}\setminus R_{\operatorname{sys}}\) have positive volume then
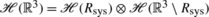 , where
, where 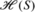 is the fermionic (or bosonic) Fock space over L
2(S). Since a fermionic wave function can be represented by a vector
is the fermionic (or bosonic) Fock space over L
2(S). Since a fermionic wave function can be represented by a vector 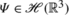 , it can indeed factorize in the splitting based on \(R_{\operatorname{sys}}\).
, it can indeed factorize in the splitting based on \(R_{\operatorname{sys}}\).From the point of view of the entire universe, from which the Hamiltonian may be regarded as fixed once and for all, the relevant choice would lie only in that of ϕ.
To see this, write ℙ(Z∈B) as 〈Ψ t |G∘ζ −1(B)|Ψ t 〉; insert (47); use 0≤G∘ζ −1(B)≤I to bound the term quadratic in ΔΨ by ∥ΔΨ∥2; use the Cauchy–Schwarz inequality and |c|<1 to bound the cross terms by 2∥ΔΨ∥; use that 1−|c|2=∥ΔΨ∥2; in total, by the triangle inequality, obtain the bound 2∥ΔΨ∥(1+∥ΔΨ∥)<3∥ΔΨ∥ provided ∥ΔΨ∥<1/2.
This assumption is to be understood in an operational sense: It is assumed that we humans can read off the result when looking at the apparatus. This is different from assuming that the result can be read off from the wave function of (the system and) the apparatus, which is notoriously not the case, a fact known as the measurement problem of quantum theory.
This assumption will be relaxed in Sect. 8, where we allow that the experiment’s run-time is not fixed before the experiment.
In this situation, it can in fact be concluded directly that \(E^{\mathrm{GRW}}_{z}=E^{\mathrm {Qu}}_{z}\). Indeed, if 〈ψ n |E z |ψ n 〉=δ z,f(n) and 0≤E z ≤I then E z =∑ n:f(n)=z |ψ n 〉〈ψ n | (and thus \(E^{\mathrm{GRW}}_{z}=E_{z}=E^{\mathrm{Qu}}_{z}\)). After all, suppose an off-diagonal entry were nonzero, c:=〈ψ n |E z |ψ m 〉≠0 for n≠m, and let ψ=αψ n +βψ m with |α|2+|β|2=1; if f(n)=z=f(m) then 〈ψ|E z |ψ〉=1+2 Re(α ∗ cβ) can be made >1 by suitable choice of α,β; if f(n)≠z≠f(m) then 〈ψ|E z |ψ〉=2 Re(α ∗ cβ) can be made negative; if f(n)=z≠f(m) then 〈ψ|E z |ψ〉=|α|2+2 Re(α ∗ cβ) can be made >1 and can be made <0.
If we want to make a similar statement about time t, the appropriate density matrix to consider is not the \(\rho_{t}^{\operatorname{sys}}\) considered in the marginal master equation but rather the random density matrix \(\operatorname {tr}_{\operatorname{env}} \vert \varPsi_{t} \rangle \langle\varPsi_{t}\vert \), from which \(\rho_{t}^{\operatorname{sys}}\) is obtained by averaging over the flashes during the time interval [0,t).
To see this, consider for example Ψ(t=0)=2−1/2(|u〉|1〉+|d〉|2〉), where |u〉,|d〉 are orthonormal vectors in
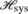 and |1〉,|2〉 in
and |1〉,|2〉 in 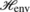 , and suppose that Ψ quickly collapses to either |u〉|1〉 or |d〉|2〉; contrast this with \(\tilde{\varPsi}(t=0) = 2^{-1/2}(\vert l \rangle \vert 1 \rangle + \vert r \rangle \vert 2 \rangle)\), where |l〉=2−1/2(|u〉+|d〉) and |r〉=2−1/2(|u〉−|d〉), and suppose that \(\tilde{\varPsi}\) quickly collapses to either |l〉|1〉 or |r〉|2〉. Then \(\rho_{\operatorname{sys}}=\frac{1}{2} \vert u \rangle \langle u\vert +\frac{1}{2} \vert d \rangle \langle d\vert =\frac {1}{2}\vert l \rangle \langle l\vert + \frac{1}{2} \vert r \rangle \langle r\vert = \tilde{\rho}_{\operatorname{sys}}\), but the \(m_{\operatorname{sys}}\) associated with |u〉 or |d〉 may be completely different from that associated with |l〉 or |r〉.
, and suppose that Ψ quickly collapses to either |u〉|1〉 or |d〉|2〉; contrast this with \(\tilde{\varPsi}(t=0) = 2^{-1/2}(\vert l \rangle \vert 1 \rangle + \vert r \rangle \vert 2 \rangle)\), where |l〉=2−1/2(|u〉+|d〉) and |r〉=2−1/2(|u〉−|d〉), and suppose that \(\tilde{\varPsi}\) quickly collapses to either |l〉|1〉 or |r〉|2〉. Then \(\rho_{\operatorname{sys}}=\frac{1}{2} \vert u \rangle \langle u\vert +\frac{1}{2} \vert d \rangle \langle d\vert =\frac {1}{2}\vert l \rangle \langle l\vert + \frac{1}{2} \vert r \rangle \langle r\vert = \tilde{\rho}_{\operatorname{sys}}\), but the \(m_{\operatorname{sys}}\) associated with |u〉 or |d〉 may be completely different from that associated with |l〉 or |r〉.The assumption that (in particular) s 2 is fixed in advance is often unrealistic, although such a situation can of course be arranged. Often, the time at which an experimenter begins the second experiment, and even which experiment to perform, will be random; it may depend on the outcome of the first experiment and on other random influences (such as the weather). This scenario is considered in Sect. 9.
Here is why such assumptions are necessary. If one of the systems “a” and “b” can be macroscopic then it makes a difference whether
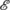 can depend only on \(\operatorname{env}\) or also on the macro-state of a or b. For example, suppose Alice and Bob carry out an EPR experiment (i.e., each performs a Stern–Gerlach experiment in the z-direction, with the two particles initially in the singlet state), “a” consists of Alice’s EPR particle, \(\operatorname{env}\) consists of Alice’s lab, “b” consists of Bob’s EPR particle and his lab, Z=ζ(Alice’s outcome), and that the choice of ζ depends on Bob’s outcome—that is where
can depend only on \(\operatorname{env}\) or also on the macro-state of a or b. For example, suppose Alice and Bob carry out an EPR experiment (i.e., each performs a Stern–Gerlach experiment in the z-direction, with the two particles initially in the singlet state), “a” consists of Alice’s EPR particle, \(\operatorname{env}\) consists of Alice’s lab, “b” consists of Bob’s EPR particle and his lab, Z=ζ(Alice’s outcome), and that the choice of ζ depends on Bob’s outcome—that is where 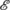 depends on b. Then it can be arranged that ℙ(Z=+1)=1 while the formalism, given
depends on b. Then it can be arranged that ℙ(Z=+1)=1 while the formalism, given 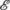 , predicts \(\mathbb{P} (Z=+1)=\frac{1}{2}=\mathbb{P}(Z=-1)\).
, predicts \(\mathbb{P} (Z=+1)=\frac{1}{2}=\mathbb{P}(Z=-1)\).Likewise, without the assumption that the choice
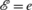 is made by the time s(e) the distribution of Z can change. For example, suppose Alice carries out 100 Stern–Gerlach experiments in the z-direction on particles in |x-up〉 and after the first +1 result declares that the last experiment was
is made by the time s(e) the distribution of Z can change. For example, suppose Alice carries out 100 Stern–Gerlach experiments in the z-direction on particles in |x-up〉 and after the first +1 result declares that the last experiment was 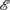 . Then ℙ(Z=+1)=1−2−100≈1 while the formalism, given
. Then ℙ(Z=+1)=1−2−100≈1 while the formalism, given 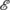 , predicts \(\mathbb{P}(Z=+1)=\frac{1}{2}=\mathbb{P}(Z=-1)\).
, predicts \(\mathbb{P}(Z=+1)=\frac{1}{2}=\mathbb{P}(Z=-1)\).The distribution of Z can also change if “a” and the apparatus are initially entangled. For example, consider again the EPR experiment and suppose that “a” consists of Alice’s EPR particle, “b” is empty, \(\operatorname{env}\) consists of Bob’s EPR particle, his lab, and Alice’s lab, Z=ζ(Alice’s outcome), and that the choice of ζ depends on Bob’s outcome. Again, it can be arranged that ℙ(Z=+1)=1.
Finally, if “a” is not isolated until s=s(e) then there is no reason to believe its density matrix at s is
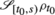 , and if “b” could interact with the apparatus then the same problem would arise as if “a” was entangled with the apparatus.
, and if “b” could interact with the apparatus then the same problem would arise as if “a” was entangled with the apparatus.Actually, it is not obvious that such an experiment is possible in GRWf. Strictly speaking, that is a gap in our argument for the possibility of obtaining probabilistic information about C [s,t). However, it seems plausible that such an experiment is possible in GRWf if it is in ordinary quantum mechanics, and there it is commonly taken for granted that every self-adjoint operator on a 2-dimensional Hilbert space (such as span{|here〉,|there〉}) is the observable for some experiment.
References
Adler, S.L.: Lower and upper bounds on CSL parameters from latent image formation and IGM heating. J. Phys. A, Math. Theor. 40, 2935–2957 (2007). arXiv:quant-ph/0605072
Allori, V., Dorato, M., Laudisa, F., Zanghì, N.: La natura delle cose, introduzione ai fondamenti e alla filosofia della fisica. Carocci, Rome (2005)
Allori, V., Goldstein, S., Tumulka, R., Zanghì, N.: On the common structure of Bohmian mechanics and the Ghirardi–Rimini–Weber theory. Br. J. Philos. Sci. 59, 353–389 (2008). arXiv:quant-ph/0603027
Allori, V., Goldstein, S., Tumulka, R., Zanghì, N.: Predictions and primitive ontology in quantum foundations: a study of examples. Br. J. Philos. Sci. (forthcoming). arXiv:1206.0019
Bassi, A., Ghirardi, G.C.: Dynamical reduction models. Phys. Rep. 379, 257–426 (2003). arXiv:quant-ph/0302164
Bassi, A., Ghirardi, G.C., Salvetti, D.G.M.: The Hilbert-space operator formalism within dynamical reduction models. J. Phys. A, Math. Theor. 40, 13755–13772 (2007). arXiv:0707.2940
Bassi, A., Salvetti, D.G.M.: The quantum theory of measurement within dynamical reduction models. J. Phys. A, Math. Theor. 40, 9859–9876 (2007). arXiv:quant-ph/0702011
Bell, J.S.: Are there quantum jumps? In: Kilmister, C.W. (ed.) Schrödinger. Centenary Celebration of a Polymath, pp. 41–52. Cambridge University Press, Cambridge (1987). Reprinted as Chap. 22 of [10]
Bell, J.S.: De Broglie–Bohm, delayed-choice double-slit experiment, and density matrix. Int. J. Quant. Chem. 14, 155–159 (1980). Reprinted as Chap. 14 of [10]
Bell, J.S.: Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press, Cambridge (1987)
Bell, J.S.: Toward an exact quantum mechanics. In: Deser, S., Finkelstein, R.J. (eds.) Themes in Contemporary Physics, vol. II, pp. 1–26. World Scientific, Teaneck (1989)
Benatti, F., Ghirardi, G.C., Grassi, R.: Describing the macroscopic world: closing the circle within the dynamical reduction program. Found. Phys. 25, 5–38 (1995)
Bohm, D.: A suggested interpretation of the quantum theory in terms of “Hidden” variables, I and II. Phys. Rev. 85, 166–193 (1952)
Choi, M.: Completely positive linear maps on complex matrices. Linear Algebra Appl. 10, 285–290 (1975)
Colin, S., Durt, T., Tumulka, R.: On superselection rules in Bohm–Bell theories. J. Phys. A, Math. Gen. 39, 15403–15419 (2006). arXiv:quant-ph/0509177
Cowan, C.W., Tumulka, R.: Epistemology of wave function collapse in quantum physics. In preparation
Davies, E.B.: Quantum Theory of Open Systems. Academic Press, San Diego (1976)
Dowker, F., Henson, J.: Spontaneous collapse models on a lattice. J. Stat. Phys. 115, 1327–1339 (2004). arXiv:quant-ph/0209051
Dowker, F., Herbauts, I.: Simulating causal wave-function collapse models. Class. Quantum Gravity 21, 1–17 (2004). arXiv:quant-ph/0401075
Dowker, F., Herbauts, I.: The status of the wave function in dynamical collapse models. Found. Phys. Lett. 18, 499–518 (2005). arXiv:quant-ph/0411050
Dürr, D., Goldstein, S., Teufel, S., Zanghì, N.: Scattering theory from microscopic first principles. Physica A 279, 416–431 (2000). arXiv:quant-ph/0001032
Dürr, D., Goldstein, S., Tumulka, R., Zanghì, N.: On the role of density matrices in Bohmian mechanics. Found. Phys. 35, 449–467 (2005). arXiv:quant-ph/0311127
Dürr, D., Goldstein, S., Zanghì, N.: Quantum equilibrium and the origin of absolute uncertainty. J. Stat. Phys. 67, 843–907 (1992). arXiv:quant-ph/0308039
Dürr, D., Goldstein, S., Zanghì, N.: Quantum equilibrium and the role of operators as observables in quantum theory. J. Stat. Phys. 116, 959–1055 (2004). arXiv:quant-ph/0308038
Dürr, D., Goldstein, S., Zanghì, N.: On the weak measurement of velocity in Bohmian mechanics. J. Stat. Phys. 134, 1023–1032 (2009). arXiv:0808.3324
Feldmann, W., Tumulka, R.: Parameter diagrams of the GRW and CSL theories of wave function collapse. J. Phys. A, Math. Theor. 45, 065304 (2012). arXiv:1109.6579
Ghirardi, G.C., Pearle, P., Rimini, A.: Markov processes in Hilbert space and continuous spontaneous localization of systems of identical particles. Phys. Rev. A (3) 42, 78–89 (1990)
Ghirardi, G.C., Rimini, A., Weber, T.: Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D, Part. Fields 34, 470–491 (1986)
Goldstein, S.: Quantum theory without observers. Physics Today, Part One, March 1998, 42–46. Part Two: April 1998, 38–42
Goldstein, S., Taylor, J., Tumulka, R., Zanghì, N.: Are all particles real? Stud. Hist. Philos. Mod. Phys. 36, 103–112 (2005). arXiv:quant-ph/0404134
Jones, G., Pearle, P., Ring, J.: Consequence for wavefunction collapse model of the Sudbury neutrino observatory experiment. Found. Phys. 34, 1467–1474 (2004). arXiv:quant-ph/0411019
Kent, A.: “Quantum jumps” and indistinguishability. Mod. Phys. Lett. A 4(19), 1839–1845 (1989)
Kraus, K.: States, Effects, and Operations. Springer, Berlin (1983)
Maudlin, T.: Non-local correlations in quantum theory: some ways the trick might be done. In: Craig, W.L., Smith, Q. (eds.) Einstein, Relativity, and Absolute Simultaneity. Routledge, London (2008)
Pearle, P.: Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 39, 2277–2289 (1989)
Pearle, P., Squires, E.: Bound state excitation, nucleon decay experiments and models of wave function collapse. Phys. Rev. Lett. 73, 1–5 (1994)
Penrose, R.: Wavefunction collapse as a real gravitational effect. In: Fokas, A., Kibble, T.W.B., Grigoriou, A., Zegarlinski, B. (eds.) Mathematical Physics 2000, pp. 266–282. Imperial College Press, London (2000)
Penrose, R.: The Road to Reality. Random House, London (2004)
Penrose, R., Rindler, W.: Spinors and Space-Time. Two-Spinor Calculus and Relativistic Fields, vol. I. Cambridge University Press, Cambridge (1984)
Rae, A.I.M.: Can GRW theory be tested by experiments on SQUIDS? J. Phys. A, Math. Gen. 23, L57–L60 (1990)
Tumulka, R.: A relativistic version of the Ghirardi–Rimini–Weber model. J. Stat. Phys. 125, 821–840 (2006). arXiv:quant-ph/0406094
Tumulka, R.: Collapse and relativity. In: Bassi, A., Dürr, D., Weber, T., Zanghì, N. (eds.) Quantum Mechanics: Are There Quantum Jumps? And On the Present Status of Quantum Mechanics. AIP Conference Proceedings, vol. 844, pp. 340–352. Am. Inst. Phys., New York (2006). arXiv:quant-ph/0602208
Tumulka, R.: On spontaneous wave function collapse and quantum field theory. Proc. R. Soc. A, Math. Phys. Eng. Sci. 462, 1897–1908 (2006). arXiv:quant-ph/0508230
Tumulka, R.: A Kolmogorov extension theorem for POVMs. Lett. Math. Phys. 84, 41–46 (2008). arXiv:0710.3605
Tumulka, R.: The point processes of the GRW theory of wave function collapse. Rev. Math. Phys. 21, 155–227 (2009). arXiv:0711.0035
Vacchini, B.: On the precise connection between the GRW master equation and master equations for the description of decoherence. J. Phys. A, Math. Theor. 40, 2463–2473 (2007)
Acknowledgements
We thank David Albert (Columbia University), Detlef Dürr (LMU München), Tim Maudlin (New York University), Daniel Victor Tausk (São Paulo), and Bassano Vacchini (Milano) for helpful discussions. S. Goldstein is supported in part by NSF Grant DMS-0504504. R. Tumulka is supported in part by NSF Grant SES-0957568 and by the Trustees Research Fellowship Program at Rutgers, the State University of New Jersey. N. Zanghì is supported in part by INFN.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Proof of the Conditional Probability Formula (40)
Note first that, for t<∞,
and
the identity operator. As a consequence,




with Ψ s =L [0,s)(f [0,s))Ψ 0/∥L [0,s)(f [0,s))Ψ 0∥.
This proves the conditional probability formula for t<∞. The one for t=∞ follows from the one for finite t because in the σ-algebra of Ω [s,∞), the family \(\mathcal {A}_{\mathrm{finite}}\) of events depending only on a finite amount of time form a ∩-stable generator, and thus the two measures \(\mathbb{P}_{\varPsi_{0}} (F_{[s,\infty)}\in\cdot |F_{[0,s )}=f_{[0,s )} )\) and \(\mathbb{P}_{\varPsi_{s}} (F_{[s,\infty)}\in\cdot )\) coincide since they coincide on \(\mathcal{A}_{\mathrm{finite}}\).
Appendix B: Check of Compatibility Conditions (56), (74), (158), and (165)
We provide the proofs of the equations expressing the compatibility property between the POVM E(⋅) and the superoperator  as defined in the various versions of the law of operators. We often use the following mathematical fact: If
as defined in the various versions of the law of operators. We often use the following mathematical fact: If  , S
a
is an operator on
, S
a
is an operator on  , and T
a∪b
is an operator on
, and T
a∪b
is an operator on  then
then
where \(\operatorname {tr}_{b}\) denotes the partial trace; the mirror image of (191) holds as well,
To check the compatibility property (56) between (70) and (71), note that





where \(\operatorname {tr}\) always means the trace, sometimes on  and sometimes on
and sometimes on  .
.
To check the compatibility property (74) between (76) and (78), note that



To check the compatibility condition between (158) and (159), note that




To check the compatibility condition (165) between (168) and (169), note that



Appendix C: Proof of the Marginal Probability Formula (115)
As a consequence of the factorization formula (81),
where \(G_{\operatorname{sys}}\) (respectively \(G_{\operatorname{env}}\)) is the POVM that would govern the system (respectively the environment) if it were alone in the universe. (In particular, the marginal of \(G_{\operatorname{sys}}\) for the first n flashes is given by
in parallel to (35).) From (208) we obtain the marginal probability formula:



with \(\rho_{\operatorname{sys}}= \operatorname {tr}_{\operatorname{env}} \vert \varPsi_{0} \rangle \langle\varPsi_{0}\vert \).
Appendix D: Proof of the Marginal Master Equation (123)
We now provide a proof of the fact, described around (124), that for two non-interacting but entangled systems a and b, also the reduced density matrix of system a evolves according to the appropriate version of the master equation (1). This follows from two ingredients: the factorization formula (82) and the fact that the solution to the master equation (1) can be expressed in terms of the L operators as
see (111). Now it follows, using f=f a ∪f b , that





which means that the reduced density matrix \(\rho_{t}^{a}\) satisfies the appropriate version of the master equation (1).
Appendix E: Proof of (172)
Indeed,



[by (173)]

[by (82)]

[carry out \(\operatorname {tr}_{\operatorname{env}}\)]

[by (111)]

[by (126)]



and since  is trace-preserving, the normalization factor \(\mathcal{N}''\) must be 1. This completes the proof of (172).
is trace-preserving, the normalization factor \(\mathcal{N}''\) must be 1. This completes the proof of (172).
Appendix F: Diagram Notation
The kind of calculations relevant to the derivation of the GRW formalism involve combinations of superoperators, some of which act on several systems, as well as the operations of tensor product and partial trace. When such calculations become more complicated, the standard notation often becomes hard to follow, as exemplified by the direct calculation in Sect. F.3 below of the joint distribution of the outcomes of two consecutive experiments. Here we introduce a diagram notation that is better suited than standard notation for this type of calculation because the terms involved can be arranged more clearly in two dimensions (as in a diagram) than in one (as in standard notation). Of the two dimensions, one represents time and the other is used for listing several systems (such as a, b, \(\operatorname{app}_{1}\), \(\operatorname{app}_{2}\), etc.). This notation is based on a similar diagram notation developed by Penrose and Rindler [39] for the tensors of general relativity.
6.1 F.1 Diagrams for Superoperators
Each diagram represents either a completely positive superoperator or a non-normalized density matrix (i.e., a positive trace-class operator). The composition  of two superoperators is represented by drawing the diagram of
of two superoperators is represented by drawing the diagram of  below that of
below that of  and drawing a line connecting the two. To this end, the diagrams have outward lines (“legs”) on top and at the bottom. For example, the following symbols can represent superoperators
and drawing a line connecting the two. To this end, the diagrams have outward lines (“legs”) on top and at the bottom. For example, the following symbols can represent superoperators  on
on  :
:

and their composition is

The symbol of a (possibly non-normalized) density matrix on  has only a leg at the bottom, e.g.,
has only a leg at the bottom, e.g.,

To apply the superoperator  to the density matrix ρ, we write the symbol of
to the density matrix ρ, we write the symbol of  below that of ρ and connect the outward lines:
below that of ρ and connect the outward lines:

To take the trace of an operator, we add a bullet  to its bottom leg, e.g.,
to its bottom leg, e.g.,

A diagram without legs, such as the right hand side of (233), represents a (non-negative) number. (It could be regarded as a completely positive superoperator on ℂ, just as a density matrix could be regarded as a completely positive superoperator from ℂ to  , i.e.,
, i.e.,  .)
.)
A superoperator on  has two upper and two lower legs, one for
has two upper and two lower legs, one for  and one for
and one for  , e.g.,
, e.g.,

The symbol of a density matrix ρ
12 on  has only two lower legs, as in
has only two lower legs, as in  . The partial trace is represented by
. The partial trace is represented by

The tensor product of two superoperators,  , is denoted by drawing the symbol of
, is denoted by drawing the symbol of  next to that of
next to that of  :
:

Since  , it is unambiguous which superoperator on
, it is unambiguous which superoperator on  the diagram
the diagram

represents. The identity superoperator I, I(ρ)=ρ, is represented by just a straight vertical line | so that legs can be extended arbitrarily.
The legs of a diagram can be thought of as representing indices of a matrix representation of a superoperator relative to a basis of the trace class (of each relevant Hilbert space). For example, let  be a basis of
be a basis of  and
and  a basis of
a basis of  . Then a density operator
. Then a density operator  can be expanded in the appropriate basis,
can be expanded in the appropriate basis,
and thus expressed by the coefficients \(\rho^{\alpha_{1}}\). The index α
1 corresponds to the leg of the diagram  for ρ. (Note though, that an upper index corresponds to a lower leg. This is because it is common, particularly in relativity theory, to write the index of an expansion coefficient as an upper index, while our convention about lower legs makes sure that, in a chain of superoperators such as in (230), the superoperators get executed from top to bottom.)
for ρ. (Note though, that an upper index corresponds to a lower leg. This is because it is common, particularly in relativity theory, to write the index of an expansion coefficient as an upper index, while our convention about lower legs makes sure that, in a chain of superoperators such as in (230), the superoperators get executed from top to bottom.)
A superoperator  can be represented by a matrix
can be represented by a matrix  according to
according to

The upper leg of the symbol for  corresponds to the index α
1, the lower leg to β
1, and connecting two legs as in (230) to summing over the corresponding index as in
corresponds to the index α
1, the lower leg to β
1, and connecting two legs as in (230) to summing over the corresponding index as in

The coefficients of a superoperator on  are of the form
are of the form  corresponding to four legs, and the coefficients of a density operator on
corresponding to four legs, and the coefficients of a density operator on  are of the form \(\rho^{\alpha _{1}\alpha _{2}}\), corresponding to two legs. The trace (or partial trace) symbol
are of the form \(\rho^{\alpha _{1}\alpha _{2}}\), corresponding to two legs. The trace (or partial trace) symbol  corresponds to the sequence of coefficients \(\operatorname {tr}B^{(1)}_{\alpha _{1}}\) or \(\operatorname {tr}B^{(2)}_{\alpha_{2}}\), whichever is appropriate.
corresponds to the sequence of coefficients \(\operatorname {tr}B^{(1)}_{\alpha _{1}}\) or \(\operatorname {tr}B^{(2)}_{\alpha_{2}}\), whichever is appropriate.
6.2 F.2 Diagram Notation Applied to GRW Theories
In GRW theories, the time evolution of the density matrix from t
1 to t
2 is given by a completely positive superoperator  , for which we introduce the symbol
, for which we introduce the symbol

Correspondingly, for the time evolution of two or three systems together we write  or
or  . The fact that
. The fact that  is trace-preserving can be expressed as follows:
is trace-preserving can be expressed as follows:

For two mutually isolated systems,

That is,  for both systems is the tensor product of one such superoperator for each system. Note that in (242), the two symbols
for both systems is the tensor product of one such superoperator for each system. Note that in (242), the two symbols  may actually represent two different superoperators; we take the symbol
may actually represent two different superoperators; we take the symbol  always to mean the “appropriate” time evolution superoperator. From (241) and (242), we immediately obtain the marginal master equation: for two mutually isolated systems,
always to mean the “appropriate” time evolution superoperator. From (241) and (242), we immediately obtain the marginal master equation: for two mutually isolated systems,

Another superoperator that comes up frequently is

where \(A\subseteq\varOmega=\varOmega_{[t_{1},t_{2})}\) is a set of flash histories. We observe the general fact that

The distribution of flashes can be expressed as follows:

Moreover, for two mutually isolated systems,

With the notation

the GRW formalism implies that

and the GRW law of operators says that

6.3 F.3 Example: Two Consecutive Experiments
As an example for the use of the diagram notation, we carry out the calculation that yields the formula (137) for the joint distribution of the outcomes of two consecutive experiments  on the same system a. This calculation amounts more or less to another derivation of the third rule of the GRW formalism.
on the same system a. This calculation amounts more or less to another derivation of the third rule of the GRW formalism.
In the diagrams that follow, the columns correspond to different systems (such as system a, system b, the apparatus), and different rows correspond to different times (with the time axis pointing downward).

[the “env” column is equal to 1, and using that b 1 is isolated from \(a\cup\operatorname{app}_{1}\cup\operatorname{app}_{2}\)]

[introducing the abbreviation  ]
]

[changing the order of the columns]

[using that \(\operatorname{app}_{1}\) is isolated from \(a\cup \operatorname{app}_{2}\) after t 1]

which is what we wanted to show, as it agrees with (137).
Rights and permissions
About this article
Cite this article
Goldstein, S., Tumulka, R. & Zanghì, N. The Quantum Formalism and the GRW Formalism. J Stat Phys 149, 142–201 (2012). https://doi.org/10.1007/s10955-012-0587-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-012-0587-6
Keywords
- Quantum theory without observers
- Ghirardi–Rimini–Weber (GRW) theory of spontaneous wave function collapse
- Empirical predictions
- Quantum measurement theory
- Predicted deviations from quantum mechanics
- Primitive ontology
- Limitations to knowledge
- Positive-operator-valued measure (POVM)
- Completely positive superoperator




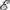 ; for example,
; for example, 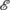 could consist of waiting for a while Δt and then “measuring position.” Then, the quantum operator associated with
could consist of waiting for a while Δt and then “measuring position.” Then, the quantum operator associated with 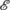 is the Heisenberg-evolved position operator,
is the Heisenberg-evolved position operator, 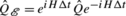 , and the reader might well expect that in GRWm or GRWf there is a different operator (in fact, a POVM) associated with
, and the reader might well expect that in GRWm or GRWf there is a different operator (in fact, a POVM) associated with 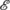 .
.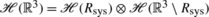 , where
, where 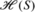 is the fermionic (or bosonic) Fock space over L
2(S). Since a fermionic wave function can be represented by a vector
is the fermionic (or bosonic) Fock space over L
2(S). Since a fermionic wave function can be represented by a vector 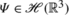 , it can indeed factorize in the splitting based on
, it can indeed factorize in the splitting based on 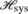 and |1〉,|2〉 in
and |1〉,|2〉 in 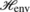 , and suppose that Ψ quickly collapses to either |u〉|1〉 or |d〉|2〉; contrast this with
, and suppose that Ψ quickly collapses to either |u〉|1〉 or |d〉|2〉; contrast this with 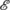 can depend only on
can depend only on 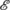 depends on b. Then it can be arranged that ℙ(Z=+1)=1 while the formalism, given
depends on b. Then it can be arranged that ℙ(Z=+1)=1 while the formalism, given 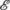 , predicts
, predicts 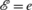 is made by the time s(e) the distribution of Z can change. For example, suppose Alice carries out 100 Stern–Gerlach experiments in the z-direction on particles in |x-up〉 and after the first +1 result declares that the last experiment was
is made by the time s(e) the distribution of Z can change. For example, suppose Alice carries out 100 Stern–Gerlach experiments in the z-direction on particles in |x-up〉 and after the first +1 result declares that the last experiment was 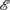 . Then ℙ(Z=+1)=1−2−100≈1 while the formalism, given
. Then ℙ(Z=+1)=1−2−100≈1 while the formalism, given 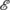 , predicts
, predicts 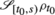 , and if “b” could interact with the apparatus then the same problem would arise as if “a” was entangled with the apparatus.
, and if “b” could interact with the apparatus then the same problem would arise as if “a” was entangled with the apparatus.