Abstract
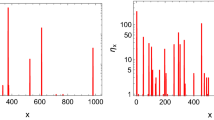
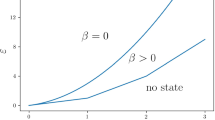
A family of m independent identically distributed random variables indexed by a chemical potential φ∈[0,γ] represents piles of particles. As φ increases to γ, the mean number of particles per site converges to a maximal density ρ c <∞. The distribution of particles conditioned on the total number of particles equal to n does not depend on φ (canonical ensemble). For fixed m, as n goes to infinity the canonical ensemble measure behave as follows: removing the site with the maximal number of particles, the distribution of particles in the remaining sites converges to the grand canonical measure with density ρ c ; the remaining particles concentrate (condensate) on a single site.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Evans, M.R.: Phase transitions in one-dimensional nonequilibrium systems. Braz. J. Phys. 30(1), 42–47 (2000)
Evans, M.R., Hanney, T.: Nonequilibrium statistical mechanics of the zero-range process and related models. J. Phys. A 38(19), R195–R240 (2005)
Evans, M.R., Majumdar, S.N., Zia, R.K.P.: Factorized steady states in mass transport models. J. Phys. A 37(25), L275–L280 (2004)
Evans, M.R., Majumdar, S.N., Zia, R.K.P.: Canonical analysis of condensation in factorised steady states. J. Stat. Phys. 123(2), 357–390 (2006)
Godrèche, C.: Dynamics of condensation in zero-range processes. J. Phys. A 36(23), 6313–6328 (2003)
Godrèche, C., Luck, J.M.: Dynamics of the condensate in zero-range processes. J. Phys. A 38(33), 7215–7237 (2005)
Großkinsky, S., Schütz, G.M., Spohn, H.: Condensation in the zero range process: stationary and dynamical properties. J. Stat. Phys. 113(34), 389–410 (2003)
Jeon, I., March, P.: Condensation transition for zero range invariant measures. In: Stochastic models (Ottawa, 1998). CMS Conf. Proc., vol. 26, pp. 233–244. Amer. Math. Soc., Providence (2000)
Jeon, I., March, P., Pittel, B.: Size of the largest cluster under zero-range invariant measures. Ann. Probab. 28(3), 1162–1194 (2000)
Kipnis, C., Landim, C.: Scaling limits of interacting particle systems. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 320. Springer, Berlin (1999)
Majumdar, S.N., Evans, M.R., Zia, R.K.: Nature of the condensate in mass transport models. Phys. Rev. Lett. 94(18), 180–601 (2005)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ferrari, P.A., Landim, C. & Sisko, V.V. Condensation for a Fixed Number of Independent Random Variables. J Stat Phys 128, 1153–1158 (2007). https://doi.org/10.1007/s10955-007-9356-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-007-9356-3