Measurement of Critical Temperatures, Critical Pressures and Densities of Acetone–Water Solutions for Simulation

Abstract

Critical temperature, critical pressure and P–T–ρ–X data of acetone–water solutions with water mole fractions in a range of 0–60% were measured to provide fundamental data for CFD simulations. Critical temperatures were determined via observing critical opalescence in fused quartz capillary tubes. Meanwhile, critical pressures were measured by heating acetone–water solutions to its critical temperature in an autoclave. The standard deviations of critical temperature and critical pressure were 0.55 K and 0.029 MPa, respectively. The results indicate that only one phase exists during mixing of acetone with water. Moreover, P–T–ρ–X data under 15 and 20 MPa in the temperature range of 460–550 K were measured in the autoclave. The relative deviation of density was 0.32%. Volume-translated Peng-Robinson and Soave–Redlich–Kwong state equations were used to illustrate the P–V–T–X relationship of acetone–water solutions, and the Peng–Robinson state equation with an average absolute relative deviation of 1.19% between fitting and experimental densities was found more accurate.

1 Introduction

4-hydroxy-2-butanone (HB) is an important intermediate for fragrances and vitamins, which is usually synthesized by aldol condensation of acetone and formaldehyde. Depending on reaction states, HB synthesis can be performed in liquid or supercritical state. Traditional liquid-phase synthesis methods [1, 2] are performed at room temperature and pressure with NaOH, KOH and basic ionic resin as catalysts. In contrast, the supercritical synthesis of HB [3,4,5] has the advantages of no additional catalyst, less waste, fast reaction speed and high yield, which is highly competitive from the perspective of green chemistry [6].

Mei et al. [3] studied the kinetics of main reactions (formation and dehydration reactions of HB) in a tube reactor where supercritical acetone was mixed and reacted with formaldehyde solution. Meanwhile, Yang et al. [4] focused on the effects of side reactions under supercritical state. Based on their studies, the supercritical synthesis of HB was fast (formaldehyde conversion can reach 90% within 3 min). In this case, the effects of mixing of acetone with formaldehyde solution should be considered especially in industrial amplification, but relative research is limited. Due to the high reaction pressure and temperature, reaction details cannot be obtained directly through experiments or production, computational fluid dynamics (CFD) is employed for simulation studies. As the main components of the synthesis system are acetone and water, the study of the supercritical synthesis process of HB can be simplified using acetone-aqueous solution, and the physical properties of acetone–water solution are required. Therefore, critical values which can determine the phase states of acetone–water solutions and densities as functions of temperature, pressure and composition are both needed in CFD simulation.

Marshall et al. [7] measured critical temperature of acetone–water solutions with a water mole fraction of 0% to 100%. However, only three experimental points were measured at synthesis temperature between 508 and 563 K [3, 4], which are not adequate for the precise calculation of critical temperatures. Furthermore, no experimental data have been reported on critical pressure of acetone–water solution. There are more experimental density data of acetone–water solution at 0.1 MPa [8,9,10,11,12,13,14,15,16,17,18,19], but few are under high pressure [20,21,22]. Schulte et al. [20] measured the density at pressures up to 28 MPa, but the water mole fractions in their work (over 98%) was significantly higher than the water content in the actual synthetic system (around 15–30% [3, 4]). Mamedov et al. [21] and Götze et al. [22] measured densities at pressures up to 150 and 250 MPa, respectively, but the highest temperatures in their work were 433 and 348 K which were much lower than synthetic temperatures. Obviously, the experimental data of acetone–water solution under synthetic conditions need to be further studied.

In this study, critical temperature, critical pressure and P–T–ρ–X data of acetone–water solutions were measured to provide physical properties for CFD simulation. Based on literatures [3,4,5] and industrial application, the water mole fraction was set at 0–60%, and the density was measured under the pressures of 15 and 20 MPa and the temperatures lower than 563 K.

2 Materials and Methods

2.1 Chemicals

Acetone (CAS: 67-64-1, purity: 0.999) was from Sinopharm Holdings, and its purity was verified by gas chromatograph. Saccharin (CAS: 81-07-2, purity: 0.980), Anthraquinone (CAS: 84-65-1, purity: 0.980) and 4-Nitrobenic acid (CAS: 62-23-7, purity: 0.980) were from Aladdin, China. All reagents were used directly without further purification.

2.2 Critical Temperature Measurements

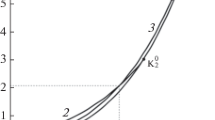
The concept of critical temperature measurement is demonstrated in Fig. 1. In a pure matter phase diagram, the transition line of gas and liquid meets at critical points where they are almost horizontal. Therefore, the point with the minimum absolute slope ($|\frac{dT}{d\rho }|$) where $\frac{{d}^{2}T}{{d\rho }^{2}}$ is equal to 0 can be identified as critical point, and the temperature is critical temperature. In addition, when temperature is close to the critical temperature, the critical opalescence [23] appears, which is another indicator for the critical temperature. For binary mixture, following the work of Scott et al. [24], the profile of critical temperature as a function of composition can be divided into 5 types. Since the critical line of acetone–water solution measured by Marshall et al. [7] was a single line, acetone–water solution is considered to be a binary mixture of the first class. Thus, the phase diagram in Fig. 1 also applies to acetone–water solutions.

Fig. 1

Description of experiment theory. T temperature, P pressure, T_c critical temperature, P_c critical pressure, ρ saturated density, ρ_c critical density, T_d experimental phase transition temperature, q solution filling ratio, q_c filling ratio at critical point

A visual method was used to determine the gas–liquid transition line (Fig. 1b). An acetone–water solution with known composition (x) was sealed in a fused quartz capillary tube (inner diameter of 300 μm, outer diameter of 665 μm and length of 2.2–2.5 cm) with a filling ratio (q = liquid length/tube length) measured at 298.15 K and 0.1 MPa (Fig. 2a). The tube was inserted horizontally and heated in a heating–cooling stage (Linkam CAP500 stage, Fig. 2b and c). By using a microscope (Nikon LV100POL), the meniscus of liquid and gas phases in the tube was observed. As the temperature of cooling-heating stage slowly increased, the meniscus became blurred, and critical opalescence appeared as the temperature and the filling ratio approached critical values. The temperature is increased slowly until a single phase occurred, at which point the temperature was denoted as T_d.

Fig. 2

Sketch of the experiment setup for critical temperature measurements. a The fused silica capillary tube with acetone–water solution. b Vertical view of the heating–cooling stage. c Cutaway view of the heating–cooling stage. S₁ the fused silica capillary tube, S₂ glass window, S₃ heating table

The preparation process of double-sealed fused silica capillary tube was illustrated as followed. Polyamide thin layer outside the fused silica capillary tube was removed by hydrogen flame. One side of the capillary tube was sealed using hydrogen flame, and the one-sealed tube was inserted vertically into a 1.5 ml centrifuge tube, which is full of ice water mixture, through the cover of the centrifuge tube. The sealed side was immersed completely into ice water mixture. Solution with known composition was injected into the one-sealed silica capillary tube using a capillary syringe. Make sure that the injected solution was apart from the unsealed side of the one-sealed silica capillary tube. Then the unsealed side of silica capillary tube was sealed using hydrogen flame. Finally, a double-sealed silica capillary tube with solution was prepared.

The density in Fig. 1a, which was the saturated density of the gas or liquid, could be calculated and replaced by the filling ratios (q) as shown in Fig. 2a through Eq. 1.

$${\rho }_{\text{single}}=\frac{{m}_{\text{solution}}}{{V}_{\text{tube}}}=\frac{{\rho }_{\text{room}}\cdot {V}_{\text{room}}}{{V}_{\text{tube}}}={\rho }_{\text{room}}\cdot \frac{\mathrm{Liquid\;length}}{\mathrm{Tube\;length}}={\rho }_{\text{room}}\cdot q$$

(1)

where ${\rho}_{\text{single}}$ was the saturated density of gas or liquid; ${m}_{\text{solution}}$ was the weight of solution in the tube; ${V}_{\text{tube}}$ was the volume of the fused silica capillary tube; ${\rho}_{\text{room}}$ was the solution density at 298.15 K and 0.1 MPa (a constant for an acetone–water solution with fixed composition); ${V}_{\text{room}}$ was the volume occupied by solution in the tube at 298.15 K and 0.1 MPa.

For the acetone–water solution with a particular composition, tubes with different filling ratios were used to obtain T_d and q values. Each data was detected at least 3 times. The transition line was obtained by polynomial fitting. The point with the lowest absolute slope of the transition line was the critical point. The corresponding T_d and q were denoted as the critical temperature and the critical filling ratio, respectively. Prior to the critical temperature measurements, saccharin, anthraquinone and 4-nitrobenzoic acid, with melting points of 503 K, 559 K, and 514 K, respectively, were chosen to correct temperature of Linkam CAP500 stage. Their melting points were measured by DSC and Linkam stage, and a temperature correction equation with an uncertainty of 0.55 K was fitted.

2.3 Critical Pressure Measurements

The critical pressure of acetone–water solutions with known composition (x) was measured by heating the solution to its critical temperature in a constant volume autoclave as shown in Fig. 3. The wall thickness of the tank (L₁) was 1.5 cm, the inner diameter of the tank (L₂) was 7 cm, the depth of the tank (L₃) was 15 cm, and the height of the tank (L₄) was 7 cm. The temperature was controlled by a thermocouple with an accuracy of 0.63 K, and the pressure was detected by a gauge with an accuracy of 0.029 MPa. The feeding pipe, the exhaust pipe and the pressure gauge were connected to the tank cover by valves. The tank volume was 543.1 ml. The weight of the solution (${m}_{\text{solution}}$) during measurements was strictly controlled according to the critical filling ratio (${q}_{\text{c}}$) and calculated by Eq. 2.

$${m}_{\text{solution}}={V}_{\text{solution}}^{0}\cdot {\rho }_{\text{solution}}^{0}={q}_{\text{c}}\cdot {V}_{\text{autoclave}}^{0}\cdot {\rho }_{\text{solution}}^{0}$$

(2)

where ${V}_{\text{solution}}^{0}\; ({\text{ml}})$ was the solution volume at 298.15 K, 0.101325 MPa; ${\rho }_{\text{solution}}^{0} ({\text{g}}\cdot {\text{ml}}^{-1})$ was the solution density at 298.15 K, 0.101325 MPa; ${V}_{\text{autoclave}}^{0} ({\text{ml}})$ was the volume of the autoclave at 298.15 K and 0.101325 MPa. The densities (${\rho }_{\text{solution}}^{0}$) of acetone–water solutions with different composition were measured by densimeters whose accuracy was 0.001 g·ml⁻¹.

Fig. 3

Schematic diagram of the autoclave used for critical pressure measurement

2.4 P–T–ρ–X Data Measurements

All P–T–ρ–X data were measured in the autoclave as shown in Fig. 3. A solution with known weight (m_solution) and composition (x) was filled into the autoclave and heated until the pressure reached 15 or 20 MPa. Furthermore, densities (${\rho }_{\text{solution}}$) under measurement conditions were calculated by Eq. 3. Thermal expansion of the tank was considered, and its effect was calculated by Eq. 4–5.

$${\rho }_{\text{solution}}=\frac{{m}_{\text{solution}}}{{V}_{\text{solution}}}=\frac{{m}_{\text{solution}}}{{V}_{\text{tank}}}$$

(3)

$${V}_{\text{tank}}={V}^{0}\cdot \beta$$

(4)

$$\beta ={(1+\alpha \cdot ({T}_{\text{solution}}-273.15))}^{3}$$

(5)

where ${V}_{\text{solution}} ({\mathrm{m}}^{3})$ was the solution volume under measurement conditions; ${V}_{\text{tank}} ({\mathrm{m}}^{3})$ was the volume of the autoclave under measurement conditions; $\beta$ was the thermal expansion coefficient of the body; $\alpha$ was the thermal expansion coefficient of 304 stainless steel $(\mathrm{i}.\mathrm{e}., 18.4\times {10}^{-6}/ \mathrm{K})$.

3 Results and Discussion

3.1 Critical Temperatures and Pressures

Figure 4 shows the experimental phase diagram of acetone–water solutions with various compositions, in which the T_d−q data was fitted by a quartic polynomial. Similar to the theory, the transition lines present upward convex trends. Note that there is always a temperature stage in each diagram, which make it easy to the critical temperature. Meanwhile, critical opalescence was observed during measurement when the temperature was close to the critical temperature.

Fig. 4

Gas–liquid T_d−q transition lines (T_d−q) for acetone–water solutions with the water mole fraction of a 0%, b 14.5%, c 26.4%, d 36.3%, e 44.6%, f 50.2%, g 57.8% and h 63.3%. T_d the temperature at which the gas–liquid meniscus completely disappeared, q filling ratio, Black point experimental points, Red line the fitted quartic polynomial line. The standard deviations were u(T_c^m) = 0.55 K, u(P_c^m) = 0.029 MPa and u(q) = 0.0012 (Color figure online)

The critical point was obtained by taking the derivative of the quartic polynomial. Table 1 presents the critical temperature (T_c^m), critical pressure (P_c^m), and corresponding filling ratio (q). It is clear that the acetone–water solution with 0–60% water mole fraction is in liquid or supercritical state under the synthesis conditions (523–563 K, 15–20 MPa), indicating that there is possibly only one phase existing during the mixing of acetone with water.

Table 1 Critical temperatures, critical pressures and corresponding filling ratios for acetone–water solutions with the water mole fractions ranging from 0 to 60%

Furthermore, the critical temperature (T_c^m) and the critical pressure (P_c^m) as functions of water mole fractions (x) are presented in Fig. 5 and Eqs. 6, 7, and the average relative deviations between experimental and fitting data for T_c^m and P_c^m were 0.043 and 0.32%, respectively. Similar to the work of Marshall et al. [7], the critical line is concave. Critical temperature and pressure are more sensitive to composition (x) when water mole fraction is bigger.

Fig. 5

Critical temperatures (T_c^m) and critical pressures (P_c^m) at various water mole fraction (x). Black points represented experimental data and red line represented fitted polynomials (Color figure online)

$${{T}_{\text{c}}}^{\text{m}}=93.56175\cdot {x}^{2}+16.3972\cdot x+508.3 \mathrm{K}$$

(6)

$${{P}_{\text{c}}}^{\text{m}}=8.41235\cdot {x}^{2}+1.51019\cdot x+4.75 \mathrm{MPa}$$

(7)

Critical temperatures in this work are compared with those in the literature [7, 25], as shown in Table 2. The discrepancy in T_c^m is less than 1 K. The difference between the critical pressure of pure acetone in literature [25] (4.70 MPa) and that in this work (4.75 MPa calculated from Eq. 7) is 0.05 MPa. These excellent agreements are a clear demonstration of the reliability of present work.

Table 2 Critical temperatures from present work and literatures

3.2 P–T–ρ–X Data

3.2.1 Verification of Density Measurements

Density of pure acetone and pure water are measured and compared with those calculated from literature [26, 27] (Table 3). The standard deviations of temperature, pressure and density are 0.63 K, 0.029 MPa and 0.3 kg·m⁻³, respectively. The relative deviation $(\left|\Delta \rho /{\rho }_{\text{ref}}\right|)$ is visualized in Fig. 6. Considering experimental safety, the maximum filling ratio of autoclave was 80–90%. As a result, the minimum temperatures were limited to 460–470 K. The average relative deviations for acetone at 15 and 20 MPa are 0.26 and 0.14%, respectively, and those of water are 0.55 and 0.33%, respectively. The relative deviations of both water and acetone are within 1% under operation conditions, which is a strong indicator of accuracy and reliability.

Table 3 Comparison of pure water and acetone densities between this work and literatures

Fig. 6

Relative deviations for pure acetone (A) and pure water (B)

3.2.2 Data of Acetone–Water Solution

Table 4 presents P–T–ρ–X data of acetone–water solution, and Fig. 7 shows the change trends. Usually, solution densities trend to decline rapidly when the solution temperature is close to the critical value, and the increase of relative pressure P_r (P_r = P_solution/P_c) can alleviate or even eliminate this change. Based on work in 3.1, the relative pressure of acetone-aqueous solution with 60% water mole fraction at 15 MPa is the minimum (1.73), which leads to a unique decreasing trend near its critical temperature (551.8 K), which also indicates that the measured critical values are compatible with P–T–ρ–X data.

Table 4 P–T–ρ–X data of acetone–water solutions

Fig. 7

Densities of acetone–water solutions of various water mole fractions at 15 MPa (A) and 20 MPa (B)^a. a The points were experimental data and the lines were simulated data

4 Data Fitting

In this paper, the P–V–T–X relation of acetone-aqueous solution is described by cubic equation of state. Prior to the simulation, the experimental mole volumes of pure substances and mixture were calculated using the density data and Eq. 8.

$${V}_{\text{exp}}=\frac{\left(1-x\right)\cdot {M}_{\text{a}}+x\cdot {M}_{\text{w}}}{1000\cdot {\rho }_{\text{solution}}}$$

(8)

where ${V}_{\text{exp}}$(m³·mol⁻¹) was the experimental mole volume of solution; x was the water mole fraction; M_a (g) and M_w (g) were the molecular mass of acetone and water, respectively; ${\rho }_{\text{solution}}$ (kg·m⁻³) was the solution density.

In this study, the solutions were in liquid or supercritical state since the measured pressures were higher than critical ones. Common two-parameter cubic equation of state, such as Soave–Redlich–Kwong (SRK) [28] and Peng–Robinson (PR) [29], appeared reasonable in gas and saturated regions but poor in the liquid region. Consequently, volume-translation equations of state (VT EOS) [30,31,32,33,34,35,36] were developed to compensate for these problems. Abudour et al. [25, 36] proposed a volume-translation Peng-Robinson equation of state (VTPR EOS) by which the P–V–T relationships of acetone, water, and acetone–water solutions (in the saturated and liquid regions) could be accurately predicted. Chen et al. [35] proposed a volume-translation Soave–Redlich–Kwong equation of state (VTSRK EOS) to make more accurate predictions for pure acetone and water. Thus, both VTPR EOSs and VTSRK EOSs was used to predict the P–V–T–X relationships of acetone, water, and acetone–water solutions in this work.

4.1 Fitting Results of Pure Substances

The detailed expressions of VTPR and VTSRK EOSs were presented below.

For the VTPR EOS of pure substances [25]:

$$P = \frac{{R - T}}{{V^{{\text{PR}}} - b^{{\text{PR}}} }} - \frac{{a^{{\text{PR}}} }}{{V^{{\text{PR}}} \cdot \left( {V^{{\text{PR}}} + b^{{\text{PR}}} } \right) + V^{{\text{PR}}} \cdot \left( {V^{{\text{PR}}} - b^{{\text{PR}}} } \right)}}$$

(9)

$$a^{{\text{PR}}} = 0.457535 \cdot \alpha \left( t \right)^{{\text{PR}}} \cdot \frac{{R^{2} T_{\text{c}}^{2} }}{{P_{\text{c}} }}$$

(10)

$$b^{{\text{PR}}} = \frac{{0.077796 \cdot R \cdot T_{\text{c}} }}{{P_{\text{c}} }}$$

(11)

$$\alpha \left( t \right)^{{\text{PR}}} = ~\exp ~\left\{ {\left( {2 + 0.836T_{\text{r}} } \right) \cdot \left( {1 - T_{\text{r}} ^{{0.134 + 0.508\omega - 0.0467\omega ^{2} }} } \right)} \right\}$$

(12)

$${{V}_{\text{VT}}}={{V}^{\text{PR}}}+{{C}_{\text{T}}^{\text{VTPR}}}$$

(13)

$${{C}_{\text{T}}}^{\text{VTPR}}=\left(\frac{R{T}_{\text{c}}}{{P}_{\text{c}}}\right)\left({C}^{\text{VTPR}}-\left(0.004+{C}^{\text{VTPR}}\right)\mathit{exp}\left(-2{d}^{\text{VTPR}}\right)\right)$$

$$-{{\delta }_{\text{c}}}^{\text{VTPR}}\cdot 0.35/(0.35+{d}^{\text{VTPR}})$$

(14)

$${{\delta }_{\text{c}}}^{\text{VTPR}}=\frac{R{T}_{\text{C}}}{{P}_{\text{C}}}(0.3074-{Z}_{\text{c}})$$

(15)

$${d}^{\text{VTPR}}=\frac{1}{R{T}_{\text{c}}}{\left(\frac{\partial P}{\partial \rho }\right)}_{\text{PR}}$$

(16)

For the VTSRK EOS of pure substances [35]:

$$P = \frac{{R \cdot T}}{{V^{{\text{SRK}}} - b^{{\text{SRK}}} }} - \frac{{a^{{\text{SRK}}} }}{{V^{{\text{SRK}}} \cdot \left( {V^{{\text{SRK}}} + b^{{\text{SRK}}} } \right)}}$$

(17)

$$a^{{\text{SRK}}} = 0.42748 \cdot \alpha \left( t \right)^{{\text{SRK}}} \cdot \frac{{R^{2} T_{\text{c}}^{2} }}{{P_{\text{c}} }}$$

(18)

$$b^{{\text{SRK}}} = \frac{{0.08664 \cdot R \cdot T_{\text{c}} }}{{P_{\text{c}} }}$$

(19)

$${\alpha (t)}^{\text{SRK}}\text{=}{{T}_{\text{r}}}^{2({\text{M}}-1)}\cdot exp\left[L\cdot (1-{T}_{\text{r}}^{2{\text{M}}})\right]$$

(20)

$$M=0.1709\cdot {\omega }^{2}-0.2063\cdot \omega +0.8787$$

(21)

$$L=0.0611\cdot {\omega }^{2}+0.7535\cdot \omega +0.1359$$

(22)

$${{V}_\text{VT}={V}^{\text{SRK}}}+{{C}_{\text{T}}}^{\text{VTSRK}}$$

(23)

$${{C}_{\text{T}}}^{\text{VTSRK}}=-{{C}_{1}}^{\text{VTSRK}}\cdot \left(\frac{R{T}_{\text{c}}}{{P}_{\text{c}}}\right)-{{\delta }_{\text{c}}}^{\text{VTSRK}}/({{C}_{2}}^{\text{VTSRK}}+{{C}_{3}}^{\text{VTSRK}}\cdot {d}^{\text{VTSRK}})$$

(24)

$${{\delta }_{\text{c}}}^{\text{VTSRK}}=\frac{R{T}_{\text{C}}}{{P}_{\text{C}}}(1/3-{Z}_{\text{c}})$$

(25)

$${d}^{\text{VTSRK}}=\frac{1}{R{T}_{\text{c}}}{\left(\frac{\partial P}{\partial \rho }\right)}_{\text{SRK}}$$

(26)

In the expressions above, P was the pressure (Pa) and T was the temperature (K); ${V}_{\text{PR}}$ and ${V}_{\text{SRK}}$ were the mole volume (m³·mol⁻¹) calculated by PR EOS and SRK EOS, respectively; R was the ideal gas constant (8.314); ${a}_{\text{PR}}$, ${b}_{\text{PR}}$, ${a}_{\text{SRK}}$ and ${b}_{\text{SRK}}$ were the parameters of PR EOS and SRK EOS; ${P}_{\text{c}}$ and ${T}_{\text{c}}$ were the critical pressure and the critical temperature of pure substance respectively; $\omega$ was the acentric factor; ${{C}_{\text{T}}}^{\text{VTPR}} \mathrm{and} \; {{C}_{\text{T}}}^{\text{VTSRK}}$ were the volume-translation term of PR EOS and SRK EOS, respectively; ${C}^{\text{VTPR}}$ and ${{C}_{1}}^{\text{VTSRK}}$, ${{C}_{2}}^{\text{VTSRK}}$, ${{C}_{3}}^{\text{VTSRK}}$ were the volume-translation parameters (VTP) of VTPR EOS and VTSRK EOS, respectively; Z_c was the critical compression factor of pure substance. The properties of pure water and acetone needed in volume-translation equation of state are listed in Table 5. These data were taken from the literature [25].

Table 5 Critical values of pure acetone and water^a

P–T–ρ–X data for pure acetone and pure water in Table 3 were used to regress the volume-translation parameters (VTP) of VTPR EOS and VTSRK EOS using the nlinfit function in Matlab. Table 6 presents VTPs of both water and acetone. Table 7 presents the fitting results (AARD and max |RD|) of VTPR EOS and VTSRK EOS. Relative deviations (RD) and the absolute average relative deviations (AARD) were calculated by Eqs. 27, 28.

$$RD=({V}_{\text{sim}}-{V}_{\text{exp}})/{V}_{\text{exp}}$$

(27)

$$AARD=(\sum_{n}\left|({V}_{\text{sim}}-{V}_{\text{exp}})/{V}_{\text{exp}}\right|)/n$$

(28)

where ${V}_{\text{sim}}$ was the mole volume calculated from equations of state; ${V}_{\text{exp}}$ was the mole volume calculated from experimental data; n was the total experimental points.

Table 6 Comparison of VTPs between this work and literatures

Table 7 AARD and max |RD| of VTPR EOS and VTSRK EOS

The experimental data used in this work are different from those in literatures [25, 35], which leads to the changes in volume-translation parameters (VTP). In contrast, the fitting parameters of VTPR EOS are more consistent with literatures [25] than those of VTSRK EOS [35], which indicates that fitting parameters of VTSRK EOS are more dependent on experimental data. However, since AARDs of all equations of state are less than 1%, VTPR and VTSRK EOSs are both suitable for density prediction of pure water and acetone.

4.2 Fitting Results of Acetone–Water Solution

Mixing rules for volume-translation terms and parameters of PR EOS and SRK EOS were required to form the equation of state for a mixture.

The following mixing rule was used for the volume-translation terms of VTPR EOS [36].

$${{C}_{\text{T}}}^{\text{mVTPR}}=\left(\frac{R{T}_{\text{c,m}}}{{P}_{\text{c,m}}}\right)\left({{C}_{1}}^{\text{mVTPR}}-\left(0.004+{C}^{\text{mVTPR}}\right)\mathit{exp}\left(-2{d}^{\text{mVTPR}}\right)\right)$$

$$-{{\delta }_{\text{c}}}^{\text{mVTPR}}\cdot 0.35/(0.35+{d}^{\text{mVTPR}})$$

(29)

$${{\delta }_{\text{c}}}^{\text{mVTPR}}=\frac{R{{T}_{\text{c}}}^{\text{m}}}{{{P}_{\text{c}}}^{\text{m}}}(0.3074-{{Z}_{\text{c}}}^{\text{m}})$$

(30)

$$d^{{\text{mVTPR}}} = \frac{1}{{RT_{\text{c}} ^{\text{m}} }}\left( {\frac{{\partial P}}{{\partial \rho }}} \right)_{{\text{PR}}}$$

(31)

$$C^{{\text{mVTPR}}} = \sum\nolimits_{i} {x_{i} } \cdot C^{{\text{iVTPR}}}$$

(32)

The following mixing rule was used for the volume-translation terms of VTSRK EOS [35].

$${{C}_{T}}^{\text{mVTSRK}}=-{{C}_{1}}^{\text{mVTSRK}}\cdot \left(\frac{R{{T}_{\text{c}}}^{\text{m}}}{{{P}_{\text{c}}}^{\text{m}}}\right)-{{\delta }_{\text{c}}}^{\text{mVTSRK}}/\left({{C}_{2}}^{\text{mVTSRK}}+{{C}_{3}}^{\text{mVTSRK}}\cdot {d}^{\text{mVTSRK}}\right)$$

(33)

$${{\delta }_{\text{c}}}^{\text{mVTSRK}}=\frac{R{{T}_{\text{c}}}^{\text{m}}}{{{P}_{\text{c}}}^{\text{m}}}(1/3-{{Z}_{\text{c}}}^{\text{m}})$$

(34)

$${d}^{\text{mVTSRK}}=\frac{1}{R{{T}_{\text{c}}}^{\text{m}}}{\left(\frac{\partial P}{\partial \rho }\right)}_{\text{SRK}}$$

(35)

$$C_{1} ^{{\text{mVTSRK}}} = \sum\nolimits_{i} {x_{i} } \cdot C_{1} ^{{\text{iVTSRK}}}$$

(36)

$$C_{2} ^{{\text{mVTSRK}}} = \sum\nolimits_{i} {x_{i} } \cdot C_{2} ^{{\text{iVTSRK}}}$$

(37)

$$C_{3} ^{{\text{mVTSRK}}} = \sum\nolimits_{i} {x_{i} } \cdot C_{3} ^{{\text{iVTSRK}}}$$

(38)

where ‘m’ in superscript and subscript represented mixture; ‘i’ in superscript represented pure substance; ${k}_{ij} \; {\mathrm{and}} \; {l}_{ij}$ were the binary interaction parameter (BIP); ${T}_{\text{c}}^{\text{m}}$ and ${P}_{\text{c}}^{\text{m}}$ were the critical temperature and pressure calculated from Eqs. 5 and 6; ${{\mathrm{Z}}_{\mathrm{c}}}^{m}$ was the critical compression factor for mixture calculated from Eqs. 38–40 [36].

$${{Z}_{\text{c}}^{\text{m}}}=\frac{{{P}_{\text{c}}}^{\text{m}}\cdot {{V}_{\text{c}}}^{\text{m}}}{R{{\text{T}}_{\text{c}}}^{\text{m}}}$$

(39)

$$ V_{\text{c}} ^{\text{m}} = \sum\nolimits_{i} {\theta _{i} } \cdot {V_{\text{c}} ^{\text{i}}} $$

(40)

$$\theta _{i} = \frac{{x_{i} \cdot ({V_{\text{c}} ^{\text{i}}} )^{{2/3}} }}{{\sum\nolimits_{i} {x_{i} } \cdot ({V_{\text{c}} ^{\text{i}}} )^{{2/3}} }}$$

(41)

One fluid mixing rule was used for the parameters of PR EOS and SRK EOS.

$$a_{\text{m}} = \sum\nolimits_{i} {\sum\nolimits_{j} {x_{i} } } x_{j} \sqrt {a_{i} a_{j} } (1 - k_{{ij}} )$$

(42)

$$b_{\text{m}} = \sum\nolimits_{i} {\sum\nolimits_{j} {x_{i} } } x_{j} \frac{{b_{i} + b_{j} }}{2}(1 - l_{{ij}} )$$

(43)

where ${k}_{ij}$ and ${l}_{ij}$ were binary interaction parameters (BIP) which needed to be regressed.

The VTPs of the pure substances (${{C}_{1}}^{\text{VTSRK}}, {{C}_{2}}^{\text{VTSRK}}, {{C}_{3}}^{\text{VTSRK}}\mathrm{and}$ ${C}^{\text{VTPR}}$) in Table 6 were used to calculate the VTPs of mixture (${{C}_{1}}^{\text{mVTSRK}}, {{C}_{2}}^{\text{mVTSRK}},{{C}_{3}}^{\text{mVTSRK}} \mathrm{and}\; {C}^{\text{mVTPR}}$). Moreover, the P–T–V–X data of the acetone–water solution in Table 4, along with the VTPs for a mixture, were used to regress the BIPs (${k}_{ij}$ and ${l}_{ij}$) by nlinfit function in Matlab. The fitting results were presented in Table 8.

Table 8 Fitting results of VTPR and VTSRK EOSs for acetone–water solutions

AARD of VTPR EOS is close to work of Abudour et al. [36] (0.6–2.3%), but a huge deviation is observed for VTSRK EOS. In fact, in work of Chen et al. [35], VTSRK EOS was only extended to hydrocarbon mixtures, and no fitting result was presented for acetone–water solution. Since VTSRK EOS has a good fitting result for pure acetone and water, the mixing rule of VTSRK EOS is considered to be inappropriate.

Critical compressibility factors of acetone–water solution (Z_c^m) with various water mole fractions (x) were calculated by Eqs. 39–41 as shown in Fig. 8. The good linear relationship indicates that Z_c^m can be calculated by Eq. 44. Abudour et al. [36] showed that ${{C}^{\text{VTPR}}}$ could be illustrated by a linear function of Z_c, which indicates that Eq. 32 is theoretically applicable with the help of Eq. 44. However, in work of Chen et al. [35], the linear relationship between ${{C}_{2}}^{\text{mVTSRK}}, {{C}_{3}}^{\text{mVTSRK}}$ and Z_c was poor, which indicates that Eqs. 37, 38 are not suitable in theory. In such a case, VTSRK EOS shows a big deviation in predicting the mole volume of acetone–water solutions.

Fig. 8

Critical compressibility factor (Z_c^m) as a function of water mole fraction (x)

$${Z_{\text{c}} ^{\text{m}}} = \sum\nolimits_{i} {x_{i} } \cdot {Z_\text{c} ^{\text{i}}}$$

(44)

VTPR EOS is more appropriate for the prediction of the mole volume of acetone–water solutions when considering the fitting results for pure substances and mixtures.

5 Conclusions

Critical temperatures and critical pressures of the acetone–water solutions with water mole fraction of 0–60% were measured. The maximum critical pressure was about 9 MPa, which indicates that only one phase (liquid or supercritical state) exists during the mixing of acetone with water at pressure over 15 MPa. Moreover, P–T–ρ–X data, at 460–550 K and 15/20 MPa, were also measured. VTPR and VTSRK EOSs were used to fit experimental data for pure water, pure acetone and water–acetone solutions. Both give good fitting results for pure substances. However, compared with VTSRK EOS, VTPR EOS had less deviation for acetone–water solution and is better suited to describe P–T–ρ–X relationships for acetone–water solutions. The data and results of this study can provide reference for CFD simulation of the supercritical synthesis of 4-hydroxy-2-butanone.

Appendix

1.1 Uncertainty

1.1.1 $T_{\text{c}}^{\text{m}}$

The uncertainty came from T_d (the phase transition temperature detected by cooling-heating stage). Before measurement, saccharin, anthraquinone and 4-nitrobenzoic acid were used to modify the temperature of the cooling-heating stage. The melting points were detected by DSC and cooling-heating stage, and the results were below (Table 9).

Table 9 The melting points read from DSC and cooling-heating stage

A calibration curve was made below.

$${{T}_{\text{modified}}^{\text{stage}}}/K=0.9454\cdot ({{T}_{\text{reading}}^{\text{stage}}}/\mathrm{K})+26.502$$

(45)

${\mathrm{T}}_{\mathrm{modified}}^{\mathrm{stage}}$, the modified temperature of cooling-heating stage. ${\mathrm{T}}_{\mathrm{reading}}^{\mathrm{stage}}$, the temperature read from cooling-heating stage. The residual deviation S was calculated as followed.

$$S=\sqrt{\frac{\sum {({T}_{\text{DSC}}-{{T}_{\text{modified}}^{\text{stage}}})}^{2}}{9-2}}=0.66 \mathrm{K}$$

(46)

The standard uncertainty u₁ was equal to S(T_d)

$$S({T}_{\text{d}})=\frac{s}{b}\times \sqrt{\frac{1}{p}+\frac{1}{n}+\frac{{({x}_{\text{a, reading}}-{x}_{\text{a}})}^{2}}{{\sum }_{1}^{\text{n}}{({x}_{i}-{x}_{\text{a}})}^{2}}}$$

(47)

where b was the slope of Eq. 45; p was the number of repeated measurements of ${T_{\text{d}}}$; n was the number of points used in temperature modification process; ${x}_\text{{a, reading}}$ was the average reading results of each ${T_{\text{d}}}$; ${x}_{\text{a}}$ was the average reading results of cooling-heating stage during modification process; ${x}_{i}$ was the reading result of cooling-heating stage during modification process. During measurement, each T_d was measured 3 times, and all three results were identical. In order to presenting the standard uncertainty of all the T_d, ${x}_\text{{a, reading}}$ was equal to the maximum of T_d during measurement. As a result, the standard uncertainty of ${{T}_{\text{c}}}^{\text{m}}$ was

$$u\left({{T}_{c}}^{m}\right)={u}_{1}=S\left({T}_{d}\right)=\frac{0.66K}{0.9454}\times \sqrt{\frac{1}{3}+\frac{1}{9}+\frac{{(560.4K-527.93K)}^{2}}{{\sum }_{1}^{9}{({x}_{i}-527.93K)}^{2}}}=0.55 \mathrm{K}$$

(48)

1.1.2 x

The water molar fraction in the solution was calculated by Eq. 49.

$$x=\frac{{m}_{\text{w}}/{M}_{\text{w}}}{{m}_{\text{w}}/{M}_{\text{w}}+{m}_{\text{a}}/{M}_{\text{a}}}$$

(49)

where $m_{\text{w}}$ and $m_{\text{a}}$ were the water mass and the acetone mass in the solution; $M_{\text{w}}$ and $M_{\text{a}}$ were the molecular weight of water and acetone.

The uncertainty originated from $m_{\text{w}}$ (u₁) and $m_{\text{a}}$ (u₂), both of which were weighed by an electronic balance with an accuracy of 0.01 g. The precision of ${\mathrm{m}}_{\mathrm{a}}$ (u₂) was also affected by the purity of acetone. By assuming that the mass was in rectangular distribution, u₁ and u₂ were calculated by eqs. 50, 51.

$${u}_{1}=0.01 \,\mathrm{ g}\times 58\mathrm{\%}\times 0.5=0.0029 \,\mathrm{ g}$$

(50)

$${u}_{2}=0.01\mathrm{ g}\times 58\mathrm{\%}\times 0.5+400\mathrm{ g}\times 0.001\times 58\mathrm{\%}\times 0.5=0.1189\mathrm{ g}$$

(51)

Moreover, the combined standard uncertainty of water molar fraction ${u}_{c}\left({x}\right)$ was calculated by Eq. 52.

$$u\left(x\right)=\sqrt{{\left(\frac{\partial x}{\partial {m}_{\mathrm{w}}}\right)}^{2}\cdot {{u}_{1}}^{2}+{\left(\frac{\partial x}{\partial {m}_{\mathrm{a}}}\right)}^{2}\cdot {{u}_{2}}^{2}}=0.00004$$

(52)

where $m_{\text{w}}\; \mathrm{ and }\; {m}_{\text{a}}$ were replaced with the average value of 20 and 400 g, respectively. In our paper, the number of valid digits of x was 3. In such a case, the standard uncertainty of x was $u\left(x\right)=0.0005$.

1.1.3 q

The filling ratio was calculated as followed.

$$q=\frac{{\text{solution}}\;{\text{length}}\;{\text{in}}\;{\text{tube}}} {{\text{tube}}\;{\text{length}}}$$

(53)

The uncertainty came from the solution length in the tube (u₁) and the tube length (u₂). The length of solution and tube were measured by a vernier caliper which had an accuracy of 0.02 mm. Under the assumption that the solution and tube had a rectangular distribution, then

$${u}_{1}={u}_{2}=0.02\;\mathrm{mm}\times 58\mathrm{\%}\times 0.5=0.0058\;\mathrm{mm}$$

(54)

$${u}_{\mathrm{r}1}={u}_{1}/\mathrm{min\;solution\;length\;during\;measurement}=0.02\;\mathrm{mm}/6\;\mathrm{mm}=0.00333$$

(55)

$${u}_{\mathrm{r}2}={u}_{2}/\mathrm{min\;tube\;length\;during\;measurement}=0.02\;\mathrm{mm}/15\;\mathrm{mm}=0.00133$$

(56)

The combined relative standard uncertainty of filling ratio ${u}_{\mathrm{c},\mathrm{ r}}\left({q}\right)$ was equal to $\sqrt{{{u}_{\mathrm{r}1}}^{2}+{{u}_{\mathrm{r}2}}^{2}}=0.0036$. The standard uncertainty of q was $u\left(q\right)={u}_{\mathrm{c},\mathrm{ r}}\left(q\right)\cdot \mathrm{max}\left(q\right)=0.0036\times 0.345=0.0012$.

1.1.4 $P_{\text{c}}^{\text{m}}$

The uncertainty of critical pressure came from the precision of the pressure gauge which had an accuracy of 0.25% full scale. By assuming that the pressure had a rectangular distribution, then

$${u}_{\mathrm{r}}=0.25\%\times 58\%=0.00145$$

(57)

The standard uncertainty of critical pressure was $u\,\left({{P}_{\text{c}}}^{\text{m}}\right)=0.00145\times 20 \, {\text{MPa}} =0.029 \, {\text{MPa}}$.

1.1.5 $\rho_{\text{solution}}$

The relative deviation of density was considered to be the average relative deviation of pure substances density (0.32%), which the temperature and pressure deviation were contained.

1.1.6 T During Density Measurement

The uncertainty of the temperature during the density measurements had its origin in the thermocouple, which had an accuracy of 0.4% (full scale). By assuming that the temperatures had a rectangular distribution, then

$${u}_{\mathrm{r}}=0.4\%\times 58\%=0.00232$$

(58)

The standard uncertainty of T was $u\left(T\right)=0.00232\times \left(546.2 \, \mathrm{K}-273.15 \, \mathrm{ K}\right)=0.63 \, \mathrm{K}$.

1.1.7 P During Density Measurement

The uncertainty of the pressure during the density measurements had its origin in the pressure gauge, which had an accuracy of 0.25% (full scale). By assuming that the pressures had a rectangular distribution, then

$${u}_{\mathrm{r}}=0.25\%\times 58\%=0.00145$$

(59)

The standard uncertainty of P was $u\left(P\right)=0.00145\times 20 \, \mathrm{MPa}=0.029 \, \mathrm{MPa}$.