Stability and Structure of Silver–l-methionine Complexes

Abstract

Stability and structure of complexes between silver (I) and l-methionine (L) deduced from potentiometric and ¹H NMR measurements allow to assume the prevailing of several protonated species. The experimental data are compatible with the formation of the following complexes: AgL, AgL₂, AgH₂L, AgH₁L₂, AgH₂L₂, AgH₃L₂ and AgH₄L₂. The coordination sites are obtained by ¹H NMR spectra, showing that only the bond between the methylthioether sulfur atom and silver (I) is responsible of the complex stability. The system is studied potentiometrically with silver and glass electrodes at 25 °C and 1.00 mol·dm⁻³ NaClO₄ as ionic medium. Amino acids containing sulfur are few and not extensively studied. In particular, l-methionine, even if it is the most important, enantiomer and their complexes with silver (I) present anticarcinogenic properties, is quite not investigated. In the same experimental conditions, l-methionine protonation constants are determined. The ¹H NMR data allow one to assume that, in moderately alkaline solution, silver (I) is bond with six membered chelate rings with sulfur and amino nitrogen, while carboxylic groups are not involved. No polynuclear species are present. The high stability of the complex with ratio 1:2 (silver (I)/l-methionine), involving also two hydrogen ions, predominating in a wide range of hydrogen ion concentration suggests to propose a study for the preparation of an electrode to measure the deprotonated l-methionine concentration.

1 Introduction

Amino acids containing sulfur are less investigated as ligands of cations [1]. Most of the studied sulfur containing amino acids contain the group –SH, like cysteine [2], but few results exist about methylthioether reagents acting as ligands [1]. Methionine (2(S) amino-4-methylmercaptobutanoic acid), as shown in Fig. 1, is an α-amino acid containing sulfur as methylthioether and a chiral carbon so that the dl-, d-, and l-enanthiomeric forms exist.

Fig. 1

Structure of methionine

Only the form l- is present in the proteins. It has important biological properties because it occupies the N-terminal of all proteins of eukaryotes and archaea and in the activated form, S-adenosylmethionine (SAM) [3] is also involved in lecithin and other phospholipids trans-sulfurization processes as in the synthesis of cysteine, carnitine and taurine.

The SAM is often present in food supplements, even for depression [4], osteo arthritis [5], and liver pathology therapies [6]. l-methionine is present in most of the food consumed daily.

On the other hand, the silver (I) complex formation is also not extensively studied [1], even if the complex formation of silver (I) deserves attention for possible application in biology and medicine.

Shukly and Mishura [7]. supposed that compounds of methionine and silver (I) could have anticarcinogenic properties. Banti and Hadjikakou [8] studied the antitumor activity of a few compounds of silver (I). Recently, Hecel et al. [9] considered silver (I) complexes as potential therapeutical reagents in pharmacy and medicine.

These references suggest studying the reactions taking place between silver (I) and l-methionine.

Only three papers are reported on the complex formation between methionine and silver (I) in the dedicated literature [1]. Lenz and Martell [10], explaining their electromotive force (emf) measures carried out at 25 °C with a glass electrode in 0.1 mol·dm⁻³ KNO₃, assumed the formation of only one complex with the constant log₁₀ K₁ = 3.17.

Pettit et al. [11] explained their data obtained at 25 °C in 0.1 mol·dm⁻³ KNO₃ with an ion-selective electrode and NMR measurements, assuming beyond the constant log₁₀ K₁ = 5.22, the presence of two complexes with participation of protons having log₁₀ β (AgHL) = 12.28 and log₁₀ β (AgH₂L₂) = 24.2, but to achieve the constants of the mixed complexes, two experimental methods were applied, which, however, gave different results.

Finally, Tombeux et al. [12], from emf measurements at 25 °C in 0.5 mol·dm⁻³ KNO₃ with glass and an ion-selective electrode, assumed also the formation of two polynuclear in silver (I) complexes: log₁₀ β (Ag₂L) = 7.46 and log₁₀ β (Ag₂L₂) = 13.41.

The above references show that few and data, with poor agreement, exist on the complex formation between silver (I) and methionine and in particular, the disagreement is relevant concerning the hydrogen ions participation and the eventual presence of polynuclear species in silver (I). Furthermore, it cannot be deduced which enanthiomeric form of methionine was employed.

Pettit and Swansk [13], in their study on complex formation of d-, l-, dl- and meso-tartaric acid, found a little difference between the protonation constants of the different enanthiomeric forms.

The aim of our research is to study the behavior of l-methionine as ligand of silver (I) in a large range of concentrations of Ag (I), l-methionine, and hydrogen ions, to find the type of interaction taking place in terms of equilibrium constants and structure. This information and the biological importance of l-methionine suggest to focus the subject of this paper on the L-enanthiomeric form as well as to deduce the stability and the structure of the formed species.

A complete and exhaustive investigation has to be performed in a large range of reagents concentrations that would provoke a variation of activity coefficients of the reagents. To minimize this effect, the method of the constant ionic medium, proposed by Biedermann and Sillèn [14], was adopted. This means that by substituting up to 15% of the ionic medium with the reagents, the activity coefficients do not change appreciably, in spite of the variation of concentrations, so that in the constant ionic medium, concentrations can substitute activities.

All measurements are carried out in 1.00 mol·dm⁻³ NaClO₄ as ionic medium, 25 °C as well as the enanthiomeric form l-methionine was employed. Solutions were prepared and kept in red light.

The equilibrium for the formation of a complex Ag_qH_pL_r (where L is methionine in completely deprotonated form) from Ag⁺ and methionine (L), is written as follows, without any preliminary hypothesis:

$$q{\text{Ag }} + p{\text{H }} + r{\text{L}} = {\text{Ag}}_{q} {\text{H}}_{p} {\text{L}}_{r} ,$$

(1)

with the constant $\beta_{p,q,r} = c_{{{\text{Ag}}_{q} {\text{H}}_{p} {\text{L}}_{r} }} c_{{{\text{Ag}}}}^{ - q} c_{{\text{H}}}^{ - p} c_{{\text{L}}}^{ - r} .$

In Eq. 1, charges are omitted, for simplicity and q ≥ 1, p ≥  ≤ 0 and r ≥ 1. When q > 1 polynuclear complexes in silver (I) are present, p ≠ 0 refers to the presence of complexes with the participation of protons. Protonated complexes correspond to p > 0, while p < 0 could referred to eventual hydroxylated species (without preliminary hypothesis a specie like Ag (OH) L could exist).

In Eq. 1 and in the following, c indicates the free concentration of the reagents, while C represents their total concentration. For example, the free concentration of deprotonated l-methionine (L = C₅H₁₀ SNO₂₋) will be indicated as c_L.

The aim of this paper is the determination of q, p, and r as well as the corresponding β_q,p,r.

To study the equilibria taking place between silver (I) and methionine, it is necessary to determine the protonation constants of the ligand in the same experimental conditions.

The main literature investigations on the protonation of methionine are collected by Powell [1], but they are incomplete and show poor agreement. Two authors [12, 15] studied the dl-methionine, other researchers did not declare the enanthiomeric form. In our paper, the reagent l-methionine, simply reported as methionine is studied.

Many papers report only the first protonation constant. Only Stypinski-Mis and Anderegg [15] worked in 1.00 mol·dm⁻³ NaClO₄, while others used diluted to 0.01 mol·dm⁻³ LiClO₄–NaClO₄ mixtures. Other studies are performed in different ionic media.

2 Experimental

2.1 Materials and Analysis

l-Methionine p.a. Sigma reagent was crystallized from bi distilled water and dried at 80 °C. The absence of water or of other impurities was verified by thermogravimetric analysis. The dissolution in water in preparing concentrated solutions was slow but checked.

A stock solution of AgClO₄ was prepared by adding a moderate excess of Ag₂O (p.a. Sigma) to about 2 mol·dm⁻³ HClO₄ and kept at about 70–80 °C for two hours to allow the formation of AgClO₄ with little residual acidity. The absence of chloride was verified. The residual acidity was determined according to Gran [16]. The concentration of silver (I) was determined by Volhard titration (with Fe(III) as visual indicator). Results of analyses agreed within ± 0.1%.

NaClO₄, HClO₄ and NaOH stock solutions were prepared and analyzed as described previously [17].

All solutions were freed from O₂ and CO₂ by bubbling nitrogen, (purity 99.999%) which was further purified by passing it through 10% NaOH, 10% H₂SO₄, distilled water and 1.00 mol·dm⁻³ NaClO₄.

2.2 Apparatus

The emf measurements, the cell arrangement and the reference electrode R.E. were described previously [18].

Ag_(s) and Ag_(s)/AgCl_(s) electrodes are prepared according to Brown [19]. To prepare the Ag_(s) and Ag_(s)/AgCl_(s) electrodes a constant current electricity generator (HP mod. 6186 C) was used.

The glass electrode potential (E_G) was measured using a Radiometer potentiometer (PHM 64) and glass electrode from the same firm. Constant values were obtained within a few minutes after each addition and remained constant for several hours. The values $E_{{\text{G}}} - E_{{\text{G}}}^{{\text{o}}}$ was reproducible within ± 0.2 mV. In the range −log₁₀ c_H ≥ 9, the response of the glass electrode was corrected on the basis of that of a H₂ electrode.

Ag_(s) electrode potential (E_Ag), measured with a Keithley 2000 Multimeter, provided constant values within half an hour after each addition, remaining constant for several hours. $E_{{{\text{Ag}}}} - E_{{{\text{Ag}}}}^{{\text{o}}}$ values were reproducible within ± 0.15 mV.

NMR measurements were conducted at 25 °C on a Bruker Unity spectrometer operating at a proton frequency of 400 MHz. The ¹H NMR spectra were collected using a 30° pulse, a sweep width of 3.7 kHz, 16 K data points, and a 0.5 s recycle delay between scans. A total of 16 scans were integrated. Spectra were referenced internally using the residual D₂O/H₂O peak at 4.80 ppm.

2.3 Method of Investigation

2.3.1 l-Methionine Protonation

The protonation constants of methionine in its completely deprotonated form indicated with L (L = C₅H₁₀ SNO₂₋), defined as follows:

$$c_{{{\text{H}}_{{_{n} }} {\text{L}}}} = c_{{{\text{H}}_{n - 1} {\text{L}}}} c_{{\text{H}}} K_{n} ,$$

(2)

where n can be 1, 2, were determined in 1.00 mol·dm⁻³ NaClO₄ and at 25 °C, by performing electromotive force (emf) measurements of the cell:

$${\text{RE}}| {\text{TS}}_{{1}} |{\text{GE}}$$

(I)

where TS₁ represents test solution: C_H mol·dm⁻³ in H⁺; (1 − C_H) mol·dm⁻³ in Na⁺; 1.00 mol·dm⁻³ in ${\text{ClO}}_{4}^{ - }$. GE indicates a glass electrode while RE is a reference electrode with following composition:

Ag_(s) | AgCl | 0.01 mol·dm⁻³ AgClO₄, 0.99 mol·dm⁻³ NaClO₄ | 1 mol·dm⁻³ NaClO₄.

At 25 °C, in millivolts and in constant ionic medium, the emf of cell Eq. 3 can be expressed as follows:

$$E_{{\text{G}}} = E_{{\text{G}}}^{{/{\text{o}}}} \_59.16\log_{10} c_{{\text{H}}} + E_{{\text{j}}} .$$

(3)

In Eq. 3, the constant $E_{{\text{G}}}^{{/{\text{o}}}}$ and E_j =  − j c_H, according to Biedermann and Sillèn [14] were determined in the first part of each measurement, where solution TS₁ had the following general composition:

C_H mol·dm⁻³ H⁺; (1 − C_H) mol·dm⁻³ in Na⁺; 1.00 mol·dm⁻³ in ${\text{ClO}}_{4}^{ - }$.

In the second part of the measurement, addition of an alkaline solution of methionine to the selected ionic medium gradually increased −log₁₀ c_H while keeping C_L constant (by addition of an adequate volume of solution having a 2C_L concentration). The results are reported below.

2.3.2 Complex Formation

The complex formation equilibrium (Eq. 1) has been little studied. The literature reports only four papers concerning the behavior of methionine as a ligand of silver (I). Furthermore, papers treating the behavior of the enanthiomer, L-methionine are not available.

The disagreement among the literature data and the lack of information about the kind of bond between silver (I) and l-methionine sulfur or amino or carboxyl groups, suggested our investigation on the equilibria taking place between methionine and silver (I) in a wide range of reagent concentration to find the existing species, with particular attention to the participation of protons and the presence of polynuclear complexes in silver (I). On the other hand, as treated below, the bond between silver (I) and methionine, is investigated.

The complex formation according to Eq. 1 is studied at 25 °C in 1.00 mol·dm⁻³ NaClO₄ by measuring the emf of the cells:

$${\text{RE}}|{\text{TS}}_{{2}} |{\text{GE}}$$

(II)

$${\text{RE}} |{\text{TS}}_{{2}} |{\text{Ag}}_{{({\text{s}})}}$$

(III)

where TS₂ represents test solution having the following general composition:

C_H mol·dm⁻³ in H⁺; C_Ag mol·dm⁻³ in Ag⁺; (1 − C_H − C_Ag) mol·dm⁻³ in Na⁺; 1.00 mol·dm⁻³ in ${\text{ClO}}_{4}^{ - }$ while Ag_(s) is a silver electrode.

At 25 °C, in millivolts and in constant ionic medium, the emf of cells (II) and (III) can be expressed respectively by Eqs. 3 and 4,

$$E_{{{\text{Ag}}}} = E_{{{\text{Ag}}}}^{{/{\text{o}}}} + 59.15\log_{10} c_{{{\text{Ag}}}} + E_{{\text{j}}} .$$

(4)

Cell constants, $E_{{\text{G}}}^{{/{\text{o}}}}$ and $E_{{{\text{Ag}}}}^{{/{\text{o}}}}$ were determined in the first part of each experiment in the absence of ligand.

The junction potential, E_j, was evaluated as E_j = (− 490 ± 10) c_H, mV·L·mol⁻¹), according to Biedermann and Sillèn [14]. In the second part of the titration, two solutions were used: an alkaline solution (1) of methionine, in the constant ionic medium and a solution (2) with Ag⁺ concentration equal to 2C_Ag, with the same C_H concentration. In this way the concentration of methionine and −log₁₀ c_H gradually increased, whereas, for each measurement, C_Ag and C_H were kept constant.

The free hydrogen ion concentration, −log₁₀ c_H, was provided by the emf measurements of cell (II), whereas, from the emf measurements of cell (III), the free silver (I) concentration −log₁₀ c_Ag was obtained.

Together with the emf measurements, in the same ionic medium, a parallel investigation with proton Nuclear Magnetic Resonance (¹H NMR) was performed looking to obtain the possible structure of the formed complexes.

3 Results and Discussion

3.1 Protonation Constants of l-Methionine

Measurements were performed at 0.010 and 0.020 mol·dm⁻³ methionine concentrations. From the material balance of the methionine, C_L, and the analytical excess of hydrogen ion, C_H, and taking into account the law of mass action, it can be written:

$$C_{{\text{L}}} = c_{{\text{L}}} + \sum {K_{1} \cdot \cdot \cdot K_{n} c_{{\text{H}}}^{n} c_{{\text{L}}} } ,$$

(5)

$$C_{{\text{H}}} = c_{{\text{H}}} + \sum {nK_{1} \cdot \cdot \cdot K_{n} c_{{\text{H}}}^{n} c_{{\text{L}}} } ,$$

(6)

where K_1···K_n represent the protonation equilibria (charges are omitted, for simplicity):

$${\text{L }} + n{\text{H }} = {\text{ H}}_{n} {\text{L}}{.}$$

Arranging C_L and C_H with c_H, experimentally measured by cell (I), the protonation function p^*, defined as the average number of protons per methionine, can be calculated as:

$$p^{*} = \frac{{C_{{\text{H}}} - c_{{\text{H}}} }}{{C_{{\text{L}}} }} = \frac{{\sum {nK_{1} \cdot \cdot \cdot K_{n} } c_{{\text{H}}}^{n} }}{{\left( {1 + \sum {K_{1} \cdot \cdot \cdot K_{n} c_{{\text{H}}}^{n} } } \right)}}.$$

(7)

The values of the constants log₁₀ K₁ and log₁₀ K₂ are obtained both applying the graphic method proposed by Sillèn [20] and by elaborating the primary data by the PC program HYPERQUAD [21]. The results show excellent agreement as:

$${\text{log}}_{{{1}0}} K_{{1}} = { 9}.{32} \pm 0.0{\text{2 and log}}_{{{1}0}} K_{{1}} K_{{2}} = { 11}.{6}0 \pm 0.0{5}{\text{.}}$$

(8)

The limits of error were estimated from the maximum shift possible for the calculated curve and experimental points for which agreement was still acceptable.

The values in (Eq. 8) are applied to calculate the theoretic curve drown on Fig. 2.

Fig. 2

Protonation function of l-methionine. Curve is calculated with the constants log₁₀ K₁ = 9.32 and log₁₀ K₁ K₂ = 11.60

3.2 Complex Formation

Experimental data were obtained for C_H = 0.025; 0.035; 0.050; 0.070 and 0.100 mol·dm⁻³ and, at the same time, C_Ag varied in the range 0.25–2.00) × 10⁻³ mol·dm⁻³. The methionine concentration increased to about 0.10 mol·dm⁻³. From emf measurements of cells (II and III) −log₁₀ c_H and −log₁₀ c_Ag are obtained.

To study reaction 1, material balance of silver (I), taking into account the law of mass action in the constant ionic medium, without preliminary hypotheses, C_Ag can be written as:

$$C_{{{\text{Ag}}}} = c_{{{\text{Ag}}}} + \sum {\sum {\sum {q\beta_{q,p,r} c_{{{\text{Ag}}}}^{q} c_{{\text{H}}}^{p} c_{{\text{L}}}^{r} } } } .$$

(9)

In Eq. 9, hydrolytic species of silver (I) are neglected. This is permissible for the investigated c_Ag and c_H ranges as estimated from results reported by Brown and Ekberg [22].

Elaborating Eq. 9, the following equation can be obtained:

$$\eta = \log_{10} \left( {\frac{{C_{{{\text{Ag}}}} }}{{c_{{{\text{Ag}}}} }}} \right) = \log_{10} \left( {1 + \sum {\sum {\sum {q\beta_{q,p,r} c_{{{\text{Ag}}}}^{q} c_{{\text{H}}}^{p} c_{{\text{L}}}^{r} } } } } \right).$$

(10)

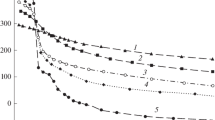
The function η is plotted versus −log₁₀ c_H in Fig. 3.

Fig. 3

The experimental data in the form η versus −log₁₀ c_H. Curves are calculated with the constants reported in Table 1

The plot of Fig. 3 shows that points obtained at the same C_H, but at different C_Ag, fall on the same curve. The function η is independent of C_Ag and so q = 1. Thus, as only mononuclear silver (I) species, like Ag H_p L_r, are present and Eq. 10 becomes:

$$\eta = \log_{10} \left( {\frac{{C_{{{\text{Ag}}}} }}{{c_{{{\text{Ag}}}} }}} \right) = \log_{10} \left( {1 + \sum {\sum {\beta_{1,p,r} c_{{^{{{\text{Ag}}}} }}^{p} c_{{_{{\text{H}}} }}^{r} } } } \right).$$

(11)

To study the complex formation between silver (I) and methionine, it is necessary to know the free.

concentration of methionine, c_L, which can be calculated from the material balance of C_H, in the constant ionic medium, by taking account of the law of mass action:

$$C_{{\text{H}}} = c_{{\text{H}}} + K_{1} c_{{\text{H}}} c_{{\text{L}}} + 2K_{1} K_{2} c_{{\text{H}}}^{2} c_{{\text{L}}} + \sum {\sum {p\beta_{1,p,r} } c_{{{\text{Ag}}}} c_{{\text{H}}}^{p} c_{{\text{L}}}^{r} } ,$$

(12)

where K₁ and K₂ are the protonation constants of methionine previously determined in the same experimental conditions and q = 1. The last term of Eq. 12 can be neglected, because in all investigated solutions, there are C_Ag ≤ 0.02 C_H.

Figure 4 shows the plot η versus −log₁₀ c_L for C_H 0.100; 0.050 and 0.025 mol·dm⁻³. It can be observed that points obtained at different C_H fall on different curves and that, as η is an increasing function of C_H, mixed complexes with assumption of protons are formed, p ≥ 0.

Fig. 4

Main of experimental data obtained at different C_H, in the form η versus −log₁₀ c_L. Curves are calculated with the constants reported in Table 1

To obtain the p and r values and the relative β_1,p,r constants, the experimental data are treated both graphical methods and elaborated with a PC program.

The graphical procedure is divided in two parts.

First, values of c_L are calculated from the data of Fig. 3. After that, the values of p and r and the constants β_1,p,r of AgH_pL_r are obtained from the set $\eta \left( {c_{{\text{H}}} ,c_{{\text{L}}} } \right)_{{c_{{{\text{Ag}}}} ,c_{{\text{H}}} }}$ according to the procedure suggested by Sillèn [23], which entails deducing from a three variable function such as η, relationships between two of the variable concentrations by keeping the third constant [20].

By applying the proposed graphic procedure, keeping c_H constant, Eq. 11 can be written as:

$$\eta = \log_{10} \left( {1 + \sum {\gamma_{r} c_{{\text{L}}}^{r} } } \right)\,{\text{where}}\,\sum {\gamma_{r} = \sum {\sum {\beta_{1,p,r} c_{{\text{H}}}^{p} } } } .$$

(13)

For each curve of Fig. 3, $\eta_{{c_{{\text{H}}} }}$ values are selected for corresponding successive −log₁₀ c_H. From the C_H and c_H values, the corresponding c_L can be calculated from Eq. 12, by neglecting its last term. In this procedure, no appreciable error is involved, because of the presence of many points. Introducing those c_L values in Eq. 13, the following expression can be obtained:

$$\phi = \log_{10} \left[ {\left( {10^{{\eta_{{c_{{\text{H}}} }} }} - 1} \right)c_{{\text{L}}}^{ - 1} } \right] = \log_{10} \left( {\sum {\gamma_{r} c_{{\text{L}}}^{r - 1} } } \right).$$

(14)

By plotting the function Φ = 10^ϕ versus c_L, for every considered −log c_H, a straight line is always obtained, then r can be only 1 or 2. For each plot, γ₁ and γ₂ respectively from extrapolation and slope can be obtained.

In Fig. 5, an example obtained for −log₁₀ c_H = 5 is plotted.

Fig. 5

The straight dependence of Φ on −log₁₀ c_L at −log₁₀ c_H = 5

By taking in to account that each methionine can assume not more than two protons, Eq. 13 can be written, without preliminary hypothesis, as:

$$\log_{10} \gamma_{1} = \log_{10} \beta_{1,0,1} + \log_{10} \left( {1 + \beta_{1,1,1} \beta_{1,0,1}^{ - 1} c_{{\text{H}}} + \beta_{1,2,1} \beta_{1,0,1}^{ - 1} c_{{\text{H}}}^{2} } \right).$$

(15)

By applying the graphical procedure proposed by Sillèn [20], it can be deduced that Eq. 18 cannot be normalized with three parameters, but it can be fitted with the following theoretical equation:

$$G = {\text{log}}_{{{1}0}} \left( {{1 } + u^{{2}} } \right).$$

(16)

This means that the 1,1,1 complex is not present in appreciable concentration, so that Eq. 15 can be simplified, as follows:

$$\log_{10} \gamma_{1} = \log_{10} \beta_{1,0,1} + \log_{10} \left( {1 + c_{{\text{H}}} + \beta_{1,2,1} \beta_{1,0,1}^{ - 1} c_{{\text{H}}}^{2} } \right).$$

(17)

By superimposing the theoretical (Eq. 16) to the points of log₁₀ γ₁, a good fit can be obtained and from the positions:

$${\text{log}}_{{{\text{1}}0}} \gamma _{{\text{1}}} - G = {\text{ log}}_{{{\text{1}}0}} \beta _{{{\text{1}},0,{\text{1}}}} \,{\text{and log}}_{{{\text{1}}0}} u = {\text{ log}}_{{{\text{1}}0}} c_{{\text{H}}} + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ log}}_{{{\text{1}}0}} \beta _{{{\text{1}},{\text{2}},{\text{1}}}} - \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ log}}_{{{\text{1}}0}} \beta _{{{\text{1}},0,{\text{1}}.}} ,$$

at the best fit, the values of log₁₀ β_1,0,1 and log₁₀ β_1,2,1 collected in Table 1 are obtained.

Table 1 Logarithms of β_pqr constant, at 25 °C and in ionic medium 1.00 mol·dm⁻³ NaClO₄, relative to generic equilibrium: qAg + pH + rL = Ag_qH_pL_r (charges are omitted, for simplicity) obtained with different equilibrium models

The elaboration of log₁₀ γ₂ is more complicated because the possibility of four protons must be considered, so that the following equation can be written:

$$\log_{10} \gamma_{2} = \log_{10} \left( {\beta_{1,0,2} + \beta_{1,1,2} c_{{\text{H}}} + \beta_{1,2,2} c_{{\text{H}}}^{2} + \beta_{1.3.2} c_{{\text{H}}}^{3} + \beta_{1,4,2} c_{{\text{H}}}^{4} } \right).$$

(18)

By taking into account that, in the range 5 ≤  −log₁₀ c_H ≤ 9, to a first approximation the terms $\beta_{1,3,2} c_{{\text{H}}}^{3}$ and $\beta_{1,4,2} c_{{\text{H}}}^{4}$ can be neglected, Eq. 18 can be reduced to:

$$\log_{10} \gamma_{2} = \log_{10} \beta_{1,0,2} + \log_{10} \left( {1 + \beta_{1,1,2} \beta_{1,0,2}^{ - 1} c_{{\text{H}}} + \beta_{1,2,2} \beta_{1,0,2}^{ - 1} c_{{\text{H}}}^{2} } \right),$$

(19)

comparable with the normalized equation:

$$Y = {\text{ log}}_{{{1}0}} \left( {{1} + R^{*} u + u^{{2}} } \right),$$

(20)

where

$${\text{log}}_{{{1}0}} \gamma_{2} - Y = {\text{ log}}_{{{1}0}} \beta_{{{1},0,{2}}} {\text{and log}}_{{{1}0}} u = {\text{ log}}_{{{1}0}} c_{{\text{H}}} + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ log}}_{{{1}0}} \beta_{{{1},{2},{2}}} - \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ log}}_{{{1}0}} \beta_{{{1},0,{2}}} ,$$

and

$${\text{log}}_{10} \beta_{1,1,2} = {\text{ log}}_{10} R^{*} + \, \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ log}}_{10} \beta_{1,2,2} + \raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$} {\text{ log}}_{10} \beta_{1,0,2} .$$

By superimposing the family of theoretical curves of Eq. 20 to the log₁₀ γ₂ points of Eq. 19 and shifting the two plots parallel to both axes, first approximations of β_1,0,2, β_1,1,2 and β_1,2,2 are obtained from the position of best fit.

Equation 18, rearranged with the introduction these values, becomes:

$$Fc_{{\text{H}}}^{ - 3} = \left[ {\gamma_{2} - \left( {\beta_{1,0,2} + \beta_{1,1,2} c_{{\text{H}}} + \beta_{1,2,2} c_{{\text{H}}}^{2} } \right)} \right] + \beta_{1,3,2} + \beta_{1,4,2} c_{{\text{H}}} .$$

(21)

Figure 6 shows the straight dependence of $Fc_{{\text{H}}}^{ - 3}$ on c_H and then β_1,3,2 is obtained from the intercept and β_1,4,2 from the slope. By repeating the procedure, accurate values of all the four constants are obtained.

Fig. 6

Straight dependence of $Fc_{{\text{H}}}^{ - 3}$ on c_H, according to Eq. 21

Next to the graphic procedure, the experimental data: total concentration of silver (I) C_Ag, of methionine C_L, the analytic excess of hydrogen ions C_H, and the free concentrations c_Ag and c_H, obtained from the emf measurements, are elaborated by applying the PC program HYPERQUAD [24].

After a lot of different trials, such as the elimination of some species or the introduction of others, the program interpreted the experimental data by assuming the same species found with the graphic method (see Table 1). In particular, a model with σ² lower than 9 is considered satisfactory. If more than one model given acceptable σ² values a χ²-test is considered next. For χ² values inferior to 12.6 the weighted residuals follow a normal distribution.

Systematic testing of different (q,p,r) complexes leads to the conclusion that acceptable agreement factors are only found with models including 7 complexes. The most relevant results of analysis of the whole set of data, comprising 345 data points (with 165 negative deviations and 180 positive deviations) of 16 titrations are summarized in Table 1. The model M2 with lowest χ² and σ² is the most reliable. All formation constants are well defined even though the model is fairly complicated consisting of 7 complexes.

The limits of error were estimated from the maximum shift possible for the calculated curve and experimental points for which agreement was still acceptable.

The constants of Table 1 are used to calculate the theoretical curves of Figs. 3 and 4.

The same constants are also used to calculate the percentage distribution of silver (I) versus −log c_H, plotted in Fig. 7.

Fig. 7

Distribution diagram of Ag(I) − l-methionine system in 0.1 mol·dm⁻³ NaClO₄ with 1.0 × 10⁻³ mol·dm⁻³ Ag(I) and 2.0 × 10^×2 mol·dm⁻³ of l-methionine

It can be observed from Fig. 7 that the complex AgH₂L₂ is predominant in a wide range 3.5 ≤ −logc_H ≤ 7, while the species AgHL is absent because it was not found at appreciable concentration (≤ 0.1%) nor by the graphic nor by the program HYPERQUAD procedures.

3.3 ¹H NMR Measurements

To confirm the results obtained by potentiometric measurements as well as to investigate on the type of bond involved between Ag⁺ and methionine, ¹H NMR spectra at different pH values and as a function of the Ag(I)/methionine ratio were collected in 1.00 mol·dm⁻³ NaClO₄ (10% D₂O). In particular, spectra from −log₁₀ c_H ~ 0 to −log₁₀ c_H ≤ 8 and from Ag(I)/methionine ratio from 0 to 2 were recorded. The chemical shifts of the protons of methionine as a function of Ag(I)/methionine ratio are reported in Fig. 8.

Fig. 8

Chemical shift, δ (ppm), of H(γ) (circles) and H(δ) (triangles) protons of methionine (v.Fig. 1) as a function of C_Ag/C_L ratio at pH 3.0 (full) and pH 7.0 (empty)

The proton chemical shifts of methionine for all pH values investigated are reported in the Supplementary Material (Table S1).

¹H NMR spectra show significant variations in chemical shifts until to a C_Ag/C_L ratio equal to 0.5 (see Table S2). This is in agreement with the formation of complexes with 1:2 stoichiometric ratio. Measurements carried out at −log₁₀ c_H = 0 show that the signal of the proton H(α) does not undergo appreciable variations, unlike the signals of the protons H(γ) and H(δ), which show variations of 0.25–0.3 ppm. This indicates the involvement of the thioether group in the formation of the AgH₂L₂ and AgH₄L₂ complexes (as can be seen from the distribution diagram in Fig. 7). The interaction between Ag⁺ ions and the carboxyl and amino groups is excluded.

Spectra recorded in solution 3 ≤ −log₁₀ c_H ≤ 7 show variations in the signals similar to those obtained at −log₁₀ c_H = 0. In this pH range, the signal of the proton H(α) is almost constant, the coordination between the carboxyl group and the silver ion can be excluded.

Investigations on solutions at −log₁₀ c_H = 8, a shift of the signal of the proton H(α) of about 0.2 ppm is observed, as well as variations of the signals H(γ) and H(δ) (about 0.3 ppm). This is in agreement with the formation of the predominant species AgHL₂ and AgL₂, where Ag⁺ ion coordinates to both the thioether group and the amino group. In all measurements carried out, no significant changes in the chemical shifts of the various protons are found for C_Ag/C_L ratio greater than 1.0. This agrees with the absence of the formation of dinuclear species that involving two silver (I) ions.

4 Conclusions

This paper shows the investigation performed on solutions silver (I) l-methionine at 25 °C and in ionic medium 1.00 mol·dm⁻³ NaClO₄, in a wide range of reagent concentration. In particular, the cation concentration varied in the range (from 0.25 to 2.00) × 10⁻³ mol·dm⁻³ and the methionine concentration increased from 0 to about 0.1 mol·dm⁻³, so that the concentration of silver (I) varied eight times and the ratio between cation and ligand arrived to about 100 times.

The protonation constants of l-methionine were also determined in the same experimental conditions.

In the studied concentration range, complexes with ratio 1:1 and 1:2 and with assumption of 1, 2, 3 and 4 protons are present, while polynuclear complexes are absent. As expected, no species with assumption of OH⁻ are present.

It seems interesting to compare the different behavior of sulfur contained in methionine with that present in cysteine.

In a previous paper [2] equilibria between cysteine and cadmium(II) were studied. Even if the ionic medium was different, the complex formation of cysteine begun at −log₁₀ c_H ≥ 4. In that case the participation of sulfur could be considered with the formation of 5 and 6 membered rings, because it was calculated that the cadmium (II) complexes with cysteine were more stable than those of serine, containing oxygen instead of sulfur. The contribute of sulfur becomes determinant at −log c_H ≥ 11. From the conclusions of paper [2] the single participation of sulfur without that of the amino acid group was excluded.

The contribute of sulfur contained in methionine is very different. From the distribution plot and from the data of Fig. 3, it is evident that the contribute of sulfur is determining, because carboxyl- and nitrogen amine in the range 1 ≤ −log₁₀ c_H ≤ 2 are protonated and silver (I) is bound only with sulfur. This sentence is supported by the ¹H NMR spectrum of Fig. 9.

Fig. 9.

¹H NMR spectra for Ag(I) − Methionine system in 1 mol dm.⁻³ NaClO₄ (10% D₂O) at −log₁₀ c_H = 3 (A) and −log₁₀ c_H = 7 (B)

The participation of sulfur to this complex can be explained observing that in methionine it is present as thioether and can expand its valence layer through their free 3d orbital.

In the range 4 ≤ −log₁₀ c_H ≤ 6, where the complex AgH₂L₂ predominates, the direct participation of sulfur is still determining. In this range the amino donor group is still protonated and the eventual formation of 7 membered rings, involving sulfur with carboxylic oxygen is not probable (as confirmed by ¹H NMR data), because of a weak stability. In the range 6 ≤ −log c_H ≤ 9, where the deprotonation of amino group occurs, the formation of six membered ring chelates with the participation of sulfur and the two amino nitrogens can be assumed.

¹H NMR spectra reported in Fig. 9, support this hypothesis, as the formation of complexes with 1: 2 stoichiometric ratio is confirmed.

In conclusion, the following scheme could represent the structure of the silver (I)—l-methionine complexes from acid solution −log₁₀ c_H ≤ 2), in neutral solution (3 ≤ −log₁₀ c_H ≤ 6) and in alkaline solution (−log c_H ≥ 8):

Scheme illustrates the fundamental role of sulfur and the 6 membered rings among sulfur, silver (I) and amino nitrogen in alkaline solution.

In addition, the formation of dinuclear species, that involving two silver (I) ions, is excluded (as confirmed by ¹H NMR spectra recorded at C_Ag/C_L = 2).

The inspection of Fig. 7, showing the presence of the only complex AgH₂L₂ in a large range of pH, could suggest the possibility to measure the free concentration of methionine. It seems possible to prepare a galvanic cell with the following composition:

$${\text{Ag }}\left| {{\text{ AgH}}_{{2}} {\text{L}}_{{2}} ,{\text{ solution S}}_{{3}} {\text{with L}}^{ - } } \right|{\text{ R}}.{\text{E}}.$$

(IV)

At 25 °C, in millivolts and in constant ionic medium, the emf of cell (IV) could be expressed as follows:

$$E_{{{\text{IV}}}} = E_{{{\text{IV}}}}^{{\text{o}}} - 59.16\log_{10} c_{{\text{L}}} .$$

(22)

In Eq. 22, $E_{{{\text{IV}}}}^{{\text{o}}}$, a constant, can be determined in the first part of each measurement, where solution S₃ has the following general composition:

C_AgH2L2 constant, C_L mol·dm⁻³ methionine; in the range 4 ≤ −log₁₀ c_H ≤ 6; 1.00 mol·dm⁻³ in Na ClO₄.

In the second part of the measurement, the concentration of a methionine solution could be measured.

The eventual preparation of a galvanic cell like (IV) can be the subject of a future approach, in order to verify the thermodynamic behavior, the possibility of interferences and any other arising difficulties. However, it can be calculated that, from the value log β_1,2,2, the presence of chloride ions ≤ 0.1 mol·dm⁻³ should not influence the response of the eventual electrode.