Evaluation of ePC-SAFT for pH Calculation in Aqueous Itaconic Acid Solutions at High Ionic Strengths

Abstract

In the context of the raw material change for sustainable production of chemicals, the selected bio-based amino acids and carboxylic acids are considered as promising platform chemicals. After fermentation, the acids are present in aqueous solutions with many side components and elevated ionic strength. The ionic strength is even further increased when pH-shift operations are applied for the separation of the target compounds. Since high ionic strengths strongly affect the solution properties, particularly the solid–liquid-equilibrium and the dissociation equilibrium in the solution, the high ionic strengths and the resulting effects on the solutions must also be taken into account in process modeling and the design of downstream processes. Various models have been reported in the literature but the majority cannot be applied for predicting the solution composition and pH at high ionic strengths. In this work, a procedure for the calculation of the composition, i.e. the distribution of the present species and pH, of aqueous itaconic acid solutions based on ePC-SAFT is developed and evaluated at different levels of ionic strengths. The ePC-SAFT parameters of itaconic acid are determined based on experimental solubility data from literature. The resulting model is validated with experimentally measured titration curves and compared with the ideal model and the Davies approximation to the Debye–Hückel model. It is demonstrated that the ePC-SAFT approach provides reliable results at high ionic strengths with lower deviations from experimental data than current literature models.

1 Introduction

Biotechnological processes represent an important basis for the sustainable production of chemicals from renewable raw materials. In these processes, mostly aqueous media with complex composition are produced, which have to be handled in downstream process steps. The development of new, and the optimization of existing, downstream processes is supported by the use of models and simulations. To ensure their validity, the process models should be able to reliably calculate the exact composition of the process media, especially the pH value. For the calculation of pH values, it is essential that the model accounts for dissociation of acids and protonation of bases.

There are two main approaches to the calculation of species concentrations at equilibrium in a multicomponent system [1]. Both approaches are based on the use of the mass action laws and therefore on the minimization of the Gibbs free energy function [2]. But the approaches differ in the solution of the mass action laws. In the equilibrium approach, the definition of equilibrium constants and mass balances yields a polynomial expression for the dissociating species. After solution of the derived polynomial, the concentrations of all remaining species can be calculated. However, the polynomial expression might yield unphysical solutions for the concentrations of the different species. This problem is circumvented by using a dynamical approach. In the dynamical approach, the kinetic rate equations for each species form a set of first-order nonlinear ordinary differential equations (ODEs), which is then solved numerically. Initialized with a physical state, the kinetic rate equations for each species converge to a physical equilibrium state. For the determination of this equilibrium state, the knowledge of the equilibrium constants is sufficient, as they define the proportion of the reaction rate constants. The different mathematical approaches have been presented in detail by Glaser et al. [1].

Compared with the equilibrium approach, the dynamical approach offers additional advantages. It can be easily applied, as the method maintains a straightforward mathematical description of the studied system [3]. The application to large multiequilibria systems, leading to large polynomial expressions in the equilibrium approach, does not require additional effort by the user in the dynamical approach. In case the reaction rate constants are known for each of the reactions, the dynamical approach may also be used for the determination of the species concentration over time and is not limited to the equilibrium state [4].

The dynamical approach has been applied to various acid–base systems [1, 3, 5]. To account for the nonidealities in real solutions, i.e. the interactions between molecules, the Davies approximation to the Debye–Hückel theory for calculating activity coefficients [6] has also already been included in the calculation approach [3, 5]. This is important, since the interaction forces between the solutes in electrolyte solutions can be substantial, and thus the deviation from the ideal case for electrolyte solutions at high ionic strength is large [7, 8]. In the work of Zars et al. [5], the effect of ionic strength on the species concentrations was investigated by a comparison of different activity models with experimental data.

However, the ionic strength in some industrially relevant processes exceed the limiting ionic strengths of 0.6 and 1.0 $\mathrm{mol \cdot L^{-1}}$ considered by Schell et al. [3] and Zars et al. [5], respectively. This applies, for example, to crystallizations, where the concentration of the target compound must exceed the solubility limit. In pH-shift crystallization processes of highly soluble amino or carboxylic acids originating from fermentations, high ionic strengths above 1.0 $\mathrm{mol \cdot L^{-1}}$ can be reached. In this range of ionic strength, the Davies approximation to the Debye–Hückel theory [6] is not valid. For the Davies equation a validity range for the ionic strength of 0.1 $\mathrm{mol \cdot L^{-1}}$ was given [9].

The ePC-SAFT equation of state is able to model phase equilibria of electrolyte solutions even at high ionic strengths [10]. The ePC-SAFT equation is based on perturbed-chain statistical associating fluid theory (PC-SAFT) [11, 12] and includes an additional electrolyte term. In literature, PC-SAFT and ePC-SAFT were used in several studies to predict densities and phase equilibria, e.g. solid-liquid equilibria, of electrolyte solutions [10, 13]. However, in literature ePC-SAFT has not yet been applied for the calculation of pH values in electrolyte solutions containing weak diprotic acids at high ionic strengths above 1.0 $\mathrm{mol \cdot L^{-1}}$.

In this work, the dynamical approach by Glaser et al. [1] is combined with the ePC-SAFT equation of state [14] to obtain a model for the calculation of species concentrations at equilibrium, including pH, in aqueous itaconic acid solutions, with validity at higher ionic strengths. The diprotic carboxylic acid is chosen as a model substance, since it represents a potential bio-based platform chemical. Thus, the model developed in this work can be used in future studies on the development of suitable downstream processes for this target molecule. The relevant ePC-SAFT parameters for itaconic acid are determined applying a procedure based on the approaches by Ruether and Sadowski [15] and Lange et al. [13]. The model is compared with the ideal model and with the Davies approximation to the Debye–Hückel theory at different ionic strengths. Additionally, the shifts in the dissociation equilibria of the itaconic acid species at increasing ionic strength are investigated.

2 Experimental

2.1 Chemicals

The chemicals used in the experiments are specified in Table 1.

Table 1 Specification of chemical samples

2.2 Titrations

Titrations of aqueous 2-methylidenebutanedioic acid (trivial name: itaconic acid (IA)) solutions with different sodium chloride (NaCl) concentrations were conducted with 20 wt% sodium hydroxide (NaOH) solution at 298.15 K. For two separate titrations, the following initial compositions were selected: 70 $\mathrm{g \cdot L^{-1}}$ IA and 0 $\mathrm{g \cdot L^{-1}}$ NaCl, and 55 $\mathrm{g \cdot L^{-1}}$ IA and 55 $\mathrm{g \cdot L^{-1}}$ NaCl. The concentrations are given in grams substance per liters solvent (water). The chosen IA concentrations are in the range of IA solubility in water at low pH and temperatures [16] and are representative for crystallization processes. The difference in the IA concentration in the initial solutions was chosen due to the reduced solubility of IA in water at increased sodium chloride concentration [16]. The solutions were stirred over night on a heated magnetic stirrer plate IKA C-MAG HS10 digital to ensure complete dissolution of solids. The titrations were carried out by adding the sodium hydroxide solution with a 50 mL burette to the continuously stirred aqueous IA solution. The temperature control was realized using a Pt100 sensor and a water bath heated by the heated magnetic stirrer plate. After each titration step and recording of the added volume, the pH value was measured with a Mettler Toledo pH electrode InLab Micro and a Mettler Toledo seven compact S210 pH meter and recorded at the steady state at 298.15 K. The pH-meter was calibrated according to manufacturer guidelines with three different buffer solutions: pH2 (Chemsolute, article 1112.1000, citrate/HCl/NaCl), pH4 (Chemsolute, article 1114.1000, citrate/NaCl/NaOH) and pH7 (Chemsolute, article 1117.1000, phosphate). The standard uncertainty of the measured pH is approximated with $\mathrm{u}_{\rm c}(\mathrm{pH})=0.05$. The standard uncertainty of the measured temperature is $\mathrm{u}_{\rm c}(T)=0.1$ K.

3 Mathematical Model

3.1 Modeling of Aqueous Electrolyte Solutions and pH Calculation

In this work, a model for aqueous electrolyte solutions containing IA, the pH modifying agents hydrochloric acid (HCl) and sodium hydroxide (NaOH) and the corresponding ions is developed. For the mathematical description of this system, a dynamical approach, describing all dissociation reactions, is chosen. First, the equilibrium state is defined for the dissociation of a monoprotic acid HA, shown in Eq. 1.

$$\begin{aligned} \mathrm{HA} + \mathrm{H}_{2}\mathrm{O} \mathop{\rightleftharpoons}\limits^{{K_{\rm a}}} \mathrm{A^{-}} + \mathrm{H_{3}\mathrm{O}^{+}} \end{aligned}$$

(1)

The thermodynamic equilibrium constant $K_{\rm a}$ describes the dissociation equilibrium. In the definition in Eq. 2, the nonidealities in the solution are taken into account by considering activities instead of molar concentrations. The nonidealities cover all interactions between molecules present in the solution.

$$\begin{aligned} K_{\rm {a}} = \frac{a_{\rm {A}^-} \cdot a_{\rm {H}_{3} {\rm{O}}^+}}{a_{\rm HA} \cdot a_{\rm {H}_2{\rm{O}}}} = \underbrace{\frac{c_{\rm {A}^-} \cdot c_{\rm {H}_{3}\text{O}^+}}{c_{\rm {HA}} \cdot c_{\rm {H}_2{\rm{O}}}}}_{Q} \cdot \underbrace{\frac{\gamma_{\rm {A}^-} \cdot \gamma_{\rm {H}_{3}\text{O}^+}}{\gamma_{\rm {HA}} \cdot \gamma_{\rm {H}_2{\rm{O}}}}}_{K_\gamma} \end{aligned}$$

(2)

In this work, $K_{\rm a}$ is divided into two terms, shown in Eq. 2. Q represents the quotient of the concentrations of the products and reactants, $K_\gamma$ represents the corresponding quotient of the activity coefficients. The conversion of activities and activity coefficients of different units is described in the appendix (Eqs. 46—48).

In dilute solutions, activity coefficients converge to unity and the equilibrium state can be described by the acid constant $K_{\rm acid}$ [3]. This component specific property is measured by titration methods and extrapolated to infinite dilution [17, 18]. Thus, it is not valid for high concentrations.

$$\begin{aligned} K_{\rm acid} = \frac{c_{\rm A^-} \cdot c_{\rm H_{3}\text{O}^+}}{c_{\rm HA}} \end{aligned}$$

(3)

In Eqs. 4 to 9, the reaction system of interest for aqueous electrolyte solutions containing IA is defined along with the corresponding equilibrium constants.

$$\begin{aligned}&\mathrm{H_2IA} + \mathrm{H_{2}\text{O}} \overset{K_{\rm a1}}{\rightleftharpoons } \mathrm{HIA^{-}} + \mathrm{H_{3}\text{O}^+} \end{aligned}$$

(4)

$$\begin{aligned}&\mathrm{HIA^{-}} + \mathrm{H_{2}\text{O}} \overset{K_{\rm a2}}{\rightleftharpoons } \mathrm{IA^{2-}} + \mathrm{H_{3}\text{O}^+} \end{aligned}$$

(5)

$$\begin{aligned}&\mathrm{H_{2}\text{O}} + \mathrm{H_{2}\text{O}} \overset{K_{\rm water}}{\rightleftharpoons } \mathrm{OH^{-}} + \mathrm{H_{3}\text{O}^+} \end{aligned}$$

(6)

$$\begin{aligned}&\mathrm{HCl} + \mathrm{H_{2}\text{O}} \overset{K_{\rm HCl}}{\rightleftharpoons } \mathrm{Cl^{-}} + \mathrm{H_{3}\text{O}^+} \end{aligned}$$

(7)

$$\begin{aligned}&\mathrm{NaOH} \overset{K_{\rm NaOH}}{\rightleftharpoons } \mathrm{OH^{-}} + \mathrm{Na^+} \end{aligned}$$

(8)

$$\begin{aligned}&\mathrm{NaCl} \overset{K_{\rm NaCl}}{\rightleftharpoons } \mathrm{Cl^{-}} + \mathrm{Na^+} \end{aligned}$$

(9)

The composition of the solution can be calculated on the basis of the rates of change of each component, applying the general mass action kinetics [19,20,21]. The rates of change of each component of the investigated reaction system are listed in Eqs. 10 to 20. The non-idealities are considered by replacing the molar concentrations with activities in the reaction kinetic [22].

$$\begin{aligned} \frac{\mathrm{d}c_{\rm H_2{\rm{IA}}}}{\mathrm{d}t} \ =&\ k_{\mathrm{1b}} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_3{\text{O}}^+} - k_{\rm 1f} \cdot a_{\rm H_2IA} \cdot a_{{\text{H}}_2{\text{O}}} \end{aligned}$$

(10)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm H{\rm{IA}}^-}}{\mathrm{d}t} =&k_{\rm 1f} \cdot a_{\rm H_2IA} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm 1b} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_3{\text{O}}^+} - k_{\rm 2f} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_2{\text{O}}} \nonumber \\&+k_{\rm 2b} \cdot a_{\rm IA^{2-}} \cdot a_{{\text{H}}_3{\text{O}}^+} \end{aligned}$$

(11)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm IA^{2-}}}{\mathrm{d}t} =&k_{\rm 2f} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_2{\text{O}}} -k_{\rm 2b} \cdot a_{\rm IA^{2-}} \cdot a_{{\text{H}}_3{\text{O}}^+} \end{aligned}$$

(12)

$$\begin{aligned} \frac{\mathrm{d}c_{{\text{H}}_2{\text{O}}}}{\mathrm{d}t} =&2 \cdot \left( k_{\rm water,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm OH^-} - k_{\rm water,f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{{\text{H}}_2{\text{O}}}\right) + k_{\rm 1b} \cdot a_{\rm H{\rm{IA}}^-} \cdot a_{{\text{H}}_3{\text{O}}^+} \nonumber \\&-k_{\rm 1f} \cdot a_{{\rm H}_{2}{\rm IA}} \cdot a_{{\text{H}}_2{\text{O}}} + k_{\rm 2b} \cdot a_{\rm IA^{2-}} \cdot a_{{\text{H}}_3{\text{O}}^+} - k_{\rm 2f} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_2{\text{O}}} \nonumber \\&-k_{\rm HCl,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm Cl^-} - k_{\rm HCl,f} \cdot a_{\rm HCl} \cdot a_{{\text{H}}_2{\text{O}}} \end{aligned}$$

(13)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm OH^-}}{\mathrm{d}t} =&k_{\rm water,f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm water,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm OH^-} + k_{\rm NaOH,f} \cdot a_{\rm NaOH} \nonumber \\&-k_{\rm NaOH,b} \cdot a_{\rm Na^+} \cdot a_{\rm OH^-} \end{aligned}$$

(14)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm HCl}}{\mathrm{d}t} =&k_{\rm HCl,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm Cl^-} - k_{\rm HCl,f} \cdot a_{\rm HCl} \cdot a_{{\text{H}}_2{\text{O}}} \end{aligned}$$

(15)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm Cl^-}}{\mathrm{d}t} =&k_{\rm HCl,f} \cdot a_{\rm HCl} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm HCl,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm Cl^-} + k_{\rm NaCl,f} \cdot a_{\rm NaCl} \nonumber \\&-k_{\rm NaCl,b} \cdot a_{\rm Cl^-} \cdot a_{\rm Na^+} \end{aligned}$$

(16)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm NaOH}}{\mathrm{d}t} =&k_{\rm NaOH,b} \cdot a_{\rm Na^+} \cdot a_{\rm OH^-} - k_{\rm NaOH,f} \cdot a_{\rm NaOH} \end{aligned}$$

(17)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm Na^+}}{\mathrm{d}t} =&k_{\rm NaOH,f} \cdot a_{\rm NaOH} - k_{\rm NaOH,b} \cdot a_{\rm Na^+} \cdot a_{\rm OH^-} + k_{\rm NaCl,f} \cdot a_{\rm NaCl} \nonumber \\&-k_{\rm NaCl,b} \cdot a_{\rm Cl^-}\cdot a_{\rm Na^+} \end{aligned}$$

(18)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm NaCl}}{\mathrm{d}t} =&k_{\rm NaCl,b} \cdot a_{\rm Cl^-} \cdot a_{\rm Na^+} - k_{\rm NaCl,f} \cdot a_{\rm NaCl} \end{aligned}$$

(19)

$$\begin{aligned} \frac{\mathrm{d}c_{{\text{H}}_3{\text{O}}^+}}{\mathrm{d}t} =&k_{\rm 1f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{\rm H_2{\rm{IA}}} - k_{\rm 1b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm HIA^-} + k_{\rm 2f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{\rm HIA^-} \nonumber \\&-k_{\rm 2b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm IA^{2-}} + k_{\rm water,f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm water,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm OH^-} \nonumber \\&+k_{\rm HCl,f} \cdot a_{\rm HCl} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm HCl,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm Cl^-} \end{aligned}$$

(20)

$k_{\rm f}$ and $k_{\rm b}$ denote the reaction rate constants for the forward and backward reaction and are connected by the equilibrium constant, as shown in Eq. 21.

$$\begin{aligned} K_{\rm a} = \frac{k_{\rm f}}{k_{\rm b}} \end{aligned}$$

(21)

Velocity constants are commonly determined in experimental investigations, but they are not documented for a wide range of substances. As suggested by Schell [3], $k_{\rm f}$ is arbitrarily set to 100 and $k_{\rm b}$ is calculated by the equilibrium constant.

In this work, ePC-SAFT is used to calculate the activity coefficients. This approach is compared to the ideal calculation ($\gamma_i = 1$) and the Davies approximation [6] to the Debye–Hückel theory [23]. In the Davies Eq. (eq 22), the activity coefficients $\gamma_z$ of ions mainly depend on the ionic strength I.

$$\begin{aligned} \log_{10}{\gamma_z} = -Az^2 \cdot \left( \frac{\sqrt{I}}{1+\sqrt{I}}-bI \right) \end{aligned}$$

(22)

The coefficient $A = \mathrm{e}^2B/(2.3038\mathrm{\pi }\epsilon \mathrm{k_B}T)$ is calculated with the electron charge $\mathrm{e}$, the static dielectric constant of water $\mathrm{\epsilon }$, the Boltzmann constant $\mathrm{k_B}$, the temperature T, $B = (2e^2\rm{N}_{\rm A}/\epsilon \mathrm{k_B}T)^{0.5}$ and the Avogadro constant $\mathrm{N_A}$ [24, 25]. At 298.15 $\mathrm{K}$, A has an approximate value of 0.5108 $\mathrm{kg}^{0.5} \cdot \mathrm{mol}^{-0.5}$ and B is approximately $0.3287 \cdot 10^8$ $\mathrm{kg}^{0.5} \cdot \mathrm{cm}^{-1} \cdot \mathrm{mol}^{-0.5}$ [25,26,27]. The Davies approximation includes the empirical parameter b with a constant value for all ions. Davies original work assigns $b = 0.2$, and this value was shown to give improved activity coefficients for large anions at low ionic strength based on conductivity measurements [6]. Schell et al. [3] showed, that $b = 0.1$ leads to more accurate results in the dihydrogen phosphate buffer system, so this value for b was chosen in this work. The ionic strength is calculated with the ion charge $z_i$ and the molar concentration $c_i$, as shown in Eq. 23.

$$\begin{aligned} I = 0.5 \cdot \sum \limits_{i} z_i^2 \cdot c_i \end{aligned}$$

(23)

The derivation of the Debye–Hückel Theory and thus also the Davies approximation are based on mole fractions as concentration unit [6, 23]. Hence, the ionic strength is calculated with the mole fraction of the ions. In diluted solutions, the mole fractions can be replaced by molar or molal concentration as a simplification [1, 3, 5]. In this work, we use molar concentrations to calculate the ionic strength (Eq. 23) and the activity coefficients (Eq. 22), even if we investigate concentrated solutions. The calculations with the Davies approximation are used as references to the ideal calculations and the ePC-SAFT model, to demonstrate the limits of the Davies approximation and the potential of ePC-SAFT at high concentrations.

In the cases of ideal calculation and the Davies approximation, the presented system of ordinary differential equations is solved. The equilibrium constants for the dissociation of IA are obtained from the acid constants $K_{\rm acid}$ at 298.15 $\mathrm{K}$ from literature [28]. Hydrochloric acid, sodium hydroxide and sodium chloride fully dissociate in water, but are considered in the defined reaction system for the purpose of a general model. The values of $K_{\rm NaOH}$ and $K_{\rm NaCl}$ are set to $10^7$, which is the reported value of the acid constant of hydrochloric acid [28], to fulfill the condition of full dissociation. $K_{\rm water}$ is calculated with the ion product of water $K_{\rm w}$ with the reported value of $10^{14}$ $\mathrm{mol^2 \cdot L^{-2}}$ [28].

In the approach with ePC-SAFT, the ordinary differential equation system is simplified. The dissociation equilibria of hydrochloric acid, sodium hydroxide and sodium chloride are neglected due to missing ePC-SAFT parameters. The simplified ordinary differential equation system is given by the Eqs. 24 to 29.

$$\begin{aligned} \frac{\mathrm{d}c_{\rm H_2{\rm{IA}}}}{\mathrm{d}t} =&k_{\mathrm{1b}} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_3{\text{O}}^+} - k_{\rm 1f} \cdot a_{\rm H_2IA} \cdot a_{{\text{H}}_2{\text{O}}} \end{aligned}$$

(24)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm H{\rm{IA}}^-}}{\mathrm{d}t} =&k_{\rm 1f} \cdot a_{\rm H_2IA} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm 1b} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_3{\text{O}}^+} - k_{\rm 2f} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_2{\text{O}}} \nonumber \\&+ k_{\rm 2b} \cdot a_{\rm IA^{2-}} \cdot a_{{\text{H}}_3{\text{O}}^+} \end{aligned}$$

(25)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm IA^{2-}}}{\mathrm{d}t} =&k_{\rm 2f} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_2{\text{O}}} -k_{\rm 2b} \cdot a_{\rm IA^{2-}} \cdot a_{{\text{H}}_3{\text{O}}^+} \end{aligned}$$

(26)

$$\begin{aligned} \frac{\mathrm{d}c_{{\text{H}}_2{\text{O}}}}{\mathrm{d}t} =&2 \cdot \left( k_{\rm water,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm OH^-} - k_{\rm water,f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{{\text{H}}_2{\text{O}}}\right) + k_{\rm 1b} \cdot a_{\rm H{\rm{IA}}^-} \cdot a_{{\text{H}}_3{\text{O}}^+} \nonumber \\&-k_{\rm 1f} \cdot a_{\rm H_2IA} \cdot a_{{\text{H}}_2{\text{O}}} + k_{\rm 2b} \cdot a_{\rm IA^{2-}} \cdot a_{{\text{H}}_3{\text{O}}^+} - k_{\rm 2f} \cdot a_{\rm HIA^-} \cdot a_{{\text{H}}_2{\text{O}}} \end{aligned}$$

(27)

$$\begin{aligned} \frac{\mathrm{d}c_{\rm OH^-}}{\mathrm{d}t} =&k_{\rm water,f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm water,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm OH^-} \end{aligned}$$

(28)

$$\begin{aligned} \frac{\mathrm{d}c_{{\text{H}}_3{\text{O}}^+}}{\mathrm{d}t} =&k_{\rm 1f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{\rm H_2IA} - k_{\rm 1b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm HIA^-} + k_{\rm 2f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{\rm H{\rm{IA}}^-} \nonumber \\&-k_{\rm 2b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm IA^{2-}} + k_{\rm water,f} \cdot a_{{\text{H}}_2{\text{O}}} \cdot a_{{\text{H}}_2{\text{O}}} - k_{\rm water,b} \cdot a_{{\text{H}}_3{\text{O}}^+} \cdot a_{\rm OH^-} \end{aligned}$$

(29)

The equilibrium constants of the dissociation of IA are fitted simultaneously with the ePC-SAFT parameters, as suggested by Lange [13]. The fitting procedure is presented in detail in Sect. 3.3.

The presented systems of ordinary differential equations (ODE) are solved with the MATLAB-solver ode23s. The results are the molar concentrations of each component. Thus the pH value in the solution can be determined as defined in Eq. 30 [29].

$$\begin{aligned} \mathrm{pH} = -\log_{10}\left( \frac{{a_{{\text{H}}_3{\text{O}}^+}}}{1 \ \mathrm{mol/L}}\right) \end{aligned}$$

(30)

In this work, the dynamical implementation is only used for the determination of the species concentrations at steady state as proposed by Glaser et al. [1]. For this purpose, the evaluation time for the ODE system was set to 0.1 $\mathrm{s}$, which ensured that the steady state concentration of each component and thus of the complete specified system was reached.

3.2 ePC-SAFT Equation of State

In this work, the dynamical approach for pH calculation by Glaser et al. [1] is combined with the ePC-SAFT equation of state for the calculation of activity coefficients. ePC-SAFT is extensively described in literature [11, 12]. Based on the residual Helmholtz energy $a^{\rm res}$, different thermodynamic quantities are calculated with ePC-SAFT. $a^{\rm res}$ takes into account the repulsion of the reference system (hc), attractive forces (disp), hydrogen-bonding interactions (assoc), as well as Coulomb interactions (ion) and is calculated with Eq. 31.

$$\begin{aligned} a^{\rm res} = a^{\rm hc} + a^{\rm disp} + a^{\rm assoc} + a^{\rm ion} \end{aligned}$$

(31)

To describe non-associating molecules, three pure component parameters, the segment diameter $\sigma$, the segment number m and the dispersion-energy parameter $\epsilon /\mathrm{k_B}$ are necessary [11]. Associating molecules require two additional pure component parameters, the association-energy parameter $\epsilon ^{\mathrm{A}_i\mathrm{B}_j}/\mathrm{k_B}$ and the association-volume parameter $\kappa ^{\mathrm{A}_i\mathrm{B}_j}$ [12]. The dispersion and association energy parameters are commonly divided by the Boltzmann constant $\mathrm{k_B}$. The pure component parameters for non-associating components in mixtures are combined with the mixing rule of Berthelot-Lorentz [30], shown in Eqs. 32 and 33.

$$\begin{aligned} \sigma_{ij}&= \frac{1}{2}\left( \sigma_i + \sigma_j\right) \end{aligned}$$

(32)

$$\begin{aligned} \epsilon_{ij}&= \sqrt{\epsilon_{i}\epsilon_{j}}\left( 1 - k_{ij}\right) \end{aligned}$$

(33)

$k_{ij}$ is the binary interaction parameter, which can be considered to adjust the dispersion-energy in mixtures. In this work, a linear dependency of $k_{ij}$ on the temperature is assumed Eq. 34).

$$\begin{aligned} k_{ij} = k_{ij\mathrm{, int}} + T \cdot k_{ij\mathrm{, slope}} \end{aligned}$$

(34)

The mixing rules from Wolbach and Sandler [31] allow the description of associating components in mixtures, shown in the Eqs. 35 and 36.

$$\begin{aligned} \epsilon ^{\mathrm{A}_i\mathrm{B}_j}&= \frac{1}{2}\left( \epsilon ^{\mathrm{A}_i\mathrm{B}_i} + \epsilon ^{\mathrm{A}_j\mathrm{B}_j}\right) \end{aligned}$$

(35)

$$\begin{aligned} \kappa ^{\mathrm{A}_i\mathrm{B}_j}&= \sqrt{\kappa ^{\mathrm{A}_i\mathrm{B}_i}\kappa ^{\mathrm{A}_j\mathrm{B}_j}}\left( \frac{\sqrt{\sigma_{ii}\sigma_{jj}}}{\frac{1}{2}\left( \sigma_{ii} + \sigma_{jj}\right) } \right) ^3 \end{aligned}$$

(36)

The ion–ion interaction is a central aspect for the description of electrolyte solutions, which is taken into account by the Helmholtz-energy contribution $a^{\rm ion}$. For this, Cameretti [14] applied a Debye–Hückel [23] term (Eq. 37) that requires no additional parameter, only the charge of the ions $z_i$.

$$\begin{aligned} \frac{a^{\rm ion}}{\mathrm{k_B} T} = -\frac{\kappa }{12 \mathrm{\pi } \mathrm{k_B} \epsilon T} \sum_{i} x_i z_i^2 \chi_i \end{aligned}$$

(37)

$\chi_i$ is defined by Eq. 38 and $\kappa$ is the Debye screening length.

$$\begin{aligned} \chi_i = \frac{3}{\left( \kappa z_i \right) ^3} \cdot \left[ \frac{3}{2} + \ln \left( 1 + \kappa z_i \right) - 2 \cdot \left( 1 + \kappa z_i \right) + \frac{1}{2} \cdot \left( 1 + \kappa z_i \right) ^2 \right] \end{aligned}$$

(38)

Besides the contribution of ion–ion interactions to the Helmholtz-energy $a^{\rm ion}$, Held et al. [10] introduce an effect on the dispersion energy $\epsilon_{ij}$ between two ions. The dispersion interaction of ions with the same charge is neglected ($\epsilon_{ij} = 0$).

The activity coefficients are calculated with the fugacity coefficients obtained from ePC-SAFT. Two definitions are relevant for the description of electrolyte solutions. They differ in their reference state, the pure substance as shown in Eq. 39 or the infinite dilution, shown in Eq. 40 [32].

$$\begin{aligned} \gamma_i^{\rm x}&= \frac{\varphi_i(T,p,x_i)}{\varphi_{0i}(T,p,x_i=1)} \end{aligned}$$

(39)

$$\begin{aligned} \gamma_i^{\mathrm{x},\infty }&= \frac{\varphi_i(T,p,x_i)}{\varphi_i^\infty (T,p,x_i)} \text { , with } x_i \rightarrow 0 \end{aligned}$$

(40)

The pure component reference state is used to calculate the activity coefficients of the solvent and the target component. The activity coefficients of the solutes that only exist in solution, in this study $\mathrm{HIA^-}$, $\mathrm{IA^{2-}}$, $\mathrm{OH^-}$, $\mathrm{H_3O^+}$, require the infinite dilution reference state.

3.3 Estimation of ePC-SAFT Parameters

For the application of the ePC-SAFT equation of state for the calculation of activity coefficients in aqueous solutions containing IA, the ePC-SAFT parameters for IA need to be determined. In this section, the determination procedure is described.

The pure component parameters are usually fitted to the liquid density and the vapor pressure of the pure component. However, pure IA exists only in the solid state under normal conditions. For this reason, the parameters are fitted to solubility data in different solvents, as suggested by Ruether and Sadowski [15]. The solid–liquid equilibrium is described with the equation according to Prausnitz et al. (Eq. 41) [33].

$$\begin{aligned} \gamma_i^{{x},{L}} = \frac{1}{x_i^L} \exp \left[ - \frac{\Delta h_{0i}^{SL}}{RT} \left( 1 - \frac{T}{T_{0i}^{SL}} \right) \right] \end{aligned}$$

(41)

$x_i^L$ is the intrinsic solubility, the mole fraction of the fully protonated IA species in solution at the limit of solubility. $\gamma_i^{{x,L}}$ is the corresponding activity coefficient in the liquid phase, $\Delta h_{0i}^{SL}$ the enthalpy of fusion at the melting temperature $T_{0i}^{SL}$ and R the universal gas constant.

In the first step of the determination procedure, the pure component parameters of IA are determined by fitting to the solubility of IA in seven organic solvents: methanol, ethanol, ethylacetate, 1-propanol, 2-propanol, acetone and acetonitrile in the temperature range from 283.15 K to 328.15 K. The experimental data are taken from Yang et al. [34]. Due to the use of organic solvents, dissociation of IA is avoided and therefore not considered. Besides the pure component parameters, the temperature-dependent binary interaction parameters of IA and the solvents are fitted. The binary interaction parameters are implemented with a temperature dependency, as shown in Eq. 34. The fitting procedure of this step is shown in Fig. 1.

Fig. 1

Fitting scheme to determine the pure component ePC-SAFT parameters of IA

First, the input data for the parameter determination procedure is listed. Temperature, pressure and the temperature-dependent solubility are given by the experimental data from Yang et al. [34]. The ePC-SAFT pure component parameters of the solvents were taken from literature and are listed in the appendix (Table 6).

At the beginning of each iteration step the fitting variables are set by the MATLAB solver. These are the pure component ePC-SAFT parameters of IA and the binary interaction parameters of IA for each solvent. With the solubility $x_{\rm IA} = x_{\rm H_2IA}$ [34], the activity coefficients $\gamma_{\rm ePC-SAFT}$ (ePC-SAFT) and $\gamma_{\rm exp}$ (Eq. 41) are calculated. The objective function, which represents the difference between the calculated activity coefficients, is formulated as a least-squares problem and solved with the MATLAB solver lsqnonlin [35]. The variable v in Fig. 2 represents the vector that contains the fitted ePC-SAFT parameters.

In the second step, the binary interaction parameters of IA and water are determined by fitting the pH-dependent solubility of IA in water at 298.15 K using the experimental data from Holtz and Goertz [16]. In this step, dissociation of IA is considered. The fitting procedure of this step is shown in Fig. 2.

Fig. 2

Fitting scheme to determine the ePC-SAFT parameters under consideration of dissociation

Again, the input data for the parameter determination procedure is listed first. Temperature, pressure and the pH-dependent solubility of IA in water are given by the experimental data from Holtz and Goertz [16]. The ePC-SAFT pure component parameters of undissociated IA are already known. The same parameters are used for the dissociated IA species, only the charge and association sites are adjusted, as suggested by Lange et al. [13]. At the beginning of each iteration step, the fitting variables are set. These are the binary interaction parameters $k_{ij}$ of the IA species and water, as well as the thermodynamic equilibrium constants of both dissociation steps $K_{\mathrm{a},1}$ and $K_{\mathrm{a},2}$. The thermodynamic equilibrium constants are integrated into the fitting procedure, as the literature values [28] were determined assuming infinite dilution. Due to the high ionic strength at the solubility limit, the literature values do not describe the dissociation equilibrium correctly. Binary interaction parameters $k_{ij}$ of zero and values from literature for the acid constants are chosen as reasonable starting points. The inner iteration loop is used to determine the solution composition, including the species distribution, and activity coefficients at each experimental data point of the pH-dependent solubility [16]. The loop starts with an estimated species distribution so that the experimental pH value is reached by the dissociation of the fully protonated IA species and initial values of $\gamma_i = 1$ (ideal case). The solution composition is calculated with the ODE reaction system defined in Eq. 24–29. The resulting composition is then used to calculate the activity coefficients with ePC-SAFT using the current parameter values for the next iteration step. If the change in composition falls below the termination criterion $\epsilon$, the calculation of the composition and the corresponding activity coefficients is finished. For the termination criterion, a value $\epsilon = 10^{-6}$ was chosen. The fitting is performed with the functions $f_1$ and $f_2$ in Eqs. 42 and 43, which represent the difference between the calculated pH value $\rm{pH}_{\rm calc}$ and the experimentally measured pH value $\rm{pH}_{\rm exp}$ and the difference between the calculated activity coefficient $\gamma_{\rm ePC-SAFT}$ for the fully protonated species and the activity coefficient obtained for the fully protonated species at solid–liquid equilibrium $\gamma_{\rm exp} = \gamma_i^{ L}$ (Eq. 41). The functions $f_1$ and $f_2$ are evaluated for each data point.

$$\begin{aligned} f_1&= \mathrm{pH}_{\rm calc} - \mathrm{pH}_{\rm exp} \end{aligned}$$

(42)

$$\begin{aligned} f_2&= \gamma_{\rm ePC-SAFT} - \gamma_{\rm exp} \end{aligned}$$

(43)

The objective function is formulated as a least-squares problem, as shown in Eq. 44 and solved with the MATLAB solver lsqnonlin. v represents again the vector that contains the fitted ePC-SAFT parameters.

$$\begin{aligned} \min_v \Vert f \Vert_2^2 = \min_v \left( f_1^2 + f_2^2 \right) \end{aligned}$$

(44)

4 Results and Discussion

4.1 Parameter Estimation and Fitting Results

The ePC-SAFT equation of state enables the calculation of activity coefficients of the components in electrolyte solutions. The ePC-SAFT parameters for the IA species obtained from the parameter estimation procedure (Sect. 3.3) are shown in Table 2. In addition, the parameters of other components considered in this work are listed in Table 2, including their literature reference.

Table 2 ePC-SAFT parameters for IA species and other components considered in this work

As mentioned in Sect. 3.3, the parameters of the different IA species only differ in the number of association sites and charge. The starting values for IA used in the determination procedure were set to the parameter values determined for succinic acid in the work by Lange at al. [13] and are listed in Appendix (Table 5). The value of the association volume is $\kappa ^{(\mathrm{A}_i\mathrm{B}_i)}/\mathrm{k_B} = 0.020069$ and therefore lies between 0.01 and 0.03, which is considered typical for organic substances [15]. The binary interaction parameters $k_{ij}$ of IA and the organic solvents are temperature-dependent, as presented in Eq. 34, and are listed in the appendix (Table 7).

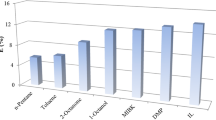
In Fig. 3, the modeling results for the solubility of IA in organic solvents based on the determined ePC-SAFT parameter set are compared to the experimental data. The predicted solubility is in good agreement with the experimental data, which demonstrates the validity of the parameter set for the protonated acid in the temperature range from 283.15 K to 328.15 K.

Fig. 3

Comparison of experimental solubility data of IA [34] and solubility data determined with ePC-SAFT for IA in different organic solvents

The binary interaction parameters of IA and water, as well as the equilibrium constants of both dissociation steps were determined based on the pH-dependent solubility data of IA [16]. The resulting parameters and dissociation constants (Eqs. 4 and 5) are listed in Tables 3 and 4, respectively.

Table 3 Binary interaction parameters of the IA species and water at 298.15 K

Table 4 Dissociation constants for IA at 298.15 K

The modeling results for the solubility of IA in water at different pH and the experimental data are compared in Fig. 4. The measured solubility in the pH range from 2.2 to 2.8 has a constant value of $x_{\mathrm{IA}}=0.0128$. Above a pH of 2.8, the solubility increases nonlinearly with increasing pH up to $x_{\mathrm{IA}}=0.0301$ at a pH of 3.77. The calculated solubility of IA is in good agreement with the experimental data, in particular in the pH range from 2.2 to 3.5. The slope of the calculated curve increases continuously with increasing pH, in accordance with the dissociation of IA. At pH values above 3.5, the deviation between calculated solubility and measured solubility increases. In the same ranges, the errors of the experimental data increase as well. The averaged relative deviation between the calculated and experimental solubility data is 4.65 $\%$ and therefore in the range of the investigation carried out by Lange et al. [13] for the pH-dependent solubility of succinic acid.

Fig. 4

Measured [16] and with ePC-SAFT calculated pH-dependent solubility of IA in water

4.2 Influence of the Ionic Strength on the pH Value

Two titrations with different NaCl concentrations were carried out to investigate the influence of the ionic strength on the equilibrium composition and thus, on the pH value. In Fig. 5, the pH values measured during these titrations are compared.

Fig. 5

Measured pH during titrations of itaconic acid solutions with different sodium chloride concentrations using sodium hydroxide solution at 298.15 $\mathrm{K}$. Mean values of 3 experiments and standard deviations of the repetition measurements are shown

The presence of NaCl leads to a decrease of the measured pH value, in agreement with Hartono et al. [37]. Comparing the data of the titration curves, the measured pH is decreased by approximately 0.2 pH units at 55 $\mathrm{g \cdot L^{-1}}$ NaCl. Since in ideal solutions the additional NaCl should not affect the measured pH, the decrease of the pH can be attributed to the interactions between the solutes and demonstrates the nonideal behavior of the system. Thus, the nonidealities influence the dissociation equilibria of IA, which was also reported for other components, like methyldiethanolamin (MDEA) [37] and 2,2,3,4,5,5-hexamethylimidazolidin-1-oxyl (HMI) [38].

The experimental data is used for the comparison and validation of different models for the calculation of activity coefficients at different levels of the ionic strength. The ideal calculation with activity coefficients equal to 1 is compared with the Davies approximation (Eq. 22) and the ePC-SAFT model (Eq. 39 and 40). A comparison and an evaluation of these models on the basis of resulting pH was chosen, since it enables the comparison with the experimental data. In addition, the obtained activity coefficients by itself are regarded not informative. In Fig. 6, the calculation results for the different models are shown for the two solutions with different NaCl concentrations.

Fig. 6

Comparison of the pH determined using different models for the calculation of activity coefficients at different NaCl concentrations: (a) 70 $\mathrm{g}\cdot \mathrm{L}^{-1}$ IA, 0 $\mathrm{g}\cdot \mathrm{L}^{-1}$ NaCl; (b) 55 $\mathrm{g}\cdot \mathrm{L}^{-1}$ IA, 55 $\mathrm{g}\cdot \mathrm{L}^{-1}$ NaCl. Experimental data is reproduced from Fig. 5. The ionic strength is calculated neglecting the activity coefficients

Figure 6a shows the titration in the absence of NaCl. The ideal calculation ($\gamma = 1$) leads to good results in the pH range from 2.5 to 4.0. In this range, the deviations are smaller than 0.16 pH units. At higher pH values, the ionic strength increases due to dissociation and the difference between calculated and measured pH value increases in the same way. The pH value is overestimated with the ideal calculation. The difference can be explained with the intensified interactions between the increased number of ions, which is neglected in the ideal calculation. The calculation with ePC-SAFT leads to qualitative similar results. In contrast to the ideal calculation, the pH value is underestimated over the entire pH range. Compared to the ideal calculation and the calculation with ePC-SAFT, the Davies approximation for the activity coefficients leads to better results in the pH range from 2.5 to 3.5. The ionic strength exceeds 0.1 $\mathrm{mol \cdot L^{-1}}$ at the third titration step, representing the reported limit for the validity of the model [9], and reaches a value of 0.25 $\mathrm{mol \cdot L^{-1}}$ at pH 3.5. Above pH 3.5, the difference between the measured and calculated pH values determined with the Davies approximation exceeds the difference determined with the ePC-SAFT approach. At a salt concentration of 55 $\mathrm{g \cdot L^{-1}}$ NaCl, shown in Fig. 6b, the deviation between the ideal calculation and the experimental data increases. The deviation is at least 0.25 pH units. In this case, the consideration of the activity coefficients with ePC-SAFT leads to excellent results in the pH range between 2.5 and 4.5. Deviations in this pH range are lower than 0.1 pH units. At pH above 4.5, the pH value is again underestimated, but the deviation to the experimental data is in the same range, as for the ideal calculations. The Davies approximation and ePC-SAFT lead to similar results in the pH range from 2.5 to 3.7. Between pH 3.7 and 5.0 the deviations of the measured and calculated pH with the Davies approximation are between 0.1 and 0.2 pH units and are therefore greater than with the ePC-SAFT calculation.

Figure 6a and b demonstrate that the activity model ePC-SAFT is able to calculate the pH value of aqueous solutions with IA up to ionic strengths of 1.75 $\mathrm{mol \cdot L^{-1}}$ accurately. Besides the more accurate pH calculation at high ionic strength, the advantage of the ePC-SAFT calculation over the ideal calculation and the Davies approximation is the knowledge of the activity coefficients of non charged components that can be used in further models, for example in crystallization or adsorption models.

4.3 Influence of the Nonidealities on the Dissociation Equilibrium

To investigate the influence of the nonidealities on the dissociation equilibrium at the different NaCl concentrations, $K_{\mathrm{a},i}$, $Q_i$ and $K_{\mathrm{\gamma },i}$, as defined in Eq. 2, are plotted in Fig. 7 as function of the ionic strength. For each titration step of each titration, the dissociation constants $K_{\mathrm{a},i}$ (Eqs. 4 and 5) are calculated as products of $Q_i$ and $K_{\mathrm{\gamma },i}$, which are obtained from the with ePC-SAFT calculated species concentrations and activity coefficients. The concentration quotients $Q_{\rm 1,Davies}$ and $Q_{\rm 2,Davies}$ are calculated with the Eqs. 2 and 22 as comparison to the ePC-SAFT approach. Using the Davies equation, the activity coefficients and therefore $K_{\mathrm{\gamma },i}$ only depend on the ionic strength and $Q_{i\mathrm{,Davies}}$ can be calculated with the knowledge of $K_{\mathrm{a},i}$ and the ionic strength as independent variable.

Fig. 7

$K_{\mathrm{a},i}$, $Q_i$ and $K_{\mathrm{\gamma },i}$ calculated with ePC-SAFT and $Q_{\rm i,Davies}$ calculated with the Davies approximation for the titrations of IA with sodium hydroxide at different NaCl concentrations (70 $\mathrm{g}\cdot \mathrm{L}^{-1}$ IA, 0 $\mathrm{g}\cdot \mathrm{L}^{-1}$ NaCl; 55 $\mathrm{g}\cdot \mathrm{L}^{-1}$ IA, 55 $\mathrm{g}\cdot \mathrm{L}^{-1}$ NaCl) as function of the calculated ionic strength

The equilibrium constants $K_{\mathrm{a},i}$ only depend on the temperature and remain constant for each dissociation step and NaCl concentration. The negative logarithm of the concentration quotient $\mathrm{p}Q_i$ for each dissociation step of IA is below the corresponding $\mathrm{p}K_{\mathrm{a},i}$ value. Schell et al. [3] and Zars et al. [5] showed for different buffer systems, using the Davies approximation, a nonlinear decrease of $\mathrm{p}Q_i$ with increasing ionic strength up to $I = 0.5$ $\mathrm{mol \cdot L^{-1}}$. This behavior can be observed for both dissociation steps of IA ($\mathrm{p}Q_1$ and $\mathrm{p}Q_2$) calculated with ePC-SAFT up to an ionic strength of 0.9 $\mathrm{mol \cdot L^{-1}}$ as well. Above this ionic strength, the concentration quotient of the first dissociation ($\mathrm{p}Q_1$) converges against the equilibrium constant $\mathrm{p}K_{\rm a,1}$ in contrast to the concentrations quotient calculated with the Davies approximation $\mathrm{p}Q_{\rm 1,Davies}$. It can be calculated that $\mathrm{p}Q_{\rm 1,Davies}$ reaches $\mathrm{p}K_{\mathrm{a},1}$ not until an ionic strength of 7.3 $\mathrm{mol \cdot L^{-1}}$. Concurrently, the difference between $\mathrm{p}Q_2$ and $\mathrm{p}Q_{\rm 2,Davies}$ increases above $I = 0.9$ $\mathrm{mol \cdot L^{-1}}$. Therefore, the calculated impact on the dissociation equilibrium differs strongly at high ionic strength ($I > 0.9$ $\mathrm{mol \cdot L^{-1}}$) between the Davies and the ePC-SAFT approach.

The impact of the increased ionic strength on the dissociation equilibrium is associated with a change of the distribution of the IA species. Figure 8 shows the relative share $\alpha$ of each acid species as a function of pH for each of the two titrations. The black lines indicate the ideal calculation neglecting the activity coefficients, the grey lines represent the calculation applying ePC-SAFT.

Fig. 8

Comparison of the IA species distributions as a function of the pH calculated with the ideal approach (black lines) and with the ePC-SAFT equation of state (grey lines). The comparison is made for the two titrations of IA with sodium hydroxide at different NaCl concentrations: a) 70 $\mathrm{g}\cdot \mathrm{L}^{-1}$ IA, 0 $\mathrm{g}\cdot \mathrm{L}^{-1}$ NaCl; b) 55 $\mathrm{g}\cdot \mathrm{L}^{-1}$ IA, 55 $\mathrm{g}\cdot \mathrm{L}^{-1}$ NaCl

The acid constant (Eq. 3) describes the dissociation equilibrium in diluted solutions, in which nonidealities can be neglected ($\gamma_i = 1$). Therefore, the intersections of the $\alpha$-curves in the Fig. 8a and 8b mark the acid constants at $\mathrm{pH}=\mathrm{p}K_{\mathrm{acid},1}=3.84$ and $\mathrm{pH}=\mathrm{p}K_{\mathrm{acid},2}=5.45$ in case of the ideal calculation method. The acid constants are not valid in concentrated solutions, because the increased ionic strength leads to a shift of these constants [37,38,39], which can be calculated with activity coefficients. The acid constants calculated with ePC-SAFT (grey lines) are shifted to lower pH values. In Fig. 8a, $\mathrm{p}K_{\mathrm{acid},1}$ is marked at pH 3.58 and $\mathrm{p}K_{\mathrm{acid},2}$ at pH 5.40. Therefore, the first dissociation equilibrium is more shifted than the second one. With increasing NaCl concentration (Fig. 8b), the influence of the ionic strength on $\mathrm{p}K_{\mathrm{acid},1}$ decreases and on $\mathrm{p}K_{\mathrm{acid},2}$ increases. The $\alpha$-curves intersect at pH = 3.67 and pH = 5.26. The investigations demonstrate that ePC-SAFT enables the consideration of the ionic strength and the influence on the dissociation equilibrium. As the dissociation equilibrium determines the actual species distribution in solution, the correct description of the dissociation equilibrium is mandatory in the design of downstream processes, e.g. in crystallization or adsorption processes. This can be demonstrated by the $\mathrm{p}K_{\rm acid,1}$-shift in Fig. 8a: Pure IA can be separated from fermentation broths by crystallization of the protonated form. For the correct calculation of the supersaturation and expected yield in the crystallization process, the correct concentration of the protonated form must be used. Comparing the species distributions of the ideal model and the ePC-SAFT model, it becomes apparent that lower supersaturation and yield is obtained with the ePC-SAFT calculation.

5 Conclusion

The dynamical approach by Glaser et al. [1] was combined with the ePC-SAFT equation of state to calculate the composition and pH in aqueous itaconic acid solutions at high ionic strengths. A two step determination procedure for the ePC-SAFT parameters of each IA species, based on the works from Ruether [15] et al. and Lange et al. [13], was applied. The calculated solubility of IA in different organic solvents are in very good agreement with the experimental data from Yang et al. [34]. The pH-dependent solubility of IA in water [16] was reproduced with an averaged relative deviation of 4.65 %. The resulting model was then compared with the ideal model and with the Davies approximation to the Debye–Hückel model and validated with titration experiments. A large influence of the ionic strength on measured pH was observed, indicating a shift in the dissociation equilibrium of itaconic acid. This impact on the dissociation equilibrium is similar to the calculations with the Davies approximation carried out by Schell et. al and Zars et al. [3, 5] at low ionic strength ($I < 1$ $\mathrm{mol \cdot L^{-1}}$). The comparison of the calculation models demonstrated that results obtained with the ePC-SAFT model are in better agreement with experimental titration data at high ionic strengths than the other models. The resulting change of the species distribution of IA compared to the ideal calculation ($\gamma_i = 1$) can be relevant for the design of downstream processes such as pH-shift-crystallization and adsorption.

Appendix

Table 5 ePC-SAFT parameters of succinic acid [13]

Table 6 ePC-SAFT parameters for the organic solvents considered in this work

Table 7 Temperature-dependent binary interaction parameters $k_{ij}\left( T\right)$ of IA and the organic solvents

In this study, the definitions of activity and activity coefficients based on different concentration measures have been taken into account. The different activities can be calculated using the following equations.

$$\begin{aligned} a_i&= \gamma_i \cdot c_i \end{aligned}$$

(45)

$$\begin{aligned} a_i^{\rm x}&= \gamma_i^{\rm x} \cdot x_i \end{aligned}$$

(46)

$$\begin{aligned} a_i^{\rm m}&= \gamma_i^{\rm m} \cdot m_i \end{aligned}$$

(47)

In the equations, x represents the mole fraction, c the molar concentration and m the molality. The different activity coefficients are related via the following equation.

$$\begin{aligned} \gamma_i^{\rm m} = x_{\rm solvent} \cdot \gamma_i^{\rm x} = \gamma_i \cdot \frac{x_{\rm solvent} \cdot v_{\rm solvent}}{v} \end{aligned}$$

(48)