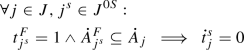Local search approaches for the test laboratory scheduling problem with variable task grouping

Abstract

The Test Laboratory Scheduling Problem (TLSP) is a real-world scheduling problem that extends the well-known Resource-Constrained Project Scheduling Problem (RCPSP) by several new constraints. Most importantly, the jobs have to be assembled out of several smaller tasks by the solver, before they can be scheduled. In this paper, we introduce different metaheuristic solution approaches for this problem. We propose four new neighborhoods that modify the grouping of tasks. In combination with neighborhoods for scheduling, they are used by our metaheuristics to produce high-quality solutions for both randomly generated and real-world instances. In particular, Simulated Annealing managed to find solutions that are competitive with the best known results and improve upon the state-of-the-art for larger instances. The algorithm is currently used for the daily planning of a large real-world laboratory.

1 Introduction

The task of testing of components and equipments is an expensive and time-consuming activity for many industrial companies. For this reason, it is extremely important that the testing process is optimized so as to save on both physical and human resources.

In this work, we consider a specific version of the testing problem, called the Test Laboratory Scheduling Problem (TLSP), which is an extension of the well-known Resource-Constrained Project Scheduling Problem (RCPSP).

For this problem, analogously to many other scheduling problems, we have to assign to each job a start time and a set of resources. In addition, as customary in scheduling as well, we have to take into account deadlines, suitability restrictions and precedences.

However, in the TLSP jobs are not atomic entities, but composed of smaller activities called tasks. The main peculiarity of the problem is that the procedure of aggregating tasks into jobs, called grouping, is not fixed, but rather part of the decision problem itself. As a consequence, the TLSP is a structured problem, composed by a grouping subproblem and a scheduling one. It is a general view in optimization that structured problems are often very difficult to solve in practice.

A restricted version of the problem, called TLSP-S, has been tackled by Mischek and Musliu (2021) and Geibinger et al. (2019). With the TLSP-S, the grouping of tasks into jobs is fixed in advance, so that the problem becomes essentially a scheduling one alone.

The general TLSP formulation has been investigated recently by Danzinger et al. (2020), by using a very-large neighborhood search (VLNS) and a Constraint Programming (CP) approach, obtaining results that outperform the ones obtained for the fixed grouping.

In this work, we investigate the possibility of using a local search approach for the general problem. To this aim, we develop four new complex neighborhoods that modify the grouping and combine them with neighborhoods affecting the schedule of the jobs. The general idea is that the two components of the problem are solved simultaneously in a cooperative fashion.

As metaheuristics for guiding the search, we experiment with the Min-Conflicts heuristic (MC) (Minton et al. 1992) and Simulated Annealing (SA) (Kirkpatrick et al. 1983). On top of both of them, we also design an iterated local search (ILS) procedure that interleaves the underlying metaheuristic with perturbation steps. As a result, we have four candidate solution methods, namely MC and SA both with and without the ILS perturbations.

All four methods, properly tuned using a statistically principled tuning procedure, are compared among each other and with the results of Danzinger et al. (2020) and Mischek and Musliu (2021) on a dataset composed of artificial and real-world instances. All instances used for this evaluation are publicly available for download.

The general outcome is that we find high-quality solutions even without the benefit of a known good grouping as in the TLSP-S, which are competitive with those of Mischek and Musliu (2021). Comparing to the state-of-the-art solver for the TLSP by Danzinger et al. (2020), we improve results on several instances. We see that we are able to obtain better results in particular on large instances, or under tight time limits. The algorithms described in this paper are used successfully in the daily scheduling of our industrial partner’s laboratory.

2 Problem definition

In the TLSP, the solver has to find a schedule for a large number of tasks, which are distributed into several projects. However, the solver first has to find a partition of the tasks into jobs, which then need to be assigned a mode, a discrete start time slot and resources. The jobs derive their properties from the tasks they contain, as described in Sect. 2.1. The final schedule must satisfy a series of hard constraints. The schedule’s quality is defined via several soft constraints or objectives¹, the final objective value is the weighted sum of all individual objectives.

The problem input consists of three parts: The first part is the environment, which defines the modes and the resources in the problem. We differentiate between three different types of resources: There are workbenches, on which tasks are performed, employees, and multiple different equipment groups. Each mode sets the number of employees required and a speed factor that is applied to the duration of jobs executed in that mode.

The second part consists of a list of projects and the tasks they contain. Each task has a real-valued duration, which must be scheduled within a time window defined by its release date and deadline. There is also a due date, which works similarly to the deadline, but violating it only results in a penalty to the solution quality. The TLSP also contains precedence constraints, but only between tasks of the same project.

Next, each task defines required resources: Up to one workbench and an arbitrary number of devices from each equipment group. As mentioned above, the number of required employees is set by the mode. The resource units that are used to fulfill the requirements of a task must be chosen from the set of available resources for the task. Similarly, there is also a set of available modes for each task. An additional restriction on the assigned employees is given in the form of preferred employees for each task, which should be assigned if possible. Further, tasks may be designated as linked. Linked tasks must be performed by the same employee(s).

Each task also belongs to a certain family. Only tasks from both the same project and family can be combined in a single job. The family also defines a setup time, which is added to the duration of each job containing tasks of that family.

Finally, each instance contains a base schedule, which can be used as a baseline and restrict the possible assignments. In particular, tasks in some jobs in the base schedule may be marked as fixed, indicating that the solver must not split up these tasks into different jobs. Some jobs may also be assigned as started. This has the effect that their start timeslot is restricted to the beginning of the schedule and the setup time is not added to their duration (it is assumed to already have been done). Usually, the available mode and resources of the tasks in a started job are also set such that the currently assigned units are the only possible assignments.

The full formal definitions of input data, job properties and constraints can be found in the “Appendix” of this paper and also the technical report by Mischek and Musliu (2018).

2.1 Job grouping

The solver has to find a partition of the tasks into jobs. The jobs derive all their properties from the tasks they contain. The general idea is that tasks within a job are not explicitly scheduled, and could be performed in any order. For this reason, a job has to fulfill all requirements of all contained tasks for its whole durations. This is a deliberate choice intended to retain a level of flexibility in the real-world execution of the schedule. It was chosen over other formulations, such as explicit scheduling of individual tasks, combined with schedule-dependent setup times (see also Mika et al. 2006) or batch scheduling approaches (e.g., Potts and Kovalyov 2000), due to a combination of circumstances in the laboratory of our industrial partner:

• Many tasks have a duration shorter than a single time slot, which is currently set at a granularity of half a (working) day per time slot. Due to flexible working hours and contracts, a finer planning granularity is infeasible to implement. As a consequence, rounding up task durations would result in unacceptable overheads. The grouping into few, longer jobs allows us to substantially decrease the impact of this problem.

• Schedule dependent setup times depend on a well-defined successor relation between tasks in a schedule, or on a certain machine. Since the requirement for additional setup times not only depends on the workbenches, but also the assigned employees and equipment, this successor relation is difficult to define and complex to evaluate for the TLSP.

• The current formulation allows tasks to be reordered within a job and even interrupted and later resumed without requiring any rescheduling. This adds a measure of robustness to the schedule, in particular since tasks are often delayed or their duration changes on short notice (see also results by Wilson et al. 2012).

• The smaller number of jobs is also easier to manage, both for the human planners in the laboratory and the employees who actually perform the tasks.

• Finally, the impact of this restriction is quite small in practice, as tasks within a family are usually very similar to each other and often share the same requirements anyway.

Consequently, the properties of a job are defined as follows:

• Its duration is the sum of the durations of the contained tasks, plus their family’s setup time (the setup time does not apply to started jobs).

• The job’s release date is the maximum among all task release dates; its target date and deadline are the minimum target date and deadline, respectively.

• The demand for each resource (workbenches, employees and each equipment group) is the maximum of the demands for each task.

• The available modes and resources of each type are the intersections of the respective task properties.

• Precedences and linking between tasks translate directly to the jobs that contain the tasks.

2.2 Constraints

Schedules are subject to a number of hard constraints. As usual for the RCPSP, all resource requirements must be met, no resource unit can be assigned to more than one job simultaneously, jobs must be scheduled between their release date and deadline and can only start after all predecessors have been completed. In addition, the TLSP also requires that the assigned mode and resource units are available for the job and linked jobs are assigned the same employees. Regarding the grouping, all tasks in a job must come from the same project and family, and fixed tasks of a job in the base schedule must also appear together in the same job in the final schedule. Finally, started jobs must start at time 0.

Once these hard constraints are fulfilled, the quality of the schedule is evaluated with respect to several objectives.

S1: Number of jobs.:

The number of jobs should be minimized.

S2: Preferred employees.:

The employees assigned to a job should be taken from the set of preferred employees.

S3: Number of employees.:

The number of employees assigned to each project should be minimized.

S4: Due date.:

The tardiness of each job after its internal due date should be minimized.

S5: Project completion time.:

The total completion time (start of the first job to end of the last) of each project should be minimized.

As discussed in the previous section, objective S1 reduces overheads (fewer setup times and losses due to rounding) and schedule fragmentation by favoring schedules with few, long jobs.

Preferred employees (S2) enable the modeling of preferences between employees that are all qualified to perform certain tasks. For example, an employee may be preferred for a particular task because they have a lot of experience in this type of work. Alternatively, employees may work only part-time or have additional duties outside the laboratory, in which case they can be marked as non-preferred for all tasks so that other employees will be scheduled first.

In practice, it has proved beneficial to have as few employees as possible cover all the tasks of a single project (S3). This enables easier communication between the client, project supervisors and the employees, but also reduces the time needed to get familiar with project-specific documentation and procedures.

Objective S4 makes the schedule more robust by ensuring that potential delays in the completion of the jobs do not cause the project to miss any deadlines.

Finally, objective S5 also helps to reduce overheads, as longer timespans between the tasks of a project would require additional effort to become familiar with project-specific procedures, as well as storage space for the devices under test between tasks. Frequent context switching due to very long and fragmented projects also adds unnecessary mental overhead to the employees.

The relative weights for these objectives depend on the usage scenarios and are currently being developed together with our industrial partner. As was done in previous work, we have used uniform weights of 1 for all objectives in our evaluations in this paper.

2.3 TLSP-S

It may happen that a suitable grouping of tasks into jobs is already known and only the scheduling part of the TLSP is of interest. This gives rise to a subproblem which we call TLSP-S, which has been tackled by Mischek and Musliu (2021); Geibinger et al. (2019).

In the TLSP-S, the jobs are already predefined (the grouping is fixed) and the solver only has to find assignments of mode, time slots and resources for each job such that all constraints are satisfied and the objective function is minimized.

As a result, job properties can be precomputed and several constraints are trivially satisfied or can be simplified. In particular, objective S1 (Number of jobs) reduces to a constant value. The results by Mischek and Musliu (2021) for the TLSP-S already include this constant and we also include it in all experiments dealing with the TLSP-S to maintain comparability with the TLSP.

3 Related literature

As mentioned in the previous sections, the TLSP is a real-life problem that has been introduced recently (Mischek and Musliu 2018, 2021). It can be classified as a project scheduling problem that includes several extensions compared to the existing problems in the literature.

Related variants of project scheduling problems have been studied extensively in the literature. The most studied variant of these problems is probably the Resource-Constrained Project Scheduling Problem (RCPSP). For surveys on literature regarding this problem and its variants, we refer to Mika et al. (2015), Hartmann and Briskorn (2010) and Brucker et al. (1999). One of the variants of the RCPSP is the Multi-Mode version (MRCPSP) (Elmaghraby 1977; Wȩglarz et al. 2011; Hartmann and Briskorn 2010; Szeredi and Schutt 2016), where each activity can be performed in one of several modes, which can affect duration and resource requirements. Of particular relevance for the TLSP(-S) is the Multi-Skill RCPSP (MSPSP) (Bellenguez and Néron 2005; Young et al. 2017), which features similar resource availability constraints.

Multiple separate projects, with project-specific constraints and objectives, appear in the Resource-Constrained Multi-Project Scheduling Problem (RCMPSP). Papers dealing with this problem include for example Gonçalves et al. (2008) and Villafáñez et al. (2019). The Multi-Mode RCMPSP (MMRCMPSP), which combines both multiple modes and multiple projects and was used for the MISTA 2013 challenge, was introduced by Wauters et al. (2016).

The TLSP has several features of previous project scheduling problems in the literature, but also includes some specific features imposed by the real-world situation, which have rarely been studied before. These include heterogeneous resources, with availability restrictions on the activities each unit of a resource can perform. While work using similar restrictions exists (Dauzère-Pérès et al. 1998; Young et al. 2017), most problem formulations either assume homogeneous, identical units of each resource or introduce additional activity modes for each feasible assignment, which quickly becomes impractical for higher resource requirements and multiple resources. Another specific feature of the TLSP(-S) is that of linked activities, which require identical assignments on a subset of the resources. A similar concept appears only in works by Salewski et al. (1997) and Drexl et al. (2000), where several activities have to be scheduled using the same mode.

Aspects similar to the grouping mechanism in the TLSP appear in other works in the form of batching (e.g., Schwindt and Trautmann 2000; Potts and Kovalyov 2000) or schedule-dependent setup times (e.g., Mika et al. 2006, 2008), although they are typically handled implicitly, i.e., the batches arise from the finished schedule, instead of the other way round.

There are few papers that deal with scheduling activities in laboratories. Scheduling of tests of experimental vehicles is considered by Bartels and Zimmermann (2009). The problem is related to the TLSP, but it uses a different resource model (in particular regarding destructive tests) and uses the number of employed vehicles as the main optimization criterion. An integer linear program for scheduling research activities for a nuclear laboratory, using a problem formulation derived from the MSPSP, but with (limited) preemption of activities is proposed by Polo Mejia et al. (2017).

Various exact, heuristic and hybrid approaches have been proposed to solve different variants of project scheduling problems (see recent surveys by Pellerin et al. (2020) and Mika et al. (2015)). A combination of memetic and hyper-heuristic methods with Monte-Carlo tree search by Asta et al. (2016) won the 2013 MISTA challenge, which dealt with the MMRCMPSP. The same problem is also treated by Ahmeti and Musliu (2018), who provided several ideas that were useful in our solver implementation for the TLSP. Examples of exact approaches based on Constraint Programming (CP) that have been used very successfully for solving specific project scheduling problems include papers by Szeredi and Schutt (2016) and Young et al. (2017).

Previous approaches for solving the TLSP-S include heuristic and exact methods (Mischek and Musliu 2021; Geibinger et al. 2019). These approaches could be applied successfully for solving realistic and practical instances. To the best of our knowledge the only approach for the TLSP has been introduced recently by Danzinger et al. (2020). That paper proposes a Constraint Programming (CP) model and a Very Large Neighborhood Search algorithm that applies the CP model to solve sub-problems. The authors showed that their solution methods can be used successfully to reach solutions that are better than those obtained by solving the TLSP-S.

4 Local search approaches

A local search framework for the TLSP-S has been described in (Mischek and Musliu 2021). In that work, different neighborhoods for the TLSP-S were implemented. One of the best performing configurations was a combination of two neighborhoods, called JobOpt and EquipmentChange. JobOpt contains moves that modify the mode, time slot, workbench and employee assignments of a single job, while EquipmentChange contains moves that replace a single assigned equipment unit by a different one. This special handling for equipment was required due to the large number of potential equipment assignments for some jobs, which made a neighborhood that simultaneously swapped all resources unwieldy in practice.

We note that the local search approach proposed by Mischek and Musliu (2021) cannot be used directly to solve the TLSP, as it does not include options to change the grouping. In this work, we propose several extensions to be able to deal with the TLSP and also investigate local search strategies. We propose four new neighborhoods that need to be added to JobOpt and EquipmentChange to make the solver suitable for TLSP, by allowing regrouping of the tasks during the search.

We also give a description of the different metaheuristics we evaluated for the TLSP in this paper. In addition to an investigation of Min-Conflicts and Simulated Annealing with the new neighborhoods, we also present a new approach based on Iterated Local Search.

4.1 New neighborhoods for variable grouping

In order to deal with the variable grouping in the TLSP, we developed four new neighborhoods that modify the task grouping.

The moves in these new neighborhoods assume that the current task grouping is valid, all jobs are scheduled within their time window, precedence constraints are satisfied, all resource requirements are fulfilled, and the assigned mode and resources are available for each job. They guarantee that these conditions still hold after the move is applied. In cases where altering the task grouping results in changing resource requirements or available resources, the solver supports different strategies to restore the validity of the resource assignments.

In the following, the time window of a job denotes the interval in which it must be scheduled. This includes both release date and deadlines, but also precedence relations to other jobs.

All neighborhoods involve two jobs, one that we call the source and the other is the target job.

4.1.1 Single task transfer

This neighborhood contains moves that transfer a single task from the source job to a target job of the same family and project. A number of restrictions apply to which tasks can be moved:

• Fixed tasks or tasks that are the only task of their job cannot be transferred (this case is handled by the Merge neighborhood).

• The mode and all resources assigned to the target job must be available for the transferred task.

• Moving the task must not introduce a cyclic dependency between jobs (see Fig. 1 for examples).

• Finally, the increased duration of the target job must still fit within its time window (including potentially updated precedence constraints).

Fig. 1

Two example scenarios where moving a task ($T_2$) from a job $J_1$ to another job $J_2$ creates a cyclic dependency between the two jobs. Arcs between tasks show the task dependencies. In both cases, job $J_2$ would have to be scheduled both before the start and after the end of job $J_1$, which is impossible. Further scenarios, potentially involving more than two jobs, exist

The modes and start times of both involved jobs are unchanged, except if it is required to move the target job forward so that its new duration does not conflict with deadlines or successor jobs.

The resource requirements of the source job may decrease due to the transferred task. In this case, two strategies are supported to remove superfluous assigned units: They can be either randomly chosen units or the worst units, i.e., those that currently cause the largest number of conflicts or the largest penalty.

Correspondingly, the resource requirements of the target job may increase. The missing resource units are chosen from the set of unassigned available resources. As with the source job, these can be either random choices or the best units for the job.

4.1.2 Merge

This neighborhood contains moves that merge two jobs of the same family and project, i.e., transfer all tasks of the source job to the target job and remove the source job from the schedule. To be candidates for a merge, the two jobs must fulfill the same requirements as for a task transfer above. The scenarios of Fig. 1 cannot happen for merges, but cyclic dependencies could still arise if there is a third job that is a successor of the source job and a predecessor of the target job, or vice versa. In this case, the two jobs cannot be merged.

As for a transfer, mode and start time of the target job are not changed, except where necessary for the job to fit into its time window. Analogously, if the resource requirements change, they need to be adjusted using either random or the best available resource units.

4.1.3 Split

The Split neighborhood covers the need of creating new jobs. A subset of the source job’s tasks are removed from it and assigned to a newly created job. Also for split moves, care must be taken to ensure that the resulting jobs do not create a cyclic dependency with each other. To ensure this, we require that for each split off task, also all successors in the source job will be split off to the new target job. It follows from this criterion that the newly created target job can be a successor of the source job, but never the other way around.

The start of the source job is adjusted to make room for the split job, if necessary (the combined duration of the reduced source job and the newly created job may be longer than the source job’s original duration due to the setup time and rounding). Otherwise, it does not change.

The resources of the source job are adjusted if the requirements have changed, using either of the two strategies described for the single task transfer neighborhood.

The target job has the same mode as the source job. Several configuration options are available to determine its start time: It can either start directly following the end of the source job, start at a random position within its time window, or start at the best possible time (with respect to the current schedule).

Regarding the resources assigned to the target job, one option is to duplicate the resource assignment of the source job and adjust it according to either of the two previously described strategies. Two alternative strategies are also supported: The resources can be assigned completely randomly from the available units or the best units from each resource can be chosen to be assigned to the job.

4.1.4 LinearSplit

The Split neighborhood contains all possible partitions of a job into two parts, except for some restrictions due to fixed tasks or other constraints. The number of these partitions rises exponentially with the number of tasks in a job, which makes it inefficient for algorithms that traverse the whole neighborhood.

To solve this problem, we developed an alternative variant of the Split neighborhood, called LinearSplit. This neighborhood randomly generates a topological ordering of the tasks in the job for each move. It contains only moves that split this ordering at a certain index, such that all tasks after this index are moved to the newly created job.

This behavior guarantees that the time required to traverse the neighborhood is linear with respect to the number of tasks in the job. The drawback is that it is no longer deterministic, in the sense that it does not always contain the same moves if applied for the same schedule and job.

The topological ordering itself is created by repeatedly choosing a random task that does not have any unchosen predecessors in the job, until all tasks have been chosen. If tasks are chosen randomly in a uniform way, the produced orderings are biased heavily toward orderings that place unconnected tasks early in the ordering. To even out the distribution, we weight tasks by the number of their successors incremented by one.

This does not completely eliminate bias (it leads to double counting of some paths), but drastically reduces it for graphs with many dependencies. A small example of this is shown in Fig. 2. The given dependency graph has 10 different topological orderings (2 orderings for the left component, 5 positions for task $T_5$ in each). Of these, 2 (20%) have node $T_5$ in the first position. With uniform weights, both node $T_1$ and node $T_5$ can be selected first with equal probability, leading to 50% of generated orderings starting with $T_5$. With our adapted weights, node $T_1$ would get a weight of 4, and thus would correctly be chosen first in 80% of all generated orderings. The remaining bias with adapted weights is seen with nodes $T_2$ and $T_3$. Assuming $T_1$ was selected first, $T_5$ appears before both $T_2$ and $T_3$ in 2 out of 8 possible orderings (25%). However, both nodes get weight 2 due to their common successor $T_4$. As a result, $T_5$ is chosen as the second node after $T_1$ only in $1/(2+2+1) = 20\%$ of all generated orderings. The discrepancy occurs due to the double-counting of node $T_4$ in the weights. In general, the remaining bias decreases the more tree-like a dependency graph is.

Unfortunately, this bias cannot be completely eliminated, as truly uniform sampling would require counting the number of all topological orderings, which is already #P-complete by itself (Brightwell and Winkler 1991).

The remaining behavior and configuration options for this neighborhood are the same as for the Split neighborhood.

Fig. 2

Example dependency graph for a job J with 5 tasks

4.2 Metaheuristics

The well-known metaheuristics Min-Conflicts (MC) and Simulated Annealing (SA) have been used by Mischek and Musliu (2021) to solve the TLSP-S. With the additional neighborhoods proposed in the previous section, they can also be useful for the TLSP. Below, we give a summary of MC and SA, and we also describe a new solution approach based on Iterated Local Search (ILS) (Lourenço et al. 2003), using either of the two metaheuristics for its inner loop.

4.2.1 Min-Conflicts heuristic

MC has been used to solve various constraint satisfaction problems. This is an iterative improvement method, where during each iteration a conflicted variable is selected randomly. The new value for the selected variable is then picked such that the number of conflicts is minimized. The main difference with other local search techniques is that MC focuses in every iteration only on variables that are involved in the violated constraints. This technique can also get stuck in a local optimum and different mechanisms can be applied to escape the local optimum. For example, noise strategies such as RandomWalk (Wallace and Freuder 1996) can be used. MC has been used successfully for the Hubble Space Telescope scheduling problem (Minton et al. 1992) and other problems including a project scheduling problem (Ahmeti and Musliu 2018, 2021) and personnel scheduling (Musliu 2005).

Our implementation of MC picks a job at random at each step and finds the best move involving the chosen job among all neighborhoods.

Note that MC typically only selects among components that violate at least one constraint. However, for the TLSP, each job is always involved in at least one soft constraint violation due to S1 (Number of jobs). Even when this constraint is ignored for this purpose, the objectives S3 (Number of employees) and S5 (Project completion time) still register penalties for most jobs. In Mischek and Musliu (2021) we also experimented with a variant that only chooses among jobs that are involved in hard constraint violations until the schedule is feasible, but that did not result in any improvements.

We also combine MC with a RandomWalk (RW) procedure (MC + RW), which chooses a random move from all neighborhoods, to enable the search to escape from local minima. At each step, RW is called instead of MC with a certain probability $p^\mathrm{RW}$.

Once MC(+RW) has performed a certain number of steps without improvement, it restarts from a new initial solution.

4.2.2 Simulated Annealing

SA selects a random move from its neighborhoods. In our implementation, each neighborhood has a certain weight, which determines the likelihood of a move being selected from this neighborhood.

Afterward, the effect of the chosen move is evaluated. If it improves the schedule, it is accepted. Otherwise, it can still be accepted with probability $\mathrm{e}^{-\varDelta / T}$, where $\varDelta$ is the difference in the objective function due to the move and T is a parameter called temperature. Higher temperatures result in higher probabilities of accepting worsening moves. In the course of the search, the temperature is successively decreased from an initial value $T^0$ to a minimum value $T^\mathrm{min}$.

Our implementation uses a cooling scheme that is designed to reach the minimum temperature right at the end of the available time. Every i steps, the current temperature T is multiplied by a cooling factor $\alpha = (\frac{T^\mathrm{min}}{T})^{\frac{i}{um}}$, where u is the remaining time and m the moves applied per second. Since m depends on both the instance and the hardware, and can even vary slightly during the search, we keep track of the elapsed time and number of moves performed so far. We then periodically update m to reflect the average speed measured so far.

4.2.3 Iterated local search

One of the main challenges for metaheuristics is escaping from local optima. Especially as the size of the instances grows, the algorithms are likely to get stuck at or around basins of low objective values. Random restarts are one way to deal with such situations and sample larger areas of the search space, but each restart means throwing away all information about the (hopefully good) solution achieved previously.

ILS also repeatedly executes runs of a metaheuristic internally. In contrast to random restarts however, ILS aims to keep as much information as possible from the previous solution between restarts to provide a good starting point for the next iteration of the inner metaheuristic, while applying a large enough perturbation to reach new areas of the search space. In essence, ILS applies a local search procedure over the search space of locally (near-)optimal solutions.

This often leads to significant improvements compared to single-run metaheuristics or random restarts (Lourenço et al. 2003).

Algorithm 1 shows the pseudocode of our implementation of ILS in the TLSP solver, which can use any other local search procedure (LS) internally. In this paper, we use either MC + RW or SA as internal heuristics. The best solution found so far is stored and whenever a new solution is not accepted after a run of LS, the current solution is reset back to best known solution.

We use the same algorithm to create the initial solution as in the single-run version of LS (greedy construction for MC + RW and random for SA).

The remaining components to determine are then the stopping criteria for the internal metaheuristic, the acceptance criterion to determine whether search should continue from the current solution, and the perturbation to apply at each restart.

Regarding the stopping criteria, MC + RW already restarts after a number of unsuccessful moves. This can be immediately reused to apply the next iteration of ILS. Since SA does not have such an intuitive stopping criterion (in particular with the dynamic cooling scheme described above), we instead provide each iteration of SA with a separate short timeout, after which it should stop. Naturally, this results in faster cooling cycles as the minimum temperature now has to be reached within the shorter available time.

The most straightforward acceptance criterion is to accept only improving or same cost solutions. However, it can be beneficial to also accept solutions that are slightly worse, in order to reach more distant areas of the search space. We have implemented two different approaches to the ILS acceptance criterion:

Threshold.:

Accepts any solution that has at most $\delta$ conflicts more than the best known solution.

Annealing.:

Works like the move acceptance criterion in SA, except that the temperature T is fixed. Takes the hard constraint weight $w^\mathrm{H}$ as additional parameter.

Finally, the perturbation can be performed either by executing a fixed number $m^\mathrm{RW}$ of steps of RW (randomwalk), or by choosing a subset of all jobs and replacing their mode, time slot and resource assignments by random values (disrupt), respecting time windows, mode and resource availabilities. The second option can be configured via the disruption strength $s^\mathrm{d}$, i.e., the fraction of jobs that is chosen, and the strategy to select jobs:

Job.:

Select randomly among all jobs.

Project.:

Select randomly among all projects and all jobs of a selected project.

JobConflict.:

Select jobs involved in conflicts first, then randomly among all jobs.

ProjectConflict.:

Select projects involved in conflicts first, then randomly among all projects.

5 Experimental evaluation

We used a set of 33 instances for our experiments, the same as were used by Danzinger et al. (2020). Thirty out of these are randomly generated based on real-world data and contain between 5 and 90 projects. The remaining three instances are real-world instances taken directly from the laboratory of our industrial partner in anonymized form. A detailed description of these instances can be found in the paper by Mischek and Musliu (2021), or at https://www.dbai.tuwien.ac.at/staff/fmischek/TLSP/, where these and additional instances are also available for download.

To make the test instances also suitable for the TLSP-S, their base schedule includes a job grouping for all tasks. The base schedules of the generated instances are otherwise empty except for some started jobs with fixed assignments. The real-world instances have a base schedule that already contains assignments for most jobs. Except where noted otherwise, we do not use the unfixed preexisting groupings or assignments in the base schedules in any way for our experiments.

The algorithms described in Sect. 4 were implemented in Java 8, as part of the solver framework first described by Mischek and Musliu (2021). Most experiments were performed on a benchmark server with 224 GB RAM and two AMD Opteron 6272 Processors each with a frequency of 2.1 GHz and 16 logical cores. This is the same machine that was also used by Danzinger et al. (2020), to ensure comparability of the results. All our solution approaches are single-threaded and, as was done by Danzinger et al. (2020), we executed two independent experiments in parallel. All experiments had a timeout of 10 min. For time reasons, we used a different machine for the automated parameter tuning, a Lenovo ThinkPad University T480s with a single Intel Core i7-8550U (1,8 GHz), containing 4 cores. In order to get comparable results, we reduced the timeout to 370 s on this machine, since this resulted in approximately the same number of moves performed per run.

5.1 Parameter tuning and configuration

In order to tune the parameters of our solution approaches, we used the automated parameter tuning framework SMAC (Hutter et al. 2011). As training data, we used a set of 30 generated instances, separate from the evaluation instances. We executed 4 instances of SMAC in parallel, in shared model mode.

To the neighborhoods used in the TLSP-S (JopOpt and EquipmentChange), we added the new neighborhoods for the TLSP. Initially, we used the TaskTransfer, Merge and Split neighborhoods for both MC + RW and SA. However, it quickly became apparent that using the Split neighborhood in MC + RW was computationally infeasible, as evaluating all possible moves could take up to eight hours for some of the larger jobs. For this reason, we replaced the Split neighborhood with the LinearSplit neighborhood in MC + RW. SA could use the Split neighborhood, as finding a random split is fast regardless of the number of tasks in a job.

Regardless of the type of splitting neighborhood used, we decided to combine it with the Merge neighborhood into a combined neighborhood (Linear)SplitMerge where both have equal weights internally. The motivation behind this decision is that they contain basically complementary moves, one creating jobs and the other removing them again. An imbalance in either direction would lead to either many fragmented jobs or few jobs with many wasted attempts to find further merge candidates.

To configure the new neighborhoods for MC + RW, we used the adjust_best strategy for resource assignments and best for the time slot assignment of the new job created by the Split neighborhood (see Sect. 4.1).

For the search parameters, we reused the best performing parameters for MC+RW and SA by Mischek and Musliu (2021) for the TLSP-S, which were also found with SMAC. For RW (performed in 10% of moves), we assigned equal weights to all neighborhoods.

5.1.1 Simulated Annealing

Since SA chooses random moves in each step, the neighborhood weights have to be carefully tuned, also taking into account the new regrouping neighborhoods.

Therefore, we need to determine the probability of choosing a move from the EquipmentChange, TaskTransfer or SplitMerge neighborhoods. The probability for the JobOpt neighborhood is then naturally computed from the other weights.

Regarding the configuration parameters, we need to determine the strategy that should be used to adjust resource assignments of existing jobs when the requirements change due to a regrouping. In addition, we need to decide how to assign both a time slot and resources to the new job created in the Split neighborhood.

Table 1 shows the list of all parameters passed to SMAC, together with their domains.

Table 1 Parameters passed to SMAC to tune the SA neighborhood configuration

5.1.2 Iterated local search

Parameters common to both heuristics used within ILS are the acceptance criterion of the outer ILS loop and the perturbation to apply before each call to the inner metaheuristic. In addition, we need to determine the cutoff for the inner metaheuristic (the maximum number of moves without improvement for MC+RW and the per-iteration timeout for SA), as shown in Table 2.

In order to keep the number of parameters to a manageable level, we decided to transfer the non-ILS-specific parameter values for the single-run versions of MC + RW and SA over to ILS.

Table 2 Parameters passed to SMAC to tune the ILS configuration

Table 3 Evaluation results for the different solution approaches

Table 3 lists the final evaluation results for MC + RW, ILS using MC + RW for the inner loop, and SA. It shows that MC + RW was unable to find feasible solutions for many of the large instances. The addition of ILS improves those results quite a bit, and produces better results for every single instance than MC+RW alone. However, it also had troubles with the large instances, including the real-world instances.

Interestingly, the best timeout for SA turned out to be 370 s, i.e., the whole time available to the solver. As a result, only a single iteration of the ILS loop (see Algorithm 1) is ever performed, which makes this configuration equivalent to SA without any restarts at all. The remaining parameters are therefore irrelevant. To rule out a mistake in the tuning process, we repeated the validation with shorter per-iteration timeouts, which all resulted in worse solutions overall. This shows that SA does not benefit from being included in an ILS algorithm, at least for the TLSP.

The situation is different for MC + RW. The best configuration contains a large number of moves without improvement before a restart (e.g., MC-moves = 1000, which is the extreme value of the domain), but the results are significantly better than MC + RW without ILS (see Sect. 5.2). The fact that the selected value is the extreme suggests that it would be worth extending the range. However, given that with 1000 moves there are already very few restarts and that without restarts the results are significantly worse, we can be confident that no improvements can come from larger values of MC-moves. Concerning the remaining parameters, it appears that smaller disruptions are preferred, since the RandomWalk disruption can affect at most 20 jobs (10 moves, at most 2 jobs affected per move). The annealing acceptance criterion with the given parameters means in practice that worsening solutions that contain at most one additional conflict are likely to be accepted (the acceptance probability is 50% at a total difference of about 69).

5.2 Evaluation results

The best results were achieved using SA, which could find at least some feasible solutions for all instances and found the best known solution for many of them, in particular large instances.

Of particular interest are the real-world instances, which proved quite difficult to solve for SA. We performed a separate analysis for these three instances to determine the cause of this discrepancy. While the generated instances closely follow the real-world data, there is one aspect that was not yet considered at the time the instances were created: Employee absences were modeled only later as blocking tasks over the period of absence, and thus appear only in the real-world instances. Intuitively, absences (partially) split the scheduling period into smaller intervals, which requires more smaller jobs that neatly fit into the gaps between the absences. Thus, the presence of absences requires a heavier focus on (re)grouping moves, which the current configuration SA with its low weight for TaskTransfer, Split and Merge is lacking. To test this hypothesis, we also performed experiments on the real-world instances with increased weights (0.05) for TaskTransfer and SplitMerge, scaling down the weights of the other neighborhoods accordingly. In this configuration, the solver could find feasible solutions for 11 out of 15 total runs (5 runs per instance). Further, SA using the original weights could find feasible solutions for 14 out of 15 runs on modified versions of the real-world instances, where all employee absences have been removed. These results indicate that employee absences require special considerations in order to find feasible schedules quickly in practice, due to the fragmentation of the scheduling period they induce.

5.2.1 Comparison to other approaches

We also compare our results for SA to those by Danzinger et al. (2020), which are currently the state of the art for the TLSP. Since that paper used timeouts of two hours per instance, we repeated our evaluations with this longer timeout. The results can be seen in Table 4.

Table 4 Comparison of results for SA with those of Danzinger et al. (2020) (VLNS and CP), with a timeout of 2 h

With this longer timeout, SA could find feasible solutions for nearly all of the runs, including the real-world instances. Compared to the previous results, while SA clearly outperforms CP, VLNS still finds better solutions on most instances.

SA still manages to find new best known solutions for the three instances where CP and VLNS could not find solutions at all, as well as for two additional instances (including one of the real-world instances). In general, the relative performance of SA is better on larger instances.

The situation looks different when we compare the performance of SA and VLNS using the original timeout of 10 min (Table 5). While VLNS still gives better results for the smaller instances, SA finds better solutions for many of the larger ones (see Fig. 3 for aggregate results).

Table 5 Comparison of results for SA (see Table 3) with those of Danzinger et al. (2020) (VLNS and CP), under a time limit of 10 min

Fig. 3

Comparison of results for the approaches in Tables 3 and 5. Results have been scaled by the best known solution for each instance. The center and right groups contain only small ($\le 20$ projects) and large instances, respectively. Only feasible results were included, which heavily influences the plots for MC + RW and ILS on large instances

5.2.2 Comparison with TLSP-S

In this section, we compare to results using SA for the TLSP-S by Mischek and Musliu (2021). Since that work did not include experiments on the three real-world instances, we have rerun the experiments for those. Note also that the SA described for the TLSP-S uses only the JobOpt and EquipmentChange neighborhoods, whose weights are proportional to the number of possible moves at each step.

When comparing results between the TLSP and the TLSP-S, we need to take into account that for the latter, the solver can (and must) use the grouping provided in the base schedule of each instance. On the one hand, the knowledge that the given grouping is already feasible makes it easier to find a conflict-free schedule. The restriction to the fixed grouping also allows the solver to simplify the search by precomputing all job properties and ignore any regrouping neighborhoods. On the other hand, while the grouping is guaranteed to be feasible, it is likely not optimal. It is easy to see that any optimal solution for the TLSP is at least as good as the optimal solution of the corresponding TLSP-S instance with any given grouping. Therefore, having a flexible grouping has the potential of better solutions, in particular when a good initial grouping for TLSP-S is not known and cannot be easily guessed.

Table 6 contains the results for SA for both the TLSP-S and the TLSP, and also a variant of the TLSP where the known grouping of the TLSP-S was used to construct the initial solution (column TLSP*). An aggregate comparison of the three approaches is shown in Fig. 4. SA for the TLSP manages to produce solutions of the same quality as SA for the TLSP-S, despite the drawback of the unknown grouping. The slight overall advantage of the TLSP can mostly be credited to a few outliers, in particular in the first instance, where a different grouping admits solutions with nearly half the penalty of the TLSP-S optimum. Providing the known grouping of the TLSP-S instance to the initial solution construction in the TLSP results in a slight improvement to several solutions, but does not lead to additional feasible solutions. Notably, it does not help with finding feasible solutions to the real-world instances.

Table 6 Results for the TLSP-S Mischek and Musliu (2021) and the TLSP (results from Table 3) using SA

5.2.3 Neighborhood analysis

In order to determine the impact of each neighborhood on the solution quality, we repeated the evaluations for SA, each time with one of the neighborhoods removed. Table 7 shows the results of these experiments.

It is immediately obvious that the JobOpt neighborhood is absolutely essential to find feasible solutions at all. This is not surprising, given that it is virtually the only neighborhood that includes mode, time slot and resource changes (the regrouping neighborhoods allow for some very restricted adjustments, but not enough to find non-trivial feasible solutions).

Fig. 4

Comparison between results for TLSP-S, TLSP and TLSP* using SA. The penalties for each instance were scaled by the best found solution among those three approaches

A similar effect appears when removing the EquipmentChange neighborhood, though much less pronounced. Since JobOpt does not modify equipment assignments, the solver basically has to try to find feasible solutions using the equipment assigned in the initial (random) construction. An interesting observation is that for those instances where a feasible solution could be found, the solution quality is not much worse than the baseline performance. This might be related to the fact that equipment assignments don’t appear in the objective function.

Removing the task transfer neighborhood has the least effect on the solutions found, probably because its effect can mostly be replicated by a corresponding split, followed by a merge. Still, this neighborhood provides a way of fine-tuning the grouping that is helpful in eliminating the last remaining conflicts.

Without the option to split and merge jobs, the number of jobs for each project (and for each family) cannot be changed from those in the initial, greedy grouping. Since this grouping often leads to infeasible schedules, it is not surprising that the task transfer neighborhood alone cannot repair the conflicts in many cases. Despite the small weight of this neighborhood (only 0.4% of moves), it has a marked impact on the ability of the solver to find feasible solutions.

6 Conclusions

In this paper, we considered the real-world scheduling problem TLSP and we proposed metaheuristic approaches for this problem. We introduced four new neighborhoods which alter the task grouping of a schedule. Combined with existing neighborhoods for the TLSP-S, which deal with mode, time slot and resource assignments, they can be used in different metaheuristics to produce high-quality solutions, for both randomly generated and real-world instances.

While a combination of Min-Conflicts and RandomWalk was unable to find feasible solutions in reasonable time for larger instances, Simulated Annealing produces results that are competitive with VLNS, the current state-of-the-art for the TLSP. For larger instances and under strict time limits, it even outperforms VLNS.

Table 7 The performance of SA, using the same configuration as in Table 3, but missing one of the neighborhoods

Our experiments also show that MC+RW profits from being included in an Iterated Local Search, while this was not the case for SA. We conjecture that longer cooling cycles are more useful than the added diversification due to the perturbation phases of ILS, in particular given the random move selection of SA.

Previously, all work on the TLSP(-S) has worked with an empty base schedule (save for fixed assignments). An interesting direction for future research would be to apply our methods also to rescheduling scenarios, where an existing schedule should be repaired or optimized.

We also aim to adapt and generalize our approaches for other laboratories, which may feature different constraints and objectives.

Finally, we plan to work on the possibility of adapting dynamically the weights of the neighborhoods during the search, by using some learning mechanisms, on the spirit of the local search hyper-heuristic methodology of Bai et al. (2012) applied for example by Pour et al. (2018) in another structured problem.

Appendices

Appendices

Formal problem definition of TLSP

The following provides the formal problem definition of the TLSP, taken directly from the technical report (Mischek and Musliu 2018):

In the TLSP, a list of projects is given, such that each project contains several tasks. For each project, the tasks must be partitioned into a set of jobs, with some restrictions on the feasible partitions. Then, those jobs must each be assigned a mode, time slots and resources. The properties and feasible assignments for each job are calculated from the tasks contained within.

A solution of TLSP is a schedule consisting of the following parts:

• A list of jobs, composed of one or multiple similar tasks within the same project.

• For each job, an assigned mode, start and end time slots, the employees scheduled to work on the job, and an assignment to a workbench and equipment.

The quality of a schedule is judged according to an objective function that is the weighted sum of several soft constraints and should be minimized. Among others, these include the number of jobs and the total completion time (start of the first job until end of the last) of each project.

1.1 Input parameters

A TLSP instance can be split into three parts: The laboratory environment, including a list of resources, a list of projects containing the tasks that should be scheduled together with their properties and the current state of the existing schedule, which might be partially or completely empty.

1.1.1 Environment

In the laboratory, resources of different kinds are available that are required to perform tasks:

• Employees $e \in E = \{1,\dots ,|E|\}$ who are qualified for different types of tasks.

• A number of workbenches $b \in B = \{1,\dots ,|B|\}$ with different facilities. (These are comparable to machines in shop scheduling problems.)

• Various auxiliary laboratory equipment groups $G_g = \{1,\dots ,|G_g|\}$, where g is the group index. These represent sets of similar devices. The set of all equipment groups is called $G^*$.

The scheduling period is composed of time slots $t \in T = \{0,\dots ,|T|-1\}$. Each time slot represents half a day of work.

Tasks are performed in one of several modes labeled $m \in M = \{1,\dots ,|M|\}$. The chosen mode influences the following properties of tasks performed under it:

• The speed factor $v_m$, which will be applied to the task’s original duration.

• The number of required employees $e_m$.

1.1.2 Projects and tasks

Given is a set P of projects labeled $p \in \{1,\dots ,|P|\}$. Each project contains tasks $\mathrm{pa} \in A_p$, with $a \in \{1,\dots ,|A_p|\}$. The set of all tasks (over all projects) is $A^* = \bigcup _{p \in P} A_p$.

Each task pa has several properties:

• It has a release date $\alpha _{pa}$ and both a due date ${\bar{\omega }_{pa}}$ and a deadline $\omega _{pa}$. The difference between the latter is that a due date violation only results in a penalty to the solution quality, while deadlines must be observed.

• $M_{pa} \subseteq M$ is the set of available modes for the task.

• The task’s duration $d_{pa}$ (in time slots, real-valued). Under any given mode $m \in M_{pa}$, this duration becomes $d_{pam} :=d_{pa} * v_{m}$.

• Most tasks must be performed on a workbench. This is indicated by the Boolean parameter $b_{pa} \in \{0, 1\}$. If required, this workbench must be chosen from the set of available workbenches $B_{pa} \subseteq B$.

• Similarly, it requires qualified employees chosen from $E_{pa} \subseteq E$. The required number depends on the mode. A further subset $E^{Pr}_{pa} \subseteq E_{pa}$ is the set of preferred employees.

• Of each equipment group $g \in G^*$, the task requires $r_{pag}$ devices, which must be taken from the set of available devices $G_{pag} \subseteq G_g$.

• A list of direct predecessors ${\mathcal {P}}_{pa} \subseteq A_{p}$, which must be completed before the task can start. Note that precedence constraints can only exist between tasks in the same project.

Each project’s tasks are partitioned into families $F_{pf} \subseteq A_{p}$, where f is the family’s index. For a given task pa, $f_{pa}$ gives the task’s family. Only tasks from the same family can be grouped into a single job.

Additionally, each family f is associated with a certain setup time $s_{pf}$, which is added to the duration of each job containing tasks of that family.

Finally, it may be required that certain tasks are performed by the same employee(s)². For this reason, each project p may define linked tasks, which must be assigned the same employee(s). Linked tasks are given by the equivalence relation $L_\mathrm{p} \subseteq A_p \times A_p$, where two tasks pa and pb are linked if and only if $({pa}, {pb}) \in L_{p}$.

1.1.3 Initial schedule

All problem instances include an initial (or base) schedule, which may be completely or partially empty. This schedule can act both as an initial solution and as a baseline, placing limits on the schedules of employees and tasks, in particular by defining fixed assignments that must not be changed.

Provided is a set of jobs $J^0$, where each job $j \in J^0$ contains the following assignments:

• The tasks in the job: ${\dot{A}}_j$

  • A fixed subset of these tasks ${\dot{A}}^F_j \subseteq {\dot{A}}_j$. All fixed tasks of a job in the base schedule must also appear together in a single job in the solution.

• The mode assigned to the job: ${\dot{m}}_{j}$

• The start and completion times of the job: ${\dot{t}}^s_{j}$ resp. ${\dot{t}}^c_{j}$

• The resources assigned to the job:

  • Workbench: ${\dot{b}}_{j}$

  • Employees: ${\dot{E}}_{j}$

  • Equipment: ${\dot{G}}_{gj}$ for equipment group g

Except for the tasks, each individual assignment may or may not be present in any given job. Fixed tasks are assumed to be empty, if not given. In all other cases, missing assignments will be referred to using the value $\epsilon$. Time slots and employees can only be assigned if also a mode assignment is given.

A subset of these jobs are the started jobs $J^{0S}$. A started job $j^s \in J^{0S}$ must fulfill the following conditions:

• It must contain at least one fixed task. It is assumed that the fixed tasks of a started job are currently being worked on.

• Its start time must be 0.

• It must contain resource assignments fulfilling all requirements.

A started job’s duration does not include a setup time. In the solution, the job containing the fixed tasks of a started job must also start at time 0. Usually, the resources available to the fixed tasks of a started job are additionally restricted to those assigned to the job, to avoid interruptions of ongoing work in case of a rescheduling.

1.2 Jobs and grouping

For various operational reasons, tasks are not scheduled directly. Instead, they are first grouped into larger units called jobs.

A single job can only contain tasks from the same project and family.

Jobs have many of the same properties as tasks, which are computed from the tasks that make up a job. The general principle is that within a job, tasks are not explicitly ordered or scheduled; therefore the job must fulfill all requirements of each associated task during its whole duration³.

Let $J = \{1,\dots ,|J|\}$ be the set of all jobs in a solution and $J_{p} \subseteq J$ be the set of jobs of a given project p. Then for a job $j \in J$, the set of tasks contained in j is ${\dot{A}}_j$. j has the following properties:

$$\begin{aligned}&{{\tilde{p}}_j \quad \text {and}\quad {\tilde{f}}_j} \end{aligned}$$

are the project and family of j.

$$\begin{aligned} {{\tilde{\alpha }}_j :=\max \limits _{{pa} \in {\dot{A}}_j} \alpha _{pa} \text {,} \quad \tilde{{\bar{\omega }}}_j :=\min \limits _{{pa} \in {\dot{A}}_j} {\bar{\omega }}_{pa} \text {,} \quad {\tilde{\omega }}_j :=\min \limits _{{pa} \in {\dot{A}}_j} \omega _{pa} } \end{aligned}$$

are the release date, due date and deadline of j, respectively.

$$\begin{aligned} {{\tilde{M}}_j :=\bigcap \limits _{{pa} \in {\dot{A}}_j} M_{pa}} \end{aligned}$$

is the set of available modes.

$$\begin{aligned}&{\tilde{d}}_{jm} :=\Big \lceil {(s_{p_jf_j} + \sum \limits _{{pa} \in {\dot{A}}_j} d_{pa}) ~*~ v_{m}\Big \rceil } \end{aligned}$$

is the (integer) duration of the job under mode m. The additional setup time is added to the total duration of the contained tasks.

$$\begin{aligned} {\tilde{b_j} :=\max _{{pa} \in {\dot{A}}_j} b_{pa}} \end{aligned}$$

is the required number of workbenches (${\tilde{b}}_j \in \{0, 1\}$).

$$\begin{aligned} {{\tilde{B}}_{j} :=\bigcap _{{pa} \in {\dot{A}}_j} B_{pa} } \end{aligned}$$

are the available workbenches for j.

$$\begin{aligned} {{\tilde{E}}_{j} :=\bigcap _{{pa} \in {\dot{A}}_j} E_{pa} } \end{aligned}$$

are the employees qualified for j.

$$\begin{aligned} {{\tilde{E}}^{Pr}_{j} :=\bigcap _{{pa} \in {\dot{A}}_j} E^{Pr}_{pa} } \end{aligned}$$

are the preferred employees of j.

$$\begin{aligned} {{\tilde{r}}_{jg} :=\max _{{pa} \in {\dot{A}}_j} r_{pag}} \end{aligned}$$

are the required units of equipment group g.

$$\begin{aligned} {{\tilde{G}}_{jg} :=\bigcap _{{pa} \in {\dot{A}}_j} G_{pag}} \end{aligned}$$

are the available devices for equipment group g.

$$\begin{aligned} {{\tilde{{\mathcal {P}}}}_j :=\{k \in J {\setminus } \{j\}: \exists {pa} \in {\dot{A}}_j, {pb} \in {\dot{A}}_k \text { s.t. } {pb} \in {\mathcal {P}}_{pa}\}} \end{aligned}$$

is the set of predecessor jobs of j. Finally,

$$\begin{aligned} {{\tilde{L}}_p :=\{(j, k) \in J \times J : j \ne k \wedge \exists \mathrm{pa} \in {\dot{A}}_j, \mathrm{pb} \in {\dot{A}}_k \text { s.t. } (\mathrm{pa}, \mathrm{pb}) \in L_\mathrm{p}\}} \end{aligned}$$

defines the linked jobs in project p.

In addition, a solution contains the following assignments for each job:

• ${\dot{t}}^s_{j} \in T$ the scheduled start time slot

• ${\dot{t}}^c_{j} \in T$ the scheduled completion time

• ${\dot{m}}_{j} \in M$ the mode in which the job should be performed

• ${\dot{b}}_{j} \in B$ the workbench assigned to the job ($\epsilon$ if no workbench is required)

• ${\dot{E}}_{j} \subseteq E$ the set of employees assigned to the job

• ${\dot{G}}_{jg} \subseteq G_g$ the set of assigned devices from equipment group g

1.3 Constraints

A solution is evaluated in terms of constraints that it should fulfill. Hard constraints must all be satisfied in any feasible schedule, while the number and degree of violations of soft constraints in a solution give a measure for its quality.

For the purpose of modeling, we introduce additional notation: The set of active jobs at time t is defined as ${\mathcal {J}}_t :=\{j \in J : {\dot{t}}^s_{j} \le t \wedge {\dot{t}}^c_{j} > t\}$.

1.3.1 Hard constraints

• H1: Job assignment. Each task must be assigned to exactly one job.

  

• H2: Job grouping. All tasks contained in a job must be from the same project and family.

  

• H3: Fixed tasks. Each group of tasks assigned to a fixed job in the base schedule must also be assigned to a single job in the solution.

  

• H4: Job duration. The interval between start and completion of a job must match the job’s duration.

  

• H5: Time Window. Each job must lie completely within the time window from the release date to the deadline.

  

• H6: Task precedence. A job can start only after all prerequisite jobs have been completed.

  

• H7: Started jobs. A job containing fixed tasks of a started job in the base schedule must start at time 0.

  

• H8: Single assignment. At any one time, each workbench, employee and device can be assigned to at most one job.

  

• H9a: Workbench requirements. Each job requiring a workbench must have a workbench assigned.

  

• H9b: Employee requirements. Each job must have enough employees assigned to cover the demand given by the selected mode.

  

• H9c: Equipment requirements. Each job must have enough devices of each equipment group assigned to cover the demand for that group.

  

• H10a: Workbench suitability. The workbench assigned to a job must be suitable for all tasks contained in it.

  

• H10b: Employee qualification. All employees assigned to a job must be qualified for all tasks contained in it.

  

• H10c: Equipment availability. The devices assigned to a job must be taken from the set of available devices for each group.

  

• H11: Linked jobs. Linked jobs must be assigned exactly the same employees.

  

1.3.2 Soft constraints

The following constraints can be used to evaluate the quality of a feasible solution. They arise from the business requirements of our industrial partner.

Each soft constraint violation induces a penalty on the solution quality, denoted as $C^{i}$, where i is the soft constraint violated.

• S1: Number of jobs. The number of jobs should be minimized.

  

• S2: Employee project preferences. The employees assigned to a job should be taken from the set of preferred employees.

  

• S3: Number of employees. The number of employees assigned to each project should be minimized.

  

• S4: Due date. The internal due date for each job should be observed.

  

• S5: Project completion time. The total completion time (start of the first job to end of the last) of each project should be minimized.

  

Constraint S1 favors fewer, longer jobs over more fragmented solutions. This helps reducing overhead (fewer setup periods necessary, rounding of fractional durations), but even more important, it reduces the complexity of the final schedule, both for the employees performing the actual tasks and any human planners in those cases where manual corrections or additions become necessary.

Constraint S2 allows defining “auxiliary” employees, which should only be used if necessary. Typically, these employees usually have other duties, but also possess the required qualifications to perform (some) tasks in the laboratory.

Constraints S3 and S5 reduce overheads by reducing the need for communication (both internal and external), (re-)familiarization with project-specific test procedures and storage space.

Constraint S4 makes the schedule more robust by encouraging tasks to be completed earlier than absolutely required, so they can still be finished on time in case of delays or other disturbances.

The overall solution quality will be determined as the weighted sum over all soft constraint violations.